I. SOME THEORETICAL ASPECTS OF TIME SERIES ANALYSIS
A. INTRODUCTION
1. The Need for Time Series Models
In many economic and industrial situations, it is necessary to predict, or forecast, the value of a particular quantity over some future time period. Often, data are available describing the past behavior of the process whose future behavior we wish to predict. In order to be able to make accurate forecasts it is desirable to be able to relate the future behavior of the process to its past behavior. In other words, we need a model of the process.
It is often the case that we are interested in predicting the behavior of a variable over the near future, based on its behavior over the recent past. In such a situation, we need a good model of the short-term behavior of the process. Depending on the application, we may or may not want the model to involve variables additional to the variable whose value we wish to forecast. In any event, we would like a model that describes the behavior of the variable of interest as accurately as possible, in terms of whatever variables are included in the model. Such a model can be used to simulate, as well as to predict, the behavior of the variable of interest.
Recently, a class of models has been investigated that can efficiently represent the short-term behavior of many of the types of time series that occur in economic and industrial contexts. These models, described by Box and Jenkins (Reference 1), are particularly useful for developing stochastic models which involve solely the single variable we wish to forecast (or simulate). They are also quite useful for situations in which the behavior of the variable to be forecast is modeled in terms of the behavior of other variables as well.
The computations associated with the analysis required to develop a Box-Jenkins model from time series data can be quite extensive. The time series analysis program, TIMES, has been developed to perform these computations and assist in the efficient development of these models.
This document summarizes the aspects of time series analysis that are considered most important for effective application of the TIMES program. A comprehensive treatment of the subject can be found in Box and Jenkins’ book (Reference 1).
2. General Considerations on Stochastic Model Construction
In general, a stochastic model describing a process expresses the variable of interest (dependent variable) in terms of other observable variables (independent variables), a random “noise” variable (“error” term), and a number of parameters. The functional form that parametrically relates the dependent variable to the independent variables can be suggested by prior physical considerations, or arise through the course of analysis of the process. The noise variable typically represents the effects of all variables (sources of variation) not explicitly taken into account in the model. Conceivably, a better understanding of the physical process generating the observations would enable construction of a model with more explanatory variables (or a different functional representation), and a “smaller” error term (i.e., a noise variable with smaller variance). An important assumption in the statistical analysis of time series is that the error terms are uncorrelated with the independent variables of the model.
The general approach to statistical model construction is to use whatever theoretical knowledge is available to suggest a functional form for the model. Statistical methods are then used to determine the number of terms necessary and to estimate values of the parameters of the model. The dynamics of many physical systems can be expressed in terms of a differential equation
(1 + c1D + c2D2 + …)Y = (1 + d1D + d1D2+ …)X
where Y is the output variable and X is the input variable, D is the differential operator, and the c’s and d’s are constants. Such simple models often describe complex systems adequately, even when the true nature of the system is not understood.
In the discrete case in which observations are taken at equally spaced intervals, the above differential equation is replaced by a difference equation
where 
denotes the
backward difference operator, defined by 
Similarly, the
complex stochastic behavior of a random process {zt} can
often successfully be described in terms of a difference equation relating {zt}
to a much simpler random process – a “white noise” process, {at},
having zero mean, constant variance, and no correlation among its members:
. (1)
We shall assume that there
are but a finite number of c’s and d’s. it is convenient here to
introduce the backward shift operator B, defined by 
, and to rewrite
the preceding equation in terms of 
. (2)
Applying the polynomial operators to zt and at, we may write this model as
or
. (3)
This equation defines the basic model investigated by Box and Jenkins. In words, the current observation is assumed to be represented in terms of a finite linear combination of previous observations, plus a white noise error term associated with the current time period, plus a finite linear combination of the white noise term associated with previous time periods.
It is often the case that more than one model can be determined to describe a process. For example, the models
(4)
and
(5)
where 
are equivalent.
Owing to errors in estimation of the coefficients, a fitted model of form (5)
might not be recognized as an alternative form of (4). Clearly the
representation (4) is a much more efficient characterization of the process {zt}.
It is a generally accepted principle of model construction that the model
adequately describing the process with the fewest parameters is chosen to
represent the process.
Box and Jenkins have succinctly described the iterative procedure by which models are determined:
1. Decide, on the basis of theory and experience, on a useful class of models;
2. Determine, using knowledge of the system and observed data, a tentative subclass of models;
3. Estimate the parameters of the tentative model from the data;
4. Apply diagnostic checks of the statistical adequacy of the fitted model.
If a lack of fit is discovered, attempt to diagnose the cause, modify the subclass of tentative models, and repeat steps (3) and (4).
This document describes the basic characteristics of time series, and the nature and properties of Box-Jenkins time series models. We shall indicate how the “statistics” associated with a time series are related to the Box-Jenkins model of the time series, and describe the diagnostic checks.
Note that a model of a process may involve both dynamic and stochastic components; i.e., the model may include other variables in addition to the white noise variable (at). Although TIMES can analyze certain models which include additional variables, this capability was not a primary motivation in its development. Because the principal application of the TIMES program is the single-variable situation, the reader is referred to Box-Jenkins’ book (Reference 1) for the (fairly involved) theory underlying the multiple-variable case.
3. Limitations Associated with Stochastic Model Construction
The purpose of the time series analysis program, TIMES, is to assist the user in inferring an underlying stochastic model form a set of real-valued observations taken at equally spaced intervals (in time or space). By the term “model” is meant a description of the stochastic process generating the observations in terms of a “small’ number of parameters (to be estimated from the observed data), and a “white noise” sequence of random variables having significantly smaller variance than that of the original process. Since, based on past observations with less error variability than the variability of the white noise process itself, deriving a model from a set of time series observations may be regarded as identifying the predictable behavior associated with the series. The remaining unpredictable component of behavior is embodied in the white noise process.
The adequacy of a model as a statistical representation of a process can be checked by testing the model “residuals”, or estimates of the white noise sequence corresponding to the process, for departure from “whiteness”. There are two principal reasons for doing this. First, the parameter values are estimated assuming whiteness of the residuals; these estimates, although biased, and “consistent” and “efficient” if the residuals are white and normally distributed. If the residuals are not white, the estimates are biased, inconsistent, and inefficient. Second, whiteness of the residuals suggests that he predictable behavior of the process which is related to the sampled information has been identified. (That is, there are no more parameters to estimate for the parametric class of model chosen.) It is important to note that it may be possible to derive a much more precise model by including additional variables in the model. Both models could be adequate statistical representations of the process, in terms of their respective variables. Selection of the variables to include in a model is guided by physical considerations or experience; time series analysis is intended to find statistically adequate models in terms of the variables that have been included in the model.
(For example, consider a stochastic process
where xt, yt and at are uncorrelated white noise processes (the at‘s being the “residuals”). If we observe only the zt and xt, we will determine the model
where the residuals are now the white noise sequence bt = byt-1 + at. Had we also observed yt however, we would derive the model
.
Both models are adequate representations of the stochastic behavior of the process zt. The latter representation, however, is more complete, more precise, and if b is large and the yt are easy to observe, likely to be more useful.)
The estimated residuals corresponding to a model are a random sample, and hence a test of their “whiteness” will be a statistical one. We can hence never be absolutely certain that the residuals are from a true white-noise process. Because of this, there may be a number of alternative models which describe a given stochastic process adequately. We cannot say for certain which is the “best” model. In general, however, one model can be chosen as being the most satisfactory on the basis of its number of parameters, or its residual error variance, or the “whiteness” of its residuals, or perhaps even on the basis of the reasonableness of the functional form of the parameters of the model.
B. NATURE OF THE TIME SERIES MODEL
1. The Mixed Autoregressive Moving Average Process
As discussed in the introduction, the general class of models that has been found to be quite useful for modeling time series has the following form:
(6)
where {zt}
is the stochastic process being modeled, {at} is a white
noise process (i.e., a sequence of uncorrelated random variables having zero
mean and constant variance), B is the backward shift operator, defined
by Bzt = zt-1, and the 
’s and 
’s are the
(unknown) parameters of the model, to be estimated from a realization of the
process (i.e., a sample of successive z’s) as noted earlier, the above
formula (6) is simply a shorthand notation for
. (7)
We assume that zt represents a deviation from a mean value. If this mean value is constant, we may drop this assumption by introducing an additional parameter, into the model:
. (8)
For simplicity, we shall drop the parameter θ0 from the following discussion.
Defining the polynomials
and
we may write the model (7) as
. (9)
There
are some cases of model (9) that are of special interest. If 
we may write the
model as
or
.
The
model is hence simply a regression model of the most recent zt
on previous zt’s, and the model is called an autoregressive
process of order p. If, on the other hand, 
then the model
becomes
or
.
Thus zt is a moving average of the “error terms”, and the process is called a moving average process of order q. The general model (9) is called a mixed autoregressive moving average process.
2. Multiplicative Seasonal Components
While the general form of the mixed autoregressive moving average model (9) is capable of modeling quite general processes zt, there are often special characteristics of a particular process that can be used to justify use of a model that has a more specific structure than (9). Such is the case in modeling processes in which seasonal behavior is inherent. A reasonable model is the following:
where s is the seasonal period; that is, the current z (zt) is related to the corresponding z’s (zt-s , zt-2s,,…) from previous periods. However, the error terms (et, et – s,,…) included in the model are expected to be correlated with nearby error terms. We hence assume a model
for the et‘s, where the at ‘s are white noise. Combining the above two expressions, we have
(10)
as a reasonable model
expressing the zt’s in terms of white noise
residuals. The model is, of course, a special case of (9) in which 
and 
.
Since the autoregressive and moving average polynomials are multiplicative combinations, we call the model a multiplicative seasonal model. In general, if we expect c seasonal components, of periods s1, s2,..., sc, then our model is
. (11)
The advantage is using the multiplicative model (11) rather than the general model (9) is, of course, that we are likely to be able to describe the behavior of the series {zt} in fewer parameters because of the special (seasonal) nature of the series. Furthermore, the special structure allows for much simpler computerized estimation of the model parameters.
3. Deterministic Components
The general model (9) is capable of describing many types of stochastic behavior of time series, including changes in level, trends, and pseudo-periodic behavior. If, on the basis of physical considerations, it is known that certain characteristics of a series are deterministic in nature, these components should be explicitly handled as separate terms in the model. For example, if a persistent linear year-to-year trend is present in a series, and it is clear that the trend corresponds, say, to growth of the economy, then this trend should be represented explicitly in the model:
where 
is the slope
parameter of the trend. Similarly, deterministic trigonometric terms might be
warranted:
.
It is important to note, however, that prior physical considerations, and not a visual examination of the observed data, should be the basis for inclusion of deterministic components. Observations sampled from a process obeying the model (9) can exhibit trends and periodicities that are stochastic in nature (i.e., they may change as the process evolves). To conclude from a visual examination of the data that such trends or periodicities were deterministic would be incorrect.
The use of a multiplicative model for time series suspected of having seasonal behavior is an example of inclusion into the model of another type of deterministic component.
C. CHARACTERISTICS OF THE TIME SERIES MODEL
This
section will describe certain aspects of the behavior of the processes defined
by (9), as a function of the parameters 
s and θ’s)
of the model:
1. Stationarity
A very
important class of stochastic processes is the class of stationary
processes. A strictly stationary process is one whose properties
are unaffected by a shift in the time origin; i.e., the joint distribution of 
is the same as
the joint distribution of 
for
any n and h. Roughly speaking, a stationary process is one in
which there are no changes in levels or trends, i.e. the process forever
fluctuates about a fixed mean. A process is weakly stationary of order r
if all its moments of order up to r are unaffected by a shift in the
time origin. The joint probability function of a Gaussian process
(i.e., process for which the at’s are normally distributed)
is characterized (i.e., completely specified) by its first and second moments,
and is strictly stationary if it is weakly stationary of order 2.
It
can be shown that a process defined by the model (9) is stationary (of order 2)
if the zeros of the polynomial 
considered
as a function of the complex variable B, are outside the unit circle. A
stationary process can be represented as
where the function
converges for 
.
It
is noted that if all the zeros of 
are
outside the unit circle, then the process is invertible, i.e., it can be
represented as
,
where the function
converges for 
2. The Autocorrelation Function
Processes that are second-order stationary are very important in time series analysis, and we shall now discuss their second-order properties. The second moments of a process are given by the autocovariance function, defined by
γk = cov (zt, zt-k)
where μ denotes the
mean of 
and E denotes the
expectation (expected value) operator. If we normalize the autocovariance
function by dividing the variance σ2 = γ0 of the
process, we obtain the autocorrelation function
.
The probability structure of a stationary Gaussian process is characterized (i.e., completely specified) by knowledge of μ and γk or, equivalently, by knowledge of μ, σ2, and ρk. Furthermore, the model of the form (9) of a stationary, invertible process is characterized by the autocorrelation function, whether it is Gaussian or not. In fact, if we define the covariance generating function
and denote 
, it can be shown
that
so that
.
Thus,
a given stationary model (9) has a unique covariance function. Also, it can be
proved that there exists only one model of the form (9) that expresses the
current observation in terms of previous history having a specified
covariance function, provided the zeros of 
and 
lie outside the
unit circle (i.e., the process is both stationary and invertible). Hence, for
stationary invertible processes, the autocorrelation function is of value in
indicating the form of the model (9) of the process. If we have a
nonstationary process, we must transform it to a stationary process if we wish
to use the autocorrelation function as a guide to model selection.
An acceptable estimate of the autocovariance function is the sample autocovariance function, defined by
where 
denotes the
sample mean,
and our observed time series is z1, z2, …zn. An acceptable estimate of the autocorrelation function is the sample autocorrelation function
γk = ck / c0.
In testing a model, it is desirable to test whether or not the estimated residuals are autocorrelated. Appendix A describes a test of the hypothesis that γk = 0, k=1,2,…, n-1, in the case of a normal distribution.
3. The Periodogram and the Spectrum
a. The Periodogram
A statistic that is useful in detecting deterministic periodicities in data (due to, e.g., sinusoidal terms or seasonality), is the periodogram. The periodogram, In*(f), is an estimate of the square of the amplitude of the cosine wave of specified frequency, f, in the time series. It is given by
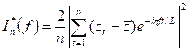
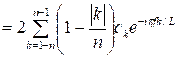
where ci is the sample autocovariance function.
Appendix B shows how the estimate of In* (f) is derived, and provides references for testing the statistical significance of it (i.e., of specified frequencies), in the case of a normal distribution.
b. The Spectrum
(Note: Since the spectrum may be somewhat less familiar to the reader than the other quantities defined in this document, it is described here in somewhat greater detail. The spectrum is not as useful a tool for assisting model development as the autocorrelation function.)
If the discrete stochastic process {zt} of the model (9) is a second order stationary process, it can be represented as
where S(f) is a stochastic process defined over the interval (-L, L), where L > 0 is arbitrary. The processes zt and S(f) are different representations of the same model; zt corresponds to representing the model in the “time domain,” and S(f) corresponds to representing the process in the “frequency domain”. While the representations are mathematically equivalent, one or the other is generally more convenient to work with, depending on the nature of the process. The models we consider arise naturally in the time domain and are hence most simply described in it (using the autocorrelation function), but we shall now see an instance in which consideration in the frequency domain (using a function called the spectral density function) is useful.
The right-hand side of the above equation is called the spectral representation of the process {zt} The second order properties of S(f) are specified by a function P(f) = var S(f), or equivalently, by the variance (σ2) of zt and a function G(f) = P(f)/σ2 called the spectral distribution function. It can be shown that
or
.
If G(f) is absolutely continuous, we have
and
,
where p(f) is called the spectrum, and g(f) is called the spectral density function. We see that the autocorrelation function is the Fourier transform of the spectral density function. Further, since g(f) is an even function, we have
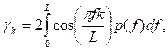
so that γk is, more specifically, twice the finite Fourier cosine transform of p(f). We hence have that
.
In
mathematical analysis, it is customary to choose L = 
so that the
frequency f is measured in units of radians per unit time. Because of
the natural occurrence of the time dimension in our models, however, it is more
natural to choose L = ½, so that f is in cycles per unit time.
In this case, the period corresponding to frequency f is simply the
reciprocal of f.
Note that
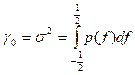
or
.
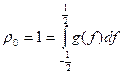Since g(f) is positive, it has the properties of a probability density function. The spectral density function in fact indicates the distribution of the variance of the time series over the frequency range.
An alternative definition of the spectrum is
where
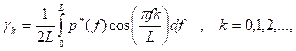
and L is taken equal to ½. That is, the coefficient of the term in brackets in the definition of the power spectrum is 2 rather than 1/(2L). this definition (with L = ½) has the property that
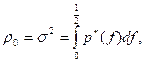
so that the spectral density function is
.
This definition arises naturally since
that is, the power spectrum is the limit of the expected value of the periodogram as the sample size increases.
For a white noise sequence, γi = 0 for i = 1, 2, …, and so its spectrum is
i.e., the spectrum is “flat’ (equal to a constant). For a sampled white noise sequence, the estimate of the spectrum (given in Appendix C) will, of course, have some variability. Appendix C describes a test of the spectrum for departures from whiteness, assuming a normal distribution. This test complements the test for zero autocorrelation using the autocorrelation function.
It is important to recognize the distinction between the periodogram and an estimate of the spectrum. The periodogram is intended to indicate the presence of deterministic periodic behavior, such as an annually recurring phenomenon, whereas an estimate of the spectrum is intended to indicate the presence of stochastic periodic behavior, such as an irregular cycle of some sort. Whereas the periodogram is intended to measure the significance of exactly specified frequencies, the spectral estimate attempts to measure the distribution of frequencies over a specified range. This difference in the intended usage of the two statistics in fact results in the inclusion of certain smoothing constants in the spectral estimate which are not present in the periodogram.
4. Behavior of a Process as a Function of its Model Parameters
The
behavior of a process defined by the model (9) can be described in general
terms as a function of the parameters of the model. If the zeros of the
polynomial 
considered as a
function of the complex variable B, are inside the unit circle, the
process exhibits explosive or increasing oscillating behavior. If the zeros
are outside the unit circle, then the process is stationary. If the roots are
on the unit circle, then the process is nonstationary, but exhibits a
homogeneous behavior as it evolves. Roughly speaking, the local behavior of
the series in this case is independent of the level of the process. In
particular, trends and changes in level are possible in this case, and so this
type of nonstationary model is potentially useful for modeling many types of
naturally occurring processes, such as sales and prices.
In particular, we shall restrict consideration to processes of the following form:
(12)
where the operators 
and 
are assumed to
have all their zeros outside the unit circle. (The invertibility restriction
on 
is not really a
restriction at all. If a noninvertible representation of the process exists,
then so does an invertible representation (in terms of a different white noise
sequence).) All of the zeros of the autoregressive operator lying on the unit
circle are contained in the difference operators (e.g., 
= 1 – B
has the zero B = 1). The variate
is thus a stationary variate,
and its model 
is
hence characterized by its autocovariance function or spectrum. The
autocorrelation function or spectral density function of wt
can hence be used as a guide to the form of the 
and 
polynomials.
The
form of the polynomial 
has a
significant effect on the behavior of the process. If the variance of the at’s
is small, then the process will behave much like the difference equation
.
The solution of this difference equation will indicate
the general behavior of the process. In fact, for a Gaussian process, this
solution is the mean. If the zeros of are complex, for
example, then the solution zt* involves sines and cosines, and so zt
will exhibit adaptive cyclic behavior. Appendix D provides some solutions to
simple linear difference equations.
D. STATISTICAL ANALYSIS OF THE TIME SERIES MODEL
1. Tentative Model Selection
a. Differencing for Stationarity
As
indicated earlier, one of the first steps in model building is to decide upon a
tentative subclass of models to be analyzed. In particular, we wish to
determine the nature of the and
polynomials: the
number of seasonal components, and the number of terms in the component
polynomials. The theory described above indicates that the autocorrelation
function and the spectrum should be of some help if we are working with a
stationary process. With this in mind, we hence seek to transform the variate zt,
which may be nonstationary, to a stationary variate. Nonstationarity is
indicated by an autocorrelation function that does not die out.
Nonstationarity is allowed for in the model (12) in the form of differences,
and so we proceed to take differences until we obtain a variate
whose autocorrelation function dies out.
b. The autocorrelation Function and Partial Autocorrelation Function
(1) Pure Moving Average Process
It can be proved that the autocorrelation function of a pure moving average process
cuts off at the order of the process. Thus if
then γq is nonzero, but γi = 0 for i >q.
Hence, if the sample autocorrelations 
are not
statistically significantly different from zero after some lag q’,
we can tentatively entertain a pure moving average process or order q’
as our model in the variate wt..
(2) Pure Autoregressive Process
Let
us define the partial autocorrelation coefficient of lag h to be the
last coefficient, 
of a
pure autoregressive process of order h. Further, let us define the h-th
sample partial autocorrelation coefficient ph as the estimate
of the last (h-th) coefficient in the autoregressive model of order h
fitted (by the method of least squares) to the time series. (The least-squares
estimate will be defined in a later section). Then, by definition, if we have
a pure autoregressive process, the partial autocorrelation coefficient cuts off
at the order of the process. Thus if
then 
is nonzero, but
= 0 for i>p.
Hence if the sample partial autocorrelation coefficients are not statistically
significantly different from zero after some lag p’ we can
tentatively entertain a pure autoregressive process of order p’
as our model in the variate wt.
(3) Mixed Autoregressive Moving Average Model
If
both 
and 
are present in
the model (in wt), then neither the autocorrelation nor
partial autocorrelation coefficients cuts off; rather, they both die out. The
behavior of the functions is still a useful guide to the form of the model,
however. Box and Jenkins provide a table illustrating this behavior as a
function of p and q.
c. The Periodogram and the Spectrum
The periodogram is used to detect the presence of deterministic components in the process. As noted earlier, caution should be taken so as not to remove stochastic periodicities by relating tentatively identified deterministic components to physical phenomena.
The spectrum, although mathematically equivalent to the autocorrelation function, is not nearly as helpful in guiding the selection of parametric models. The principal use of the spectrum will be as a test for whiteness of residuals, to be described later.
2. Estimation
a. Least-Squares Estimates
The procedure used to derive estimates of the parameters of the model is that of least-squares. The least-squares estimates are used because they have a number of desirable statistical properties, and they are easily computed. Provided the residuals are normally distributed, uncorrelated, and have constant variance, they are asymptotically (i.e., for large sample sizes) efficient (i.e., their sampling variance is less than the sampling variance of any other linear estimates) and consistent (for large samples there is, loosely speaking, a high probability that the parameter estimate is close to the parameter being estimated).
b. Maximum Likelihood Estimates
An alternative method to least-squares for obtaining estimates is the method of maximum likelihood. In this procedure, a distribution is assumed for the at’s. This distribution involves the unknown parameters of the model. Those values are then chosen for the parameters that maximize the probability (“likelihood”) of having observed the particular sample of at’s that were actually observed. Although maximum likelihood estimates are identical to least-squares estimates in the case of normally distributed at’s there are a number of advantages associated with knowledge of the entire likelihood function (as a function of the parameters):
1. Restriction of the parameters to certain regions (of stationarity or invertibility) are easily handled.
2. Alternative models that, statistically speaking, are about as good as the least-squares model, may be identified.
3. Parameter
redundancies, such as a common factor in and , would be
recognized (the maximum would tend to lie along a line or plane).
3. Diagnostic Checking
a. Hypothesis Testing
In the course of analysis of a tentatively proposed model, it is necessary to make various statistical tests of hypotheses concerning the values of parameters or the shapes of distributions. Such tests of hypotheses assume a particular distribution for the at’s. Note that none of the estimates (except the maximum likelihood estimates) depends on the distribution form. In what follows, we shall present tests based on the assumption of a normal distribution of the at’s . Usually, the tests will still be appropriate if the at’s deviate somewhat from normality. In any event, it is possible to test the hypothesis of normality of the residuals (at’s) by means of a Kolmogorov-Smirnov test of goodness of fit.
b. Significance of Parameters
In
model building, it is generally less undesirable to risk introduction of an
unnecessary parameter into the model, than to omit a necessary one.
Nevertheless, it is desirable to be able to test whether or not the estimated ’s and 
’s of the fitted
model
are statistically significantly different from zero.
Let us denote the vector of all estimates by β, i.e.,
.
The covariance matrix, S, of β is computed as described in Appendix E. Let us define Hotelling’s T2 statistic:
where β0 is the test value of β, in this case, the vector of p+q zeros. Then, under the hypothesis β = β0, the quantity
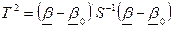
has an F-distribution with p+q and n-p-q degrees of freedom, where n is the number of observations. To perform a 95% significance level test of the hypothesis
we simply compute F and reject the hypothesis if
F > F.95 (p+q, n-p-q) ,
where F.95(p+q, n-p-q) is the 95% critical value of the F-distribution with parameters p+q and n-p-q.
c. Analysis of Residuals
(1) Autocorrelation Analysis
Perhaps the most important test of the statistical adequacy of a fitted model
is a test of whether or not
the model residuals 
corresponding
to the estimates 
and 
are white noise. (The
model residuals 
are
estimates of the (unobservable) at’s. Although
even for a “correct” model these estimates are slightly correlated, for “large”
samples their (sample) autocorrelation function approaches the autocorrelation
function of the at’s.) Evidence to the contrary
indicates that the model is incorrect or incomplete, and should be revised.
Appendix A presents a test for whiteness in terms of the autocorrelation
function.
The autocorrelation behavior of the residuals of a fitted model can be used as a guide to revising the model. For example, suppose that we have tentatively fitted the model
and that the model residuals
are correlated.
If the correlation function of the 
’s
suggests a model of the form
then the new model
should be examined.
(2) Periodogram Analysis
If seasonal components are suspected, computation of the periodogram of the residuals of a fitted model should indicate whether or not the model should be revised to reflect such behavior. See Appendix B.
(3) Spectral Analysis
Appendix C presents a test for whiteness of the residuals of a model in terms of the spectrum.
d. Over-fitting
After we have derived a model whose residuals satisfy the preceding tests, we should allow for additional parameters in the fitted model, and determine whether or not their estimates are statistically significantly different from zero. If they are, then there is cause for concern that we have not identified the model correctly. For example, if we have fitted the model
we should also examine
or
to see whether or not the additional parameters are significant.
e. Independent Estimates from Different Data
It is possible that the parameters of a process being modeled are not constant over time. If so, we are in danger of constructing a model that describes a certain period of history well, but that is of little predictive value. For this reason, it is desirable to derive parameter estimates from separate sections of time series history, and to compare the results.
In actual practice, it would be best to review parameter estimates as new data become available, to guard against model changes. (If the parameters must be changed frequently, this should be taken as evidence that the model is not adequate to describe the process well. In such as case, a different time series representation should be sought, or perhaps an “adaptive” model, such as a Kalman filter.)
E. SIMULATION AND FORECASTING
1. Simulation
In some instances, a model is constructed in order to allow simulation of a process. For example, it could be desired to examine the effect of sales variability on a new inventory policy, starting from the current sales position. In such a case, we not only need to know the parameters of the model
but also the variance of at and the distribution of at.
The variance of at is estimated as part of the least-squares estimation procedure. To estimate the form of the distribution of at, the model residuals (at’s) corresponding to the estimated parameters should be used to construct a histogram. The shape of the histogram will generally suggest a parametric class of distributions (such as normal) from which the at’s could be regarded as being sampled. The Kolmogorov-Smirnov test of goodness of fit could be used to test an hypothesis regarding a choice for the distribution of the at’s.
To simulate the process
we simply write it in the form
.
If we have past history, zt-1 ,…, zt-p, from an actual realization of the time series, then we substitute these values in the above expression. The value at is drawn from the identified distribution of the residuals. The values at-1, at-2 .,…,, at-q, must be estimated from the past data. A simple recursive procedure for doing so will be described later in the section on forecasting. Thus all of the quantities on the right-hand side of the above expression are known, and we can compute the value for zt. The new values at and zt are in turn used, with a new sampled value at+1, to compute zt+1, and so on.
If we have no past history, then it is necessary to determine initial values for z1 ,…, zp and a1 ,…, aq. The initial at’s are obtained simply by sampling. The initial zt’s should be drawn from a distribution of initial values. Such a distribution would be determined by analysis of the initial values. Such a distribution would be determined by analysis of the initial values of actual time series, or by subjective considerations. Note, of course, that the initial zt’s are correlated, so that they cannot be independently sampled. If the at’s are normally distributed, then a regression model for z2 conditional on z1, and z3 conditional on z2 and z1, is a legitimate procedure for sampling the initial values z1 ,…, zp.
2. Forecasting
A useful property of the time series model (9) is that it is easy to derive a forecasting function for it. The forecasting function can be expressed simply; it has the property that it minimizes the expected squared deviation of the forecast from the actual value.
a. Derivation of the Least-Squares Forecaster
(Note: The reader who is not interested in the details of the derivation of the least-squares forecaster may omit reading this section.)
Solving the difference equation represented by the model (9), we may write
= 
where C(t) is the
complementary function (general solution of the homogeneous equation), and 
is a particular
solution of the complete equation. Consider a forecaster 
of
that is a linear
function of the at’s:
.
Since
the forecast error is
.
Assuming that the at’s are uncorrelated with mean zero and variance σ2 the mean squared error is
.
This
quantity is minimized by setting 
Hence
the least-squares forecaster is
Since
and
and
,
we have
so that
or
.
Identifying
coefficients of powers of B, and denoting 
we have
…
(or
).
Thus
the 
may be calculated
recursively.
The
variance of the error in the forecast 
is given by
var 
Thus the variance of the one-ahead forecast is simply σ2. The variance of forecasts further out approaches var (zt).
b. Computation of the Forecast
Note that
(13)
and that
where E(zt+k) denotes the conditional expectation of zt+k, given zt, zt-1, ….
In
actual practice, the 
are not
necessary to compute the forecast 
All
that is required is to write down the model (9) with all terms but 
on the right-hand
side. We then substitute in the right-hand side, as required, the following:
1.
(observed);
2.
(computed from
(13));
3.
for 
4.
zeros for 
Thus we simply substitute known quantities and replace unknown quantities by their expected values.
It is noted that
so
that, once 
is known, the
forecasts 
can be readily
computed from the quantities 
.
Recall
that in the section on simulation we needed estimates of the past at’s
in order to start the simulation process. The formula (13) provides the means
for obtaining these estimates. That is, we simply start forecasting one step
ahead from the beginning of our historical time series (assuming zeros for a1,
a0, a-1, a-2, …). For each time t the
difference between the realized value of the series at time t and the
forecast 
of zt
made at time t-1 is an estimate of at.
c. Eventual Forecast Function
After
steps into the
future, the forecast is a
solution of the autoregressive part of the process set equal to zero:
. (14)
This
solution is called the eventual forecast function. Note that if q>(p+d)
= P, say, then the eventual forecast function is the unique curve (whose
form is specified by the solution to (14) passing through the last P of
the forecasts 
then
both the actual forecast and the eventual forecast function are the unique
curve (determined by 
) that
passes through the first P forecasts 
.
For example, for autoregressive functions of the form
,
the eventual forecast function is given by
i.e., a straight line. For
we have
.
II. THE TIME SERIES ANALYSIS PROGRAM TIMES
The time series analysis program TIMES is capable of performing all the computations described in the preceding sections, except the computation of the likelihood function. The TIMES program consists of two subprograms: ESTIMATE, which estimates the model parameters and analyzes the model residuals; and PROJECTOR, which computes projections. The PROJECTOR program may be used in either of two modes: in the SIMULATE mode, to compute simulations; and in the FORECAST mode, to compute forecasts. We shall now describe the capabilities of these programs in somewhat more detail.
A. THE ESTIMATION PROGRAM “ESTIMATE”
The ESTIMATE program estimates the parameters of a mixed autoregressive moving average time series model having multiplicative seasonal components. Sine terms, cosine terms, and exogenous variates may also be included in the models. In addition to estimating parameters, the program also computes the mean, variance, histogram, autocorrelation function, partial autocorrelation function, and spectrum of the residuals of the estimated model.
The
program is designed to work with the actual data, or to transform to
logarithms. To run the program, the user must specify the number, c, of
multiplicative (seasonal) components additional to the basic component, the
periods sc, …s1 of the seasons, the respective
difference parameters, 
the
orders of the 
polynomials
and the orders of
the 
polynomials, 
In addition, it
is possible to use the operators
instead of
in which case the 
must be
specified as different from unities. It is possible to combine several
different time series (of equal length) as the basis for estimating the overall
model parameters, and an option is available for subtracting the mean of each
series from the observations of the series. Further, it is possible to include
deterministic sine and cosine terms, in which case the frequencies must be
specified. Finally, one can include exogenous variables, whose values are the
same or different for corresponding observations of different series, and an
overall mean. In these latter cases, the program estimates the mean, the
coefficients of the sine and cosine terms, and the coefficients of the
exogenous variates. Thus the model analyzed by ESTIMATE is
t
= 1, …, m; j = 1, …, n
where ztj denotes
the t-th observation in the j-th series, and where the user
specifies the s’s, d’s, F’s (0<Fi<
½), G’s(0<Gi< ½), and the X’s and Y’s.
As noted earlier, the operators 
can
be replaced by 
by specifying
the different from
unity.
In
the case of a nonlinear model 
present,
or more than one polynomial),
it is necessary to specify an iteration cutoff value (e.g., .005), a maximum
number of iterations (e.g., 20), and a stepsize fraction (e.g., .5).
Specifically, the program performs the following computations:
- Estimation of parameters.
- Covariance matrix of parameter estimates.
- Hotelling’s T2 test of significance of all parameter estimates.
- Calculation of residuals; histogram of residuals.
- Mean and variance of residuals.
- Autocorrelation and partial autocorrelation functions of residuals; correlogram (plot of autocorrelation function).
- Chi-square test of significance of autocorrelations.
- Periodogram and estimate of spectrum of residuals.
- Fisher’s test of significance of periodogram.
- Kolmogoroff-Smirnov test of significance of spectrum.
Based on an examination of the above statistics, the user decides whether or not the model is an adequate statistical representation of the stochastic process generating the time series data. If it is not, then he modifies its structure in accordance with the theory outlined in the text, and runs the program again.
A separate manual (Reference 2) describes the procedures for using the ESTIMATE program.
B. THE PROJECTION PROGRAM “PROJECTOR”
Once a statistically adequate model had been derived, it can be used to simulate future realizations, or outcomes, of the stochastic process being modeled. The PROJECTOR program computes these simulations. Reference 2 describes the procedures for using the PROJECTOR program. The PROJECTOR program can simulate any model of the form specified above.
The estimated time series model can also be used to compute forecasts, or predictions, of future observations of the time series. The program PROJECTOR computes these forecasts. Also, upper and lower one-standard deviation limits for each forecast value are computed by the program. The user inputs the parameter estimates computed by ESTIMATE. The PROJECTOR program can forecast any model of the form given above. Reference 2 describes the procedures for using the PROJECTOR program.
REFERENCES
1. G.E.P. Box and G.M.
Jenkins, Time Series Analysis, Forecasting, and Control,
Holden-Day, Inc., San Francisco, Calif., 1970, 1976, 1994 (with Gregory
Reinsel).
2. TIMES Reference Manual, Volume II, User’s Manual, Lambda Corporation, Arlington, Virginia, Revised March, 1971.
APPENDIX A. AUTOCORRELATION ANALYSIS
The usefulness of the autocorrelation function as a guide in model selection has already been described in the text. This appendix will present tests of the significance of the individual autocorrelations and of the autocorrelation function as a whole. The latter test is, of course, a test of “whiteness”.
The autocovariance function, γk, of a discrete stochastic process {at} is defined as
γk = cov (at, at+k )
i.e., it is the covariance between two values, at and at+k considered as a function of their distance apart, k. The time difference k is called the lag.
We have
γo= cov (at, at) = σ2
where σ2 = var at. The autocorrelation function ρk is defined as
ρk = yk / y0 = yk / σ2 .
(A normal stationary process is completely specified by its mean and its autocovariance function.)
An unbiased estimate of the autocorrelation function, ρk, is the sample autocorrelation function
rk = ck / c0
where
and
.
If rk denotes the k-th correlation coefficient, then Bartlett (Reference A-1) has proved that
and
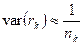
where nk is the size of the sample used to estimate rk.
Under the white noise hypothesis, we have
.
The
sample autocorrelations are thus approximately a sample of uncorrelated random
variables with mean 0, variance 1/nk. (Since the at’s
are computed from estimated values for the 
’s and
’s, this
approximation is not very good for autocorrelations of small lag. The quantity
1/nk is an approximate upper bound, however. See Reference
A-3 for discussion.) For samples of 30 or more, they are approximately
normally distributed (Reference A-2). Whenever the residuals are based on
estimated parameters (’s and’s) rather than
true values, biases are introduced into the distribution of the
autocorrelations. These biases are removed by replacing nk
by nk – (number of estimated parameters).
Using the preceding results, a test statistic for the hypothesis that the process is a pure moving average process of order k-1 is given by
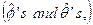
where sk is approximately distributed as a unit normal variate. Hence sk < 1.96 would be a 95% acceptance region. In order to test for whiteness, we test the significance of p autocorrelation coefficients using the statistic
where χ2 is
distributed as a χ2 variate with p-v degrees of
freedom, and v is the number of estimated parameters 
.
The
hypothesis of zero autocorrelations is rejected for 
.. It
is helpful to plot the set of autocorrelations on a graph, showing upper and
lower significance levels for the individual autocorrelations. Such a plot is
called a correlogram.
REFERENCES
A-1. Bartlett, M.S., “On the Theoretical Specification and Sampling Properties of Autocorrelated Time Series,” Journal of the Royal Statistical Society, Series B, Volume 8, 1946.
A-2. Anderson, R.L., “Distribution of the Serial Correlation Coefficient,” Annals of Mathematical Statistics, Volume 13, 1942.
A-3. Box, G.E.P. and Pierce, D.A., “Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models,” Journal of the American Statistical Association, Volume 65, No. 332, December, 1970
APPENDIX B. PERIODOGRAM ANALYSIS
This Appendix will describe the periodogram, a statistic designed to detect the presence of deterministic periodicities in a time series.
Suppose that, instead of the model (9), the appropriate time series model for sales is of the form
(B-1)
i.e., deterministic
components of periods 1/fi, i = 1, …, r are present.
This section will show how it is possible to identify these frequencies using
the raw periodogram (see Box and Jenkins [Reference B-1] or Wilks [Reference
B-2] for further discussion). For simplicity of discussion, we shall ignore
the 
and θ
terms and write the model (B-1) as
. (B-2)
In actuality, all parameters must be estimated simultaneously.
Let us suppose for convenience than n = 2r+1, and that n corresponds to a complete number of cycles of each frequency fi so that we may set
fi = i/n , i = 1, 2, …, r .
Note that we are trying to estimate those harmonics (fi) of the fundamental frequency 1/(2r+1) that correspond to periods greater that twice the time interval length.
Denoting
and 
, the model (B-2)
becomes
. (B-3)
The
least-squares estimates of 
can
be shown to be
.
The model (B-3) may be written
, (B-4)
where tan 
The quantity
is an estimate of the square
of the amplitude of the cosine wave of frequency ft in
zt. Defining j = 
we may write
.
Since
= 
we have
.
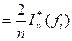
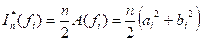
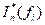
Hence
.
is an alternative expression
for the periodogram. The quantity 
is
the sum of squares attributable to the coefficients ai and bi
and so the can be used to
construct an analysis of variance table to test their significance. Box and
Jenkins illustrate this method. Alternatively, Wilks shows how to test for
significance of the largest periodogram component.
REFERENCES
B-1. Box, G.E.P., and Jenkins, G.M., Time Series Analysis, Forecasting, and Control, Holden-Day, Inc., San Francisco, Calif., 1970.
B-2. Wilks, S.S., Mathematical Statistics, John Wiley and Sons, New York, 1962.
APPENDIX C. SPECTRAL ANALYSIS
This Appendix will present a description of the statistic used to estimate the spectrum of a time series, and a test for “whiteness” i.e., of deviation of the spectrum from a constant line.
1. Definition of the Spectrum
The power spectrum of the discrete time series {at} is defined as
i.e., it is the Fourier cosine transform of the theoretical covariance function.
It follows that
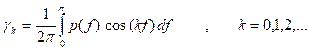
i.e., γk is
the Fourier transform of the power spectrum. Choosing 
we have
and
.
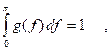The value L = ½ is also a popular choice. It is a somewhat more natural choice, since the frequency is then measured in units of cycles per second, rather than radians per second. The spectrum is defined over a finite range (e.g., - ½, ½) for discrete (lattice) processes since any sine curve of frequency > ½ is indistinguishable from some sine curve with frequency < ½ on a lattice of unit time period spacing.
The spectral density function is defined by
.
Since
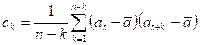
and g(f) is positive, it has the properties of a probability density function.
2. Estimates of the Spectrum
a. Raw Periodogram
A natural (but poor) estimate of the power spectrum is the periodogram:
where
.
An alternative definition of the periodogram is
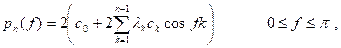
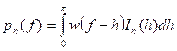
i.e., there is an additional factor (1 – k/n) introduced. The above estimate is slightly better than the one given earlier, but the asymptotic properties are the same. The periodogram thus has the same form as the power spectrum, with the estimated covariances substituted for the theoretical covariances. That is, it is the Fourier cosine transform of the sample autocovariance function. (It is also seen to be the square of the Fourier transform of the data.) It is a poor estimate of the power spectrum, since its variance (for fixed f) does not decrease to zero as the sample size (n) increases, i.e., it is not a consistent estimate.
b. Smoothed Periodogram
It can be shown that the modified estimate
is consistent (variance decreases to zero as n increases), using the appropriate values for the weights (λ’s). This estimate is called the “smoothed” periodogram, as opposed to the “raw” periodogram. Such weighted estimates are equivalent to estimates of the form
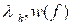
i.e., a weighted average of the periodogram over some band of frequencies. Thus we do not have a consistent estimate of the power spectrum at a single frequency; we do have, however, a consistent estimate of a smoothed power spectrum. It is noted, however, that the integral of the raw periodogram is a consistent estimate of the spectral distribution function:
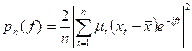
The
weight function 
is
called a lag window; the weight function w(f) is called a spectral
window. The pair (
) of
corresponding weights is called a window pair; they are Fourier transforms of
each other.
The weighting can also be applied to the data itself,
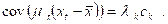
in which case the weight
function 
is called a data
window. The lag window, which is equivalent (in an expected value sense) to
this data window, is
since
The
Fourier transform, υ(f), of is
called the frequency window, and the equivalent spectral window (Fourier
transform of ) is
Blackman and Tukey (Reference C-1) present a thorough discussion of smoothing. As Box and Jenkins note, the impracticability of estimating the spectral density function at an exact frequency is analogous to that of estimating an ordinary density function at an exact point using a histogram. By choosing suitably large intervals, the histogram successfully estimates the probability mass in the intervals; if the interval is too small, the estimate oscillates wildly along the axis, and from sample to sample. Similarly, by choosing a suitably broad spectral window, the smoothed periodogram successfully estimates the spectral mass over the window; if the window is too small, the variance of the corresponding estimate is so large that the estimate is useless.
c. Weight Functions
Bartlett introduced the weights
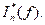
where the parameter mn
is an integer less than n such that mn
and mn/n
as n
(say ~ n1/3).
A
number of other weighting functions have been considered for use with 
Daniell
introduced the weights
These
weights require computation of all n - 1 covariances, unfortunately.
(Once again, mn and mn/n
as n
).
Approximations to the preceding weight function are given by Hanning:
and by von Hann:
Perhaps the simplest weights are
,
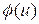resulting in a “truncated” periodogram. This estimate has the unpleasant property, however, that it can be negative.
3. White Noise
A sequence {at} of uncorrelated random variables having constant mean and variance is called a “white noise” sequence. A white noise sequence is hence one that has zero autocorrelation function, and constant spectral density function, equal to 1/π = .318. A test for zero autocorrelation function was given in Appendix A, assuming normality of the at’s.
4. A Test for Whiteness
A test for constant spectral density function is given by Grenander and Rosenblatt (Reference C-2). We have
where 
is the normal
distribution function and
where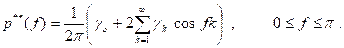 
.
The quantity F*(f) is the un-normalized spectral distribution function,
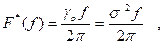
where the following definition is used for the spectrum:
Note that
and that in particular,
.
The quantity G(π) is estimated by
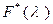
where 
The quantity 
is the estimate
of 
defined by
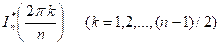
i.e., the integral of the Bartlett smoothed periodgram.
For
a 95% level of significance test of the hypothesis that the spectral density
function is constant, we determine 
and
reject the hypothesis if
D =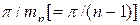 
.
This test is not very satisfactory, however, since σ2 is usually unknown. Replacing σ2 by an estimate results in accepting the null hypothesis more often than we should.
Since estimates of only n - 1 autocorrelations are available, estimates of n -1 different spectral mass densities contain all of the autocorrelation information of the sample, even though the estimate spectrum is plotted as a continuous curve. In fact, Hannan (Reference C-3) shows that the raw periodogram estimates
are uncorrelated for normal processes.
Such
is not the case, however, for the smoothed estimates 
The weight
function w(f) used for smoothing the periodogram overlaps for adjacent
estimated spectral masses (frequency distance 
apart), resulting
in high correlation between them. There is little overlap for next-adjacent
estimates (distance 2π/(n-1) apart), however, and they are hence
essentially uncorrelated. The “resolution” of the smoothed periodogram
(minimum frequency distances between essentially uncorrelated spectral mass
estimates) is hence2π/(n-1). See Blackman and Tukey (Reference C-1) or
Hannan (Reference C-3) for further discussion of this point.
We shall describe a test for whiteness that does not require knowledge of the true variance (σ2) of the process. It can be shown that, under the hypothesis of whiteness, each of the quantities
has the same distribution. A test of whether or not the spectral distribution function
differs significantly from a white noise spectral distribution function
can be tested using the Kolmogoroff-Smirnov test for goodness of fit. The test statistic is
and the 100p% critical value
for the test statistic is (approximately) 
where λp
(the p-th percentile point of the distribution of the test statistic)
equals 1.36 for p = .95 and 1.02 for p = .75. Reference C-4 may
be consulted for additional details concerning the preceding test.
REFERENCES
C-1. Blackman, R.B., and Tukey, J.W., The Measurement of Power Spectra, Dover Publications, New York, 1959.
C-2. Grenander, U., and Rosenblatt, M., Statistical Analysis of Stationary Time Series, John Wiley and Sons, New York, 1957.
C-3. Hannan, E.J., Time Series Analysis, John Wiley and Sons, New York, 1960.
C-4. Jenkins, G.M. and Watts, D.G., Spectral Analysis and its Applications, Holden-Day, San Francisco, 1968.
APPENDIX D. LINEAR DIFFERENCE EQUATIONS
As indicated in the text, the difference equation solution of the autoregressive part of the time series model is the median value of the process. This Appendix presents a fundamental result from the theory of linear difference equations, namely the solution of a linear second order difference equation.
Consider the difference equation
where 
. Let m1
and m2 denote the two roots of the corresponding indicial
(auxiliary, characteristic) equation:
.
The general solution of the above difference equation is given by
if m1 and m2 are real and unequal, by
if m1 = m2, and by
if m1 and m2 are the complex conjugates r(cos θ + sin θ).
The general solution to the difference equation
is given by
zt = general solution to the homogenous equation
(obtained by setting et = 0 in the above)
+ particular solution of the complete equation.
If the roots m1 and m2 are unequal, then a particular solution of the complete equation is
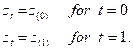
where
If m1 = m2 = m, then a particular solution of the complete equation is
The constants of the general solution are chosen to satisfy the initial conditions
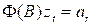
Goldberg (Reference D-1) provides a readable introduction to difference equations.
REFERENCES
D-1. Goldberg, Samuel, Introduction to Difference Equations, Science Editions, Inc., John Wiley and Sons, Inc., New York, 1961.
APPENDIX E. LEAST-SQUARES AND MAXIMUM LIKELIHOOD ESTIMATION
1. Introduction
This Appendix shows the derivation of the least-squares estimates of the parameters of the model
and gives the formula for the likelihood function in the case of normally distributed at’s.
The
analysis in the case of multiplicative seasonal components is similar and will
not be described here. It is noted that if we have a nonseasonal pure autoregressive
model, the model is what is known as a linear model, and the estimation
is straightforward. If any θ’s are present, however, or if there is
more than one 
polynomial,
then the model is not linear, and iterative procedures are employed to find the
least-squares estimates.
2. Least-Squares Estimates
a. Pure Autoregressive Model
In the case of the pure autoregressive model, the least-squares estimates are easy to compute. We have
or
where
and
.
Suppose we have n observations. Denoting the vector of the n-p most recent observations by
and the error vector (i.e., vector of random components) by
we have
where
.
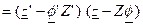This
model is linear in the ’s, and
so it is easy to calculate the least-squares estimates of the ’s, given by the
values which minimize the residual sum of squares:
.
Applying vector differentiation, we have
= 
.
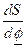
Hence,
setting 
equal to the null
vector, we have
or
or
or
as the least squares estimate
of 
.The estimate of
the variance-covariance matrix of 
is
where 
, the estimate of
the variance of at, is given by
b. Mixed Autoregressive Moving Average Model
We
shall now determine the least-squares estimates in the case of the mixed
autoregressive moving average model. Suppose that the zeros of 
are outside the
unit circle. We may then invert the process and write
Considering
as a function of 
and the z’s
up to and including zt, we expand at in a Taylor series about some trial value 
where
.
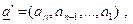Denoting:
and
and denoting the matrix whose
(i, t)-th element is 
we
may write the above as
or
which is a linear model in
the deviations 
of the
trial value 
from the true
value 
As before, the
least-squares estimates for are
We
calculate the new trial value 
,
and repeat the above process to obtain 
and hence 
. This process is
continued until 
converges.
If a sufficiently bad initial trial value for is used, the
iteration might not converge. Box and Jenkins suggest means for picking
“reasonable” trial values. In practice, zero initial values are satisfactory.
For each iteration the values of the quantities at0 and Xit0 are calculated iteratively as follows.
Since
we have
since
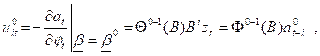
we have
since
we have
3. Maximum Likelihood Estimates
The
above procedure for obtaining estimates of the ’s and θ’s
produces so- called “least-squares” estimates; i.e., the estimates are chosen
so as to minimize the sum of squares of the deviations of the observations from
their expectations.
An
alternative procedure for obtaining estimates is to choose those values for the
’s and θ’s that
maximize the likelihood function (i.e., the probability function of a1,…,an,
considered as a function of the ’s
and θ’s). For the case in which the a’s are normally
distributed, the maximum likelihood estimates are the same as the least-squares
estimates. In addition, the maximum likelihood procedure is useful in that
knowledge of the entire likelihood function (and not just its maximum) can
provide insight into the behavior of the model as the parameters are varied
from their maximizing values. This would enable one to determine more useful
forms of the time series model which, statistically speaking, are about as
good. Also, parameter redundancies caused by common factors in the 
and 
polynomials would
be recognized (the maximum might tend to lie along a line).
Another
reason for using the maximum likelihood method is that we are restricting our parameters so
that the zeros of are
outside the unit circle. The least-squares procedure is not designed to handle
such a restriction. Using the maximum likelihood method, however, we may
simply choose the parameter estimates corresponding to the maximum value of the
likelihood function in the acceptable region.
Note that it is, of course, necessary to assume a distribution for the at’s if we wish to use the maximum likelihood method.
4. The Likelihood Function
As noted above, we assume normality of the random variation (at’s) of the time series. The probability density function of the at’s is hence
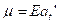
where 
and 
. For given
values of the parameters μ and σ2 the probability
density function indicates the “likelihood” of an outcome a’1 ,…,
a’n. If the parameters are known, then a set of intuitively
appealing estimates are those values for which f is maximized. The
function f, considered as a function of the parameters, is called the likelihood
function, and will be denoted by L. The maximizing parameter values
are called maximum likelihood estimates. Maximum likelihood estimates
can be shown to have desirable statistical properties. In the case of a normal
distribution (as above), the least-squares estimates and the maximum likelihood
estimates are identical.
The likelihood function is
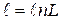
It
is convenient to work with the log-likelihood function, 
(a monotonic
function of L):
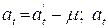
Let
us denote 
has zero
expectation.
Note
that in the time series situation, we cannot observe the at’s
directly. Instead, we can only compute them, given values for the ’s and θ’s
Since
the at’s depend on the parameters (’s and θ’s)
of the time series model and on previous observations, we write
where 
and 
Since
at depends on and
θ, so does 
, and so
we write 
for completeness.
In general, our model is
where
so that
If
all of the θ’s are zero, the model is linear (in the coefficients of the
zt’s) and at involves only z1,…,
zn, given values for the ’s and d:
Calculation
of the maximum likelihood estimates of the ’s , μ, and
σ2 is straightforward in this case:
and the ’s as given
previously. If any of the θ’s are nonzero, however, the model is
nonlinear and at depends on an infinite number of
unobservable zt’s (namely z0, z-1, z-2,
…).
Writing the at’s recursively, we have
Hence,
in addition to μ, σ2, the θ’s and the ’s we must
estimate a0, a-1, … , a1-q and z0,
z-1, … , z1-p. With a large number of observations,
however, it is justifiable simply to ignore a1, a2, …,
ap, and set at, p < t < q equal
to zero. Then we need estimate only μ, σ2, the θ’s
and the ’s.
APPENDIX F. TRANSFORMATION OF DATA
One of the underlying assumptions in the least-squares estimation procedure is that the variance of the at’s are homoscedastic, or constant for varying t. If this is not true, then the estimates are still unbiased, but their sampling variances are inflated. A Bartlett’s M-test can be applied to test whether or not the variances of different series to be pooled for estimation purposes are heteroscedastic. In addition to variance differences from series to series, it may be that the variance of the same series changes over the length of the series. To enable efficient estimation, it is desirable to transform the data so that the variance is comparable for all the observations.
If m = E(X), and var X = f(m), then a transformation which will usually result in a random variable with constant variance is
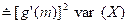
since, by Taylor’s theorem,
var
(Y) 
= 
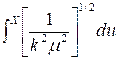
= 1
provided suitable regularity conditions are satisfied. For example, if the magnitude of observation-to-observation variations in zt appear to be proportional to the local mean level, the logarithmic transformation is appropriate, since, letting SD(X) = μ, or var(X) = k2μ2 we have
g(X)
= 
= 
= 
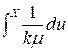
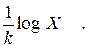
Note that transformation of the data has the effect that the estimates are “least-squares” with respect to the transformed scale, not the original scale.
Forecasting in the Case of a Logarithmic Transformation
It
is of interest to observe the effect of a data transformation on forecasts.
Suppose that fluctuations in the original time series are proportional to the
level of the time series, so that it is appropriate to apply a logarithmic
transformation to the data. Let us denote the untransformed variate by zt’.
To forecast zt’, we compute the least-squares forecast of the
logarithm, zt, of zt’ and exponentiate the
result. Although, the forecast logarithm is the expected value (mean) of zt,
the exponentiated result is not the expected value of the original variate, zt’.
It is, however, the median of the distribution of zt’, if the
zt’s are normally distributed. The median value, 
,of zt’
at time t is used rather than the mean value, 
, to forecast zt’
at time t for the following reason. Suppose that zt’
obeys a lognormal distribution. The median is considered more appropriate than
the mean as a forecaster for a lognormal distribution, since the mean value of
a lognormal distribution is unduly influenced by extremely improbable,
extremely large values. For example, the mean can be thousands of times larger
than the .99 percentile point of the distribution.
Note, however, that the median forecaster is biased low. This follows form Jensen’s inequality:
where E is the expectation operator. It follows that
exp(least squares forecast log sales) < least squares forecast sales;
i.e., the forecaster is biased low. The bias increases as the variability (var at) increases. In particular, if zt’ is lognormally distributed,
then
and
The bias is the factor exp(σ2/2) which increases as σ2 increases.
APPENDIX G. EXPONENTIAL SMOOTHING
A procedure that has been widely used in forecasting is exponential smoothing. This Appendix will show that the use of exponential smoothing in fact corresponds to use of a particular model of the form
Suppose that
and that
so that our model is
(G-1)
The lead-one least-squares forecaster associated with this model is
where 
and 
denotes the
one-step-ahead forecast made from time t. We may hence write
(G-2)
From this expression, we can obtain an alternative expression for the least-squares forecaster:
… =
(G-3)
which would readily have been derived from representing the process as
or
or
or
so that
The expression (G-3) is called an exponentially weighted moving average, and use of this forecaster is called (single) exponential smoothing. Although single exponential smoothing has been uncritically applied to forecast sales (having only changes in level), it is obviously appropriate only when the model (G-1) is a valid statistical representation of the sales time series. The program TIMES provides the means for determining whether or not the model (G-1) is appropriate, and for determining the correct model, if it is not.
FndID(238)
FndTitle(TIMES Box-Jenkins Forecasting System Reference Manual Volume I TECHNICAL BACKGROUND)
FndDescription(TIMES Box-Jenkins Forecasting System Reference Manual Volume I TECHNICAL BACKGROUND)
FndKeywords(Box-Jenkins; forecasting; mathematical forecasting; time series analysis; TIMES)