MISSING DATA, WEIGHTING AND EXTREME VALUES: LECTURE NOTES
Joseph George Caldwell, PhD (Statistics)
1432 N Camino Mateo, Tucson, AZ 85745-3311 USA
Tel. (001)(520)222-3446, E-Mail jcaldwell9@yahoo.com
July 13, 2016
Copyright © 2016 Joseph George Caldwell. All rights reserved.
Contents
3. APPROACHES TO TREATMENT OF MISSING DATA.. 5
4. MISSING DATA IN EXPERIMENTS. 6
6. AVAILABLE-CASE ANALYSIS. 25
8. SINGLE-VALUE IMPUTATION.. 27
10. CALIBRATION WEIGHTING (GENERALIZED REGRESSION ESTIMATES, GREG). 35
11. LIKELIHOOD-BASED PROCEDURES. 38
13. NONIGNORABLE MISSING DATA.. 44
OUTLINE
REFERENCES
TYPES OF MISSING DATA (MCAR, MAR, MNAR; IGNORABILITY))
APPROACHES TO TREATMENT OF MISSING DATA
MISSING DATA IN EXPERIMENTS
AD-HOC PROCEDURES
COMPLETE- CASE ANALYSIS
WEIGHTED COMPLETE-CASE ANALYSIS
BASE WEIGHTS
ADJUSTMENT FOR ELIGIBILITY
ADJUSTMENT FOR NONRESPONSE (WEIGHTING CLASSES; RESPONSE HOMOGENEITY GROUPS)
ESTIMATION OF WEIGHTS
WEIGHTING-CLASS ESTIMATOR
PROPENSITY SCORING MODELS
CLASSIFICATION AND REGRESSION TREE MODELS (CART)
AVAILABLE –CASE ANALYSIS
IMPUTATION
SINGLE-VALUE IMPUTATION
EXPLICIT MODELS
UNCONDITIONAL MEAN
CONDITIONAL MEAN
ADJUSTMENT CELLS
REGRESSION IMPUTATION
BUCK'S METHOD
IMPUTING DRAWS FROM A PREDICTIVE DISTRIBUTION
STOCHASTIC REGRESSION IMPUTATION
IMPLICIT MODELS
SUBSTITUTION
HOT DECK
COLD DECK
ESTIMATION OF UNCERTAINTY
MULTIPLE IMPUTATION
CALIBRATION WEIGHTING (GREG)
LIKELIHOOD-BASED PROCEDURES
MAXIMUM-LIKELIHOOD METHOD
IGNORABLE MISSINGNESS
ESTIMATION OF PARAMETERS
ANALYTICAL METHODS
NUMERICAL METHODS
NEWTON-RAPHSON
EM ALGORITHM
DEMING-STEPHAN ITERATIVE PROPORTIONAL FITTING
BAYESIAN METHODS
GIBBS SAMPLING
NONIGNORABLE MISSING DATA
EXTREME VALUES
1. REFERENCES
REFERENCE FOR MISSING DATA:
Roderick J. A. Little and Donald B. Rubin, Statistical Analysis with Missing Data, 2nd edition, Wiley 2002 (381 pages)
REFERENCES FOR WEIGHTING:
Richard Valliant, Jill A. Dever and Frauke Kreuter, Practical Tools for Designing and Weighting Sample Surveys, Springer, 2013 (comprehensive discussion of weighting; 670 pages)
Carl-Erik Särndal, Bengt Swensson and Jan Wretman, Model Assisted Survey Sampling, Springer, 2003 (summary information on weighting; 694 pages)
THIS PRESENTATION WILL FOLLOW THE ORGANIZATION AND NOTATION OF THESE REFERENCES.
THE FOCUS IS ON “LOST” DATA (NONRESPONSE AND TRUNCATION) RATHER THAN UNOBSERVABLE DATA (SAMPLE SELECTION)
INFORMAL PROCEDURES (IMPLICIT MODELS) VS. EXPLICIT MODELS
MODELS BASED ON STATISTICAL PROPERTIES OF DATA (LIKELIHOOD-BASED) VS. OTHERS
BAYESIAN AND CLASSICAL (TRADITIONAL, FREQUENTIST)
2. TYPES OF MISSING VALUES
DEPENDENT VARIABLES (“Ys”)
INDEPENDENT VARIABLES (“Xs”)
EITHER MAY BE IMPUTED (OR OTHERWISE ACCOUNTED FOR), BUT IMPUTATION OF DEPENDENT VARIABLES IS USUALLY RESTRICTED TO DESIGNED EXPERIMENTS OR MULTIVARIATE ANALYSIS (MORE THAN ONE DEPENDENT VARIABLE).
IN GENERAL, CAPITAL LETTERS WILL BE USED TO REFER TO RANDOM VARIABLES (FUNCTIONS DEFINED ON SAMPLE SPACES), AND LOWER-CASE LETTERS TO REALIZATIONS OF RANDOM VARIABLES (BASED ON OUTCOMES OF EXPERIMENTS).
POTENTIAL SOURCE OF CONFUSION WITH THE WORD "RESPONSE":
THE INDEPENDENT VARIABLES MAY BE REFERRED TO AS EXPLANATORY VARIABLES OR REGRESSOR VARIABLES. THE DEPENDENT VARIABLES MAY BE REFERRED TO AS OUTCOME VARIABLES, REGRESSANDS, OR RESPONSE VARIABLES. IF AN OBSERVATION OCCURS (I.E., IF THE DATA ARE NOT MISSING), IT IS OFTEN SAID THAT A RESPONSE WAS OBTAINED, OR THAT A RESPONSE OCCURRED. A PROBLEM THAT ARISES IS THAT THE TERM “RESPONSE” IS AMBIGUOUS – IT MAY REFER EITHER TO THE VALUE OF AN OBSERVED OUTCOME VARIABLE (A MEASUREMENT ON AN EXPERIMENTAL UNIT) OR TO THE EVENT THAT AN OUTCOME WAS OBSERVED. FOR THIS REASON, WE SHALL GENERALLY USE THE TERM “MISSING” OR “NON-MISSING” TO REFER TO THE OCCURRENCE OR NON-OCCURRENCE OF MISSING DATA, RATHER THAN THE TERMS “RESPONDING / NON-RESPONDING” OR “RESPONSE / NON-RESPONSE.”
TYPES OF NONRESPONSE:
MISSING COMPLETELY AT RANDOM (MCAR): THE MISSING-DATA EVENT IS RANDOM (THE COMPLETE CASES ARE A SIMPLE RANDOM SAMPLE OF THE SAMPLE OF ALL CASES).
MISSING AT RANDOM (MAR): THE MISSING-DATA EVENT DOES NOT DEPEND ON THE MISSING DATA (BUT MAY DEPEND ON OBSERVED EXPLANATORY VARIABLES).
MISSING NOT AT RANDOM (MNAR, OR "NOT MISSING AT RANDOM", NMAR): ALL OTHER CASES; THE PROBABILITY OF NONRESPONSE MAY DEPEND ON THE MISSING DATA. EXAMPLE: A PROBABILITY SAMPLE OF ELIGIBLE PEOPLE ARE SELECTED FOR A JOB TRAINING COURSE, BUT A SUBSTANTIAL PROPORTION OF THE SAMPLE DECLINES TO PARTICIPATE, AND IT IS KNOWN THAT THE PARTICIPATION DECISION IS RELATED TO UNOBSERVED (UNMEASURED) PERSONAL CHARACTERISTICS SUCH AS CONFIDENCE, THAT ARE RELATED TO OUTCOME.
3. APPROACHES TO TREATMENT OF MISSING DATA
AD-HOC PROCEDURES
COMPLETE- CASE ANALYSIS
WEIGHTED COMPLETE-CASE ANALYSIS
BASE WEIGHTS
ADJUSTMENT FOR ELIGIBILITY
ADJUSTMENT FOR NONRESPONSE (WEIGHTING CLASSES; RESPONSE HOMOGENEITY GROUPS)
ESTIMATION OF WEIGHTS
WEIGHTING-CLASS ESTIMATOR
PROPENSITY SCORING MODELS
CLASSIFICATION AND REGRESSION TREE MODELS (CART)
AVAILABLE –CASE ANALYSIS
IMPUTATION
SINGLE-VALUE IMPUTATION
EXPLICIT MODELS
UNCONDITIONAL MEAN
CONDITIONAL MEAN
ADJUSTMENT CELLS
REGRESSION IMPUTATION
BUCK'S METHOD
IMPUTING DRAWS FROM A PREDICTIVE DISTRIBUTION
STOCHASTIC REGRESSION IMPUTATION
IMPLICIT MODELS
SUBSTITUTION
HOT DECK
COLD DECK
ESTIMATION OF UNCERTAINTY
MULTIPLE IMPUTATION
CALIBRATION WEIGHTING (GREG)
LIKELIHOOD-BASED PROCEDURES
MAXIMUM-LIKELIHOOD METHOD
IGNORABLE MISSINGNESS
ESTIMATION OF PARAMETERS
ANALYTICAL METHODS
NUMERICAL METHODS
NEWTON-RAPHSON
EM ALGORITHM
DEMING-STEPHAN ITERATIVE PROPORTIONAL FITTING
BAYESIAN METHODS
GIBBS SAMPLING
NONIGNORABLE MISSING DATA
4. MISSING DATA IN EXPERIMENTS
MOTIVATION: EXPERIMENTAL DESIGNS ARE HIGHLY STRUCTURED (BALANCED), ENABLING CONVENIENT APPLICATION OF SPECIALIZED (DESIGN-SPECIFIC) SOFTWARE FOR ANALYSIS (E.G., ANALYSIS OF VARIANCE). THE EXPLANATORY VARIABLES (“Xs”) ARE RARELY MISSING, SINCE THE EXPERIMENTER USUALLY HAS CONTROL OF THOSE. WHAT IS USUALLY MISSING IS A RESPONSE (Y) VARIABLE. BY ESTIMATING A MISSING Y VALUE, DESIGN-SPECIFIC STATISTICAL-ANALYSIS SOFTWARE MAY BE USED TO ANALYZE THE DATA AND PRESENT RESULTS.
THE FOLLOWING PROCEDURES APPLY WHEN ONLY A SINGLE OUTCOME VARIABLE IS MISSING, AND NO PREDICTOR (DESIGN) VARIABLES ARE MISSING.
THE STANDARD APPROACH TO ESTIMATION OF MISSING RESPONSES IN EXPERIMENTAL DESIGNS IS TO APPLY THE METHOD OF LEAST SQUARES, I.E., TO DETERMINE THE MISSING VALUE(S) TO MINIMIZE THE ERROR SUM OF SQUARES. THIS APPROACH MAKES NO ASSUMPTIONS ABOUT THE DISTRIBUTION OF THE RANDOM VARIABLES.
THIS APPROACH PRODUCES "LEAST SQUARES" ESTIMATES OF THE MODEL PARAMETERS AND OF THE RESIDUAL ERRORS. THESE ESTIMATES ARE MAXIMUM LIKELIHOOD ESTIMATES WHEN THE MODEL ERROR TERMS ARE NORMALLY DISTRIBUTED WITH CONSTANT VARIANCE, BUT NOT NECESSARILY OTHERWISE. THE ESTIMATED COVARIANCE MATRIX OF THE PARAMETER ESTIMATES IS TOO SMALL (I.E., SMALLER THAN FOR THE GENERAL-LINEAR-MODEL ANALYSIS OF THE AVAILABLE DATA), LEADING TO INFLATED VALUES FOR THE “F” STATISTIC USED TO TEST THE SIGNIFICANCE OF EFFECTS ASSOCIATED WITH MULTIPLE DEGREES OF FREEDOM (SUCH AS A TREATMENT HAVING MORE THAN TWO LEVELS). ALSO, THE DEGREES OF FREEDOM FOR “t” TESTS MUST BE ADJUSTED TO TAKE INTO ACCOUNT THE MISSING DATA.
SEVERAL METHODS ARE AVAILABLE USING THIS APPROACH:
· YATES’ METHOD
· ITERATIVE METHODS (HARTLEY; HEALY AND WESTMACOTT)
· ANCOVA WITH MISSING-VALUE COVARIATES (BARTLETT’S METHOD)
THESE METHODS ASSUME THAT THE OCCURRENCE OF MISSING DATA DOES NOT DEPEND ON THE MISSING VALUES (I.E., THE MISSING DATA PHENOMENON IS MISSING COMPLETELY AT RANDOM (MCAR) OR MISSING AT RANDOM (MAR)) AND THAT THE PARAMETERS OF THE MISSING-DATA PROCESS ARE DISTINCT FROM (I.E., IN DISTRIBUTIONS SEPARATE FROM (UNRELATED TO)) THE OUTCOME MODEL PARAMETERS. (NOTE THAT, DEPENDING ON WHAT DATA ARE MISSING, SOME EFFECTS MAY NOT BE ESTIMABLE.)
YATES’ METHOD (FOR EXPERIMENTAL DESIGNS)
THE MISSING VALUE (OR VALUES) ARE ESTIMATED BY THE METHOD OF LEAST SQUARES. BECAUSE OF THE HIGH STRUCTURE OF THE DESIGN, THIS LEADS TO A SIMPLE FORMULA FOR THE MISSING VALUE. THE VALUE IS SUBSTITUTED AND DESIGN-SPECIFIC SOFTWARE IS USED TO ANALYZE THE DATA.
THIS APPROACH WAS OF GREATER INTEREST PRIOR TO THE WIDESPREAD AVAILABILITY OF STATISTICAL ANALYSIS COMPUTER SOFTWARE, AND THERE WAS STRONG (COMPUTATIONAL) REASON TO MAINTAIN THE ORIGINAL DESIGN STRUCTURE. TODAY, GENERAL-LINEAR-MODEL SOFTWARE WOULD TYPICALLY BE USED TO ANALYZE THE DATA.
FEW SOCIO-ECONOMIC EVALUATION STUDIES USE HIGHLY STRUCTURED DESIGNS, SO THIS APPROACH IS OF LIMITED USE IN THAT FIELD.
FORMULAS ARE PRESENTED IN A NUMBER OF BOOKS AND ARTICLES ON EXPERIMENTAL DESIGN:
William G. Cochran and Gertrude M. Cox, Experimental Designs, 2nd ed, Wiley (1957, 1950)
Wilkinson, G. N., "Estimation of missing values for the analysis of incomplete data," Biometrics, Vol. 14, 1958, pp. 257-286; and "The analysis of variance and derivation of standard errors for incomplete data," pp. 360-384.
STANDARD EXPERIMENTAL DESIGNS:
· FRACTIONAL FACTORIAL DESIGNS
· RANDOMIZED BLOCKS
· BALANCED INCOMPLETE BLOCKS
· LATIN SQUARES
· LATTICE SQUARES
· SPLIT-PLOT.
EXAMPLE OF A FORMULA FOR A MISSING VALUE:
RANDOMIZED BLOCK DESIGN WITH T TREATMENTS AND B BLOCKS, THE FORMULA FOR A MISSING VALUE IN TREATMENT t AND BLOCK b IS
![]()
where
![]() = missing value of Y for treatment t and block b
= missing value of Y for treatment t and block b
![]() = sum of the observed values of Y for treatment t
= sum of the observed values of Y for treatment t
![]() = sum of the observed values of Y for block b
= sum of the observed values of Y for block b
![]() = sum of all observed values of Y.
= sum of all observed values of Y.
ITERATIVE METHODS (FOR EXPERIMENTAL DESIGNS)
COMMONLY USED METHOD DESCRIBED BY HEALY AND WESTMACOTT:
1. SUBSTITUTE TRIAL VALUES FOR ALL MISSING VALUES (E.G., MEANS)
2. PERFORM COMPLETE-DATA ANALYSIS TO ESTIMATE MODEL PARAMETERS
3. USE THE ESTIMATED MODEL TO ESTIMATE MISSING VALUES
4. SUBSTITUTE ESTIMATED MISSING VALUES AND REPEAT STEPS 2 AND 3 UNTIL RESIDUAL SUM OF SQUARES STOPS DECREASING
THIS PROCEDURE IS AN EXAMPLE OF AN EM ALGORITHM, WHICH WILL BE DISCUSSED LATER, RELATIVE TO NON-EXPERIMENTAL DESIGNS.
ANCOVA WITH MISSING-VALUE COVARIATES (BARTLETT’S METHOD) (FOR EXPERIMENTAL DESIGNS)
1. SPECIFY A GUESS VALUE FOR EACH MISSING VALUE (E.G., A MEAN).
2. DEFINE A MISSING-VALUE COVARIATE (INDICATOR VARIABLE, 0 = NONMISSING, 1 = MISSING) FOR EACH MISSING VALUE.
3. SUBTRACT THE ESTIMATED COEFFICIENT FOR EACH COVARIATE FROM THE GUESS VALUE. THIS IS THE LEAST-SQUARES ESTIMATE OF THE MISSING VALUE.
ADVANTAGES:
· NONITERATIVE.
· METHOD WARNS OF SINGULAR DESIGN MATRIX (NONESTIMABLE PARAMETER CONTRASTS)
· METHOD PRODUCES CORRECT ESTIMATES OF EFFECTS, RESIDUAL SUM OF SQUARES, STANDARD ERRORS OF PARAMETER ESTIMATES, SUMS OF SQUARES DUE TO EFFECTS AND F TESTS.
· METHOD MAY BE IMPLEMENTED BY MEANS OF A SERIES OF ANOVA PROCEDURES.
AS WITH YATES’ METHOD, THIS METHOD WAS ATTRACTIVE PRIOR TO THE ADVENT OF DIGITAL COMPUTERS, WHEN THE COMPUTATIONAL BURDEN ASSOCIATED WITH CORRUPTED DESIGNS WAS HEAVY.
5. AD-HOC PROCEDURES
THE PRECEDING SECTION (ON MISSING DATA IN EXPERIMENTAL DESIGNS) ADDRESSED THE SITUATION IN WHICH (A VALUE OF OR VALUES OF) A SINGLE RESPONSE VARIABLE COULD BE MISSING.
WE WILL NOW ADDRESS SITUATIONS IN WHICH ANY OF THE VARIABLES (RESPONSE OR EXPLANATORY) MAY BE MISSING, FOR ARBITRARY SAMPLE DESIGNS.
THIS PRESENTATION DEALS WITH MISSING DATA FOR WHICH THE MISSINGNESS MECHANISM IS RANDOM, NOT DETERMINISTIC. FOR DETERMINISTIC MISSINGNESS, THE WEIGHTING-CLASS METHOD DESCRIBED LATER MAY BE USED (NONRESPONSE BIAS IS DECREASED BY GROUPING THE DATA INTO CLASSES FOR WHICH THE RESPONDENTS AND NONRESPONDENTS HAVE, AS NEARLY AS POSSIBLE, THE SAME MEANS).
THE SIMPLEST APPROACH IS TO ANALYZE ONLY THOSE OBSERVATIONS THAT HAVE NO MISSING DATA, I.E., THE “COMPLETE” CASES.
ADVANTAGES:
· SIMPLE (USE BASIC, STANDARD SOFTWARE)
· COMPARABILITY OF STATISTICS (ALL BASED ON SAME DATA SET)
DISADVANTAGES:
· LOSS OF PRECISION, IF THERE ARE MANY CASES HAVING MISSING VARIABLES
· BIAS IF THE MISSING-DATA MECHANISM IS NOT MISSING COMPLETELY AT RANDOM (MCAR).
TYPES OF MISSINGNESS
MISSING COMPLETELY AT RANDOM (MCAR): THE MISSING-DATA EVENT IS RANDOM (THE COMPLETE CASES ARE A SIMPLE RANDOM SAMPLE OF THE SAMPLE OF ALL CASES).
MISSING AT RANDOM (MAR): THE MISSING-DATA EVENT DOES NOT DEPEND ON THE MISSING DATA (BUT MAY DEPEND ON OBSERVED EXPLANATORY VARIABLES).
MISSING NOT AT RANDOM (OR NOT MISSING AT RANDOM): ALL OTHER CASES; THE PROBABILITY OF NONRESPONSE MAY DEPEND ON THE DEPENDENT VARIABLE, OR ON THE MISSING DATA. EXAMPLE: A PROBABILITY SAMPLE OF ELIGIBLE PEOPLE ARE SELECTED FOR A JOB TRAINING COURSE, BUT A SUBSTANTIAL PROPORTION OF THE SAMPLE DECLINES TO PARTICIPATE, AND IT IS KNOWN THAT THE PARTICIPATION DECISION IS RELATED TO PERSONAL CHARACTERISTICS SUCH AS CONFIDENCE, THAT ARE RELATED TO OUTCOME AND NOT OBSERVED.
THIS APPROACH (WEIGHTED COMPLETE-CASE ANALYSIS) IS USEFUL IF THE PROPORTION OF MISSING (NON-COMPLETE) CASES IS SMALL AND THERE IS LIMITED COVARIATE INFORMATION AVAILABLE (SO THAT MORE ELABORATE METHODS MAY NOT BE USED).
NOTE: IF THERE ARE MANY VARIABLES OF INTEREST IN AN ANALYSIS, AND MISSING VALUES MAY OCCUR IN MANY OF THEM, THEN THE NUMBER OF OBSERVATIONS HAVING NO MISSING VALUES MAY BE VERY SMALL, AND THE COMPLETE-CASE APPROACH IS NOT PRACTICAL.
IF THE VARIABLES ARE STOCHASTICALLY DEPENDENT (E.G., CORRELATED), THEN THIS APPROACH IS NOT EFFICIENT:
· OBSERVED VALUES ARE DROPPED FOR VARIABLES WHEN OTHER VARIABLES ARE MISSING (“THROWING DATA AWAY”)
· THE NON-MISSING VARIABLES CONTAIN INFORMATION ABOUT THE MISSING VARIABLES (“THROWING INFORMATION AWAY”).
IF THE MISSING VALUES ARE MCAR, THEN THERE IS A LOSS IN PRECISION ASSOCIATED WITH MISSING DATA, BUT NO BIAS, AS A RESULT OF THE MISSING DATA. OTHERWISE, ESTIMATES MAY BE BIASED, WHERE THE BIAS DEPENDS ON THE DIFFERENCE BETWEEN THE COMPLETE CASES AND THE MISSING CASES WITH RESPECT TO THE VARIABLES OF INTEREST.
FOR EXAMPLE, IF μCC and μIC DENOTE THE MEANS FOR THE COMPLETE-CASE AND INCOMPLETE-CASE OBSERVATIONS, RESPECTIVELY, AND IF pCC DENOTES THE PROPORTION OF COMPLETE CASES, THEN THE BIAS IS
μCC – μ = (1 - pCC) (μCC – μIC),
WHERE μ IS THE POPULATION (OVERALL) MEAN. FOR REGRESSION ANALYSIS, THE COEFFICIENTS ARE BIASED IF THE PROBABILITY OF BEING COMPLETE GIVEN THE EXPLANATORY VARIABLES DEPENDS ON Y (OR, EQUIVALENTLY, ON THE MODEL ERROR TERM).
NOTE THAT OBSERVATIONS MAY BE OMITTED BASED ON THE VALUE OF THE INDEPENDENT VARIABLES (Xs) WITHOUT INTRODUCING BIASES INTO ESTIMATES. IN FACT, DATA ARE FREQUENTLY CULLED (PRUNED, TRIMMED) FROM ANALYSIS SETS BASED ON THE VALUES OF EXPLANATORY VARIABLES, TO REDUCE DEPENDENCE OF THE MODEL ON THE PARTICULAR SAMPLE. (SEE THE FOLLOWING FOR A DISCUSSION OF THIS TOPIC. HO, DANIEL, KOSUKE IMAI, GARY KING, AND ELIZABETH STUART. "MATCHING AS NONPARAMETRIC PREPROCESSING FOR REDUCING MODEL DEPENDENCE IN PARAMETRIC CAUSAL INFERENCE." POLITICAL ANALYSIS 15 (2007): 199-236 (POSTED AT INTERNET WEBSITE http://gking.harvard.edu/gking/files/matchp.pdf).)
WEIGHTED COMPLETE-CASE ANALYSIS
A STANDARD APPROACH TO REDUCING THE BIAS ASSOCIATED WITH COMPLETE-CASE ANALYSIS IS TO MODIFY THE HORVITZ-THOMPSON ESTIMATOR USED IN SAMPLE SURVEY TO ACCOUNT FOR MISSING (NONRESPONDING) VALUES.
THE WEIGHTS ARE DETERMINED SO THAT THE WEIGHTED MEAN IS AN UNBIASED (OR REDUCED-BIAS) ESTIMATE OF THE POPULATION MEAN. THE VARIANCE OF THE ESTIMATOR IS DETERMINED USING THE BOOTSTRAPPING METHOD.
WITH THIS APPROACH, THERE IS NO IMPUTATION OF MISSING DATA. WEIGHTS ARE CALCULATED TAKING INTO ACCOUNT THE SAMPLE DESIGN, ELIGIBILITY AND NONRESPONSE AT THE LEVEL OF THE OBSERVATION (NOT THE INDIVIDUAL ITEM WITHIN AN OBSERVATION).
IF THIS APPROACH WERE APPLIED TO INCOMPLETE CASES (ITEM NONRESPONSE), THE WEIGHTS WOULD DIFFER FOR EACH VARIABLE CONSIDERED, DEPENDING ON ITS INDIVIDUAL RESPONSE PATTERN.) THIS IS USUALLY NOT PRACTICAL, SINCE IT MAY LEAD TO A LARGE NUMBER OF SETS OF WEIGHTS. USUALLY, ONLY ONE SET OF WEIGHTS (THE OBSERVATION WEIGHTS) IS DETERMINED FOR A DATA SET.
ANOTHER REASON WHY WEIGHTING IS USED TO ADDRESS UNIT NONRESPONSE AND NOT ITEM NONRESPONSE IS THAT IN UNIT NONRESPONSE, THE QUESTIONNAIRE IS BLANK, EXCEPT FOR DESIGN INFORMATION. IN THIS CASE, NOT MUCH DATA IS AVAILABLE ON WHICH TO BASE A NONRESPONSE MODEL. IN THE CASE OF ITEM NONRESPONSE (IN NON-BLANK QUESTIONNAIRES), DATA ARE AVAILABLE FOR SOME ITEMS, AND IT MAY BE POSSIBLE TO DEVELOP A MUCH BETTER MODEL TO ADDRESS NONRESPONSE (TO ESTIMATE BOTH THE PROBABILITY OF NONRESPONSE AND THE MISSING VALUE).
(TERMINOLOGY: A SAMPLE DESIGN MAY INCLUDE A NUMBER OF LEVELS OF SAMPLING, SUCH AS SAMPLING OF A FIRST-STAGE SAMPLE OF VILLAGES AND A SECOND-STAGE SAMPLE OF HOUSEHOLDS WITHIN VILLAGES. THE UNITS OF SAMPLING AT EACH LEVEL ARE CALLED SAMPLE UNITS. AT THE LOWEST LEVEL OF SAMPLING, THEY ARE CALLED ULTIMATE UNITS OR ELEMENTS. THE MEASUREMENTS ON A SAMPLE UNIT ARE CALLED OBSERVATIONS. THE MEASUREMENT ON EACH SAMPLE UNIT MAY BE VECTOR-VALUED, AS IN THE CASE OF A QUESTIONNAIRE WITH MANY QUESTIONS. THE COMPONENTS OF THE OBSERVATION VECTOR ARE CALLED ITEMS. NONRESPONSE (MISSING DATA) MAY OCCUR EITHER AT THE LEVEL OF A SAMPLE UNIT (UNIT NONRESPONSE, OBSEERVATION RESPONSE) OR AT THE LEVEL OF AN ITEM WITHIN A SAMPLE UNIT (ITEM NONRESPONSE).)
IF, FOR A SAMPLE OF SIZE n, p1i DENOTES THE PROBABILITY OF INCLUSION IN THE SAMPLE FOR THE i-th SAMPLE UNIT, WITH RESPONSE yi, THEN THE HORVITZ-THOMPSON (H-T) ESTIMATOR OF THE POPULATION TOTAL IS
![]() .
.
IF WE DEFINE wi = 1/p1i AS THE WEIGHT FOR THE i-th UNIT, THEN THIS MAY BE WRITTEN AS
![]() .
.
THE H-T ESTIMATE OF THE POPULATION MEAN IS
![]() .
.
THE EXPRESSION "PROBABILITY OF SELECTION" IS SOMETIMES USED FOR "PROBABILITY OF INCLUSION." THIS MAY LEAD TO SOME CONFUSION. THE PROBABILITY OF INCLUSION IS USUALLY THE SAME AS THE PROBABILITY OF SELECTION, BUT IT MAY BE DIFFERENT. FOR EXAMPLE, IF A SAMPLE OF INDIVIDUALS IS SELECTED FROM A LIST OF INDIVIDUALS, BUT WHENEVER SOMEONE IS SELECTED FOR THE SAMPLE HIS MARRIAGE PARTNER IS INCLUDED IN THE SAMPLE, THEN THE INCLUSION PROBABILITY DIFFERS FROM THE SELECTION PROBABILITY. (DESPITE THE AMBIGUITY, THE TERM "PROBABILITY OF SELECTION" IS OFTEN USED IN PLACE OF "PROBABILITY OF INCLUSION.")
WHEN THE SAMPLE WEIGHTS ARE DEFINED, AS ABOVE, AS THE RECIPROCALS OF THE INCLUSION PROBABILITIES, THEN IT FOLLOWS THAT
![]()
SO THAT THE EXPRESSION FOR THE ESTIMATE OF THE POPULATION MEAN MAY BE WRITTEN AS
![]() .
.
IT IS IMPORTANT TO RECOGNIZE THAT SAMPLE WEIGHTS ARE SOMETIMES NORMALIZED TO SUM TO A VALUE OTHER THAN THE SAMPLE SIZE (n), SUCH AS THE POPULATION TOTAL. IN THIS CASE, IT IS NO LONGER TRUE THAT
![]()
IN THIS CASE, THE FIRST EXPRESSION FOR THE SAMPLE MEAN (WITH DENOMINATOR n) IS NOT CORRECT, AND THE SECOND EXPRESSION MUST BE USED. (THIS USUALLY CAUSES NO PROBLEMS IN DATA ANALYSIS, SINCE STATISTICAL SOFTWARE ALWAYS USES THE LATTER EXPRESSION (SO THAT IT DOES NOT MATTER WHAT THE SAMPLE WEIGHTS ARE NORMALIZED TO).
THE PRECEDING FORMULAS ASSUME NO MISSING VALUES (NO NONRESPONSE).
IF, GIVEN SELECTION, THE PROBABILITY OF OBTAINING A RESPONSE FOR THE i-th SAMPLE UNIT IS p2i, THEN THE PROBABILITY OF INCLUSION AND RESPONSE IS
Pr(inclusion and response) = Pr(inclusion) Pr(response | inclusion) = p1i p2i,
AND THE H-T ESTIMATE OF THE POPULATION TOTAL AND MEAN IS GIVEN BY FORMULAS SIMILAR TO ABOVE, WHERE THE WEIGHT FOR THE i-th SAMPLE UNIT IS wi = 1/(p1i p2i). THE FORMULA FOR THE ESTIMATED TOTAL IS THE SAME, AND THE FORMULA FOR THE ESTIMATED MEAN IS
![]() .
.
WHERE r DENOTES THE NUMBER OF RESPONDING UNITS (AND
![]()
(WITH wi = 1/(p1i p2i)).
A PROBLEM THAT ARISES HERE IS THAT THE RESPONSE PROBABILITY (p2i) IS NOT KNOWN. THIS PROBLEM IS ADDRESSED BY ESTIMATING IT FROM DATA THAT ARE OBSERVED FOR BOTH RESPONDENTS AND NONRESPONDENTS (SUCH AS DESIGN VARIABLES OR COVARIATES THAT ARE KNOWN FOR BOTH RESPONDENTS AND NONRESPONDENTS).
THIS APPROACH IS APPLIED TO ADDRESS MISSING VALUES IN THE CASE IN WHICH AN ENTIRE OBSERVATION IS MISSING (I.E., UNIT NONRESPONSE, AS OPPOSED TO ITEM NONRESPONSE), SO THAT A SINGLE SET OF WEIGHTS IS INVOLVED FOR A DATA SET, NO MATTER HOW MANY OBSERVED VARIABLES (Y) THERE ARE.
THE WEIGHTS BASED ON THE PROBABILITIES OF INCLUSION ARE REFERRED TO AS “BASE WEIGHTS.” THE WEIGHTS BASED ON INCLUSION AND RESPONSE ARE CALLED WEIGHTS ADJUSTED FOR NONRESPONSE. OTHER ADJUSTMENTS MAY BE MADE. FOR EXAMPLE, IF A SAMPLE FRAME IS NOT PERFECT, SOME SAMPLE UNITS MAY BE DETERMINED TO BE OUT OF SCOPE, OR INELIGIBLE, AND REMOVED FROM THE SAMPLE. IN THIS CASE, WEIGHTS WOULD BE ADJUSTED FOR IN-SCOPE / ELIGIBILITY: p1i WOULD REFER TO THE PROBABILITY OF INCLUSION IN THE SAMPLE, p2i TO THE PROBABILITY OF ELIGIBILITY, GIVEN INCLUSION, AND p3i TO THE PROBABILITY OF RESPONSE, GIVEN INCLUSION AND ELIGIBILITY, SO THAT THE UNCONDITIONAL PROBABILITY OF INCLUSION IS pi = p1i p2i p3i, AND THE WEIGHT ADJUSTED FOR ELIGIBILITY AND RESPONSE WOULD BE wi = 1/pi.
ESTIMATION OF WEIGHTS
THE PRECEDING DISCUSSION DESCRIBES HOW TO APPLY WEIGHTS, ASSUMING THAT THE PROBABILITIES OF INCLUSION, ELIGIBILITY AND NONRESPONSE ARE KNOWN. IN GENERAL, THE PROBABILITIES OF INCLUSION ARE KNOWN (FROM THE SURVEY DESIGN AND SAMPLE SELECTION SPECIFICATION), BUT THE PROBABILITIES ASSOCIATED WITH ELIGIBILITY OR NONRESPONSE ARE NOT, AND MUST BE ESTIMATED FROM THE DATA.
FOR SIMPLICITY, IN WHAT FOLLOWS WE SHALL NO LONGER REFER TO ELIGIBILITY, AND DISCUSS ONLY NONRESPONSE.
IF THERE IS VERY LITTLE NONRESPONSE, IT WOULD BE DIFFICULT TO ESTIMATE A NONRESPONSE MODEL, AND THE NATURE OF THE NONRESPONSE WOULD BE GUIDED MAINLY BY JUDGMENT. IF THERE IS SUBSTANTIAL NONRESPONSE, STATISTICAL MODELING TECHNIQUES CAN BE APPLIED TO ESTIMATE A NONRESPONSE MODEL AND ESTIMATE NONRESPONSE PROBABILITIES FROM IT. APPROACHES TO ESTIMATION OF WEIGHTS INCLUDE THE FOLLOWING:
WEIGHTING-CLASS MODELS
PROPENSITY-SCORE REGRESSION MODELS
CLASSIFICATION AND REGRESSION-TREE (CART) MODELS.
THESE PROCEDURES WILL NOW BE SUMMARIZED. THE WEIGHTING-CLASS PROCEDURE IS SIMPLEST. PROPENSITY-SCORE-BASED MODELS AND CART MODELS HAVE SEVERAL ADVANTAGES OVER WEIGHTING-CLASS ESTIMATORS:
1. IF CATEGORICAL VARIABLES ARE CROSS-CLASSIFIED, MANY WEIGHTING CATEGORIES RESULT. WITH PROPENSITY-SCORE (PS) BASED AND CART-BASED MODELS, CATEGORICAL VARIABLES NEED NOT BE COMPLETELY INTERACTED.
2. PS AND CART MODELS MAY INCLUDE CONTINUOUS VARIABLES (EITHER ALONE OR WITH CATEGORICAL VARIABLES).
3. PS AND CART MODELS ARE MORE GENERAL THAN CATEGORICAL MODELS, AND FORM A SOUNDER BASIS FOR FINDING A GOOD NONRESPONSE MODEL (WHICH COULD BE A WEIGHTING-CLASS MODEL).
WEIGHTING-CLASS ESTIMATOR
DIVIDE THE SAMPLE INTO CATEGORIES (“WEIGHTING CLASSES”; "RESPONSE HOMOGENEITY GROUPS") ON THE BASIS OF VARIABLES THAT ARE KNOWN FOR BOTH RESPONDENTS AND NONRESPONDENTS (E.G., DESIGN VARIABLES). IT IS DESIRED THAT WITHIN EACH CLASS THE SAMPLE IS RANDOM (MCAR). LET ni DENOTE THE SAMPLE SIZE WITHIN EACH CATEGORY AND ri DENOTE THE NUMBER OF RESPONDENTS. THEN THE PROBABILITY OF RESPONSE FOR EACH WEIGHTING CLASS IS ri/ni, AND THE WEIGHT FOR ALL OBSERVATIONS IN THAT CLASS (NORMALIZED TO SUM TO THE TOTAL RESPONDENT SAMPLE SIZE, r) IS
![]()
WHERE ![]() .
.
DISCUSSION OF WEIGHTING-CLASS ESTIMATORS IS PRESENTED IN LITTLE AND RUBIN, IN SÄRNDAL, SWENSSON AND WRETMAN, AND IN VALLIANT, DEVER AND KREUTER. LITTLE AND RUBIN USE THE TERMINOLOGY WEIGHTING-CLASS ESTIMATOR. SÄRNDAL ET AL. USE THE TERM RESPONSE HOMOGENEITY GROUP (RHG) ESTIMATOR. THE DISCUSSION IN SÄRNDAL IS MORE DETAILED.
GUIDANCE ON FORMING WEIGHTING CLASSES
THE FOLLOWING GUIDELINES ARE SUGGESTED FOR FORMING WEIGHTING CLASSES:
1. FORM CLASSES IN WHICH THE RESPONSE PROBABILITY IS SIMILAR WITHIN EACH CLASS.
2. FORM CLASSES SUCH THAT THE MEAN-SQUARED-ERROR OF ESTIMATES IS MINIMIZED. MEAN-SQUARED-ERROR IS THE VARIANCE PLUS THE SQUARE OF THE BIAS. VARIANCE IS REDUCED BY SPECIFYING WEIGHTING CLASSES THAT ARE RELATED TO Y (THIS, FOR EXAMPLE, IS AN OBJECTIVE OF STRATIFICATION). BIAS IS REDUCED BY SPECIFYING WEIGHTING CLASSES THAT RELATE TO THE RESPONSE EVENT.
IN DECIDING ON THE WEIGHTING CLASSES, THERE IS A TRADEOFF BETWEEN PRECISION AND BIAS. A LARGE NUMBER OF WEIGHTING CLASSES MAY DECREASE BIAS BUT DECREASE PRECISION. A SMALL NUMBER OF WEIGHTING CLASSES MAY INCREASE PRECISION BUT INCREASE BIAS.
3. WEIGHTING CLASSES ARE GENERALLY BASED ON DESIGN VARIABLES, SINCE THEY ARE AVAILABLE FOR NONRESPONDENTS. (IN SINGLE-ROUND SURVEYS, THE ONLY DATA AVAILABLE FOR BOTH RESPONDENTS AND NONRESPONDENTS ARE USUALLY THE DESIGN VARIABLES. FOR PANEL-DATA (MULTI-ROUND, OR MULTI-WAVE) STUDIES, A SUBSTANTIAL AMOUNT OF DATA MA BE AVAILABLE FOR NONRESPONENTS IN THE SECOND ROUNG WHO RESPONDED IN THE FIRST ROUND.) FOR SIMPLICITY, EVEN IF WEIGHTING CLASSES ARE BASED ON MORE VARIABLES THAN THE DESIGN VARIABLES, WEIGHTING CLASSES SHOULD BE CONTAINED WITHIN THE SAMPLE DESIGN CATEGORIES.
NOTE THAT EVERY WEIGHTING CLASS MUST CONTAIN SOME SAMPLE UNITS.
A SIMPLE (AND OFTEN USED) EXAMPLE OF WEIGHTING CLASSES IS A TWO-STAGE SAMPLE DESIGN, WHERE EACH FIRST-STAGE SAMPLE UNIT IS A WEIGHT CLASS. FOR EXAMPLE, THE FIRST-STAGE SAMPLE UNITS MAY BE VILLAGES AND THE SECOND-STAGE SAMPLE UNITS HOUSEHOLDS. THE RESPONSE PROBABILITY IS CALCULATED FOR EACH ULTIMATE SAMPLE UNIT (ELEMENT, IN THIS CASE, HOUSEHOLD, AS THE PROPORTION OF HOUSEHOLDS RESPONDING IN THE VILLAGE). A POTENTIAL PROBLEM WITH THIS APPROACH IS THAT, SINCE THE WITHIN-VILLAGE SAMPLE SIZES MAY BE SMALL, THE SAMPLE WEIGHTS MAY VARY CONSIDERABLY, LEADING TO DECREASED PRECISION. A BETTER APPROACH WOULD TYPICALLY BE TO FORM LARGER WEIGHTING CLASSES (E.G., STRATA, OR REGION OF THE COUNTRY, OR URBAN/RURAL).
VARIANCE INCREASE FROM NONRESPONSE WEIGHTING
NONRESPONSE WEIGHTING INCREASES THE VARIANCE OF ESTIMATES. FOR RANDOM SAMPLING WITHIN WEIGHTING CLASSES, THE FOLLOWING FORMULA (SEE LITTLE AND RUBIN) SHOWS THE MAGNITUDE OF THIS INCREASE:
![]()
WHERE cv(wi) IS THE COEFFICIENT OF VARIATION OF THE WEIGHTS (RELATIVE STANDARD DEVIATION = STANDARD DEVIATION / MEAN). HENCE THE SQUARE OF THE COEFFICIENT OF VARIATION OF THE WEIGHTS IS A MEASURE OF THE RELATIVE INCREASE IN THE VARIANCE OF THE MEAN DUE TO WEIGHTING.
THIS FORMULA SHOWS THAT IT IS DESIRABLE, FROM THE VIEWPOINT OF KEEPING THE VARIANCE INCREASE SMALL, THAT THE VARIATION IN THE WEIGHTS NOT BE GREAT.
PROPENSITY-SCORE-BASED WEIGHTING CLASSES.
WEIGHTING CLASS ESTIMATORS ARE USED WHEN THE SET OF VARIABLES ON WHICH THEY ARE BASED IS LIMITED. IN SOME SITUATIONS, MANY VARIABLES MAY BE AVAILABLE TO CONSTRUCT A MODEL OF THE PROBABILITY OF MISSING. IN THESE SITUATIONS THE WEIGHTING-CLASS APPROACH IS NOT PRACTICAL: FORMING WEIGHT CLASSES (OR “CELLS”) BY JOINTLY “CROSSING” VARIABLE CATEGORIES RESULTS IN CELLS HAVING NONRESPONDENTS AND NO RESPONDENTS, RESULTING IN INFINITE WEIGHTS.
IN THIS CASE, THE STANDARD APPROACH IS TO USE A GENERALIZED LINEAR MODEL TO ESTIMATE A BINARY REGRESSION MODEL (TYPICALLY A LOGISTIC REGRESSION MODEL) THAT SPECIFIES THE PROBABILITY OF NON-MISSING, OR “RESPONSE PROPENSITY SCORE,” AS A FUNCTION OF THE OBSERVED VARIABLES. UNDER THE ASSUMPTION THAT THE DATA ARE MISSING AT RANDOM (MAR), IT CAN BE SHOWN THAT THE DATA WITHIN STRATA DEFINED BY THE RESPONSE PROPENSITY SCORE ARE A RANDOM SAMPLE. THE PROOF IS AS FOLLOWS:
Let Y denote a set of response (outcome) variables, M the missingness indicator, and X the set of variables on which missingness depends. Under the assumption that the data are missing at random,
Pr(M | X, Y) = Pr(M | X).
The response propensity is
p(xi) = Pr(mi = 0 | xi).
It is assumed that this is positive for all xi. Then
Pr(mi = 0 | yi, p(xi)) = E[Pr(mi = 0 | yi, xi) | yi, p(xi)]
=E[Pr(mi = 0 | xi) | yi, p(xi)] (by the MAR assumption)
= E[p(xi) | yi, p(xi)] by definition of p(xi)
= p(xi) for all xi.
Hence
Pr[M | p(X), Y] = Pr[M | p(X)]
i.e., the respondents within a stratum defined by the response propensity score are a random sample.
IN PRACTICE, THE PROPENSITY SCORE IS ESTIMATED USING A LOGISTIC REGRESSION MODEL.
THE ESTIMATED PROPENSITY
SCORES MAY BE USED IN TWO WAYS. FIRST, TO DEFINE WEIGHTING CLASSES (I.E., A
NUMBER OF STRATA IN WHICH THE PROPENSITY SCORE, AND HENCE THE WEIGHT (ITS
RECIPROCAL) IS APPROXIMATELY CONSTANT); OR SECOND, TO DEFINE THE WEIGHTS
DIRECTLY FOR EACH OBSERVATION (AS THE RECIPROCAL, ![]() ). A DISADVANTAGE OF THE LATTER METHOD IS THAT THE WEIGHTS MAY VARY
SUBSTANTIALLY (IF SOME OF THE PROPENSITY SCORES ARE QUITE SMALL), LEADING TO
LARGE VARIANCES OF THE ESTIMATORS. TO ADDRESS THIS PROBLEM, LIMITS MAY BE
PLACED ON THE RANGE OF THE WEIGHTS.
). A DISADVANTAGE OF THE LATTER METHOD IS THAT THE WEIGHTS MAY VARY
SUBSTANTIALLY (IF SOME OF THE PROPENSITY SCORES ARE QUITE SMALL), LEADING TO
LARGE VARIANCES OF THE ESTIMATORS. TO ADDRESS THIS PROBLEM, LIMITS MAY BE
PLACED ON THE RANGE OF THE WEIGHTS.
REGRESSION-TREE MODELS (CART)
ANOTHER PROCEDURE FOR ESTIMATING PROPENSITY SCORES IS TO APPLY THE CART (CLASSIFICATION AND REGRESSION TREE) APPROACH. THIS METHOD GENERALLY WORKS WELL. IT IS AN AUTOMATED PROCESS, WHEREAS THE PROPENSITY-SCORE-BASED MODEL REQUIRES MANUAL SPECIFICATION OF THE MODEL STRUCTURE.
THE PRECEDING APPROACHES PROVIDE ESTIMATES OF NONRESPONSE WEIGHTS, NOT TRUE VALUES. THEY ARE SUBJECT TO SAMPLING ERROR. THE USE OF ESTIMATED WEIGHTS MAY INTRODUCE BIASES AND INCREASE VARIANCE OVER THE LEVELS ASSOCIATED WITH THE USE OF TRUE WEIGHTS.
THE PREVIOUS EXAMPLES HAVE SHOWN HOW TO ESTIMATE WEIGHTS AT A LOW LEVEL OF COMPLICATION. MANY STATISTICAL PROGRAM PACKAGES ARE DESIGNED TO USE SAMPLE WEIGHTS. A SINGLE SET OF WEIGHTS IS INCLUDED IN THE DATA SET (DELIVERED TO THE CLIENT) AS A VARIABLE (ONE VALUE FOR EACH OBSERVATION), AND THE NAME OF THE WEIGHT VARIABLE IS SPECIFIED TO THE ANALYSIS PROCEDURE (PROGRAM). NOT ALL ANALYSIS ROUTINES CAN USE WEIGHTS, BUT MANY DO.
THE ADVANTAGE TO HAVING SAMPLE WEIGHTS AVAILABLE IS THAT UNBIASED OR REDUCED-BIAS ESTIMATES MAY BE OBTAINED WITH "BASIC" STATISTICAL SOFTWARE DESIGNED FOR USE WITH SIMPLE RANDOM SAMPLES, WITHOUT THE NEED FOR MORE ADVANCED SOFTWARE THAT PERFORMS ESTIMATION FOR COMPLEX SURVEYS. THE MAJOR DISADVANTAGE IS THAT, SINCE THESE BASIC PROGRAMS DO NOT TAKE INTO ACCOUNT THE SAMPLE DESIGN (E.G., STRATIFICATION, CLUSTERING), THEY DO NOT PROVIDE PROPER ESTIMATES OF THE STANDARD ERRORS OF THE WEIGHTED ESTIMATES. (BOOTSTRAPPING COULD BE USED, BUT IT WOULD TYPICALLY NOT BE USED IN A "BASIC" STATISTICAL SOFTWARE PROGRAM.)
THE SINGLE SET OF WEIGHTS CORRESPONDS TO UNIT NONRESPONSE, NOT ITEM NONRESPONSE. THE WEIGHTS ARE CALCULATED FOR THE ENTIRE SAMPLE (NOT FOR SUBPOPULATIONS / DOMAINS OF STUDY), TAKING INTO ACCOUNT THE SAMPLE DESIGN, ELIGIBILITY, AND NONRESPONSE. (FOR EXAMPLE, IN THE VILLAGE-HOUSEHOLD EXAMPLE MENTIONED EARLIER, THE WEIGHTS WOULD BE CALCULATED FOR EACH HOUSEHOLD. IF ALL VILLAGES RESPONDED, THE CALCULATION IS STRAIGHTFORWARD. IF VILLAGE-LEVEL NONRESPONSE OCCURRED, THE WEIGHTS WOULD STILL BE CALCULATED FOR EACH RESPONDING UNIT (HOUSEHOLD), BUT THE CALCULATION OF THE WEIGHTS WOULD BE MORE COMPLICATED, TAKING INTO ACCOUNT VILLAGE-LEVEL NONRESPONSE, NOT JUST HOUSEHOLD-LEVEL RESPONSE.)
NOTE THAT SAMPLE WEIGHTS ARE DIFFERENT FOR DIFFERENT DOMAINS OF STUDY (SUBPOPULATIONS, SUCH AS ALL MEN OR ALL WOMEN, OR SUCH AS INDIVIDUAL STRATA OF A STRATIFIED DESIGN). (THE REASON FOR THIS IS THAT THE COMPOSITION OF THE WEIGHTING CLASSES WOULD BE DIFFERENT.) THE STANDARD APPROACH IS TO CALCULATE A SINGLE SET OF WEIGHTS (I.E., A SINGLE WEIGHT VARIABLE) AND INCLUDE THEM IN THE SAMPLE DATA FILE FOR THE TOTAL RESPONDING POPULATION, NOT SEVERAL WEIGHT SETS FOR DIFFERENT SUBPOPULATIONS.)
THE SAMPLE WEIGHTS WILL BE APPROPRIATE (I.E., LEAD TO UNBIASED OR CONSISTENT ESTIMATES OF MEANS) UNDER CERTAIN ASSUMPTIONS, SUCH AS MISSING COMPLETELY AT RANDOM OR MISSING AT RANDOM. THESE ASSUMPTIONS SHOULD BE CLEARLY STATED IN THE ANALYSIS DOCUMENTATION.
FOR SURVEY DATA, THE SAMPLE DESIGN SHOULD BE TAKEN INTO ACCOUNT IN CONSTRUCTING ESTIMATES (WITH OR WITHOUT MISSING DATA). USING SAMPLE WEIGHTS ALONE, WITHOUT FULL CONSIDERATION OF THE SAMPLE DESIGN, WILL PRODUCE GOOD VALUES FOR MEANS (EXPECTED VALUES), BUT THE VARIANCES WILL NOT BE CORRECT (AND SO CONFIDENCE INTERVALS WILL NOT BE CORRECT). IF THE SAMPLE DESIGN IS CORRECTLY TAKEN INTO ACCOUNT, FORMULAS ARE AVAILABLE FOR ESTIMATING THE VARIANCES OF WEIGHTED ESTIMATES, TAKING INTO ACCOUNT THE MISSING VALUES.
TO EMPHASIZE THIS POINT, WEIGHTS ARE NOT A SUBSTITUTE FOR THE SAMPLE DESIGN. THEY CAN REDUCE BIAS BY ADJUSTING FOR NONRESPONSE AND ELIGIBILITY, BUT, BY THEMSELVES, THEY DO NOT REFLECT SAMPLE DESIGN FEATURES SUCH AS STRATIFICATION, CLUSTERING AND NONREPLACEMENT SAMPLING. THEY REFLECT SIMPLY THE PROBABILITIES OF SELECTION OF THE DESIGN, NOT THE MORE COMPLEX STRUCTURAL FEATURES. IF STATISTICAL SOFTWARE IS USED FOR DATA ANALYSIS, BOTH THE WEIGHTS AND THE SAMPLE DESIGN MUST BE SPECIFIED TO THE ANALYSIS PROCEDURE.
HANDLING OF MISSING DATA CAN BE VERY COMPLEX, COMPLICATED, AND TIME-CONSUMING. MOST DESCRIPTIVE SURVEY ANALYSIS IS CONDUCTED USING A SINGLE SET OF WEIGHTS AND ARE APPROPRIATE FOR MCAR OR MAR MISSING DATA. ANALYTICAL SURVEYS (USED TO SUPPORT IMPACT ANALYSIS) MUST ADDRESS NON-MAR SAMPLE SELECTION, AND REQUIRES SUBSTANTIALLY GREATER ANALYSIS EFFORT.
POST-STRATIFICATION AND RAKING TO KNOWN MARGINS
FOR A SAMPLE DESIGN IN WHICH THE SAMPLE INCLUSION PROBABILITIES ARE EQUAL FOR ALL UNITS, IT CAN BE SHOWN THAT THE WEIGHTING-CLASS ESTIMATOR IS
![]()
WHERE ![]() IS THE RESPONDENT MEAN IN CLASS j AND
IS THE RESPONDENT MEAN IN CLASS j AND ![]() IS THE TOTAL SAMPLE SIZE (BOTH RESPONDENTS AND NONRESPONDENTS).
IS THE TOTAL SAMPLE SIZE (BOTH RESPONDENTS AND NONRESPONDENTS).
NOTE THAT nj/n IS AN ESTIMATE OF THE PROPORTION OF THE POPULATION IN WEIGHTING CLASS j. IN SOME APPLICATIONS, THIS PROPORTION IS KNOWN, AND A BETTER ESTIMATE OF THE MEAN IS THE POST-STRATIFIED ESTIMATE:
![]()
SIMILARLY, THE PROCEDURE OF RAKING OF CROSS-TABULATIONS TO KNOWN MARGINAL TOTALS (DEMING-STEPHAN RAKING, ITERATIVE PROPORTIONAL FITTING) MAY PRODUCE BETTER ESTIMATES THAN THE WEIGHTING-CLASS ESTIMATOR.
A MORE GENERAL METHOD FOR MATCHING ESTIMATES TO KNOWN TOTALS WILL BE DISCUSSED LATER, UNDER THE HEADING "GENERALIZED REGRESSION ESTIMATORS."
ESTIMATION OF VARIANCES FOR WEIGHTED ESTIMATES
IN GENERAL, THE PROBLEM OF ESTIMATING THE VARIANCES OF WEIGHTED ESTIMATES IS DIFFICULT ANALYTICALLY. A MAJOR PROBLEM IS ASSOCIATED WITH THE FACT THAT THE WEIGHTS ARE ESTIMATES, NOT KNOWN NUMBERS. STATISTICAL PROGRAM PACKAGES THAT ALLOW FOR SPECIFICATION OF A SURVEY DESIGN AND INCORPORATION OF WEIGHTS TYPICALLY TREAT THE WEIGHTS AS KNOWN. THE APPROPRIATE PROCEDURE FOR ESTIMATING THE VARIANCES OF WEIGHTED ESTIMATES IS TO USE A RESAMPLING METHOD SUCH AS THE JACKKNIFE OR BOOTSTRAPPING.
(THIS IS DONE BY SELECTING A NUMBER OF RANDOM SUBSAMPLES FROM THE AVAILABLE SAMPLE, CALCULATING THE WEIGHTED ESTIMATE FOR EACH SUBSAMPLE, AND ESTIMATING THE VARIANCE OF THE ESTIMATOR DIRECTLY FROM THESE ESTIMATES. TYPICALLY, FOR ESTIMATION OF MEANS, THE WEIGHTED ESTIMATES WOULD BE DETERMINED USING THE SINGLE SET OF WEIGHTS FOR THE COMPLETE SAMPLE, RATHER THAN ESTIMATING WEIGHTS ANEW FOR EACH BOOTSTRAP SUBSAMPLE. THE PREFERRED METHOD IS TO RECALCULATE THE WEIGHTS ANEW FOR EACH BOOTSTRAP SAMPLE.)
SUMMARY OF WEIGHTED COMPLETE-CASE ANALYSIS
WEIGHTED COMPLETE-CASE ANALYSIS IS A STRAIGHTFORWARD AND COMMONLY USED METHOD FOR REDUCING BIAS FROM MISSING DATA. A MAJOR ADVANTAGE IS THAT THE WEIGHTS ARE THE SAME FOR ALL VARIABLES. A MAJOR DISADVANTAGE IS THAT INCOMPLETE CASES ARE DISCARDED. THIS METHOD IS MOST USEFUL WHEN COVARIATE INFORMATION IS LIMITED AND THE SAMPLE SIZE IS LARGE (SO THAT BIAS IS A MORE SERIOUS PROBLEM THAN PRECISION (VARIANCE), AND OTHER APPROACHES ARE NOT USEFUL).
6. AVAILABLE-CASE ANALYSIS
IN SITUATIONS IN WHICH THERE ARE A CONSIDERABLE NUMBER OF ITEMS IN EACH OBSERVATION, COMPLETE-CASE ANALYSIS MAY NOT BE FEASIBLE. FOR EXAMPLE, IF IN A QUESTIONNAIRE THERE ARE 20 VARIABLES THAT MAY BE MISSING, AND EACH OF THESE VARIABLES HAS A 10 PERCENT CHANCE (INDEPENDENTLY) OF BEING MISSING, THEN THE EXPECTED PROPORTION OF COMPLETE CASES (OBSERVATIONS) IS .920 = .12.
IN SUCH CASES, A PROCEDURE THAT MAY BE USED FOR AN ESTIMATE OF INTEREST IS TO USE ALL OF THE CASES FOR WHICH DATA ARE AVAILABLE TO CALCULATE THAT SPECIFIC ESTIMATE. DISADVANTAGES OF THIS APPROACH ARE THAT ESTIMATES BASED ON DIFFERENT VARIABLES (HAVING DIFFERENT MISSING VALUE PATTERNS) ARE BASED ON DIFFERENT SUBSAMPLES. THE ESTIMATES ARE HENCE NOT COMPARABLE. IF IT IS DESIRABLE TO USE WEIGHTING CLASSES (INSTEAD OF AN MCAR ASSUMPTION), THEN SOME INSTANCES OF EACH VARIABLE MUST OCCUR IN EACH WEIGHTING CLASS. ESTIMATION OF COVARIANCE MATRICES IS PROBLEMATIC, BECAUSE THERE IS NO GUARANTEE THAT AN ESTIMATED CORRELATION WOULD FALL IN THE RANGE (-1,1), OR THAT THE ESTIMATED MATRIX WILL BE POSITIVE DEFINITE (WHICH WOULD CAUSE SEVERE PROBLEMS IN REGRESSION ANALYSIS).
IN GENERAL, THE AVAILABLE-CASE APPROACH IS USEFUL ONLY IF THE MISSINGNESS PHENOMENON IS MCAR AND THE CORRELATIONS AMONG VARIABLES ARE MODEST.
7. IMPUTATION
THE MAJOR PROBLEM ASSOCIATED WITH THE COMPLETE-CASE AND AVAILABLE-CASE APPROACHES TO MISSING DATA IS THAT THEY ARE WASTEFUL OF DATA: THEY DO NOT MAKE USE OF OBSERVATIONS HAVING ANY MISSING ITEMS, EVEN IF THE ITEM OF INTEREST IS NOT MISSING.
ACCURACY OF ESTIMATES MAY BE IMPROVED BY USING METHODS THAT ARE NOT SO WASTEFUL OF DATA. THERE ARE TWO GENERAL APPROACHES TO MAKING USE OF ALL OF THE OBSERVATIONS. ONE IS TO CONSIDER THE JOINT PROBABILITY DISTRIBUTION OF ALL VARIABLES, INCLUDING THOSE RELATED TO NONRESPONSE. THAT APPROACH IS TECHNICALLY CHALLENGING, AND WILL BE CONSIDERED LATER. A SIMPLER APPROACH, WHICH IS WIDELY USED BUT NOT AS METHODOLOGICALLY SOUND, IS THE METHOD OF IMPUTATION.
IN THE METHOD OF IMPUTATION, MISSING VALUES ARE ESTIMATED FOR MISSING ITEMS, USING A VARIETY OF AD-HOC PROCEDURES.
THE MISSING VALUES ARE ESTIMATED FROM A PREDICTIVE DISTRIBUTION THAT IS ESTIMATED FROM THE OBSERVED DATA. THERE ARE TWO APPROACHES TO THE IMPUTATION METHOD. IN EXPLICIT MODELING, A FORMAL STATISTICAL MODEL IS SPECIFIED. IN IMPLICIT MODELING, A PROCEDURE IS SPECIFIED, WHICH IMPLIES AN UNDERLYING MODEL (FOR WHICH THE PROCEDURE IS APPROPRIATE).
TWO MAJOR CATEGORIES OF IMPUTATION ARE SINGLE-VALUE IMPUTATION AND MULTIPLE IMPUTATION. WE WILL NOW DISCUSS METHODS IN THESE TWO CATEGORIES.
NOTE THAT IF ALL OF THE ITEMS (VARIABLES) OF AN OBSERVATION ON A SAMPLE UNIT ARE MISSING, THE METHODS TO BE DESCRIBED ARE NOT USED (TO IMPUTE VALUES FOR ALL ITEMS). USUALLY, SUCH OBSERVATIONS (BLANK QUESTIONNAIRES, EXCEPT FOR SAMPLE-DESIGN INFORMATION) ARE DELETED FROM THE DATA SET AND WEIGHTS ARE CONSTRUCTED BASED ON THE RESPONSE RATES FOR OBSERVATIONS HAVING AT LEAST ONE RESPONDING ITEM (JUST AS THEY WERE IN THE PRECEDING SECTION, DEALING WITH WEIGHTED COMPLETE-CASE ANALYSIS). LOGICALLY (AS MENTIONED EARLIER) A DIFFERENT SET OF SAMPLE WEIGHTS SHOULD BE CONSTRUCTED FOR EACH ITEM (SINCE EACH MAY HAVE A DIFFERENT NONRESPONSE PROBABILITY AND MISSING VALUE PATTERN), BUT THIS IS NOT DONE. THE ESTIMATED RESPONSE PROBABILITY (AND THE SINGLE WEIGHT INCLUDED IN THE DATA SET) REFERS TO UNIT RESPONSE (OBSERVATION RESPONSE), NOT TO ITEM RESPONSE.
8. SINGLE-VALUE IMPUTATION
SINGLE-VALUE IMPUTATION MAY INVOLVE SPECIFICATION OF A MODEL (EXPLICIT MODELING) OR SPECIFICATION OF A PROCEDURE (IMPLICIT MODELING) WHICH IMPLIES A MODEL (FOR WHICH THE PROCEDURE IS APPROPRIATE).
FOR SINGLE-VALUE IMPUTATION, THE MAJOR CATEGORIES OF EXPLICIT MODELING ARE:
MEAN IMPUTATION (UNCONDITIONAL AND CONDITIONAL)
ADJUSTMENT CELLS
REGRESSION IMPUTATION
STOCHASTIC REGRESSION IMPUTATION.
THE MAJOR CATEGORIES OF IMPLICIT MODELING ARE:
SUBSTITUTION
HOT-DECK IMPUTATION
COLD-DECK IMPUTATION.
SINGLE IMPUTATION METHODS
UNCONDITIONAL MEAN
IN UNCONDITIONAL MEAN IMPUTATION OF A MISSING VALUE FOR AN ITEM (SAY, THE j-TH ITEM OF THE i-TH UNIT), THE MISSING VALUE IS REPLACED BY THE MEAN OF THAT ITEM FOR THE RESPONDING OBSERVATIONS (I.E., FROM THE AVAILABLE CASES FOR THAT ITEM). UNDER MCAR, THE ESTIMATED MEAN OF THE OBSERVED AND IMPUTED VALUES IS CORRECT, BUT THE SAMPLE VARIANCE IS UNDERESTIMATED BY THE FACTOR (n(j) – 1)/(n – 1), WHERE n(j) DENOTES THE NUMBER OF AVAILABLE CASES FOR THE j-TH ITEM. MEAN IMPUTATION DISTORTS THE SAMPLE DISTRIBUTION BY PLACING ALL OF THE MISSING VALUES AT THE MEAN OF THE DISTRIBUTION. AS A RESULT, ESTIMATES OF DISTRIBUTIONAL CHARACTERISTICS SUCH AS VARIANCES AND PERCENTILES ARE NOT CORRECT. ALSO, CROSSTABULATION TABLES INVOLVING THE IMPUTED ITEM ARE ALSO NOT CORRECT, BECAUSE ALL OF THE MISSING VALUES ARE PLACED AT THE MEAN VALUE. COVARIANCES ARE ALSO UNDERESTIMATED.
BECAUSE OF ALL OF THE AFOREMENTIONED PROBLEMS, MEAN IMPUTATION IS NOT RECOMMENDED.
CONDITIONAL MEAN
A SUBSTANTIAL IMPROVEMENT OVER UNCONDITIONAL-MEAN IMPUTATION IS TO IMPUTE MEANS THAT ARE CONDITIONED ON THE VALUES OF OBSERVED ITEMS. NOT ONLY DOES THIS APPROACH GENERALLY INCREASE PRECISION AND DECREASE BIAS OVER UNCONDITIONAL-MEAN IMPUTATION, BUT IT INTRODUCES DISTRIBUTIONAL VARIATION IN THE IMPUTED VALUE.
TWO METHODS FOR IMPUTING CONDITIONAL MEANS ARE ADJUSTMENT CELLS AND REGRESSION.
ADJUSTMENT CELLS
A SIMPLE METHOD OF IMPUTATION THAT INCORPORATES DISTRIBUTIONAL CHARACTERISTICS OF THE IMPUTED VALUE IS TO FORM ADJUSTMENT CLASSES BASED ON THE OBSERVED VARIABLES, AND CLASSIFY THE RESPONDENTS AND NONRESPONDENTS INTO THE CLASSES. THE ADJUSTMENT CLASSES ARE SIMILAR TO THE WEIGHTING CLASSES CONSIDERED EARLIER. THEY ARE CONSTRUCTED BY TAKING INTO ACCOUNT OBSERVED VARIABLES THAT ARE BELIEVED TO HAVE A RELATIONSHIP TO THE MISSING VARIABLE.
AS WAS THE CASE FOR THE WEIGHTING-CLASS ESTIMATOR, THE ADJUSTMENT-CLASS ESTIMATOR FOR THE MEAN IS OBTAINED BY WEIGHTING THE MEAN FOR EACH CLASS BY THE INVERSE OF THE PROPORTION OF RESPONDENTS IN EACH CLASS (I.E., BY 1/(rj/nj) WHERE rj IS THE NUMBER OF RESPONDENTS IN CLASS j):
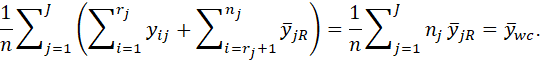
AS IN THE CASE OF WEIGHTING-CLASS ESTIMATES, AN IMPROVED ESTIMATE CAN BE OBTAINED BY POST-STRATIFICATION, IF THE POPULATION PROPORTIONS ARE KNOWN FOR EACH ADJUSTMENT CLASS.
REGRESSION IMPUTATION
THE PRECEDING METHOD OF ADJUSTMENT CELLS WORKS WELL IF THE ADJUSTMENT CELLS ARE DEFINED BY A SMALL NUMBER OF VARIABLES. IT IS PARTICULARLY USEFUL FOR LOW LEVELS OF RESPONSE, WHERE INSUFFICIENT DATA ARE AVAILABLE TO DEVELOP A MODEL USING STATISTICAL ESTIMATION PROCEDURES (BUT A REASONABLE MODEL MAY BE SPECIFIED BASED ON JUDGMENT / EXPERIENCE).
IF THE DATA SET IS LARGE AND THERE IS SUBSTANTIAL NONRESPONSE, IT MAY BE FEASIBLE TO DEVELOP A REGRESSION MODEL THAT DESCRIBES THE RELATIONSHIP OF ONE ITEM TO ANOTHER ITEM, OR TO SEVERAL OTHER ITEMS. THIS REGRESSION MODEL MAY THEN BE USED TO ESTIMATE MISSING VALUES FOR THE DEPENDENT VARIABLE.
SUPPOSE THAT Y1, ..., YK-1 ARE FULLY OBSERVED AND THAT YK IS OBSERVED FOR THE FIRST r OBSERVATIONS AND MISSING FOR THE LAST n-r OBSERVATIONS. A REGRESSION EQUATION IS CONSTRUCTED FOR YK AS A FUNCTION OF Y1, ..., YK-1. SUPPOSE THAT CASE i HAS yiK MISSING AND Yi1, ..., Yi,K-1 NOT MISSING. THE MISSING VALUE IS IMPUTED AS
![]()
WHERE ![]() IS THE INTERCEPT AND
IS THE INTERCEPT AND ![]() IS THE COEFFICIENT OF Yj IN THE REGRESSION OF YK
ON Y1, ..., YK-1.
IS THE COEFFICIENT OF Yj IN THE REGRESSION OF YK
ON Y1, ..., YK-1.
IF THE OBSERVED VARIABLES ARE INDICATOR VARIABLES FOR CATEGORIES, THE PREDICTIONS ARE ESTIMATED RESPONDENT MEANS FOR THE CATEGORIES, AND THE METHOD IS EQUIVALENT TO THE METHOD OF ADJUSTMENT CELLS. OTHERWISE, THE REGRESSION IMPUTATION APPROACH IS MORE GENERAL, AND CAN BE EXTENDED TO THE CASE OF CONTINUOUS AND CATEGORICAL VARIABLES AND VARIABLE INTERACTIONS.
BUCK'S METHOD
THE PRECEDING METHOD (REGRESSION IMPUTATION) WAS DESCRIBED FOR THE CASE OF UNIVARIATE RESPONSE, I.E., MISSING VALUES OCCUR IN A SINGLE ITEM. BUCK'S METHOD IS A GENERALIZATION OF THE REGRESSION-IMPUTATION METHOD TO THE CASE WHERE REGRESSION IMPUTATION IS DONE FOR AN ARBITRARY NUMBER OF MISSING ITEMS, EACH WITH A SEPARATE REGRESSION MODEL. WHILE THIS MAY APPEAR TO BE A FORMIDABLE UNDERTAKING, IT CAN IN FACT BE IMPLEMENTED EFFICIENTLY USING THE SWEEP OPERATOR, BASED ON ESTIMATED MEANS AND A COVARIANCE MATRIX ESTIMATED FROM COMPLETE CASES.
MEANS ESTIMATED FROM BUCK'S METHOD ARE CONSISTENT UNDER THE ASSUMPTION OF MCAR, ASSUMING THAT THE REGRESSION MODELS (SHOWN HERE AS LINEAR REGRESSION MODELS) ARE CORRECTLY SPECIFIED. THEY ARE ALSO CONSISTENT UNDER THE ASSUMPTION OF MAR, WHERE IT IS ASSUMED THAT MISSINGNESS DEPENDS ON THE REGRESSOR VARIABLES. VARIANCES AND COVARIANCES ARE UNDERESTIMATED (SINCE MISSING OBSERVATIONS ARE REPLACED BY CONDITIONAL MEANS), AND SHOULD BE ADJUSTED TO ACCOUNT FOR THIS, OR NUMERICAL METHODS (SUCH AS BOOTSTRAPPING) USED. (THE BOOTSTRAPPING IS DONE BY SELECTING A NUMBER OF SUBSAMPLES AND THEN PERFORMING THE IMPUTATION DE NOVO FOR EACH SUBSAMPLE, NOT BY USING IMPUTATIONS CALCULATED FROM THE WHOLE SAMPLE.)
IMPUTING DRAWS FROM A PREDICTIVE DISTRIBUTION
THE PRECEDING METHODS OF IMPUTING MEANS HAS THE DISADVANTAGE THAT IT UNDERESTIMATES VARIANCES AND COVARIANCES. FACTORS MAY BE APPLIED TO CORRECT FOR THE UNDERESTIMATION. AN ALTERNATIVE APPROACH IS TO IMPUTE VALUES USING A MEAN PLUS A DRAW FROM A PREDICTIVE DISTRIBUTION.
STOCHASTIC REGRESSION IMPUTATION
IN THE CASE OF REGRESSION IMPUTATION, THE MISSING ITEM IS ESTIMATED AS THE REGRESSION ESTIMATE PLUS A DRAW OF A RANDOM NUMBER FROM THE DISTRIBUTION OF THE MODEL RESIDUALS. THAT IS, THE IMPUTATION IS A CONDITIONAL DRAW:
![]()
WHERE ziK IS A
RANDOM NORMAL VARIATE WITH MEAN 0 AND VARIANCE EQUAL TO ![]() , THE VARIANCE OF THE MODEL
RESIDUALS.
, THE VARIANCE OF THE MODEL
RESIDUALS.
IMPLICIT MODELS
THE PRECEDING METHODS OF IMPUTATION INVOLVE ESTIMATION OF MODELS FROM WHICH IMPUTED VALUES ARE ESTIMATED. SEVERAL IMPUTATION METHODS ARE SPECIFIED BY MEANS OF PROCEDURES, OR ALGORITHMS, WITHOUT SPECIFYING A MODEL. THESE METHODS INCLUDE SUBSTITUTION, THE HOT-DECK PROCEDURE AND THE COLD-DECK PROCEDURE. THESE METHODS ARE RANDOM-DRAW METHODS.
SUBSTITUTION
IN SAMPLE SURVEYS, NONRESPONSE INVARIABLY OCCURS. USUALLY, THE SURVEY FIELD ORGANIZATION IS UNDER CONTRACT TO DELIVER A SAMPLE OF SPECIFIED SIZE. TO ACCOMMODATE NONRESPONSE, THE CONTRACTOR MUST EITHER SELECT A LARGER SAMPLE THAN IS ULTIMATELY NEEDED. A PROBLEM WITH THIS IS THAT THE FINAL SAMPLE SIZE IS VARIABLE, AND, IF THE ANTICIPATED NONRESPONSE WAS NOT ESTIMATED WELL, THE FINAL SAMPLE MAY BE SUBSTANTIALLY TOO SMALL OR TOO LARGE.
A COMMON METHOD USED IN SAMPLE SURVEY, WHEN A MISSING UNIT IS ENCOUNTERED, IS TO SUBSTITUTE A SIMILAR UNIT, E.G., FROM THE SAME SAMPLE CLUSTER OR STRATUM. FOR EXAMPLE, IF NO ONE IS AT HOME AT A SELECTED HOUSEHOLD, A REPLACEMENT HOUSEHOLD MAY BE SAMPLED FROM THE SAME BLOCK OR VILLAGE. THE BIAS ASSOCIATED WITH SUBSTITUTION IS KEPT LOW BY REPLACING NONRESPONDENTS AT RANDOM FROM A POPULATION SIMILAR TO THE MISSING UNIT (E.G., FROM THE SAME BLOCK OR VILLAGE). (REPLACEMENT PROCEDURES SHOULD BE DESCRIBED IN DETAIL FOR THE FIELD PERSONNEL.)
HOT-DECK IMPUTATION
IN HOT-DECK IMPUTATION, MISSING VALUES ARE SELECTED FROM SIMILAR RESPONDING UNITS. SIMILARITY IS DETERMINED BY MATCHING ON VARIABLES THAT ARE AVAILABLE BOTH FOR THE MISSING UNIT AND A NONMISSING UNIT.
IF SEVERAL ITEMS ARE MISSING, IT IS BETTER TO IMPUTE THEM JOINTLY, RATHER THAN INDEPENDENTLY (SO THAT ASSOCIATIONS AMONG MISSING ITEMS (CHARACTERISTICS OF THE JOINT DISTRIBUTION) ARE PRESERVED).
COLD-DECK IMPUTATION
IN COLD-DECK IMPUTATION, MISSING VALUES ARE SELECTED FROM SIMILAR UNITS IN A DIFFERENT SAMPLE, SUCH AS DATA FROM A PREVIOUS CENSUS OR PANEL SURVEY.
ESTIMATION OF IMPUTATION UNCERTAINTY (ADJUSTMENTS, ULTIMATE CLUSTERS, RESAMPLING (JACKKNIFE, BOOTSTRAP), MULTIPLE IMPUTATION)
THE MISSING-DATA IMPUTATION METHODS DESCRIBED ABOVE PROVIDE CONSISTENT ESTIMATES OF MEANS UNDER CERTAIN ASSUMPTIONS, BUT THE ESTIMATES OF UNCERTAINTY (VARIANCES, COVARIANCES) ARE OFTEN NOT CORRECT. METHODS FOR ADDRESSING THIS PROBLEM INCLUDE THE FOLLOWING:
ADJUSTMENT FORMULAS
ESTIMATION OF VARIANCES FROM ULTIMATE CLUSTERS
RESAMPLING METHODS (JACKKNIFE, BOOTSTRAP)
MULTIPLE IMPUTATION.
ADJUSTMENT FORMULAS
EXAMPLES OF ADJUSTMENT FORMULAS TO CORRECT SAMPLE VARIANCES AND COVARIANCES WERE MENTIONED EARLIER. THESE PROCEDURES ARE USEFUL WHEN IT CAN BE ASSUMED THAT, WITHIN A WEIGHTING CLASS OR ADJUSTMENT CELL, MISSINGNESS IS MCAR.
ULTIMATE CLUSTERS
IN MOST SAMPLE SURVEYS, NONRESPONSE OCCURS AT A LOW LEVEL OF SAMPLING, SUCH AS THE HOUSEHOLD, OR, IN SOME CASES, THE VILLAGE. IF NO NONRESPONSE OCCURS AT A PARTICULAR LEVEL OF SAMPLING UNITS, THEN IT MAY BE POSSIBLE TO ESTIMATE VARIANCES FROM THOSE UNITS, IF THE IMPUTATION METHODS USED AT A LOWER LEVEL OF SAMPLING ARE UNBIASED. LITTLE AND RUBIN DISCUSS THIS PROCEDURE.
RESAMPLING METHODS (JACKKNIFE, BOOTSTRAP)
VARIANCES OF ESTIMATORS MAY BE ESTIMATED BY SELECTING RANDOM SUBSAMPLES FROM THE OBSERVED DATA, CALCULATING THE ESTIMATE FOR EACH SUBSAMPLE, PERFORMING THIS OPERATION A NUMBER OF TIMES (INDEPENDENTLY), AND CALCULATING THE VARIANCE OF THE ESTIMATOR FROM THE ESTIMATES FOR THE SAMPLE OF SUBSAMPLES
TO APPLY THIS METHOD TO IMPUTED DATA, THE BOOTSTRAP SAMPLE IS SELECTED FROM THE OBSERVED (UNIMPUTED) DATA, THE IMPUTATION PROCEDURE IS APPLIED TO EACH BOOTSTRAP SAMPLE, THE ESTIMATES OF INTEREST ARE CALCULATED FROM THE IMPUTED DATA, AND THE VARIANCE OF THE ESTIMATE IS CALCULATED FROM THE SAMPLE THUS OBTAINED.
BOOTSTRAP CAPABILITY IS INCLUDED IN ALL MAJOR STATISTICAL SOFTWARE PACKAGES.
9. MULTIPLE IMPUTATION
MULTIPLE IMPUTATION IS THE PROCEDURE OF CALCULATING A NUMBER OF IMPUTED VALUES, SAMPLED FROM AN APPROPRIATE CONDITIONAL DISTRIBUTION, FOR EACH MISSING VALUE. AN ESTIMATE OF INTEREST IS THEN CALCULATED USING THE FIRST IMPUTED VALUE FOR EACH MISSING ITEM, THEN THE SECOND, AND SO ON.
MULTIPLE IMPUTATION IS SIMILAR TO RESAMPLING, EXCEPT THAT A COMPLETE DATA SET IS CONSTRUCTED WITH A SMALL NUMBER OF MULTIPLE IMPUTATIONS (E.G., 10 FOR EACH MISSING ITEM). THE IMPUTED VALUES ARE STORED IN THE DATA SET, AVAILABLE FOR USE BY FUTURE USERS. WITH RESAMPLING, THE RESAMPLED VALUES ARE NOT STORED. FOR EXAMPLE, A SAMPLE OF 200 BOOTSTRAP SAMPLES MAY BE SELECTED AND THE VARIANCE OF INTEREST ESTIMATED. THE USE OF BOOTSTRAPPING REQUIRES ACCESS TO A STATISTICAL SOFTWARE PACKAGE THAT SUPPORTS BOOTSTRAPPING. WITH MULTIPLE IMPUTATION, THE DATA ANALYST CAN ANALYZE THE DATA USING COMPLETE-DATA ALGORITHMS, AND THEN ESTIMATE THE VARIANCE OVER THE SAMPLE OF RESULTS FROM THE MULTIPLE IMPUTATIONS.
MULTIPLE IMPUTATION WAS OF GREATER INTEREST A NUMBER OF YEARS AGO, BEFORE RESAMPLING WAS COMMONLY AVAILABLE IN STATISTICAL SOFTWARE PACKAGES.
LITTLE AND RUBIN COMPARE MULTIPLE IMPUTATION TO RESAMPLING (PP. 89-91 OP. CIT.).
TO IMPLEMENT THE PROCEDURES DESCRIBED ABOVE FOR HANDLING MISSING DATA, THE STANDARD APPROACH IS TO CONSTRUCT A "COMMAND" FILE IN A STATISTICAL SOFTWARE PACKAGE (SUCH AS STATA), AND PROGRAM ALL OF THE STEPS DESIRED. THE COMMAND FILE IS SAVED. IF IT IS DESIRED TO MODIFY THE ANALYSIS AT ANY POINT, APPROPRIATE MODIFICATIONS ARE MADE TO THE COMMAND FILE, AND IT IS RE-EXECUTED. WITH THIS APPROACH, NO IMPUTED VALUES ARE STORED IN THE DATA SET.
10. CALIBRATION WEIGHTING (GENERALIZED REGRESSION ESTIMATES, GREG)
TWO METHODS FOR ADJUSTING SURVEY ESTIMATES SO THAT THEY MATCH MARGINAL DISTRIBUTIONS OF KNOWN POPULATION TOTALS WERE MENTIONED EARLIER (POSTSTRATIFICATION AND DEMING-STEPHAN RAKING). OTHER METHODS INCLUDE RATIO AND REGRESSION ESTIMATORS FROM STANDARD SAMPLE SURVEY METHODOLOGY. A GENERAL METHOD FOR MATCHING KNOWN TOTALS IS GENERALIZED REGRESSION ESTIMATION OR GREG.
SINCE GENERALIZED REGRESSION ESTIMATION IS NOT DISCUSSED IN MANY BOOKS ON SAMPLE SURVEY, WE PROVIDE A NUMBER OF REFERENCES TO IT HERE:
SÄRNDAL, CARL-ERIK, BENGT SWENSSON AND JAN WRETMAN, MODEL ASSISTED SURVEY SAMPLING, SPRINGER, 1992
VALLIANT, RICHARD, JILL A. DEVER AND FRAUKE KREUTER, PRACTICAL TOOLS FOR DESIGNING AND WEIGHTING SURVEY SAMPLES, SPRINGER, 2013
RAO, J. N. K, SMALL AREA ESTIMATION, WILEY, 2003
LOHR, SHARON L., SAMPLING: DESIGN AND ANALYSIS, DUXBURY PRESS, 1999.
THE MOST DETAILED DESCRIPTION OF THE PROCEDURE IS PRESENTED IN THE FIRST REFERENCE (SÄRNDAL ET AL.). HERE, WE FOLLOW THE PRESENTATION OF VALLIANT ET AL.
LET
![]()
BE THE ESTIMATOR OF THE POPULATION TOTAL BASED ON THE INPUT WEIGHTS (I.E., WEIGHTS THAT ACCOUNT FOR THE SAMPLE DESIGN, ELIGIBILITY AND NONRESPONSE). THE INDEX s REFERS TO THE SAMPLE. LET
![]()
DENOTE THE VECTOR OF POPULATION TOTALS OF p AUXILIARY VARIABLES.
LET
![]()
DENOTE THE TOTALS OF THE AUXILIARY VARIABLES BASED ON THE di WEIGHTS, WHERE xi DENOTES THE VECTOR OF AUXILIARY VARIABLES FOR THE i-th SAMPLE UNIT.
LET D = diag(di) DENOTE THE n x n DIAGONAL MATRIX OF INPUT WEIGHTS.
LET
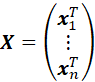
DENOTE THE n x p MATRIX OF AUXILIARY VARIABLES FOR THE n SAMPLE UNITS,
y = (y1,...,yn)T BE THE VECTOR OF y's (RESPONSE VARIABLES) FOR THE SAMPLE UNITS, AND V = DIAG (vi) BE AN n x n DIAGONAL MATRIX OF VALUES ASSOCIATE WITH A LINEAR (REGRESSION) MODEL.
THEN THE GENERALIZED REGRESSION (GREG) ESTIMATOR OF THE POPULATION TOTAL FOR y IS
![]()
THE ESTIMATED TOTAL FOR A y IS CALCULATED AS
![]()
WHERE wi = digi. THE TERM IN BRACKETS IS CALLED A g-WEIGHT OR CALIBRATION ADJUSTMENT (OR CALIBRATION FACTOR OR CALIBRATION WEIGHT). THE WEIGHTS wi DO NOT DEPEND ON ANY SAMPLE DATA (y's), JUST ON DESIGN VARIABLES AND AUXILIARY VARIABLES), SO THAT THE SAME WEIGHTS MAY BE USED FOR ANY ANALYSIS VARIABLE (y).
ALTHOUGH THE PRECEDING DISCUSSION REFERS TO ESTIMATION OF TOTALS, THE SAME WEIGHTS ARE USED TO ESTIMATE OTHER QUANTITIES. FOR EXAMPLE, THE ESTIMATED POPULATION MEAN IS
![]()
THE VECTOR ![]() IS AN ESTIMATOR OF THE SLOPE IN THE MODEL
IS AN ESTIMATOR OF THE SLOPE IN THE MODEL
![]()
WHERE THE єi
HAVE MEAN ZERO AND VARIANCE vi. IN THE CASE OF SIMPLE RANDOM
SAMPLING WITH REPLACEMENT AND BASE WEIGHTS (I.E., THE INPUT WEIGHTS REFLECT THE
DESIGN ONLY, NOT OTHER FACTORS SUCH AS NONRESPONSE), ![]() REDUCES TO (XTX)-1XTy,
THE USUAL EXPRESSION FOR A REGRESSION-MODEL ESTIMATE.
REDUCES TO (XTX)-1XTy,
THE USUAL EXPRESSION FOR A REGRESSION-MODEL ESTIMATE.
IF THE SAMPLE FRAME COVERS
THE ENTIRE POPULATION OF INTEREST, THE GREG ESTIMATOR IS APPROXIMATELY UNBIASED
IN REPEATED SAMPLING, AND ![]() IS A CONSISTENT ESTIMATE OF THE POPULATION TOTAL.
IS A CONSISTENT ESTIMATE OF THE POPULATION TOTAL.
THE GREG INCLUDES SIMPLER (FAMILIAR) METHODS, SUCH AS (ONE-VARIABLE) RATIO AND REGRESSION ESTIMATES AND POST-STRATIFICATION.
11. LIKELIHOOD-BASED PROCEDURES
WHILE MANY OF THE PROCEDURES DESCRIBED ABOVE ARE REASONABLE, BASED IN THEORY, AND PRODUCE GOOD RESULTS, THEY ARE CLASSIFIED AS "AD-HOC" SINCE THEY ARE NOT BASED ON A COMPREHENSIVE (COMPLETE, DETAILED) MODEL OF THE OBSERVED DATA. THIS SECTION DESCRIBES MISSING-DATA APPROACHES THAT ARE BASED ON THE JOINT PROBABILITY DISTRIBUTION FUNCTION OF THE OBSERVED DATA, TAKING INTO ACCOUNT BOTH THE OUTCOME OF OBSERVED DATA AND THE MISSING-DATA PHENOMENON, CONSIDERED TOGETHER.
THE METHODS DISCUSSED IN THIS SECTION INVOLVE THE LIKELIHOOD-BASED METHODS OF MAXIMUM-LIKELIHOOD ESTIMATION AND BAYESIAN ESTIMATION. A DETAILED DESCRIPTION OF THESE METHODS IS PRESENTED IN A SEPARATE PRESENTATION ("REVIEW OF STATISTICAL INFERENCE (REVIEW OF THEORY NEDED AS BACKGROUND FOR OTHER COURSES)"). THIS PRESENTATION WILL DISCUSS GENERAL CONCEPTS FOR THESE TOPICS, AT A LOW LEVEL OF DETAIL.
THE LIKELIHOOD FUNCTION OF A SAMPLE IS THE JOINT PROBABILITY DISTRIBUTION FUNCTION OF THE SAMPLE, CONSIDERED AS A FUNCTION OF THE PARAMETERS GIVEN THE SAMPLE, INSTEAD OF AS A FUNCTION OF THE SAMPLE GIVEN THE PARAMETERS.
THAT IS, IF f(Y|θ) IS THE PROBABILITY DENSITY FUNCTION OF THE RANDOM VARIABLE OF INTEREST, THEN A LIKELIHOOD FUNCTION IS ANY FUNCTION OF θ PROPORTIONAL TO f(Y|θ). MANY DISTRIBUTIONS OF INTEREST INVOLVE EXPONENTIAL FUNCTIONS, AND IT IS GENERALLY MORE CONVENIENT TO WORK WITH THE LOGARITHM OF THE LIKELIHOOD FUNCTION.
EXAMPLE (NORMAL DISTRIBUTION):
THE DENSITY FUNCTION OF THE A (SCALAR) RANDOM VARIABLE HAVING A NORMAL DISTRIBUTION WITH MEAN μ AND VARIANCE σ2 IS
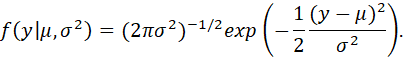
THE LIKELIHOOD FUNCTION IS HENCE
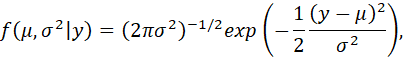
AND THE LOG-LIKELIHOOD FUNCTION IS
![]()
(THE ADDITIVE CONSTANT ln(2π) MAY BE DROPPED BECAUSE THE LIKELIHOOD FUNCTION IS ANY FUNCTION PROPORTIONAL TO THE DENSITY FUNCTION.)
FOR A SAMPLE Y = (y1,...,yn)' OF INDEPENDENT OBSERVATIONS DRAWN FROM THE SAME NORMAL DISTRIBUTION, THE JOINT PROBABILITY DENSITY FUNCTION IS
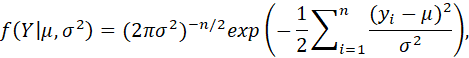
AND THE LOG-LIKELIHOOD FUNCTION IS
![]()
MAXIMUM LIKELIHOOD ESTIMATORS OF THE PARAMETERS (μ,σ2) ARE THE VALUES THAT MAXIMIZE THE LIKEIHOOD FUNCTION OR LOG-LIKELIHOOD FUNCTION).
THE PRECEDING FORMULAS REFER TO THE CASE IN WHICH THERE ARE NO MISSING DATA. IF DATA MAY BE MISSING, THE MISSINGNESS PHENOMENON MUST BE REPRESENTED IN THE JOINT PROBABILITY DENSITY FUNCTION.
SUPPOSE THAT Y = (yij) IS AN n x k MATRIX OF OBSERVATIONS MEASURED FOR k VARIABLES. LET Mij DENOTE A MISSING-VALUE INDICATOR, THAT TAKES THE VALUE 1 IF AN OBSERVATION COMPONENT IS MISSING AND 0 IF IT IS OBSERVED:
![]()
THE FULL MODEL IS SPECIFIED BY THE JOINT PROBABILITY DISTRIBUTION OF M AND Y:
![]()
WHERE THE PARAMETER ψ IDENTIFIES THE DISTRIBUTION OF THE MISSING-DATA MECHANISM.
THERE ARE TWO GENERAL APPROACHES TO THE PROBLEM OF ADDRESSING MISSING DATA, DEPENDING ON HOW THE PRECEDING JOINT DISTRIBUTION IS HANDLED.
WITH THE FIRST APPROACH, THE JOINT DISTRIBUTION IS FACTORED (USING THE PROPERTIES OF CONDITIONAL PROBABILITY) AS FOLLOWS:
![]()
IF THE PARAMETER SPACES FOR θ AND ψ ARE DISTINCT (I.E., THE DISTRIBUTION f(Y|θ,ψ) IS f(Y|θ) AND THE DISTRIBUTION f(M|θ,ψ) IS f(M|ψ)), THEN THE PRECEDING MAY BE WRITTEN AS
![]()
THE FULL RANDOM VARIABLE Y MAY BE PARTITIONED INTO TWO PARTS: THE OBSERVED PART, Yobs, AND THE MISSING PART, Ymis, AS Y = (Yobs, Ymis). THE DISTRIBUTION OF THE OBSERVED DATA IS OBTAINED BY INTEGRATING Ymis OUT OF THE JOINT DENSITY:
![]()
IF THE MISSING-DATA MECHANISM DOES NOT DEPEND ON THE MISSING VALUES, Ymis, (THAT IS, IF
![]()
THEN THE PRECEDING REDUCES TO
![]()
BUT
![]()
IS SIMPLY THE MARGINAL DISTRIBUTION OF Yobs, f(Yobs)|θ), IGNORING THE MISSING-DATA MECHANISM. SO UNDER THE CONDITION THAT THE MISSING-DATA MECHANISM DOES NOT DEPEND ON THE MISSING VALUES, THE PRECEDING REDUCES TO
![]()
THE CONDITION THAT THE MISSING-DATA MECHANISM DOES NOT DEPEND ON Ymis WAS PREVIOUSLY CALLED "MISSING AT RANDOM" OR "MAR". THAT IS, THE CONDITION OF MAR IS EQUIVALENT TO THE CONDITION THAT THE MARGINAL DISTRIBUTION OF Y IS EQUAL TO THE MARGINAL DISTRIBUTION OF Y IGNORING THE MISSING-DATA MECHANISM. FOR THIS REASON, THIS CONDITION OF MAR IS ALSO CALLED "IGNORABILITY" (I.E., IGNORABILITY OF THE MISSING-DATA MECHANISM).
TO SUMMARIZE, THE CONDITION OF IGNORABILITY IS THAT THE MISSING DATA ARE MISSING AT RANDOM (MAR) AND THE PARAMETERS θ AND ψ ARE DISTINCT (IN THE SENSE THAT THE JOINT PARAMETER SPACE OF (θ,ψ) IS THE PRODUCT OF THE PARAMETER SPACES OF θ AND ψ).
THE IMPORTANCE OF THE PRECEDING RESULT IS THAT IF THE MISSING-DATA MECHANISM IS IGNORABLE, THEN THE JOINT LIKELIHOOD FUNCTION OF THE OBSERVED MEASUREMENTS AND THE MISSING-DATA EVENTS IS PROPORTIONAL TO THE LIKELIHOOD FUNCTION OF THE OBSERVED MEASUREMENT (SINCE THE FACTOR
![]()
DOES NOT INVOLVE θ). THIS MEANS THAT MAXIMUM-LIKELIHOOD ESTIMATORS OF θ MAY BE OBTAINED SIMPLY BY MAXIMIZING THE LIKELIHOOD FUNCTION OF THE OBSERVED DATA, IGNORING THE MISSING-DATA MECHANISM.
SIMILAR RESULTS CAN BE OBTAINED FOR BAYESIAN ESTIMATION. THESE ARE DISCUSSED IN LITTLE AND RUBIN, AND WILL NOT BE DISCUSSED HERE. THE CONDITION OF IGNORABILITY IS THAT THE MISSING DATA ARE MAR AND THAT THE JOINT PRIOR DISTRIBUTION OF θ AND ψ CAN BE FACTORED: p(θ,ψ) = p(θ)p(ψ).
ESTIMATION OF PARAMETERS
ANALYTIC METHODS
JUST BECAUSE INFERENCE CAN BE DONE IGNORING THE MISSING-DATA MECHANISM DOES NOT MEAN THAT THE ESTIMATION PROBLEM IS SIMPLE. IT IS, IN FACT, QUITE COMPLICATED, BECAUSE THE JOINT DISTRIBUTION FUNCTION IS COMPRISED OF FACTORS (ONE FOR EACH OBSERVATION) THAT MAY HAVE DIFFERENT FUNCTIONAL FORMS, DEPENDING ON THE MISSING-DATA PATTERN. BECAUSE OF THIS, THE STANDARD PROCEDURE OF DIFFERENTIATING WITH RESPECT TO THE PARAMETERS AND SETTING THE DERIVATIVES EQUAL TO ZERO RARELY WORKS.
LITTLE AND RUBIN DISCUSS SOME HIGHLY STRUCTURED SITUATIONS IN WHICH ANALYTICAL PROCEDURES MAY BE APPLIED. EVEN THOSE USUALLY REQUIRE A LOT OF NUMERICAL PROCESSING, SUCH AS USE OF THE SWEEP OPERATOR.
NUMERICAL METHODS
THE STANDARD PROCEDURE FOR HANDLING MISSING DATA, EVEN IN THE CASE OF MAR, IS TO EMPLOY NUMERICAL METHODS. THESE INCLUDE THE EXPECTATION-MAXIMIZATION (EM) ALGORITHM AND EXTENSIONS, THE NEWTON-RAPHSON METHOD, AND ITERATIVE PROPORTIONAL FITTING (FOR CONTINGENCY TABLES).
BAYESIAN ESTIMATION
THE SITUATION IS SIMILAR FOR BAYESIAN ESTIMATION. IN ADDITION TO THE EM ALGORITHM AND EXTENSIONS, THE GIBBS SAMPLER IS USED TO DETERMINE ESTIMATION SOLUTIONS BY NUMERICAL METHODS.
(FROM WIKIPEDIA: "In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled.
"Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inference such as the expectation-maximization algorithm (EM).
"As with other MCMC algorithms, Gibbs sampling generates a Markov chain of samples, each of which is correlated with nearby samples. As a result, care must be taken if independent samples are desired (typically by thinning the resulting chain of samples by only taking every nth value, e.g. every 100th value). In addition, samples from the beginning of the chain (the burn-in period) may not accurately represent the desired distribution.")
13. NONIGNORABLE MISSING DATA
THE PRECEDING SECTION ADDRESSED THE SITUATION IN WHICH MISSINGNESS DID NOT DEPEND ON THE MISSING DATA, THAT IS, MAR OR IGNORABILITY OF THE MISSING-DATA MECHANISM. WITH THAT APPROACH, THE MISSING DATA Ymis COULD BE INTEGRATED OUT OF THE JOINT DENSITY OF THE MEASURED DATA (Y = (Yobs, Ymis)) AND THE MISSING-DATA INDICATOR VARIABLE (M).
IF THE CONDITION OF MAR (IGNORABILITY) DOES NOT HOLD, THEN ESTIMATION MUST BE BASED ON THE FULL JOINT LIKELIHOOD FUNCTION, INVOLVING BOTH THE MEASURED VARIABLES AND THE MISSINGNESS INDICATOR. WHILE THE ESTIMATION APPROACHES ARE THE SAME AS THOSE JUST DESCRIBED (E.G., EM, NEWTON-RAPHSON, GIBBS SAMPLING), THE SITUATION IS COMPLICATED SUBSTANTIALLY BY THE NEED TO MODEL THE MISSING-DATA MECHANISM.
THERE ARE TWO BASIC APPROACHES TO DOING THIS, CALLED SELECTION MODELS AND PATTERN MODELS. THESE WILL NOW BE DESCRIBED BRIEFLY. WE CONSIDER ONLY THE CASE OF SAMPLES IN WHICH THE SAMPLE COMPONENTS ARE INDEPENDENT.
IN THE PRECEDING SECTION, DEALING WITH MAR, THE JOINT DENSITY FUNCTION WAS FACTORED AS
![]()
WHERE THE FIRST FACTOR ON THE RIGHT-HAND SIDE IS THE DISTRIBUTION OF Y IN THE POPULATION, THE SECOND FACTOR IS THE DISTRIBUTION OF THE INCIDENCE OF MISSING DATA CONDITIONAL ON Y, AND θ AND ψ ARE DISTINCT. THE PRECEDING FACTORIZATION GIVES RISE TO AN APPROACH CALLED SELECTION MODELS.
AN ALTERNATIVE FACTORIZATION IS
![]()
THIS FACTORIZATION GIVES RISE TO AN APPROACH CALLED PATTERN-MIXTURE MODELS.
FOR A SAMPLE OF OBSERVATIONS, THE JOINT DENSITY OF THE OBSERVED DATA AND THE MISSING-DATA INDICATOR IS
![]()
THIS FACTORIZATION REVEALS A FUNDAMENTAL PROBLEM, NAMELY, THAT THERE IS NO INFORMATION FROM THE SAMPLE ON WHICH TO ESTIMATE THE SECOND PRODUCT (SINCE ALL OF THE DATA ARE MISSING FOR THAT FACTOR).
UNLIKE THE CASE OF IGNORABILITY, THERE IS NO WAY TO INTEGRATE THE MISSING DATA OUT OF THE JOINT DENSITY, SO THAT ESTIMATION MAY BE BASED SOLELY ON THE OBSERVED DATA.
THIS FUNDAMENTAL PROBLEM IS NOT SO APPARENT FROM THE SELECTION-MODEL FACTORIZATION, BUT IT IS NEVERTHELESS TRUE.
ONE WAY OUT OF THIS DILEMMA IS TO INCORPORATE RESTRICTIONS ON THE MODEL, THAT ESTABLISH RELATIONSHIPS BETWEEN THE NONRESPONDENTS AND THE RESPONDENTS. LITTLE AND RUBIN PRESENT SOME EXAMPLES OF THIS. THIS IS ANALOGOUS TO THE METHOD OF INTRODUCING A CORRELATION BETWEEN THE SELECTION MODEL AND THE OUTCOME MODEL IN AN ECONOMETRIC (HECKMAN) SELECTION MODEL.
ANOTHER APPROACH IS TO MAXIMIZE THE FULL LIKELIHOOD FUNCTION. TO DO SO, IT IS NECESSARY TO SPECIFY A MODEL FORM FOR THE MISSING-DATA MECHANISM (JUST AS IS DONE FOR THE MEASURED VARIABLES). IN GENERAL, THE MODELING PROBLEM IS DIFFICULT, BECAUSE IT IS OFTEN NOT CLEAR WHAT VARIABLES AFFECT NONRESPONSE, AND THE SAMPLE OF NONRESPONDENTS MAY NOT BE VERY LARGE. USUALLY, A MORE SATISFACTORY SOLUTION IS TO USE A SAMPLE DESIGN, SUCH AS A PANEL SURVEY, IN WHICH THE VARIABLES THAT AFFECT SELECTION ARE TIME-INVARIANT (SUCH AS PERSONALITY CHARACTERISTICS), AND MAY BE REMOVED FROM CONSIDERATION BY DIFFERENCING (I.E., A "FIXED-EFFECTS" TRANSFORMATION). THIS APPROACH IS DISCUSSED IN DETAIL IN ANOTHER PRESENTATION.
14. EXTREME VALUES
A COMMON PROBLEM IN DATA ANALYSIS IS THAT OF DECIDING WHETHER AN UNUSUAL VALUE SHOULD BE DISCARDED, BECAUSE IT APPEARS TO BE ERRONEOUS. SUCH VALUES ARE CALLED EXTREME VALUES OR OUTLIERS. THIS ISSUE IS INCLUDED IN THIS PRESENTATION ON MISSING DATA BECAUSE IF A VALUE IS DISCARDED, IT BECOMES MISSING, AND FALLS WITHIN THE PURVIEW OF THIS PRESENTATION.
THE STANDARD APPROACH FOR IDENTIFICATION OF OUTLIERS IS TO POSIT A DISTRIBUTION FOR A VARIABLE OF INTEREST AND TO CLASSIFY AS OUTLIERS THOSE OBSERVATIONS FOR WHICH THE PROBABILITY OF OBTAINING THEIR VALUE OR A MORE EXTREME ONE IS VERY SMALL.
SOME OF THE TESTS FOR OUTLIERS INCLUDE:
THE MODIFIED THOMPSON TAU TEST
GRUBB'S TEST
DIXON'S Q TEST
MAHALANOBIS DISTANCE
INFLUENCE AND LEVERAGE MEASURES, SUCH AS COOK'S D.
THESE AND OTHER TESTS ARE INCLUDED IN STATISTICAL SOFTWARE PACKAGES, AND WILL NOT BE DISCUSSED HERE.
WHEN A DECISION IS MADE TO DISCARD THE VALUE OF AN ITEM BECAUSE IT IS DECIDED THAT IT IS IN ERROR, THEN THAT ITEM BECOMES MISSING, AND IT IS TREATED IN ACCORDANCE WITH THE PROCEDURES DESCRIBED IN THIS PRESENTATION.
FndID(214)
FndTitle(MISSING DATA, WEIGHTING AND EXTREME VALUES: LECTURE NOTES)
FndDescription(MISSING DATA, WEIGHTING AND EXTREME VALUES: LECTURE NOTES)
FndKeywords(statistical methods; monitoring and evaluation; statistics course; short course; sample survey; causal inference; statistical design and analysis; sample size determination; missing data; weighting; extreme values)