STATISTICAL DESIGN AND ANALYSIS IN EVALUATION: LECTURE NOTES

These notes are intended to accompany a lecture, using a board or projector to augment the oral presentation. They have been prepared so that the student may listen to the presentation without having to take notes.

The lecture may be accompanied by examples and handouts, which are not included in these notes.

The course may also include in-class student exercises.

The course may be covered in two six-hour days (three hours in morning, three hours in afternoon), or in four half days (three hours per day). The split-up sessions are intended to accommodate clients whose employees would find it inconvenient or impractical to allocate an entire day, or three days in sequence, to a course.

The course is intended for any class size, but a smaller class size (e.g., 10-30 students) is better for interactive discussion (responses to student questions, clarifications, additional examples).

The topics covered in the two-day course are:

Day 1: Statistical Design in Evaluation

Day 2: Statistical Analysis in Evaluation

Day 1 includes discussion of causal modeling, impact measures and estimators, basic evaluation designs, and principles and techniques of design and analysis for evaluation. Day 2 is concerned with impact analysis.

The level and scope of the course; managing expectations

This course is an introductory course on statistical design and analysis in evaluation. It assumes that the student has taken a prerequisite course in “college math,” and it requires a little prior knowledge of calculus (e.g., to understand the meaning of a continuous probability distribution and expectation). For students having knowledge of calculus (or some background in probability and statistics, say from an elementary course in statistics), some additional information may be presented. This additional material is marked with the notation optional. These optional sections (few in number) are omitted from the course presentation.

Attendees should be somewhat familiar with basic statistical concepts, such as probability, discrete and continuous probability distributions, expectation, the mean and variance of a distribution, the normal distribution, the binomial distribution, estimation and hypothesis testing, confidence intervals, and regression and correlation. Needed material from these topics is reviewed, but this review is not sufficient (too much material, too quickly) for a person having no previous knowledge of probability or statistics. Ideally, a person attending this course would have previously taken an elementary course in statistics. A person with no previous training in statistics could follow much of the lecture, but it would be expecting a lot to absorb the basic concepts of statistics or econometrics “on the fly,” in addition to the material specific to sample survey.

This course would be useful for a person who is familiar with techniques of sample survey design for descriptive surveys (used to estimate overall characteristics of populations and subpopulations, such as totals, means and proportions) and wishes to learn the basic concepts of analytical surveys (used to estimate relationships and to test hypotheses, such as whether a program has a positive impact).

As background material for the course, the following reference texts are recommended:

Gertler, Paul J., Sebastian Martinez, Patrick Premand, Laura B. Rawlings, and Christel M. J. Vermeersch, Impact Evaluation in Practice, The World Bank, 2011. (This reference is conceptual, not technical.)

This course builds on material in other courses and articles of the author, including the course in Sample Survey Design and Analysis: A Three-Day Course, and the article Sample Survey Design for Evaluation. These are posted at http://www.foundationwebsite.org.

The sample survey course addresses mainly the design and analysis of descriptive surveys (used for monitoring), with some coverage of analytical surveys (used for impact assessment). The article includes discussion of concepts in design of analytical surveys. The present course presents this material and also includes material on analysis of analytical surveys. Examples of statistical power analysis are presented using the author’s Microsoft Excel computer program, JGCSampleSiizeProgram, posted at http://www.foundationwebsite.org.

This course is intended to cover a broad range of topics in sample survey and econometric design and analysis. To do so, it does not cover each topic in great detail. The concern is with known results and how and when to apply them, not in proving them.

The course is introductory and conceptual, but somewhat technical, relatively comprehensive, and certainly intensive. At the end of the course, a person with some mathematical ability should be able to recognize which basic type of evaluation and sample design is appropriate in a given situation, be able to estimate the sample size required to produce a specified level of precision or power, and be able to conduct standard analyses of the collected sample data (using the Stata statistical program package).

There is no way, however, that a two-day course will make an “instant survey statistician” or “econometrician” out of anyone. In a survey design situation that is complex or that will involve large amounts of time, effort, or money, the advice of an expert sample survey statistician or econometrician should be sought.

The course is basically conceptual and discusses technical terms, but no time is spent on working through detailed examples, such as numerical calculation of formulas. Someone wishing to construct an actual evaluation or survey design and analyze the survey data would likely want to consult a reference text to review detailed examples and gain expertise by working through exercises.

This course is an ideal introduction for a project director or government technical (project) officer who wishes to understand the basic concepts of sample survey and evaluation design in order to effectively manage or monitor a project involving sample survey and econometric design and analysis. With the background of this course, the project manager should be able to sense what type of survey design is appropriate in a given situation, and be able to converse meaningfully with a consulting survey statistician or econometrician on a project involving a sample survey.

While it is possible to present a course on sample survey or econometrics with virtually no reference to mathematical symbology, such a course would not be of use to a person who actually wanted to design a survey and analyze survey data. This course is not a “no-math” course. While it is introductory and does not require extensive knowledge or use of calculus, it does require some familiarity with mathematics at the “college math” level, and a some background in introductory calculus and statistics. Persons with little mathematical background could attend the course and understand much of the conceptual material, but it is unlikely that they would be able to implement the methodology properly.

Nobody likes unpleasant surprises. One of the purposes for publishing these notes on the Internet is so that prospective students may quickly peruse them and assess whether the material is too advanced for them, given their present background in mathematics.

The course covers a lot of material in a short time. These notes will enable the student to pay attention to the lecture without having to take notes. It is not expected that everything will “sink in” in a two-day course, and it is recommended that the student who wishes to apply the techniques in practice acquire a reference text for study, or attend a formal course in which many homework exercises will “fix” the concepts.

Each attendee to the course is asked to complete a course evaluation. One of the questions asked is whether the course should spend less time on many topics (as it does), or concentrate on a smaller number of topics.

The course is comprehensive, but it is certainly not exhaustive. It provides an introduction to the major aspects of sample survey design and analysis in evaluation. There are many specialized topics that it does not cover, and it does not address every possible combination of survey design elements.

These notes are available for review by anyone considering enrolling in the course. The notes do not contain all of the exercises, examples, and handouts that may be included in the presentation.

It is not expected for the student to memorize the various formulas presented, but it is expected that some of the major ones would be familiar and recognized, by the end of the course (e.g., the formula for a double-difference measure and a double-difference estimator, and a general linear statistical model). A certain amount of course material (e.g., examples, supplementary material, details) is included as “background,” to place the essential concepts in context. It is not expected that the student remember all of the material presented, and the really important concepts will be identified and stressed.

In a usual academic course, the material covered here would be written out by the professor, over the course of 48 one-hour class sessions. If all of the material covered here were written out, it would not be possible to cover it in a two-day course. Hence, in addition to obviating the need for taking notes, the course notes enable much more material to be covered than would be possible in a usual course. It is recognized that there is a learning advantage to the student’s writing his own notes, but this benefit has been sacrificed in order to cover much material in a short time. The material presented in the notes is available in a variety of reference texts on sample survey, experimental design and evaluation. The essential feature of the course is the lecture and in-class interaction, not the notes. The notes are made available simply to enable the student to take full advantage of these aspects.

The course lasts 12 hours. This is about 1/4 of the class time of a “three-unit” college semester (three hours per week for 16 weeks, or 48 hours). The college course, however, would include substantial amounts of homework, which this course does not include.

Sample survey and econometric modeling and analysis involve a lot of formulas. There are a number of different designs and estimation techniques, and each of them involves its own formulas (or procedures, such as resampling) for calculating estimates and standard errors of estimates. These course notes include a number of formulas, for reference, but no class time is spent in working with the formulas. They are too many and too complicated to learn well in a two-day course. The class time is spent in discussing concepts, examples, and approaches, not with working through complicated estimation formulas. A few detailed numerical examples may be worked out in the early part of the course, so that the student may become familiar with the computational requirements of the estimation formulas. After that, formulas will be shown in order to illustrate concepts and general forms, but no further calculations will be made using them. Discussion of statistical computer software for performing the calculations is included.

Note on course content. If presented on an advertised basis (individual enrollments), the course follows these notes closely. If presented for a single client, the content may be modified somewhat to suit the client’s interests.

The pace of the course, the selection of topics, and the time spent on various topics may be adjusted a little by the instructor, in order to address specific concerns or interests of the students.

While these notes parallel the lecture, not every item included in the notes is necessarily included in the lecture, and not every item included in the lecture is included in the notes. The notes are intended to reduce the requirement for the student to take copious notes during the lecture. They are not intended to be a detailed recording of the lecture. For additional detail and examples, the student should consult reference textbooks on sample survey design or econometric analysis.

This course covers both estimation (point and interval estimation) and hypothesis testing. It differs from a standard course on sample survey design, which is concerned mainly with sampling from finite populations and estimation of overall features of the population and subpopulations, rather than with estimation of relationships and tests of hypotheses about a process or conceptually infinite population.

Course Pricing

At present, the course is not given on an advertised basis, but only “in-house” at a client’s facility. The price is negotiated. The estimated price for the course, conducted over a two-day period at a client's facility, is USD10,000 plus travel and lodging expense for two people. If the course is conducted over more days, the price is estimated at USD 5,000 per day plus travel and lodging expenses.

This price is all-inclusive, subject to the following limitations. Half payment is requested in advance, and half payment upon completion. Travel and per diem (meals, lodging and incidental) expense for the course staff are charged in accordance with US Government maximum travel per diem allowances (or international-organization allowances) for the travel (from presenter’s home base to client’s location, time spent at the client’s location, and return to the presenter’s home base).

It is agreed that the client will download the course notes from the Internet website http://www.foundationwebsite.org, and print sufficient copies for all attendees. Note: The Internet version of the course notes does not include handouts. These supplementary items, if available, will be e-mailed (as computer files) to the client prior to the course. If the client does not print the course notes and/or the supplementary items, the course will be presented without course notes and/or supplementary items. This is not the intended format, or the format that has been used successfully in the past for similar courses. As discussed, much material is presented, and it is not possible to write out this material during a two-day course. At the same time, restricting the course to a lecture, without benefit of the notes, would lose much. The course is intended to be a lecture supplemented with the Course Notes.

The client is expected to provide a comfortable environment conducive to learning. If the client does not have suitable accommodations at its own facility, it is recommended that facilities be procured at a local commercial hotel, many of which have excellent facilities for seminars. It is requested that the client provide a computer (with a Microsoft Windows operating system), computer-driven projector and projection screen, for displaying the Course Notes. It is also requested that a medium be provided for ad-hoc classroom presentation by the lecturer. For small groups, this may be a wall board (with chalk or markers) or “flip-chart-and-easel” (with marking pen). For larger groups it is recommended that a “view-graph” projector be available (for displaying writing using markers on clear acetate sheets).

It is requested that the client provide snacks and drinks for the breaks. The client is encouraged to provide lunch to presenters and attendees for full-day sessions, but this is at the client’s discretion. (This was the practice when a similar course was presented on an advertised basis at a commercial hotel, and it works well (it keeps the class together, and avoids late returns to class after lunch).)

2. Course Schedule

Course Schedule

Day 1: Causal Modeling, Impact Measures and Estimators, Basic Evaluation Designs, and Principles and Techniques of Design and Analysis for Evaluation

9:00 - 9:20 Introduction; Course Objectives and Outline; Overview of First Day's Course Content

9:20 -10:00 Causal Models

10:00 -10:30 Impact Measures and Impact Estimators

10:30 -10:45 Break

10:45 -12:00 Basic Evaluation Design / Models / Estimators

12:00 - 1:00 Lunch

1:00 - 2:30 Sample Survey Design for Evaluation (Principles of Experimental Design;

Descriptive and Analytical Surveys; Sample Survey Design Techniques)

2:30 - 2:45 Break

2:45 - 4:00 Sample Survey Design for Evaluation (Matching; Estimation of Sample Size; Sample Selection Procedures); Survey of References; Outline of Topics for Second Day; Questions and Answers

Day 2: Impact Analysis

9:00 - 9:15 Overview of Second Day's Course Content

9:15 - 9:45 Parametric Estimation and Hypothesis Testing (General Linear Statistical Model (Regression Model); Logistic Regression Model)

9:45 - 10:30 Impact Analysis

10:30 -10:45 Break

10:45 -12:00 Impact Analysis

12:00 - 1:00 Lunch

1:00 - 2:30 Impact Analysis

2:30 - 2:45 Break

2:45 - 3:30 Analysis of Baseline Data

3:30 - 4:00 Computer Software for Analysis of Survey Data; Questions and Answers

3. Course Syllabus

Course Syllabus

Day 1: Causal Modeling, Impact Measures and Estimators, Basic Evaluation Designs, and Principles and Techniques of Design and Analysis for Evaluation

1. Introduction

· Course Objectives and Outline

· Overview of First Day's Course Content

2. Causal Modeling

· Causal Modeling (Pearl Graphical Approach to Causal Modeling)

· Causal Relationship; Causal Structure (Causal Graph, Path Diagram, Directed Acyclic Graph)

· Equational Model (Structural Equation Model)

· Causal Effect

· Potential Outcomes, Counterfactuals, Neyman-Fisher-Cox-Rubin Causal Model)

3. Impact Measures

· Review of Impact Measures

· Counterfactual Model

· Matching and Regression Analysis

4. Basic Evaluation Designs / Models / Estimators

· Designs Based on Randomization

· Two-Group Designs

· Interrupted Time-Series Design

· Four-Group Designs

· Quasi-Experimental Designs

· Observational Data

5. Sample Survey Design for Evaluation

· Principles of Experimental Design

· Descriptive Surveys vs. Analytical Surveys

· Sample Survey Design Techniques

· Use of Matching to Improve Precision and Power

· Estimation of Sample Size for Descriptive Surveys

· Estimation of Sample Size for Analytical Surveys

· Statistical Tests of Hypothesis

· Sample Selection Procedures

6. Survey of References; Outline of Topics for Second Day; Questions and Answers

Day 2: Parametric Estimation, Analysis of Baseline Data, Impact Analysis, Use of Stata Statistical Program Package

1. Overview Of Second Day’s Course Content

· Parametric Estimation and Hypothesis Testing (General Linear Statistical Model, Logistic Regression Model; Two-Step M-Estimators)

· Impact Analysis (Design-Based Estimates, Model-Based Estimates, Model Specification, Use of Matching to Reduce Model Dependence, Estimators Baseed on Ignorability (Conditional Independence), Selection vs. Outcome Models (Two-Step Models), Estimation of Standard Errors, Estimation Based on Combining Regression and Propensity-Score Matching (Matching Estimators, Doubly-Robust Matching/Regression Approach), Instrumental-Variable Estimators, Local Average Treatment Effect (LATE), Intention-to-Treat Effect (ITT), Regression Discontinuity Design, Responses Discrete or in a Limited Range, Multivalued (Categorical) Treatment Variable, Multiple Treatment Variables, Panel Data (Fixed-Effects Model, Random-Effects Model), Treatment of Missing Values, Use of Weights, Estimation of Standard Errors)

· Analysis of Baseline Data (Descriptive Surveys, Analytical Surveys)

· Use of Stata Statistical Program Package (Summary Description and Examples)

· Survey of References

· Questions and Answers

2. Parametric Estimation and Hypothesis Testing

· Properties of Estimators

· Estimation Procedures

· General Linear Statistical Model

· Generalized Linear Statistical Model

· Principle of Conditional Error

3. Impact Analysis

· Design-Based Estimates

· Model-Based Estimates

· Model Specification

· Use of Matching to Reduce Model Dependence

· Estimators Based on Ignorability (Conditional Independence)

· Selection vs. Outcome Models (Two-Step Models)

· Estimation of Standard Errors

· Estimation Based on Combining Regression and Propensity-Score Matching (Matching Estimators; Doubly Robust Matching/Regression Approach)

· Instrumental-Variable Estimators

· Local Average Treatment Effect (LATE), Intention-to-Treat Effect (ITT)

· Regression-Discontinuity Design

· Responses Discrete or in a Limited Range

· Multivalued (Categorical) Treatment Variable

· Multiple Treatment Variables

· Panel Data (Fixed-Effects Model, Random-Effects Model)

· Treatment of Missing Values

· Use of Weights

· Estimation of Standard Errors

4. Analysis of Baseline Data

· Descriptive Surveys

· Analytical Surveys

5. Use of Stata Statistical Program Package

· Summary Description of Stata

· Examples

6. Survey of References; Questions and Answers

4. Course Critique Form

Course Critique Form

Dear Participant:

We appreciate your attendance and are interested in your comments in order to improve our course. Please answer the following questions, adding additional comments as necessary, and send the form back in the attached envelope. Thank you.

Date of course_________________ Location of course_______________________________

Course Content

1. How useful do you consider the information?_______________________________

2. Was the material presented in sufficient detail?_____________________________

3. Were there some topics you would have preferred more discussion on? Yes__ No___

If so, which ones?_________________________________________________________

Course Delivery

1. Were the presentations effective?____________________________________________

2. Were the visual aids helpful?___________________________________________

3. Were the Course Notes sufficiently detailed?________________________________

Facilities

1. Was the seating arrangement satisfactory?_____________________________________

2. Were the meals satisfactory?_________________________________________________

3. Was parking adequate?______________________________________________________

4. Is the location convenient?__________________________________________________

General

1. How did you find out about this course?____________________________________

Brochure in mail_________________

Organizational channels___________

Associate_______________________

Internet_________________________

Other (specify)___________________

2. Did you have sufficient registration time?___________________

3. Did you feel the course was as you expected it to be, from the flyer?

____________________________________________________________________

4. Did you feel the course was as you expected it to be, from the Course Notes (if examined on the Internet)?______________________________________________

5. If from out of town: Did you stay at the hotel where the course was presented? _____

6. This course was presented to provide a broad overview of Statistical Design and Analysis in Evaluation. Would you have preferred to concentrate on fewer topics?_________________________________________________________________

7. Have you ever attended a course on Statistical Design and Analysis in Evaluation before?

Yes_____ No_____

8. Would you prefer a more detailed course of 3-4 days,_____

or a less detailed course of 1 day?_____

9. Would you prefer a more advanced course,_____

or a less advanced course?_____

10. Compared to other short courses of which you are familiar, was the cost of this course:

About right______________

Rather high______________

Lower than expected______

11. What additional seminars might you be interested in?

Sample Survey Design and Analysis________

Time Series Analysis, Forecasting and Control________

Biostatistics_______________

Experimental Design________

Quality Control_____________

Evaluation Research________

Introduction to Statistics and Data Analysis____________

Simulation and Modeling______________

Optimization_______________

Other (specify)______________

Additional Comments:_____________________________________________________________

Name (optional)______________________________________________________________

Organization (optional)__________________________________________________________

5. Résumé of Course Developer

Joseph George Caldwell, Ph.D. (Statistics)

Consultant in Statistics, Economics, Operations Research and Computer Science

Professional Profile: Career in management consulting, system development, research, and teaching. Directed projects in strategic planning, policy analysis, program evaluation, economics, public finance, statistics, operations research / systems analysis, and information technology for US, state and foreign governments, and US and foreign organizations. Areas of expertise include health, education, vocational rehabilitation, welfare, public finance (tax policy analysis, Medicaid and AFDC financing), agriculture, civil rights, economic development, energy, environment, population, and defense (US Army, Navy, Air Force, Department of Defense). Considerable overseas experience.

2005- Semi-retired. Consultant in Statistics and Information Technology, Spartanburg, South Carolina, and Tucson, Arizona, USA. Consultant on research design for impact evaluation of development projects (assignments in Honduras, Ghana, Burkina Faso, Namibia and other African countries funded mainly by Millennium Challenge Corporation); also computer / communication system development work in Timor Leste funded by UNDP and in Guinea and Liberia funded by US Agency for International Development).

2001-2005 Management Consultant / System Developer, Clearwater, Florida. System development work in Zambia (funded by US Agency for International Development).

1999-2001 Director of Management Systems, Bank of Botswana (Botswana’s central bank).

1991-1998 Management Consultant / Statistician / System Developer, Clearwater, Florida. Clients included First Union National Bank (Wachovia, Wells Fargo), Charlotte; US Agency for International Development, Egypt, Malawi, Ghana; Asian Development Bank, Bangladesh; Canada Trust Bank, Toronto, Canada.

1989-1991 President, Vista Research Corporation, Tucson, Arizona. Research in artificial intelligence for noncommunications electronic warfare systems (work on automated scenario generation, funded by US Army Communications-Electronic Command).

1982-1991 Director of Research and Development and Principal Scientist, US Army Electronic Proving Ground’s Electromagnetic Environmental Test Facility / Bell Technical Operations and Combustion Engineering; Adjunct Professor of Statistics, University of Arizona; Principal Engineer, Singer Systems and Software Engineering; Tucson and Sierra Vista, Arizona.

1964-1982 Consultant or employee to firms in South Carolina, North Carolina, Virginia, Maryland, District of Columbia, Haiti, Philippines.

Education: PhD, Statistics, University of North Carolina at Chapel Hill (1966)

BS, Mathematics, Carnegie Mellon University, Pittsburgh, PA (1962)

Graduate of Spartanburg High School, Spartanburg, SC (1958)

Personal: Born March 23, 1942, in Kingston, Ontario, Canada.

Nationality: United States of America, Canada.

Author of articles and books on divers topics (e.g., population, environment, economics, politics, defense and music, including The Late Great United States (2008); Can America Survive? (1999); The Value-Added Tax: A New Tax System for the United States (1987); How to Play the Guitar by Ear (for mathematicians and physicists) (2000). See Internet website http://www.foundationwebsite.org to view these and other articles.

Contact information: 1432 N Camino Mateo, Tucson, AZ 85745-3311USA, e-mail jcaldwell9@yahoo.com

File: ResumeOfCourseDeveloper20110210.docx

6. Day 1: Causal Modeling

DAY 1: CAUSAL MODELING, IMPACT MEASURES AND ESTIMATORS, BASIC EVALUATION DESIGNS, AND PRINCIPLES AND TECHNIQUES OF DESIGN AND ANALYSIS FOR EVALUATION

6.1. Overview of First Day's Course Content

INTRODUCTION; COURSE OBJECTIVES AND OUTLINE; OVERVIEW OF FIRST DAY’S COURSE CONTENT

CAUSAL MODELING (PEARL GRAPHICAL APPROACH TO CAUSAL MODELING; POTENTIAL OUTCOMES, COUNTERFACTUALS, NEYMAN-FISHER-COX-RUBIN CAUSAL MODEL)
IMPACT MEASURES
BASIC EVALUATION DESIGNS / MODELS / ESTIMATORS
SAMPLE SURVEY DESIGN FOR EVALUATION
SURVEY OF REFERENCES; OUTLINE OF TOPICS FOR SECOND DAY; QUESTIONS AND ANSWERS

6.2. Causal Modeling

CAUSAL MODELING

GOAL: TO ASSESS THE CAUSAL EFFECT (CAUSAL IMPACT, IMPACT) OF A PROJECT OR PROGRAM

CAUSAL EFFECT: DEFINED WITH RESPECT TO A CAUSAL MODEL. REFERENCES:

Pearl, Judea, Causality: Models, Reasoning, and Inference, Cambridge University Press, 2000.

Morgan, Stephen L. and Christopher Winship, Counterfactuals and Causal Inference: Methods and Principles for Social Research, Cambridge University Press, 2007.

Holland, Paul W. Statistics and Causal Inference, Journal of the American Statistical Association, Vol. 81, No. 396, pp. 945-960, 1986.

Rosenbaum, Paul R. and Donald B. Rubin, “The central role of the propensity score in observational studies for causal effects,” Biometrika (1983), Vol. 70, No. 1, pp. 41-55.

Dawid, A. P., Causal Inference without Counterfactuals, Journal of the American Statistical Association, Vol. 95, No. 450, pp. 407-448, 2000.

Additional references on structural equation modeling:

Muliak, Stanley A., Linear Causal Modeling with Structural Equations, Chapman and Hall / CRC, 2009.

Duncan, O. D., Introduction to Structural Equation Models, Academic Press, 1975

Goldberger, A. S. and O. D. Duncan, Structural Equation Models in the Social Sciences, Seminar Press, 1973.

Kline, Rex B., Principles and Practice of Structural Equation Modeling 3^rd edition, Guilford Press, 2011.

Schumacker, Randall E. and Richard G. Lomax, A Beginner’s Guide to Structural Equation Modeling 3^rd edition, Routledge, 2010.

Everitt, B. S., An Introduction to Latent Variable Models, Chapman and Hall, 1984.

Loehlin, John C., Latent Variable Models: An Introduction to Factor, Path and Structural Equation Analysis 4^th edition, Routledge, 2004.

WHY THE INTEREST IN CAUSAL MODELING? MODEL IDENTIFICATION. (IS THE MODEL “IDENTIFIED”?) THE CORRECT SPECIFICATION OF A MODEL (VARIABLES, RELATIONSHIPS, PARAMETER VALUES) CANNOT BE INFERRED FROM SAMPLE DATA. THE MODEL PARAMETERS CANNOT BE ESTIMATED UNLESS CERTAIN TECHNICAL ASSUMPTIONS HOLD, AND THOSE ASSUMPTIONS FLOW FROM THE CAUSAL MODEL. ESTIMABILITY OF MODEL PARAMETERS IS DETERMINED BY THE CAUSAL MODEL.

THE CAUSAL MODEL SHOWS, FOR EXAMPLE, WHICH VARIABLES OF A MODEL ARE ENDOGENOUS (AND REQUIRE SPECIAL TREATMENT IN REGRESSION ANALYSIS), AND WHICH VARIABLES MAY SERVE AS INSTRUMENTAL VARIABLES FOR THEM.

NOTE: SOME VARIATION IN TERMINOLOGY. STATISTICIANS OFTEN USE THE TERM “CORRECTLY SPECIFIED” OR “ESTIMABLE” INSTEAD OF “IDENTIFIED.”

FOR PROGRAM EVALUATION APPLICATIONS, WE ASK: WHAT IS EFFECT OF A CAUSE, NOT WHAT IS THE CAUSE OF AN EFFECT.

ASSOCIATIONAL RELATIONSHIP: A VARIABLE X HAS AN ASSOCIATIONAL RELATIONSHIP TO A VARIABLE Y IF THE PROBABILITY DISTRIBUTION OF Y CONDITIONAL ON X DIFFERS FOR DIFFERENT VALUES OF X.

A CAUSAL RELATION DIFFERS FROM AN ASSOCIATIONAL RELATION

“CORRELATION IS NOT CAUSATION.” “NO CAUSATION WITHOUT MANIPULATION (INTERVENTION).” TO ESTIMATE THE EFFECT OF CHANGES TO A VARIABLE IN A SYSTEM, ONE MUST MAKE FORCED CHANGES TO THE VARIABLE.

CAUSAL MODELING SUBSUMES (INCLUDES) STATISTICAL MODELING. STATISTICS TEXTS AVOID MENTION OF CAUSALITY (CAUSAL, CAUSAL EFFECT), PREFERRING “EFFECT.” CAUSALITY MAY BE INFERRED FROM EXPERIMENTAL DESIGNS HAVING RANDOMIZED ASSIGNMENT TO TREATMENT. IN OTHER CASES, NEED A CAUSAL MODEL AS A BASIS FOR MAKING CAUSAL INFERENCES. THE CAUSAL MODEL IS USED TO GUIDE MODEL IDENTIFICATION, AND STATISTICAL INFERENCE IS USED TO ESTIMATE MODEL PARAMETERS FOR AN IDENTIFIED MODEL.

DIFFERENCES IN THE ROLES OF CAUSAL MODELING AND STATISTICAL ANALYSIS.

CAUSAL MODELING ASSISTS MODEL IDENTIFICATION.

STATISTICAL ANALYSIS IS USED TO ESTIMATE PARAMETERS IN IDENTIFIED MODELS.

DIFFERENCES IN DESCRIPTIVE SURVEY DESIGN AND ANALYSIS AND ANALYTICAL SURVEY DESIGN AND ANALYSIS

DESCRIPTIVE SURVEY APPROACH: ESTIMATE CHARACTERISTICS (TOTALS, MEANS, PROPORTIONS) OF AN EXISTING FINITE POPULATION AND SUBPOPULATIONS. HAS NOTHING TO DO WITH A CAUSAL MODEL, AND DOES NOT NEED A CAUSAL MODEL. NOT CONCERNED WITH INFERENCES ABOUT CAUSE-AND-EFFECT RELATIONSHIPS.

THE POPULATION IS REGARDED AS FIXED. THE RANDOM VARIABLE OF INTEREST IS THE PROBABILITY OF SELECTION OF UNITS FOR THE SAMPLE. CONCERNED WITH PRECISION OF ESTIMATES (STANDARD ERRORS AND CONFIDENCE INTERVALS). IF SAMPLE ENTIRE POPULATION, STANDARD ERRORS ARE ZERO (FINITE POPULATION CORRECTION, OR FPC). DESIGN-BASED ESTIMATES.

ANALYTICAL SURVEY APPROACH: ESTIMATE CHARACTERISTICS OF A PROCESS, OR CAUSAL EFFECT OF AN INTERVENTION; RELATIONSHIP OF OUTCOME VARIABLES TO INPUT VARIABLES; TESTS OF HYPOTHESIS ABOUT OVERALL IMPACT, OR RELATIONSHIP OF IMPACT TO EXPLANATORY VARIABLES. THE RANDOM VARIABLES OF INTEREST ARE ALL VARIABLES OF A MODEL DESCRIBING THE PROCESS OF INTEREST. CONCERNED WITH POWER OF TESTS OF HYPOTHESIS ABOUT PROCESS CHARACTERISTICS (E.G., IS EFFECT OF TREATMENT INTERVENTION POSITIVE). CONCEPTUALLY INFINITE POPULATION: EVEN IF SAMPLE ENTIRE PHYSICAL POPULATION, STILL HAVE SAMPLING VARIATION. MODEL-BASED OR MODEL-ASSISTED ESTIMATES. INCORPORATES ASPECTS OF EXPERIMENTAL DESIGN.

ANALYTICAL SURVEY DESIGN AND ANALYSIS IS SUBSTANTIALLY MORE DIFFICULT THAN DESCRIPTIVE SURVEY DESIGN AND ANALYSIS. IT REQUIRES CONSIDERATION OF CAUSAL MODELS, AND INCORPORATES ELEMENTS OF EXPERIMENTAL DESIGN (THE FIELD OF DESIGN OF EXPERIMENTS) AND ECONOMETRICS. THIS TWO-DAY COURSE IN STATISTICAL DESIGN AND ANALYSIS IN EVALUATION WILL DESCRIBE THE ESSENTIAL BASIC CONCEPTS AND PROVIDE SOME DETAIL FOR MOST-USED TECHNIQUES.

REFERENCES ON DESCRIPTIVE SURVEY DESIGN AND ANALYSIS:

Cochran, William G., Sampling Techniques 3^rd edition, Wiley, 1977.

Sheaffer, Richard L., William Mendenhall, R. Lyman Ott and Kenneth G. GeRow, Elementary Survey Sampling 7^th edition, Cengage Learning, 2011. (Or any earlier edition, such as 2^nd, Duxbury Press, 1979)

REFERENCES ON ANALYTICAL SURVEY DESIGN AND ANALYSIS:

Lohr, Sharon L., Sampling: Design and Analysis, 2nd ed., Cengage Learning, 2009.

Thompson, Steven K., Sampling 3rd edition, Wiley, 2012.

Lehtonen, Risto and Erkki Pahkinen, Practical Methods for Design and Analysis of Complex Surveys 2^nd edition, Wiley, 2004.

Rao, J. N. K. and D. R. Bellhouse, “History and Development of the Theoretical Foundations of Survey Based Estimation and Analysis,” Survey Methodology, June 1990, Vol. 16, No. 1, pp. 3-29, Statistics Canada.

REFERENCES ON EXPERIMENTAL DESIGN:

Kuehl, Robert O., Design of Experiments: Statistical Principles of Research Design and Analysis, 2^nd edition, Brooks/Cole/Cengage, 2000.

Cochran, William G. and Gertrude M. Cox, Experimental Designs, Wiley, 1957.

REFERENCES ON CAUSAL MODELING

Pearl, Judea, Causality: Models, Reasoning, and Inference, Cambridge University Press, 2000.

Morgan, Stephen L. and Christopher Winship, Counterfactuals and Causal Inference: Methods and Principles for Social Research, Cambridge University Press, 2007.

Holland, Paul W. Statistics and Causal Inference, Journal of the American Statistical Association, Vol. 81, No. 396, pp. 945-960, 1986.

Dawid, A. P., Causal Inference without Counterfactuals, Journal of the American Statistical Association, Vol. 95, No. 450, pp. 407-448, 2000.

REFERENCE ON CAUSAL ANALYSIS (IN THE PARTICULAR FIELD OF ECONOMETRICS):

Wooldridge, Jeffrey M., Econometric Analysis of Cross Section and Panel Data 2^nd edition, The MIT Press, 2010.

CAUSAL MODEL; CAUSAL EFFECT; POTENTIAL OUTCOMES, COUNTERFACTUALS

EARLY DEVELOPMENT: CHARLES SPEARMAN (FACTOR ANALYSIS, 1904), SEWELL WRIGHT (PATH ANALYSIS, 1918), O. D. DUNCAN (STRUCTURAL EQUATION MODELING, 1966).

TWO MAIN KINDS OF CAUSAL MODELS:

RECURSIVE (NO FEEDBACK LOOPS, CAUSAL EFFECTS UNIDIRECTIONAL, DISTURBANCES UNCORRELATED; IDENTIFIED; ORDINARY LEAST SQUARES)

NONRECURSIVE (FEEDBACK LOOPS, CORRELATED DISTURBANCES; SOME NONIDENTIFIED; INDIRECT LEAST SQUARES, TWO-STAGE LEAST SQUARES, FULL INFORMATION MAXIMUM LIKELIHOOD)

(THE TERM “RECURSIVE” IS MISLEADING – IT REFERS TO THE METHOD OF SOLVING STRUCTURAL EQUATIONS, NOT TO THE CAUSAL FLOW IN A PATH DIAGRAM.

(A RECURSIVE MODEL IS HIERARCHICAL: ALL ENDOGENOUS VARIABLES CAN BE ARRANGED IN A SEQUENCE X₁, X₂,…,X_m SUCH THAT FOR ANY X_i AND X_j where i<j, X_j IS NOT A CAUSE OF X_i. HENCE THE FIRST ENDOGENOUS VARIABLE IS INFLUENCED ONLY BY EXOGENOUS VARIABLES, THE SECOND IS INFLUENCED ONLY BY EXOGENOUS VARIABLES AND THE FIRST ENDOGENOUS VARIABLE, AND SO ON.)

SOME DESCRIPTION OF CAUSAL MODELING, IN THE RECURSIVE CASE (THE FOLLOWING IS DERIVED FROM PEARL OP. CIT.)

CAUSAL RELATIONSHIP: IF THE PROBABILITY DISTRIBUTION OF Y CHANGES WHEN A RANDOMLY-TIMED FORCED CHANGE IS MADE IN X, THEN WE SAY THAT THERE IS A CAUSAL RELATIONSHIP BETWEEN X AND Y (AND THAT X HAS A CAUSAL INFLUENCE ON Y).

NOTE THAT THE CAUSAL MODEL IS NOT INFERRED FROM PROBABILISTIC ASSOCIATIONS. CAUSAL RELATIONSHIPS ARE SPECIFIED IN A CAUSAL MODEL. THE STRENGTH OF THOSE RELATIONSHIPS MAY BE SPECIFIED BY PROBABILITY DISTRIBUTIONS, BUT THE CAUSAL RELATIONSHIPS ARE NOT DERIVED FROM ASSOCIATIONAL RELATIONSHIPS. THE CAUSAL MODEL PROVIDES INFORMATION ON HOW CAUSAL EFFECTS SHOULD BE ESTIMATED (I.E., ON ESTIMABILITY, OR IDENTIFIABILITY).

NOTATION: DENOTE RANDOM VARIABLES BY UPPER-CASE LETTERS (E.G., X, Y, U, V, W). DENOTE SPECIFIC REALIZATIONS OF RANDOM VARIABLES BY LOWER-CASE LETTERS (E.G., x, y, u, v, w). WILL USUALLY DENOTE VECTORS USING UNDERSCORES OR BOLD FACE (E.G., x’ = (x₁, x₂ ,…, x_n) OR x’ = (x₁, x₂ ,…, x_n), BUT OCCASIONALLY x = (x₁, x₂ ,…, x_n). WILL USUALLY DENOTE COLUMN VECTORS WITHOUT PRIMES AND ROW VECTORS WITH PRIMES.

CAUSAL STRUCTURE (CAUSAL GRAPH, PATH DIAGRAM): A CAUSAL STRUCTURE OF A SET OF VARIABLES IS A DIRECTED ACYCLIC GRAPH (DAG) IN WHICH EACH NODE REPRESENTS A VARIABLE AND EACH LINK REPRESENTS A CAUSAL RELATIONSHIP BETWEEN THE LINKED VARIABLES.

EXAMPLE OF DAG [SHOW GRAPH}.

z → w → y

where

z = education on exercise

w = exercise

y = health

z = random assignment to treatment

w = treatment

y = outcome

z AFFECTS w, BUT NOT y DIRECTLY. z IS CALLED AN INSTRUMENT FOR w.

CAUSAL MODEL: THE PROBABILITY DISTRIBUTIONS ASSOCIATED WITH A CAUSAL STRUCTURE. THE PROBABILITY DISTRIBUTION FOR VARIABLE (NODE) x IS CONDITIONAL ONLY ON ITS PARENT VARIABLES (NODES), AND, CONDITIONAL ON THE PARENT VALUES, x IS INDEPENDENT OF ALL OTHER VARIABLES. (NOTE: PEARL DEFINES A DETERMINISTIC CAUSAL MODEL, AND THEN A PROBABILISTIC CAUSAL MODEL.)

MORE SPECIFICALLY, EQUATIONAL MODEL (STRUCTURAL EQUATION MODEL):

FOR EACH VARIABLE (NODE) x_i, x_i = f_i(pa_i, u_i), I = 1,…,n, WHERE f_i DENOTES A FUNCTIONAL RELATIONSHIP, pa_i DENOTES THE VALUES OF PARENT VARIABLES, u_i DENOTE BACKGROUND (EXOGENOUS) VARIABLES, AND P(u) DENOTES THE JOINT PROBABILITY DISTRIBUTION OF THE u, WHICH ARE ASSUMED TO BE INDEPENDENT. WE DO NOT KNOW THE f_i OR P. (u MAY DENOTE A SINGLE u_i OR A VECTOR OF ALL u_i.)

NOTATION: U DENOTES THE SET OF ALL BACKGROUND (EXOGENOUS) VARIABLES, AND V DENOTES THE SET OF ALL VARIABLES DETERMINED BY VARIABLES IN THE MODEL (I.E., ENDOGENOUS VARIABLES). LOWER-CASE LETTERS ARE REALIZATIONS OF UPPER-CASE RANDOM VARIABLES.

TERMINOLOGY:

ENDOGENOUS VARIABLES: VARIABLES THE CAUSES OF WHICH ARE EXPLICITLY REPRESENTED IN THE CAUSAL MODEL

PREDETERMINED VARIABLES: VARIABLES THE CAUSES OF WHICH ARE NOT EXPLICITLY REPRESENTED IN THE MODEL

LAGGED ENDOGENOUS VARIABLES HAVE VALUES EQUAL TO THE VALUES OF ENDOGENOUS VARIABLES AT PREVIOUS TIMES

EXOGENOUS VARIABLES (BACKGROUND VARIABLES): VALUES DETERMINED OUTSIDE THE MODEL (NOT PRIOR VALUES OF ENDOGENOUS VARIABLES)

THE EQUALITY SIGNS IN THE EQUATIONAL MODEL IMPLY “IS DETERMINED BY.” (CAUSATION, NOT SIMPLE ASSOCIATION.)

NOTE: THE MODEL IS MARKOVIAN, I.E., THE DISTRIBUTION DEPENDS ONLY ON THE VALUES OF THE PARENT VARIABLES, AND NO PREVIOUS ANCESTOR NODES. FOR DIFFERENT POPULATION UNITS, THE RESPONSES ARE INDEPENDENT, GIVEN THE PARENT VARIABLES. THIS IS CALLED THE STABLE UNIT TREATMENT VALUE ASSUMPTION (SUTVA, THE NO-MACRO-EFFECTS ASSUMPTION, OR THE PARTIAL-EQUILIBRIUM ASSUMPTION). (FOR EXAMPLE, INDIVIDUALS DO NOT COMPETE FOR RESOURCES.)

MORE COMPLICATED EXAMPLE OF STRUCTURAL EQUATIONS. PRICE AND DEMAND EQUATIONS:

q = b₁ p + d₁ i + u₁

p = b₂q + d₂ w + u₂

where

q = quantity of household demand for a product

p = unit price of product

i = household income

w = wage rate for producing the product

u_i = error terms.

CAUSAL MODELING = PATH ANALYSIS, LATENT-VARIABLE MODELING. STRUCTURAL EQUATION MODELING (SEM) (ALTERNATIVE REPRESENTATIONS OF CAUSAL INFORMATION – EQUATIONS RATHER THAN GRAPHS). IN SOME FIELDS (PROCESS CONTROL, BIOLOGY, PSYCHOLOGY), MODELS MAY BE COMPLEX.

IN THE FIELD OF EVALUATION IN INTERNATIONAL DEVELOPMENT, THE CAUSAL MODELS ARE USUALLY SIMPLE, INVOLVING VARIABLES THAT AFFECT SELECTION FOR TREATMENT, A TREATMENT VARIABLE (USUALLY A SINGLE BINARY VARIABLE), AND A NUMBER OF COVARIATES. CONSIDERATION OF THE CAUSAL MODEL STRUCTURE (DIAGRAM) INDICATES VALID STATISTICAL MODELS TO USE FOR PARAMETER ESTIMATION (E.G., INSTRUMENTAL VARIABLES).

EXAMPLE: DIRECT FEEDBACK LOOP (SHOW GRAPH).

EXAMPLE: PANEL MODEL FOR LONGITUDINAL DATA (SHOW GRAPH)

RECIPROCAL CAUSATION REPRESENTED BY CROSS-LAG DIRECT EFFECTS BETWEEN RESPONSE AND EXPLANATORY VARIABLES MEASURED AT DIFFERENT TIMES. NO DIRECT FEEDBACK LOOP.

NOTATION: WILL GENERALLY (BUT NOT ALWAYS) USE UPPER-CASE LETTERS (X, Y, Z…) TO DENOTE RANDOM VARIABLES (FUNCTIONS DEFINED ON A SAMPLE SPACE), AND LOWER-CASE LETTERS TO DENOTE SPECIFIC REALIZATIONS (NUMERICAL VALUES, x, y, z…). WILL USE GREEK LETTERS TO DENOTE POPULATION VALUES (“TRUE” VALUES), AND CARETS OR BARS TO DENOTE SAMPLE ESTIMATES.

CAUSAL EFFECT: GIVEN TWO DISJOINT SETS OF VARIABLES, X AND Y, THE CAUSAL EFFECT OF X ON Y, DENOTED P(y|) OR AS P(y|do(x)), IS A FUNCTION FROM X TO THE SPACE OF PROBABILITY DISTRIBUTIONS ON Y. FOR EACH REALIZATION x OF X, P(y|do(x)) GIVES THE PROBABILITY OF Y = y INDUCED BY DELETING FROM THE EQUATIONAL MODEL ALL EQUATIONS CORRESPONDING TO VARIABLES IN X AND SUBSTITUTING X = x IN THE REMAINING EQUATIONS. (ALTERNATIVELY (ROSENBAUM AND RUBIN), THE CAUSAL EFFECT IS THE DIFFERENCE E(Y|do(x₁)) – E(Y|do(x₂)), WHERE x₁ AND x₂ ARE TWO DISTINCT REALIZATIONS OF X.)

COMPARE STATISTICAL P(y|see x) TO CAUSAL P(y|do(x)). CAUSAL MODEL IS ONTOLOGICAL (RELATES TO HOW THINGS ARE), STATISTICAL MODEL IS EPISTEMOLOGICAL (RELATES TO HOW THINGS APPEAR (BELIEF, KNOWLEDGE)).

EVERYTHING MAY HAVE A CAUSE, BUT NOT EVERYTHING CAN BE A CAUSE (ATTRIBUTES ARE NEVER CAUSES).

TO ESTABLISH CAUSALITY REQUIRES EXPERIMENTATION (RANDOM, FORCED CHANGES IN EXPLANATORY (“PARENT”) VARIABLES).

PHILOSOPHICALLY (METAPHYSICALLY), A TIME VARIABLE IS REQUIRED TO ESTABLISH CAUSALITY; CAUSAL MODEL ENABLES PREDICTION. CAUSALITY MAY BE INFERRED FROM EXPERIMENTS (E.G., USING AN EXPERIMENTAL DESIGN IN WHICH TREATMENT IS RANDOMLY ASSIGNED).

ALTERNATIVE MODELS: MODEL PREFERENCE:

CAUSAL INFLUENCE: A VARIABLE X IS SAID TO HAVE A CAUSAL INFLUENCE ON A VARIABLE Y IF A DIRECTED PATH FROM X TO Y EXISTS IN EVERY MINIMAL STRUCTURE CONSISTENT WITH THE DATA. (A MINIMAL THEORY IS ONE THAT IS SIMPLER THAN OTHERS IN SOME SENSE, AND CONSISTENT WITH THE DATA.) OCCAM’S RAZOR: PREFER SIMPLER EXPLANATIONS (POPPER: SIMPLER MODEL LESS EASY TO FALSIFY, FEWER OPPORTUNITIES FOR OVERFITTING THE DATA.)

COUNTERFACTUALS MODEL (POTENTIAL OUTCOMES MODEL; RUBIN CAUSAL MODEL; NEYMAN-RUBIN CAUSAL MODEL; NEYMAN-FISHER-COX-RUBIN CAUSAL MODEL)

A SUBMODEL, M_x, OF A CAUSAL MODEL, CORRESPONDING TO A PARTICULAR REALIZATION x IN X, IS THE CAUSAL MODEL DETERMINED BY DELETING ALL FUNCTIONS f_i CORRESPONDING TO MEMBERS OF THE SET X AND REPLACING THEM WITH THE SET OF CONSTANT FUNCTIONS X = x.

EFFECT OF ACTION (CAUSAL EFFECT): THE EFFECT OF ACTION do(X = x) ON A CAUSAL MODEL M IS GIVEN BY THE SUBMODEL M_x.

POTENTIAL RESPONSE: LET X AND Y BE TWO SUBSETS OF VARIABLES IN V. THE POTENTIAL RESPONSE OF Y TO ACTION do(X = x) IS THE SOLUTION, Y_x(u) (OR Y(x,u)), FOR Y IN THE SET OF EQUATIONS f_i IN THE SUBMODEL M_x.

COUNTERFACTUAL: LET X AND Y BE TWO SUBSETS OF VARIABLES IN V. THE SENTENCE “THE VALUE THAT Y WOULD HAVE OBTAINED, HAD X BEEN x” IS INTERPRETED AS DENOTING THE POTENTIAL RESPONSE Y_x(u).

THE TERM COUNTERFACTUAL IS OFTEN MISUSED IN PLACE OF THE TERM POTENTIAL OUTCOME. POTENTIAL OUTCOMES ALWAYS EXIST IN CONCEPT. A COUNTERFACTUAL EXISTS ONLY AFTER ONE OF THE POTENTIAL OUTCOMES HAS BEEN PHYSICALLY REALIZED.

A CAUSAL MODEL IS A BASIS FOR PREDICTION. THE POTENTIAL OUTCOMES / COUNTERFACTUAL TERMINOLOGY IS USEFUL FOR EXPLANATION, BUT IS A DIFFICULT APPROACH TO CAUSAL MODEL SPECIFICATION. IT IS NOT AS COMPLETE A FRAMEWORK AS THE PEARL APPROACH (I.E., MAY FAIL TO CERTIFY SOME VALID CONCLUSIONS). IT ENCOUNTERS DIFFICULTIES FROM A QUANTUM-THEORETIC VIEWPOINT, AND IS REJECTED BY SOME (E.G., DAWID). IN THE NEYMAN-RUBIN FRAMEWORK, Y_x(u)) IS VIEWED AS A PRIMITIVE (UNDEFINED QUANTITY), WHEREAS IN THE PEARL FRAMEWORK, IT IS A DERIVED QUANTITY. A SIGNIFICANT ADVANTAGE OF THE PEARL FRAMEWORK IS THAT IT PROVIDES A BASIS FOR DETERMINING (BY EXAMINING THE DAG) WHICH INFERENCES ARE IDENTIFIABLE (ESTIMABLE) (“INTERVENTION CALCULUS,” GRAPHICAL TESTS OF IDENTIFIABLITY, NOT ADDRESSED HERE). THE COUNTERFACTUALS APPROACH REQUIRES ASSUMPTIONS ABOUT THE CONDITIONAL INDEPENDENCE OF COUNTERFACTUAL OUTCOMES,

CONDITIONAL INDEPENDENCE: X AND Y ARE SAID TO BE CONDITIONALLY INDEPENDENT GIVEN Z IF P(x|y,z) = P(x|z) WHENEVER P(y,z)>0.

NOTATION (CONDITIONAL INDEPENDENCE, MUCH USED IN COUNTERFACTUALS APPROACH):

y╨w|x : y IS (CONDITIONALLY) INDEPENDENT OF w GIVEN x

y┴w|x: y IS UNCORRELATED WITH (ORTHOGONAL TO) w GIVEN x

ADJUSTMENT FOR OTHER VARIABLES: COVARIATES, CONCOMMITANTS, AND CONFOUNDERS

X AND Y ARE CONFOUNDED WHEN THERE IS A THIRD VARIABLE Z THAT INFLUENCES BOTH X AND Y (Z IS CALLED A CONFOUNDER OF X AND Y).

TWO VARIABLES X AND Y ARE NOT CONFOUNDED IF AND ONLY IF EVERY VARIABLE Z THAT IS NOT AFFECTED BY X IS EITHER (1) UNASSOCIATED WITH X; OR (2) UNASSOCIATED WITH Y, CONDITIONAL ON X.

SIMPSON’S PARADOX: ANY STATISTICAL RELATIONSHIP BETWEEN TWO VARIABLES MAY BE REVERSED BY INCLUDING ADDITIONAL FACTORS IN THE MODEL. FOR EXAMPLE (FROM PEARL), “…WE MAY FIND THAT STUDENTS WHO SMOKE OBTAIN HIGHER GRADES THAN THOSE WHO DO NOT SMOKE BUT, ADJUSTING FOR AGE, SMOKERS OBTAIN LOWER GRADES IN EVERY AGE GROUP AND, FURTHER ADJUSTING FOR FAMILY INCOME, SMOKERS AGAIN OBTAIN HIGHER GRADES THAN NONSMOKERS IN EVERY INCOME-AGE GROUP, AND SO ON.”

(TECHNICAL DEFINITION OF SIMPSON’S PARADOX:

E(y|w=1) – E(y|w=0) > (<) 0, while E(y|x,w=1) – E(y|x,w=0) < (>) 0 for all x.)

THE ADJUSTMENT PROBLEM: WHAT COVARIATES SHOULD BE INCLUDED IN A MODEL? CANNOT BE DETERMINED FROM DATA – RESTS ON ASSUMPTIONS.

THE POTENTIAL-OUTCOMES APPROACH. AS PRESENTED BY ROSENBAUM AND RUBIN, HAS SOME PROBLEMS. THE COUNTERFACTUAL (THE VALUE THAT Y WOULD HAVE BEEN, HAD X BEEN x)) IS TAKEN AS A PRIMITIVE, NOT A DERIVED CONSTRUCT. THAT APPROACH DOES NOT SPECIFY A MATHEMATICAL MODEL FROM WHICH CAUSAL CONSISTENCY MAY BE ESTABLISHED, OR FOR ADDRESSING THE ISSUE OF COMPLETENESS (WHETHER THE RELATIONSHIPS AT HAND ARE SUFFICIENT FOR DETERMINING THE VALIDITY OF ALL INFERENCES).

IGNORABILITY: “Z IS AN ADMISSIBLE SET OF COVARIATES IF, GIVEN Z, THE VALUE THAT Y WOULD OBTAIN HAD X BEEN x IS INDEPENDENT OF X.” COUNTERFACTUALS ARE NOT OBSERVABLE, AND ASSESSMENT OF CONDITIONAL INDEPENDENCE IS DIFFICULT.

PEARL PRESENTS A METHOD, BASED ON ANALYSIS OF CAUSAL GRAPHS, FOR SOLVING THE ADJUSTMENT PROBLEM.

TESTING FOR IDENTIFICATION. PEARL PRESENTS GRAPHICAL TESTS OF IDENTIFIABILITY (OF CAUSAL EFFECTS): BACK-DOOR CRITERION, FRONT-DOOR CRITERION. METHODOLOGY INCLUDES ANALYSIS OF PRIMITIVE INTERVENTIONS (do(x)) AND COMPLEX PLANS (“do x if you see z” or “do x with probability p if you see p”).

OTHER METHODS FOR TESTING FOR IDENTIFICATION ARE DISCUSSED IN BERRY (Nonrecursive Causal Models). (VERIFY THAT CAN SOLVE FOR SIMULTANEOUS-EQUATION MODEL PARAMETERS, GIVEN VALUES FOR THE REDUCED EQUATION.) OVERIDENTIFICATION / MULTIPLE SOLUTIONS.

SUMMARY AND CONCLUSION: PEARL’S APPROACH TO CAUSAL MODELING IS A SOUND MATHEMATICAL BASIS FOR ESTIMATING CAUSAL EFFECTS. NEYMAN-RUBIN POTENTIAL- OUTCOMES MODEL CAN BE REPRESENTED IN THIS FRAMEWORK, AND IS USEFUL FOR EXPLANATION. THE MODELS THAT ARISE IN INTERNATIONAL DEVELOPMENT APPLICATIONS ARE RELATIVELY SIMPLE, AND RESTRICTING DISCUSSION TO THE POTENTIAL-OUTCOMES APPROACH IS ADEQUATE.

6.3. Impact Measures

IMPACT MEASURES

SEQUENCE OF IMPLEMENTATION OF INTERVENTION: INPUT-PROCESS-OUTPUT-OUTCOME-IMPACT

IMPACT MEASURES:

OBSERVED TREATMENT EFFECT (OTE): DIFFERENCE IN MEAN OUTCOMES FOR TREATED AND UNTREATED SAMPLE UNITS

AVERAGE TREATMENT EFFECT (ATE): AVERAGE EFFECT OF TREATMENT ON A RANDOMLY SELECTED MEMBER OF THE ELIGIBLE (TARGET) POPULATION

AVERAGE TREATMENT EFFECT ON THE TREATED (ATT, TOT): AVERAGE EFFECT OF TREATMENT FOR TREATED INDIVIDUALS

INTENTION-TO-TREAT EFFECT (ITT): AVERAGE EFFECT OF TREATMENT FOR THOSE SELECTED (BY RANDOMIZATION) FOR TREATMENT

LOCAL AVERAGE TREATMENT EFFECT (LATE): EFFECT OF TREATMENT ON “COMPLIERS” (INDIVIDUALS WHO TAKE TREATMENT IF OFFERED AND DO NOT TAKE TREATMENT IF NOT OFFERED)

PARTIAL TREATMENT EFFECT (PTE): CHANGE IN ATE PER UNIT CHANGE IN A TREATMENT VARIABLE

MARGINAL TREATMENT EFFECT (MTE): AVERAGE EFFECT OF TREATMENT FOR THOSE “JUST ELIGIBLE” FOR A PROGRAM

QUANTILE TREATMENT EFFECT (QTE): AVERAGE EFFECT OF TREATMENT AT A QUANTILE OF A DISTRIBUTION

WILL DESCRIBE MOST, BUT NOT ALL, OF THE PRECEDING IMPACT MEASURES, AND DISCUSS A FEW IN DETAIL.

WILL FIRST DEVELOP THEORY FOR THE CASE OF A SINGLE BINARY TREATMENT VARIABLE, IN THE CASE OF A SINGLE CROSS-SECTIONAL DESIGN (TWO SAMPLES, ONE TREATED AND THE OTHER NOT TREATED; TREATMENT SAMPLE AND COMPARISON SAMPLE (USE THE TERM “CONTROL” MAINLY IN EXPERIMENTS WITH RANDOMIZED ASSIGNMENT TO TREATMENT)).

THE TERM “GROUP” MAY REFER EITHER TO A SAMPLE OR A POPULATION (E.G., “TREATMENT GROUP” MAY REFER TO THE ENTIRE TREATED POPULATION, OR TO A SAMPLE FROM THAT POPULATION).

POTENTIAL OUTCOMES MODEL (SOMETIMES CALLED THE COUNTERFACTUAL MODEL):

FOR EACH SAMPLE UNIT (INDEX i), THERE ARE TWO POTENTIAL OUTCOMES:

y_i = y_0i if i-th unit is untreated

= y_1i if i-th unit is treated

IMPACT OF TREATMENT ON THE i-TH UNIT IS y_1i – y_0i

IF DEFINE TREATMENT INDICATOR VARIABLE

w_i = 0 if i-th unit is untreated

= 1 if i-th unit is treated

THEN

y_i = y_0i + (y_1i – y_0i)w_i.

FOR SIMPLICITY, DROP INDEX i (USED IN FORMULAS), AND WRITE:

y = y₀ + (y₁ – y₀)w.

PRIMARY GOAL OF EVALUATION IS TO ESTIMATE THE AVERAGE TREATMENT EFFECT (ATE), OR EXPECTED TREATMENT EFFECT:

ATE = E(y₁ – y₀),

OR TO ESTIMATE THE AVERAGE TREATMENT EFFECT ON THE TREATED (ATT)

ATT = E(y₁ – y₀ | w=1) = E(y₁ | w=1) – E(y₀ | w=1).

EXPRESSIONS SUCH AS E(y₁ | w =1) ARE CONDITIONAL EXPECTATIONS.

NOTE THAT

E(y | w=1) = E(y₀ + (y₁ – y₀)w | w=1) = E(y₁ | w=1)

AND

E(y | w=0) = E(y₀ + (y₁ – y₀)w | w=0) = E(y₀ | w=0).

EXAMPLE:

EFFECT OF AN EDUCATION OR TRAINING PROGRAM ON EARNINGS (E.G., FARMER TRAINING AND DEVELOPMENT ASSISTANCE (FTDA) PROGRAM IN HONDURAS).

ATE IS THE AVERAGE INCREASE IN EARNINGS FOR A RANDOMLY SELECTED MEMBER OF THE POPULATION. (THIS IS WHAT IS OF PRIMARY INTEREST TO A GOVERNMENT POLICY MAKER.)

ATT IS THE AVERAGE INCREASE IN EARNINGS FOR PROGRAM GRADUATES.

ATT IS PROBABLY HIGHER THAN ATE, SINCE GRADUATES ARE LIKELY TO BE MORE MOTIVATED, AMBITIOUS AND ABLE THAN THE GENERAL POPULATION; OR BECAUSE THE PROGRAM IMPLEMENTER MAY SELECT PARTICIPANTS WHO ARE MORE LIKELY TO SUCCEED.

AS A RESULT, THE OTE IS PROBABLY HIGHER THAN THE ATE. OTE WOULD LIKELY BE A BIASED-HIGH ESTIMATE OF ATE.

FORMULAS FOR ATE AND ATT:

ATE = E(y₁ – y₀) = E(y₁) – E(y₀)

= E(y₁|w=1) P(w=1) + E(y₁|w=0) P(w=0) - E(y₀|w=1) P(w=1) – E(y₀|w=0) P(w=0).

FROM THIS EXPRESSION, CAN OBTAIN:

OTE = E(y|w=1) – E(y|w=0)

= E(y₁|w=1) – E(y₀|w=0)

= E(y₁ – y0) + [E(y₀|w=1) – E(y₀|w=0)] + (1–P(w=1)) [E(y₁ – y₀ | w=1) – E(y₁ – y₀|w=0)]

= ATE +Selection Bias + Differential Treatment Effect.

WE ALSO HAVE:

OTE = E(y|w=1) – E(y|w=0)

= E(y₁|w=1) – E(y₀|w=0)

= [E(y₀|w=1) – E(y₀|w=1)] + [E(y₀|w=1) – E(y₀|w=0)]

= ATT + Selection Bias.

NOTE THAT ATE AND ATT DIFFER ONLY BY THE DIFFERENTIAL TREATMENT EFFECT.

IF WE ASSIGN TREATMENT BY RANDOMIZATION, THE POTENTIAL OUTCOMES y₀ and y₁ ARE INDEPENDENT OF TREATMENT, w. IN THIS CASE:

E(y₀|w=1) = E(y₀|w=0),

SO THE SELECTION BIAS IS ZERO, SO THAT OTE = ATT; AND

E(y₁ – y₀)|w=1) = E(y₁ – y₀|w=0)

SO THE DIFFERENTIAL TREATMENT EFFECT IS ALSO ZERO, SO THAT ATE=ATT (=OTE).

AN ALTERNATIVE WAY OF SHOWING THE LATTER RESULT IS TO WRITE

y₀ = μ₀ + v₀

and

y₁ = μ₁ + v₁

where

μ_i = E(y_i), i = 0, 1

and

E(v_i) = 0

(THAT IS, SPLIT y_i INTO ITS MEAN PLUS A RANDOM COMPONENT). IN THIS NOTATION,

y₁ – y₀ = μ₁ – μ₀ + v₁ – v₀ = ATE + v₁ – v₀.

TAKING EXPECTATIONS ON BOTH SIDES OF THE EQUATION, CONDITIONAL ON w = 1, YIELDS

E(y₁ – y₀|w=1) = ATE + E(v₁ – v₀|w=1)

ATT = ATT + E(v₁ – v₀|w=1).

THAT IS, ATT AND ATE DIFFER BY THE DIFFERENTIAL TREATMENT EFFECT.

IN SUMMARY, UNDER THE ASSUMPTION OF INDEPENDENCE OF (y₀, y₁) and w, ATT EQUALS ATE, AND BOTH MAY BE ESTIMATED AS THE DIFFERENCE IN MEANS BETWEEN THE TREATED AND UNTREATED POPULATIONS.

THIS RESULT UNDERSCORES THE DESIRABILITY OF USING RANDOMIZED ASSIGNMENT OF TREATMENT – THE ANALYSIS IS STRAIGHTFORWARD, AND THE ESTIMATES ARE UNBIASED.

FOR MANY APPLICATIONS IN INTERNATIONAL DEVELOPMENT, IT IS NOT FEASIBLE TO RANDOMLY ASSIGN TREATMENT. MUCH OF THE SUBJECT OF STATISTICAL DESIGN AND ANALYSIS ADDRESSES THE ISSUE OF WHAT TO DO IN THAT CASE.

NOTE: THE PRECEDING DISCUSSED OTE, ATE AND ATT. THE OTHER IMPACT ESTIMATORS LISTED EARLIER WILL BE ADDRESSED LATER.

ALTERNATIVES TO RANDOMIZED ASSIGNMENT OF TREATMENT: CONDITIONAL INDEPENDENCE (“IGNORABILITY OF TREATMENT”)

TWO TECHNIQUES: MATCHING AND REGRESSION ANALYSIS (REGRESSION ADJUSTMENT, COVARIATE ADJUSTMENT).

MATCHING: SELECT COMPARISON SAMPLE TO BE SIMILAR TO THE TREATMENT SAMPLE WITH RESPECT TO OBSERVABLE VARIABLES (THAT ARE BELIEVED TO HAVE AN EFFECT ON OUTCOME).

REGRESSION ADJUSTMENT: DEVELOP A STATISTICAL MODEL THAT ESTIMATES PARAMETERS OF THE CAUSAL MODEL, AND USE THIS AS A BASIS FOR ESTIMATING IMPACT (AVERAGE TREATMENT EFFECT OR PARTIAL TREATMENT EFFECT).

KEY RESULT: MATCHING AND REGRESSION CAN BE COMBINED TO PRODUCE CONSISTENT ESTIMATES IF EITHER THE REGRESSION MODEL OR THE MATCHING MODEL IS CORRECTLY SPECIFIED. THIS APPROACH IS SAID TO BE DOUBLY ROBUST.

REFERENCES ON MATCHING:

Rosenbaum, Paul R. and Donald B. Rubin, “The central role of the propensity score in observational studies for causal effects,” Biometrika (1983), Vol. 70, No. 1, pp. 41-55.

Ho, Daniel, Kosuke Imai, Gary King, and Elizabeth Stuart. "Matching as Nonparametric Preprocessing for Reducing Model Dependence in Parametric Causal Inference." Political Analysis 15 (2007): 199-236 (posted at Internet website http://gking.harvard.edu/gking/files/matchp.pdf).

IDEAL SITUATION: WANT INDEPENDENCE OF POTENTIAL OUTCOMES (y₀, y₁) AND TREATMENT w (E.G., AS IN AN EXPERIMENTAL DESIGN (RANDOMIZED ASSIGNMENT TO TREATMENT)).

ACHIEVABLE GOAL: CONDITIONAL INDEPENDENCE OF (y₀, y₁) AND TREATMENT w, CONDITIONAL ON OBSERVED COVARIATES x. (BOLD LETTERS WILL NOW BE USED TO DENOTE VECTORS.) THIS CONDITION IS CALLED CONDITIONAL INDEPENDENCE, IGNORABILITY OR UNCONFOUNDEDNESS. IF, IN ADDITION, 0 < P(w=1|x) < 1, THE CONDITION IS CALLED STRONG IGNORABILITY (FOR ANY SETTING OF x IN THE POPULATION, THERE IS A CHANCE OF SEEING UNITS IN THE TREATMENT AND COMPARISON GROUPS). THE TERM “IGNORABLE” IS USED SINCE, CONDITIONAL ON x, THE POTENTIAL OUTCOMES FOR A UNIT DO NOT DEPEND ON TREATMENT (w), I.E., TREATMENT STATUS OR MECHANISM MAY BE “IGNORED" (WHEN COMPARING THE POTENTIAL OUTCOMES).

A BALANCING SCORE IS ANY FUNCTION OF THE COVARIATES, b(x), SUCH THAT THE CONDITIONAL DISTRIBUTION OF x GIVEN b(x) IS INDEPENDENT OF TREATMENT (I.E., THE SAME FOR TREATMENT AND COMPARISON UNITS). ROSENBAUM AND RUBIN SHOWED THAT THE “COARSEST” BALANCING SCORE IS THE PROPENSITY SCORE, WHICH IS THE PROBABILITY OF BELONGING TO THE TREATMENT GROUP, e(x) = P(w=1|x).

FURTHERMORE, IF TREATMENT IS STRONGLY IGNORABLE (I.E., UNDER THE ASSUMPTION OF CONDITIONAL INDEPENDENCE), THE DIFFERENCE BETWEEN THE TREATMENT AND COMPARISON MEANS CONDITIONAL ON ANY VALUE OF A BALANCING SCORE IS AN UNBIASED ESTIMATE OF THE ATE AT THE VALUE. HENCE, PAIR MATCHING, SUBGROUP MATCHING, OR COVARIATE ADJUSTMENT ON THE PROPENSITY SCORE PRODUCES UNBIASED ESTIMATES OF TREATMENT EFFECTS (UNDER THE ASSUMPTION OF STRONG IGNORABILITY).

ROSENBAUM AND RUBIN’S RESULT IS FOR THE TRUE PROPENSITY SCORE. IN PRACTICE, WE CAN MATCH ONLY ON OBSERVABLE COVARIATES (x), AND IT IS NECESSARY TO ASSUME CONDITIONAL INDEPENDENCE, GIVEN MATCHING ON OBSERVABLES.

REFERENCES ON IMPACT ESTIMATORS IN THE POTENTIAL-OUTCOMES FRAMEWORK:

Morgan, Stephen L. and Christopher Winship, Counterfactuals and Causal Inference: Methods and Principles for Social Research, Cambridge University Press, 2007.

Lee, Myoung-Jae, Micro-Econometrics for Policy, Program and Treatment Effects, Oxford University Press, 2005.

Angrist, Joshua D. and Jörn-Steffen Pischke, Mostly Harmless Econometrics: An Empiricist’s Companion, Princeton University Press, 2009.

PRECISION, BIAS AND ACCURACY

PRECISION (RELIABILITY) REFERS TO VARIATION OF A PARAMETER ESTIMATOR AROUND ITS EXPECTED VALUE. IT IS MEASURED BY THE STANDARD ERROR (STANDARD DEVIATION) OF THE ESTIMATOR.

BIAS (VALIDITY) IS THE DIFFERENCE BETWEEN THE EXPECTED VALUE OF AN ESTIMATOR AND THE (TRUE) VALUE OF THE PARAMETER BEING ESTIMATED.

ACCURACY IS A COMBINATION MEASURE OF PRECISION AND BIAS. IT REFERS TO VARIATION OF A PARAMETER ESTIMATOR AROUND THE (TRUE) VALUE OF THE PARAMETER BEING ESTIMATED. IT IS MEASURED BY THE ROOT MEAN SQUARED ERROR, MSE, EQUAL TO THE SQUARE ROOT OF THE VARIANCE OF THE ESTIMATOR PLUS THE SQUARE OF THE BIAS.

UNBIASEDNESS AND CONSISTENCY

AN ESTIMATOR IS UNBIASED IF ITS EXPECTED VALUE IS EQUAL TO THE (TRUE) VALUE OF THE PARAMETER BEING ESTIMATED.

AN ESTIMATOR IS CONSISTENT IF ITS EXPECTED VALUE CONVERGES TO THE (TRUE) VALUE OF THE PARAMETER BEING ESTIMATED, AS THE SAMPLE SIZE BECOMES VERY LARGE.

IN EVALUATION (ECONOMETRICS, ANALYTICAL SURVEYS), EXPLANATORY VARIABLES ARE USUALLY VIEWED AS RANDOM VARIABLES, NOT AS FIXED QUANTITIES, AND ATTENTION FOCUSES ON ASYMPTOTIC PROPERTIES OF ESTIMATORS (I.E., ON CONSISTENCY).

INTERNAL VALIDITY AND EXTERNAL VALIDITY

INTERNAL VALIDITY OF AN ESTIMATOR REFERS TO ITS ACCURACY RELATIVE TO THE POPULATION UNDER STUDY. (USE A CONSISTENT ESTIMATOR.)

EXTERNAL VALIDITY OF AN ESTIMATOR REFERS TO ITS ACCURACY RELATIVE TO A LARGER POPULATION OF INTEREST. (SELECT A PROBABILITY SAMPLE FROM THE TARGET POPULATION.)

6.4. Basic Evaluation Designs; Models; Estimators

BASIC EVALUATION DESIGNS / MODELS / ESTIMATORS

EXAMPLE DESIGNS TO BE DISCUSSED:

DESIGNS BASED ON RANDOMIZATION

TWO-GROUP DESIGNS

TREATMENT/CONTROL DESIGN

PRETEST/POSTTEST DESIGN

INTERRUPTED TIME-SERIES DESIGN

FOUR-GROUP DESIGN

QUASI-EXPERIMENTAL DESIGNS

OBSERVATIONAL DATA

DESIGNS BASED ON RANDOMIZATION

NOTE: RANDOMIZATION SHOULD OCCUR AT THE LEVEL OF THE ULTIMATE SAMPLING UNIT, E.G., AT THE HOUSEHOLD LEVEL. IN MANY EVALUATION STUDIES, IT OCCURS AT A HIGHER ADMINISTRATIVE LEVEL, SUCH AS A VILLAGE, CENSUS ENUMERATION AREA, OR DISTRICT. THIS TYPE OF RANDOMIZATION (USUALLY REFERRED TO AS “CLUSTER RANDOMIZATION”) PRESENTS PROBLEMS, WHICH WILL BE DISCUSSED LATER. (SUCH DESIGNS SHOULD BE CLASSIFIED AS “QUASI-EXPERIMENTAL” DESIGNS.)

TWO-GROUP DESIGNS

TREATMENT/CONTROL DESIGN

RANDOMLY SELECT A UNIT FROM THE POPULATION OF INTEREST (TARGET POPULATION, ELIGIBLE POPULATION), AND RANDOMLY ASSIGN EACH UNIT TO TREATMENT OR CONTROL (NON-TREATMENT). APPLY THE TREATMENT TO THOSE SELECTED FOR TREATMENT, AND MAKE OBSERVATION.

DESIGN USEFUL IF RESULTS OCCUR QUICKLY.

NOTE TWO TYPES OF RANDOMIZATION:

RANDOM SELECTION FROM THE POPULATION (FOR EXTERNAL VALIDITY)

RANDOM ASSIGNMENT TO TREATMENT (FOR INTERNAL VALIDITY)

STATISTICAL MODEL:

y_i = α + β w_i + e_i

y = α + β w + e

where

y = outcome variable (explained variable, dependent variable, response variable, regressand)

w = treatment variable (explanatory variable, independent variable, regressor); = 0 if untreated, 1 if treated

e = error term (mean zero, independent of each other and independent of w).

NOTE: UNDER THE POTENTIAL-OUTCOMES CONCEPTUAL FRAMEWORK, THE PRECEDING MODEL APPLIES TO EACH UNIT, ALTHOUGH ONLY ONE OUTCOME IS OBSERVED FOR EACH UNIT (I.E., FOR w = 0 OR FOR w = 1, BUT NOT BOTH).

IMPACT MEASURE:

ATE = DIFFERENCE IN MEANS OF POTENTIAL OUTCOMES

= E(y₁ – y₀) = E(y|w=1) – E(y|w=0) = (α + β) – (α) = β.

NOTE: ARE AVERAGING OVER THE POPULATION OF UNITS.

IMPACT ESTIMATOR:

DIFFERENCE IN MEANS OF TREATMENT AND CONTROL GROUPS

= (α + β) – (α) = β.

NOTE: ARE AVERAGING OVER THE SAMPLE UNITS.

BECAUSE OF RANDOMIZED ASSIGNMENT TO TREATMENT, THE DISTRIBUTION OF EVERY VARIABLE EXCEPT TREATMENT IS THE SAME FOR THE TREATMENT AND CONTROL SAMPLES.

PRETEST/POSTTEST DESIGN (“BEFORE/AFTER,” “REFLEXIVE” DESIGN)

RANDOMLY SELECT A UNIT FROM THE POPULATION OF INTEREST (TARGET POPULATION, ELIGIBLE POPULATION). MAKE OBSERVATIONS AT TWO POINTS IN TIME (PRETEST/POSTTEST, BEFORE/AFTER).

NOTE: JUST ONE TYPE OF RANDOMIZATION: RANDOM SELECTION FROM THE POPULATION (FOR EXTERNAL VALIDITY), BUT NO RANDOM ASSIGNMENT TO TREATMENT (FOR INTERNAL VALIDITY).

MODEL, IMPACT MEASURE AND IMPACT ESTIMATOR SAME AS ABOVE.

DESIGN MAY BE APPROPRIATE FOR ASSESSING AN IMPACT THAT MANIFESTS QUICKLY.

IF THE TIME BETWEEN SURVEYS IS LONG, MANY VARIABLES THAT MAY AFFECT OUTCOME MAY CHANGE OVER TIME, AND THE POSTULATED MODEL MAY BE INVALID, IN WHICH CASE THE DIFFERENCE IN THE TWO SAMPLE MEANS (BEFORE AND AFTER) WOULD NOT BE AN UNBIASED ESTIMATE OF THE IMPACT MEASURE.

INTERRUPTED TIME-SERIES DESIGN

MAY BE USEFUL IN FINANCIAL INTERVENTIONS, WHERE MUCH MONTHLY DATA IS AVAILABLE:

y₁, y₂, y₃, …y_t, intervention, y_t+1, y_t+2,…y_n

INTERVENTION AT A RANDOM TIME.

MAY HAVE MANY TIME SERIES (E.G., MANY BANKS).

STATISTICAL MODEL: AUTOREGRESSIVE INTEGRATED MOVING AVERAGE (ARIMA) MODEL OR AUTOREGRESSIVE CONDITIONAL HETEROSKEDASTICITY (ARCH) MODEL, E.G., ARMA(1,1)

y_t = x_tβ + ρ(y_t-1 – x_t-1β) + θε_t-1 + ε_t.

THE IMPACT IS ONE OF THE β COEFFICIENTS.

[SHOW GRAPH.]

FOUR-GROUP DESIGN (TREATMENT BEFORE, TREATMENT AFTER, CONTROL BEFORE, CONTROL AFTER)

POSSIBLE MODEL SPECIFICATION (REPRESENTATION):

Time 1 Time 2

t=0 t=1

Control Group w=0 w=0

Treatment Group w=0 w=1

RANDOMIZED ASSIGNMENT OF TREATMENT.

DESIGN USEFUL IF RESULTS REQUIRE SOME TIME TO OCCUR, AND IF VARIABLES OTHER THAN TREATMENT THAT AFFECT OUTCOME HAVE THE SAME VALUES FOR THE TREATMENT AND CONTROL SAMPLES.

STATISTICAL MODEL:

y = α + θt + ϕw + e.

EFFECT (IMPACT) IS COEFFICIENT, ϕ, OF TREATMENT VARIABLE, w.

ALTERNATIVE MODEL SPECIFICATION (MORE USEFUL LATER ON, TO ACCOUNT FOR SELECTION EFFECTS):

Time 1 Time 2

t=0 t=1

Control Group w=0 w=0

Treatment Group w=1 w=1

STATISTICAL MODEL:

y = α + θt + ϕw + δtw + e.

EFFECT IS COEFFICIENT, δ, OF THE INTERACTION EFFECT OF TREATMENT AND TIME.

BECAUSE OF RANDOMIZED ASSIGNMENT TO TREATMENT, ϕ=0 (NO DIFFERENCE BETWEEN TREATMENT AND CONTROL GROUPS AT TIME 0 (THE BASELINE)). LATER, THIS ASSUMPTION WILL BE DROPPED.

IMPACT MEASURE:

DOUBLE-DIFFERENCE MEASURE:

DD = (μ_T1 – μ_T0) – (μ_C1 – μ_C0)

WHERE THE FIRST SUBSCRIPT SPECIFIES TREATMENT OR CONTROL GROUP (T OR C, CORRESPONDING (IN THE ALTERNATIVE MODEL REPRESENTATION) TO w = 1 OR w = 0) AND THE SECOND SUBSCRIPT SPECIFIES TIME (t = 0 OR t = 1).

DOUBLE-DIFFERENCE ESTIMATOR:

THE TREMENDOUS ADVANTAGE OF THE RANDOMIZED-ASSIGNMENT, IF ALL COVARIATES HAVE THE SAME VALUES (OR TIME-VARY THE SAME WAY) FOR THE TREATMENT AND CONTROL GROUPS, IS THAT THE ESTIMATOR DOES NOT HAVE TO TAKE ANY COVARIATES INTO ACCOUNT. THAT IS, THE “RAW” DOUBLE-DIFFERENCE ESTIMATOR (OTE) IS AN UNBIASED ESTIMATE OF IMPACT.

THE FACT IS, OVER TIME, MANY VARIABLES AFFECTING OUTCOME, OTHER THAN TREATMENT, MAY VARY DIFFERENTLY FOR THE TREATMENT AND CONTROL GROUPS, AND TAKING THIS INTO ACCOUNT WILL BE NECESSARY EVEN FOR A RANDOMIZED FOUR-GROUP (BEFORE AND AFTER) DESIGN.

QUASI-EXPERIMENTAL DESIGNS

QUASI-EXPERIMENTAL DESIGNS HAVE STRUCTURE SIMILAR TO RANDOMIZED DESIGNS, BUT LACK PROPER RANDOMIZED ASSIGNMENT TO TREATMENT. THE COMPARISON SAMPLE IS NOT FORMED BY RANDOMIZED ASSIGNMENT TO TREATMENT, BUT BY MATCHING.

A NUMBER OF MATCHING PROCEDURES IS AVAILABLE, INCLUDING JUDGMENT MATCHING AND VARIOUS NUMERICAL-ALGORITHM PROCEDURES. MATCHING IS DONE USING AVAILABLE DATA ON VARIABLES THAT MAY AFFECT OUTCOME (OR SELECTION). SINCE DATA ARE AVAILABLE GENERALLY FOR ADMINISTRATIVE UNITS SUCH AS VILLAGES, CENSUS ENUMERATION AREAS, AND DISTRICTS, MATCHING IS GENERALLY DONE AT THOSE LEVELS, NOT AT THE LEVEL OF THE HOUSEHOLD (ULTIMATE SAMPLE UNIT).

NOTE THAT MATCHING IS DONE ON INDEPENDENT VARIABLES, NOT ON DEPENDENT VARIABLES. MATCHING ON DEPENDENT VARIABLES CAN INTRODUCE REGRESSION-EFFECT BIAS (AS IN THE WESTINGHOUSE – OHIO STATE EVALUATION OF THE HEAD START PROGRAM).

MATCHING ADJUSTS FOR OVERT BIAS (IMBALANCE IN A COVARIATE), BUT NOT HIDDEN BIAS.

REGRESSION-EFFECT BIAS (REGRESSION TO THE MEAN):

FRANCIS GALTON: CHILDREN’S (ADULT) HEIGHT IS A WEIGHTED AVERAGE OF PARENTS’ HEIGHT AND THE POPULATION AVERAGE HEIGHT, I.E., IT “REGRESSES” TO THE POPULATION MEAN.

EXPLANATION (EXAMPLE FROM ANGRIST, OP. CIT. P. 108):

HEIGHT IS STATIONARY (DOES NOT CHANGE MUCH OVER TIME).

BIVARIATE PLOT SHOWS CLEAR LINEAR RELATIONSHIP [SHOW GRAPH].

y =child height

x = parent height

y = α + β x + e

Since height is not changing over time (i.e., across generations), the mean and variance of x and y are the same. Hence

β = cov(y,x)/var(x) = cov(y,x)/sqrt(var(y) var(x)) = ρ_xy

and

α = E(y) – βE(x) = μ(1 – β) = μ(1 – ρ_xy)

where ρ_xy is the intergenerational correlation coefficient in height and μ = E(y) = E(x) is the population mean height.

Hence the conditional expectation of y given x is

E(y|x) = α + βx = μ(1 – ρ_xy) + ρ_xy x

i.e., the height of an adult child is a weighted average of his parents’ height and the population mean.

THE PHENOMENON OF REGRESSION TO THE MEAN OCCURS WHENEVER MATCHING IS DONE ON AN IMPRECISE PRE-MEASURE OF THE DEPENDENT VARIABLE (E.G., SELECTING A CONTROL GROUP FROM A GENERAL POPULATION TO MATCH TO A LESS-ABLE POPULATION, USING TEST SCORES).

TYPES OF MATCHING

MATCHING PRIOR TO RANDOMIZED ASSIGNMENT TO TREATMENT. THIS IS NOT THE TYPE OF MATCHING DISCUSSED HERE, FOR CONSTRUCTION OF CONTROL GROUPS WHEN RANDOMIZED ASSIGNMENT HAS NOT BEEN DONE. THAT TYPE OF MATCHING (“BLOCKING” FOR LOCAL CONTROL) IS USED FOR “MATCHED PAIRS” DESIGNS, TO IMPROVE PRECISION. IT HAS NOTHING TO DO WITH THE PRESENT TOPIC.

EX-ANTE MATCHING. MATCHING PRIOR TO CONDUCT OF THE SURVEY, DURING SURVEY DESIGN. USUALLY CONDUCTED AT AN AGGREGATE LEVEL, SUCH AS VILLAGE, CENSUS ENUMERATION AREA OR DISTRICT (FOR WHICH DATA ARE AVAILABLE FOR USE IN SURVEY DESIGN).

EX-POST MATCHING. MATCHING DONE ON THE FULL DATA SET (E.G., AT THE HOUSEHOLD LEVEL), DURING ANALYSIS (TO REDUCE MODEL DEPENDENCE ON THE DATA). ALSO CALLED TRIMMING, PRUNING OR CULLING OF THE SAMPLE. “DISCARDS,” “THROWS AWAY,” OR “LOSES” DATA. OF LIMITED USE IN INTERNATIONAL DEVELOPMENT APPLICATIONS, WHICH TYPICALLY INVOLVE TWO-STAGE SAMPLE DESIGNS WITH SMALL FIRST-STAGE SAMPLE SIZES. CANNOT AFFORD TO LOSE DATA. USE PRIMARILY REGRESSION ADJUSTMENT, NOT EX-POST MATCHING, FOR DATA ANALYSIS IN THIS FIELD.

MANY MATCHING TECHNIQUES AVAILABLE, E.G.,:

EXACT MATCHING

DISTRIBUTION MATCHING

MATCHING ON A SCORE (MEASURE OF CLOSENESS)

NEAREST-NEIGHBOR(S) MATCHING

MAHALANOBIS-DISTANCE MATCHING

PROPENSITY-SCORE MATCHING

NEAREST-NEIGHBOR

RADIUS (CALIPER)

STRATIFIED

KERNEL (WEIGHTING)

IMPORTANCE-FUNCTION MATCHING

SELECTION-CRITERION-SCORE MATCHING FOR REGRESSION-DISCONTINUITY DESIGN

OPTIMAL MATCHING

SEE HO ET AL. ARTICLE FOR DETAILS ON MANY OF THE PRECEDING. SEE “MATCHIT” SOFTWARE FOR IMPLEMENTATION.

“JUDGMENT MATCHING” – ALL MATCHING METHODS ARE “JUDGMENT MATCHING.” REMEMBER: CAN MATCH “AT WILL” ON EXPLANATORY VARIABLES.

ALL MATCHING TECHNIQUES ARE BASED ON OBSERVABLES (AVAILABLE EX ANTE OR EX POST).

WITH EX ANTE MATCHING (IN DESIGN), WILL ALMOST INVARIABLY USE REGRESSION ADJUSTMENT AFTER THE FULL DATA SET IS AVAILABLE. USE OF MATCHING ALONE IS INADEQUATE MEANS OF REDUCING BIAS.

WHAT VARIABLES TO INCLUDE AS MATCH VARIABLES? THOSE THAT ARE BELIEVED TO HAVE AN EFFECT ON OUTCOME, BASED ON A CAUSAL MODEL. WITH RESPECT TO PRECISION, MATCHING ON VARIABLES RELATED TO SELECTION IS OF VALUE ONLY TO THE EXTENT THAT THE VARIABLES AFFECTING SELECTION ALSO AFFECT OUTCOME. WITH RESPECT TO BIAS, MATCHING ON VARIABLES RELATED TO SELECTION IS USEFUL (E.G., PROPENSITY-SCORE MATCHING), AS LONG AS THOSE VARIABLES ALSO AFFECT OUTCOME.

EXACT MATCHING:

MATCH EACH TREATMENT UNIT TO ALL POSSIBLE COMPARISON UNITS HAVING EXACTLY THE SAME VALUE ON ALL (MATCH) COVARIATES. FOR EACH TREATMENT UNIT, SELECT A MATCHING COMPARISON UNIT RANDOMLY.

ADVANTAGES: SIMPLICITY, PROBABILITY DISTRIBUTIONS MATCH EXACTLY FOR ALL MATCH VARIABLES. JOINT PROBABILITY DISTRIBUTION MATCHES.

DISADVANTAGES: IN MANY APPLICATIONS, CANNOT FIND EXACT MATCHES (UNLESS CLASSIFICATION CATEGORIES ARE VERY “COURSE”) “CURSE OF DIMENSIONALITY.”

DISTRIBUTION MATCHING:

DISCARD UNITS OUTSIDE OF COMMON SUPPORT. SUBSAMPLE.

DISADVANTAGE: IF MATCH MARGINAL DISTRIBUTIONS, THEN JOINT PROBABILITY DISTRIBUTION DOESN’T MATCH (UNLESS INDEPENDENT).

MATCHING ON A SCORE: DEFINE A MEASURE OF “CLOSENESS” OF UNITS. MATCH CLOSE UNITS (TYPICALLY ONE TO ONE OR ONE TO MANY). ADDRESSES THE “CURSE OF DIMENSIONALITY” (SINCE MATCH ON A SCALAR SCORE).

MAHALANOBIS-DISTANCE MATCHING: IF V IS THE VARIANCE-COVARIANCE MATRIX OF THE MATCH VARIABLES, THE DISTANCE BETWEEN TWO UNITS WITH MATCH VALUES x₁ AND x₂ IS D = (x₁-x₂)’V(x₁-x₂). MATCH NEAREST NEIGHBORS.

DISADVANTAGES: LOW FACE VALIDITY. DOES NOT TAKE INTO ACCOUNT IMPORTANCE OF VARIABLES IN AFFECTING OUTCOME. NO THEORETICAL ADVANTAGES. MOST APPROPRIATE FOR APPLICATIONS INVOLVING THE NORMAL DISTRIBUTION, WHICH IS CHARACTERIZED BY THE MEAN VECTOR AND VARIANCE-COVARIANCE MATRIX.

PROPENSITY-SCORE MATCHING:

ESTIMATE THE PROPENSITY SCORE, WHICH IS THE PROBABILITY OF SELECTION FOR TREATMENT = Pr(w=1|x) (LOGISTIC REGRESSION MODEL). VARIOUS MATCHING PROCEDURES (NEAREST-NEIGHBOR, RADIUS, STRATIFIED, KERNEL).

ADVANTAGE: ROSENBAUM AND RUBIN (1983): UNDER THE ASSUMPTION OF CONDITIONAL INDEPENDENCE (“IGNORABILITY”) OF OUTCOMES (y₀, y₁) AND w GIVEN x, DIFFERENCE OF MEANS OF TREATMENT AND COMPARISON SAMPLES WILL BE UNBIASED ESTIMATE OF IMPACT (ATE = E(y₁ – y₀)).

DISADVANTAGES: UNITS THAT MATCH ON PROPENSITY SCORE MAY BE VERY DIFFERENT WITH RESPECT TO VARIABLES THAT HAVE AN IMPORTANT EFFECT ON OUTCOME, SO THAT THE PRECISION AND POWER OF THE MATCHED SAMPLES MAY BE VERY POOR. IN MANY CASES, THE ASSUMPTION CONDITIONAL INDEPENDENCE IS TENUOUS. SACRIFICING PRECISION AND POWER ON A TENUOUS HOPE THAT THE BIAS MAY BE REDUCED IS UNREASONABLE.

IMPORTANCE-SCORE MATCHING:

ASSIGN WEIGHTS REFLECTING THE IMPORTANCE OF EACH MATCH VARIABLE IN AFFECTING OUTCOMES OF INTEREST. FOR EACH UNIT, CALCULATE THE WEIGHTED SUM OF MATCH VARIABLES. DISTANCE BETWEEN UNITS IS THE DIFFERENCE IN THE WEIGHTED SUM. MATCH NEAREST NEIGHBORS.

ADVANTAGES: SIMPLE. BASED ON CAUSAL MODEL. RESULTS IN MATCHES WITH HIGH PRECISION AND POWER, AND LOW BIAS.

SELECTION-CRITERION-SCORE MATCHING FOR REGRESSION-DISCONTINUITY DESIGN:

IN SOME PROGRAMS, THE TREATMENT POPULATION IS DETERMINED BY USE OF A SCORE, SUCH AS A “PROXY MEANS TEST” SCORE IN A CONDITIONAL-CASH-TRANSFER (CCT) PROGRAM. TREATMENT AND COMPARISON SAMPLES MAY BE OBTAINED BY SELECTING UNITS JUST BELOW AND JUST ABOVE THE CUT-OFF SCORE.

ADVANTAGES: SIMPLE TO IMPLEMENT.

DISADVANTAGES: LIMITS SCOPE OF INFERENCE (EXTERNAL VALIDITY), BECAUSE IT IS RESTRICTED TO THE POPULATION CLOSE TO THE CUT-OFF THRESHOLD. CUT-OFF SCORE FOCUSES ON NEED FOR SERVICE, AND IGNORES THE IMPORTANCE OF VARIABLES THAT AFFECT OUTCOMES OF INTEREST (LOW PRECISION AND POWER).

OPTIMAL MATCHING:

NEAREST-NEIGHBOR MATCHING DEPENDS ON THE ORDER (SEQUENCE) OF THE MATCH, AND, FOR SMALL TREATMENT AND CONTROL POPULATIONS, THE MATCH MAY BE POOR FOR THE LAST MATCHES. OPTIMAL MATCHING SEEKS TO MATCH TO FIND THE MINIMAL VALUE FOR THE AVERAGE DISTANCE.

ADVANTAGE: MAY IMPROVE PRECISION AND POWER OVER NEAREST-NEIGHBOR APPROACH.

DISADVANTAGE: MORE COMPLEX.

REMEMBER: IN ALL INSTANCES, WILL STILL HAVE TO USE COVARIATE ADJUSTMENT (EVEN FOR PROPENSITY-SCORE MATCHING, BECAUSE THE CONDITIONAL INDEPENDENCE ASSUMPTION MAY NOT BE JUSTIFIED (AND THIS MAY BE ADDRESSED WHEN THE FULL DATA SET IS AVAILABLE)). IN PARTICULAR, IF DO MATCHING ON FIRST-STAGE SAMPLE UNITS, WILL HAVE TO COVARIATE-ADJUST WHEN FULL DATA SET IS AVAILABLE.

OBSERVATIONAL DATA

EXPERIMENT: AN EMPIRICAL INVESTIGATION IN WHICH ASSIGNMENT OF TREATMENT TO UNITS (SUBJECTS) IS CONTROLLED BY THE EXPERIMENTOR (INVESTIGATOR, RESEARCHER).

OBSERVATIONAL DATA: NO CONTROL OF ASSIGNMENT OF TREATMENT TO UNITS. (GOAL IS STILL THE SAME: ASSESS CAUSE-AND-EFFECT RELATIONSHIPS.)

IN THE ANALYSIS OF OBSERVATIONAL DATA, THERE IS LITTLE OR NO DESIGN STRUCTURE, AND NO CONTROL OVER THE ASSIGNMENT OF TREATMENT TO UNITS. THERE MAY BE ONE OR MORE CONTROL GROUPS AVAILABLE, BUT THEY ARE NOT CONSTRUCTED BY THE INVESTIGATOR. LOW EXTERNAL AND INTERNAL VALIDITY.

MATCHING AND COVARIATE ADJUSTMENT (OR CONTINGENCY TABLES) ARE DONE IN THE ANALYSIS, NOT IN THE DESIGN.

6.5. Sample Survey Design for Evaluation

SAMPLE SURVEY DESIGN FOR EVALUATION

SAMPLE SURVEY DESIGN FOR EVALUATION IS ANALYTICAL SURVEY DESIGN, WHICH COMBINES ELEMENTS OF DESCRIPTIVE SAMPLE SURVEY DESIGN AND EXPERIMENTAL DESIGN (DESIGN OF EXPERIMENTS).

PRINCIPLES OF EXPERIMENTAL DESIGN

RANDOMIZATION (TO ESTABLISH CAUSALITY)

REPLICATION (FOR ESTIMATION OF EXPERIMENTAL ERROR)

SYMMETRY (FOR EASE OF COMPUTATION AND TO ACHIEVE UNAMBIGUOUS RESULTS (ORTHOGONALITY))

LOCAL CONTROL (TO INCREASE PRECISION AND POWER)

FOR MULTIPLE TREATMENT VARIABLES AND LEVELS, EXPERIMENTAL DESIGNS ARE ELABORATE, E.G., FRACTIONAL FACTORIAL DESIGNS, BALANCED INCOMPLETE BLOCK DESIGNS, LATIN SQUARE DESIGNS. FOR DEVELOPMENT APPLICATIONS, OFTEN HAVE A SINGLE BIVARIATE TREATMENT VARIABLE (TREATED VS. UNTREATED). DESIGNS ARE SIMPLE, BUT THE PRINCIPLES OF EXPERIMENTAL DESIGN STILL APPLY, AND PLAY AN IMPORTANT ROLE.

ALSO VERY IMPORTANT ARE ASPECTS OF DESCRIPTIVE SAMPLE SURVEY DESIGN (STRATIFICATION, CLUSTER SAMPLING, MULTISTAGE SAMPLING), BUT WITH SOME MODIFICATION TO INCORPORATE DESIGN CONSIDERATIONS (MARGINAL STRATIFICATION; MATCHING; INTRODUCTION OF CORRELATIONS (FOR DIFFERENCE ESTIMATES); BALANCE AND SPREAD; ORTHOGONALIZATION OF COVARIATES); POWER ANALYSIS VS. PRECISION ANALYSIS); RANDOM EFFECTS; NO FPC.

DATA ANALYSIS (CONSIDERED IN DAY 2) IS RADICALLY DIFFERENT FOR ANALYTICAL SURVEY DESIGNS COMPARED TO DESCRIPTIVE SURVEY DESIGNS.

DESCRIPTIVE SURVEYS VS. ANALYTICAL SURVEYS

DESCRIPTIVE SURVEY:

ESTIMATE THE CHARACTERISTICS (TOTALS, MEANS, PROPORTIONS) FOR A POPULATION OR SUBPOPULATIONS. FIXED, FINITE POPULATION. DESIGN-BASED ESTIMATES. CLOSED-FORM FORMULAS FOR ESTIMATES AND STANDARD ERRORS. FINITE POPULATION CORRECTION (FPC) (PRECISION BECOMES PERFECT WHEN SAMPLE SIZE APPROACHES FINITE POPULATION SIZE). THE RANDOM VARIABLES OF INTEREST ARE THE EVENTS OF INCLUSION IN THE SAMPLE, NOT THE VARIABLES BEING MEASURED ON THE SAMPLE UNITS. FOCUS ON PRECISION OF POINT ESTIMATES AND (CONFIDENCE INTERVALS), NOT ON TESTS OF HYPOTHESIS. SAMPLE SIZE ESTIMATION BASED ON PRECISION ANALYSIS.

ANALYTICAL SURVEY:

ESTIMATE THE CHARACTERISTICS OF A PROCESS THAT AFFECTS OR GENERATES THE FINITE POPULATION BEING SURVEYED. IMPACT OF AN INTERVENTION, OR RELATIONSHIP OF IMPACT TO EXPLANATORY VARIABLES. MODEL-BASED (MODEL-ASSISTED) ESTIMATES. FINITE POPULATION BEING SURVEYED IS SIMPLY A REALIZATION OF AN INFINITE COLLECTION OF SAMPLES THAT THE PROCESS COULD PRODUCE. FPC DOES NOT APPLY. THE RANDOM VARIABLES OF INTEREST ARE THE VARIABLES BEING MEASURED ON THE SAMPLE UNITS. FOCUS ON POWER OF TESTS OF HYPOTHESIS ABOUT IMPACT. SAMPLE SIZE ESTIMATION BASED ON POWER ANALYSIS.

SAMPLE SURVEY DESIGN TECHNIQUES

CLUSTER SAMPLING

MULTISTAGE SAMPLING

STRATIFIED SAMPLING

ORDINARY STRATIFICATION

MARGINAL STRATIFICATION

TWO-PHASE SAMPLING

USE OF MATCHING TO IMPROVE PRECISION AND POWER

ESTIMATION OF SAMPLE SIZE FOR DESCRIPTIVE SURVEYS

ESTIMATION OF SAMPLE SIZE FOR ANALYTICAL SURVEYS

SAMPLE SELECTION PROCEDURES

CLUSTER SAMPLING

EFFICIENCY OF A DESIGN REFERS TO THE RATIO OF THE PRECISION OR POWER OF AN ESTIMATE TO SURVEY COST (MORE EFFICIENT DESIGN HAS HIGHER PRECISION (LOWER STANDARD ERRORS OF ESTIMATES) AND POWER).

DESIGN EFFECT. THE STANDARD MEASURE OF THE EFFICIENCY OF A DESIGN IS THE RATIO OF THE VARIANCE (OF AN ESTIMATOR) FOR THE DESIGN TO THE VARIANCE USING A SIMPLE RANDOM SAMPLE OF THE SAME SIZE. THIS IS CALLED KISH’S DESIGN EFFECT, OR “DEFF.” IT IS CALLED THE “MOULTON FACTOR” BY SOME ECONOMISTS.

CLUSTER SAMPLING. THE COST OF COLLECTING DATA FROM A SIMPLE RANDOM SAMPLE OF HOUSEHOLDS DISTRIBUTED OVER A LARGE GEOGRAPHIC AREA MAY BE VERY HIGH. IT MAY BE MUCH MORE EFFICIENT TO SELECT A RANDOM SAMPLE OF SMALL AREAS, AND SURVEY THE HOUSEHOLDS IN THE SELECTED AREAS. THE AREAS ARE CALLED “CLUSTERS,” AND THIS TYPE OF SAMPLING IS CALLED “CLUSTER SAMPLING.” THE CLUSTERS MAY BE DEFINED BY THE INVESTIGATOR, BUT MORE LIKELY ARE EXISTING ADMINISTRATIVE GROUPINGS, SUCH AS VILLAGES, CENSUS ENUMERATION AREAS, OR DISTRICTS.

THE EFFICIENCY OF CLUSTER SAMPLING DEPENDS ON THE RELATIVE COST OF SAMPLING CLUSTERS VS. UNITS WITHIN CLUSTERS, AND ON THE INTERNAL HOMOGENEITY OF THE CLUSTERS RELATIVE TO A VARIABLE OF INTEREST.

THE PRECISION OF CLUSTER SAMPLING FOR ESTIMATING THE MEAN OF A VARIABLE OF INTEREST DEPENDS ON THE INTERNAL HOMOGENEITY OF THE CLUSTERS RELATIVE TO THE GENERAL POPULATION.

IF THE VARIATION (FOR A PARTICULAR RESPONSE VARIABLE) IN UNITS WITHIN A CLUSTER IS THE SAME AS THE VARIATION FOR THE GENERAL POPULATION, CLUSTER SAMPLING HAS THE SAME PRECISION AS A SIMPLE RANDOM SAMPLE OF THE SAME (TOTAL UNIT) SIZE (FOR ESTIMATING THE MEAN OF THAT VARIABLE). IF THE VARIATION IS LESS, THE PRECISION OF CLUSTER SAMPLING IS LESS, AND IF THE VARIATION IS GREATER (WHICH IS UNUSUAL), THE PRECISION IS GREATER. IF ALL OF THE UNITS WITHIN A CLUSTER ARE IDENTICAL, THEN THE PRECISION IS THE SAME AS FOR A SIMPLE RANDOM SAMPLE OF SIZE EQUAL TO THE NUMBER OF CLUSTERS.

THE INTERNAL HOMOGENEITY OF A CLUSTER IS MEASURED BY THE INTRA-CLUSTER CORRELATION COEFFICIENT (DENOTED icc OR ρ). IT VARIES FOR EACH VARIABLE OF INTEREST. IT IS EQUAL TO 1 IF ALL OF THE UNITS WITHIN A CLUSTER ARE IDENTICAL (WITH RESPECT TO THE VARIABLE OF INTEREST), AND EQUAL TO 0 IF THE UNITS WITHIN A CLUSTER HAVE THE SAME VARIABILITY AS THE GENERAL POPULATION. FOR MOST VARIABLES, IT IS POSITIVE (I.E., PRECISION IS DECREASED BY CLUSTER SAMPLING), BUT NOT ALWAYS (E.G., THE GENDER OF RESIDENTS IN TWO-MEMBER HOUSEHOLDS IS NEGATIVELY CORRELATED).

THE VALUE OF ρ TENDS TO DECREASE AS THE CLUSTER SIZE (NUMBER OF UNITS IN THE CLUSTER) INCREASES.

IF s² DENOTES THE VARIANCE OF UNITS IN THE POPULATION AND s_w² DENOTES THE WITHIN-CLUSTER VARIANCE OF UNITS, THEN (APPROXIMATELY)

ρ = 1 – s_w²/s²,

AND THE DESIGN EFFECT IS GIVEN BY

deff = 1 + (M-1)ρ,

WHERE M DENOTES THE NUMBER OF UNITS IN EACH CLUSTER (I.E., THE “CLUSTER SIZE”).

MULTISTAGE SAMPLING

CLUSTER SAMPLING IS NOT USED A LOT, BECAUSE IT IS USUALLY INEFFICIENT TO MEASURE (INTERVIEW) ALL UNITS WITHIN A CLUSTER. AT SOME POINT, IT BECOMES MORE EFFICIENT TO SAMPLE MORE CLUSTERS THAN TO COLLECT ADDITIONAL INFORMATION ABOUT THE CLUSTERS ALREADY IN THE SAMPLE (SINCE THEY OFTEN TEND TO BE SIMILAR). INSTEAD, IT IS MORE EFFICIENT TO SELECT A SAMPLE OF UNITS WITHIN EACH CLUSTER, THAN TO SELECT ALL OF THEM. THIS PROCEDURE IS CALLED MULTISTAGE SAMPLING. IN THIS CASE, THE CLUSTERS ARE REFERRED TO AS FIRST-STAGE SAMPLE UNITS OR PRIMARY SAMPLING UNITS (PSUs), AND THE UNITS WITHIN THE FIRST-STAGE SAMPLE UNITS ARE CALLED SECOND-STAGE SAMPLE UNITS OR “ULTIMATE SAMPLE UNITS.”

THE WITHIN-PSU SAMPLE SIZE MAY BE FIXED (DENOTED m) OR VARIABLE (DENOTED m_i). IN MANY APPLICATIONS, IT IS EFFICIENT (ADMINISTRATIVELY CONVENIENT) TO USE A FIXED WITHIN-PSU SAMPLE SIZE, m. FOR LARGE SAMPLE SIZES OF SIMILAR PSUs, RESULTS SIMILAR TO THOSE PRESENTED ABOVE HOLD:

ρ = 1 – s_w²/s²,

AND

deff = 1 + (m-1)ρ.

IT IS OF INTEREST TO DETERMINE THE OPTIMAL VALUE OF m, GIVEN THE VALUES OF ρ AND THE COSTS OF SAMPLING FIRST- AND SECOND-STAGE SAMPLE UNITS, c₁ and c₂, WHERE THE MARGINAL SURVEY COST IS GIVEN BY

C = c₁ n + c₂ nm

WHERE n IS THE NUMBER OF FIRST-STAGE SAMPLE UNITS AND m IS THE NUMBER OF SECOND-STAGE SAMPLE UNITS:

m_opt = sqrt( (c₁/c₂) (1-ρ)/ρ) ).

IF C IS SPECIFIED, THEN THE FIRST-STAGE SAMPLE SIZE, n, IS DETERMINED BY SOLVING THE COST EQUATION.

THE INTERESTING FEATURE OF THE PRECEDING RESULT IS THAT THE OPTIMAL VALUE OF m DOES NOT DEPEND ON n.

IN DESCRIPTIVE SURVEYS, IT IS USUALLY EFFICIENT TO HAVE THE PROBABILITY OF SELECTION OF THE ULTIMATE SAMPLE UNITS UNIFORM. THIS IS ACCOMPLISHED EITHER BY SELECTING THE PSUs WITH FIXED PROBABILITIES AND SETTING THE WITHIN-PSU SAMPLE SIZE PROPORTIONAL TO THE PSU SIZE, OR BY SELECTING THE PSUs WITH PROBABILITIES PROPORTIONAL TO SIZE AND SETTING THE WITHIN-PSU SAMPLE SIZE EQUAL TO A CONSTANT (I.E., TO m). (THE LATTER METHOD IS THE ONE USUALLY EMPLOYED, FOR REASONS OF EFFICIENCY AND CONVENIENCE IN FIELD WORK.)

STRATIFIED SAMPLING

FOR DESCRIPTIVE SURVEYS: ORDINARY STRATIFICATION

DIVIDE THE POPULATION INTO SUBPOPULATIONS (CATEGORIES, “STRATA”), AND SELECT A SAMPLE FROM EACH.

IN DEVELOPMENT APPLICATIONS, ARE USUALLY STRATIFYING FIRST-STAGE UNITS, SINCE DATA ARE AVAILABLE FOR THAT LEVEL, FOR USE IN SURVEY DESIGN (UNLESS DO A LISTING SURVEY).

REASONS FOR USING STRATIFICATION IN DESCRIPTIVE SURVEYS:

WANT ESTIMATES FOR SUBPOPULATIONS

ADMINISTRATIVE CONVENIENCE

DIFFERENT SAMPLING APPROACHES

GAIN IN PRECISION IF STRATA ARE INTERNALLY HOMOGENEOUS

(EQUIVALENT TO MULTISTAGE SAMPLING, WHERE A SAMPLE IS SELECTED FROM EVERY FIRST-STAGE SAMPLE UNIT IN THE POPULATION.)

ESTIMATE POPULATION MEAN AS A WEIGHTED AVERAGE OF STRATUM MEANS:

[FORMULAS]

NEED TO DETERMINE THE NUMBER OF STRATUM CATEGORIES, THE STRATUM BAOUNDARIES, AND THE ALLOCATION OF THE SAMPLE TO THE STRATA. OPTIMAL (NEYMAN) ALLOCATION, DALENIUS BOUNDARIES.

ORDINARY STRATIFICATION USUALLY DONE WITH ONE OR TWO VARIABLES OF STRATIFICATION. WITH MANY VARIABLES OF STRATIFICATION, THE NUMBER OF STRATA IN A CROSS-STRATIFICATION BECOMES VERY LARGE, EASILY EXCEEDING THE SAMPLE SIZE. MANY STRATA CONTAIN 0 OR 1 UNIT (UNLESS COLLAPSE STRATA). DIFFICULT TO CONTROL SELECTION PROBABILITIES. LOW PRECISION, NO ADVANTAGE.

OTHER METHODS: TWO-WAY STRATIFICATION, CONTROLLED SELECTION. USEFUL FOR A FEW VARIABLES OF STRATIFICATION AND SMALL SAMPLE SIZES (E.G., STRATIFICATION OF PSUs).

FOR ANALYTICAL SURVEYS: MARGINAL STRATIFICATION

SPECIFY VARIABLE PROBABILITIES OF SELECTION, SO THAT THE EXPECTED NUMBER OF UNITS IN EACH MARGINAL STRATUM CATEGORY (“CELL”) IS AS DESIRED.

REASONS FOR MARGINAL STRATIFICATION IN ANALYTICAL SURVEYS:

WORKS FOR ANY NUMBER OF VARIABLES, ANY NUMBER OF LEVELS PER VARIABLE

WANT TO CONTROL VARIATION (SPREAD, BALANCE, ORTHOGONALITY) FOR A LARGE NUMBER OF VARIABLES

APPROACH:

IDENTIFY VARIABLES (HAVING PRE-SURVEY DATA AVAILABLE) THAT AFFECT OUTCOME (BASED ON CAUSAL MODEL); ELIMINATE OR COMBINE CAUSALLY-REDUNDANT VARIABLES.

SET A SMALL NUMBER (<10) OF STRATA FOR EACH VARIABLE (NATURAL OR OTHERWISE)

SPECIFY A DESIRED ALLOCATION FOR THE MARGINAL DISTRIBUTION OF EACH VARIABLE OF STRATIFICATION. (THIS DETERMINES DESIRED SAMPLING FRACTIONS.)

USE AN ALGORITHM TO DETERMINE VARIABLE SELECTION PROBABILITIES TO ACHIEVE DESIRED ALLOCATION AS CLOSELY AS POSSIBLE, TAKING INTO ACCOUNT THE RELATIVE IMPORTANCE OF THE VARIABLES IN AFFECTING OUTCOME.

TWO-PHASE SAMPLING

A PROBABILITY SAMPLE IS ONE IN WHICH THE PROBABILITIES OF SELECTION OF THE ULTIMATE SAMPLE UNITS IS KNOWN, OR EQUAL TO A CONSTANT.

IF PROBABILITY SAMPLING IS USED, THE THEORY OF STATISTICS MAY BE APPLIED TO MAKE INFERENCES FROM THE SAMPLE DATA.

IN ORDER TO SELECT A PROBABILITY SAMPLE, IT IS DESIRABLE TO HAVE A SAMPLE FRAME (OR FRAME OR SAMPLING FRAME). A SAMPLE FRAME IS A COMPLETE, ACCURATE, UP-TO-DATE LIST OF THE PSUs AND A COMPLETE, ACCURATE UP-TO-DATE LIST OF THE UNITS WITHIN EACH SAMPLED PSU.

IF A SAMPLE FRAME IS NOT AVAILABLE, IT MAY BE ADVANTAGEOUS TO ALLOCATE PROJECT RESOURCES TO CONSTRUCTING ONE. ADVANTAGES: BETTER KNOWLEDGE OF POPULATION SIZES AND HENCE, SELECTION PROBABILITIES (REDUCE BIAS). ABLE TO STRATIFY (USE FIRST SURVEY TO ESTIMATE STRATUM WEIGHTS), AND THEREBY IMPROVE PRECISION.

GIVEN COST OF CLASSIFICATION PER UNIT AND COST OF MEASURING A UNIT IN EACH STRATUM, CAN DETERMINE OPTIMAL CHOICES FOR THE FIRST-PHASE SAMPLE SIZE (TO MEASURE AUXILIARY VARIATES) AND SECOND-PHASE SAMPLE SIZE.

USE OF MATCHING TO IMPROVE PRECISION AND POWER

TWO SITUATIONS FOR MATCHING:

FOR RANDOMIZED DESIGNS (MATCHING PRIOR TO RANDOMIZED ASSIGNMENT)

FOR QUASI-EXPERIMENTAL DESIGNS (TO FORM COMPARISON GROUPS; MATCHING AFTER SELECTION FOR TREATMENT)

FOR RANDOMIZED DESIGNS (MATCHED-PAIRS DESIGNS)

DOUBLE-MATCHED-PAIRS DESIGN

INTERVIEW OF SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS

MATCHING PRIOR TO RANDOMIZED ASSIGNMENT TO TREATMENT

REASON WHY MATCHING IS IMPORTANT: IT INTRODUCES A CORRELATION INTO VARIABLES IN MATCHED PAIRS, AND REDUCES VARIANCE OF ESTIMATES OF DIFFERENCES. THIS IMPROVES PRECISION OF DIFFERENCE ESTIMATES AND POWER OF TESTS OF HYPOTHESIS ABOUT DIFFERENCE MEASURES. (PAIR MATCHING INTRODUCES NO BIAS AS LONG AS THE MATCHING CRITERIA (MATCH VARIABLES) ARE UNRELATED TO THE DEPENDENT VARIABLES.)

TWO SAMPLES OF SIZE n₁ AND n₂. ASSUME n₁ = n₂ = n. ASSUME EQUAL VARIANCE, σ².

IF INDEPENDENT:

IF MATCHED: LET ρ DENOTE THE CORRELATION BETWEEN MATCHED UNITS. THAT IS, cov(x₁, x₂ ) = ρσ². SAMPLE OF n MATCHED PAIRS OF x₁ – x₂. var(x₁ – x₂) = σ₁² + σ₂² – 2 cov(x₁,x₂) = σ² + σ² - 2ρσ² = (1-ρ)2σ². IT FOLLOWS THAT

FOUR SAMPLES (TREATMENT BEFORE, TREATMENT AFTER, CONTROL BEFORE, CONTROL AFTER):

IF INDEPENDENT:

IF MATCH BEFORE AND AFTER (REINTERVIEW OF SAME HOUSEHOLDS): LET ρ₁₂ DENOTE THE CORRELATION BETWEEN MATCHED UNITS. THEN

IF MATCH TREATMENTS AND CONTROLS: LET ρ₁₃ DENOTE THE CORRELATION BETWEEN MATCHED UNITS. THEN

IF MATCH BEFORE AND AFTER, AND TREATMENTS AND CONTROLS (“DOUBLE-MATCHED” DESIGN): NUMBER THE GROUPS 1: TREATMENT BEFORE; 2: TREATMENT AFTER; 3: CONTROL BEFORE; 4: CONTROL AFTER. DENOTE THE CORRELATIONS BETWEEN GROUPS i AND j AS ρ_ij. THEN

INTRODUCTION OF CORRELATIONS (USE OF MATCHING) BETWEEN THE GROUPS ALLOWS FOR A SUBSTANTIAL REDUCTION IN THE VARIANCE OF DIFFERENCE ESTIMATORS.

HOW TO MATCH?

MATCH ON VARIABLES THAT HAVE AN EFFECT ON OUTCOME. IN SAMPLE SURVEY, CANNOT MATCH “AT WILL.” MUST WORK WITH EXISTING FINITE POPULATION. MATCHING WILL INVOLVE TRADE-OFFS – GOOD MATCHES ON SOME VARIABLES WILL RESULT IN POOR MATCHES ON OTHERS. TAKE INTO ACCOUNT THE RELATIVE IMPORTANCE OF THE VARIABLES IN AFFECTING OUTCOME, ACCORDING TO CAUSAL MODEL.

DO NOT MATCH ON THE PROPENSITY SCORE. UNITS HAVING SIMILAR PROPENSITY SCORES MAY HAVE VERY DIFFERENT VALUES FOR VARIABLES THAT HAVE AN IMPORTANT EFFECT ON OUTCOME. EXAMPLE: ABILITY TO JUMP. MATCH ON WHETHER IN THE ARMED SERVICES. (ALSO, IN THE DESIGN STAGE OF A SURVEY THE ESTIMATED PROPENSITY SCORE MAY BE VERY UNRELIABLE.)

IN DEVELOPMENT APPLICATIONS, USUALLY MATCH FIRST-STAGE SAMPLE UNITS (PSUs, CLUSTERS): “CLUSTER-MATCH,” “CLUSTER-RANDOMIZED” DESIGN.

IMPORTANT NOTE: RANDOMIZED ASSIGNMENT OF PSUs DOES NOT CONSTITUTE RANDOMIZED ASSIGNMENT OF THE ULTIMATE SAMPLE UNITS.

THREE APPROACHES:

RANDOMIZE ASSIGNMENT OF SAMPLE UNITS WITHIN TREATMENT AND CONTROL UNITS

SELECT TREATMENT UNITS WITHIN TREATMENT AND CONTROL UNITS IN EXACTLY THE SAME WAY

STRATIFY EACH PSU INTO A CERTAINTY STRATUM OF TREATMENT UNITS AND A STRATUM OF NON-TREATMENT UNITS

IN LAST TWO CASES, MUST ADJUST FOR SELECTION EFFECTS BY REGRESSION ANALYSIS.

RECOMMENDED APPROACH: MATCH ON A “DISTANCE” MEASURE (SCORE) THAT TAKES INTO ACCOUNT THE RELATIVE IMPORTANCE OF EACH MATCH VARIABLE ON OUTCOMES OF INTEREST. MATCH ALL UNITS OF THE POPULATION (FORM INTO “MATCH SETS” (MATCHED PAIRS, TRIPLETS, QUADRUPLETS OR QUINTUPLETS, AS DATA AVAILABILITY PERMITS – EXTRAS ARE INCLUDED FOR REPLACEMENTS)). (BLOCKING.) ASSIGN ONE UNIT OF EACH PAIR TO TREATMENT AND ONE TO CONTROL. APPLY MARGINAL STRATIFICATION TO THE TREATMENT UNITS TO SELECT THE SAMPLE. PROBABILITIES OF INCLUSION OF EACH UNIT CAN BE DETERMINED FROM THE PROBABILITIES OF SELECTION OF EACH UNIT.

[DESCRIBE IN GREATER DETAIL. SHOW FORMULA.]

AFTER FORM MATCH SETS (PAIRS OR GROUPS), RANDOMLY ASSIGN ONE TO TREATMENT AND ONE TO CONTROL.

MATCHING FOR QUASI-EXPERIMENTAL DESIGNS

TREATMENT SAMPLE IS ALREADY SELECTED.

DO MATCHING IN THE USUAL WAY.

ESTIMATION OF SAMPLE SIZE

TWO MAIN AREAS OF STATISTICAL INFERENCE: ESTIMATION OF PARAMETERS AND TESTING OF HYPOTHESES. DESCRIPTIVE SURVEYS ARE CONCERNED MORE WITH PARAMETER ESTIMATION, AND ANALYTICAL SURVEYS ARE CONCERNED MORE WITH TESTS OF HYPOTHESES.

APPROACH TO SAMPLE SIZE DETERMINATION:

SPECIFY FORMULA FOR PRECISION (DESCRIPTIVE SURVEYS) OR POWER (ANALYTICAL SURVEYS) IN TERMS OF SAMPLE SIZE, AND SOLVE FORMULA FOR SAMPLE SIZE

USUAL APPROACH (E.G., WILLIAM T. GRANT FOUNDATION “OPTIMAL DESIGN” (OD) SOFTWARE): SPECIFY MODEL SOLELY IN TERMS OF SEVERAL VARIANCES OR FIXED-EFFECT SUMS OF SQUARES. DIFFICULT FOR COMPLEX MODELS (E.G., OD DOES NOT ADDRESS DESIGNS INVOLVING MATCHING OR PANEL SAMPLING; USES “REPEATED MEASURES WITH POLYNOMIAL TRAJECTORY”).

PROBLEM: NOT VERY INTUITIVE, AND DIFFICULT TO SPECIFY VALUES OF VARIANCES OR FIXED-EFFECT SUMS OF SQUARES.

RECOMMENDED APPROACH: TO EXTENT POSSIBLE, SPECIFY MODEL IN TERMS OF CORRELATIONS. SIMPLER FORMULAS, MORE INTUITIVE.

NOTE: FOR THIS ANALYSIS, AND ALL TO FOLLOW, IT IS ASSUMED THAT SAMPLE SIZES ARE SUFFICIENTLY LARGE (E.G., >30) SO THAT THE LAW OF LARGE NUMBERS AND CENTRAL LIMIT THEOREMS APPLY. ALSO, THE FPC IS IGNORED.

PROPERTIES OF ESTIMATORS: BIAS (UNBIASEDNESS), PRECISION (MINIMUM VARIANCE), ACCURACY, CONSISTENCY.

POINT ESTIMATES (E.G., MEAN), INTERVAL ESTIMATES (E.G., CONFIDENCE INTERVAL).

SOME NOTATION:

E(x) = μ (or μ_x)

var(x) = E(x-μ)² = σ² (or σ_x²)

sd(x) = sqrt(var(x)) = σ

cov(x,y) = E((x-μ_x)(y-μ_y))

corr(x,y) = cov(x,y)/(sd(x)sd(y)) = ρ or ρ_xy.

WILL MAKE USE OF

E(x + y) = E(x) + E(y)

E(cx) = cE(x)

var(cx) = c² var(x)

var(x+y) = var(x) + var(y) + 2ρ_xy sd(x) sd(y) = σ_x² + σ_y² + 2ρ_xy σ_x σ_y

(Check: If x=y, then ρ_xy=1, and var(x+x) = var(2x) = 4 var(x) and var(x-x) = var(0) = 0.)

If x and y are independent, then ρ_xy = 0, so var(x+y) = var(x) + var(y) and var(x-y) = var(x) + var(y).

Define sample mean = .

The standard deviation of an estimate (e.g., the estimated mean) is called the standard error of the estimate.

se() = sqrt(var())

For simple random sampling (SRS), can show E() = μ, so sample mean is an unbiased estimate of the population mean.

For simple random sampling (SRS), var() = σ²/n and se() = σ/.

For any design, deff ≡ (variance for the design) / (variance for SRS), so var() = deff σ²/n or se() = σ/

E.g., for multistage sampling, deff = (1 + (m-1)ρ), so var() = deff σ²/n = (1 + (m-1)ρ) σ²/n.

If x is a binomial random variate (values 0 or 1, Pr(x=1) = p; “sampling for proportions”), then E(x) = p, var(x) = p(1-p) = pq, and var() = var() = pq/n.

ESTIMATION OF SAMPLE SIZE FOR DESCRIPTIVE SURVEYS

STATISTICAL PRECISION ANALYSIS: INVESTIGATION OF THE RELATIONSHIP BETWEEN SAMPLE SIZE AND THE PRECISION OF ESTIMATES.

MOTIVATION FOR PRECISION ANALYSIS: TO ASSURE THAT THE SAMPLE ESTIMATES WILL BE OF USEFUL PRECISION.

TWO APPROACHES: SPECIFY LEVEL OF PRECISION AND DERIVE CORRESPONDING SAMPLE SIZE; OR SPECIFY SAMPLE SIZE AND DERIVE CORRESPONDING PRECISION.

NOTE: “SAMPLE SIZE” REFERS BOTH TO PSU SAMPLE SIZE AND ULTIMATE-UNIT SAMPLE SIZE.

CONCEPTS: SAMPLING DISTRIBUTION OF AN ESTIMATOR; LAW OF LARGE NUMBERS; CENTRAL LIMIT THEOREM; POINT ESTIMATE; INTERVAL ESTIMATE; CONFIDENCE INTERVAL. THESE CONCEPTS ARE DISCUSSED IN ANY BOOK ON INTRODUCTION TO THE THEORY OF STATISTICS (E.G., Introduction to the Theory of Statistics by Alexander M. Mood, Franklin A. Graybill and Duane C Boes 3^rd edition, McGraw Hill, 1974).

[GRAPH OF NORMAL DISTRIBUTION (DENSITY FUNCTION), SHOWING PERCENTILE POINTS α/2 AND 1-α/2]

[GRAPH OF SAMPLING DISTRIBUTION (DENSITY FUNCTION) OF , SHOWING A NUMBER OF DENSITIES CORRESPONDING TO DIFFERENT SAMPLE SIZES.]

CONFIDENCE INTERVAL:

Random sample x’ = (x₁, …,x_n) from density f(x;θ).

Statistics T₁=t₁(x) and T₂=t₂(x) such that T₁<=T₂ for which P_θ[T₁<τ(θ)<T₂]=γ, where γ does not depend on θ. (In the figure, γ=1-α.)

The random interval (T₁,T₂) is called a 100γ percent confidence interval for τ(θ).

γ is called the confidence coefficient.

T₁ and T₂ (or realized values t₁ and t₂) are called lower and upper confidence limits, respectively, for τ(θ).

EXAMPLE:

Sample mean , sample standard deviation , se() = =

The statistic has (approximately) a normal distribution, N(μ,σ) = N(0,1).

Hence P[-1.96 < Z < 1.96] = .95

or P[-1.96 < < 1.96] = .95

or P[--1.96 < < -+1.96] = .95

or P[+1.96 > > 1.96] = .95

or P[1.96 < < 1.96] = .95.

So (1.96, 1.96) is a 95% confidence interval for μ.

CASE 1: SINGLE SAMPLE: ESTIMATION OF POPULATION MEAN

PRECISION ANALYSIS: SPECIFY LEVEL OF PRECISION, AND DERIVE CORRESPONDING SAMPLE SIZE.

ESTIMATION OF SAMPLE SIZE FOR ESTIMATING A POPULATION MEAN, BASED ON A SINGLE SAMPLE.

POINT ESTIMATION: SPECIFY THE DESIRED STANDARD ERROR, se.

KNOW se() = σ/.

SET se = σ/ AND SOLVE FOR n:

n = deff σ²/ se².

EXAMPLE 1.1. POINT ESTIMATION: DETERMINE SAMPLE SIZE REQUIRED TO ESTIMATE MEAN INCOME WITH A $10 STANDARD ERROR.

NEED TO KNOW STANDARD DEVIATION OF INCOME. ASSUME THAT IT IS $100.

NEED TO KNOW TYPE OF SAMPLING (SAMPLE DESIGN). ASSUME SRS. HENCE deff=1.

n = deff σ²/ se² = 1 100² / 10² = 100.

EXAMPLE 1,2. POINT ESTIMATION: DETERMINE SAMPLE SIZE REQUIRED TO ESTIMATE MEAN INCOME WITH A RELATIVE STANDARD ERROR OF 5%. (NOTE: RELATIVE STANDARD ERROR = STANDARD ERROR / MEAN. RELATIVE STANDARD DEVIATION = σ/μ IS CALLED THE COEFFICIENT OF VARIATION. σ²/μ² IS CALLED THE RELATIVE VARIANCE, OR REL VARIANCE.)

NEED TO KNOW THE RELATIVE STANDARD ERROR OF INCOME. OFTEN IN THE RANGE .5 TO 2. ASSUME 1.0. ASSUME SRS, AS BEFORE.

n = deff σ²/ se² = deff (σ/μ)²/ (se/μ)² = 1 1² / .05² = 400.

EXAMPLE 1.3. INTERVAL ESTIMATION: DETERMINE SAMPLE SIZE SUCH THAT A 95% CONFIDENCE INTERVAL FOR THE MEAN IS OF SIZE (WIDTH) 10. HALF THE WIDTH OF THE 95% CONFIDENCE INTERVAL IS OFTEN CALLED THE ERROR BOUND, DENOTED BY E. SO IN THIS EXAMPLE, THE ERROR BOUND IS E = 10/2 = 5. OTHERWISE SAME AS EXAMPLE 1 (deff = 1, σ = 100).

95% confidence interval: = =

SO SET , or 1.96σ/ = E, WHERE E = 5.

SOLVING FOR n:

n = deff (1.96 σ / E)² = 1 (1.96 100 / 5)² = 1536.64 ≈ 1,537.

EXAMPLE 1.4. INTERVAL ESTIMATION: 95% CONFIDENCE INTERVAL FOR PROPORTION. DETERMINE SAMPLE SIZE SUCH THAT A 95% CONFIDENCE INTERVAL FOR AN ESTIMATED PROPORTION IS +/- 3% (E.G., TELEVISION POLLS).

TO KNOW σ, MUST SPECIFY p. “WORST CASE” IS p=.5, FOR WHICH σ=.

PROCEEDING AS ABOVE,

95% confidence interval: =

SO SET , or 1.96σ/ = .03.

SOLVING FOR n:

n = deff (1.96 σ / .03)² = 1 (1.96 .5 / .03)² = 1,067.11 ≈ 1,067.

MOST TELEVISION POLLS SET “SAMPLING ERROR” OR “ERROR BOUND” AT +/- 3%, AND USE A SAMPLE SIZE OF 1000-1200.

PRECEDING EXAMPLES ASSUMED SIMPLE RANDOM SAMPLING (SRS), WITH deff = 1.

IF USE CLUSTER SAMPLING OR MULTISTAGE SAMPLING, WILL HAVE A DIFFERENT VALUE FOR deff.

EXAMPLE 1.5. FOR EXAMPLE, SUPPOSE, IN EXAMPLE 1.3, THAT WE ARE USING A TWO-STAGE SAMPLE DESIGN – SAMPLES OF VILLAGES WITH SUBSAMPLES OF m = 10 HOUSEHOLDS PER VILLAGE. MUST SPECIFY A VALUE FOR THE INTRA-CLUSTER CORRELATION COEFFICIENT, icc (or ρ) AND THE WITHIN-PSU SAMPLE SIZE, m, IN ORDER TO CALCULATE THE DESIGN EFFECT.

deff = 1 + (m-1)icc.

THE VALUE OF icc DEPENDS ON THE VARIABLE BEING MEASURED. FOR MANY HOUSEHOLD VARIABLES, icc IS IN THE RANGE .05-.15. (ASSUME VALUE BASED ON EXPERIENCE, OR FROM ANALYSIS OF EXISTING DATA.)

deff = 1 + (m-1)icc = 1 + (10 – 1).1 = 1.9

n = deff (1.96 σ / 5)² = 1.9 (1.96 100 / 5)² = 2919.16 ≈ 2,919.

THE SAMPLE SIZE VARIES AS deff. THE “CLUSTER EFFECT” ON SAMPLE SIZE IS SUBSTANTIAL, EVEN FOR SMALL VALUES OF icc.

CASE 2: TWO SAMPLES; ESTIMATION OF DIFFERENCE IN GROUP MEANS (“SINGLE DIFFERENCE”)

GROUPS 1 AND 2, GROUP MEANS μ₁ AND μ₂, GROUP STANDARD DEVIATIONS σ₁ AND σ₂, SAMPLE MEANS and , INTERGROUP CORRELATION ρ₁₂. (USE icc, INSTEAD OF ρ, FOR INTRA-CLUSTER CORRELATION COEFFICIENT TO AVOID CONFUSION.)

ESTIMATE .

THEORY PROCEEDS SAME AS ABOVE (CASE 1), WHERE REPLACE by .

se() = sqrt{ deff [ σ₁²/n₁ + σ₂²/n₂ - 2ρ₁₂σ₁σ₂/ ]}.

IF INDEPENDENT SAMPLES, THEN ρ₁₂ = 0.

se() = sqrt{ deff [ 2 (1 - ρ₁₂) σ²/n ] }.

NOTE THAT IF WE ASSUME THE SAME TOTAL SAMPLE SIZE AS IN CASE 1, THEN THE VALUE OF n IN THIS EXPRESSION (I.E., THE PER-GROUP SAMPLE SIZE) IS n/2 OF THE CASE 1 VALUE. IF ρ₁₂ = 0 (INDEPENDENT SAMPLES), THE VARIANCE IS FOUR TIMES AS LARGE AS IN CASE 1, SO THE SAMPLE SIZE WILL BE FOUR TIMES AS LARGE.

EXAMPLE 2.1. (SIMILAR TO EXAMPLE 1.3.) INTERVAL ESTIMATION: DETERMINE SAMPLE SIZE SUCH THAT A 95% CONFIDENCE INTERVAL FOR THE DIFFERENCE IN MEANS IS OF SIZE (WIDTH) 10, I.E., ERROR BOUND E = 5. deff = 1. σ = 100. ASSUME INDEPENDENT SAMPLES, I.E., ρ₁₂=0.

95% confidence interval: = =

SO SET , or 1.96 sqrt{ deff [ 2 (1 - ρ₁₂) σ²/n ] } = E, WHERE E = 5.

SOLVING FOR n:

n = deff 2 (1 – ρ₁₂) (1.96 σ / E)² = 1 2 (1 – 0) (1.96 100 / 5)² = 3073.28 ≈ 3,073.

THIS IS THE PER-GROUP SAMPLE SIZE, I.E., THE SAMPLE IS FOUR TIMES AS LARGE AS IN EXAMPLE 1.3.

(NOTE: THIS RESULT MAY SEEM TO DIFFER FROM THE EXAMPLES PRESENTED EARLIER, WHEN EXAMINING THE VARIANCE OF MATCHED SAMPLES. FOR THE PREVIOUS EXAMPLES, THE SAMPLE SIZE WAS n FOR EVERY GROUP. HERE IT IS n/2.)

THE SAMPLE SIZES FOR ESTIMATING DIFFERENCES ARE VERY LARGE, IF USE INDEPENDENT SAMPLES. VARIANCE OF THE ESTIMATED DIFFERENCE IS REDUCED BY INTRODUCING CORRELATIONS BETWEEN THE GROUPS, E.G., BY INTERVIEWING THE SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS (IN A BEFORE-AFTER DESIGN), OR BY MATCHING TREATMENT AND CONTROL UNITS (IN A TREATMENT-CONTROL DESIGN).

EXAMPLE 2.2. SAME AS EXAMPLE 2.1, BUT ρ₁₂ = .5.

THE PER-GROUP SAMPLE SIZE DECREASES FROM 3,073 TO HALF THAT VALUE, 1,537.

GUIDANCE FOR SPECIFYING ρ₁₂.

FOR BEFORE-AFTER DESIGN, IF INTERVIEW SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS, SET A HIGH VALUE FOR ρ₁₂, SUCH AS .5.

FOR TREATMENT-CONTROL WITH MATCHING OF PSUs, SET MODEST VALUE, E.G., ρ₁₂ = .3.

CASE 3: FOUR SAMPLES (TREATMENT BEFORE, TREATMENT AFTER, COMPARISON BEFORE, COMPARISON AFTER): ESTIMATION OF DOUBLE DIFFERENCE OF GROUP MEANS.

GROUPS:

1: TREATMENT BEFORE

2: TREATMENT AFTER

3: COMPARISON BEFORE

4: COMPARISON AFTER

GROUP MEANS μ₁, μ₂, μ₃ AND μ₄, GROUP STANDARD DEVIATIONS σ₁, σ2, σ3 AND σ₄, SAMPLE MEANS , , and .

INTERGROUP CORRELATIONS:

GROUP 1 (TRT BEFORE) ---ρ₁₂--- GROUP 2 (TRT AFTER)

| ρ₂₃ |

ρ₁₃ ρ₂₄

| ρ₁₄ |

GROUP 3 (COMP BEFORE) ---ρ₃₄--- GROUP 4 (COMP AFTER)

CORRELATIONS ρ₁₂, ρ₁₃, AND ρ₃₄ ARE “REAL,” ρ₂₃, ρ₂₄, AND ρ₃₄ ARE “ARTIFACTUAL.”

ESTIMATE .

THEORY PROCEEDS SAME AS ABOVE (CASE 1), WHERE REPLACE by .

se() = sqrt{ deff [ σ₁²/n₁ + σ₂²/n₂ + σ₃²/n₃ + σ₄²/n₄ - 2ρ₁₂σ₁σ₂/ - 2ρ₁₃σ₁σ₃/ + 2ρ₁₄σ₁σ₄/ + 2ρ₂₃σ₂σ₃/ - 2ρ₂₄σ₂σ₄/ - 2ρ₃₄σ₃σ₄/ ]}.

IF ALL FOUR SAMPLES ARE INDEPENDENT, THEN ALL OF THE ρ’s are zero.

IF DON’T INTERVIEW SAME HOUSEHOLDS IN BOTH ROUNDS, THEN ρ₁₂=0.

IF DON’T MATCH TREATMENT AND COMPARISON UNITS, THEN ρ₁₃=0.

GUIDANCE ON SETTING VALUES OF ρ’s: AS ABOVE (CASE 2).

NOTE THAT THE COVARIANCE MATRIX MUST BE POSITIVE DEFINITE.

NOTE: FOR ESTIMATING DIFFERENCES, IT IS MOST EFFICIENT FOR THE GROUPS SAMPLE SIZES TO BE THE SAME (I.E., A “BALANCED” DESIGN). WILL ASSUME THIS IN THE EXAMPLES THAT FOLLOW. FOR SIMPLICITY, WILL ASSUME σ₁ = σ₂ = σ₃ = σ₄ = σ. DENOTE n₁ = n₂ = n₃ = n₄ = n. FOR SIMPLICITY, WILL (UNREALISTICALLY) ASSUME ρ₁₂ = ρ₁₃ = ρ₁₄ = ρ₂₃ = ρ₂₄ = ρ₃₄ = ρ. IN THIS CASE,

se() = sqrt{ deff [ 4 (1 - ρ) σ²/n ] }.

NOTE THAT IF WE ASSUME THE SAME TOTAL SAMPLE SIZE AS IN CASE 1, THEN THE VALUE OF n IN THIS EXPRESSION (I.E., THE PER-GROUP SAMPLE SIZE) IS n/4 OF THE CASE 1 VALUE. IF ALL ρ’s = 0 (E.G., INDEPENDENT SAMPLES), THE VARIANCE IS SIXTEEN TIMES AS LARGE AS IN CASE 1, SO THE SAMPLE SIZE WILL BE SIXTEEN TIMES AS LARGE.

EXAMPLE 3.1. (SIMILAR TO EXAMPLE 1.3.) INTERVAL ESTIMATION: DETERMINE SAMPLE SIZE SUCH THAT A 95% CONFIDENCE INTERVAL FOR THE DIFFERENCE IN MEANS IS OF SIZE (WIDTH) 10, I.E., ERROR BOUND E = 5. deff = 1. σ = 100. ASSUME INDEPENDENT SAMPLES, I.E., ALL ρ’s =0.

95% confidence interval: = =

SO SET , or 1.96 sqrt{ deff [ 4 (1 - ρ) σ²/n ] } = E, WHERE E = 5.

SOLVING FOR n:

n = deff 4 (1 – ρ) (1.96 σ / E)² = 1 2 (1 – 0) (1.96 100 / 5)² = 6146.56 ≈ 6,147.

THIS IS THE PER-GROUP SAMPLE SIZE, I.E., THE SAMPLE IS SIXTEEN TIMES AS LARGE AS IN EXAMPLE 1.3.

THE SAMPLE SIZES FOR ESTIMATING DOUBLE DIFFERENCES ARE VERY LARGE, IF USE INDEPENDENT SAMPLES. VARIANCE OF THE ESTIMATED DOUBLE DIFFERENCE IS REDUCED BY INTRODUCING CORRELATIONS BETWEEN THE GROUPS, E.G., BY INTERVIEWING THE SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS (IN A BEFORE-AFTER DESIGN), OR BY MATCHING TREATMENT AND CONTROL UNITS (IN A TREATMENT-CONTROL DESIGN).

EXAMPLE 3.2. SAME AS EXAMPLE 3.1, BUT ρ = .5.

THE PER-GROUP SAMPLE SIZE DECREASES FROM 6,147 TO HALF THAT VALUE, 3,073.

[HANDOUTS: COMPUTER-PROGRAM PRINTOUTS]

ESTIMATION OF SAMPLE SIZE FOR ANALYTICAL SURVEYS

STATISTICAL POWER ANALYSIS: INVESTIGATION OF THE RELATIONSHIP BETWEEN SAMPLE SIZE AND THE PROBABILITY OF DETECTING AN EFFECT OF A SPECIFIED SIZE.

MOTIVATION FOR POWER ANALYSIS: LEHMANN: “THERE IS LITTLE POINT IN CARRYING OUT AN EXPERIMENT WHICH HAS ONLY A SMALL CHANCE OF DETECTING THE EFFECT BEING SOUGHT WHEN IT EXISTS.”

TWO APPROACHES: SPECIFY LEVEL OF POWER AND DERIVE CORRESPONDING SAMPLE SIZE; OR SPECIFY SAMPLE SIZE AND DERIVE CORRESPONDING POWER.

NOTE: “SAMPLE SIZE” REFERS BOTH TO PSU SAMPLE SIZE AND TO ULTIMATE-UNIT SAMPLE SIZE.

CONCEPTS (ADDITIONAL TO THOSE ADDRESSED ABOVE, IN SECTION ON DESCRIPTIVE SURVEYS): STATISTICAL TESTS OF HYPOTHESIS.

[ONE-SAMPLE CASE: GRAPH OF SAMPLING DISTRIBUTION (DENSITY FUNCTION) OF DISPLACED TO THE RIGHT OF THE ORIGIN, SHOWING A NUMBER OF DENSITIES CORRESPONDING TO DIFFERENT SAMPLE SIZES.]

[TWO-SAMPLE CASE. SHOW TWO DENSITY FUNCTIONS. CAN REDUCE TO ONE-SAMPLE CASE.]

STATISTICAL TESTS OF HYPOTHESIS:

Statistical hypothesis: A statement (assertion or conjecture) about the distribution of one or more random variables. If the hypothesis completely specifies the distribution, it is a simple hypothesis; otherwise it is a composite hypothesis. Denote an hypothesis by H.

Test of a statistical hypothesis: a rule or procedure for deciding whether to reject a statistical hypothesis. Denote a test by T.

Nonrandomized test; critical region; critical function. Sample x’ = (x₁, …, x_n) in sample space χ. Subset (region) C ϵ χ. If reject H if and only if x ϵ C, then C is called the critical region of the test. If define the indicator function ψ(x) = 1 if x ϵ C, 0 otherwise, then ψ is called the critical function.

Null hypothesis; alternative hypothesis. Customary to refer to H as the null hypothesis, and denote it by H₀. The complementary hypothesis not-H is referred to as the alternative hypothesis, denoted by H₁. If H₀ is not rejected, we say that it is accepted.

Types of error. Observe a sample and make a decision (accept or reject H₀). If reject H₀ when it is true, have made a Type I error. If accept H₀ when it is false, have made a Type II error. The probability of making a Type I error is called the size of the Type I error, and the probability of making a Type II error is called the size of the Type II error. If H₀ is a simple hypothesis, the size of the Type I error is called the size of the critical region, or the size of the test. Some writers refer to the size of the test as the significance level of the test.

Notation:

Pr[Type I error] = α (significance level)

Pr[Type II error] = β. 1 – β is called the power of the test

Power function: Suppose that the distribution function of x is a function of a parameter θ (denote f(x;θ) or f_θ(x)). The power function of a test, T, denoted by π(θ), is the probability that H₀ is rejected when the sampling distribution is parameterized by θ.

Simple likelihood-ratio test (simple null and alternative); most powerful test; Neyman-Pearson lemma.

Example, for a test of the hypothesis that the mean of a distribution is zero vs. the alternative that the mean is D>0. (A “one-sided” test.)

[GRAPHS OF DENSITY FOR H₀ AND DENSITY FOR H₁.]

Case 1: Specify power and sample size, and determine minimum detectable effect, D.

Test statistic: sample mean, . Standard error se(). Population mean μ.

Use test of size (significance level) α and power β.

Want to determine the value, D, that the population mean must exceed. D is called the “minimum detectable effect.”

STANDARD VALUES FOR α AND β ARE α=.05 AND β=.1 (POWER 1 – β = .90), IN WHICH CASE AND .

NOTE THAT THE PRECEDING IS A ONE-SIDED TEST. ONE-SIDED TESTS ARE USUAL IN EVALUATION, WHERE THE DIRECTION OF THE IMPACT IS RELATIVELY CERTAIN. (FOR TWO-SIDED TESTS, WOULD USE, FOR α=.05, IN WHICH CASE .

THE PRECEDING RESULT IS VERY GENERAL. IT MAY BE USED FOR ONE-GROUP, TWO-GROUP, AND FOUR-GROUP DESIGNS, WITH ANY TYPE OF SAMPLING (SRS, MULTISTAGE), AND ANY ESTIMATOR, (MEAN, SINGLE DIFFERENCE, DOUBLE DIFFERENCE), SIMPLY BY SUBSTITUTING THE APPROPRIATE VALUE FOR .

FOR EXAMPLE, FOR SIMPLE RANDOM SAMPLING WITH A ONE-GROUP DESIGN,

FOR ANY OTHER TYPE OF SAMPLING (FOR A ONE-GROUP) DESIGN,

FOR EXAMPLE, WITH MULTISTAGE SAMPLING, deff = 1 + (m-1)icc.

Case 2. One-group design. Specify α, β, and D, and determine the required sample size.

Use the same equation as above,

but substitute the appropriate formula for . That is,

Solving for n:

For example, suppose that we are using two-stage sampling with subsample size m=10 in each PSU. For a variable for which the intra-PSU correlation coefficient is icc = .1, the formula for the design effect is deff = 1 + (m-1)icc = 1 + (10 – 1).1 = 1.9. If α = .05 and β = .1, then and . Let us suppose that the coefficient of variation of a variable of interest is 1.0, and that we wish to detect a minimum detectable effect equal to 10% of this value. Then σ/D = 1/.1 = 10. Substituting these values yields

n = (1.645 + 1.282)² 1.9 10² = 1628.

SUMMARY: TO ESTIMATE SAMPLE SIZE FOR AN ANALYTICAL SURVEY, THE FOLLOWING MUST BE SPECIFIED:

THE IMPACT ESTIMATOR TO BE USED

THE TEST PARAMETERS (POWER LEVEL, 1-β, AND SIGNIFICANCE LEVEL, α)

THE MINIMUM DETECTABLE EFFECT

CHARACTERISTICS OF THE SAMPLED POPULATION (MEANS, STANDARD DEVIATIONS, INTRA-PSU CORRELATION COEFFICIENT (IF MULTISTAGE SAMPLING IS USED)

THE SAMPLE DESIGN TO BE USED FOR THE SAMPLE SURVEY TO COLLECT QUANTITATIVE DATA

ALTERNATIVELY (RATHER THAN SPECIFYING THE POWER AND DETERMINING THE SAMPLE SIZE), IT MAY BE USEFUL TO SPECIFY THE SAMPLE SIZE AND DETERMINE THE POWER (OR THE POWER FUNCTION (I.E., THE POWER, AS A FUNCTION OF THE MINIMUM DETECTABLE EFFECT).

THE PRECEDING EXAMPLES HAVE SHOWN FORMULAS FOR A ONE-GROUP DESIGN AND A MEAN. THE FORMULAS FOR TWO-GROUP DESIGN AND A SINGLE-DIFFERENCE ESTIMATOR, OR FOR A FOUR-GROUP DESIGN AND A DOUBLE-DIFFERENCE ESTIMATOR, ARE SIMILAR. ALL THAT CHANGES IS THE EXPRESSION FOR THE STANDARD ERROR OF THE ESTIMATOR.

FOR EXAMPLE, FOR A FOUR-GROUP DESIGN AND A DOUBLE-DIFFERENCE ESTIMATOR OF IMPACT, THE FORMULA FOR SAMPLE SIZE AS A FUNCTION OF THE VARIOUS PARAMETERS IS:

n = (z_α + z_β)² varf / D²

where

n = sample size

D = minimum detectable effect

z_α = standard normal deviate having probability α to the right, where α denotes the significance level of the one-sided test of hypothesis that D exceeds zero (i.e., the probability of making a Type I error of deciding that D exceeds zero when in fact it does not)

z_β = standard normal deviate having probability β to the right, where 1 – β denotes the power of the test (i.e., the probability of deciding that D exceeds zero when it does). (β denotes the probability of making a Type II error of deciding that D does not exceed zero when in fact it does.)

varf = variance factor for impact estimator.

The value of var is given by

varf = deff (1 – R²) [σ₁² + σ₂² + σ₃² + σ₄² -2ρ₁₂σ₁σ₂ – 2 ρ₁₃σ₁σ₃ + 2ρ₁₄σ₁σ₄ + 2ρ₂₃σ₂σ₃ - 2ρ₂₄σ₂σ₄ - 2ρ₃₄σ₃σ₄]

where

the four design groups are designated by the indices 1 (treatment before), 2 (treatment after), 3 (comparison before) and 4 (comparison after)

σ_i² = variance for group i

ρ_ij = coefficient of correlation between groups i and j

deff = Kish’s design effect (to reflect the effect of two-stage sampling (“clustering”), if used) (deff is the ratio of the variance of the estimator under the design to the variance using a simple random sample of the same size)

R² = multiple correlation coefficient (from regression model, if used) (this factor represents the effect of marginal stratification to achieve adequate variation in explanatory variables).

[EXAMPLES: HANDOUTS]

THE POWER ANALYSIS IS DONE TO ASSIST DETERMINATION OF SAMPLE DESIGN AND SAMPLE SIZE. ONCE THE SAMPLE HAS BEEN SELECTED, THE ROLE OF POWER ANALYSIS IS FINISHED.

SAMPLE SELECTION PROCEDURES

USUALLY SELECTION WITHOUT REPLACEMENT, WITH VARIABLE PROBABILITIES (TO EFFECT MARGINAL STRATIFICATION).

USUALLY MATCHING OF TREATMENT AND CONTROL PSUs.

USE A RANDOMIZED LIST OF THE ENTIRE POPULATION, TO ALLOW FOR SELECTION OF REPLACEMENTS.

REPLACEMENTS

WITH RANDOM LIST, SIMPLY GO FURTHER DOWN THE LIST FOR PSUS, SELECT REPLACEMENT UNITS FROM THE SAME PSU (TO REDUCE BIAS).

TO AVOID REPLACEMENT OF A MATCHED PSU PAIR WHEN ONE FAILS TO RESPOND, SELECT MATCH SETS (TRIPLETS, QUADRUPLETS).

WITHIN-PSU SELECTION

SYSTEMATIC SAMPLING WITH TWO RANDOM STARTS.

FROM LIST OR USING A STRUCTURED “RANDOM WALK.”

KEEP TRACK OF REPLACEMENTS, TO ENABLE CORRECT CALCULATION OF SAMPLE WEIGHTS.

REVIEW OF A TYPICAL SAMPLE DESIGN (HANDOUT).

SURVEY OF REFERENCES

QUESTIONS AND ANSWERS FOR DAY 1

OUTLINE OF TOPICS FOR SECOND DAY

END OF DAY 1

7. Day 2: Causal Analysis

DAY 2: PARAMETRIC ESTIMATION, ANALYSIS OF BASELINE DATA, IMPACT ANALYSIS, USE OF STATA STATISTICAL PROGRAM PACKAGE

7.1. Overview of Second Day's Course Content

OVERVIEW OF SECOND DAY’S COURSE CONTENT

PARAMETRIC ESTIMATION (GENERAL LINEAR STATISTICAL MODEL; LOGISTIC REGRESSION MODEL; TWO-STEP M-ESTIMATORS)

· IMPACT ANALYSIS (DESIGN-BASED ESTIMATES, MODEL-BASED ESTIMATES, MODEL SPECIFICATION, USE OF MATCHING TO REDUCE MODEL DEPENDENCE, ESTIMATORS BASED ON IGNORABILITY (CONDITIONAL INDEPENDENCE), SELECTION VS. OUTCOME MODELS (TWO-STEP MODELS), ESTIMATION OF STANDARD ERRORS, ESTIMATION BASED ON COMBINING REGRESSION AND PROPENSITY-SCORE MATCHING (MATCHING ESTIMATORS, DOUBLY-ROBUST MATCHING/REGRESSION APPROACH), INSTRUMENTAL-VARIABLE ESTIMATORS, LOCAL AVERAGE TREATMENT EFFECT (LATE), INTENTION-TO-TREAT EFFECT (ITT), REGRESSION DISCONTINUITY DESIGN, RESPONSES DISCRETE OR IN A LIMITED RANGE, MULTIVALUED (CATEGORICAL) TREATMENT VARIABLE, MULTIPLE TREATMENT VARIABLES, PANEL DATA (FIXED-EFFECTS MODEL, RANDOM-EFFECTS MODEL), TREATMENT OF MISSING VALUES, USE OF WEIGHTS, ESTIMATION OF STANDARD ERRORS)

ANALYSIS OF BASELINE DATA (DESCRIPTIVE SURVEYS, ANALYTICAL SURVEYS)
USE OF STATA STATISTICAL PROGRAM PACKAGE (SUMMARY DESCRIPTION AND EXAMPLES)
SURVEY OF REFERENCES
QUESTIONS AND ANSWERS

7.2. Parametric Estimation and Hypothesis Testing

PARAMETRIC ESTIMATION AND HYPOTHESIS TESTING

WILL FOCUS ON PARAMETER ESTIMATION RATHER THAN HYPOTHESIS TESTING

MANY PROCEDURES FOR ANALYSIS OF RELATIONSHIPS

NONPARAMETRIC METHODS: CATEGORICAL DATA ANALYSIS (CROSS-CLASSIFIED TABLES, CONTINGENCY TABLES)

PARAMETRIC METHODS: GENERAL LINEAR STATISTICAL MODEL (GLM, LEAST-SQUARES); MAXIMUM LIKELIHOOD (ML); M-ESTIMATORS; BAYESIAN ESTIMATES (MINIMIZE AVERAGE RISK/LOSS); MINIMAX ESTIMATES (MINIMIZE MAXIMUM RISK/LOSS).

WILL FOCUS ON PARAMETRIC METHODS (GLM, ML, M):

GENERAL LINEAR STATISTICAL MODEL (GLM): “MULTIPLE REGRESSION” MODEL (MR); ANALYSIS OF VARIANCE (ANOVA)

GENERALIZED LINEAR STATISTICAL MODEL (GLM): LOGISTIC REGRESSION MODEL (LR)

LIKELIHOOD RATIO: MAKE ASSUMPTIONS ABOUT THE UNDERLYING DISTRIBUTION

M-ESTIMATORS: USE A MORE GENERAL OPTIMIZATION CRITERION (USEFUL FOR NONLINEAR MODELS)

PROPERTIES OF ESTIMATORS:

UNBIASEDNESS: EXPECTED VALUE OF ESTIMATOR EQUALS VALUE OF PARAMETER BEING ESTIMATED

MINIMUM-VARIANCE: PRECISION IS NO LESS THAN OTHER ESTIMATORS BASED ON THE SAME SAMPLE

SUFFICIENCY: CONTAINS ALL OF THE INFORMATION IN THE SAMPLE THAT IS RELEVANT TO ESTIMATION OF THE PARAMETER

ASYMPTOTIC EFFICIENCY: AS THE SAMPLE SIZE INCREASES, THE PRECISION OF THE ESTIMATOR IS AS HIGH AS POSSIBLE (ACHIEVES THEORETICAL LOWER BOUND FOR THE VARIANCE)

CONSISTENCY: CONVERGES TO THE DESIRED VALUE AS THE SAMPLE SIZE BECOMES LARGE (ASYMPTOTIC (LARGE-SAMPLE) PROPERTY, VS. SMALL-SAMPLE PROPERTY)

ASYMPTOTIC NORMALITY

NOTE THAT IN MANY INSTANCES, THE “SAMPLE ANALOG” OF A FUNCTION IS A REASONABLE ESTIMATOR FOR A PARAMETER, E.G., THE SAMPLE MEAN IS A REASONABLE ESTIMATOR FOR THE POPULATION MEAN. (COUNTEREXAMPLE: SAMPLE SPECTRUM IS NOT A CONSISTENT ESTIMATOR FOR THE TRUE SPECTRUM.) ALSO, SAMPLE MOMENTS ARE CONSISTENT ESTIMATORS OF POPULATION MOMENTS.

ESTIMATION PROCEDURES:

LEAST-SQUARES

NONLINEAR LEAST SQUARES

M-ESTIMATOR

TWO-STEP M-ESTIMATOR (FIRST-STEP SELECTION MODEL + SECOND-STEP OUTCOME MODEL)

MAXIMUM LIKELIHOOD

IN ECONOMIC APPLICATIONS, FOCUS MAINLY ON THE REDUCED MODEL, AND ON ESTIMATION OF A SINGLE EQUATION AT A TIME (LIMITED INFORMATION LEAST-SQUARES ESTIMATIONS VS. FULL INFORMATION MAXIMUM LIKELIHOOD (MULTIVARIATE ANALYSIS)).

ESTIMATION OF STANDARD ERRORS:

FOR SIMPLE MODELS, CLOSED-FORM EXPRESSIONS ARE AVAILABLE

FOR COMPLEX MODELS, USE RESAMPLING METHODS (JACKKNIFE, BOOTSTRAP)

TESTS OF HYPOTHESIS (MORE LATER):

DIFFICULT, BECAUSE OF CONFOUNDING

PRINCIPLE OF CONDITIONAL ERROR

REFERENCES:

Wooldridge, Jeffrey M., Econometric Analysis of Cross Sectional and Panel Data 2^nd edition, MIT Press, 2010.

Mood, Alexander M., Graybill, Franklin A. and Duane C. Boes, Introduction to the Theory of Statistics 3^rd edition, McGraw Hill, 1974.

Dobson, Annette J., An Introduction to Generalized Linear Models 2^nd edition, Chapman & Hall, 2002.

Draper, Norman and Harry Smith, Applied Regression Analysis, Wiley, 1966.

Hosmer, David W. and Stanley Lemshow, Applied Logisitic Regression, Wiley, 1989.

Kuehl, Robert O. Design of Experiments: Statistical Principles of Research Design and Analysis 2^nd edition, Brooks/Cole/Cengage Learning, 2000.

Everitt, B. S., An Introduction to Latent Variable Models, Chapman and Hall, 1984.

Technical references:

Lehmann, E. L., Theory of Point Estimation, Wiley, 1983.

Lehmann, E. L., Testing Statistical Hypotheses 2^nd edition, Wiley, 1986.

Rao, C. Radhakrishna Rao, Linear Statistical Infernence and Its Applications 2^nd edition, Wiley, 1973 (1^st edition 1965).

GENERAL LINEAR STATISTICAL MODEL (GENERAL LINEAR MODEL (GLM), LINEAR MODEL)

y_j = β₁x_1j + β₂x_2j + … + β_kx_kj + e_j

where

j = observation index, j = 1,…,n

n = sample size

y = response variable (explained variable, dependent variable, regressand)

β_i = model parameter (regression coefficient), i = 1,…,k

k = number of model parameters

x_ij = explanatory variable (independent variable, regressor), i = 1,…,k; j = 1,…,n

e_j = model error term (or residuals), independently distributed and independent of the x’s, with mean zero and variance σ² (i.e., E(e) = 0, var(e_j) = σ², e_j1╨ e_j2 and e_j1╨x_j2 for all j1, j2).

THE ASSUMPTION THAT THE ERRORS ARE INDEPENDENT CORRESPONDS TO THE STABLE UNIT TREATMENT VALUE ASSUMPTION (SUTVA) (NO-MACRO-EFFECTS ASSUMPTION, PARTIAL-EQUILIBRIUM ASSUMPTION). EXAMPLE: JOB-TRAINING PROGRAM IN A STABLE ECONOMY.

NOTE: IF THE FIRST VARIABLE IS UNITY, THEN β₁= mean. IF THE FIRST VARIABLE IS UNITY, THEN IT IS CUSTOMARY TO START THE INDEX AT 0 (SO THAT THE MEAN IS β₀).

Will usually drop the observation index, and write:

y = β₁x₁ + β₂x₂ + … + β_kx_k + e

MATRIX NOTATION: THE PREVIOUS EQUATION IS WRITTEN AS

y = x’β + e

where β’ = (β₁,…,β_k) and x’ = (x₁, …,x_k) (boldface denotes vectors; prime denotes matrix transpose; absence of a prime on a vector denotes a column vector; prime on a vector denotes a row vector). (Note: Contrary to standard vector notation, Wooldridge defines the model in terms of a row vector x: y = xβ + e.)

and the full sample is written as

y = Xβ + e

where y’ = (y₁,…,y_n), X' = (x₁,…,x_n) and e’ = (e₁,….,e_n).

X IS CALLED THE DATA MATRIX. IN MOST INSTANCES, x₁=1, AND β₁ IS THE MEAN.

THE “LEAST-SQUARES” (GAUSS-MARKOV) ESTIMATE OF β MINIMIZES THE SUM OF SQUARES OF THE RESIDUALS:

UNDER THE ASSUMPTION THAT THE MATRIX X’X (THE “CROSSPRODUCTS” MATRIX) IS OF FULL RANK (INVERTIBLE), IT IS GIVEN BY

(THE “INVERTIBLE” CONDITION MEANS THAT THERE CANNOT BE ANY LINEAR DEPENDENCIES IN THE x VARIABLES. FOR EXAMPLE, INCLUDE ONLY n-1 INDICATOR VARIABLES (“DUMMY” VARIABLES) FOR A CATEGORICAL VARIABLE HAVING n CATEGORIES. THE ESTIMATOR IS DEFINED IN TERMS OF CONDITIONAL INVERSES OTHERWISE.)

THE LEAST-SQUARES ESTIMATES ARE OF INTEREST BECAUSE THEY ARE SIMPLE IN FORM (MATRIX OPERATIONS) AND HAVE DESIRABLE STATISTICAL PROPERTIES (E.G., UNBIASEDNESS, CONSISTENCY, ASYMPTOTIC EFFICIENCY, ASYMPTOTIC NORMALITY). THEY WORK WELL FOR MANY PROBLEMS.

IN THE CASE OF A MODEL WITH A MEAN AND A SINGLE EXPLANATORY VARIABLE,

y = β₀ + β₁x + e

THE LEAST-SQUARES ESTIMATES ARE

= sample mean

= (sample covariance of x and y) / (sample variance of x).

WHY IS THE ASSUMPTION THAT THE EXPLANATORY VARIABLES AND THE ERROR TERMS ARE UNCORRELATED IMPORTANT?

CONSIDER THE SIMPLE EXAMPLE:

Model y = βx + e

where y, x and e have zero mean, but x may be correlated with e.

Multiply through by x:

xy = βx² + xe.

Take expectations:

Exy = βEx² + E(xe)

or, because of zero means,

cov(x,y) = βvar(x) + cov(x,e).

Solving for β:

β = cov(x,y)/var(x) – cov(x,e)/var(x).

But the correct estimate for β is the first term on the right-hand side. The second term, which is the coefficient of the regression of e on x, is a bias.

ENDOGENEITY (E.G., SIMULTANEOUS EQUATIONS) IS A CAUSE OF CORRELATION BETWEEN REGRESSORS AND ERROR TERMS.

EXAMPLE (J. Johnston, Econometric Methods 2^nd edition (McGraw Hill, 1960), pp. 341-344):

Income-determination model consisting of a consumption function and an income identity:

Ct = α + βY_t + u_t

Y_t = Ct + Z_t

where

C = consumption expenditure

Y = income

Z = nonconsumption expenditure

u = stochastic disturbance term

t = time period.

Substituting the first equation in the second:

Y_t = α + βY_t + Z_t + u_t

Y_t = α/(1-β) + Z_t/(1 – β) + u_t/(1 – β)

so that Y_t is influenced by u_t.

E(Y_t) = α/(1 – β) + Z_t/(1 – β)

and

E{u_t[Y_t – E(Y_t)]} = E(u_t²)/(1 – β) ≠ 0.

The disturbance term and the explanatory variable in the consumption equation are correlated, and direct application of OLS to that equation will not yield unbiased or consistent estimates of α and β.

IN MANY APPLICATIONS, THE x ARE FIXED EFFECTS (FIXED NUMBERS, NOT RANDOM VARIABLES), AND THEREFORE CERTAINLY UNCORRELATED WITH THE MODEL ERROR TERMS. UNDER THE STATED ASSUMPTIONS, THE LEAST-SQUARES ESTIMATES ARE UNBIASED AND MINIMUM VARIANCE.

IN ECONOMIC (AND EVALUATION) APPLICATIONS, THE x ARE RANDOM VARIABLES. UNDER THE STATED ASSUMPTIONS, THE LEAST-SQUARES ESTIMATES ARE CONSISTENT AND ASYMPTOTICALLY NORMALLY DISTRIBUTED.

VARIANCE OF ESTIMATORS DEPENDS ON ASSUMPTIONS (FIXED EFFECTS, HOMOSCEDASTICITY).

IF FIXED EFFECTS AND CONSTANT VARIANCE, COVARIANCE MATRIX OF THE β’s IS

WHERE ESTIMATE σ² BY

THIS MODEL IS CALLED A LINEAR MODEL BECAUSE IT IS LINEAR IN THE PARAMETERS. THE EXPLANATORY VARIABLES MAY BE NONLINEAR (E.G., x², x₁x₂, ln(x)).

THE EXPLANATORY VARIABLES MAY BE CONTINUOUS OR DISCONTINUOUS. THE RESPONSE VARIABLE IS MORE CONSTRAINED (SO THAT LINEARITY ASSUMPTION HOLDS).

FOR EXAMPLE, AN INDICATOR (BINARY, DICHOTOMOUS) VARIABLE THAT DENOTES SEX:

x = 1 for males, 0 for females

OR A DESIGN VARIABLE:

x = 1 for region A, 0 otherwise.

OR THE INTERACTION EFFECT OF TREATMENT AND TIME:

x₁ (treatment) = 1 if treated, 0 if not treated

x₂ (time, survey round) = 0 for time 1 (before), 1 for time 2 (after).

Measure of impact = interaction effect of treatment and time = coefficient of x₁x₂ in regression model

THREE KEY ASSUMPTIONS:

HOMOSCEDASTICITY: VARIANCE OF THE MODEL ERROR TERMS IS CONSTANT

INDEPENDENCE: MODEL ERROR TERMS ARE INDEPENDENT OF EACH OTHER AND OF THE x’s (NO ENDOGENEITY; SUTVA)

LINEARITY: THE MODEL IS LINEAR IN THE PARAMETERS

IF THESE ASSUMPTIONS ARE VIOLATED, THE PARAMETER ESTIMATES MAY BE SERIOUSLY BIASED, AND MODEL PREDICTIONS MAY BE ABSURD (E.G., LINEAR PROBABILITY MODEL (LPM)).

APPROACHES WHEN ASSUMPTIONS ARE VIOLATED

HETEROSCEDASTICITY

VARIANCE-STABILIZING TRANSFORMATION

IF THE “RAW” DATA DO NOT SATISFY THE HOMOSCEDASTICITY ASSUMPTION, IT MAY BE POSSIBLE TO TRANSFORM THE RESPONSE VARIABLE (y) SO THAT IT DOES. EXAMPLE: LOGARITHM OF INCOME MAY HAVE CONSTANT VARIANCE.

HETEROSCEDASTICITY-CONISTENT (HETEROSCEDASTIC-ROBUST) STANDARD ERRORS (EIKER-HUBER-WHITE (BOSE ROY JOHNSON HOTELLING? – IN USE AT UNC CHAPEL HILL IN 1962) SANDWICH ESTIMATOR).

IF MODEL IS NOT WELL-SPECIFIED IN TERMS OF CAUSAL VARIABLE, INCLUDE DESIGN PARAMETERS (E.G., CLUSTER VARIABLE).

FIXED EFFECTS VS. RANDOM EFFECTS

ENDOGENEITY

ENDOGENEITY: CORRELATION OF AN x WITH e. USUALLY THE RESULT OF:

OMITTED VARIABLES

MEASUREMENT ERROR (“ERRORS IN VARIABLES”)

SIMULTANEITY (SIMULTANEOUS-EQUATION MODEL)

METHODS FOR DEALING WITH ENDOGENEITY:

INDIRECT LEAST-SQUARES: PUT THE SIMULTANEOUS EQUATION IN “REDUCED FORM” (A SINGLE EQUATION), AND APPLY ORDINARY LEAST SQUARES (OLS).

METHOD OF INSTRUMENTAL VARIABALES: TWO-STAGE LEAST SQUARES (2SLS)

FULL-INFORMATION MAXIMUM LIKELIHOOD (FIML)

METHOD OF INSTRUMENTAL VARIABLES (IV).

IF AN x IS CORRELATED WITH THE e’s, REPLACE IT WITH A VARIABLE (z) THAT, CONDITIONAL ON THE OTHER x’s, IS CORRELATED WITH IT BUT NOT WITH THE ERROR TERMS. SUCH A VARIABLE IS CALLED AN INSTRUMENTAL VARIABLE (IV).

CONCEPTUALLY, A “TWO-STEP” PROCEDURE IS USED: REGRESS THE ENDOGENOUS VARIABLE ON THE IV AND THE OTHER (EXOGENOUS) VARIABLES, AND REPLACE THE ENDOGENOUS VARIABLE WITH THIS ESTIMATE () IN THE REGRESSION MODEL. SHORTCOMING: ESTIMATES OF ERRORS NOT CORRECT.

CORRECT PROCEDURE (TWO-STAGE LEAST SQUARES, 2SLS): IF x_k IS THE ENDOGENOUS VARIABLE, THEN DENOTE z’ = (x₁, x₂,…,x_k-1,z_k)

DIFFICULTIES WITH IV METHOD:

IV ESTIMATES ARE BIASED (BUT CONSISTENT)

IF IV IS NOT HIGHLY CORRELATED WITH THE ENDOGENOUS VARIABLE, THE METHOD WORKS POORLY: BIAS AND LOW PRECISION. MAY BE BETTER TO USE OLS EVEN THOUGH BIASED.

NONLINEARITY

EXAMPLE: THE CASE OF A BIVARIATE RESPONSE VARIABLE, E.G., LINEAR PROBABILITY MODEL (LPM). THIS MODEL DOES NOT FIT WELL. IF A LINEAR MODEL IS USED IN THIS SITUATION, SOME OF THE PREDICTIONS WILL BE OUTSIDE THE RANGE (0,1). MUCH BETTER TO TRANSFORM THE MODEL PARAMETER (I.E., REPARAMETERIZE THE MODEL).

THIS LEADS US TO THE GENERALIZED LINEAR MODEL (ALSO GLM).

GENERALIZED LINEAR MODEL

THE GENERAL LINEAR MODEL IS OF THE FORM

E(y) = μ = x’β.

THE GENERALIZED LINEAR MODEL IS OF THE FORM

g(μ) = x’β.

THE FUNCTION g(μ) IS CALLED A LINK FUNCTION.

EXAMPLE. BINARY RESPONSE VARIABLE. LOGISTIC REGRESSION MODEL.

SUPPOSE y IS A BINARY VARIABLE, E.G.,

y = 1 if treated, 0 if not treated

Define

p = probability of treatment

and the link function

g(p) = log(p/(1-p)) = x’β

that is,

p = e^x^’β / (1 + e^x^’β )

NOTE THAT IN THIS MODEL, p IS RESTRICTED TO THE INTERVAL (0,1).

THE ONLY PROBLEM WITH THIS FORMULATION IS THAT THE METHOD OF LEAST SQUARES CANNOT BE USED TO ESTIMATE THE MODEL PARAMETERS. INSTEAD, THE METHOD OF MAXIMUM LIKELIHOOD IS USED.

ALTERNATIVES TO LOGISTIC REGRESSION MODEL: PROBIT REGRESSION MODEL

ADVANTAGES OF LOGISTIC REGRESSION MODEL (LOG ODDS MODEL):

FOR DISCUSSION OF THE GENERALIZED LINEAR MODEL, SEE THE FOLLOWING REFERENCES:

Agresti, Alan, An Introduction to Categorical Data Analysis, Wiley, 1996.

Agresti, Alan, Categorical Data Analysis, Wiley, 1990

Generalized Linear Model

Response variable Y (binary).

Latent variable X (continuous, -∞<x<∞)

Distribution function

F(x) = P(X<=x), -∞<x<∞

For example, F(x) may be the normal distribution, in which case the model is called a probit model, or a logistic distribution, in which case the model is called a logit or logistic model. From Agresti (1996), “The probit model was introduced in 1934 for models in toxicology. The logistic regression model was not studied until about a decade later, but it is now much more popular than the probit. Partly this is because one can also interpret the logistic regression effects using odds ratios. Thus, one can fit those models to data from case-controlled studies, because one can estimate odds ratios for such data.”

Link function g(.) specifies how μ = E(Y) relates to the linear function of the explanatory variables:

g(μ) = x’β

Mean function μ(.) specifies how the linear function relates to the mean:

μ(x’β) = g^-1(x’β)

Simplest link function g(μ) = μ corresponds to general linear model.

Canonical parameter, θ: a “natural” parameter for a distribution, such as the mean, μ, for a normal distribution, p for a binomial distribution, and λ for a Poisson distribution).

Canonical link function: the one that expresses the canonical parameter (θ) in terms of μ, i.e., θ = b(μ).

Table of canonical link functions (from Wikipedia http://en.wikipedia.org/wiki/Generalized_linear_model)

Canonical Link Functions
Distribution	Name	Link Function	Mean Function
Normal	Identity
Exponential	Inverse
Gamma	Inverse
Inverse Gaussian	Inverse squared
Poisson	Log
Binomial	Logit
Multinomial	Logit

So, for example, if the raw data followed a Poisson distribution, w would use a Poisson loglinear model, which is a GLM that assumes a Poisson distribution for Y and uses the log link function:

log μ = α + βx,

μ = exp^{(α + βx)} = e^α(e^β)x.

M-ESTIMATORS, NONLINEAR LEAST SQUARES (NLS) ESTIMATORS

MORE GENERAL FRAMEWORKS (THAN ORDINARY LEAST SQUARES) FOR PARAMETER ESTIMATION INCLUDE NONLINEAR LEAST SQUARES AND M-ESTIMATION.

SUPPOSE

E(y | x) = m(x,θ₀) for some parameter value θ₀ (a “correctly specified model for the conditional mean”)

ESTIMATE θ AS THE VALUE OF θ₀ THAT MINIMIZES THE EXPECTED SQUARED ERROR BETWEEN y AND m(x, θ), I.E., θ₀ SOLVES THE PROBLEM

min_θ E{[y – m(x,θ)]²}.

THE NLS ESTIMATOR OF θ₀, , SOLVES THE PROBLEM

MORE GENERALLY, LET q(x) DENOTE A FUNCTION OF THE RANDOM VARIABLE x. AN M-ESTIMATOR OF θ₀ SOLVES THE PROBLEM

THIS IS THE SAMPLE ANALOGY OF SOLVING THE POPULATION PROBLEM

THE LEAST-SQUARES APPROACHES ARE SIMPLY COMPUTATIONAL PROCEDURES THAT WORK RATHER WELL. THE PROPERTIES OF THE ESTIMATORS DEPEND ON THE UNDERLYING PROBABILITY DISTRIBUTIONS (E.G., NORMAL, POISSON, BINOMIAL). THE MAXIMUM-LIKELIHOOD ESTIMATORS (E.G., THE LOGISTIC-REGRESSION MODEL) ARE WELL-GROUNDED IN THEORY.

(THE PRECEDING SUMMARY IS A GENERALIZATION. FOR NONLINEAR MODELS, IT CAN BE SHOWN THAT THE ESTIMATE FOR WHICH THE CONDITIONAL EXPECTATION OF THE REGRESSION-MODEL ERROR TERMS, GIVEN THE EXPLANATORY VARIABLES, IS THE LEAST-SQUARES ESTIMATOR. SEE WOOLDRIDGE OP. CIT, PP. 397-401.)

RECOMMENDED APPROACH TO MODEL SELECTION: SEEK A MATHEMATICAL REPRESENTATION THAT HAS HIGH “FACE VALIDITY” WITH RESPECT TO REPRESENTING THE CAUSAL MODEL. E.G., USE OF A FIRST-STEP LOGISTIC REGRESSION SELECTION MODEL FOLLOWED BY A SECOND-STEP OUTCOME REGRESSION MODEL. FIXED-EFFECTS VS. RANDOM –EFFECTS ASSUMPTION GUIDED BY CAUSAL MODEL.

THE CAUSAL MODEL MAY BE REPRESENTED BY STRUCTURAL EQUATIONS. THE STATISTICAL MODEL (ESTIMABLE MODEL) IS USUALLY A “REDUCED-FORM” SINGLE-EQUATION REPRESENTATION.

RECOMMENDED APPROACH TO ESTIMATION OF STANDARD ERRORS: FOR SIMPLE MODELS, USE STANDARD (CLOSED-FORM) ESTIMATORS. USE HETEROSCEDASTICITY-ROBUST ESTIMATORS WHEN APPROPRIATE. IF NEED TO ACCOUNT FOR DESIGN FEATURES (E.G., CLUSTER), SEEK A BETTER MODEL. FOR COMPLEX MODELS, USE BOOTSTRAPPING.

SURPRISING RESULT (pp. 500-502 and 925 of Wooldrdige) (WILL USE LATER): CONSIDER A “TWO-STEP” M-ESTIMATOR, SUCH AS ESTIMATING THE PROBABILITY OF SELECTION IN THE FIRST STEP USING VARIATES z AND USING THAT ESTIMATE TO ESTIMATE OUTCOME IN THE SECOND STEP USING VARIATES v. ASSUME THAT THE FIRST-STEP ESTIMATOR IS A MAXIMUM LIKELIHOOD ESTIMATOR. UNDER THE CONDITIONAL INDEPENDENCE ASSUMPTION THAT v AND w (TREATMENT) ARE INDEPENDENT CONDITIONAL ON z, THEN THE STANDARD ERRORS OBTAINED BY IGNORING THE VARIABILITY IN THE FIRST-STEP ESTIMATOR ARE CONSERVATIVE.

ASSESSMENT OF QUALITY OF ESTIMATES

CANNOT INFER CAUSALITY FROM SAMPLE DATA, ANY MORE THAN CAN INFER RANDOMNESS FROM SAMPLE DATA. RANDOMNESS IS A PROCESS, NOT AN ASPECT OF THE DATA. CAUSALITY IS AN INTRINSIC PROPERTY OF PHYSICAL EXISTENCE, NOT AN ASPECT OF THE DATA.

ESTIMATOR VALIDITY AND PRECISION: ADDRESSED ABOVE (PRECISION, BIAS, MSE).

FOR IMPACT ESTIMATORS THAT ARE REGRESSION-MODEL COEFFICIENTS, STANDARD ERROR IS PROVIDED AS A DEFAULT PROGRAM OUTPUT. CAN ALSO OBTAIN ESTIMATE OF STANDARD ERROR OF A LINEAR FUNCTION (WILL SHOW LATER). FOR MORE COMPLEX ESTIMATORS, CAN USE RESAMPLING (BOOTSTRAPPING).

SO ESTIMATION OF PRECISION IS NOT A PROBLEM, AS LONG AS THE SAMPLE SIZE IS ADEQUATE.

DEGREES OF FREEDOM: SAMPLE SIZE LESS NUMBER OF PARAMETERS ESTIMATED.

FOR COMPLEX MODELS, PREFER SEVERAL HUNDRED DEGREES OF FREEDOM FOR ERROR-VARIANCE ESTIMATION.

TUKEY: “WITH FIVE PARAMETERS I CAN FIT AN ELEPHANT.” DISREGARDING “NUISANCE” PARAMETERS, A STATISTICAL MODEL SHOULD BE SUCH A GOOD REPRESENTATION OF REALITY THAT ONLY A FEW PARAMETERS ARE REQUIRED. EXAMPLE: BOX-JENKINS TIME SERIES MODELS USUALLY REQUIRE JUST 2-5 PARAMETERS.

OVERALL MODEL FIT:

MODEL FACE VALIDITY

MEASURES OF MODEL FIT (FOR COMPARING ALTERNATIVE MODELS):

COEFFICIENT OF DETERMINATION (R² = SQUARE OF MULTIPLE CORRELATION COEFFICIENT)

VARIOUS FIT MEASURES, SUCH AS:

CHI-SQUARE STATISTIC

ROOT MEAN SQUARE ERROR OF APPROXIMATION (RMSEA)

AKAIKE INFORMATION CRITERION (AIC): = χ² + k(k-1) – 2df where k is the number of parameters and df is the degrees of freedom of the model, or -2 ln(L) + 2k where ln(L) is the maximized log-likelihood of the model.

BAYESIAN INFORMATION CRITERION (BIC) = χ² + ln(n)[k(k-1}/2 – df] or -2 ln(L) + k ln(n).

(Reference: Measuring Model Fit, by David A. Kenny, posted at http://davidakenny.net/cm/fit.htm (September 4, 2011).)

ALTERNATIVE MODEL REPRESENTATIONS

BECAUSE OF MULTICOLLINEARITY (CORRELATION AMONG VARIABLES; LACK OF ORTHOGONALITY) MANY ALTERNATIVE REPRESENTATIONS HAVE SIMILAR FIT (SIMPSON’S PARADOX). BECAUSE OF LACK OF FORCED CHANGES, CANNOT INTERPRET MODEL COEFFICIENTS AS RESPONSE TO FORCED CHANGES. INCLUDE EXPLANATORY VARIABLES, BUT DO NOT READ MUCH INTO INDIVIDUAL COEFFICIENTS, OTHER THAN FORCED-CHANGE ONES (SUCH AS TREATMENT). ESTIMATES PROVIDE HYPOTHESES, NOT CONCLUSIONS.

EXAMPLE:

TWO DEGREES OF FREEDOM ASSOCIATED WITH A VARIABLE.

REPRESENTATION 1: LINEAR AND QUADRATIC COMPONENTS

ORTHOGONAL POLYNOMIALS

IF COMPONENTS ARE CORRELATED, EFFECTS ARE CONFOUNDED

IF COMPONENTS ARE ORTHOGONAL, EFFECTS ARE UNCORRELATED

If x = 0, 1 and 2, then x and x² are correlated, and effects confounded.

x x²

0 0

1 1

2 4

Cross-product (vector inner product): x’x² = 0x0 + 1x1 +2x4 = 0 + 1 + 8 = 9

sd(x) = **

sd(x²) = **

cov(x, x²) = **

corr(x, x²) = **

If define x with three values, -1, 0 and 1, then x and x² are orthogonal.

x x²

-1 1

0 0

1 1

Cross-product: 0

sd(x) =

sd(x²) =

cov(x, x²) = 0

corr(x, x²) = 0

IN THIS CASE, WITH ZERO CORRELATION BETWEEN x AND x², THE LINEAR AND QUADRATIC EFFECTS ARE UNCONFOUNDED.

WHEN INCLUDE INTERACTION EFFECTS IN A MODEL, MAKE SURE TO DE-MEAN THE COVARIATES, OR ELSE COEFFICIENT OF INTERACTION OF TREATMENT AND TIME WILL NOT BE UNBIASED ESTIMATE OF IMPACT. WILL DISCUSS LATER.

Continuing the example, suppose that a variable has three levels, involving two sub-variables:

Type of ownership of a firm:

Private

Public for-profit

Public not-for-profit

Define indicator variables x₁ for private/ profit and x₂ for-profit/not-for-profit.

x₁ x₂

Private -2 0

Pubic for-profit 1 -1

Public non-for-profit 1 1

Cross-product: -2x0 + 1x(-1) + 1x1 = 0.

Variables are orthogonal.

Model coefficients are not confounded, easy to interpret.

THESE EFFECTS (DEFINED BY SUBSTANTIVELY MEANINGFUL COMPARISONS (CONTRASTS)) ARE MUCH MORE INFORMATIVE (GREATER FACE VALIDITY) THAN THE LINEAR AND QUADRATIC COMPARISONS, WHICH HAVE NO SUBSTANTIVE MEANING. BOTH REPRESENTATIONS USE TWO DEGREES OF FREEDOM, AND WOULD PROVIDE IDENTICAL COEFFICIENT OF DETERMINATION (R²). THE INDIVIDUAL EFFECTS (SINGLE DEGREES OF FREEDOM) CAN BE INTERPRETED IN ONE REPRESENTATION, BUT NOT THE OTHER. (EXTREME EXAMPLE: 10 DISTRICTS. DEFINE 10 DISTRICT INDICATOR VARIABLES. WOULD NEVER CONSIDER REPRESENTING DISTRICT USING A NINE-DEGREE POLYNOMIAL.) DON’T BLINDLY INTRODUCE A MÉLANGE OF FUNCTIONAL FORMS INTO A MODEL (LINEAR, QUADRATIC, LOGARITHMIC). ("FLEXIBLE" REGRESSION MODELS.)

A NOTE ON UNBIASEDNESS:

AN ESTIMATED MEAN MAY BE UNBIASED EVEN THOUGH THE MODEL COEFFICIENTS ARE BIASED. FOR EXAMPLE, MAY WISH TO FORECAST (PREDICT) SALES (Y), AS A FUNCTION OF A NUMBER OF OBSERVED VALUES (X’s), INCLUDING ADVERTISING BUDGET. IN THIS CASE, THERE IS NO NEED FOR UNBIASED OR CONSISTENT ESTIMATES OF THE MODEL COEFFICIENTS. IF, HOWEVER, WE WISH TO PREDICT THE EFFECT OF A FORCED CHANGE IN THE ADVERTISING BUDGET, WE WANT A GOOD ESTIMATE OF THE EFFECT OF CHANGING THE BUDGET, IN WHICH CASE THE COEFFICIENT MATTERS VERY MUCH.

7.3. Impact Analysis

IMPACT ANALYSIS

WILL NOW DISCUSS IMPACT ESTIMATION IN THE CASE OF A FOUR-GROUP DESIGN (PRETEST/POSTTEST/COMPARISON GROUP).

THE PRESENTATION USES THE APPROACH AND NOTATION OF WOOLDRIDGE OP. CIT.

A. DESIGN-BASED ESTIMATES: ESTIMATES FOR HIGHLY STRUCTURED EXPERIMENTAL DESIGNS WITH RANDOMIZED ASSIGNMENT TO TREATMENT

[GRAPH, SHOWING SAME STARTING POINT FOR TREATMENT AND CONTROL GROUPS.]

MAIN FEATURE: NOT NECESSARY TO DEFINE THE CAUSAL MODEL (NO ECONOMIC THEORY, NO ECONOMIC MODEL (OTHER THAN TREATMENT VARIABLE)). WITH RANDOMIZED ASSIGNMENT TO TREATMENT, DON’T NEED ONE (OTHER THAN TREATMENT) TO INFER CAUSAL IMPACT. ESTIMATES OF IMPACT WILL BE BASED ON DESIGN PARAMETERS (AND PERHAPS A FEW COVARIATES), NOT ON A STRUCTURAL-EQUATION MODEL.

CASE 1 (SIMPLEST CASE): PRETEST/POSTTEST RANDOMIZED ASSIGNMENT TO TREATMENT, WITH SIMPLE RANDOM SAMPLING IN EACH GROUP. NO IMPORTANT HIDDEN VARIABLES. (OTHER THAN TREATMENT, NO FACTORS (EVENTS) THAT MIGHT AFFECT THE TREATMENT AND CONTROL OUTCOMES DIFFERENTLY AND SUBSTANTIALLY.)

MODEL:

Let t denote survey round: t = 0 for baseline (before, time 1) and t = 1 for endline (after, time 2).

Let T denote treatment: T = 0 for control unit and T = 1 for treatment unit (same value in baseline and endline).

Important note: The variable T may or may not be considered to be a function of time, T_t. In the preceding model formulation, a treatment unit is distinguished as such from Round 0, and the value of the treatment indicator does not change in time (for the same unit). In some model formulations, a treatment unit is not distinguished as such until the second round. While either formulation works well for the present case (randomized assignment to treatment), the convention adopted here works better for cases (considered later) in which randomized assignment is lacking, and it is necessary to distinguish the treatment and control groups in Round 0 (baseline). In the convention adopted here, impact is the interaction effect of treatment and time. In the alternative representation, impact in the present case would be the treatment effect.

Response y_Tt

Allow for a mean, β₀, a “round” (or time) effect, β₁, a “treatment” effect, β₂ (which is zero in the case of randomized assignment), and an interaction effect of round and treatment, β₃:

Control before: y₀₀ = β₀ + e

Control after: y₀₁ = β₀ + β₁ + e

Treatment before: y₁₀ = β₀ + β₂ + e

Treatment after: y₁₁ = β₀ + β₁ + β₂ + β₃ + e

y_Tt = β₀ + β₁t + β₂T + β₃tT + e

Impact is the interaction effect of time and treatment, i.e., the coefficient, β₃, on the interaction variable tT.

May obtain this estimate as a double difference, or as the coefficient of T in a regression model.

DD measure = (Ey₁₁ – Ey₁₀) – (Ey₀₁ – Ey₀₀) = β₀ + β₁ + β₂ + β₃ – β₀ – β₂ - β₀ – β₁ + β₀ = β₃.

DD estimator = .

THIS DESIGN CAN BE SUBSTANTIALLY IMPROVED ON, BY INTERVIEWING THE SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS.

CASE 2: PRETEST/POSTTEST RANDOMIZED ASSIGNMENT TO TREATMENT, MATCHING OVER TIME.

EACH HOUSEHOLD IS A “BLOCK.” THIS DESIGN ACHIEVES A SUBSTANTIAL INCREASE IN PRECISION OVER THE PREVIOUS DESIGN, BECAUSE OF THE INTRODUCTION OF WITHIN-HOUSEHOLD CORRELATION INTO THE DESIGN.

Let h_i denote an indicator variable (“dummy” variable) for the i-th household:

h_i = 1 if the unit is in the i-th household, 0 otherwise, i = 1, n_hh (where n_hh denotes the number of households).

The model becomes

y_{Tth1h2…hnhh-1} = β₀ + β₁t + β₂T + β₃tT + β₄h₁ + + β_nhh+2h_nhh-1 + e

A DIFFICULTY WITH THIS MODEL IS THAT IT INCLUDES A VERY LARGE NUMBER OF PARAMETERS (I.E., ONE FOR EACH HOUSEHOLD) THAT ARE OF NO INTEREST. THESE ARE CALLED “NUISANCE” PARAMETERS. IN A “STRAIGHTFORWARD” ANALYSIS, INCLUDING THESE PARAMETERS WOULD REQUIRE THE DEFINITION OF A LARGE NUMBER OF EXPLANATORY VARIABLES AND THE INVERSION OF A LARGE CROSSPRODUCTS MATRIX. STATISTICAL PROGRAM PACKAGES (E.G., STATA) CAN HANDLE THIS PROBLEM EFFECTIVELY (I.E., WITHOUT DEFINING THE NUISANCE VARIABLES AND WITHOUT INVERTING AN UNNECESSARILY LARGE MATRIX).

AS BEFORE, THE IMPACT IS THE COEFFICIENT β₃ ON THE TIME x TREATMENT VARIABLE (tT).

THE PRECISION OF THIS DESIGN CAN BE INCREASED BY MATCHING THE TREATMENT AND CONTROL GROUPS IN SOME WAY. THE MOST FREQUENT WAY OF DOING THIS IS TO MATCH AT A LOW ADMINISTRATIVE LEVEL, SUCH AS VILLAGE, CENSUS ENUMERATION AREA OR DISTRICT.

CASE 3: PRETEST/POSTTEST “CLUSTER” RANDOMIZED ASSIGNMENT TO TREATMENT, WITH MATCHING OVER TIME. (I.E., A “DOUBLE-MATCHED” DESIGN, WITH TEMPORAL AND CROSS-SECTIONAL MATCHING.)

Let ms_i denote an indicator variable (“dummy” variable) for the i-th match set (e.g., pair of matched villages):

ms_i = 1 if the unit is in the i-th match set, 0 otherwise, i = 1, n_ms (where n_ms denotes the number of match sets).

The model becomes

y_{Tth1h2…hnhh-1ms1ms2…nms-1} = β₀ + β₁t + β₂T + β₃tT + β₄h₁ +… + β_nhh+2h_nhh-1 + β_nhh+3ms₁ + … + β_nhh+nms+1ms_nms-1 + e.

AS BEFORE, STATISTICAL SOFTWARE PACKAGES CAN HANDLE THE SUBSTANTIAL NUMBER OF DUMMY VARIABLES ASSOCIATED WITH THE TREATMENT/CONTROL MATCH SETS.

AS BEFORE, THE IMPACT IS THE COEFFICIENT β₃ ON THE TIME x TREATMENT VARIABLE (tT).

NOTE ON MODEL SIMPLIFICATION:

THE HOUSEHOLD NUISANCE PARAMETERS MAY BE ELIMINATED BY TRANSFORMING THE DATA BY TAKING DIFFERENCES WITHIN HOUSEHOLDS, OR BY DE-MEANING THE DATA BY SUBTRACTING THE HOUSEHOLD MEAN FROM EACH OBSERVATION. IN THE CASE OF TWO SURVEY ROUNDS, THESE TWO APPROACHES PRODUCE IDENTICAL ESTIMATES. (IN TIME SERIES APPLICATIONS (WITH MORE THAN TWO TIME PERIODS), THEY PRODUCE DIFFERENT RESULTS.)

THE DIFFERENCING APPROACH REDUCES THE SIZE OF THE SAMPLE TO THE NUMBER OF HOUSEHOLDS HAVING DATA IN BOTH ROUNDS.

THIS TRANSFORMATION IS CALLED A “FIXED-EFFECTS” TRANSFORMATION” (WILL BE ADDRESSED LATER).

EVEN THOUGH THE PRECEDING DESIGNS ARE RANDOMIZED, IT IS QUITE POSSIBLE THAT THERE ARE SOME OBSERVED VARIABLES THAT AFFECT OUTCOME THAT MAY HAVE CHANGED OVER TIME. THESE VARIABLES (COVARIATES) ARE INCLUDE IN THE MODEL.

NOTE: EVEN THOUGH THERE MAY HAVE BEEN RELATIVELY FEW MATCH VARIABLES AVAILABLE FOR DESIGN, AFTER THE SURVEY HAS BEEN CONDUCTED THERE ARE A LARGE NUMBER OF COVARIATES AVAILABLE FROM THE QUESTIONNAIRE.

CASE 4: PRETEST/POSTTEST “CLUSTER” RANDOMIZED ASSIGNMENT TO TREATMENT, WITH TEMPORAL AND CROSS-SECTIONAL MATCHING, ADJUSTING FOR COVARIATES.

THIS IS STILL CONSIDERED A “DESIGN-BASED” ESTIMATE, EVEN THOUGH COVARIATES ARE INVOLVED. THE COVARIATES ARE SIMPLY OBSERVED, NOT THE RESULT OF FORCED CHANGES. THEY ARE ASSUMED TO BE EXOGENOUS, FIXED EFFECTS. THE MODEL IS AN “ANALYSIS OF COVARIANCE” MODEL. SIMILAR TO THE USE OF RATIO AND REGRESSION ESTIMATES IN DESCRIPTIVE SAMPLE SURVEY. (INCREASE PRECISION, BUT LITTLE MEANING READ INTO THE COVARIATE COEFFICIENTS – SIMILAR TO NUISANCE PARAMETERS.)

ROLE OF COVARIATES: BETTER MODEL REPRESENTATION (INCREASE PRECISION, LOWER BIAS)

REPRESENT EVENTS THAT HAPPENED OVER THE COURSE OF THE STUDY (E.G., INTRODUCTION OF HEALTH CLINICS IN SOME DISTRICTS).

REPRESENT DIFFERENCES IN TREATMENT AND CONTROL UNITS, EVEN THOUGH RANDOMIZED ASSIGNMENT.

NOTE: FOR THE PRESENT EXAMPLE, FOR SIMPLICITY, THE COVARIATES WILL BE ASSUMED TO CONSTANT IN TIME. THIS ASSUMPTION WILL BE DROPPED LATER.

Let (x₁,…,x_k) represent k covariates.

The model becomes

y_{Tth1h2…hnhh-1ms1ms2…nms-1} = β₀ + β₁t + β₂T + β₃tT + β₄h₁ +… + β_nhh+2h_nhh-1 + β_nhh+3ms₁ + … + β_nhh+nms+1ms_nms-1 + β_nhh+nms+2x₁ + … + β_nhh+nms+k+1x_k + e.

AS DISCUSSED BEFORE, IT IS DIFFICULT TO READ MUCH INTO COVARIATE COEFFICIENTS UNLESS FORCED (RANDOM) CHANGES HAVE BEEN MADE IN THE VARIABLES, AND THE VARIABLES ARE ORTHOGONAL (AS IN A HIGHLY STRUCTURED DESIGNED EXPERIMENT, SUCH AS A FRACTIONAL FACTORIAL DESIGN).

FOR CLARITY IN DISCUSSION, IT IS MOST USEFUL IS TO REPRESENT ONLY THE FORCED-CHANGE VARIABLES EXPLICITLY IN THE MODEL, AND REPRESENT ALL OTHERS AS A “GENERIC” x’β TERM. USING THIS APPROACH, THE PRECEDING MODEL IS SHOWN, FOR EXAMPLE, AS:

y_Tt = x’β + αt + γT + δtT + e

(WHERE, BECAUSE OF RANDOMIZATION, γ=0). IN MOST CASES, THE INDIVIDUAL-VARIABLE TERMS IN x’β HAVE LITTLE MEANING (BECAUSE OF LACK OF FORCED CHANGES AND LACK OF ORTHOGONALITY (CONFOUNDING; SIMPSON’S PARADOX).

THE PRECEDING DISCUSSION HAS FOCUSED ON THE GENERAL LINEAR MODEL, WHICH IS APPROPRIATE, FOR EXAMPLE, FOR CONTINUOUS RESPONSE VARIABLES. FOR BINARY RESPONSE VARIABLES, WOULD USE A GENERALIZED LINEAR MODEL, SUCH AS A LOGISTIC REGRESSION MODEL.

THE MAIN POINT TO THE PRECEDING IS THAT, EVEN IF THE DESIGN IS BASED ON RANDOMIZED ASSIGNMENT TO TREATMENT, THE MODEL USED TO ANALYZE THE DATA WILL BE A “REGRESSION-ADJUSTED” (COVARIATE ADJUSTED) MODEL.

IT SHOULD NOT BE ANTICIPATED THAT THE USE OF A HIGHLY STRUCTURED RANDOMIZED-ASSIGNMENT-TO-TREATMENT DESIGN WILL ENABLE THE USE OF THE SIMPLE DOUBLE-DIFFERENCE ESTIMATOR TO ESTIMATE IMPACT.

THE MEASURE OF IMPACT IS THE DOUBLE-DIFFERENCE MEASURE (μ₁₁ – μ₁₀) – (μ₀₁ – μ₀₀), BUT THE ESTIMATOR OF IMPACT IS RARELY THE SAMPLE DOUBLE-DIFFERENCE ESTIMATOR. THE IMPACT ESTIMATE IS USUALLY A COEFFICIENT IN A REGRESSION MODEL. THIS ESTIMATE IS CALLED A “REGRESSION-ADJUSTED” DOUBLE-DIFFERENCE ESTIMATE. THIS DESCRIPTOR IS SOMEWHAT MISLEADING, BECAUSE IT IS THE MODEL THAT IS ADJUSTED, NOT THE MEASURE, AND THE ESTIMATOR (THE REGRESSION COEFFICIENT) IS NOT REPRESENTED AS AN “ADJUSTMENT” TO THE RAW DOUBLE-DIFFERENCE ESTIMATOR.

THIS IS WHY, WHEN A DESIGN GETS “MESSED UP” (CORRUPTED) SOMEWHAT BY NONRESPONSE, IT USUALLY DOESN’T AFFECT THE ANALYSIS MUCH – COMPLEX REGRESSION ESTIMATORS WILL BE REQUIRED IN ANY EVENT.

NOTE THAT THE PRECEDING MODEL FOCUSES ON OUTCOME, NOT ON SELECTION OR ATTRITION. SELECTION BIASES ARE REMOVED BY RANDOMIZED ASSIGNMENT TO TREATMENT. IF ATTRITION IS A PROBLEM, IT WILL BE ADDRESSED IN THE “MODEL-BASED” APPROACH, TO BE DISCUSSED.

B. MODEL-BASED ESTIMATES. STATISTICAL ANALYSIS USED TO ESTIMATE PARAMETERS IN A CAUSAL MODEL

WITH THE DESIGN-BASED APPROACH, RANDOMIZED ASSIGNMENT TO TREATMENT WAS THE BASIS FOR CAUSAL INFERENCE. NO NEED FOR A CAUSAL MODEL (OTHER THAN TREATMENT).

MODEL-BASED APPROACH. CAUSAL MODEL IS SPECIFIED VIA CAUSAL DIAGRAM OR STRUCTURAL EQUATIONS. STATISTICAL ANALYSIS IS USED TO ESTIMATE MODEL PARAMETERS. STRUCTURAL-EQUATION MODELING.

IN PHYSICAL SCIENCES, INTRODUCE FORCED RANDOM VARIATION (CHANGES) INTO EXPLANATORY VARIABLES, ACCORDING TO A HIGHLY STRUCTURED DESIGN (E.G., FRACTIONAL FACTORIAL, LATIN SQUARE, PARTIALLY BALANCED INCOMPLETE BLOCKS).

IN SOCIAL AND ECONOMIC SCIENCES, CAN USUALLY INTRODUCE FORCED CHANGES INTO JUST A FEW VARIABLES (E.G., TREATMENT, SURVEY ROUND), AND OFTEN WORK WITH A BINARY TREATMENT VARIABLE (INCLUDED OR NOT INCLUDED IN THE PROGRAM; RECEIPT OR NON-RECEIPT OF PROGRAM SERVICES).

BECAUSE OF LACK OF RANDOMIZED ASSIGNMENT TO TREATMENT, AND LACK OF FORCED CHANGES IN EXPLANATORY VARIABLES, PROPERTIES OF ESTIMATES ARE BASED ON ASSUMPTIONS, SUCH AS CONDITIONAL INDEPENDENCE.

THE BIASING EFFECTS OF LACK OF RANDOMIZATION ARE MITIGATED THROUGH THE USE OF PROCEDURES SUCH AS:

EX ANTE AND EX POST MATCHING

USE OF MODELS THAT REPRESENT SELECTION AND ATTRITION

USE OF MODEL-BASED ESTIMATORS

THE MATHEMATICAL FORM OF THE MODEL USED TO REPRESENT OUTCOME WILL BE AS IN CASE 4 DISCUSSED ABOVE (GLM), BUT THE ASSUMPTIONS WILL BE DIFFERENT.

TAKING EX ANTE MATCHING INTO ACCOUNT

EX ANTE MATCHING: MATCHING AS PART OF THE DESIGN, PRIOR TO THE SURVEY.

SUMMARY OF ROLE OF MATCHING

ASSUME SAME HOUSEHOLDS INTERVIEWED IN BOTH SURVEY ROUNDS. DISCUSSION HERE PERTAINS TO MATCHING OF TREATMENT AND CONTROL SAMPLES (I.E., CROSS-SECTIONAL MATCHING, NOT TEMPORAL MATCHING).

IN AN EXPERIMENTAL DESIGN WITH RANDOMIZED ASSIGNMENT TO TREATMENT, MATCHING IS USED PRIOR TO RANDOMIZED ASSIGNMENT TO TREATMENT, TO INCREASE PRECISION, NOT BIAS (SINCE BIAS IS REMOVED BY RANDOMIZED ASSIGNMENT TO TREATMENT. (“MATCHED PAIRS” DESIGN; LOCAL CONTROL.)

USE A MATCHING TECHNIQUE TO FORM MATCHED PAIRS (OR MATCH SETS OF MORE THAN TWO, TO ALLOW FOR REPLACEMENTS). ONE MEMBER OF EACH MATCH SET IS ASSIGNED TO TREATMENT AND ONE TO CONTROL. MATCHING IS USUALLY DONE USING ADMINISTRATIVE UNITS SUCH AS VILLAGES OR DISTRICTS, NOT AT THE HOUSEHOLD LEVEL (BECAUSE OF LIMITATIONS ON DATA FOR SURVEY DESIGN).

IN A QUASI-EXPERIMENTAL DESIGN, THE PURPOSE OF EX ANTE MATCHING IS TO CAUSE THE DISTRIBUTIONS OF VARIABLES THAT MAY AFFECT OUTCOME TO BE SIMILAR FOR THE TREATMENT AND CONTROL SAMPLES. THE PRIMARY GOAL IS TO REDUCE BIAS, BUT PRECISION IS ALSO AFFECTED.

IN A QUASI-EXPERIMENTAL DESIGN, EX ANTE MATCHING IS USED TO INCREASE PRECISION AND TO REDUCE BIAS (ASSOCIATED WITH LACK OF RANDOMIZED ASSIGNMENT TO TREATMENT).

MATCHING MAY BE DONE AT TWO LEVELS: MATCHING OF UNITS AND DISTRIBUTIONAL MATCHING. UNIT MATCHING IS PREFERRED SINCE IT CAUSES THE JOINT DISTRIBUTION OF MATCH VARIABLES TO BE SIMILAR (FOR TREATMENT AND CONTROL GROUPS), NOT JUST THE MARGINAL DISTRIBUTIONS.

EX ANTE MATCHING WAS DONE ON (MATCH) VARIABLES AVAILABLE PRIOR TO THE SURVEY. IN THE ANALYSIS PHASE, THE EX ANTE MATCHING IS “HISTORY.” IT MUST BE TAKEN INTO ACCOUNT IN THE ANALYSIS, BUT IS A GIVEN.

IF DISTRIBUTIONAL MATCHING WAS DONE, THE DESIGN IS NOT MATCHED CROSS-SECTIONALLY. DATA ARE ANALYZED AS IF THEY WERE TWO INDEPENDENT SAMPLES.

IF MATCHING WAS DONE ON HIGHER-LEVEL UNITS (E.G., VILLAGES OR HOUSEHOLDS), THEN THE MATCH SETS MUST BE SPECIFIED IN THE MODEL (AS WAS DISCUSSED EARLIER). (NOTE: MANY RESEARCHERS FAIL TO ACCOUNT FOR THE EX ANTE MATCHING, IN THE DATA ANALYSIS.)

THE ROLE OF EX POST MATCHING

EX POST MATCHING: MATCHING IN THE DATA ANALYSIS PHASE

TWO KINDS OF EX POST MATCHING:

DATA TRIMMING, CULLING OR PRUNING, TO REDUCE MODEL DEPENDENCE

MATCHING ESTIMATORS

C. USE OF MATCHING TO REDUCE MODEL DEPENDENCE

MODEL DEPENDENCE: [DEFINITION**]

[GRAPH ILLUSTRATING MODEL DEPENDENCE]

EX POST MATCHING TO REDUCE MODEL DEPENDENCE

DATA TRIMMING: AS LONG AS THE TRIMMING IS DONE ON EXPLANATORY VARIABLES OF A MODEL, NO BIASES ARE INTRODUCED IN ESTIMATES IN ESTIMATES OF MODEL PARAMETERS, IF THE MODEL IS CORRECTLY SPECIFIED AND ESTIMABLE.

EX POST MATCHING IS USUALLY RESTRICTED TO REMOVAL OF NON-COMMON SUPPORTS IN EXPLANATORY VARIABLES THAT ARE BELIEVED TO HAVE A SUBSTANTIAL EFFECT ON OUTCOMES OF INTEREST. NO EFFORT TO MODIFY “SHAPE” OF DISTRIBUTIONS – THAT WILL BE TAKEN INTO ACCOUNT IN A REGRESSION MODEL.

DATA TRIMMING “LOSES” DATA. MIGHT HAVE DELETERIOUS EFFECT ON PRECISION (OR MIGHT HELP).

NOTE THAT EX POST MATCHING ADDRESSES BOTH SELECTION AND ATTRITION.

NOTE THAT EX POST MATCHING INCLUDES MANY MORE MATCH VARIABLES THAN EX ANTE MATCHING (I.E., ALL OF THE SURVEY VARIABLES, NOT JUST THE DESIGN VARIABLES).

A COMBINATION OF MATCHING AND REGRESSION ESTIMATION IS “DOUBLY ROBUST”: IF EITHER THE MATCHING IS CORRECT (I.E., RESULTS IN THE SAME DISTRIBUTIONS FOR TREATMENTS AND CONTROLS) OR THE REGRESSION MODEL IS CORRECT (I..E., CORRECTLY SPECIFIED), BUT NOT NECESSARILY BOTH, THEN THE ESTIMATES WILL BE CORRECT.

THE PRECEDING DISCUSSION RELATES TO MATCHING ON INDIVIDUAL VARIABLES. MATCHING MAY ALSO BE DONE ON COMPOSITE SCORES, SUCH AS A PROPENSITY SCORE. THIS WILL BE DISCUSSED IN THE NEXT SECTION.

D. ESTIMATORS BASED ON IGNORABILITY (CONDITIONAL INDEPENDENCE)

THIS SECTION WILL PRESENT RESULTS FOR A TWO-GROUP DESIGN (TREATMENT/CONTROL). A LATER SECTION WILL DESCRIBE MODIFICATIONS FOR THE FOUR-GROUP DESIGN (“PANEL DATA”: TREATMENT BEFORE, TREATMENT AFTER, CONTROL BEFORE, CONTROL AFTER).

WE WISH TO ESTIMATE THE (UNCONDITIONAL) AVERAGE TREATMENT EFFECT, ATE:

ATE = E(y₁ – y₀)

AND/OR THE AVERAGE TREATMENT EFFECT ON THE TREATED, ATT:

ATT = E(y₁ – y₀|w=1).

A NUMBER OF ESTIMATORS WILL BE PRESENTED, OF VARYING COMPLEXITY. CHOICE OF MODEL DEPENDS MAINLY ON ASSESSMENT OF “FACE VALIDITY” (I.E., THE EXTENT TO WHICH THE VARIABLES AND STRUCTURE RESEMBLE REALITY), AND THE EXTENT TO WHICH MODEL TECHNICAL ASSUMPTIONS ARE SATISFIED).

FACTORS TO CONSIDER:

SELECTION FOR TREATMENT (BY PROGRAM PERSONNEL AND BY ELIGIBLE CLIENT)

NONRESPONSE (TO SURVEY QUESTIONNAIRE)

ATTRITION (LEAVING THE PROGRAM BETWEEN SURVEY ROUNDS)

EXPLANATORY VARIABLES

STRUCTURAL RELATIONSHIP OF OUTCOMES OF INTEREST TO EXPLANATORY VARIABLES (CAUSAL MODEL STRUCTURE)

STATISTICAL FACTORS:

ENDOGENEITY (CORRELATION BETWEEN EXPLANATORY VARIABLES AND MODEL ERROR TERMS)

HETEROSCEDASTICITY

LINEARITY

NOTE: THE FOLLOWING TAKES INTO ACCOUNT SELECTION (FOR TREATMENT) FROM ALL SOURCES.

NOTE: WILL PRESENT RESULTS FIRST FOR A TWO-GROUP (TREATMENT/CONTROL) DESIGN, THEN SHOW MODIFICATIONS FOR FOUR-GROUP (PANEL DATA) DESIGN.

ASSUMPTIONS FOR ESTIMATING ATE:

ASSUMPTION ATE1 (IGNORABILITY):. CONDITIONAL ON x, w AND THE POTENTIAL OUTCOMES (RESPONSE) (y₀, y₁) ARE INDEPENDENT. ALSO CALLED: CONDITIONAL INDEPENDENCE OF RESPONSE AND TREATMENT; IGNORABILITY OF TREATMENT; UNCONFOUNDEDNESS OF TREATMENT.

NOTE: IF w IS A DETERMINISTIC FUNCTION OF x, THIS ASSUMPTION CALLED SELECTION ON OBSERVABLES.

THE ASSUMPTION OF IGNORABILITY IS NOT TESTABLE, SINCE WE OBSERVE ONLY (y, w, x), AND NOT BOTH POTENTIAL OUTCOMES y₀ AND y₁.

(WEAKER) ASSUMPTION ATE1’ (IGNORABILITY IN MEAN): E(y₀|x,w) = E(y₀,x) AND E(y₁|x,w) = E(y₁|x).

ASSUMPTION ATE2: (OVERLAP): FOR ALL x IN THE SUPPORT OF THE COVARIATES, 0 < P(w=1|x) < 1.

NOTE: p(x) = P(w=1|x) IS CALLED THE PROPENSITY SCORE.

NOTE: ASSUMPTIONS 1 AND 2 COMBINED ARE CALLED STRONG IGNORABILITY.

ASSUMPTIONS FOR ESTIMATING ATT:

ASSUMPTION ATT1’ (IGNORABILITY IN MEAN): E(y₀|x,w) = E(y₀,x).

ASSUMPTION ATT2 (OVERLAP): FOR ALL x IN THE SUPPORT OF THE COVARIATES, P(w=1|x) < 1. (NOTE THAT THIS IS WEAKER THAN ASSUMPTION ATE2.)

GUIDANCE FOR SELECTION OF COVARIATES (x):

DO NOT INCLUDE VARIABLES THAT MAY BE AFFECTED BY TREATMENT (THIS WILL INTRODUCE A BIAS)

GOOD CANDIDATES: VARIABLES MEASURED PRIOR TO TREATMENT ASSIGNMENT, INCLUDING PAST OUTCOMES ON y.

DO NOT SELECT CANDIDATES FOR INSTRUMENTAL VARIABLES FOR w (I.E., VARIABLES THAT ARE RELATED TO w BUT INDEPENDENT OF UNOBSERVABLES THAT AFFECT (y₀, y₁))

CONSTRUCT A DIRECTED ACYCLIC GRAPH THAT DISPLAYS THE CAUSAL RELATIONSHIPS AMONG THE MODEL VARIABLES, FOLLOWING THE THEORY PRESENTED IN PEARL OP. CIT. CONDITION ON COVARIATES THAT SATISFY THE "BACK DOOR" OR "FRONT DOOR" ESTIMABILITY CRITERIA.

DEFINE THE TWO POTENTIAL-OUTCOME CONDITIONAL MEANS:

μ₀(x) = E(y₀|x)

μ₁(x) = E(y₁|x)

NOTE THAT THESE FUNCTIONS ARE UNKNOWN.

THE AVERAGE TREATMENT EFFECT CONDITIONAL ON x IS

ATE(x) = E(y₁ – y₀|x) = μ₁(x) - μ₀(x)

AND THE AVERAGE TREATMENT EFFECT ON THE TREATED CONDITIONAL ON x IS

ATT(x) = E(y₁ – y₀|x, w=1).

IDENTIFICATION PROBLEM: ARE ATE AND ATT IDENTIFIED (ESTIMABLE)?

FIRST APPROACH TO ESTABLISHING IDENTIFICATION (REGRESSION-FUNCTION-BASED APPROACH)

DEFINE

m₀(x) = E(y|x, w=0)

and

m₁(x) = E(y|x, w=1).

UNDER ASSUMPTION ATE1’,

ATE(x) = m₁(x) – m₀(x)

AND UNDER THE ADDITIONAL ASSUMPTION ATE2,

ATE = E[m₁(x) – m₂(x)].

UNDER ASSUMPTION ATT1’,

ATT(x) = m₁(x) – m₀(x),

AND UNDER THE ADDITIONAL ASSUMPTION ATT2,

ATT = E(m₁(x) – m₀(x)|w=1].

THE PRECEDING RESULTS, BASED ON REGRESSION FUNCTIONS E(y|x,w=0) and E(y|x,w=1) ARE THE BASIS FOR REGRESSION-ADJUSTMENT ESTIMATORS:

SECOND APPROACH TO ESTABLISHING IDENTIFICATION (PROPENSITY-SCORE-BASED APPROACH; PROPENSITY-SCORE WEIGHTING)

IT CAN BE SHOWN THAT

AND

THESE RESULTS, BASED ON THE PROPENSITY SCORE (p(x)), ARE THE BASIS FOR PROPENSITY-SCORE-BASED ESTIMATORS:

NOTE: THE PRECEDING ESTIMATORS ARE SIMILAR TO THE HORVITZ-THOMPSON ESTIMATORS OF DESCRIPTIVE SAMPLE SURVEY. THE VARIANCE OF THE ESTIMATORS IS LARGE WHEN VALUES OF THE PROPENSITY SCORE ARE VERY SMALL OR VERY LARGE. IN PRACTICE, DROP OBSERVATIONS HAVING PROPENSITY SCORES BELOW .1 OR ABOVE .9.

ADDITIONAL PROPENSITY-SCORE-BASED ESTIMATORS:

REGRESSION-ADJUSTED PROPENSITY-SCORE-BASED ESTIMATE:

Regress

MODIFIED REGRESSION-ADJUSTED PROPENSITY-SCORE-BASED ESTIMATE:

Regress

where is a consistent estimate of ρ = E[p(x_i)] = P(w_i = 1).

If is from a logistic regression model that includes an intercept, the two estimates and are identical.

E. ESTIMATION OF STANDARD ERRORS

THE REGRESSION-ADJUSTMENT ESTIMATORS ARE SAMPLE AVERAGES OF REGRESSION ESTIMATES. COMPLICATED: USE BOOTSTRAPPING TO ESTIMATE THE STANDARD ERRORS OF THE ESTIMATES.

THE PROPENSITY-SCORE-BASED ESTIMATORS ARE MORE COMPLICATED. THEY ARE TWO-STEP ESTIMATORS (FIRST STEP: ESTIMATE THE PROPENSITY SCORE; SECOND STEP: ESTIMATE IMPACT USING THE ESTIMATED PROPENSITY SCORE). COMPLICATED: USE BOOTSTRAPPING TO ESTIMATE THE STANDARD ERRORS OF THE ESTIMATES.

NOTE: THE PROPENSITY-SCORE-BASED ESTIMATORS ARE TWO-STEP M-ESTIMATORS IN WHICH THE FIRST STEP IS A MAXIMUM-LIKELIHOOD ESTIMATOR. HENCE CAN APPLY THE “SURPRISING RESULT” CITED EARLIER, AND OBTAIN CONSERVATIVE ESTIMATES OF THE STANDARD ERRORS BY IGNORING THE FACT THAT THE PROPENSITY SCORE IS AN ESTIMATE. (WHY?: COMPUTER RUNNING TIMES CAN BE VERY LONG WITH BOOTSTRAPPING.)

F. TESTING STATISTICAL HYPOTHESES

THREE STANDARD APPROACHES:

IMPACT ESTIMATOR IS A REGRESSION COEFFICIENT. TEST OF HYPOTHESIS OF ZERO IMPACT IS TEST OF HYPOTHESIS THAT THE COEFFICIENT IS ZERO. SHOWN IN ANALYSIS OF VARIANCE TABLE OUTPUT BY REGRESSION PROGRAM.

IMPACT ESTIMATOR IS A LINEAR CONTRAST (E.G., SINGLE DIFFERENCE). VARIANCE OF IS V = (XX’)^-1σ². VARIANCE OF LINEAR FUNCTION c’β IS c’Vc (CALCULATED BY COMPUTER PROGRAM).

PRINCIPLE OF CONDITIONAL ERROR: ESTIMATE RESIDUAL VARIANCES FOR A “FULL” MODEL AND A “REDUCED” MODEL (UNDER THE NULL HYPOTHESIS). COMPARE VARIANCES USING AN F DISTRIBUTION (ANALYSIS OF VARIANCE).

IF f REFERS TO THE “FULL” MODEL AND r TO THE “REDUCED” MODEL, AND SSE REFERS TO “SUM OF SQUARES,” THEN

(THE RATIO OF TWO CHI-SQUARED VARIATES DIVIDED BY THEIR RESPECTIVE DEGREES OF FREEDOM). (SEE KUEHL, OP. CIT, P. 57 FOR DISCUSSION OF THIS FORMULA,)

G. ESTIMATION BASED ON COMBINING REGRESSION AND PROPENSITY-SCORE MATCHING

ESTIMATOR ON PAGE 932 OF WOOLDRIDGE OP. CIT.

H. MATCHING ESTIMATORS

SIMILAR TO THE PROPENSITY-SCORE-BASED ESTIMATION APPROACH (SAME IGNORABILITY/OVERLAP ASSUMPTIONS), BUT USING MORE GENERAL MATCHING TECHNIQUES

MULTIDIMENSIONAL MATCHING ON THE FULL SET OF COVARIATES

MAHALANOBIS-DISTANCE MATCHING

IMPORTANCE-SCORE MATCHING

PRECISION CAN BE SUBSTANTIALLY IMPROVED IF THE RELATIONSHIP OF OUTCOMES TO MATCH VARIABLES IS STRONG (SIMILAR TO STRATIFICATION IN A DESCRIPTIVE SURVEY). MAY BE MUCH MORE PRECISE THAN PROPENSITY-SCORE MATCHING.

APPROACH:

AS BEFORE, ESTIMATE CONDITIONAL ATE:

ATE(x) = E(y|w=1,x) – E(y|w=0,x),

AND THEN AVERAGE OVER THE DISTRIBUTION OF x (BY AVERAGING OVER THE SAMPLE).

LACK OF OVERLAP (BETWEEN TREATMENT AND CONTROL GROUPS) CAUSES PROBLEMS (JUST AS FOR REGRESSION-ADJUSTMENT AND PROPENSITY-SCORE-BASED ESTIMATORS).

IF MATCH ON THE PROPENSITY-SCORE, THIS IS CALLED PROPENSITY-SCORE MATCHING (VS. PROPENSITY-SCORE WEIGHTING CONSIDERED EARLIER).

FOR BOOTSTRAP ESTIMATION OF STANDARD ERRORS, PREFERABLE TO MATCH ON SEVERAL NEAREST-NEIGHBORS, RATHER THAN A SINGLE ONE. (IF MATCH ON NEAREST NEIGHBOR, RESAMPLING PRODUCES THE SAME BOOTSTRAP SAMPLE EVERY TIME.)

I. INSTRUMENTAL VARIABLE ESTIMATORS

IF THE IGNORABILITY ASSUMPTIONS CANNOT BE JUSTIFIED, THEN MAY USE THE METHOD OF INSTRUMENTAL VARIABLES TO ESTIMATE IMPACT.

DO NOT ASSUME INDEPENDENCE OF (y₀, y₁) AND w GIVEN x.

INSTEAD, ASSUME THE AVAILABILITY OF INSTRUMENTS z THAT ARE INDEPENDENT OF (y₀, x). (THAT IS, z IS CORRELATED WITH w BUT INDEPENDENT OF OUTCOME (y₀, x). WEAKER ASSUMPTIONS SUFFICE.)

PROCEDURE:

ESTIMATE THE BINARY RESPONSE P(w=1|x,z) = G(x,z,γ) BY MAXIMUM LIKELIHOOD, WHERE γ ARE PARAMETERS (E.G., OF A LOGIT OR PROBIT MODEL).

FROM THIS MODEL, ESTIMATE THE PROPENSITY SCORES . DENOTE .

ESTIMATE THE EQUATION

y = δ + τw + x’β + e

BY INSTRUMENTAL VARIABLES USING INSTRUMENTS 1, , AND x.

SEE WOOLDRIDGE PP. 937-940 FOR DETAILS.

NOTE THAT ESTIMATION OF THE PARAMETERS γ IN THE FIRST STAGE MAY BE IGNORED IN ESTIMATING THE 2SLS MODEL. (2SLS WITH GENERATED INSTRUMENTS.)

NOTE ALSO THAT SINCE G IS BEING USED AS AN INSTRUMENT FOR w, THE MODEL FOR G DOES NOT HAVE TO BE CORRECTLY SPECIFIED.

REMEMBER THAT 2SLS ESTIMATES ARE BIASED. TO INVOKE CONSISTENCY, NEED LARGE SAMPLES.

J. INTENTION-TO-TREAT (ITT) ESTIMATOR

SUPPOSE THAT THE DESIGN IS AN EXPERIMENTAL DESIGN WITH RANDOMIZED ASSIGNMENT TO TREATMENT.

THE INTENTION TO TREAT (ITT) ESTIMATE OF IMPACT IS OBTAINED BY APPLYING THE ESTIMATION FORMULAS FOR THE EXPERIMENTAL DESIGN TO THE OBSERVED OUTCOME, WHETHER OR NOT TREATMENT WAS ACTUALLY RECEIVED.

BY DEFINITION, THERE IS NO “SELECTION” BIAS IN THIS ESTIMATOR.

LET z DENOTE THE INTENTION TO TREAT.

THE RELATIONSHIP OF ATE TO ITT IS

ATE = ITT/[P(w=1|z=1) – P(w=1|z=0)].

IF P(w=1|z=0) = 0, THEN

ATE = ITT/P(w=1|z=1).

THIS FORMULA IS KNOWN AS THE “BLOOM RESULT” (AFTER HOWARD BLOOM, 1994).

K. LOCAL AVERAGE TREATMENT EFFECT (LATE) ESTIMATOR

IN THE INSTRUMENTAL-VARIABLE CASE CONSIDERED ABOVE, AN INSTRUMENTAL VARIABLE (z) WAS INTRODUCED FOR THE TREATMENT VARIABLE, w.

POTENTIAL OUTCOMES (y₀, y₁) WERE INTRODUCED FOR THE OUTCOME, y:

y = y₀ if w=0

y = y₁ if w=1

y = y₀ + w(y₁ – y₀).

MAY ALSO CONSIDER POTENTIAL TREATMENTS:

w = w₀ if z=0

w = w₁ if z=1

IN WHICH CASE

w = (1-z)w₀ + zw₁ = w₀ + z(w₁ – w₀)

AND (SUBSTITUTING IN y = y₀ + w(y₁ – y₀))

y = y₀ +w₀(y₁ - y₀) + z(w₁ – w₀)(y₁ – y₀).

IT IS ASSUMED THAT z IS INDEPENDENT OF (y₀, y₁, w₀, w₁).

IF WE DEFINE:

Never-takers: w₀ = 0, w₁ = 0

Compliers: w₀ = 0, w₁ = 1

Defiers: w₀ = 1, w₁ = 0

Always-takers: w₀ = 1, w₁ = 1

UNDER CERTAIN ASSUMPTIONS (CALLED THE “LATE” ASSUMPTIONS), IT CAN BE SHOWN THAT THE EXPECTED TREATMENT EFFECT ON THE COMPLIERS IS GIVEN BY

LATE = E(y₁ – y₀|w₁=1, w₀=0) = (Effect of z on y) / (Effect of z on w) = [E(y|z=1) – E(y|z=0)] / [E(w|z=1) – E(w|z=0)].

ESTIMATE LATE BY USING THE SAMPLE ANALOGS OF THE EXPECTATIONS.

INTERESTING ASPECT OF LATE: CANNOT OBSERVE THE COMPLIERS.

THE LATE ASSUMPTIONS ARE

1. P(w=1|z) is a nonconstant function of z

2. Independence of z and (y₀, y₁, w₀, w₁)

3. Monotonicity: For all i, either w_1i >= w_0i or w_1i <= w_0i

FOR AN EXPERIMENTAL DESIGN, THERE IS NO NEED TO CONSIDER COVARIATES. THE INSTRUMENTAL VARIABLE, z, IS SELECTION FOR TREATMENT IN THE DESIGN.

IF THE DESIGN HAS BEEN CORRUPTED, THE LATE MAY BE CALCULATED AS THE ITT, OR COVARIATES MAY BE TAKEN INTO ACCOUNT:

THE FORMULA FOR THE LATE WHEN COVARIATES ARE INCLUDED IS:

L. REGRESSION-DISCONTINUITY ((RD) DESIGN

SHARP REGRESSION-DISCONTINUITY (SRD) DESIGN: THERE IS A SINGLE COVARIATE x_i, THAT DETERMINES TREATMENT:

w_i = I(x_i >=c) (WHERE I(.) IS THE UNIT INDICATOR FUNCTION).

CANNOT APPLY PREVIOUS METHODS, SUCH AS PROPENSITY-SCORE WEIGHTING, BECAUSE THERE IS NO OVERLAP. (IGNORABILITY HOLDS BECAUSE w IS A DETERMINISTIC FUNCTION OF x, SO E(y_g|x,w) = E(y_g|x), g=0,1).)

USE OF REGRESSION ADJUSTMENT WOULD REQUIRE EXTRAPOLATION BEYOND THE RANGE OF THE DATA.

APPROACH: ESTIMATE THE AVERAGE TREATMENT EFFECT AT THE DISCONTINUITY POINT:

ATE(c) = τ_c = E(y1 – y0|x=c) = μ₁(c) - μ₀(c).

NO EXTERNAL VALIDITY.

ASSUMPTION: THE MEAN FUNCTIONS μ₁(x) - μ₀(x) ARE CONTINUOUS AT c.

PROCEDURE: ESTIMATE THE TWO REGRESSION FUNCTIONS ABOVE AND BELOW c, AND EVALUATE AT c. THE IMPACT IS THE DIFFERENCE IN THESE VALUES.

LINEAR REGRESSION ESTIMATOR:

DEFINE

μ_0c = μ₀(c)

and

μ_1c = μ₁(c)

DEFINE

y₀ = μ_0c + β₀(x - c) + u₀

y₁ = μ_1c + β₁(x - c) + u₁

SO THAT

y = (1 - w)y₀ + wy₁ = μ_c + τ_cw + β₀(x - c) + δw(x – c) + r

where

r = u₀ +w(u₁ – u₀) and δ = β₁ – β₀.

THE ESTIMATE OF IMPACT IS THE ESTIMATE OF τ_c (THE JUMP IN THE LINEAR FUNCTION AT x = c).

TO ESTIMATE τ_c, REGRESS y on 1, w_i, (x_i – c) and w_i(x_i-c).

RESTRICT DATA TO A SMALL BAND AROUND c.

FUZZY REGRESSION-DISCONTINUITY (FRD) DESIGN: THE PROBABILITY OF TREATMENT CHANGES DISCONTINUOUSLY AT x = c:

P(w=1|x) = F(x).

See pp 957-958 of Wooldridge op. cit. for details.

M. RESPONSES DISCRETE OR IN A LIMITED RANGE

SIMILAR METHODS

E.G., IF RESPONSE IS POISSON, USE POISSON DISTRIBUTION IN MAXIMUM LIKELIHOOD

CONTINUOUS, BUT DATA CENSORED OR TRUNCATED

DATA CENSORING (E.G., OBSERVATION IS “TOP-CODED” OR RESPONSE MISSING)

TRUNCATED (DISTRIBUTION IS “CUT OFF,” OBSERVATIONS DELETED; SELECTION ON BASIS OF RESPONSE)

EXAMPLE: CENSORED NORMAL REGRESSION MODEL

CENSORED TOBIT MODEL:

Latent variable y* = x’β + u, where u≈N(0, σ²)

Observe y=max(0, y*)

ESTIMATION:

OLS INCONSISTENT (SIMILAR TO HIDDEN VARIABLE); USE MAXIMUM LIKELIHOOD. (COMPLICATED, DETAILS OMITTED.)

EXAMPLE: TRUNCATED NORMAL REGRESSION MODEL

TRUNCATED TOBIT MODEL:

EXAMPLE: WAGE OFFER AND LABOR FORCE PARTICIPATION

Wage model: y₁ = x₁’β₁ + u₁

Labor force participation model: y₂ = I(xδ₂ + v₂ > 0) (indicator function)

where (x, y₂) is always observed, and y₁ is observed only when y₂ = 1

Not reasonable to assume wage = 0 when person is not a labor force participant

OLS INCONSISTENT: SELECTION BIAS.

USE TOBIT SELECTION MODEL:

y₁ = x₁’β₁ + u₁

y₂ = max(0, x’δ₂ + v₂)

TWO-STEP MODEL: ESTIMATE δ₂ FROM THE MODEL. E.G., FIRST-STEP PROBIT MODEL

P(y_i2=1)|x_i) = Φ(x’_iδ₂)

using all observations.

Estimate β₁using OLS on the selected sample. (Details complicated, omitted.)

N. MULTIVALUED (CATEGORICAL) TREATMENT VARIABLE

CATEGORICAL, NON-BINARY: E.G., THREE VALUES: CONTROL (0), TREATMENT 1 (1), TREATMENT 2 (2)

SIMILAR ESTIMATION TECHNIQUES APPLY: E.G., ESTIMATE AVERAGE TREATMENT EFFECT FOR EACH TREATMENT LEVEL VS. CONTROL.

O. MULTIPLE TREATMENT VARIABLES

INSTEAD OF SCALAR TREATMENT VARIABLE, w, HAVE VECTOR TREATMENT VARIABLE, w.

MAY CONSIDER MORE ELABORATE RESEARCH DESIGN, E.G., TWO VARIABLES AT TWO LEVELS = FOUR COMBINATIONS OF TREATMENT VARIABLES. THIS IS AN “ORTHOGONAL” DESIGN.

MODELS SIMILAR TO BEFORE. TREATMENT VARIABLES ARE “SPECIAL” (HIGH INTEREST) EXPLANATORY VARIABLES. MORE EFFECTS OF INTEREST.

SIMILAR ESTIMATION TECHNIQUES APPLY, ALTHOUGH SOMEWHAT MORE COMPLICATED.

P. PANEL DATA

SECTION A DESCRIBED THE FOUR-GROUP MODEL (TREATMENT BEFORE, TREATMENT AFTER, CONTROL BEFORE, CONTROL AFTER) IN THE CASE OF RANDOMIZED ASSIGNMENT TO TREATMENT:

MODEL:

y_Tt = x’β + αt + γT + δtT + e

AND SECTIONS D-N DESCRIBED ESTIMATION FOR THE TWO-GROUP MODEL (TREATMENT/CONTROL), IN THE POTENTIAL- OUTCOMES CONCEPTUAL FRAMEWORK (LACK OF RANDOMIZED ASSIGNMENT TO TREATMENT).

THAT APPROACH WAS TAKEN TO SIMPLIFY THE PRESENTATION.

THIS SECTION DESCRIBES EXTENSIONS OF THE THEORY TO THE GENERAL FOUR-GROUP CASE (NON-RANDOMIZED ASSIGNMENT TO TREATMENT).

[GRAPH, SHOWING DIFFERENT STARTING POINTS FOR TREATMENT AND CONTROL GROUPS.]

MAIN FEATURES:

WITH RANDOMIZED ASSIGNMENT TO TREATMENT, IT WAS NOT NECESSARY TO DEFINE THE CAUSAL MODEL (ECONOMIC MODEL). LACKING THIS, IT IS NECESSARY TO SPECIFY THE CAUSAL MODEL. CAUSAL EFFECT WAS COEFFICIENT OF TREATMENT VARIABLE (w). COVARIATES WERE “INCIDENTAL” (DESIGN EFFECTS, ASSOCIATION).

WITH RANDOMIZED ASSIGNMENT TO TREATMENT, THE TREATMENT AND CONTROL GROUPS WERE THE SAME AT BASELINE (“STARTED FROM THE SAME POINT”). LACKING THIS, THE CAUSAL EFFECT IS THE COEFFICIENT OF THE INTERACTION EFFECT OF TREATMENT (w) AND TIME (SURVEY ROUND, t). COVARIATES INCLUDE DESIGN EFFECTS AND CAUSAL VARIABLES.

CASE 1 PREVIOUS MODEL (RANDOMIZED ASSIGNMENT TO TREATMENT, NO COVARIATES):

y_Tt = x’β + αt + γT + δtT + e

WHERE, BECAUSE OF RANDOMIZED ASSIGNMENT TO TREATMENT, γ=0.

WE NOW ALLOW FOR THE FACT THAT, BECAUSE OF LACK OF RANDOMIZED ASSIGNMENT TO TREATMENT, THE TREATMENT AND CONTROL GROUPS MAY DIFFER AT BASELINE.

THE MODEL FOR THIS EXAMPLE (CASE 1) DOES NOT INCLUDE COVARIATES. REALISTIC MODELS WILL INCLUDE COVARIATES, IN ACCORDANCE WITH THE CAUSAL MODEL.

IN THE PREVIOUS CONSIDERATION OF COVARIATES (“CASE 4”), THEY WERE ASSUMED TO BE EXOGENOUS, FIXED EFFECTS. BOTH OF THESE ASSUMPTIONS WILL NOW BE DROPPED (I.E., THEY MAY NOW BE ENDOGENOUS AND RANDOM).

ASSUMPTIONS ARE NOW REQUIRED CONCERNING THE RELATIONSHIP OF EXPLANATORY VARIABLES (COVARIATES) AND ERROR TERMS OVER TIME (I.E., BETWEEN ROUNDS). THESE ASSUMPTIONS ARE COMPLICATED, BUT ESSENTIAL TO TAKE INTO ACCOUNT.

THESE ASSUMPTIONS ARE REPRESENTED IN THE CAUSAL MODEL.

FIXED-EFFECTS OR RANDOM EFFECTS

IN ECONOMETRIC APPLICATIONS AND EVALUATION STUDIES, COVARIATES (I.E., VARIABLES EXCLUDING TREATMENT AND DESIGN VARIABLES) ARE USUALLY ASSUMED TO BE RANDOM VARIABLES (“RANDOM EFFECTS”).

IN THIS CASE, ASSUMPTIONS MUST BE MADE ABOUT THE RELATIONSHIP BETWEEN THE COVARIATES AND THE MODEL ERROR TERMS.

A KEY CONSIDERATION IS OMITTED VARIABLES, OR UNOBSERVED EFFECTS. MANY OF THE UNOBSERVED EFFECTS ARE REMOVED BY DIFFERENCING (E.G., A SINGLE-DIFFERENCE OR DOUBLE-DIFFERENCE IMPACT ESTIMATE).

THE UNOBSERVED EFFECTS MODEL (UEM) IS:

y_t = x_t’β + c + u_t, t=0,1

WHERE c DENOTES AN UNOBSERVED TIME-CONSTANT VARIABLE (UNOBSERVED COMPONENT, LATENT VARIABLE, UNOBSERVED HETEROGENEITY INDIVIDUAL EFFECT, IDIOSYNCHATIC DISTURBANCES).

RANDOM-EFFECTS MODEL:

IF c IS A RANDOM VARIABLE, THE FOLLOWING ORTHOGONALITY ASSUMPTIONS (AMONG OTHERS) ARE REQUIRED TO OBTAIN CONSISTENT ESTIMATORS OF THE PARAMETERS (β):

E(u_t|X,c) = 0, t=0,1 (the error terms are uncorrelated with X, given c)

E(c|X) = E(c) = 0 (c is uncorrelated with X)

where X = (x₁,x₂) (and the subscript t on x_t refers to time (t)).

THE RANDOM-EFFECTS APPROACH TO ESTIMATING β IS EQUIVALENT TO PLACING c IN THE MODEL ERROR TERM.

IF c IS A RANDOM VARIABLE, THE COMPOSITE ERROR c + u_t IS SERIALLY CORRELATED. IN ORDER TO OBTAIN CONSISTENT (GENERALIZED) LEAST-SQUARES ESTIMATES, NEED TO ASSUME ORTHOGONALITY OF X AND c.

THE PRECEDING ASSUMPTIONS MEAN THAT THE UNOBSERVED EFFECT IS UNCORRELATED WITH THE OBSERVED COVARIATES AND THE MODEL ERROR TERMS (I.E., c AND X ARE ORTHOGONAL).

THE VARIANCES OF THE ESTIMATES DEPEND ON THE VARIANCE OF c (SO THAT TESTING HYPOTHESES IS LIKE A RANDOM-EFFECTS ANOVA).

WHETHER THE ORTHOGONALITY ASSUMPTIONS ARE JUSTIFIED IS INFERRED FROM THE CAUSAL MODEL.

(THE OTHER ASSUMPTIONS REQUIRED FOR A FIXED-EFFECTS ANALYSIS ARE THAT A CERTAIN QUADRATIC FORM IS POSITIVE DEFINITE (OF FULL RANK), AND THAT, CONDITIONAL ON c AND THE COVARIATES, THE MODEL ERROR TERMS ARE UNCORRELATED AND HAVE CONSTANT VARIANCE, AND THE VARIANCE OF c CONDITIONAL ON THE COVARIATES IS A CONSTANT.)

FIXED-EFFECTS MODEL:

IF c IS A FIXED EFFECT, IT MAY BE ARBITRARILY RELATED TO THE COVARIATES X.

THE KEY ASSUMPTION FOR THE FIXED-EFFECTS MODEL IS:

E(u_t|X,c) = 0, t=0,1 (the error terms are uncorrelated with X, given c).

THE SECOND ASSUMPTION OF THE RANDOM-EFFECTS MODEL, VIZ.,

E(c|X) = E(c) = 0 (c is uncorrelated with X)

IS NOT REQUIRED. IN OTHER WORDS, E(c|X) IS ALLOWED TO BE ANY FUNCTION OF X.

THE FIXED-EFFECTS MODEL IS HENCE MORE “ROBUST” THAN THE RANDOM EFFECTS MODEL, WITH RESPECT TO TECHNICAL ASSUMPTIONS.

IN THE FIXED-EFFECTS MODEL, c IS CONFOUNDED WITH x_t’β. HENCE WE HAVE TO ELIMINATE IT FROM THE MODEL. THIS IS DONE EITHER BY DE-MEANING THE OBSERVATIONS FOR MATCHED UNITS (HOUSEHOLDS) OVER TIME, OR BY DIFFERENCING MATCHED UNITS OVER TIME. (THIS REMOVES ALL UNOBSERVED VARIABLES THAT ARE CONSTANT WITHIN HOUSEHOLDS.) THESE TRANSFORMATIONS ARE CALLED FIXED-EFFECTS TRANSFORMATIONS OR “WITHIN” TRANSFORMATIONS.

IN THE FIXED-EFFECTS MODEL, THE LEAST-SQUARES ESTIMATES OF β ARE UNBIASED CONDITIONAL ON X.

UNDER THE ASSUMPTION THAT THE MODEL ERRORS ARE UNCORRELATED CONDITIONAL ON X AND c, THE LEAST-SQUARES ESTIMATES ARE EFFICIENT.

WHICH APPROACH TO USE?

FOR BOTH APPROACHES, DECIDING WHETHER THE TECHNICAL ASSUMPTIONS HOLD IS DIFFICULT TO JUSTIFY – MODELS ARE TOO COMPLEX.

RANDOM-EFFECTS MODEL IS MORE IN LINE WITH THE CAUSAL MODEL FOR EVALUATION. MORE DIFFICULT TO DETECT CHANGE (LIKE RANDOM-EFFECTS ANOVA, THE VARIANCE OF THE DENOMINATOR OF THE F STATISTIC CONTAINS THE “RESIDUAL” VARIANCE PLUS THE VARIANCE OF THE EXPLANATORY VARIABLES).

FIXED-EFFECTS MODEL IS MORE ROBUST. INFERENTIAL SCOPE IS RESTRICTED TO THE FIXED VALUES OF THE EXPLANATORY VARIABLES. THIS CAN MAKE A BIG DIFFERENCE IF HAVE A RELATIVELY SMALL SAMPLE OF PSUs (E.G., DISTRICTS, VILLAGES). HAVE A MUCH BETTER CHANCE OF DETECTING EFFECTS.

SOLUTION:

TAKE FULL ADVANTAGE OF THE FACT THAT MANY EVALUATION STUDIES INVOLVE INTERVIEW OF THE SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS.

THIS IS DONE VIA THE FIXED-EFFECTS TRANSFORMATION (DE-MEANING OR DIFFERENCING).

POTENTIAL PROBLEM: THIS MAKES USE OF DATA FOR WHICH INTERVIEWS ARE AVAILABLE IN BOTH SURVEY ROUNDS. MAKE EXCEPTIONAL EFFORTS TO KEEP SECOND-ROUND NONRESPONSE LOW.

FIXED-EFFECTS MODEL IS MUCH USED IN POLICY ANALYSIS AND EVALUATION. THE POLICY VARIABLE (TREATMENT VARIABLE, w) MAY BE CORRELATED WITH AVERAGE VALUE OF THE ERROR TERM FOR MATCHED UNITS BETWEEN ROUNDS. ALL THAT IS REQUIRED IS THAT THE DEMEANED ERROR TERMS BE UNCORRELATED WITH THE COVARIATES (SEE WOOLDRIDGE OP. CIT. pp. 278-279).

FIXED-EFFECTS APPROACH, BASED ON “WITHIN” DATA, IS USELESS FOR ASSESSING THE EFFECT OF A TIME-CONSTANT VARIABLE IN A PANEL-DATA STUDY. THE VARIABLE “DROPS OUT.” SOLUTION: USE RANDOM EFFECTS MODEL (“BETWEEN” MODEL), OR INCLUDE INTERACTIONS WITH SURVEY ROUND (WHICH DOES NOT DROP OUT). (E.G., SIZE OF FARM, SEX OF HEAD OF HOUSEHOLD, DISTANCE TO CLINIC, AND VILLAGE CHARACTERISTICS MAY DROP OUT, BUT THE INTERACTION OF THESE VARIABLES WITH SURVEY ROUND DOES NOT.)

RECOMMENDED APPROACH: CONSIDER AND COMPARE BOTH RANDOM-EFFECTS AND FIXED-EFFECTS MODELS. IN GENERAL, RELY ON FIXED-EFFECTS MODEL AND FIXED-EFFECTS TRANSFORMATION (SIMPLER ASSUMPTIONS, MORE ROBUST).

THE EQUIVALENCE OF A RANDOM-EFFECTS MODEL AND A FIXED-EFFECTS MODEL FOR THE SAME DATA SET IS TESTED USING THE HAUSMAN TEST. IF THE TWO MODELS ARE NOT STATISTICALLY SIGNIFICANTLY DIFFERENT, THEN THE RANDOM-EFFECTS MODEL IS USED (BECAUSE THE FIXED-EFFECTS MODEL IS CONSISTENT AND THE RANDOM-EFFECTS MODEL IS EFFICIENT).

KEEP IN MIND: FIXED-EFFECTS MODEL CORRESPONDS TO A MORE RESTRICTED SCOPE OF INFERENCE. (E.G., IN RANDOM-EFFECTS MODEL, SAMPLE PSUs ARE VIEWED AS A RANDOM SAMPLE; IN FIXED-EFFECTS MODEL, THEY BECOME THE POPULATION OF INTEREST. RANDOM EFFECTS MORE DIFFICULT TO FIND (ALLOWS FOR VARIATION IN PSU MEANS). RANDOM-EFFECTS ANOVA: COMPONENTS OF VARIANCE, VARIANCE OF “REDUCED” MODEL INCLUDES RESIDUAL VARIANCE AND PSU VARIANCE.

VERY IMPORTANT NOTE: WHEN INCLUDING INTERACTION TERMS OF COVARIATES WITH TREATMENT, MUST DE-MEAN THE COVARIATE TERMS, OR WILL NOT OBTAIN AN UNBIASED ESTIMATE OF IMPACT.

NOTE ON MODEL SPECIFICATION:

MODEL SHOULD NOT DEPEND ON PSU (CLUSTER, FIRST-STAGE SAMPLE UNIT). IF IT DOES, LOOK FOR AN IMPROVED SPECIFICATION.

Q. TREATMENT OF MISSING VALUES

REASONS FOR MISSING VALUES:

NONRESPONSE IN BASELINE (REFUSALS, NOT AT HOME, CANNOT LOCATE (DEFECTIVE FRAME))

NONRESPONSE IN ENDLINE (SAME, PLUS DIED, MOVED)

ATTRITION (WITHDRAWAL FROM PROGRAM)

NOTE: REPLACEMENT HOUSEHOLDS ARE MORE PROBLEMATIC IN PANEL SURVEYS (THE REPLACEMENT HOUSEHOLD MAY DIFFER ON MANY VARIABLES, INTRODUCING SUBSTANTIAL ERROR INTO THE INTER-ROUND HOUSEHOLD DIFFERENCE.)

IT IS ESSENTIAL TO KEEP TRACK OF ALL BASELINE UNITS (HOUSEHOLDS), TO IMPLEMENT SELECTION MODEL.

REFERENCES ON MISSING VALUES:

Little, Roderick J. A. Little and Donald B. Rubin, Statistical Analysis with Missing Data 2^nd edition, Wiley, 2002 (1^st edition 1987).

Rubin, Donald B, Multiple Imputation for Nonresponse in Surveys, Wiley, 1987.

MISSING VALUES ARE A VERY SERIOUS PROBLEM IN MODEL-BASED ESTIMATION, BECAUSE OF CASEWISE DELETION (IF AN OBSERVATION DOES NOT HAVE VALUES FOR ALL VARIABLES, IT IS DROPPED FROM THE DATA SET).

IMPERATIVE TO IMPUTE MISSING VALUES.

APPROACHES:

SUBSTITUTION OF MEANS (OR MEDIANS) FOR MISSING VALUES

SUBSTITUTION OF REGRESSION ESTIMATE (BASED ON NON-MISSING VALUES) FOR MISSING VALUES (SUBSTITUTION OF “CONDITIONAL MEANS,” BUCK’S METHOD)

LIKELIHOOD-BASED (MODEL-BASED) ESTIMATION OF MISSING VALUES: MAXIMUM-LIKELIHOOD AND BAYES MODELS.

COMPLETE DATA MATRIX Y = (yij)

MISSING-DATA INDICATOR MATRIX, M = (Mij).

MISSING COMPLETELY AT RANDOM (MCAR): MISSINGNESS (DISTRIBUTION OF M) DOES NOT DEPEND ON THE VALUES OF THE DATA, MISSING OR OBSERVED.

MISSING AT RANDOM (MAR): MISSINGNESS DEPENDS ONLY ON THE NON-MISSING VALUES.

NOT MISSING AT RANDOM (NMAR): DISTRIBUTION OF M DEPENDS ON THE MISSING VALUES IN THE DATA MATRIX, Y.

EXPECTATION-MAXIMIZATION (EM) ALGORITHM FOR FINDING MAXIMUM-LIKELIHOOD ESTIMATES FROM INCOMPLETE DATA (AVOIDS ANALYTICAL PROBLEMS):

REPLACE MISSING VALUES BY ESTIMATED VALUES

ESTIMATE PARAMETERS

RE-ESTIMATE MISSING VALUES ASSUMING THAT THE NEW PARAMETER ESTIMATES ARE CORRECT

ITERATE PREVIOUS STEP (RE-ESTIMATION OF PARAMETERS) UNTIL CONVERGENCE

NOTE: BOOTSTRAP ESTIMATION PROCESS REQUIRES FULL DATA SET: MUST IMPUTE MISSING VALUES PRIOR TO APPLYING.

R. USE OF WEIGHTS

FOUR TYPES OF WEIGHTS (STATA):

FREQUENCY WEIGHTS (fweights) INDICATE DUPLICATED OBSERVATIONS

SAMPLING WEIGHTS (pweights) DENOTE RECIPROCALS (INVERSES) OF THE PROBABILITY OF INCLUSION BECAUSE OF THE SAMPLE DESIGN. E.G., “EXPANSION FACTORS” USED TO ESTIMATE POPULATION TOTALS.

ANALYTIC WEIGHTS (aweights) ARE INVERSELY PROPORTIONAL TO THE VARIANCE OF AN OBSERVATION. (E.G., OBSERVATIONS ARE MEANS, AND THE WEIGHTS ARE THE NUMBER OF UNITS ON WHICH THE MEAN IS BASED.)

IMPORTANCE WEIGHTS (iweights) INDICATE THE “IMPORTANCE” OF AN OBSERVATION (NO FORMAL DEFINITION).

IN EVALUATION, ATTENTION FOCUSES ON pweights.

IF A REGRESSION MODEL IS CORRECTLY SPECIFIED (IDENTIFIED), DO NOT NEED THE WEIGHTS. (SO THE LARGE VARIATION IN WEIGHTS THAT IS OFTEN A FEATURE OF ANALYTICAL DESIGNS IS NOT A PROBLEM.)

ESTIMATE MODELS WITH AND WITHOUT WEIGHTS: RESULTS SHOULD BE SIMILAR.

NOTE: THE SAMPLE DESIGN WILL SPECIFY THE PROBABILITY OF SELECTION FOR EACH PSU, BUT THE SELECTION OF WITHIN-PSU UNITS IS USUALLY DONE IN THE FIELD (NO SAMPLE FRAME FOR HOUSEHOLDS). IT IS IMPORTANT TO DO THE WITHIN-PSU SAMPLING IN A WAY SUCH THAT THE PROBABILITY OF SELECTION IS KNOWN FOR EACH SAMPLE UNIT.

FOR EXAMPLE, SELECT TWO OR THREE RANDOM STARTING POINTS, AND SELECT “EVERY K-TH” HOUSEHOLD IN RANDOM DIRECTIONS. KEEP TRACK OF NUMBER OF HOUSEHOLDS AT EACH POINT. (COMPACT SEGMENTS.)

NOTE: IF USE SYSTEMATIC SAMPLING WITH A SINGLE RANDOM START (WITHIN PSU), CANNOT ESTIMATE THE WITHIN-PSU VARIANCE. THIS IS NOT A PROBLEM IN DESCRIPTIVE SURVEYS IF THE FIRST-STAGE FPC IS SMALL. IT IS NOT A PROBLEM UNDER THE “RANDOM-EFFECTS” ASSUMPTION (INFINITE POPULATION). IT IS A POTENTIAL PROBLEM UNDER THE “FIXED-EFFECTS” ASSUMPTION, IF THE NUMBER OF PSUs IS NOT VERY LARGE. BEST TO USE SYSTEMATIC SAMPLING WITH AT LEAST TWO RANDOM STARTS.

S. ESTIMATION OF STANDARD ERRORS

IT IS ESSENTIAL TO BE ABLE TO ESTIMATE THE STANDARD ERRORS OF ESTIMATES, TO ESTIMATE CONFIDENCE INTERVALS AND TO CONDUCT TESTS OF HYPOTHESES.

USE IMPACT ESTIMATORS FOR WHICH STANDARD ERRORS CAN BE ESTIMATED (E.G., NEAREST-NEIGHBOR MATCHING ESTIMATOR PRESENTS A PROBLEM).

FOR SIMPLE MODELS, CLOSED-FORM FORMULAS ARE AVAILABLE. FOR COMPLEX MODELS, USE RESAMPLING TECHNIQUES (E.G., BOOTSTRAPPING, JACKKNIFE).

USE TRANSFORMATIONS AND MODEL SPECIFICATION ARTFULLY, SO THAT STANDARD ERRORS ARE SMALL AND MODEL ERROR TERMS ARE HOMOSCEDASTIC.

FOR TWO-STEP M-ESTIMATORS (E.G., FIRST-STEP LOGISTIC REGRESSION SELECTION MODEL + SECOND-STEP OUTCOME REGRESSION MODEL), MAY IGNORE THE FACT THAT THE FIRST-STEP PARAMETER ESTIMATE IS AN ESTIMATE, AND OBTAIN CONSERVATIVE ESTIMATES OF STANDARD ERRORS.

IN STATA, THERE ARE SEVERAL OPTIONS AVAILABLE FOR ESTIMATION OF STANDARD ERRORS:

HETEROSCEDASTICITY-ROBUST ESTIMATES (EICKER-HUBER-WHITE “SANDWICH” ESTIMATOR)

“CLUSTER” OPTION (RECOGNIZES CLUSTERING – SHOULD NOT BE NECESSARY IF MODEL IS WELL SPECIFIED)

BOOTSTRAPPING (AS AN OPTION IN MANY PROCEDURES, BUT WILL HAVE TO WRITE A .ado FILE FOR COMPLEX ESTIMATORS (E.G., TWO-STEP SELECTION MODEL).

IF ASSUME A RANDOM-EFFECTS MODEL, AND UNEXPECTEDLY LITTLE IS SIGNIFICANT, THEN USE A FIXED-EFFECTS MODEL (BUT RECOGNIZE THAT THE SCOPE OF INFERENCE IS RESTRICTED).

INSTRUMENTAL-VARIABLE MODELS WORK WELL ONLY IF GOOD INSTRUMENTS ARE AVAILABLE (UNCORRELATED WITH MODEL ERROR TERM BUT HIGHLY CORRELATED WITH THE ENDOGENOUS VARIABLE, CONDITIONAL ON COVARIATES).

7.4. Analysis of Baseline Data

ANALYSIS OF BASELINE DATA

DESCRIPTIVE SURVEYS

MAIN ASPECTS:

RESPONSE RATES

DESCRIPTIVE STATISTICS

ERROR PROFILE

EXCERPT FROM COURSE, SAMPLE SURVEY DESIGN AND ANALYSIS (DAY 2)

PART III. HOW TO ANALYZE SURVEY DATA

I. STANDARD ESTIMATION PROCEDURES FOR DESCRIPTIVE SURVEYS

A. SUMMARY OF PROCEDURES

1. PRELIMINARY ANALYSIS (LARGE DATA SETS)

DO THE FOLLOWING FOR THE ENTIRE SAMPLE AND FOR SUBPOPULATIONS OF INTEREST (E.G., BY STRATUM). THIS IS A STANDARD NONRESPONSE ANALYSIS AND “NONPARAMETRIC” SUMMARY OF THE SAMPLE DATA. (A “FIRST-CUT” LOOK AT THE SAMPLE DATA MAY IGNORE COMPLEXITIES OF THE SAMPLE DESIGN (AND TESTS OF SIGNIFICANCE), AND SIMPLY PRESENT ESTIMATES OF CHARACTERISTICS OF THE SAMPLE.)

UNIVARIATE ANALYSIS:

UNIT (QUESTIONAIRE) NONRESPONSE. CALCULATE PROPORTION OF SAMPLE UNITS RESPONDING. CATEGORIZE BY REASON. NOTE VARIABLES CORRELATED WITH NONRESPONSE.
ITEM NONRESPONSE. DEFINE A NO-RESPONSE INDICATOR VARIABLE FOR EACH VARIABLE. NOTE VARIABLES HAVING HIGH LEVEL OF NONRESPONSE, AND VARIABLES CORRELATED WITH NONRESPONSE.
FOR INTERVAL-SCALE VARIABLES, COMPUTE MEAN OR PERCENTAGE, MEDIAN, MIN, MAX, RANGE, VARIANCE, STANDARD DEVIATION, HISTOGRAM.
FOR CATEGORICAL VARIABLES COMPUTE MIN, MAX, RANGE AND HISTOGRAM.
FOR GEOGRAPHIC DATA, PLOT ALL SAMPLE UNITS ON A MAP.

BIVARIATE ANALYSIS:

RECODE ALL INTERVAL-SCALE VARIABLES BY QUINTILE
RECODE ALL CATEGORICAL VARIABLES HAVING MORE THAN 10 CATEGORIES INTO TEN OR LESS CATEGORIES (PREFERABLY 5 OR LESS). DEFINE INDICATOR VARIABLES FOR HIGH-INTEREST CATEGORIES.
CALCULATE CRAMER COEFFICIENT OF ASSOCIATION FOR ALL VARIABLES (I.E., EACH VARIABLE WITH EACH OTHER). NOTE STRONG CORRELATIONS.
CONSTRUCT TABLES OR GRAPHS (SCATTER PLOTS, LOESS / LOWESS (LOCALLY WEIGHTED SCATTERPLOT SMOOTHING) CURVES) TO ILLUSTRATE STRONG RELATIONSHIPS.

2. PLANNED ANALYSIS

FOR TOTAL POPULATION AND SUBPOPULATIONS OF INTEREST, SUMMARIZE NONRESPONSE PATTERNS
ADJUST SAMPLE WEIGHTS FOR NONRESPONSE
CALCULATE ESTIMATES INTEREST (USE APPROPRIATE FORMULAS OR PROCEDURES)
CROSSTABS OF INTEREST (BY STRATUM OR WEIGHTED)
COMPUTE EXPANSION ESTIMATES
CONDUCT TESTS OF SIGNIFICANCE

3. SPECIAL ANALYSES

ALTERNATIVE ESTIMATORS (RATIO, REGRESSION)
POSTSTRATIFICATION
ADDITIONAL SUBPOPULATIONS
REDEFINE NONRESPONSE STRATA, RECOMPUTE ESTIMATES
RESAMPLING ESTIMATES OF VARIANCES
TABLES OF GENERALIZED VARIANCES
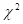(CHI-SQUARED) TESTS FOR CLUSTER-SAMPLE CROSSTABS

ANALYTICAL SURVEYS

MAIN ASPECTS:

RESPONSE RATES

MEASURES OF PRECISION OF ESTIMATES VS. MEASURES OF MATCH QUALITY

TEST OF RANDOMIZED ASSIGNMENT TO TREATMENT

ASSESSMENT OF COMMON SUPPORT

MAIN POINT: IN A PANEL SURVEY, THE FINAL ANALYSIS (OF IMPACT) WILL PROBABLY INVOLVE THE FIXED-EFFECTS TRANSFORMATION (E.G., DIFFERENCING OF HOUSEHOLDS), AND MANY VARIABLES WILL “DROP OUT.” THERE IS NO POINT TO CONSTRUCTING MODELS OF THE RELATIONSHIPS OF RESPONSE VARIABLES TO EXPLANATORY VARIABLES FOR THE BASELINE DATA, WHEN THESE MODELS WILL EVENTUALLY BE IRRELEVANT.

INSTEAD, FOCUS ON ASPECTS OF THE BASELINE DATA THAT ASSESS THE USEFULNESS OF THE DATA FOR THE ENDLINE ANALYSIS.

USUALLY WILL NOT HAVE RANDOMIZED ASSIGNMENT TO TREATMENT, OR IF DO, IT IS A “CLUSTER-RANDOMIZED” DESIGN. SO IT IS OF INTEREST TO COMPARE THE TREATMENT AND CONTROL POPULATIONS, TO ASSESS THE QUALITY OF THE RANDOMIZED ASSIGNMENT TO TREATMENT.

WHEN DO ESTIMATION OF IMPACT VIA REGRESSION ANALYSIS, A MAJOR CONCERN WILL BE THE COMMON SUPPORT OF VARIABLES THAT ARE BELIEVED TO AFFECT OUTCOME (OF THE DIFFERENCES, NOT OF THE ORIGINAL DATA).

SO, IT IS OF INTEREST TO COMPARE THE SUPPORTS OF IMPORTANT EXPLANATORY VARIABLES.

THIS CAN BE CUMBERSOME, SINCE, AFTER THE BASELINE, THERE WILL BE MANY EXPLANATORY VARIABLES, AND MANY OF THEM WILL BE RELATED TO OUTCOMES OF INTEREST. TO REDUCE THE MAGNITUDE OF THE PROBLEM, DEVELOP A PROPENSITY-SCORE MODEL (SELECTION, NONRESPONSE), AND COMPARE THE DISTRIBUTIONS OF THE PROPENSITY SCORES FOR THE TREATMENT AND CONTROL GROUPS. (THE PARTICULAR VARIABLES IN THE MODEL ARE NOT HIGHLY IMPORTANT, SINCE THEY WILL BE CORRELATED (CONFOUNDED).)

[GRAPH SHOWING TWO PROPENSITY-SCORE DISTRIBUTIONS]

NOTE: SIGNIFICANCE LEVELS SHOULD BE REPORTED ONLY WHEN THE PROBABILITY STRUCTURE OF THE DESIGN IS PROPERLY TAKEN INTO ACCOUNT (E.G., TWO-STAGE SAMPLING). WHEN MATCHING IS INVOLVED, THE SAMPLES ARE NOT INDEPENDENT SAMPLES. SIGNIFICANCE LEVELS (“p” VALUES) MAY BE USED AS “MEASURES OF SIMILARITY,” BUT THEY DO NOT REPRESENT PROBABILITIES.

7.5. Use of Stata Statistical Program Package

USE OF STATA STATISTICAL PROGRAM PACKAGE

REFERENCES

Stata Reference Manuals

Kohler, Ulrich and Frauke Kreuter, Data Analysis Using Stata 2^nd edition, Stata Press, 2005, 2009.

Hamilton, Lawrence C., Statistics with Stata, Duxbury/Thomson/Brooks/Cole, 2006.

Khandker, Shahidur R., Gayatri B. Koolwal and Hussain A. Samad, Handbook on Impact Evaluation: Quantitative Methods and Practices, The World Bank, 2010.

SUMMARY DESCRIPTION OF STATA

INTERACTIVE, .do COMMAND FILES (COLLECTION OF STATA COMMANDS), AND .ado FILES (A PROGRAM, CONSISTING OF A NUMBER OF STATA COMMANDS).

NOTE: THE KHANDKER REFERENCE INCLUDES INTERACTIVE EXAMPLES ON THE WORLD BANK WEBSITE, AT http://go.worldbank.org/FE8098BI60

EXAMPLES

LIST DATA:

sort by treatment

list treatment tothhinc

COUNT DATA:

count

count if treatment=0

SUMMARIZE DATA (SUMMARY STATISTICS, SUCH AS MEAN AND VARIANCE):

summarize tothhinc

FREQUENCY DISTRIBUTIONS (TABULATIONS)

tab tothhinc

tab tothhinc if Round=0

MULTI-WAY TABLES (TABLES)

table inc1 inc2 inc3, contents(freq) by(treatment)

GENERATE NEW VARIABLES

generate inctot=inc1+inc2+inc3

MODIFY VARIABLES

generate senior=1 if age>64

replace senior=0 if age<=65

LABELING VARIABLES

label variable senior “Senior (age>64)”

LABELING VALUES

label define sexlabel 0 “Female” 1 “Male”

label values sex sexlabel

GRAPHS

histogram inctot

twoway (scatter inctot incemp), ytitle(Total Household Income) xtitle(Employee Income) title(Total Household Income vs. Employee Income)

TWO-SAMPLE RANDOMIZED DESIGN

TWO-SAMPLE t-Test

ttest inctot, by(treatment)

REGRESSION MODEL

Regress inctot treatment

LOGISTIC REGRESSION MODEL

logistic treatment education farmsize

PROPENSITY-SCORE MODEL

pscore treatment education farmsize

AVERAGE TREATMENT EFFECT ON THE TREATED USING THE “RADIUS MATCHING” MATCHING ESTIMATOR

attr inctot treatment, pscore(ps98) radius(0.001) comsup

FOUR-GROUP RANDOMIZED DESIGN

Generate new observations by differencing income for matching households by survey round (not shown).

Apply t-test to differences:

ttest inctotd, by(treatment)

Model

y = α + βT + γt + δDDTt + e

(data setup not shown)

generate RndTrt=Round*treatment

regress inctot Round treatment RndTrt

May include covariates:

regress inctot Round treatment RndTrt age educ farmsize

FIXED-EFFECTS MODEL

(xtset panelvar timevar)

xtset hhid Round

xtreg inctot Round treatment RndTrt, fe

May include covariates:

xtreg inctot Round treatment RndTrt age educ farmsize, fe

INSTRUMENTAL-VARIABLE MODEL:

ivreg and xtivreg commands

Suppose Treated is an endogenous variable, and P is an estimated propensity score for Treated.

xtivreg inctot educ agemployees farmsize equipmentvalue farmrentalvalue (Treated RoundTreated = P RoundP), fe

REGRESSION DISCONTINUITY

rd_sharp, rd_fuzzy

RECOMMENDED .do FILE HEADER TEMPLATE:

version 10.0

set more off

clear

capture log close

*In the following line, specify the name of the folder in which the data files are located.

global direct1 "C:\DataAnalysis\Project1\"

log using "$direct1\Do10Project1ImpactEstimation.log", replace

*Place file header following the preceding statement, so it shows up in the log file.

*File name: Do10Project1ImpactEstimation.do

*Project: Project 1 Program Evaluation

*Creator: Joseph Caldwell

*Date created: 22 January 2012

*Modifier: Joseph Caldwell

*Date modified: 23 January 2012

*Purpose: Estimate impact for Project 1 program.

*Input file: Project1Data.dta.

*Output files: Project1ImpactEstimation.dta, Project1PropensityScores.dta.

*Log file: Do10Project1ImpactEstimation.log

*Repeat, as comments, commands prior to turning log on:

*version 10.0

*set more off

*clear

*capture log close

*In the following line, specify the name of the folder in which the data files are located.

*global direct1 "C:\DataAnalysis\Project1\"

*log using "$direct1\Do10Project1ImpactEstimation.log", replace

set memory 100m

set matsize 800

set linesize 100

REVIEW OF A TYPICAL PROJECT FINAL REPORT.

SURVEY OF REFERENCES

QUESTIONS AND ANSWERS FOR DAY 2

END OF DAY 2

8. References

Reference List

Statistical Design and Analysis in Evaluation

Causal Modeling

Pearl, Judea, Causality: Models, Reasoning, and Inference, 2nd ed., Cambridge University Press, 2009.

Morgan, Stephen L. and Christopher Winship, Counterfactuals and Causal Inference: Methods and Principles for Social Research, Cambridge University Press, 2007.

Holland, Paul W. Statistics and Causal Inference, Journal of the American Statistical Association, Vol. 81, No. 396, pp. 945-960, 1986.

Dawid, A. P., Causal Inference without Counterfactuals, Journal of the American Statistical Association, Vol. 95, No. 450, pp. 407-448, 2000.

Additional references on structural equation modeling:

Muliak, Stanley A., Linear Causal Modeling with Structural Equations, Chapman and Hall / CRC, 2009.

Berry, William D., Nonrecursive Causal Models, Sage Publications, 1984

Asher, Herbert, Causal Modeling 2^nd edition, Sage Publications, 1983

Duncan, O. D., Introduction to Structural Equation Models, Academic Press, 1975

Goldberger, A. S. and O. D. Duncan, Structural Equation Models in the Social Sciences, Seminar Press, 1973.

Kline, Rex B., Principles and Practice of Structural Equation Modeling 3^rd edition, Guilford Press, 2011.

Schumacker, Randall E. and Richard G. Lomax, A Beginner’s Guide to Structural Equation Modeling 3^rd edition, Routledge, 2010.

Everitt, B. S., An Introduction to Latent Variable Models, Chapman and Hall, 1984.

Loehlin, John C., Latent Variable Models: An Introduction to Factor, Path and Structural Equation Analysis 4^th edition, Routledge, 2004.

Evaluation

Khandker, Shahidur R., Gayatri B. Koolwal, and Hussair A. Samad, Handbook on Impact Evaluation: Quantitative Methods and Practices, The World Bank, 2010. (This reference includes some technical material, including examples of Stata procedures. Posted at The World Bank Internet website at http://go.worldbank.org/FE8098BI60.)

Econometrics

Wooldridge, Jeffrey M., Econometric Analysis of Cross Section and Panel Data 2^nd edition, The MIT Press, 2010.

Angrist, Joshua D. and Jörn-Steffen Pischke, Mostly Harmless Econometrics: An Empiricist’s Companion, Princeton University Press, 2009.

Morgan, Stephen L. and Christopher Winship, Counterfactuals and Causal Inference: Methods and Principles for Social Research, Cambridge University Press, 2007.

Lee, Myoung-Jae, Micro-Econometrics for Policy, Program and Treatment Effects, Oxford University Press, 2005.

Matching

Rosenbaum, Paul R. and Donald B. Rubin, “The central role of the propensity score in observational studies for causal effects,” Biometrika (1983), Vol. 70, No. 1, pp. 41-55.

General statistics (undergraduate-level mathematical statistics)

Mood, Alexander M., Franklin Graybill and Duane C. Boes, Introduction to the Theory of Statistics, 3^rd edition, McGraw Hill, 1974

Snedecor, George W. and William G. Cochran, Statistical Methods, 8^th edition, Iowa State University Press, 1989

Brunk, H. D., An Introduction to Mathematical Statistics, Ginn and Company, 1960

Dobson, Annette J., An Introduction to Generalized Linear Models 2^nd edition, Chapman & Hall, 2002.

Draper, Norman and Harry Smith, Applied Regression Analysis, Wiley, 1966.

Hosmer, David W. and Stanley Lemshow, Applied Logistic Regression, Wiley, 1989.

Technical references on estimation and test of hypotheses:

Lehmann, E. L., Theory of Point Estimation, Wiley, 1983.

Lehmann, E. L., Testing Statistical Hypotheses 2^nd edition, Wiley, 1986.

Rao, C. Radhakrishna Rao, Linear Statistical Infernence and Its Applications 2^nd edition, Wiley, 1973 (1^st edition 1965).

General statistics (less mathematical)

Crow, Edwin L., Frances A. Davis and Margaret W. Maxfield, Statistics Manual: With Examples Taken from Ordnance Development, Dover Publications, 1960

Downie, N. M. and R. W. Heath, Basic Statistical Methods, 4^th edition, Harper & Row, 1974

Survey sampling, less mathematical

Sheaffer, Richard L., William Mendenhall, R. Lyman Ott and Kenneth G. Geow, Elementary Survey Sampling 7^th edition, Cengage Learning, 2011. (Or any earlier edition, such as 2^nd, Duxbury Press, 1979)

Des Raj, The Design of Sample Surveys, McGraw-Hill, Inc., 1972

Kish, Leslie, Survey Sampling, John Wiley & Sons, 1965

Survey sampling, mathematical

Cochran, William G., Sampling Techniques, 3^rd edition, John Wiley & Sons, Inc., 1977

Des Raj, Sampling Theory, McGraw-Hill, Inc., 1968

Hansen, Morris H., William N. Hurwitz and William G. Madow, Sample Survey Methods and Theory, volumes 1 and 2, John Wiley & Sons, Inc., 1953

Survey sampling, additional references (mix of mathematical and less mathematical)

Lohr, Sharon, Sampling: Design and Analysis, 2nd ed., Cengage Learning, 2011

Kott, Phillip S., Sample Survey Theory and Methods: A Correspondence Course, Sept. 12, 2006. May be downloaded free from http://www.nass.usda.gov/research/reports/course%20notes%200906.pdf This course has the prerequisite of one preious college-level course in statistics. It uses Sharon Lohr’s Sampling: Design and Analysis as a required text.

Rubin, Donald B., Multiple Imputation for Nonresponse in Surveys, John Wiley & Sons, 1987

Little, Roderick J. A. and Donald B. Rubin, Statistical Analysis with Missing Data, John Wiley & Sons, 1987

Caldwell, Joseph G., Sample Survey Design and Analysis: A Comprehensive Three-Day Course with Application to Monitoring and Evaluation, Notes for a three-day course are posted at Internet websites http://www.foundationwebsite.org/SampleSurvey3DayCourseDayOne.pdf , http://www.foundationwebsite.org/SampleSurvey3DayCourseDayTwo.pdf and http://www.foundationwebsite.org/SampleSurvey3DayCourseDayThree.pdf .)

Rao, J. N. K. and D. R. Bellhouse, “History and Development of the Theoretical Foundations of Survey Based Estimation and Analysis,” Survey Methodology, June 1990, Statistics Canada

Risto Lehtonen and Erikki Pahkinen, Practical Methods for Design and Analysis of Complex Surveys, 2^nd edition, Wiley, 2004

Thompson, Steven K., Sampling, 3rd edition, Wiley, 2012

Statistical Power Analysis

Spybrook, Jessaca, Stephen W. Raudenbush, Richard Congden and Andrés Martínez, Optimal Design for Longitudinal and Multilevel Research: Documentation for the “Optimal Design” Software, William T. Grant Foundation, 2009. Software posted at Internet website http://www.wtgrantfoundation.org/resources/consultation-service-and-optimal-design#Optimal%20Design%20Software.

Cohen, Jacob, Statistical Power Analysis for the Behavioral Sciences, 2^nd edition, Lawrence Erlbaum, 1988.

Bloom, Howard S., editor, Learning More from Social Experiments: Evolving Analytic Approaches, Sage, 2005.

References on Experimental Design and Quasi-experimental Design

Kuehl, Robert O. Design of Experiments: Statistical Principles of Research Design and Analysis, 2^nd edition, Brooks/Cole/Cengage, 2000.

Cochran, William G. and Gertrude M. Cox, Experimental Designs, 2^nd edition, Wiley, 1950, 1957

Campbell, Donald T. and Julian C. Stanley, Experimental and Quasi-Experimental Designs for Research, Rand McNally, 1966. Reprinted from Handbook of Research on Teaching, N. L. Gage (editor), Rand Mcnally, 1963.

Cook, Thomas D. and Donald T. Campbell, Quasi-Experimentation: Design and Analysis Issues for Field Settings Houghton Mifflin, 1979

References on use of Stata statistical program software

Kohler, Ulrich and Frauke Kreuter, Data Analysis Using Stata 2^nd edition, Stata Press, 2005, 2009.

Hamilton, Lawrence C., Statistics with Stata, Duxbury/Thomson/Brooks/Cole, 2006.

Khandker, Shahidur R., Gayatri B. Koolwal and Hussain A. Samad, Handbook on Impact Evaluation: Quantitative Methods and Practices, The World Bank, 2010.

Additional Material on Sample Survey Design for Evaluation

Caldwell, Joseph George, “Sample Survey Design for Evaluation,” posted at http://www.foundationwebsite.org/SampleSureyDesignForEvaluation.pdf .

Reference on analysis of categorical data (binary response):

Agresti, Alan, An Introduction to Categorical Data Analysis, Wiley, 1996.

Agresti, Alan, Categorical Data Analysis, Wiley, 1990.

FndID(212)

FndTitle(STATISTICAL DESIGN AND ANALYSIS IN EVALUATION: LECTURE NOTES)

FndDescription(STATISTICAL DESIGN AND ANALYSIS IN EVALUATION: LECTURE NOTES)

FndKeywords(statistical methods; monitoring and evaluation; statistics course; short course; sample survey; causal inference; statistical design and analysis; sample size determination)