CAUSAL INFERENCE AND MATCHING: LECTURE NOTES (PREVIOUS TITLE: MATCHING IN EVALUATION DESIGN: CONCEPTS, PRACTICES AND PITFALLS, USE AND ABUSE: LECTURE NOTES)

THIS PRESENTATION SUMMARIZES THE THEORY ASSOCIATED WITH MATCHING IN THE DESIGN OF SAMPLE SURVEYS CONDUCTED TO OBTAIN DATA FOR ESTIMATION OF THE IMPACT OF A PROGRAM INTERVENTION. THE USE OF MATCHING IS VERY IMPORTANT, BOTH IN EXPERIMENTAL DESIGNS AND IN QUASI-EXPERIMENTAL DESIGNS (USED TO ANALYZE OBSERVATIONAL (NON-EXPERIMENTAL) DATA). FOR EXPERIMENTAL DESIGN, IT IS USED TO INCREASE PRECISION AND POWER; FOR QUASI-EXPERIMENTAL DESIGNS IT IS USED ALSO TO DECREASE BIAS.

MANY ASPECTS OF MATCHING ARE NOT WIDELY UNDERSTOOD, AND IT IS A PRIMARY PURPOSE OF THIS PRESENTATION TO CLARIFY THEM IN TERMS OF THOROUGH DESCRIPTION AND SIMPLE EXAMPLES. IN PARTICULAR, THERE IS CONSIDERABLE MISINFORMATION ABOUT THE SIMILARITIES AND DIFFERENCES OF ALTERNATIVE APPROACHES TO IMPACT ESTIMATION (CAUSAL MODELING AND ANALYSIS). THIS PRESENTATION DESCRIBES TWO CAUSAL-ANALYSIS APPROACHES IN DETAIL, AND COMPARES THEIR CHARACTERISTICS, ADVANTAGES AND DISADVANTAGES, WITH PARTICULAR ATTENTION TO MATCHING.

THIS PRESENTATION IS CONCERNED MAINLY WITH CONCEPTS, WITH LITTLE ATTENTION TO TECHNICAL PROCEDURES FOR MATCHING. SOME MENTION IS MADE OF TECHNICAL PROCEDURES FOR MATCHING AND OF COMPUTER SOFTWARE SOURCES FOR MATCHING.

THESE PRESENTATION NOTES ARE INTENDED TO COMPLEMENT LECTURES, AND MAY NOT INCLUDE ALL OF THE VISUAL PRESENTATIONS USED IN THE LECTURE. THERE IS SOME REDUNDANCY IN THE PRESENTATION. IN ADDRESSING A PARTICULAR TOPIC, A POINT THAT HAS ALREADY BEEN MADE IN A PREVIOUS TOPIC MAY BE REPEATED, FOR COMPLETENESS AND BETTER FLOW OF THE PRESENTATION.

WE ARE CONCERNED HERE MAINLY WITH MATCHING IN DESIGN, NOT WITH MATCHING IN ANALYSIS. MATCHING IN DESIGN IS CONCERNED WITH METHODS FOR SELECTING SAMPLE UNITS. IT FOCUSES ON EXPERIMENTAL DESIGN AND SAMPLE SURVEY DESIGN, RATHER THAN ON ANALYSIS (STATISTICAL INFERENCE: ESTIMATION AND HYPOTHESIS TESTING).

IT IS NOT POSSIBLE TO REASONABLY SEPARATE DESIGN FROM ANALYSIS – BOTH SHOULD BE CONSIDERED JOINTLY. ALTHOUGH THIS PRESENTATION FOCUSES ON MATCHING IN DESIGN, MATCHING IN ANALYSIS IS CONSIDERED TO THE EXTENT THAT IT PROMOTES AN UNDERSTANDING OF THE IMPORTANCE AND USE OF MATCHING IN DESIGN. MATCHING IN ANALYSIS IS CONSIDERED IN DETAIL IN A SEPARATE PRESENTATION.

MATCHING MAY BE DONE EITHER (OR BOTH) IN DESIGN (“EX ANTE”) OR IN ANALYSIS (“EX POST”). THE PROCEDURES FOR MATCHING IN THESE TWO INSTANCES ARE SIMILAR IN CONCEPT, BUT THERE ARE SUBSTANTIAL DIFFERENCES. IN DESIGN, MATCHING IS DONE USING DATA THAT ARE AVAILABLE PRIOR TO THE SURVEY, WHEREAS IN ANALYSIS, MATCHING MAKES USE OF THE DATA COLLECTED IN THE SURVEY INSTRUMENTS. IN DESIGN, MATCHING IS DONE AT THE LOWEST (MOST DETAILED) LEVEL OF SAMPLING FOR WHICH USEFUL MATCH DATA ARE AVAILABLE PRIOR TO THE SURVEY FOR USE IN DESIGN, SUCH AS A DISTRICT OR VILLAGE. IN ANALYSIS, MATCHING MAY BE DONE FOR THE ULTIMATE SAMPLE UNIT (OR “ELEMENT”), SUCH AS A HOUSEHOLD OR TEACHER.

BECAUSE OF THE LIMITED NUMBER OF VARIABLES AND POSSIBLY SMALL SAMPLE SIZE (WHEN MATCHING HIGHER-LEVEL SAMPLING UNITS), MATCHING IN DESIGN IS CONCERNED ONLY WITH THE MOST BASIC MODELS AND ESTIMATORS; IN ANALYSIS, A MUCH BROADER RANGE OF MODELS AND ESTIMATORS IS AVAILABLE FOR CONSIDERATION.

IN BOTH ANALYSIS AND DESIGN, THE PURPOSE OF MATCHING IS TO REDUCE BIAS, INCREASE PRECISION OF ESTIMATES OF INTEREST, AND INCREASE THE POWER OF TESTS OF HYPOTHESIS.

A POPULAR METHOD OF MATCHING IS TO MATCH ON THE ESTIMATED PROPENSITY SCORE (THE ESTIMATED PROBABILITY OF ASSIGNMENT TO TREATMENT, GIVEN OBSERVED COVARIATES). IF ALL IMPORTANT VARIABLES AFFECTING ASSIGNMENT TO TREATMENT ARE OBSERVED, PROPENSITY-SCORE MATCHING REDUCES SELECTION BIAS. PROPENSITY-SCORE MATCHING MAY INCREASE OR DECREASE PRECISION AND POWER.

SOME OF THE ASPECTS OF MATCHING THAT ARE ADDRESSED IN THIS PRESENTATION ARE THE FOLLOWING.

1. PAIR MATCHING

2. MATCHING OF TREATMENT AND COMPARISON GROUPS

3. THE ROLE OF MATCHING IN INCREASING PRECISION AND POWER

4. THE ROLE OF MATCHING IN REDUCING BIAS

5. CAUSAL MODELING

6. SUMMARY OF NEYMAN-RUBIN (POTENTIAL OUTCOMES) APPROACHES TO CAUSAL MODELING (THE ROSENBAUM-RUBIN APPROACH, THE HECKMAN APPROACH, AND OTHERS)

7. THE ROLE OF THE PROPENSITY SCORE IN MATCHING

8. THE USE OF MATCHING TO REDUCE MODEL DEPENDENCY (DATA TRIMMING, CULLING, PRUNING); RELATIONSHIP TO MARGINAL STRATIFICATION

9. THE USE OF MATCHING TO REDUCE CONFOUNDING

10. SUMMARY OF MATCHING PROCEDURES AND COMPUTER SOFTWARE FOR MATCHING

11. THE DOUBLY ROBUST NATURE OF MATCHING AND COVARIATE ADJUSTMENT

12. A PROBLEM WITH PROPENSITY-SCORE MATCHING

13. RECOMMENDED APPROACH TO MATCHING IN EVALUATION DESIGN.

THE KNOWLEDGE PREREQUISITES FOR THIS PRESENTATION ARE A BASIC COURSE IN STATISTICS, INCLUDING BASIC KNOWLEDGE OF THE GENERAL LINEAR STATISTICAL MODEL (REGRESSION ANALYSIS, ANALYSIS OF VARIANCE); AND A BASIC COURSE IN SAMPLE SURVEY DESIGN AND ANALYSIS, INCLUDING KNOWLEDGE OF STRATIFICATION AND TWO-STAGE SURVEY DESIGN. STATISTICAL MODELS WILL BE DESCRIBED USING VECTOR NOTATION (VECTORS AND VECTOR PRODUCTS, BUT NO MORE COMPLICATED MATRIX ALGEBRA). IT IS IMPORTANT TO UNDERSTAND THE BASIC ASSUMPTIONS UNDERLYING A MULTIPLE REGRESSION MODEL, SUCH AS THE REQUIREMENT FOR THE EXPLANATORY VARIABLES TO BE UNCORRELATED WITH THE MODEL ERROR TERMS IN ORDER TO AVOID BIASES IN THE PARAMETER ESTIMATES.

(NOTE ON NOTATION: IN THIS REPORT WE SHALL DENOTE VECTORS EITHER IN BOLDFACE OR BY UNDERLINING (BOLDFACE IN MICROSOFT WORD EQUATION FORMULAS AND BOLDFACE OR UNDERLINING IN PLAIN TEXT). IN THE TEXT,WE WILL TEND TO USE UNDERLINING, SINCE IT SHOW UP BETTER.)

EXAMPLES OF TEXTS THAT WOULD PROVIDE A GOOD BACKGROUND FOR THIS PRESENTATION ARE:

1. WASSERMAN, LARRY, ALL OF STATISTICS: A CONCISE COURSE IN STATISTICAL INFERENCE, SPRINGER, 2004

2. LOHR, SHARON L., SAMPLING: DESIGN AND ANALYSIS, DUXBURY PRESS, 1999

3. SCHEAFFER, RICHARD L., WILLIAM MENDENHALL AND LYMAN OTT, ELEMENTARY SURVEY SAMPLING, 5^TH EDITION, CENGAGE LEARNING, 1995.

NO PREVIOUS KNOWLEDGE OF CAUSAL MODELING AND ANALYSIS IS ASSUMED; BASIC INFORMATION ON THAT SUBJECT IS PROVIDED.

A BOOK THAT PRESENTS A COMPREHENSIVE AND DETAILED THEORY OF MATCHED SAMPLING FOR CAUSAL EFFECTS IS:

RUBIN, DONALD B., MATCHED SAMPLING FOR CAUSAL EFFECTS, CAMBRIDGE UNIVERSITY PRESS, 2000.

THAT BOOK IS WELL WORTH READING AS COMPLEMENTATION TO THIS PRESENTATION. IT IS TECHNICALLY MORE DETAILED THAN THIS PRESENTATION, BUT MUCH OF THE DISCUSSION AND TEXT IS QUITE READABLE.

AS GENERAL BACKGROUND FOR THIS PRESENTATION, IT IS SUGGESTED THAT ONE OR MORE OF THE FOLLOWING NON-TECHNICAL REFERENCES ON EVALUATION BE REVIEWED.

1. GERTLER, PAUL J., SEBASTIAN MARTINEZ, PATRICK PREMAND, LAURA B. RAWLINGS AND CHRISTEL M. J. VERMEERSCH, IMPACT EVALUATION IN PRACTICE, THE WORLD BANK, 2011 (AVAILABLE FROM INTERNET)

2. KHANDKER, SHAHIDUR R., GAYATRI B. KOOLWAL, AND HUSSAIN A. SAMAD, HANDBOOK ON IMPACT EVALUATION, QUANTITATIVE METHODS AND PRACTICES, THE WORLD BANK, 2010 (AVAILABLE FROM INTERNET)

3. ROSSI, PETER H., MARK W. LIPSEY AND HOWARD E. FREEMAN, EVALUATION, A SYSTEMATIC APPROACH, 7^TH EDITION, SAGE PUBLICATIONS, 2004

4. IMAS, LINDA G. MORRA AND RAY C. RIST, THE ROAD TO RESULTS, THE WORLD BANK, 2009 (AVAILABLE FROM INTERNET)

5. KUSEK, JODY ZALL AND RAY C. RIST, TEN STEPS TO A RESULTS-BASED MONITORING AND EVALUATION SYSTEM, THE WORLD BANK, 2004

6. CLARK, MARI AND ROLF SARTORIUS, MONITORING AND EVALUATION, SOME TOOLS, METHODS AND APPROACHES, THE WORLD BANK, 2004 (AVAILABLE FROM INTERNET)

7. LEEUW, FRANS AND JOS VAESSEN, IMPACT EVALUATIONS AND DEVELOPMENT, NONIE GUIDANCE ON IMPACT EVALUATION, NONIE / THE WORLD BANK, 2009

8. WILSON, DAVID, MANUEL OPERATIONNEL DE SUIVI ET D’EVALUATION, THE WORLD BANK, 2003 (AVAILABLE FROM INTERNET)

9. BAKER, JUDY L., EVALUATING THE IMPACT OF DEVELOPMENT PROJECTS ON POVERTY, A HANDBOOK FOR PRACTITIONERS, THE WORLD BANK, 2000 (AVAILABLE FROM INTERNET)

10. NICHOLS, AUSTIN, CAUSAL INFERENCE WITH OBSERVATIONAL DATA, HTTP://WWW.STATA.COM/MEETING/GERMANY09/NICHOLS.PDF (AVAILABLE FROM INTERNET)

REFERENCES ON CAUSAL MODELING AND ANALYSIS INCLUDE THE FOLLOWING:

1. HOLLAND, PAUL W., “STATISTICS AND CAUSAL INFERENCE,” JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, DEC. 1986, VOL. 81, NO. 396, PP. 945 – 960. (THIS ARTICLE IS LIMITED TO CONSIDERATION OF EXPERIMENTAL DATA, NOT OBSERVATIONAL DATA.)

2. ROSENBAUM, PAUL R. AND DONALD B. RUBIN, “THE CENTRAL ROLE OF THE PROPENSITY SCORE IN OBSERVATIONAL STUDIES FOR CAUSAL EFFECTS,” BIOMETRIKA, (1983), VOL. 70, NO. 1, PP. 41-55.

3. PEARL, JUDEA, CAUSALITY: MODELS, REASONING, AND INFERENCE, 2^ND EDITION, CAMBRIDGE UNIVERSITY PRESS, 2009 (1^ST ED. 2000)

4. CARTWRIGHT, NANCY, HUNTING CAUSES AND USING THEM: APPROACHES IN PHILOSOPHY AND ECONOMICS, CAMBRIDGE UNIVERSITY PRESS, 2007

5. MORGAN, STEPHEN L. AND CHRISTOPHER WINSHIP, COUNTERFACTUALS AND CAUSAL INFERENCE: METHODS AND PRINCIPLES FOR SOCIAL RESEARCH, CAMBRIDGE UNIVERSITY PRESS, 2007

6. ANGRIST, JOSHUA D. AND JÖRN-STEFFEN PISCHKE, MOSTLY HARMLESS ECONOMETRICS: AN EMPIRICIST’S COMPANION, PRINCETON UNIVERSITY PRESS, 2009

7. LEE, MYOUNG-JAE, MICRO-ECONOMICS FOR POLICY, PROGRAM AND TREATMENT EFFECTS, OXFORD UNIVERSITY PRESS, 2005

8. RUBIN, DONALD B., MATCHED SAMPLING FOR CAUSAL EFFECTS, CAMBRIDGE UNIVERSITY PRESS, 2000.

9. FREEDMAN, DAVID A., EDITED BY DAVID COLLIER, JASJEET S SEKHON AND PHILIP B. STARK, STATISTICAL MODELS AND CAUSAL INFERENCE: A DIALOGUE WITH THE SOCIAL SCIENCES, CAMBRIDGE UNIVERSITY PRESS, 2010

10. MULAIK, STANLEY A., LINEAR CAUSAL MODELING WITH STRUCTURAL EQUATIONS (CRC PRESS, 2009)

11. DECHTER, RINA, HECTOR GEFFNER AND JOSEPH Y. HALPERN, HEURISTICS, PROBABILITY AND CAUSALITY: A TRIBUTE TO JUDEA PEARL, COLLEGE PUBLICATIONS (KING'S COLLEGE LONDON), 2010

12. HECKMAN, JAMES J. AND EDWARD J. VYTLACIL, “ECONOMETRIC EVALUATION OF SOCIAL PROGRAMS, PART I: CAUSAL MODELS, STRUCTURAL MODELS AND ECONOMETRIC POLICY EVALUATION,” HANDBOOK OF ECONOMETRICS, VOL. 6B, CHAPTER 70, PP. 4779 – 4874, (SEE ALSO PART II (CHAPTER 71, PP. 4875 – 5143) AND PART III, PP. 5145 – 5303), ELSEVIER, 2007. AN EXTRACT OF PART I IS ECONOMETRIC CAUSALITY BY JAMES J. HECKMAN, NATIONAL BUREAU OF ECONOMIC RESEARCH WORKING PAPER 13934, APRIL 2008, POSTED AT INTERNET WEBSITE http://www.nber.org/papers/w13934 .

13. WOOLDRIDGE, JEFFREY M., ECONOMETRIC ANALYSIS OF CROSS SECTION AND PANEL DATA, 2^ND ED., THE MIT PRESS, 2010 (1^ST ED. 2002).

14. GREENE, WILLIAM H., ECONOMETRIC ANALYSIS, 7^TH EDITION, PRENTICE HALL, 2012

THE FIRST TWELVE PUBLICATIONS LISTED DEAL MAINLY WITH THEORETICAL CONCEPTS, AND THE LAST TWO DEAL WITH STATISITICAL PROCEDURES FOR ESTIMATION.

GENERAL OBSERVATIONS ON FOCUS AND SCOPE OF PRESENTATION; MEASURES OF IMPACT; ESTIMATION OBJECTIVES

THIS PRESENTATION IS CONCERNED WITH THE CONSTRUCTION OF GOOD DESIGNS AND GOOD ESTIMATES OF THE IMPACT OF A PROGRAM. IT IS PROFOUNDLY CONCERNED WITH CAUSAL MODELING AND ANALYSIS. CAUSAL ANALYSIS MAY ADDRESS EITHER ESTIMATION OF THE EFFECTS OF CAUSES OR IDENTIFICATION OF THE CAUSES OF EFFECTS. THIS PRESENTATION IS CONCERNED WITH ESTIMATION OF THE EFFECTS OF CAUSES, NOT WITH IDENTIFICATION OF THE CAUSES OF EFFECTS. IT IS CONCERNED WITH GENERAL CAUSATION – THE AVERAGE EFFECT OF A PROGRAM INTERVENTION ON A POPULATION (E.G., WHAT IS THE AVERAGE EFFECT OF CIGARETTE SMOKING ON A POPULATION), NOT WITH SINGULAR CAUSATION (THE EFFECT OF AN INTERVENTION OR EVENT ON A SINGLE INDIVIDUAL, SUCH AS WHETHER CIGARETTE SMOKING KILLED A PARTICULAR INDIVIDUAL).

THERE ARE A NUMBER OF IMPACT MEASURES THAT ARE USED IN PROGRAM EVALUATION, INCLUDING THE AVERAGE TREATMENT EFFECT (ATE), THE AVERAGE TREATMENT EFFECT ON THE TREATED (ATT), THE MARGINAL TREATMENT EFFECT (MTE), AND THE LOCAL AVERAGE TREATMENT EFFECT (LATE). THERE ARE ALSO AVERAGE TREATMENT EFFECTS CONDITIONAL ON THE VALUES OF VARIABLES (“COVARIATES”) OTHER THAN TREATMENT VARIABLES. ALSO, THERE ARE MEASURES OF IMPACT THAT ARE NOT AVERAGES AT ALL, SUCH AS THE ENTIRE DISTRIBUTION OF OUTCOME, CONDITIONAL ON OTHER VARIABLES (BOTH CAUSAL OR NONCAUSAL).

THE TWO MOST WIDELY USED IMPACT MEASURES ARE THE AVERAGE TREATMENT EFFECT (ATE) AND THE AVERAGE EFFECT OF TREATMENT ON THE TREATED (ATT). (ANOTHER TERM FOR THE ATE IS THE AVERAGE CAUSAL EFFECT (ACE).) THESE MEASURES ARE OF INTEREST FOR THE ENTIRE POPULATION OF INTEREST (E.G., THE POPULATION OF ENTITIES (E.G., PERSONS, HOUSEHOLDS) ELIGIBLE FOR PROGRAM SERVICES), OR FOR SPECIAL SUBPOPULATIONS, SUCH AS MALES AND FEMALES, PERSONS IN A PARTICULAR REGION, OR PERSONS RECEIVING SERVICES.

THE ATE IS DEFINED AS THE AVERAGE EFFECT OF TREATMENT ON A UNIT (E.G., PERSON, HOUSEHOLD) RANDOMLY SELECTED FROM THE POPULATION AND RANDOMLY ASSIGNED TO TREATMENT (THAT IS, INDEPENDENTLY AT RANDOM). THIS DEFINITION IS PROBLEMATIC BECAUSE IT IS NOT POSSIBLE TO OBSERVE THE SAME INDIVIDUAL IN BOTH TREATED AND UNTREATED STATES (SO THAT IT IS NOT POSSIBLE TO OBSERVE THE EFFECT OF TREATMENT ON AN INDIVIDUAL). THAT IS, IT IS NOT POSSIBLE TO OBSERVE THE QUANTITY OF INTEREST (THE TREATMENT EFFECT) ON AN INDIVIDUAL SAMPLE UNIT. IT IS PROBLEMATIC ALSO BECAUSE IT MAY NOT BE POSSIBLE (FOR PHYSICAL OR ETHICAL REASONS) TO ASSIGN TREATMENT TO AN INDIVIDUAL. IT IS PROBLEMATIC ALSO BECAUSE IT IS DEFINED RELATIVE TO A PARTICULAR POPULATION – IF THE POPULATION CHANGES, THE AVERAGE TREATMENT EFFECT CHANGES.

ALTERNATIVELY, THE ATE MAY BE DEFINED AS THE DIFFERENCE IN MEAN OUTCOME BETWEEN A RANDOM SAMPLE OF INDIVIDUALS WHO ARE TREATED (AFTER SELECTION) AND A RANDOM SAMPLE OF INDIVIDUALS WHO ARE NOT TREATED (AFTER SELECTION). OR, IT MAY BE DEFINED AS THE DIFFERENCE IN MEANS FOR THE TREATED AND UNTREATED UNITS OF A RANDOM SAMPLE OF INDIVIDUALS, WHERE TREATMENT IS RANDOMLY ASSIGNED TO EACH INDIVIDUAL (AFTER RANDOM SELECTION FROM THE POPULATION UNDER STUDY). ALL OF THE PRECEDING DESCRIPTIONS ARE WIDELY USED, BUT THEY ARE NOT VERY GOOD DEFINITIONS SINCE THEY CONFLATE THE CONCEPT OF ATE WITH A PROCEDURE FOR DETERMINING IT (I.E., USING RANDOM SELECTION FROM A POPULATION AND RANDOM ASSIGNMENT TO TREATMENT). THE ATE WILL BE DEFINED MORE PRECISELY LATER, IN TERMS OF A THEORY OF POTENTIAL OUTCOMES.

THERE ARE REASONS WHY ATTENTION FOCUSES ON THE AVERAGE TREATMENT EFFECT AS THE MOST COMMONLY USED MEASURE OF IMPACT. IT IS PERHAPS THE SIMPLEST MEASURE, BOTH CONCEPTUALLY AND TECHNICALLY, AND ITS STATISTICAL PROPERTIES ARE EASY TO DETERMINE. UNBIASED ESTIMATES OF IT ARE AVAILABLE WITH MINIMAL ASSUMPTIONS. IT IS NOT NECESSARY TO ESTIMATE THE ENTIRE DISTRIBUTION OF OUTCOME. IT IS A LINEAR MEASURE, AND POSSESSES ADDITIVITY PROPERTIES (SUCH AS THE ATE FOR A POPULATION BEING A LINEAR COMBINATION OF THE ATEs FOR SUBPOPULATIONS).

THE OBJECTIVE OF A SURVEY IN SUPPORT OF PROGRAM EVALUATION IS TO OBTAIN AN ESTIMATE OF ATE (OR ATT OR OTHER IMPACT MEASURE) THAT IS OF HIGH PRECISION AND LOW BIAS, AND TO BE ABLE TO MAKE POWERFUL STATISTICAL TESTS OF HYPOTHESES ABOUT IMPACT. (THE TECHNICAL TERMS USED HERE WILL BE DEFINED LATER.) MATCHING – THE TOPIC OF THIS PRESENTATION – IS A VERY EFFECTIVE TOOL FOR INCREASING PRECISION AND POWER AND FOR REDUCING BIAS.

IF PROGRAM SERVICES ARE RANDOMLY ASSIGNED TO UNITS THAT ARE RANDOMLY SELECTED FROM THE POPULATION (E.G., IF AN EXPERIMENT IS CONDUCTED), IT IS STRAIGHTFORWARD TO OBTAIN GOOD ESTIMATES OF THE ATE, SUCH AS THE DIFFERENCE IN MEAN IMPROVEMENT BETWEEN THE TREATED AND UNTREATED SAMPLES. (BY THE TERM “RANDOMLY SELECTED” MEANS THAT PROBABILITY SAMPLING IS USED AS A BASIS FOR SELECTING SAMPLE UNITS, BUT THE UNITS DO NOT HAVE TO BE SELECTED WITH EQUAL PROBABILITIES, I.E., WITH SIMPLE RANDOM SAMPLING.)

IF THE UNITS ARE SELECTED FROM THE POPULATION OR ASSIGNED TO TREATMENT IN SOME OTHER WAY (NON-PROBABILITY-BASED), SUCH AS RESPONDING TO PREFERENCES OF PROGRAM STAFF (E.G., “CHERRY PICKING,” “CREAMING,” OR POLITICAL PREFERENCE) OR OF POTENTIAL CLIENTS (E.G., SELF-SELECTION), SIMPLE ESTIMATORS SUCH AS THE DIFFERENCE IN MEANS BETWEEN THE TREATED AND UNTREATED MAY BE SERIOUSLY BIASED ESTIMATES OF THE ATE (DEFINED AS THE EFFECT ON A RANDOMLY SELECTED INDIVIDUAL). THE BIAS THAT MAY BE INTRODUCED BY NONRANDOM SELECTION FROM THE POPULATION OR BY NONRANDOM ASSIGNMENT TO TREATMENT IS REFERRED TO AS A “SELECTION BIAS.” (IT IS NOT REFERRED TO AS “ASSIGNMENT BIAS”.) THIS PRESENTATION WILL DESCRIBE MATCHING PROCEDURES TO REDUCE THE SELECTION BIAS IN ESTIMATES, AS WELL AS TO INCREASE PRECISION OF ESTIMATES AND POWER OF TESTS OF HYPOTHESES.

IT WAS MENTIONED THAT SELECTION BIAS MAY BE ELIMINATED BY USING RANDOM ASSIGNMENT OF TREATMENT TO UNITS, AS IN AN EXPERIMENTAL DESIGN. THERE ARE A NUMBER OF REASONS WHY RANDOM ASSIGNMENT MAY NOT BE FEASIBLE IN SOCIAL AND ECONOMIC EVALUATIONS, AND MANY SUCH STUDIES MAKE USE OF ANALYSIS OF OBSERVATIONAL DATA, SUCH AS IN A QUASI-EXPERIMENTAL DESIGN. MATCHING IS OF VALUE BOTH FOR EXPERIMENTAL DESIGNS (RANDOMIZED EXPERIMENTS) AND FOR QUASI-EXPERIMENTAL DESIGNS (OBSERVATIONAL DATA) – IT IS USED TO REDUCE BIAS FOR QUASI-EXPERIMENTAL DESIGNS, AND TO INCREASE PRECISION AND POWER FOR BOTH EXPERIMENTAL AND QUASI-EXPERIMENTAL DESIGNS.

IT IS SOMETIMES SAID, IN DESIGN AND ANALYSIS ASSOCIATED WITH IMPACT ESTIMATION, THAT MATCHING TENDS TO BE USED MORE BY STATISTICIANS, AND REGRESSION ANALYSIS MORE BY ECONOMISTS. THEORETICALLY, IF EITHER THE MATCHING MODEL IS CORRECT OR THE REGRESSION MODEL IS CORRECT (BUT NOT NECESSARILY BOTH), THEN IMPACT ESTIMATES WILL BE CORRECT (UNBIASED). THAT IS, THE APPROACH OF USING BOTH MATCHING AND REGRESSION ANALYSIS IS SAID TO BE “DOUBLY ROBUST.” MATCHING MAY BE USED WITH OR WITHOUT REGRESSION ANALYSIS. MATCHING MAY BE USED “EX ANTE” IN DESIGN OR “EX POST” IN ANALYSIS, WHEREAS REGRESSION ANALYSIS IS USED ONLY IN THE LATTER. FOR SOME METHODS, SUCH AS THE ROSENBAUM AND RUBIN APPROACH TO BE DISCUSSED IN DETAIL IN THIS PRESENTATION, MATCHING IS VERY IMPORTANT (I.E., IF REGRESSION ADJUSTMENT IS NOT USED, THE IMPORTANCE OF MATCHING INCREASES).

2. CAUSAL INFERENCE; DISCUSSION OF EXPERIMENTAL AND OBSERVATIONAL STUDIES

CAUSAL INFERENCE

THE SCIENCE OF ESTIMATING THE EFFECTS OF CHANGES IN CERTAIN VARIABLES ON OTHER VARIABLES IS CALLED CAUSAL INFERENCE, CAUSAL ANALYSIS OR CAUSAL MODELING (WE WILL DISTINGUISH AMONG THESE TERMS LATER). CAUSAL INFERENCE IS BASED ON DATA. SOMETIMES THE DATA ARE OBTAINED FROM A DESIGNED EXPERIMENT, AND SOMETIMES THEY ARE OBTAINED FROM OBSERVATIONAL DATA (PASSIVELY OBSERVED DATA IN WHICH THE EXPERIMENTER HAS NOT MADE FORCED CHANGES IN THE EXPLANATORY VARIABLES).

CAUSAL INFERENCE INCLUDES BOTH THE PROBLEM OF INFERRING THE "EFFECTS OF CAUSES" (I.E., ESTIMATING THE MAGNITUDE OF CHANGES INDUCED IN SOME VARIABLES BY CHANGES (FORCED OR OTHERWISE) IN OTHER VARIABLES) AND THE PROBLEM OF INFERRING THE "CAUSES OF EFFECTS" (I.E., DECIDING ON THE MOST LIKELY EVENT OR MOST SIGNIFICANT EVENT ASSOCIATED WITH AN OBSERVED EFFECT, OUT OF A GROUP OF EVENTS). THIS PRESENTATION DEALS ALMOST EXCLUSIVELY WITH THE FORMER PROBLEM, SINCE THAT PROBLEM IS THE MAIN GOAL OF PROGRAM IMPACT EVALUATION. THE LATTER PROBLEM IS OF INTEREST MORE IN LEGAL PROCEEDINGS, WHERE IT IS DESIRED TO ESTABLISH THE MAIN CAUSE OF AN EVENT. THE PROBLEM OF INFERRING THE EFFECTS OF CAUSES IS USUALLY CONCERNED WITH ESTIMATION OF THE AVERAGE EFFECT OVER A POPULATION (E.G., THE AVERAGE IMPACT OF A LABOR TRAINING PROGRAM OVER A POPULATION OF INTEREST, OR OF A MEDICAL DRUG ON ALLEVIATING ILLNESS), WHEREAS THE PROBLEM OF INFERRING THE CAUSES OF EFFECTS IS USUALLY CONCERNED WITH INFERENCE ABOUT A SINGLE INDIVIDUAL (E.G., TO ESTABLISH LIABILITY, WAS AN INDIVIDUAL'S DEATH IN AN AUTOMOBILE ACCIDENT CAUSED BY POOR BRAKES OR BY BAD WEATHER). SEE THE ARTICLES BY HAMMOND AND DAWID (REFERENCES CITED LATER) FOR DISCUSSION OF THIS POINT.

IN THIS PRESENTATION, WE WILL DESCRIBE A NUMBER OF PROCEDURES FOR CONDUCTING CAUSAL INFERENCE. THESE PROCEDURES WILL BE BASED ON MATHEMATICAL AND STATISTICAL MODELS, AND THEY WILL TAKE INTO ACCOUNT HOW THE DATA WERE COLLECTED, I.E., USING A DESIGNED EXPERIMENT OR PASSIVE OBSERVATION. CAUSAL INFERENCE MAY BE DONE IN BOTH SETTINGS. THE SETTING AFFECTS BOTH HOW THE DATA ARE ANALYZED AND WHAT KINDS OF INFERENCE ARE APPROPRIATE.

CAUSAL ANALYSIS USING EXPERIMENTAL DATA

AN EXPERIMENT IS A STUDY IN WHICH THE ASSIGNMENT OF TREATMENT LEVELS TO SUBJECTS IS CONTROLLED BY THE EXPERIMENTER. (“TREATMENT” MAY REFER TO A SINGLE PROCEDURE, OR TO A COMPLEX PROTOCOL INVOLVING MANY EXPERIMENTAL CONDITIONS, SUCH AS IN A FRACTIONAL FACTORIAL EXPERIMENTAL DESIGN HAVING MANY TREATMENT VARIABLES AND LEVELS.) AN OBSERVATIONAL STUDY IS A STUDY IN WHICH THIS CONTROL IS LACKING. A DESIGNED EXPERIMENT IS A PLANNED EXPERIMENT THAT POSSESSES FEATURES (SUCH AS RANDOMIZATION, SYMMETRY AND REPLICATION) THAT SUPPORT OBTAINING GOOD ESTIMATES FROM THE DATA. (A DESIGNED EXPERIMENT IS OFTEN REFERRED TO AS AN EXPERIMENTAL DESIGN (ED). ALTHOUGH THIS USAGE IS WIDESPREAD, IT IS A LITTLE “LOOSE,” SINCE A DESIGNED EXPERIMENT IS AN EXPERIMENT, WHEREAS AN EXPERIMENTAL DESIGN IS A STRUCTURED PLAN FOR AN EXPERIMENT – A DESIGN, NOT AN EXPERIMENT.)

(NOTE ON ABBREVIATIONS. WE SHALL USE THE FOLLOWING TERMS AND ABBREVIATIONS RELATED TO EXPERIMENTAL AND QUASI-EXPERIMENTAL DESIGNS: EXPERIMENTAL DESIGN (ED); DESIGNED EXPERIMENT (DE); RANDOMIZED EXPERIMENT (RE); RANDOMIZED CONTROLLED TRIAL (RCT); QUASI-EXPERIMENTAL DESIGN (QED); OBSERVATIONAL DATA (OD); PASSIVELY OBSERVED DATA (POD).)

MATHEMATICAL / STATISTICAL MODELS ARE USED FOR A VARIETY OF PURPOSES, SUCH AS SUMMARIZING (DESCRIBING) A POPULATION, ESTIMATING THE CHANGES THAT WILL OCCUR IN ONE VARIABLE IF CERTAIN CHANGES ARE OBSERVED IN OTHER VARIABLES, AND ESTIMATING THE CHANGES THAT WILL OCCUR IN ONE VARIABLE IF FORCED CHANGES ARE MADE IN OTHER VARIABLES. (ESTIMATION OF THE EFFECTS OF CHANGES IS USUALLY CALLED PREDICTION; ESTIMATION OF VALUES AT SPECIFIED FUTURE TIMES IS USUALLY CALLED FORECASTING.)

IN ORDER FOR A MODEL TO PREDICT WITH HIGH CONFIDENCE THE EFFECT OF MAKING A CHANGE IN ONE VARIABLE (AN EXPLANATORY VARIABLE, OR CAUSAL VARIABLE) ON ANOTHER VARIABLE (A RESPONSE VARIABLE, OR EFFECT VARIABLE), IT IS NECESSARY THAT THE MODEL BE DEVELOPED WITH DATA IN WHICH CONTROLLED MANIPULATIONS HAVE BEEN MADE IN THE EXPLANATORY VARIABLE. THIS IS DONE FOR DESIGNED EXPERIMENTS: THE ESSENTIAL ASPECT OF AN EXPERIMENT IS THAT THE EXPERIMENTER EXERCISES CONTROL OVER THE ASSIGNMENT TO TREATMENT LEVELS. FOR A DETAILED DISCUSSION OF THIS POINT, SEE “USE AND ABUSE OF REGRESSION” BY GEORGE E. P. BOX, TECHNOMETRICS, VOL. 8, NO. 4 (NOV. 1966), PP. 625-629.

AS A FINAL REMARK IN THIS ARTICLE, BOX OBSERVES, "TO FIND OUT WHAT HAPPENS TO A SYSTEM WHEN YOU INTERFERE WITH IT YOU HAVE TO INTERFERE WITH IT (NOT JUST PASSIVELY OBSERVE IT)." THE POINT THAT BOX MAKES, VERY FORCEFULLY, IS THAT A REGRESSION MODEL CONSTRUCTED FROM PASSIVELY OBSERVED DATA CANNOT RELIABLY BE USED TO ESTIMATE THE EFFECT THAT FORCED CHANGES IN THE EXPLANATORY VARIABLES ("X's") WILL HAVE ON THE DEPENDENT VARIABLE ("Y"). THE PROBLEM IS THAT, WITHOUT CONTROLLED MANIPULATION OF THE MODEL EXPLANATORY VARIABLES, THERE MAY EXIST HIDDEN VARIABLES THAT ARE CORRELATED WITH THE EXPLANATORY VARIABLES. THESE HIDDEN VARIABLES MAY INTRODUCE A CORRELATION BETWEEN THE MODEL RESIDUAL (ERROR TERM), IN WHICH CASE THE ESTIMATES OF THE MODEL PARAMETERS (REGRESSION COEFFICIENTS) WILL BE BIASED ESTIMATES OF THE CAUSAL EFFECT OF THE MODEL EXPLANATORY VARIABLES ON THE DEPENDENT VARIABLE. THEY WILL ACCURATELY REFLECT THE EFFECT OF THE EXPLANATORY VARIABLES ON THE DEPENDENT VARIABLE IF THE SYSTEM CONTINUES TO OPERATE AS IT DID FOR THE COLLECTED DATA, BUT NOT THE EFFECT OF THE EXPLANATORY VARIABLES ON THE DEPENDENT VARIABLE IF FORCED CHANGES ARE MADE IN THE EXPLANATORY VARIABLES.

CAUSAL ANALYSIS USING OBSERVATIONAL DATA

IF THERE ARE NO HIDDEN VARIABLES, AND THE REGRESSION MODEL IS CORRECTLY SPECIFIED ("TRUE"), THEN EVEN THOUGH THE MODEL IS CONSTRUCTED FROM PASSIVELY OBSERVED DATA IT MAY, UNDER CERTAIN ASSUMPTIONS, BE USED TO PREDICT THE EFFECT OF FORCED CHANGES. (THE MAIN ASSUMPTION THAT THE MODEL IS CORRECTLY SPECIFIED (I.E., THAT THE MODEL RESIDUALS ARE UNCORRELATED WITH THE EXPLANATORY VARIABLES)). THE MAJOR DIFFICULTY THAT ARISES IS THAT IT IS OFTEN DIFFICULT TO REPRESENT WITH CONFIDENCE THAT ANY MODEL IS AN ACCURATE REPRESENTATION OF (CAUSAL) REALITY, WITHOUT MAKING RANDOMIZATION-BASED MANIPULATIONS OF THE EXPLANATORY VARIABLES. THIS POINT WILL BE DISCUSSED IN DETAIL, LATER. IF IT CANNOT BE REASONABLY ASSUMED THAT THE CAUSAL MODEL IS A REASONABLE REPRESENTATION OF REALITY, I.E., THAT THE CAUSAL MODEL IS CORRECTLY SPECIFIED, THEN BOX'S ASSERTION THAT A MODEL DERIVED FROM ANALYSIS OF PASSIVELY OBSERVED DATA CANNOT BE USED TO ESTIMATE THE EFFECT OF FORCED CHANGES IN THE EXPLANATORY VARIABLES STANDS.

CAUSAL INFERENCES MAY BE BASED ON OBSERVATIONAL DATA, IF APPROPRIATE ASSUMPTIONS ARE MADE. THESE INFERENCES WILL BE DIFFERENT FROM THOSE BASED ON EXPERIMENTAL DATA. THEY WILL INVOLVE DIFFERENT ASSUMPTIONS AND A DIFFERENT SCOPE OF INFERENCE (EXTERNAL VALIDITY). THEY ARE NEVERTHELESS CAUSAL INFERENCES.

IN THIS PRESENTATION WE SHALL MAKE MUCH USE OF MATHEMATICAL MODELS. IN HIS BOOK ON RESPONSE SURFACE METHODOLOGY WITH NORMAN R. DRAPER BOX WROTE THAT "ESSENTIALLY, ALL MODELS ARE WRONG, BUT SOME ARE USEFUL."

THE ACT OF MAKING CONTROLLED MANIPULATIONS IN AN EXPLANATORY VARIABLE IS REFERRED TO AS “SETTING,” “DOING,” “FIXING,” “MANIPULATING” OR “CONTROLLING” THE EXPLANATORY VARIABLES, OR “MAKING AN INTERVENTION.” THE FIELD OF CAUSAL INFERENCE IS CONCERNED WITH ESTIMATING THE PROBABILITY DISTRIBUTION OF ONE RANDOM VARIABLE WHEN CONTROLLED MANIPULATIONS (FORCED CHANGES) ARE MADE IN ANOTHER.

THIS DISTRIBUTION DIFFERS FROM THE USUAL CONDITIONAL DISTRIBUTION OF ONE RANDOM VARIABLE ON ANOTHER WHEN BOTH ARE PASSIVELY OBSERVED. THAT DISTRIBUTION IS CALLED THE CONDITIONAL PROBABILITY DISTRIBUTION OF THE FIRST VARIABLE GIVEN THE SECOND. A SOURCE OF CONFUSION IS THAT BOTH OF THE PRECEDING DISTRIBUTIONS ARE CONDITIONAL DISTRIBUTIONS, INVOLVING THE SAME VARIABLES, BUT UNDER DIFFERENT CONDITIONS. TO REDUCE CONFUSION, WE SHALL REFER TO THE FIRST DISTRIBUTION AS THE CAUSAL-EFFECT DISTRIBUTION (OR "FORCED-CHANGE" DISTRIBUTION) AND THE SECOND ONE AS THE ASSOCIATIONAL DISTRIBUTION (OR "PASSIVELY OBSERVED" DISTRIBUTION), IF IT IS NOT CLEAR FROM CONTEXT WHICH DISTRIBUTION IS BEING REFERRED TO.

A FURTHER SOURCE OF CONFUSION IS THAT THE USUAL (ASSOCIATIONAL) CONDITIONAL DISTRIBUTION IS ALSO REFERRED TO AS THE CONDITIONAL DISTRIBUTION GIVEN, FIXING, OR HOLDING FIXED ANOTHER VARIABLE. THESE ARE THE SAME TERMS THAT ARE USED WHEN REFERRING TO THE CAUSAL-EFFECT DISTRIBUTION.

RANDOMIZED ASSIGNMENT TO TREATMENT IS A WAY OF MAKING FORCED CHANGES IN EXPLANATORY VARIABLES. RANDOMIZED SELECTION FROM A POPULATION IS A WAY OF SETTING A VARIABLE FOR WHICH A FORCED CHANGE CANNOT BE MADE. THE USE OF RANDOMIZED FORCED CHANGES IS IMPORTANT BECAUSE IT ENABLES THE ESTIMATION OF CAUSAL EFFECTS WITH HIGH VALIDITY, BUT IT IS NOT ESSENTIAL TO USEFUL CAUSAL ANALYSIS (IF APPROPRIATE ASSUMPTIONS ARE MADE AND CAN BE JUSTIFIED).

IN REALITY (AS OPPOSED TO IN A THOUGHT EXPERIMENT, OR IN A CAUSAL MODEL), NOT ALL EXPLANATORY VARIABLES MAY BE MANIPULATED. FOR EXAMPLE, SEX AND RACE MAY BE OBSERVED, BUT NOT FORCIBLY CHANGED. IN AN EXPERIMENT, EXPERIMENTAL UNITS MAY BE SELECTED HAVING THESE ATTRIBUTES, BUT THE ATTRIBUTE CANNOT BE IMPOSED ON A RANDOMLY SELECTED EXPERIMENTAL UNIT. SUCH FACTORS CAN BE INCLUDED IN THE ANALYSIS AS COVARIATES, AND ONE MAY SPEAK OF THE “EFFECT” OF THESE VARIABLES ON AN OUTCOME VARIABLE, SUCH AS INCOME. IN THIS CASE, HOWEVER, WHAT IS BEING MEASURED AND ESTIMATED IS THE ASSOCIATION OF THESE VARIABLES WITH THE OUTCOME VARIABLE, NOT THE EFFECT OF MAKING A “FORCED CHANGE” IN THEM. THESE VARIABLES MAY BE SURROGATES FOR OTHER VARIABLES THAT ARE MANIPULABLE. (IN THE CASE OF SUCH VARIABLES, “RANDOM SELECTION” OR “RANDOM ASSIGNMENT” REFERS TO SELECTING AN INDIVIDUAL FROM A SUBPOPULATION THAT POSSESSES THE ATTRIBUTE. FOR EXAMPLE, TO CONSTRUCT A SAMPLE INCLUDING INDIVIDUALS OF VARIOUS RACES, INDIVIDUALS WOULD BE SELECTED BY RACE AND THEN ASSIGNED TO TREATMENT – IT IS NOT CONCEIVED TO ASSIGN RACE. IN THIS SITUATION, THERE IS NO “FORCED CHANGE” OR ASSIGNMENT, BUT THERE MAY OR MAY NOT BE RANDOM SELECTION.)

SOME AUTHORS (E.G., RUBIN AND HOLLAND) OBJECT TO REFERRING TO VARIABLES THAT CANNOT BE MANIPULATED (IN PRINCIPLE) AS CAUSAL VARIABLES – “NO CAUSATION WITHOUT MANIPULATION.” THIS POSITION IS RATHER EXTREME, ALTHOUGH IT SHOULD BE NOTED THAT IT WAS PRESENTED IN AN ARTICLE ON ANALYSIS OF EXPERIMENTAL DATA, NOT OBSERVATIONAL DATA. FOR EXAMPLE, THE SUN'S RISING EACH MORNING IS REASONABLY VIEWED AS A CAUSAL VARIABLE, BUT IT IS NOT SUBJECT TO MANIPULATION. A REASONABLE INTERPRETATION OF THE RUBIN/HOLLAND VIEWPOINT (OF NO CAUSATION WITHOUT MANIPULATION) IS THAT IT IS NOT POSSIBLE TO UNEQUIVOCALLY ESTIMATE (OR TO ESTIMATE WITH HIGH CONFIDENCE) THE EFFECT OF MAKING CHANGES IN A VARIABLE THAT CANNOT BE MANIPULATED. EVEN THIS MODIFIED ASSERTION IS VERY STRINGENT – IF A CAUSAL MODEL IS POSITED FOR A CERTAIN PASSIVELY-OBSERVED DATA SET, CAUSAL EFFECTS MAY CERTAINLY BE ESTIMATED FROM THE MODEL AND DATA. THE VALIDITY OF THESE ESTIMATES DEPENDS ON THE VALIDITY OF THE MODEL I.E., THE REASONABLENESS OF THE ASSUMPTIONS MADE IN THE MODEL. IT IS NOT REASONABLE TO ASSERT THAT CAUSAL ANALYSIS CANNOT BE DONE IF EXPERIMENTAL DATA ARE NOT POSSIBLE.

BY ITSELF, A PROBABILITY MODEL DOES NOT SPECIFY CAUSAL RELATIONSHIPS. IT SPECIFIES JUST ASSOCIATIONAL RELATIONSHIPS. IN ORDER TO MAKE CAUSAL INFERENCES, ADDITIONAL INFORMATION IS REQUIRED. THERE ARE TWO BASIC APPROACHES TO CAUSAL INFERENCE. THE FIRST APPROACH, OFTEN CALLED THE "STATISTICAL" APPROACH, IS TO SPECIFY CONDITIONS (SUCH AS CONDITIONAL INDEPENDENCE) UNDER WHICH PARTICULAR ESTIMATES ARE ESTIMATES OF CAUSAL EFFECTS. THE SECOND APPROACH TO CAUSAL INFERENCE, WHICH MAY BE CALLED THE "CAUSAL MODELING" APPROACH, IS TO SPECIFY A COMPLETE CAUSAL MODEL, AND THEN DERIVE CAUSAL ESTIMATES FROM THE MODEL (AND DATA). (BY "COMPLETE" IS MEANT A MODEL THAT IDENTIFIES ALL MAJOR VARIABLES AFFECTING OUTPUTS OF INTEREST, AND THEIR CAUSAL RELATIONSHIPS, IN SITUATIONS OF INTEREST.)

THE FIRST APPROACH (THE "STATISTICAL" APPROACH) IS A "MINIMALIST" APPROACH, SINCE IT REQUIRES FEWER ASSUMPTIONS. UNFORTUNATELY, THIS APPARENT SIMPLICITY IS ILLUSORY, SINCE, ABSENT AN EXPLICIT CAUSAL MODEL, IT IS DIFFICULT TO JUSTIFY THOSE ASSUMPTIONS. FOR EXAMPLE, IT IS EASIER TO DEFEND AN ASSUMPTION OF CONDITIONAL INDEPENDENCE (NEEDED TO JUSTIFY CERTAIN CAUSAL ESTIMATES) FROM A COMPLETE DESCRIPTION OF A CAUSAL MODEL AND A SAMPLING SCHEME, THAN IN THE ABSENCE OF A DESCRIPTION OF THE MODEL.

IN SOME INSTANCES, IT IS QUITE UNNECESSARY TO SPECIFY A COMPLETE CAUSAL MODEL (I.E., ALL OF THE MAJOR VARIABLES THAT AFFECT OUTCOME). FOR EXAMPLE, IN A DESIGNED EXPERIMENT, WITH RANDOMIZATION USED TO SPECIFY THE LEVELS OF EXPLANATORY VARIABLES, THE MODEL SPECIFICATION MAY BE RESTRICTED TO THE OUTPUT VARIABLES OF INTEREST AND THE RANDOMIZED EXPLANATORY VARIABLES (IGNORING ALL OTHER VARIABLES THAT AFFECT OUTCOME). (A MORE DETAILED MODEL, INCLUDING COVARIATES, COULD BE CONSIDERED, TO IMPROVE PRECISION OF ESTIMATES, BUT THIS IS NOT NECESSARY.) WITH RANDOMIZATION AND ORTHOGONALITY OF TREATMENT LEVELS, THE TREATMENT EFFECT ESTIMATES ARE UNBIASED ESTIMATES OF CAUSAL EFFECTS.

UNFORTUNATELY, THE SIMPLICITY OF THE RANDOMIZED EXPERIMENT DOES NOT CARRY OVER INTO THE ANALYSIS OF OBSERVATIONAL DATA. ABSENT A RANDOMIZED EXPERIMENTAL DESIGN, IT BECOMES NECESSARY TO SPECIFY A COMPLETE CAUSAL MODEL, IN ORDER TO MAKE CLEAR AND JUSTIFY THE ASSUMPTIONS REQUIRED TO OBTAIN CONSISTENT ESTIMATES OF CAUSAL EFFECTS. (USE OF THE WORD "COMPLETE" MAY BE A LITTLE MISLEADING. IN A RANDOMIZED EXPERIMENT, THE MODEL INCLUDING THE OUTPUT VARIABLES AND THE RANDOMIZED EXPLANATORY VARIABLES WOULD CERTAINLY BE CONSIDERED "COMPLETE," WITH RESPECT TO ANALYSIS NEEDS.)

IN THE CAUSAL MODELS TO BE DISCUSSED LATER, WE WILL INCLUDE ATTRIBUTES THAT CANNOT BE MANIPULATED AS “CAUSAL VARIABLES,” ALONG WITH THOSE THAT CAN BE MANIPULATED. THEY ARE CONSIDERED TO “HAVE AN EFFECT” ON OTHER VARIABLES, EVEN THOUGH THEY CANNOT BE MANIPULATED FOR AN INDIVIDUAL UNIT, AND THE “EFFECT” IS SIMPLY AN ASSOCIATION.

MOST STATISTICS TEXTS DO NOT USE THE WORD “CAUSAL,” EXCEPT PERHAPS WHEN DISCUSSING EXPERIMENTAL DESIGNS. THEY USUALLY SPEAK ONLY OF “EFFECTS.” THEY OFTEN DO NOT DISTINGUISH BETWEEN VARIOUS SELECTION METHODS (FORCED CHANGES, RANDOM SELECTION, PASSIVE OBSERVATION) IN ESTIMATION, SINCE THE ESTIMATES ARE AFFECTED ONLY BY ASSOCIATIONAL RELATIONSHIPS (THE JOINT PROBABILITY DISTRIBUTION, OR LIKELIHOOD FUNCTION, OF THE SAMPLE), NOT CAUSAL ONES, AND THE PROBABILISTIC ASSOCIATION BETWEEN VARIABLES DOES NOT DEPEND ON OR REFLECT THE SELECTION METHOD (FORCED OR UNFORCED), BUT JUST THE RESULT. IT IS NOT POSSIBLE TO SPECIFY CAUSAL RELATIONSHIPS SOLELY IN TERMS OF PROBABILITY DISTRIBUTIONS. CAUSAL RELATIONSHIPS MUST BE SPECIFIED ADDITIONAL TO STATEMENTS ABOUT THE PROBABILISTIC RELATIONSHIPS AMONG VARIABLES. A PROBABILITY DISTRIBUTION MAY DESCRIBE A CAUSAL RELATIONSHIP, BUT IT DOES NOT IMPLY ONE.

THE RELUCTANCE OF STATISTICIANS TO USE THE WORD "CAUSAL" IS A LITTLE DIFFICULT TO UNDERSTAND. STATISTICAL ANALYSIS HAS BEEN APPLIED TO MANY SUBSTANTIVE FIELDS, AND MANY PEOPLE ARE COMFORTABLE WITH DESCRIPTORS SUCH AS "BIOMETRICS," "ECONOMETRICS," "PSYCHOMETRICS," AND "STATISTICAL MECHANICS" IN REFERRING TO AREAS OF SCIENCE THAT MAKE GOOD USE OF STATISTICAL METHODS. THE APPLICATION OF STATISTICAL METHODS TO THE INVESTIGATION OF CAUSAL PHENOMENA IS AS "LEGITIMATE" AS ANY OF THESE OTHER APPLICATIONS.

MOST STATISTICS TEXTS DO NOT MAKE AN ISSUE OUT OF THE SELECTION METHOD (FORCED OR PASSIVELY OBSERVED). THE REASON WHY IS THAT IS MOST OF THEM DEAL SOLELY WITH ASSOCIATIONAL STATISTICS – PROBABILISTIC RELATIONSHIPS, WHETHER OR NOT THEY REPRESENT CAUSAL RELATIONSHIPS. SUCH ASSOCIATIONAL RELATIONSHIPS ARE DESCRIPTIVE FEATURES OF A PROCESS, AND MAY OR MAY NOT REPRESENT THE INTRINSIC PHYSICAL (CAUSAL) NATURE OF THE PROCESS (DEPENDING ON CONDITIONS AND ASSUMPTIONS).

3. MATCHING IN DESIGNED EXPERIMENTS

IN THE INTRODUCTION TO THIS PRESENTATION, IT WAS STATED THAT THIS PRESENTATION IS CONCERNED WITH MATCHING IN SAMPLE SURVEY. THAT STATEMENT WAS NOT INTENDED TO EXCLUDE EXPERIMENTAL DESIGNS FROM DISCUSSION. SAMPLE SURVEY IS A SCIENTIFIC METHOD FOR COLLECTING DATA FROM A POPULATION. A SAMPLE SURVEY MAY COLLECT DATA FOR AN EXPERIMENTAL DESIGN OR FOR AN OBSERVATIONAL STUDY.

THIS PRESENTATION FOCUSES MAINLY ON ANALYSIS OF OBSERVATIONAL DATA, RATHER THAN ON DATA FROM DESIGNED EXPERIMENTS. THERE ARE SEVERAL REASONS FOR THIS FOCUS. FIRST, THIS PRESENTATION IS ABOUT MATCHING IN EVALUATION DESIGN, AND MOST EVALUATION STUDIES INVOLVE OBSERVATIONAL DATA, NOT EXPERIMENTAL DATA. SECOND, A PRIMARY MOTIVATION FOR MATCHING IS REDUCTION OF BIAS CAUSED BY NON-INDEPENDENT SELECTION FOR TREATMENT, WHICH OCCURS IN OBSERVATIONAL STUDIES, NOT (HOPEFULLY!) IN EXPERIMENTAL STUDIES. WHILE MATCHING IS AN INTEGRAL PART OF SOME EXPERIMENTAL DESIGNS (E.G., MATCHED-PAIRS DESIGNS), IT IS NOT A MAJOR FEATURE OF MANY EXPERIMENTAL DESIGNS. FOR OBSERVATIONAL STUDIES, HOWEVER, MATCHING IS COMMON FEATURE, BOTH IN STUDY DESIGN AND IN ANALYSIS.

FOR THE PRECEDING REASONS, THIS SECTION ON MATCHING IN EXPERIMENTAL DESIGN IS BRIEF. BECAUSE OF THE LIMITED DISCUSSION OF EXPERIMENTAL DESIGN, NO BACKGROUND IN THAT SUBJECT IS ASSUMED. REFERENCES ON THE SUBJECT INCLUDE:

1. KUEHL, ROBERT O., DESIGN OF EXPERIMENTS: STATISTICAL PRINCIPLES OF RESEARCH DESIGN AND ANALYSIS, 2ND ED., BROOKS/COLE CENGAGE LEARNING, 2000

2. COCHRAN, WILLIAM G. AND GERTRUDE M. COX, EXPERIMENTAL DESIGNS, 2ND ED., WILEY, 1957.

3. COX, D. R., PLANNING OF EXPERIMENTS, WILEY, 1958

RANDOMIZED SELECTION AND RANDOMIZED ASSIGNMENT TO TREATMENT; PROBABILITY SAMPLING

IN A DESIGNED EXPERIMENT, RANDOMIZATION IS USED TO SELECT EXPERIMENTAL UNITS FROM A POPULATION OF INTEREST AND TO ASSIGN TREATMENT LEVELS TO THE SELECTED EXPERIMENTAL UNITS. NOTE THAT THERE ARE TWO ASPECTS TO RANDOMIZATION IN AN EXPERIMENT – RANDOMIZED SELECTION OF SAMPLE UNITS FROM THE POPULATION AND RANDOMIZED ASSIGNMENT OF TREATMENT LEVELS TO THEM (ALTHOUGH THESE TWO ASPECTS MAY BE IMPLEMENTED SIMULTANEOUSLY).

IN SOME APPLICATIONS, EXPERIMENTAL UNITS ARE SELECTED FROM A HYPOTHETICAL OR PHYSICALLY UNREALIZED (OR “METAPHYSICAL”) POPULATION, SUCH AS ALL UNITS THAT MAY HYPOTHETICALLY BE PRODUCED ON A MACHINE, AND THE SAMPLE IS THOSE UNITS ACTUALLY PRODUCED IN A RANDOMLY SELECTED PERIOD. IN THIS CASE, THE PROBABILITY OF SELECTION IS CONCEIVED TO BE A PROBABILITY DENSITY FUNCTION OVER A CONCEPTUALLY INFINITE POPULATION AND IT IS ASSUMED THAT EVERY UNIT OF THE HYPOTHETICAL POPULATION HAS AN EQUAL CHANCE (PROBABILITY OR PROBABILITY DENSITY) OF SELECTION.

IN MANY SOCIO-ECONOMIC APPLICATIONS, THE EXPERIMENTAL UNITS ARE NOT "CREATED" OR "GENERATED" AS IN LABORATORY EXPERIMENTS, BUT ARE SELECTED FROM AN EXISTING POPULATION, USING THE METHODS OF SAMPLE SURVEY. IN THE CASE OF SAMPLE SURVEY, THE POPULATION UNITS MAY CORRESPOND TO AN ACTUAL (EXTANT) PHYSICAL POPULATION (SUCH AS ALL OF THE HOUSEHOLDS IN A REGION AT A PARTICULAR TIME), AND THE PROBABILITIES OF SELECTION ARE NONZERO FOR EACH MEMBER OF THE POPULATION. THIS POPULATION MAY BE OF INTEREST IN ITS OWN RIGHT, OR IT MAY BE CONCEIVED TO BE A RANDOMLY SELECTED POPULATION FROM A CONCEPTUALLY INFINITE “SUPERPOPULATION” OF POPULATIONS GENERATED BY SOME PROCESS (SUCH AS A PROGRAM INTERVENTION).

FOCUS ON THE BINARY-TREATMENT CASE

FOR MUCH OF THIS PRESENTATION, WE SHALL RESTRICT CONSIDERATION PRIMARILY TO THE “BINARY” TREATMENT CASE, IN WHICH THERE ARE JUST TWO TREATMENT LEVELS, “TREATED” AND “UNTREATED.” THE UNTREATED UNITS WILL BE REFERRED TO AS “COMPARISON” UNITS (OR, IN THE CASE OF A DESIGNED EXPERIMENT, AS “CONTROL” UNITS). AT SOME POINT WE WILL RELAX THIS RESTRICTION TO THE BINARY-TREATMENT CASE. THE REASON FOR FOCUSING ON THIS SPECIAL CASE IS THAT IT OCCURS OFTEN IN PRACTICE, AND IT IS A GOOD BASIS FOR EXPLANATION OF FUNDAMENTAL CONCEPTS.

THE TERMS “RANDOMLY SELECTED,” “SELECTED AT RANDOM,” OR “RANDOMLY ASSIGNED” MEANS THAT A KNOWN RANDOMIZATION PROCESS IS INVOLVED IN THE SELECTION OF EXPERIMENTAL UNITS FROM THE POPULATION OF INTEREST AND IN ASSIGNMENT TO TREATMENT. THE TERM “KNOWN” HERE MEANS THAT THE PROBABILITY OF SELECTION IS NONZERO AND KNOWN (OR KNOWN TO BE NONZERO AND EQUAL WITHIN WELL-DEFINED POPULATION GROUPS). IN ORDER TO USE MAKE INFERENCES AND TEST HYPOTHESES USING STATISTICAL THEORY, IT IS ESSENTIAL THAT THE PROBABILITIES ASSOCIATED WITH THE RANDOMIZATION PROCESS BE NONZERO AND KNOWN (OR KNOWN TO BE NONZERO AND EQUAL FOR SPECIFIED SUBPOPULATIONS). IF THERE IS SOME SORT OF RANDOMIZATION PROCESS INVOLVED IN SELECTING THE UNITS FROM THE POPULATION AND ASSIGNING THEM TO TREATMENT LEVELS, BUT THE PROBABILITIES ASSOCIATED WITH THE PROCESS ARE NOT KNOWN (OR NOT KNOWN TO BE CONSTANT WITHIN WELL-DEFINED STRATA), THAT RANDOMIZATION IS OF LITTLE VALUE. THE TERM “ASSIGNED TO TREATMENT” IS GENERALLY USED IN EXPERIMENTAL DESIGN, AND THE TERM “SELECTION FOR TREATMENT” IS GENERALLY USED IN SOCIAL AND ECONOMIC STUDIES (OBSERVATIONAL DATA).

FOR SIMPLICITY, WE SHALL STOP ADDING THE COMMENT "OR KNOWN TO BE NONZERO AND EQUAL FOR THE POPULATION OR SPECIFIED POPULATION SUBGROUPS" TO THE PHRASE "PROBABILITY OF SELECTION ARE NONZERO AND KNOWN," AND ASSUME THAT THIS CONDITION ALWAYS HOLDS.

(BY SAYING THAT THE “PROBABILITIES ARE KNOWN” MEANS THAT THE JOINT PROBABILITY DISTRIBUTION OF SELECTION IS KNOWN FOR ALL SAMPLE UNITS. THIS ALLOWS FOR THE FACT THAT THE SELECTION OF VARIOUS UNITS MAY BE CORRELATED, AS, FOR EXAMPLE, IN THE CASE OF MULTISTAGE SAMPLING OR SAMPLING WITHOUT REPLACEMENT (IN WHICH CASE THE CORRELATIONS AMONG THE SELECTION EVENTS MUST BE KNOWN FOR THE SELECTED SAMPLE UNITS).)

IN THE CASE OF A DESIGNED EXPERIMENT, THE PROBABILITIES OF SELECTION FROM THE POPULATION MAY BE RELATED TO ANY KNOWN VARIABLES INDEPENDENT OF THE OUTCOME (RESPONSE). ALL THAT IS REQUIRED IS THAT THE PROBABILITIES (OR PROBABILITY DENSITIES) BE NONZERO AND KNOWN. FOR A DESIGNED EXPERIMENT, THE NUMBERS OF TREATED AND UNTREATED UNITS ARE OFTEN SPECIFIED FOR CERTAIN GROUPS (E.G., BALANCED WITHIN STRATA, BLOCKS OR HIGHER-LEVEL SAMPLE UNITS). IN ANY EVENT, THE PROBABILITY OF ASSIGNMENT TO TREATMENT MUST BE KNOWN, OR CONSTANT OVERALL, OR CONSTANT WITHIN DESIGN STRATA (SUBPOPULATIONS ASSOCIATED WITH SPECIFIED VALUES OF DESIGN VARIABLES), OR A KNOWN FUNCTION OF KNOWN (OBSERVED) VARIABLES.

IF THE PROBABILITY OF SELECTION FROM THE POPULATION IS NONZERO AND KNOWN AND THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS NONZERO AND KNOWN, IT IS AN EASY MATTER TO CONSTRUCT GOOD ESTIMATES OF IMPACT, E.G., USING THE MAXIMUM-LIKELIHOOD PRINCIPLE OR BAYES’ RULE (SINCE THE PROBABILITY DISTRIBUTION OF THE SAMPLE IS FULLY SPECIFIED). IN A DESIGNED EXPERIMENT, THESE PROBABILITY DISTRIBUTIONS ARE UNDER CONTROL OF THE EXPERIMENTER, AND ARE KNOWN. FOR OBSERVATIONAL DATA AND QUASI-EXPERIMENTAL DESIGNS, THEY ARE NOT KNOWN. (THEY MAY, HOWEVER, BE ESTIMATED – THAT IS IN FACT THE SUBJECT OF MUCH OF THIS PRESENTATION.)

THERE ARE MANY WAYS THAT A RANDOMIZATION PROCESS MAY BE IMPLEMENTED. ALL THAT IS REQUIRED FOR ANALYSIS IS THAT IT BE DONE IN SUCH A WAY THAT THE PROBABILITY MODEL FOR WHATEVER PROCESS IS EMPLOYED BE KNOWN (AND POSITIVE FOR ALL UNITS OF INTEREST). CONCEPTUALLY, PERHAPS THE SIMPLEST APPROACH IS TO RANDOMLY SELECT A UNIT FROM A POPULATION AND THEN RANDOMLY ASSIGN THE UNIT TO A TREATMENT LEVEL. IN THIS CASE, THE TOTAL SAMPLE SIZE WOULD BE FIXED, BUT THE NUMBERS OF TREATMENT AND COMPARISON UNITS WOULD BE RANDOM. ALTERNATIVELY, IT MAY BE DECIDED BEFORE THE UNIT IS SELECTED FROM THE POPULATION WHETHER IT WILL BE A TREATMENT UNIT OR A COMPARISON UNIT, AND THEN THE UNIT IS RANDOMLY SELECTED FROM THE POPULATION. THIS IS USUALLY THE CASE IN A DESIGNED EXPERIMENT OR SAMPLE SURVEY, WHERE IT IS DECIDED EXACTLY HOW MANY TREATMENT UNITS AND HOW MANY CONTROL (COMPARISON) UNITS WILL BE IN THE SAMPLE. (IT IS ALSO THE PROCEDURE THAT WOULD BE USED TO RANDOMLY “ASSIGN” A VARIABLE SUCH AS RACE OR SEX, THAT MAY NOT BE FORCIBLY IMPOSED ON A UNIT.)

FROM A TECHNICAL VIEWPOINT, THERE IS NO DISTINCTION BETWEEN THE EXPRESSION “THE UNIT IS ASSIGNED TO TREATMENT” AND “TREATMENT IS ASSIGNED TO THE UNIT,” BUT THERE COULD BE A DEFINITE OPERATIONAL DIFFERENCE IN THESE EXPRESSIONS.

THE TERMS “SELECTION FOR TREATMENT” AND “ASSIGNMENT TO TREATMENT” ARE USED WHEN THERE ARE TWO TREATMENT LEVELS (BINARY TREATMENT), TREATED AND UNTREATED. WHEN THERE ARE MORE THAN TWO TREATMENT LEVELS OR THE TREATMENT LEVEL IS CONTINUOUS (INTERVAL LEVEL OF MEASUREMENT), THE TERM “ASSIGNMENT TO TREATMENT LEVEL” IS USED. THIS PRESENTATION IS RESTRICTED MAINLY TO THE CASE OF BINARY TREATMENT.

THE TERMS “PARTICIPATION” AND “PARTICIPANT” ARE OFTEN USED IN PROGRAM EVALUATION, IN LIEU OF “TREATMENT” AND “TREATED.” A PARTICIPANT IS A PERSON RECEIVING THE ASSIGNED PROGRAM SERVICES. THE TERM “PARTICIPATION” MAKES EXPLICIT THE FACT THAT ASSIGNMENT TO TREATMENT MAY INVOLVE DECISIONS ON THE PARTS OF BOTH THE INDIVIDUAL AND THE PROGRAM, AND THAT IN A LONGITUDINAL STUDY CLIENTS MAY BE LOST OVER TIME (ATTRITION). IN THIS PRESENTATION, WE SHALL GENERALLY USE THE TERM “TREATMENT” RATHER THAN “PARTICIPATION.”

TO SUMMARIZE, THE TERM “RANDOMIZATION” IMPLIES THE USE OF PROBABILITY SAMPLING (I.E., EACH UNIT OF THE POPULATION HAS A KNOWN (OR EQUAL) NONZERO PROBABILITY (OR PROBABILITY DENSITY) OF SELECTION, AND THAT THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS KNOWN (OR EQUAL)). IF THE SAMPLING IS CORRELATED (E.G., THE CASE OF SAMPLING WITHOUT REPLACEMENT), THE JOINT CORRELATIONS OF THE SELECTION EVENTS MUST BE KNOWN. THE TERM “RANDOMIZATION” DOES NOT NECESSARILY MEAN THAT THE SELECTION OR ASSIGNMENT IS BY MEANS OF SIMPLE RANDOM SAMPLING. THE RANDOM SAMPLING MAY BE CONTROLLED BY A COMPLEX SAMPLE SURVEY DESIGN AND SAMPLING PROCEDURE, SUCH AS ONE INVOLVING STRATIFIED SAMPLING OR MULTISTAGE SAMPLING, AND COMPLEX SAMPLE SELECTION PROCEDURES (E.G., USING RAO-HARTLEY-COCHRAN SELECTION OF FIRST-STAGE SAMPLE UNITS).

RANDOMIZATION IS USED TO ENABLE THE CONSTRUCTION OF UNBIASED OR CONSISTENT ESTIMATES. (THE BIAS OF AN ESTIMATOR IS THE DIFFERENCE BETWEEN THE EXPECTED VALUE (EXPECTATION) OF THE ESTIMATOR AND THE TRUE (POPULATION) VALUE OF THE QUANTITY BEING ESTIMATED. AN UNBIASED ESTIMATOR IS ONE FOR WHICH THE EXPECTED VALUE IS EQUAL TO THE POPULATION VALUE OF THE QUANTITY BEING ESTIMATED, I.E., THE BIAS IS ZERO. BIAS IS ALWAYS RELATIVE TO THE QUANTITY BEING ESTIMATED. A CONSISTENT ESTIMATOR IS ONE FOR WHICH THE BIAS DECREASES TO ZERO AS THE SAMPLE SIZE INCREASES.)

EVEN WITH RANDOMIZATION, BIAS IS POSSIBLE, E.G., INTRODUCED BY THE USE OF A PARTICULAR ESTIMATOR (SUCH AS A RATIO ESTIMATOR, OR AN INSTRUMENTAL VARIABLE). BIAS MAY EVEN BE COMPLETELY ACCEPTABLE, E.G., IN PREFERRING A BIASED ESTIMATOR WITH SMALL MEAN-SQUARED ERROR OVER AN UNBIASED ONE WITH A LARGE MEAN-SQUARED ERROR. (THE MEAN-SQUARED ERROR (MSE) IS THE VARIANCE PLUS THE SQUARE OF THE BIAS. THE ROOT-MEAN-SQUARED ERROR (RMSE) IS THE SQUARE ROOT OF THE MSE.)

IN EXPERIMENTAL DESIGN, THE PURPOSE OF MATCHING IS TO INCREASE PRECISION AND POWER, NOT TO REDUCE OR REMOVE BIAS INTRODUCED BY A LACK OF RANDOMIZATION (SINCE (WITH RANDOMIZATION AND THE USE OF PROPER ANALYSIS PROCEDURES) IT IS ZERO).

FOUR MAIN PRINCIPLES OF EXPERIMENTAL DESIGN ARE:

RANDOMIZATION (RANDOM SELECTION OF EXPERIMENTAL UNITS AND RANDOM ASSIGNMENT OF TREATMENT LEVELS TO THEM). RANDOMIZATION ENABLES:

· ESTIMATION OF EXPERIMENTAL ERROR

· REDUCTION OF BIAS

· ATTRIBUTION OF CAUSALITY

REPLICATION

ENABLES ESTIMATION OF EXPERIMENTAL ERROR (TO SUPPORT ESTIMATION OF STANDARD ERRORS, AND HENCE CONFIDENCE INTERVALS AND TESTS OF HYPOTHESES)

SYMMETRY / BALANCE / ORTHOGONALITY

ADVANTAGES: EASE OF ANALYSIS; INCREASED PRECISION; DISAMBIGUATION OF EFFECT ESTIMATES (I.E., TO REDUCE CONFOUNDING OF EFFECTS)

EXAMPLES: RANDOMIZED BLOCKS DESIGNS; BALANCED INCOMPLETE BLOCKS DESIGNS; PARTIALLY BALANCED INCOMPLETE BLOCKS DESIGNS; LATIN SQUARE / GRECO-LATIN SQUARE DESIGNS; FRACTIONAL FACTORIAL DESIGNS; MATCHED-PAIRS DESIGNS

LOCAL CONTROL

PURPOSE: INCREASE PRECISION AND POWER

METHODS: BLOCKING (E.G., RANDOMIZED BLOCKS); MATCHING PRIOR TO RANDOMIZED ASSIGNMENT (“MATCHED PAIRS” DESIGN)

TO REPEAT: FOR A DESIGNED EXPERIMENT, THE PURPOSE OF MATCHING IS TO INCREASE PRECISION AND POWER, NOT TO REDUCE BIAS CAUSED BY A LACK OF RANDOMIZATION

MATCHING IN EXPERIMENTAL DESIGN: TWO EXAMPLES

IN THE FOLLOWING, THE TERM “MEASURE” REFERS TO A POPULATION ATTRIBUTE (SUCH AS A MEAN), AND THE TERM “ESTIMATE” REFERS TO A SAMPLE STATISTIC.

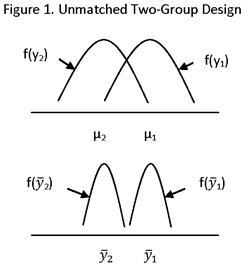
UNMATCHED TWO-GROUP DESIGN

MEASURE OF IMPACT: DIFFERENCE IN POPULATION MEANS, μ₁ – μ₂, WHERE SUBSCRIPT 1 DENOTES TREATMENT AND 2 DENOTES CONTROL.

ESTIMATE OF IMPACT: DIFFERENCE IN SAMPLE MEANS, , WHERE y DENOTES AN OUTCOME OF INTEREST.

WHERE

σ₁² = POPULATION VARIANCE FOR TREATMENT

σ₂² = POPULATION VARIANCE FOR CONTROL

n₁ = SAMPLE SIZE FOR TREATMENT

n₂ = SAMPLE SIZE FOR CONTROL.

MATCHED-PAIRS DESIGN

MATCHED PAIRS OF UNITS ARE FORMED SUCH THAT EACH MEMBER OF A PAIR IS SIMILAR TO THE OTHER MEMBER WITH RESPECT TO VARIABLES CONSIDERED TO HAVE A SUBSTANTIAL RELATIONSHIP TO ASSIGNMENT TO TREATMENT OR TO OUTCOMES OF INTEREST (I.E., OUTCOMES FOR WHICH ESTIMATES OF IMPACT ARE DESIRED). INDIVIDUAL UNITS MAY BE PAIRED (IF PRE-SURVEY DATA ARE AVAILABLE AT THE INDIVIDUAL LEVEL), OR GROUPS OF UNITS, SUCH AS PLOTS OF LAND OR VILLAGES, MAY BE PAIRED. MATCHING IS DONE AT THE LOWEST LEVEL OF AGGREGATION FOR WHICH PRE-SURVEY DATA ARE AVAILABLE FOR USE IN DESIGN.

(MATCHING IMPROVES PRECISION (VIA AN INCREASE IN "LOCAL CONTROL"). IT DOES NOT INTRODUCE A BIAS IN THE ESTIMATED MEANS SINCE AFTER MATCHING IT IS STILL THE CASE THAT THE MEANS ARE INDEPENDENT OF ALL OTHER VARIABLES (SINCE THEY ARE IDENTICAL FOR MATCHING UNITS, WITH RESPECT TO THE MATCH VARIABLES).)

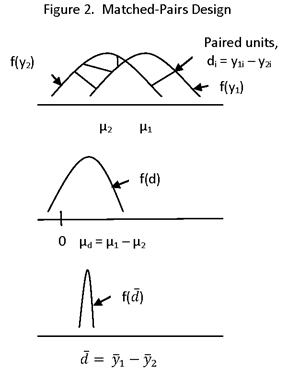
NOTE: WE ARE NOT MATCHING ON AN IMPRECISE PREMEASURE OF THE OUTCOME VARIABLE. SINCE THE PREMEASURE MAY BE CORRELATED WITH THE OUTCOME (I.E., THE DEPENDENT VARIABLE) THAT PROCEDURE WOULD INTRODUCE A REGRESSION-EFFECT BIAS. WE ARE MATCHING ON EXOGENOUS VARIABLES THAT AFFECT OUTCOMES OF INTEREST BUT ARE NOT AFFECTED BY THEM.

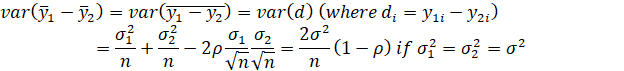
WHERE

ρ =INTRA-PAIR CORRELATION COEFFICIENT (I.E., THE CORRELATION BETWEEN UNITS WITHIN THE SAME PAIR).

(NOTE THAT SINCE THE OBSERVATIONS ARE PAIRED, n₁ = n₂ = n.)

IF THE INTRA-PAIR CORRELATION IS HIGH, THE USE OF MATCHED PAIRS PRODUCES A SUBSTANTIAL INCREASE IN PRECISION AND POWER FOR A SPECIFIED SAMPLE SIZE, OR ALLOWS A SUBSTANTIAL DECREASE IN SAMPLE SIZE FOR A GIVEN LEVEL OF PRECISION OR POWER.

NOTE THAT THE INTRA-PAIR CORRELATION IS NOT THE SAME AS THE INTRA-GROUP (WITHIN-GROUP) CORRELATION, WHERE “GROUP” REFERS TO THE TWO DESIGN GROUPS, TREATED AND UNTREATED. FOR EXAMPLE, IF THE UNITS IN EACH PAIR WERE IDENTICAL, THE INTRA-PAIR CORRELATION WOULD BE 1.0, BUT THE INTRA-GROUP CORRELATION COULD TAKE A WIDE RANGE OF VALUES (E.G., ZERO, IF THE GROUP CONSISTED OF A SIMPLE RANDOM SAMPLE FROM THE POPULATION). THE BETWEEN-GROUP (INTER-GROUP) CORRELATION IS THE SAME AS THE CORRELATION BETWEEN THE MEANS OF THE TREATED AND UNTREATED UNITS.

NOTE ALSO THAT THE INTRA-PAIR CORRELATION IS UNRELATED TO THE INTER-GROUP CORRELATION. FOR EXAMPLE, THE GROUPS COULD BE IDENTICAL, BUT RANDOMLY MATCHED, IN WHICH CASE THE INTER-GROUP CORRELATION IS 1.0 BUT THE INTRA-PAIR CORRELATION IS ZERO; OR THE GROUPS COULD BE IDENTICAL AND PERFECTLY MATCHED, IN WHICH CASE BOTH THE INTER-GROUP AND INTRA-PAIR CORRELATIONS ARE 1.0.

MATCHING IS DONE AT THE LOWEST LEVEL FOR WHICH DATA ARE AVAILABLE PRIOR TO THE SURVEY, FOR USE IN DESIGN. MATCHING AT THE LOWEST LEVEL OF SAMPLING (THE ULTIMATE SAMPLE UNIT, OR “ELEMENT”) IS CALLED A “MATCHED PAIRS” DESIGN. MATCHING AT HIGHER LEVELS IS CALLED “MATCHED BLOCKS” OR SIMPLY A “MATCHED DESIGN.”

NOTE THAT IN AN ED, MATCHING IS USED ONLY TO INCREASE PRECISION AND POWER, NOT TO REDUCE BIAS. FOR EDs, BIAS REDUCTION IS ADDRESSED BY RANDOMIZATION, NOT BY MATCHING.

4. MATCHING IN QUASI-EXPERIMENTAL DESIGNS

4.1. GENERAL CONSIDERATIONS

WE SHALL NOW PRESENT SOME GENERAL BACKGROUND ON QUASI-EXPERIMENTAL DESIGNS. REFERENCES ON THIS TOPIC INCLUDE THE FOLLOWING:

1. CAMPBELL, DONALD T. AND JULIAN C. STANLEY, EXPERIMENTAL AND QUASI-EXPERIMENTAL DESIGNS FOR RESEARCH, AMERICAN EDUCATIONAL RESEARCH ASSOCIATION, 1963

2. COOK, THOMAS D. AND DONALD T. CAMPBELL, QUASI-EXPERIMENTATION: DESIGN AND ANALYSIS ISSUES FOR FIELD SETTINGS, HOUGHTON MIFFLIN COMPANY, 1979

3. SHADISH, WILLIAM R., THOMAS D. COOK AND DONALD T. CAMPBELL, EXPERIMENTAL AND QUASI-EXPERIMENTAL DESIGNS FOR GENERALIZED CAUSAL INFERENCE, WADSWORTH CENGAGE LEARNING, 2002

4. ROSENBAUM, PAUL R., OBSERVATIONAL STUDIES 2^ND EDITION, SPRINGER, 2002 (1^ST ED. 1995)

AS MENTIONED EARLIER, AN EXPERIMENT IS A STUDY IN WHICH THE ASSIGNMENT OF TREATMENT LEVELS TO SUBJECTS IS CONTROLLED BY THE EXPERIMENTER. AN OBSERVATIONAL STUDY IS A STUDY IN WHICH THIS CONTROL IS LACKING. A DESIGNED EXPERIMENT (DE) IS A PLANNED EXPERIMENT THAT POSSESSES FEATURES (SUCH AS RANDOMIZATION AND SYMMETRY) THAT SUPPORT OBTAINING GOOD ESTIMATES FROM THE DATA. (“GOOD” REFERS TO DESIRABLE ESTIMATOR PROPERTIES SUCH AS HIGH PRECISION, LOW BIAS AND CONSISTENCY.)

A QUASI-EXPERIMENTAL DESIGN (QED) MAY BE DEFINED IN TWO DIFFERENT WAYS, NOT EQUIVALENT. ON THE ONE HAND, A QUASI-EXPERIMENTAL DESIGN MAY BE DEFINED AS AN OBSERVATIONAL STUDY THAT POSSESSES SOME OF THE APPARENT FEATURES (STRUCTURE) OF AN EXPERIMENTAL DESIGN (SUCH AS SYMMETRY AND BALANCE (E.G., USING COMPARISON GROUPS, MATCHING, AND ORTHOGONAL EXPLANATORY VARIABLES)), BUT RANDOMIZATION IS NOT USED TO SELECT EXPERIMENTAL UNITS AND TO ASSIGN TREATMENT LEVELS TO EXPERIMENTAL UNITS (OR SOME ASPECT OF RANDOMIZATION IS LACKING, SUCH AS KNOWLEDGE OF THE PROBABILITY MODEL DESCRIBING THE RANDOMIZATION PROCESS). THIS DEFINITION WOULD APPLY TO THE MANY QEDs DISCUSSED BY CAMPBELL AND COOK (OP. CIT.), SUCH AS THE NON-EQUIVALENT CONTROL GROUP DESIGN OR THE INTERRUPTED TIME SERIES DESIGN.

ON THE OTHER HAND, A QED MAY BE DEFINED AS AN OBSERVATIONAL DATA SET FOR WHICH STEPS HAVE BEEN TAKEN TO COMPENSATE FOR THE LACK OF RANDOMIZATION, BY MODELING OR BY THE INTRODUCTION OF MATCHING IN THE DESIGN OR ANALYSIS. EXAMPLES OF THIS ARE THE ROSENBAUM-RUBIN AND HECKMAN IMPLEMENTATIONS OF THE NEYMAN-RUBIN CAUSAL MODEL.

IN THIS PRESENTATION, WE SHALL USE MAINLY THE LATTER DEFINITION. ANALYSIS OF OBSERVATIONAL DATA WILL ALWAYS INVOLVE A MODEL OF THE PROBABILISTIC STRUCTURE AND CAUSAL STRUCTURE OF THE DATA, AND THE ESTIMATES OF QUANTITIES OF INTEREST WILL BE BASED ON THIS MODEL. (SOME STATISTICIANS PREFER TO RESTRICT CONSIDERATION TO THE DATA SET AT HAND, WITHOUT REFERENCE TO EXTERNAL OR “PRIOR” INFORMATION, SUCH AS IS DONE IN A BAYESIAN APPROACH. THAT “DATA-CENTRIC” APPROACH WORKS FINE FOR ASSOCIATIONAL ANALYSIS, BUT NOT AT ALL FOR CAUSAL ANALYSIS. IT IS IMPOSSIBLE TO MAKE CREDIBLE CAUSAL ESTIMATES WITHOUT SPECIFICATION OF A CAUSAL MODEL ASSOCIATED WITH THE DATA SET. CAUSAL RELATIONSHIPS CANNOT BE INFERRED FROM DATA ALONE, OR FROM PROBABILITY DISTRIBUTIONS ALONE.)

THE ISSUE OF CONTROLLED MANIPULATION (FORCED CHANGE)

THE ESSENTIAL DIFFERENCE BETWEEN AN EXPERIMENT AND AN OBSERVATIONAL STUDY IS THAT IN AN EXPERIMENT, CONTROLLED MANIPULATIONS (OR RANDOM SELECTION AND ASSIGNMENT TO TREATMENT) ARE MADE IN EXPLANATORY VARIABLES.

IN DESIGNED EXPERIMENTS, CONTROLLED MANIPULATIONS (FORCED CHANGES) ARE MADE. THE REASON FOR USING THIS APPROACH IS THAT IF ASSIGNMENT TO TREATMENT (OR TREATMENT LEVEL) IS DONE USING RANDOMIZATION, THE DISTRIBUTION OF ALL OTHER VARIABLES IS THE SAME FOR THE TREATMENT AND CONTROL GROUPS, IN WHICH CASE IT IS POSSIBLE TO OBTAIN UNBIASED ESTIMATES OF THE EFFECT OF TREATMENT (WITH RESPECT TO THE SETTING OF THE EXPERIMENT).

AS DISCUSSED EARLIER, IN A DESIGNED EXPERIMENT THE TREATMENT VARIABLES MAY BE ORTHOGONALIZED AND RANDOMLY ASSIGNED, IN WHICH CASE THE CORRELATIONS AMONG THE TREATMENT VARIABLES ARE ZERO, AND THE EFFECTS ARE UNCONFOUNDED. IF EXPLANATORY VARIABLES ARE RANDOMLY SELECTED BUT NOT ACTIVELY SET (E.G., RACE), THEN THEY MAY BE CORRELATED WITH OTHER EXPLANATORY VARIABLES AND IT MAY NOT BE POSSIBLE TO OBTAIN AN UNCONFOUNDED ESTIMATES OF MULTIPLE EFFECTS.

IN THE PRECEDING, WE HAVE FREQUENTLY REFERRED TO FORCED CHANGES AND TO RANDOMIZATION. BOTH OF THESE ARE IMPORTANT IN DESIGNED EXPERIMENTS, AND EITHER OF THEM MAY OCCUR IN OBSERVATIONAL STUDIES. ALTHOUGH THERE IS A CLOSE RELATIONSHIP BETWEEN THE USE OF FORCED CHANGES AND RANDOMIZATION, THERE IS AN IMPORTANT DISTINCTION. RANDOMIZATION MAY BE USED WITH OR WITHOUT FORCED CHANGES. FOR EXAMPLE, RANDOMIZATION MAY BE USED TO SELECT EXPERIMENTAL UNITS FROM A POPULATION, PRIOR TO ASSIGNMENT TO TREATMENT. HERE, IN THE SELECTION OF THE UNITS FROM THE POPULATION, THERE IS NO FORCED CHANGE INVOLVED. IN THE RANDOMIZED ASSIGNMENT TO TREATMENT, HOWEVER, FORCED CHANGE IS INVOLVED. THE USE OF RANDOMIZED FORCED CHANGES IS VERY USEFUL BECAUSE IT AFFORDS A WAY OF ASSURING THAT CERTAIN VARIABLES ARE INDEPENDENT OF OTHER VARIABLES. EVEN WITHOUT THE USE OF RANDOMIZATION, HOWEVER, THE USE OF FORCED CHANGES IS USEFUL BECAUSE IT IS POSSIBLE THAT WHEN FORCED CHANGES ARE MADE IN CERTAIN VARIABLES, THE WAY THAT OTHER VARIABLES VARY MAY NOT BE THE SAME AS FOR A SYSTEM UNDER PASSIVE OBSERVATION, AND IT IS IMPORTANT TO KNOW THIS. THIS IS THE ISSUE OF "STABILITY" (OR "FAITHFULNESS," "INVARIANCE" OR "MODULARITY") OF PROBABILISTIC RELATIONSHIPS IN A CAUSAL MODEL IN WHICH CHANGES ARE ASSUMED (SUCH AS HOLDING CERTAIN VARIABLES FIXED WHILE OTHERS ARE ALLOWED TO VARY). MORE WILL BE SAID ABOUT THIS LATER.

A QUASI-EXPERIMENTAL DESIGN (IN THE CONTEXT OF THIS PRESENTATION) IS AN ANALYTICAL FRAMEWORK FOR ANALYSIS OF OBSERVATIONAL DATA. FOR OBSERVATIONAL DATA, CONTROLLED MANIPULATION OR RANDOM SELECTION MAY OR MAY NOT HAVE BEEN MADE IN EXPLANATORY VARIABLES. AN EXPERIMENTAL DESIGN IS BASED ON A RANDOMIZATION PROCESS FOR WHICH THE PROBABILITY MODEL IS KNOWN, AND FOR A QED, RANDOMIZATION IS MISSING OR THE PROBABILITY MODEL IS UNKNOWN, AND, TO MAKE USE OF STATISTICAL ANALYSIS, IT MUST BE ASSUMED OR ESTIMATED. THE TERM “RANDOMIZATION PROCESS” REFERS TO PROBABILITY SELECTION OF EXPERIMENTAL UNITS FROM A WELL-DEFINED POPULATION AND TO ASSIGNMENT OF TREATMENT LEVELS TO THE SAMPLE UNITS USING PROBABILITY SAMPLING.

USE OF RANDOMIZED ASSIGNMENT OF TREATMENT MAY BE INFEASIBLE FOR A NUMBER OF REASONS:

PHYSICALLY IMPOSSIBLE

ETHICAL REASONS

LEGAL REASONS

SELF-SELECTION

NONCOMPLIANCE.

THROUGH THE USE OF MODELING AND ANALYSIS, IT IS POSSIBLE TO OVERCOME A LACK OF RANDOMIZATION AND LACK OF FORCED CHANGES IN A DATA SET, AND CONDUCT USEFUL CAUSAL ANALYSIS USING THE METHODS OF PROBABILITY AND STATISTICS. THE INFERENCES MADE IN THIS CONTEXT WILL NOT BE AS STRONG AS THOSE MADE USING DESIGNED EXPERIMENTS, BUT THEY CAN BE USEFUL AND VALID, SUBJECT TO CERTAIN ASSUMPTIONS (SUCH AS THE STABILITY OF THE CAUSAL MODEL).

ASSOCIATIONAL INFERENCE VS. CAUSAL INFERENCE

FROM THE SAME DATA SET, IT IS POSSIBLE TO MAKE BOTH ASSOCIATIONAL INFERENCES AND CAUSAL INFERENCES. ASSOCIATIONAL INFERENCES ARE SIMPLY DESCRIPTIVE. THEY MAY BE MADE BASED ON THE SAMPLE DESIGN OR EXPERIMENTAL DESIGN ALONE, WITH NO CONSIDERATION OF A CAUSAL MODEL (OR A SELECTION METHOD). CAUSAL INFERENCES INVOLVE ASSUMPTIONS ABOUT A CAUSAL MODEL, SAMPLE DESIGN, AND DATA (TO ESTIMATE MODEL CHARACTERISTICS AND CAUSAL EFFECTS).

THE DEFINITION OF "CAUSAL EFFECT"

SOME RESEARCHERS (E.G., RUBIN AND HOLLAND) ASSERT THAT CAUSAL INFERENCES MAY NOT BE MADE FOR VARIABLES THAT CANNOT BE PHYSICALLY MANIPULATED (SUCH AS SEX AND RACE). RUBIN CHARACTERIZES THIS VIEW AS “NO CAUSATION WITHOUT MANIPULATION.” IN THIS CASE ONLY ASSOCIATIVE (DESCRIPTIVE) INFERENCES MAY BE MADE. OTHER RESEARCHERS DO NOT AGREE WITH THIS VIEWPOINT – IN THE EXAMPLE JUST GIVEN THEY WOULD DEEM IT APPROPRIATE TO REFER TO A CAUSAL EFFECT OF SEX OR RACE. AS DISCUSSED EARLIER, CAUSAL INFERENCES MAY BE MADE IN THE ABSENCE OF MANIPULATION, GIVEN A CAUSAL MODEL (SUCH AS JUDEA PEARL'S). (THE ARTICLE BY HOLLAND ("STATISTICS AND CAUSAL INFERENCE," OP. CIT.) WHICH INCLUDES THE ASSERTION ABOUT "NO CAUSATION WITHOUT MANIPULATION" NOTES SPECIFICALLY (SEC. 4.5, P. 949) THAT THE DISCUSSION RELATES TO EXPERIMENTAL DATA, NOT TO OBSERVATIONAL DATA ("NONRANDOMIZED STUDIES".)

IN THIS PRESENTATION WE SHALL ALLOW USE OF THE TERM “CAUSAL EFFECT” TO REFER EITHER TO SITUATIONS IN WHICH FORCED CHANGES CAN BE MADE IN AN EXPLANATORY VARIABLE (E.G., TREATMENT) OR WHEN THE EXPLANATORY VARIABLE IS SELECTED BY RANDOM SAMPLING (E.G., RACE OR SEX). IT IS AGREED, HOWEVER, THAT ONLY THE FORMER SITUATION (FORCED CHANGES) CORRESPONDS TO THE PHYSICAL CONCEPT OF CAUSE AND EFFECT, AND THAT THE LATTER IS MERELY AN ASSOCIATION. IN BOTH CASES, THE ESTIMATED CAUSAL EFFECT WILL HAVE THE SAME VALUE. AS LONG AS ONE CLEARLY SPECIFIES THE SELECTION METHOD, AND ACCEPTS THAT THE SCOPE OF INFERENCE OF THE ANALYSIS RESULTS DEPENDS ON THE SELECTION METHOD, NO CONFUSION EXISTS RELATIVE TO THIS ISSUE.

THE ISSUE OF FORCED CHANGE

AN ESSENTIAL CONSIDERATION IN CAUSAL INFERENCE IS THAT CAUSAL INFERENCES APPLY TO THE SETTING FROM WHICH THE DATA WERE OBTAINED (I.E., TO THE SELECTION METHOD, FORCED CHANGE OR PASSIVE OBSERVATION). IF THE SETTING IS AN EXPERIMENT WITH FORCED CHANGES IN CERTAIN EXPLANATORY VARIABLES, THEN THE CAUSAL INFERENCES REFER TO THAT SETTING (AND MAY BE USED TO PREDICT OUTCOMES OF FUTURE SIMILAR EXPERIMENTS). IF THE SETTING IS OBSERVATIONAL (PASSIVELY OBSERVED DATA), THEN THE CAUSAL INFERENCES REFER TO THAT SETTING (AND MAY BE USED TO PREDICT OUTCOMES OF FUTURE SIMILAR SETTINGS). IN BOTH CASES, THEY ARE CAUSAL INFERENCES (BASED ON DIFFERENT CAUSAL MODELS WITH DIFFERENT ASSUMPTIONS), BUT THE SCOPE OF INFERENCE, OR EXTERNAL VALIDITY, IS QUITE DIFFERENT.

CAUSAL INFERENCE WHEN FORCED CHANGES CANNOT BE MADE

WITH RESPECT TO MAKING PREDICTIONS BASED ON ESTIMATES OBTAINED FROM A MODEL, THE NATURE OF THE PREDICTIONS THAT ARE APPROPRIATE IS DETERMINED BY THE NATURE OF THE DATA. IF THERE IS NO ACTIVE MANIPULATION INVOLVED IN THE ASSIGNMENT OF TREATMENT LEVELS, ALL THAT CAN BE DONE IS TO ESTIMATE CAUSAL EFFECTS FROM OBSERVED ASSOCIATIONS IN PASSIVELY OBSERVED DATA. FOR EXAMPLE, UNITS MAY BE SELECTED FROM A POPULATION BY RACE, BUT RACE CANNOT BE ASSIGNED (BARRING GENETIC ENGINEERING). HENCE, WITH RESPECT TO RACE, CAUSAL INFERENCES MUST BE BASED ON ESTIMATION OF ASSOCIATIONS. THE ESTIMATED EFFECT IS THE EFFECT ASSOCIATED WITH SELECTING A PERSON OF A SPECIFIED RACE, NOT THE EFFECT OF “CHANGING” RACE ON OTHER VARIABLES. THE CAUSAL ESTIMATES MAY ADJUST FOR THE FACT THAT THE TREATMENT DISTRIBUTION DEPENDS ON OTHER MODEL VARIABLES, BUT THERE IS NO WAY IT CAN ADJUST FOR THE FACT THAT THE OBSERVED VARIATION IS PASSIVELY OBSERVED AND NOT FORCIBLY MANIPULATED.

CAUSAL INFERENCE WHEN FORCED CHANGES CAN BE MADE, BUT WERE NOT

IN SOME SITUATIONS, OBSERVATIONAL DATA ARE AVAILABLE FOR VARIABLES FOR WHICH FORCED CHANGES COULD HAVE BEEN MADE, BUT WERE NOT. IF IT IS DESIRED TO MAKE ASSERTIONS ABOUT THE EFFECTS OF FORCED CHANGES IN THIS SITUATION, IT IS NECESSARY TO MAKE ASSUMPTIONS ABOUT THE STABILITY OF THE CAUSAL MODEL (I.E., THAT THE PROBABILISTIC ASSOCIATIONS REMAIN THE SAME IF FORCED CHANGES ARE MADE AS FOR THE PASSIVELY OBSERVED SYSTEM). MORE WILL BE SAID ABOUT THIS LATER.

THE NATURE OF THE DATA DETERMINES THE SCOPE OF INFERENCE

AS G. E. P. BOX ASSERTED, THE USE TO WHICH ESTIMATES ARE PUT DEPENDS ON THE NATURE OF THE DATA OR, MORE SPECIFICALLY, ON THE NATURE OF THE SELECTION METHOD. IF ESTIMATES ARE BASED ON A MODEL IN WHICH FORCED CHANGES ARE MADE IN EXPLANATORY VARIABLES (E.G., A PROGRAM INTERVENTION), THEN THOSE ESTIMATES MAY BE REPRESENTED AS PREDICTIONS OF THE EFFECTS TO BE OBSERVED IF FORCED CHANGES ARE MADE IN THOSE VARIABLES. IF ESTIMATES ARE BASED ON A MODEL IN WHICH THE EXPLANATORY VARIABLES ARE SELECTED (E.G., RACE CANNOT BE FORCIBLY CHANGED BUT ONLY PASSIVELY OBSERVED; RACE IS "SELECTED," NOT "ASSIGNED": INDIVIDUALS OF A PARTICULAR RACE ARE RANDOMLY SELECTED FROM THAT SUBPOPULATION), THEN THE ESTIMATES MAY BE REPRESENTED AS PREDICTIONS OF THE EFFECT TO BE OBSERVED IF THE VARIABLE IS SELECTED. IN BOTH CASES, THE ESTIMATES ARE “CAUSAL ESTIMATES” (AND WOULD BE EQUAL IN MAGNITUDE) BUT THE SCOPE OF INFERENCE DIFFERS.

THE FORMULAS USED TO ESTIMATE CAUSAL EFFECTS (TO BE PRESENTED LATER) ADJUST FOR THE FACT THAT TREATMENT IS NOT RANDOMLY ASSIGNED. THESE ESTIMATES, HOWEVER, ARE EXACTLY THE SAME WHETHER THE CAUSAL VARIABLE IS ONE FOR WHICH FORCED CHANGES MIGHT HAVE BEEN MADE (E.G., TREATMENT) AS FOR ONE, SUCH AS RACE, FOR WHICH FORCED CHANGES CANNOT BE MADE. ALTHOUGH THE COMPUTATIONS ARE THE SAME IN THESE TWO CASES, THE CONCEPTUAL FRAMEWORK IS QUITE DIFFERENT.

AS DISCUSSED EARLIER, A CAUSAL EFFECT IS OFTEN DESCRIBED AS THE AVERAGE EFFECT OF A TREATMENT ON AN INDIVIDUAL WHO IS RANDOMLY SELECTED FROM THE POPULATION. AS MENTIONED, THIS IS NOT A VERY SATISFYING DEFINITION, SINCE IT IS BASED ON A PROCESS THAT MAY BE PHYSICALLY IMPOSSIBLE TO IMPLEMENT. IN THE ARTICLE, “THE CENTRAL ROLE OF THE PROPENSITY SCORE IN OBSERVATIONAL STUDIES FOR CAUSAL EFFECTS,” (OP. CIT.) ROSENBAUM AND RUBIN DESCRIBE A "REALIZABLE" CONCEPTUAL PROCEDURE FOR ESTIMATING A CAUSAL EFFECT FROM OBSERVATIONAL DATA (PARAPHRASED):

"Suppose a specific value of the vector of covariates x is randomly sampled from the entire population of units, that is, both treated and control units together, and then a treatment unit and a control unit are found both having this value for the vector of covariates. In this two-step sampling process, the expected difference in response is

E_x{E(r₁|x,z=1) – E(r₀|x,z=0)},

where E_x denotes expectation with respect to the distribution of x in the entire population of units. If treatment (z) and response (r₁, r₀) are conditionally independent given x, then the preceding expression equals

E_x{E(r₁|x) – E(r₀|x)},

which is the average treatment effect, E(r₁) – E(r₀)."

AT THIS POINT OF THE PRESENTATION, DO NOT BE CONCERNED WITH THE TECHNICAL DETAILS OF THE PRECEDING EXCERPT. THE SIGNIFICANT POINT IS THAT THE AVERAGE TREATMENT EFFECT MAY BE DEFINED IN TERMS OF SAMPLING FROM THE POPULATION, NOT IN TERMS OF ASSIGNING TREATMENT TO A RANDOMLY SELECTED INDIVIDUAL.

SOME AUTHORS REPRESENT THE ESTIMATE OBTAINED FROM THIS PROCEDURE TO BE THE CAUSAL EFFECT OF "SETTING" THE VALUES OF THE TREATMENT VARIABLE AT 0 AND 1 AND TAKING THE DIFFERENCE IN MEANS. THIS IS NOT AT ALL WHAT ROSENBAUM AND RUBIN HAVE DONE. IT SHOULD BE RECOGNIZED THAT REPRESENTING THE CAUSAL EFFECT THIS WAY REQUIRES A VERY STRONG ASSUMPTION, VIZ., THAT OF STABILITY – THAT THE PROBABILITY DISTRIBUTIONS OF THE MODEL VARIABLES REMAIN THE SAME WHETHER THE UNITS ARE PASSIVELY OBSERVED OR FORCIBLY CHANGED. THE CAUSAL EFFECT IS THE SAME WHETHER THE ASSUMPTION OF STABILITY IS MADE OR NOT. THIS ASSUMPTION IS REQUIRED ONLY IF IT IS DESIRED TO REPRESENT THAT THE ESTIMATED CAUSAL EFFECT IS WHAT WOULD RESULT IF TREATMENT WERE FORCIBLY IMPOSED (E.G., ON A RANDOMLY SELECTED INDIVIDUAL). IT IS EMPHASIZED THAT THIS ASSUMPTION IS OPTIONAL. THE ESTIMATED CAUSAL EFFECT IS THE SAME WITH OR WITHOUT THIS ASSUMPTION. WHAT DIFFERS IS THE SCOPE OF INFERENCE: WHETHER THE CAUSAL EFFECT IS VIEWED AS THE RESULT OF SAMPLING (AS R&R DESCRIBE) OR AS THE RESULT OF "SETTING" A CAUSAL VARIABLE (I.E., RANDOMLY ASSIGNING TREATMENT TO A RANDOMLY SELECTED INDIVIDUAL).

THE ROLE OF PROBABILITY SAMPLING

IN ORDER TO APPLY STATISTICAL THEORY TO ANALYSIS OF DATA (WHETHER ASSOCIATIVE OR CAUSAL), IT IS NECESSARY TO USE PROBABILITY SAMPLING, I.E., TO SELECT A SAMPLE OF DATA FROM A POPULATION USING KNOWN PROBABILITIES (OR CONSTANT PROBABILITIES). ALSO, TO ESTIMATE THE EFFECT OF A TREATMENT IT IS NECESSARY TO KNOW, OR BE ABLE TO ESTIMATE, THE PROBABILITY OF ASSIGNMENT TO TREATMENT.

IN GENERAL, THE TERMS “SELECTION FOR TREATMENT” OR “ASSIGNMENT TO TREATMENT” MEAN ASSIGNMENT OF A SAMPLE UNIT TO TREATMENT WITH A KNOWN PROBABILITY AFTER THE UNIT HAS BEEN SELECTED FROM THE POPULATION OF INTEREST WITH A KNOWN PROBABILITY (OR PROBABILITY DENSITY), OR THE UNIT IS SELECTED AT RANDOM (USING PROBABILITY SAMPLING) FROM THE POPULATION AFTER IT IS DECIDED WHICH TREATMENT LEVEL IS TO BE ASSIGNED TO IT. (AS DISCUSSED EARLIER, THE RANDOMIZATION PROCESS MAY BE DONE IN ANY WAY SUCH THAT THE JOINT PROBABILITY DISTRIBUTION OF THE OBSERVATIONS IS KNOWN.)

IN SOME APPLICATIONS, UNITS ARE SELECTED DIRECTLY FROM THE POPULATION AND ASSIGNED TO TREATMENT, WITHOUT IDENTIFYING THE PROBABILITY OF SELECTION (OR PROBABILITY DENSITY OF SELECTION) OF THE UNIT FROM THE GENERAL POPULATION. WHEN THIS IS DONE, AND THE PROBABILITIES OF SELECTION OF UNITS FROM THE POPULATION ARE NOT KNOWN (OR KNOWN TO BE CONSTANT WITHIN DESIGN STRATA), IT IS NOT POSSIBLE TO PRODUCE “DESIGN-BASED” ESTIMATES OF QUANTITIES (SINCE THE DESIGN SELECTION PROBABILITIES ARE NOT KNOWN). IN THIS CASE, ALL ESTIMATES ARE “MODEL-BASED” ESTIMATES. THE EXPRESSION “PROBABILITY OF ASSIGNMENT TO TREATMENT” DOES NOT REFER TO THE PROBABILITY OF SELECTING (SUBSAMPLING) A TREATED UNIT FROM A POOL OF ALREADY-TREATED UNITS – IT REFERS TO THE PROBABILITY OF ASSIGNMENT TO TREATMENT FOR A RANDOMLY SELECTED UNIT FROM A NEVER-TREATED POPULATION.

IF THE LACK OF RANDOMIZATION IS THAT EXPERIMENTAL UNITS ARE NOT SELECTED USING PROBABILITY SAMPLING FROM A WELL-DEFINED POPULATION OF INTEREST, THERE IS LITTLE THAT USE OF A QED OR MATCHING CAN DO TO ADDRESS THIS ISSUE FROM THE PERSPECTIVE OF CONSTRUCTING UNBIASED DESIGN-BASED ESTIMATES. THE INFERENCES WILL PERTAIN TO THE SELECTED SAMPLE, AND WILL BE VALID TO THE EXTENT THAT THE SAMPLE IS REPRESENTATIVE OF THE POPULATION OF INTEREST. IF PROBABILITY SAMPLING IS NOT USED TO SELECT THE SAMPLE, THEN MODEL-BASED ESTIMATES MUST BE USED TO MAKE STATISTICAL INFERENCES ABOUT THE ESTIMATES AND A HYPOTHETICAL PROCESS THAT IS CONCEIVED TO HAVE GENERATED THE POPULATION. FOR MODEL-BASED ESTIMATION, IT IS DESIRABLE TO HAVE SUBSTANTIAL VARIATION IN CAUSAL VARIABLES OF INTEREST (OR SURROGATES FOR THEM), AND HAVE LOW CORRELATION AMONG THEM (TO REDUCE CONFOUNDING OF EFFECTS).

(THIS PRESENTATION DEALS MAINLY WITH MODEL-BASED ESTIMATES. DESIGN-BASED ESTIMATES ARE USED MAINLY IN DESCRIPTIVE SURVEYS, WHERE THE OBJECTIVE IS TO ESTIMATE FEATURES OF A FIXED, FINITE POPULATION (AND THE ESTIMATES OF INTEREST ARE ASSOCIATIONAL, NOT CAUSAL). MODEL-BASED ESTIMATES ARE USED IN ANALYTICAL SURVEYS, WHERE IT IS DESIRED TO DESCRIBE CAUSAL RELATIONSHIPS AMONG VARIABLES, SUCH AS THE RELATIONSHIP OF OUTCOME TO TREATMENT. THE TERMINOLOGY IS MISLEADING, SINCE BOTH TYPES OF ESTIMATES ARE IN FACT BASED ON MODELS – FOR DESIGN-BASED ESTIMATES THE MODEL (A “SAMPLE SELECTION” MODEL) DESCRIBES THE PROBABILITY DISTRIBUTION OF THE SAMPLE SELECTION INDICATOR VARIABLE. FOR MODEL-BASED ESTIMATES THE MODEL (A “PROCESS MODEL”) DESCRIBES THE PROBABILITY DISTRIBUTION OF AN OUTCOME VARIABLE IN TERMS OF A RANDOM PROCESS THAT GENERATES OBSERVED UNITS, WHERE THE RANDOM PROCESS DEPENDS ON SPECIFIED CHARACTERISTICS OF THE UNITS. (THE TERM “MODEL-BASED” OFTEN REFERS TO A CAUSAL MODEL, BUT NOT NECESSARILY.)

(THE WAY THAT COVARIATES ARE HANDLED DIFFERS IN THE TWO APPROACHES. FOR DESIGN-BASED ESTIMATES, THE COVARIATES ARE SIMPLY ADDITIONAL CHARACTERISTICS OF THE SAMPLE UNIT, WITHOUT RESTRICTION (I.E., CONSIDERATION OF THEIR STATISTICAL PROPERTIES). FOR MODEL-BASED ESTIMATES, THE COVARIATES ARE MODEL VARIABLES (EITHER FIXED NUMBERS OR RANDOM VARIABLES, AND THEY MAY BE ADDED TO OR DELETED FROM A MODEL ONLY IF IT REMAINS CORRECTLY SPECIFIED, IF THE OBJECTIVE IS TO ESTIMATE INDIVIDUAL MODEL PARAMETERS). FOR MORE DISCUSSION OF THIS POINT, SEE MODEL ASSISTED SURVEY SAMPLING BY CARL-ERIK SÄRNDAL, BENGT SWENSSON AND JAN WRETMAN (SPRINGER, 1992); PRACTICAL TOOLS FOR DESIGNING AND WEIGHTING SURVEY SAMPLES BY RICHARD VALLIANT, JILL A. DEVER, AND FRAUKE KREUTER (SPRINGER, 2013); SMALL AREA ESTIMATION BY J. N. K. RAO (WILEY, 2003); AND “HISTORY AND DEVELOPMENT OF THE THEORETICAL FOUNDATIONS OF SURVEY BASED ESTIMATION AND ANALYSIS” BY J. N. K. RAO AND D. R. BELLHOUSE, SURVEY METHODOLOGY, JUNE 1990, VOL. 16, NO. 1, PP. 3-29, STATISTICS CANADA.)

ESTIMABILITY, IDENTIFIABILITY, AND CONFOUNDEDNESS

THREE CONCEPTS THAT ARE MUCH USED IN CAUSAL ANALYSIS AND MODEL BUILDING ARE ESTIMABILITY, IDENTIFIABILITY AND CONFOUNDEDNESS. THESE AND RELATED TERMS WILL NOW BE DEFINED AND DISCUSSED.

AN ESTIMABLE PARAMETER (OR STATISTICAL FUNCTIONAL) IS A MEASURABLE FUNCTION OF THE POPULATION’S CUMULATIVE PROBABILITY DISTRIBUTION, SUCH AS A MEAN, MEDIAN, OR VARIANCE. (IN THIS CONTEXT, A MEASURABLE FUNCTION IS ONE ABOUT WHICH PROBABILITY STATEMENTS MAY BE MADE.)

LET θ DENOTE A PARAMETER OF A DISTRIBUTION (I.E., A CONSTANT ON WHICH THE DISTRIBUTION DEPENDS), AND LET g(θ) DENOTE A REAL-VALUED FUNCTION OF θ. IF THERE EXISTS AN UNBIASED ESTIMATOR, δ(X), OF g, THEN g IS SAID TO BE U-ESTIMABLE (“U” FOR UNBIASED). IN THIS PRESENTATION, WE SHALL BE CONCERNED WITH U-ESTIMABILITY. FOR EASE OF PRESENTATION, WE SHALL USE THE TERM “ESTIMABLE” FOR “U-ESTIMABLE” (AS IS OFTEN (USUALLY) DONE).

IN SIMPLE STATISTICAL PROBLEMS, THE GOAL IS TO ESTIMATE A FEW SIMPLE CHARACTERISTICS OF A DISTRIBUTION, SUCH AS THE MEAN OR VARIANCE. IN MORE COMPLEX PROBLEMS, THE JOINT PROBABILITY DISTRIBUTION (LIKELIHOOD FUNCTION) OF THE DATA SAMPLE IS DEFINED IMPLICITLY BY MEANS OF A MODEL, SUCH AS A SET OF LINEAR EQUATIONS. FOR COMPLEX MODELS, IT MAY NOT BE IMMEDIATELY CLEAR WHETHER ALL OF THE MODEL PARAMETERS ARE ESTIMABLE. A SITUATION THAT COMMONLY ARISES IS WHEN THERE ARE MULTIPLE VALUES OF A PARAMETER THAT CORRESPOND TO THE SAME DISTRIBUTION (E.G., WHEN THE CROSS-PRODUCTS MATRIX IN A REGRESSION MODEL IS NOT OF FULL RANK). THE MULTIPLE PARAMETER VALUES THAT CORRESPOND TO THE SAME DISTRIBUTION ARE SAID TO BE “OBSERVATIONALLY EQUIVALENT.” IN THIS CASE THE MODEL IS IDENTIFIABLE UNDER CERTAIN CONDITIONS (OR “RESTRICTIONS” OR “EXCLUSION RESTRICTIONS”).

A PARAMETRIC MODEL IS SAID TO BE IDENTIFIABLE IF THERE IS A ONE-TO-ONE CORRESPONDENCE BETWEEN THE PROBABILITY DISTRIBUTION ASSOCIATED WITH THE MODEL AND THE MODEL PARAMETERS. THAT IS, DISTINCT VALUES OF THE MODEL PARAMETERS CORRESPOND TO DISTINCT PROBABILITY DISTRIBUTIONS. A MODEL IS IDENTIFIABLE IF IT IS THEORETICALLY POSSIBLE TO DETERMINE THE TRUE VALUE OF A MODEL’S PARAMETERS WITH AN INFINITE NUMBER OF OBSERVATIONS. IF A MODEL IS SPECIFIED BY A SET OF EQUATIONS, THE MODEL IS IDENTIFIABLE IF THE EQUATIONS HAVE A UNIQUE SOLUTION WHEN THE VARIANCES OF THE RANDOM VARIABLES ASSOCIATED WITH THE MODEL ARE SET TO ZERO.

A COMMON PROBLEM IN STATISTICS IS TO DETERMINE CONDITIONS UNDER WHICH A MODEL IS IDENTIFIABLE. MANY MODELS IN ECONOMETRICS AND CAUSAL MODELING ARE LINEAR STATISTICAL MODELS, DEFINED BY A SET OF LINEAR EQUATIONS AND A COVARIANCE MATRIX FOR THE MODEL DISTURBANCES. IN SUCH CASES, REQUIREMENTS FOR IDENTIFIABILITY ARE USUALLY STATED IN TERMS OF CONDITIONS ON THE COEFFICIENTS OF THE SYSTEM OF LINEAR EQUATIONS DEFINING THE MODEL (“COEFFICIENT RESTRICTIONS”) OR ON THE COVARIANCE MATRIX OF THE MODEL RESIDUAL TERMS (“COVARIANCE RESTRICTIONS”). (FOR NONRECURSIVE MODELS (SIMULTANEOUS CAUSALITY), THERE ARE TWO CLASSES OF COEFFICIENT RESTRICTIONS: RANK AND ORDER RESTRICTIONS. THE ORDER CONDITION REQUIRES THAT IN A MODEL DEFINED BY K LINEAR EQUATIONS, EACH EQUATION MUST EXCLUDE AT LEAST K-1 MODEL VARIABLES. THE RANK RESTRICTION IMPOSES A RESTRICTION ON THE RANKS OF CERTAIN DETERMINANTS OF THE MODEL COEFFICIENTS.)

FOR A REFERENCE ON ESTIMABILITY IN LINEAR MODELS, SEE SAS/STAT 9.2 USER’S GUIDE: THE FOUR TYPES OF ESTIMABLE FUNCTIONS (BOOK EXCERPT), SAS Institute Inc. 2008. SAS/STAT® 9.2 User’s Guide. Cary, NC: SAS Institute Inc., POSTED AT http://support.sas.com/documentation/cdl/en/statugestimable/61763/PDF/default/statugestimable.pdf . OR “A SIMPLE APPROACH FOR FINDING ESTIMABLE FUNCTIONS IN LINEAR MODELS” BY R. K. ELSWICK, JR., CHRIS GENNINGS, VERNON M. CHINCHILLI AND KATHRYN S. DAWSON, THE AMERICAN STATISTICIAN, VOL. 45, NO. 1. (FEB. 1991), PP. 51-53.

A MODEL IS IDENTIFIED ONLY IF ALL OF ITS PARAMETERS ARE ESTIMABLE. IN SOME APPLICATIONS, IT IS NOT DESIRED TO ESTIMATE ALL OF THE MODEL PARAMETERS. IF A CERTAIN SUBSET OF MODEL PARAMETERS IS ESTIMABLE, THEN THE MODEL IS SAID TO BE PARTIALLY IDENTIFIABLE. (EXAMPLES OF APPLICATIONS IN WHICH IT IS NOT NECESSARY TO IDENTIFY ALL MODEL VARIABLES INCLUDE FORECASTING, WHERE THE OBJECTIVE IS TO PREDICT THE DEPENDENT VARIABLE, AND THE MODEL COEFFICIENTS ARE INCIDENTAL; AND A LOGISTIC REGRESSION MODEL OF SELECTION, WHERE THE MODEL COEFFICIENTS HAVE NO ECONOMIC MEANING.) EVEN IF INTEREST CENTERS ON A SINGLE COEFFICIENT IN A LINEAR REGRESSION MODEL (E.G., THE COEFFICIENT OF A BINARY TREATMENT INDICATOR VARIABLE), THEN IT IS NECESSARY THAT ALL OF THE MODEL COEFFICIENTS BE ESTIMABLE, I.E., THE MODEL BE IDENTIFIED.

THE PRECEDING PROCEDURES FOR ASSESSING ESTIMABILITY AND IDENTIFIABILITY OFTEN INVOLVE MATRIX ALGEBRA (DETERMINANTS AND INVERSES OF MATRICES). LATER, WE SHALL DESCRIBE METHODS FOR ASSESSING ESTIMABILITY BY SIMPLER, GRAPHICAL, METHODS.

CONFOUNDING

A SUBSTANTIAL PROBLEM WITH THE ANALYSIS OF PASSIVELY OBSERVED VARIABLES IS THE ISSUE OF CONFOUNDING. CONFOUNDING REFERS TO THE INABILITY TO OBTAIN AN UNBIASED ESTIMATE OF A DESIRED QUANTITY, BECAUSE OF THE PRESENCE OF MORE THAN ONE EXPLANATORY VARIABLE IN A MODEL. THE SOURCE OF CONFOUNDING IS THAT MANY EXPLANATORY VARIABLES OF INTEREST MAY BE CORRELATED, AND WITHOUT MAKING INDEPENDENT FORCED CHANGES IN THEM (AND ORTHOGONALIZING THEM) IT MAY BE DIFFICULT TO ASCRIBE OBSERVED OUTCOMES (EFFECTS) TO THEM (IF THE GOAL IS TO DECIDE ON THE CAUSE OF EFFECTS) OR TO ESTIMATE THE MAGNITUDE OF THEIR EFFECT (IF THE GOAL IS TO ESTIMATE THE EFFECTS OF CAUSES). (IT MAY BE SAID THAT CONFOUNDING IS CAUSED BY THE PRESENCE OF A VARIABLE THAT AFFECTS BOTH AN EXPLANATORY VARIABLE OF INTEREST AND THE DEPENDENT VARIABLE, BUT THIS IS INCLUDED IN THE DEFINITION JUST GIVEN.)

IT MAY BE THAT INTERESTING HYPOTHESES ABOUT POTENTIAL CAUSAL RELATIONSHIPS MAY BE FORMED FROM A DESCRIPTIVE ANALYSIS OF PASSIVELY OBSERVED DATA, BUT IF CONFOUNDING IS PRESENT THE ANALYSIS MAY NOT BE A SOUND BASIS FOR MAKING CAUSAL INFERENCES AND PREDICTION OF THE CHANGES TO BE EXPECTED IN OUTCOME FOLLOWING CHANGES IN EXPLANATORY VARIABLES.

THE TERM “CONFOUNDING” (AND RELATED TERMS SUCH AS CONFOUNDED AND UNCONFOUNDED) REFERS TO THE INTRODUCTION OF BIASES INTO ESTIMATES OF EFFECTS BECAUSE OF THE PRESENCE OF MORE THAN ONE EXPLANATORY VARIABLE IN A MODEL. (THIS DEFINITION ASSUMES THAT THE FOCUS OF AN INVESTIGATION IS ESTIMATION OF THE EFFECTS OF CAUSES, NOT MAKING A DECISION ABOUT THE CAUSE OF AN EFFECT. IN THE LATTER CASE, CONFOUNDING REFERS TO THE INABILITY TO DISTINGUISH THE CAUSE OF AN EFFECT.) AN EFFECT MAY BE DEFINED IN VARIOUS WAYS, SUCH AS A SUM OF SQUARES (OF A DETERMINISTIC VARIABLE), A VARIANCE (OF A RANDOM VARIABLE), A DIFFERENCE IN MEANS (E.G., OF TREATED AND UNTREATED UNITS), OR A PARAMETER IN A REGRESSION MODEL (SUCH AS THE COEFFICIENT OF A TREATMENT INDICATOR VARIABLE). FOR EXAMPLE, IN PROGRAM EVALUATION AN EFFECT OF INTEREST MAY BE THE AVERAGE TREATMENT EFFECT.

THE TERM CONFOUNDING MAY REFER EITHER TO A CAUSAL MODEL OR TO A DATA SET. FOR EXAMPLE, VARIABLES MAY BE CONFOUNDED IN A MODEL, SO THAT THE MODEL MAY NOT BE IDENTIFIED NO MATTER HOW LARGE THE SAMPLE; OR, THEY MAY BE UNCONFOUNDED IN A MODEL BUT CONFOUNDED IN A DATA SET (BECAUSE OF CORRELATIONS IN THE SAMPLE DATA). IN THIS PRESENTATION, WE SHALL GENERALLY BE CONCERNED WITH CONFOUNDING RELATIVE TO A MODEL, NOT A DATA SET (THE LATTER BEING ADDRESSED IN A PRESENTATION ON DATA ANALYSIS).

CONFOUNDING OCCURS, FOR EXAMPLE, WHEN AN EXPLANATORY VARIABLE Z AFFECTS ANOTHER EXPLANATORY VARIABLE X AND THE OUTCOME VARIABLE Y. THE VARIABLE Z IS CALLED THE CONFOUNDING VARIABLE OR A CONFOUNDER. IN THIS CASE, THE AVERAGE EFFECT OF Y ON X IN THE SAMPLE IS AN UNBIASED ESTIMATE OF THE AVERAGE EFFECT OF Y ON X IN THE POPULATION, BUT IT MAY BE A SEVERELY BIASED ESTIMATE OF THE AVERAGE EFFECT OF X ON Y CONDITIONAL ON Z (I.E., ON OTHER VARIABLES SUCH AS AGE, SEX OR RACE). (IT IS IMPORTANT TO RECALL THAT THE BIAS IN AN ESTIMATOR IS ALWAYS RELATIVE TO WHAT ENTITY IS BEING ESTIMATED.)

BIASES DUE TO CONFOUNDING MAY BE REDUCED OR REMOVED BY MAKING CHANGES TO THE CAUSAL MODEL DESIGN OR TO THE DATA SET. THESE PROCEDURES INCLUDE RANDOMIZED ASSIGNMENT TO TREATMENT, AND RESPECIFICATION OF THE MODEL (E.G., BY ADDING ADDITIONAL VARIABLES OR BY ORTHOGONALIZING EXPLANATORY VARIABLES).

CONFOUNDING IS BEST DEFINED WITH RESPECT TO A CAUSAL MODEL. ATTEMPTS TO DEFINE IT STRICTLY IN TERMS OF ASSOCIATIVE (DESCRIPTIVE) STATISTICS HAVE INVARIABLY FAILED (SEE PEARL, OP. CIT. FOR DISCUSSION OF THIS). ALTHOUGH THE CONCEPT OF CONFOUNDING IS THE SAME IN CAUSAL MODELING AND ASSOCIATIVE STATISTICS, THE TERMINOLOGY IS SLIGHTLY DIFFERENT. IN DESCRIPTIVE STATISTICS, IT IS SAID THAT EXPLANATORY VARIABLES ARE CORRELATED OR DEPENDENT, AND THAT (OUTCOME) EFFECTS ARE CORRELATED OR CONFOUNDED. THAT IS, THE TERM “CONFOUNDED” REFERS TO THE EFFECTS, NOT TO THE EXPLANATORY VARIABLES THAT INFLUENCE THE EFFECTS. IN STATISTICAL CAUSAL MODELING, IT IS SAID THAT EXPLANATORY VARIABLES ARE CONFOUNDED WHEN (IN ATTEMPTING TO DECIDE ON THE CAUSE OF AN EFFECT) IT IS NOT CLEAR WHICH OF THEM IS A CAUSE OF A PARTICULAR EFFECT, OR WHEN (IN ESTIMATING THE EFFECT OF A CAUSE) THEY ARE BOTH CAUSES AND ARE CORRELATED, SO THAT THE EFFECTS OF THEM CANNOT BE DISTINGUISHED (“DISENTANGLED”).

THE TERM “CONFOUNDED” IS DEFINED DIFFERENTLY IN CAUSAL MODELING AND ASSOCIATIVE STATISTICAL ANALYSIS. IN CAUSAL MODELING, A CAUSAL VARIABLE X AND AN EFFECT VARIABLE Y ARE SAID TO BE UNCONFOUNDED (WITH RESPECT TO A SPECIFIED CAUSAL MODEL) IF THE AVERAGE CAUSAL EFFECT IS EQUAL TO THE AVERAGE OBSERVED EFFECT. SPECIFICALLY, PEARL’S DEFINITION OF NO-CONFOUNDING IS THAT TWO VARIABLES X AND Y IN A MODEL ARE NOT CONFOUNDED IF THE OBSERVED TREATMENT EFFECT IS AN UNBIASED ESTIMATE OF THE AVERAGE (EXPECTED) TREATMENT EFFECT (ON A RANDOMLY SELECTED INDIVIDUAL). (MORE SPECIFICALLY, THE REQUIREMENT FOR UNCONFOUNDEDNESS IS THAT THE PEARL CAUSAL EFFECT P(Y|do(x)) BE EQUAL TO THE CONDITIONAL DISTRIBUTION P(Y|X); WE SHALL DEFINE THE PEARL CAUSAL EFFECT LATER.)

A SIMPLE DEFINITION OF UNCONFOUNDEDNESS IN ASSOCIATIVE STATISTICS IS THAT TWO EFFECTS ARE SAID TO BE CONFOUNDED IF THEY ARE ASSOCIATED (E.G., CORRELATED OR COLLINEAR). (FOR EXAMPLE, IN A FRACTIONAL FACTORIAL EXPERIMENTAL DESIGN WITH SIX FACTORS, A, B, C, D, E, AND F, IT MAY BE THAT THE DESIGN IS CONFIGURED SO THAT THE A EFFECT IS (TOTALLY) CONFOUNDED WITH THE BCDEF INTERACTION EFFECT. OR, IN AN ANALYSIS OF VARIANCE (OF INCOME, SAY, ON TREATMENT AND RACE), TREATMENT MAY BE CORRELATED WITH RACE, SO THAT THE EFFECTS OF TREATMENT (T) AND RACE (R) ARE COMMINGLED (AND MAY BE ESTIMATED BY PARTITIONING THE TOTAL SUM OF SQUARES IN ALTERNATIVE WAYS, SUCH AS T AND R COMBINED, T AND R|T, OR R AND T|R.)

AN EXPERIMENTAL DESIGN IS SET UP SO THAT THE EFFECTS OF INTEREST (MAIN EFFECTS AND LOW-ORDER INTERACTIONS) ARE NOT CONFOUNDED (CORRELATED) WITH EACH OTHER. THIS IS DONE BY “ORTHOGONALIZING” THE DESIGN SO THAT THE CORRELATION (INNER PRODUCT) BETWEEN THE EXPLANATORY VARIABLES IS ZERO OVER THE SAMPLE (E.G., SUCH THAT EACH LEVEL OF ONE EXPLANATORY VARIABLE OCCURS WITH ALL LEVELS OF OTHER EXPLANATORY VARIABLES). (FOR FACTORIAL EXPERIMENTAL DESIGNS HAVING MANY VARIABLES AND LEVELS, IT IS NOT POSSIBLE FOR ALL MAIN EFFECTS AND HIGHER-ORDER INTERACTIONS TO BE ORTHOGONALIZED. THE DESIGN IS STRUCTURED (AS A FRACTIONAL FACTORIAL DESIGN) SO THAT NO EFFECTS OF INTEREST ARE CORRELATED WITH EACH OTHER (EFFECTS OF INTEREST ARE DELIBERATELY (AND TOTALLY) CONFOUNDED WITH VERY-HIGH-ORDER INTERACTIONS, WHICH ARE UNLIKELY TO BE SIGNIFICANT).)

WHEN EXPLANATORY VARIABLES ARE ORTHOGONALIZED IN A SURVEY OR EXPERIMENTAL DESIGN OR DATA SET, THE ASSOCIATED EFFECTS ARE UNCORRELATED. THEY MAY OR MAY NOT BE UNCORRELATED IN THE POPULATION.

IN AN EXPERIMENTAL DESIGN, CONFOUNDING CAN BE AVOIDED BY ORTHOGONALIZING THE EXPLANATORY VARIABLES. THIS CAN BE DONE FOR VARIABLES FOR WHICH FORCED CHANGES CAN BE MADE, BUT NOT NECESSARILY FOR VARIABLES THAT MAY SIMPLY BE OBSERVED (OR EVEN RANDOMLY SELECTED) SUCH AS RACE (SINCE THEY MAY BE PHYSICALLY RELATED SO THAT THEY CANNOT BE INDEPENDENTLY SET (SPECIFIED)).

FOR OBSERVATIONAL (PASSIVELY OBSERVED) DATA, CONFOUNDING IS MORE DIFFICULT TO ADDRESS. THERE ARE TWO ISSUES, OR TYPES OF CONFOUNDING. IF AN EFFECT IS CONFOUNDED WITH RESPECT TO A MODEL, THE MODEL MUST BE RESPECIFIED (E.G., RECONFIGURED, OR VARIABLES ADDED) SO THAT THE CONFOUNDING IS REMOVED. IF AN EFFECT IS UNCONFOUNDED WITH RESPECT TO THE MODEL BUT CONFOUNDED IN THE DATA SET, THEN ADDITIONAL DATA MAY BE COLLECTED TO REMOVE THE CONFOUNDING. AN ORTHOGONAL SET OF VARIABLES COULD BE SELECTED FROM A SET OF OBSERVATIONAL DATA, BUT IN THE ABSENCE OF FORCED CONTROL OF THOSE VARIABLES, THIS WOULD SUCCEED SOLELY IN ELIMINATING THE CORRELATION AMONG THE ESTIMATED ASSOCIATIVE EFFECTS AND CAUSAL EFFECTS, BUT NOT AMONG THE CAUSAL VARIABLES AND MODEL RESIDUALS.

THE SIGNIFICANCE OF CONFOUNDING IN THE MODEL IS THAT CAUSAL EFFECTS MAY NOT BE REPRESENTED AS INDEPENDENT OF EACH OTHER, EVEN IF THE ESTIMATES ARE UNCORRELATED. THEY REFLECT THE CAUSAL EFFECTS IF ALL OF THE CAUSAL VARIABLES CONTINUE TO OPERATE AS THEY DID FOR THE OBSERVED DATA SET.

CONFOUNDING IS ADDRESSED IN CAUSAL MODELING BY DETERMINING THE ESTIMABILITY OF A CAUSAL EFFECT FROM A CAUSAL DIAGRAM (E.G., USING PEARL’S BACK-DOOR CRITERION). IF A CAUSAL EFFECT IS ESTIMABLE AS THE CONDITIONAL DISTRIBUTION OF THE OUTCOME VARIABLE ON THE CAUSAL VARIABLE, AN UNBIASED ESTIMATE MAY BE OBTAINED, AND THE EFFECT IS SAID TO BE UNCONFOUNDED.

ORTHOGONALIZATION WITH RESPECT TO EXPERIMENTAL DATA (CONTROLLED VARIATION, FORCED CHANGES) IS DIFFERENT IN CHARACTER FROM ORTHOGONALIZATION FOR OBSERVATIONAL DATA (I.E., SELECTING A SAMPLE OF ORTHOGONAL VARIABLES FROM PASSIVELY OBSERVED DATA, WITHOUT MAKING FORCED CHANGES IN THE VARIABLES). THE FORMER REDUCES CONFOUNDING OF ESTIMATES OF CAUSAL EFFECTS BOTH IN THE MODEL AND IN THE DATA SET AND ENABLES PREDICTION OF CHANGES IN OUTCOME ASSOCIATED WITH INDEPENDENT CHANGES IN INPUTS (EXPLANATORY VARIABLES). THE LATTER REDUCES CONFOUNDING OF ASSOCIATIVE EFFECTS IN THE DATA SET (BUT NOT IN THE MODEL), AND SIMPLY PRESENTS A CLEARER PICTURE OF ASSOCIATIONS. IT DOES NOT ENABLE PREDICTION OF THE EFFECTS OF MAKING FORCED CHANGES IN EXPLANATORY VARIABLES (IF THEY WERE NOT MADE FOR THE DATA SET).

NOTE THAT IT MAY NOT BE POSSIBLE TO ORTHOGONALIZE THE CONTROLLED ASSIGNMENT OF ALL EXPLANATORY VARIABLES IN A DESIGNED EXPERIMENT. FOR EXAMPLE, WITH RESPECT TO RACE AND MALARIA RESISTANCE, UNITS MAY BE SELECTED FROM A POPULATION SO THAT RACE AND MALARIA RESISTANCE ARE ORTHOGONAL TO EACH OTHER AND ORTHOGONAL TO OTHER DESIGN VARIABLES, BUT IT IS NOT POSSIBLE TO SELECT POPULATION UNITS AND ASSIGN RACE AND MALARIA RESISTANCE TO THEM INDEPENDENTLY. (IN THIS CASE UNCONFOUNDED (UNBIASED) ESTIMATES MAY BE MADE OF THE EFFECTS ASSOCIATED WITH RACE AND MALARIA RESISTANCE INDEPENDENTLY, BUT THE EXPERIMENT COULD NOT BE USED AS A BASIS FOR ESTIMATING THE EFFECT OF MAKING INDEPENDENT “FORCED CHANGES” IN RACE OR MALARIA RESISTANCE (SINCE THIS CANNOT BE DONE).)

[END OF SECTION ON CONFOUNDING]

DESIGN-BASED, MODEL-BASED AND MODEL-ASSISTED ESTIMATES

A DESIGN-BASED ESTIMATE IS ONE THAT IS BASED ON THE SAMPLE DESIGN (SAMPLE DESIGN STRUCTURE AND SAMPLE SELECTION PROBABILITIES). A MODEL-BASED ESTIMATE IS ONE THAT IS BASED ON A MATHEMATICAL MODEL OF A PROCESS. IT MAY OR MAY NOT INCORPORATE THE SELECTION PROBABILITIES OF THE DESIGN. AN ESTIMATOR IS DESIGN-UNBIASED IF IT IS UNBIASED WITH RESPECT TO THE MODEL REPRESENTED BY THE SAMPLE DESIGN. AN ESTIMATOR IS MODEL-UNBIASED IF IT IS UNBIASED WITH RESPECT TO THE PROCESS MODEL. SURVEYS DESIGNED TO CONSTRUCT DESIGN-BASED ESTIMATES (OF POPULATION CHARACTERISTICS) ARE CALLED DESCRIPTIVE SURVEYS. SURVEYS DESIGNED TO CONSTRUCT MODEL-BASED ESTIMATES (OF PROCESS CHARACTERISTICS) ARE CALLED ANALYTICAL SURVEYS.

SOME ESTIMATORS INCORPORATE ASPECTS OF BOTH A SAMPLE DESIGN AND A PROCESS MODEL. SUCH ESTIMATES ARE CALLED MODEL-ASSISTED ESTIMATES. NOTE THAT IF A VARIABLE IS INCLUDED IN A MODEL-BASED ESTIMATE, IT MUST BE INCLUDED IN SUCH A WAY THAT THE PROCESS MODEL IS CORRECTLY SPECIFIED. ON THE OTHER HAND, A DESIGN-BASED ESTIMATE IS CORRECT EVEN IF THE PROCESS MODEL IS INCORRECTLY SPECIFIED OR CRUDELY SPECIFIED – IT GAINS PRECISION FROM ASSOCIATIONAL RELATIONSHIPS, NOT FROM CORRECT SPECIFICATION OF A CAUSAL MODEL. IF A COVARIATE IS INCLUDED IN A DESIGN-BASED ESTIMATE (E.G., A RATIO ESTIMATE OR A REGRESSION ESTIMATE IN AN ORDINARY SAMPLE SURVEY), THERE IS NO CONSIDERATION OF A PROCESS MODEL, AND NO CHANGES ARE MADE TO THE SELECTION PROBABILITY MODEL. INCLUSION OF THE COVARIATE MAY REDUCE THE STANDARD ERROR OF THE DESIGN-BASED ESTIMATE, WITHOUT ANY CONSIDERATION OF A PROCESS MODEL. (FOR MORE ON THIS TOPIC, CONSULT REFERENCES ON THE DESIGN AND ANALYSIS OF ANALYTICAL SURVEYS. USEFUL REFERENCES INCLUDE THOSE CITED JUST EARLIER.)

THE ROLES OF MATCHING IN A QUASI-EXPERIMENTAL DESIGN

THE GOAL IN USING A QUASI-EXPERIMENTAL DESIGN IS TO INCORPORATE FEATURES, SUCH AS MATCHING AND MODELING, THAT ARE LIKELY TO REDUCE BIASES INTRODUCED BY LACK OF RANDOMIZATION. THE EFFECTIVENESS OF A QED IS DETERMINED BY THESE FEATURES, NOT BY THE APPARENT SIMILARITY OF THE DESIGN STRUCTURE TO THAT OF AN EXPERIMENTAL DESIGN. (THE DESIGN STRUCTURE MAY OF A QED (E.G., ORTHOGONALIZATION OF EXPLANATORY VARIABLES) MAY REDUCE BIAS ASSOCIATED WITH CONFOUNDING.)

THE FUNDAMENTAL DIFFERENCE BETWEEN MATCHING IN AN ED AND MATCHING IN A QED IS THAT IN AN ED THE MATCHING IS DONE PRIOR TO RANDOMIZED ASSIGNMENT TO TREATMENT, WHEREAS IN A QED, MATCHING IS DONE AFTER UNITS HAVE BEEN ASSIGNED TO TREATMENT. AS IN THE CASE OF MATCHING IN AN ED, THE MATCHING IS DONE ON VARIABLES, AVAILABLE FOR USE IN SURVEY DESIGN, THAT ARE CONSIDERED TO HAVE A SUBSTANTIAL EFFECT ON SELECTION FOR TREATMENT OR ON OUTCOMES OF INTEREST (OR ON BOTH – WHICH VARIABLES ARE MORE IMPORTANT DEPENDS ON THE STRENGTH OF THE RELATIONSHIP).

IN A QED THE MATCHING IS DONE BY SELECTING A PROBABILITY SAMPLE (OR ALL) OF UNITS FROM THE (ALREADY) TREATED POPULATION AND MATCHING THEM TO SIMILAR UNITS IN THE AVAILABLE UNTREATED POPULATION.

IN THE DESIGN OF ANY APPLICATION, IT IS USEFUL TO SPECIFY WHAT IMPACT ESTIMATES ARE OF INTEREST, SUCH AS THE ATE, THE OTE, THE ATT, OR A MARGINAL TREATMENT EFFECT (MTE). THE REASON FOR THIS IS THAT THE OPTIMAL SAMPLE SIZE AND SAMPLE ALLOCATION DIFFER DEPENDING ON WHETHER IT IS DESIRED TO ESTIMATE A MEAN (SUCH AS THE ATE) OR A DISTRIBUTIONAL CHARACTERISTIC (SUCH AS THE MTE). IN THIS PRESENTATION, WE WILL FOCUS ON ESTIMATION OF THE ATE AND ATT.

THE PURPOSE OF MATCHING IN A QED: INCREASED PRECISION, REDUCTION IN BIAS, AND REDUCTION IN MODEL DEPENDENCE; DOUBLE ROBUSTNESS OF MATCHING AND REGRESSION ADJUSTMENT

IN EXPERIMENTAL DESIGN, THE MAIN PURPOSE OF MATCHING IS TO INCREASE PRECISION. IT CAN ALSO BE USED TO INTRODUCE ORTHOGONALITY. BECAUSE OF RANDOMIZED SELECTION AND ASSIGNMENT, BIAS IS NOT A PROBLEM. CONFOUNDING IS CONTROLLED BY ORTHOGONALIZATION OR BY DELIBERATE CONFOUNDING OF HIGH-ORDER AND LOW-ORDER INTERACTIONS. IN A QED, MATCHING CAN BE USED TO INCREASE PRECISION, BUT IT ALSO PLAYS OTHER IMPORTANT ROLES. THOSE ARE REDUCTION IN BIAS ASSOCIATED WITH A LACK OF RANDOMIZATION AND REDUCTION IN MODEL DEPENDENCE (I.E., ON THE BIAS INTRODUCED BY INCORRECT MODEL SPECIFICATION).

THIS PRESENTATION DISCUSSES THE ROLE OF MATCHING IN DESIGN TO INCREASE PRECISION AND REDUCE SELECTION BIAS. DISCUSSION OF MATCHING TO REDUCE MODEL DEPENDENCE IS ADDRESSED IN A SEPARATE PRESENTATION ON ANALYSIS.

MATCHING MAY BE DONE WITH OR WITHOUT REGRESSION ANALYSIS. IF THE MATCHING MODEL IS CORRECT OR THE REGRESSION MODEL IS CORRECT, THEN THE ESTIMATE OF IMPACT WILL BE CORRECT. IT IS ONLY NECESSARY THAT ONE OF THEM BE CORRECT. BECAUSE OF THIS PROPERTY, THE APPROACH OF USING BOTH METHODS IS SAID TO BE “DOUBLY ROBUST.” SEE WOOLDRIDGE OP. CIT. (2ND ED., PP. 930-34) FOR A PROOF AND DISCUSSION OF THIS PROPERTY.

MATCHING MAY BE DONE EX ANTE, IN DESIGN, PRIOR TO THE COLLECTION OF DATA, OR EX POST, AFTER THE DATA ARE AVAILABLE. IT IS MORE EFFECTIVE EX POST, WHEN DATA ON MORE VARIABLES ARE AVAILABLE, BUT IT MAY BE INEFFICIENT (BECAUSE IT MAY INVOLVE PRUNING, CULLING OR TRIMMING OF DATA). A REASONABLE “MIDDLE OF THE ROAD” APPROACH IS TO USE MATCHING IN DESIGN AND REGRESSION ADJUSTMENT IN DATA ANALYSIS (SINCE THE REGRESSION ANALYSIS UTILIZES ALL OF THE SAMPLE DATA, WHEREAS MATCHING IN THE ANALYSIS PHASE INVOLVES DISCARDING DATA).

DESIGNS FOR ASSESSING IMPACT

A COMMON DESIGN USED IN EVALUATION STUDIES INTENDED TO ESTIMATE THE AVERAGE TREATMENT EFFECT IS THE PRETEST-POSTTEST-MATCHED-COMPARISON-GROUP DESIGN. THIS DESIGN MAY BE EITHER AN EXPERIMENTAL DESIGN OR A QUASI-EXPERIMENTAL DESIGN. THIS DESIGN WILL BE USED TO ILLUSTRATE CONCEPTS, WHICH APPLY READILY TO OTHER DESIGNS. (NOTE: IT IS CUSTOMARY TO USE THE TERM “COMPARISON GROUP” FOR QEDs, RATHER THAN THE TERM “CONTROL GROUP” (WHICH IS GENERALLY USED FOR EDs).)

THE WORD “GROUP” MAY REFER EITHER TO A POPULATION OR TO A SAMPLE (OR A SUBPOPULATION OR SUBSAMPLE), DEPENDING ON CONTEXT. IT MAY REFER TO THE SETS (“POOLS”) OF TREATED AND UNTREATED UNITS AVAILABLE FROM OBSERVATIONAL DATA, OR TO SAMPLES OF THOSE SETS.

PRETEST-POSTTEST-MATCHED-COMPARISON-GROUP DESIGN: SELECT TREATMENT AND COMPARISON SAMPLES AT TWO (OR MORE) DIFFERENT TIMES (BASELINE, (MIDTERM, FOLLOW-UP,) ENDLINE).

THERE ARE FOUR DESIGN GROUPS:

AS DISCUSSED EARLIER, A STANDARD MEASURE OF IMPACT IN EVALUATION STUDIES IS THE AVERAGE TREATMENT EFFECT (ATE), WHICH IS THE EXPECTED EFFECT OF TREATMENT FOR A RANDOMLY SELECTED INDIVIDUAL. FOR A SAMPLE OF RANDOMLY SELECTED INDIVIDUALS THIS IS ESTIMATED AS THE DIFFERENCE IN OUTCOME BETWEEN TREATED AND UNTREATED UNITS. FOR AN EXPERIMENTAL DESIGN STRUCTURED AS ABOVE, AN UNBIASED ESTIMATOR OF THE ATE IS THE DOUBLE-DIFFERENCE (DD) ESTIMATOR (SOMETIMES CALLED A “DIFFERENCE-IN-DIFFERENCE” ESTIMATOR), WHICH IS THE DIFFERENCE, BETWEEN THE TREATED AND UNTREATED UNITS, OF THE DIFFERENCE IN GROUP MEANS BEFORE AND AFTER TREATMENT. (IT IS UNDERSTOOD HERE THAT THE “GROUP MEAN” IS AN UNBIASED ESTIMATE CONSTRUCTED IN ACCORDANCE WITH THE SAMPLE DESIGN USED FOR THE GROUP, E.G., SIMPLE RANDOM SAMPLING, TWO-STAGE SAMPLING, OR STRATIFIED SAMPLING.)

FOR A QUASI-EXPERIMENTAL DESIGN STRUCTURED AS ABOVE, THE DOUBLE-DIFFERENCE ESTIMATOR MAY BE A BIASED ESTIMATE OF THE ATE. THE REASON FOR THIS IS THAT IN A QED, UNLIKE THE CASE FOR THE EXPERIMENTAL DESIGN, TREATMENT IS NOT RANDOMLY ASSIGNED. IN A TRAINING PROGRAM, FOR EXAMPLE, THE MOST-ABLE APPLICANTS MAY BE SELECTED. THE ATE IS THE AVERAGE EFFECT OF THE PROGRAM INTERVENTION FOR A RANDOMLY SELECTED INDIVIDUAL. IF RANDOM SELECTION IS NOT USED, THE DOUBLE DIFFERENCE IN MEANS COULD BE VERY DIFFERENT FROM THE ATE.

HYPOTHETICAL DISTRIBUTIONS (POTENTIAL OUTCOMES; COUNTERFACTUALS)

IN THE DISCUSSION THAT FOLLOWS, TO FACILITATE THE EXPLANATION OF CONCEPTS, WE WILL MAKE REFERENCE TO TWO HYPOTHETICAL POPULATIONS. THESE POPULATIONS CORRESPOND TO THE (POTENTIAL) HYPOTHETICAL OUTCOMES OF AN EXPERIMENT (SUCH AS A PROGRAM INTERVENTION). BEFORE DEFINING THESE TWO HYPOTHETICAL POPULATIONS, CONSIDER FIRST THE PHYSICAL (ACTUAL, REAL, EXTANT) POPULATION OF ALL ELIGIBLE UNITS (PEOPLE, HOUSEHOLDS, DISTRICTS – WHATEVER THE UNIT OF INTERVENTION). BECAUSE OF THE PROGRAM INTERVENTION, EACH UNIT OF THIS POPULATION MAY BE TREATED OR MAY BE UNTREATED. WE MAY HENCE DEFINE, FOR EACH UNIT, TWO POTENTIAL OUTCOMES ASSOCIATED WITH THE PROGRAM INTERVENTION – THE OUTCOME, Y₀, IF UNTREATED, AND THE OUTCOME, Y₁, IF TREATED (OR Y_i0 AND Y_i1, IF THE UNIT INDEX IS INCLUDED). THESE TWO OUTCOMES, Y₀ AND Y₁, ARE CALLED POTENTIAL OUTCOMES.

IT IS EMPHASIZED THAT HERE WE ARE STILL FOCUSING ON THE BINARY-TREATMENT CASE (IN WHICH THERE ARE TWO TREATMENT LEVELS, "TREATED" AND "UNTREATED." THE "POTENTIAL OUTCOMES" FRAMEWORK IS DISCUSSED MAINLY WITH RESPECT TO THIS CASE.

AFTER IT HAS BEEN DECIDED WHETHER TO TREAT A UNIT, AND THE PROGRAM INTERVENTION HAS OCCURRED, THE OUTCOME WILL BE ONE OF THESE OR THE OTHER. IN OTHER WORDS, FOR EACH UNIT OF THE POPULATION, WE MAY OBSERVE EITHER Y₀ (IF THE UNIT IS UNTREATED) OR Y₁ (IF THE UNIT IS TREATED), BUT NOT BOTH. THE OUTCOME THAT IS OBSERVED (DENOTED BY Y) IS CALLED THE “FACTUAL” OUTCOME, AND THE OTHER (UNOBSERVED) OUTCOME IS CALLED THE “COUNTERFACTUAL” OUTCOME.

NOTE THAT THERE ARE TWO REAL POPULATIONS – THE POPULATION OF (PROGRAM-ELIGIBLE) UNITS PRIOR TO TREATMENT, AND THE POPULATION OF ALL UNITS AFTER TREATMENT (INCLUDING BOTH THE TREATED AND UNTREATED). THESE MAY BE REFERRED TO AS THE “PRETREATMENT” POPULATION AND THE “POSTTREATMENT” POPULATION.

THE FIRST HYPOTHETICAL POPULATION TO BE DEFINED IS THE POPULATION OF OUTCOMES OF ALL PROGRAM-ELIGIBLE UNITS, IF ALL ARE UNTREATED. THIS POPULATION WILL BE REFERRED TO AS THE “PROGRAM-ELIGIBLE POPULATION IF UNTREATED.” THE SECOND HYPOTHETICAL POPULATION IS THE POPULATION OF OUTCOMES OF ALL PROGRAM-ELIGIBLE UNITS, IF ALL ARE TREATED. THIS POPULATION WILL BE REFERRED TO AS THE “PROGRAM-ELIGIBLE POPULATION IF TREATED.” NOTE THAT EACH OF THESE TWO HYPOTHETICAL POPULATIONS CONTAINS EXACTLY THE SAME NUMBER OF UNITS AS THE TWO PHYSICAL (REAL) POPULATIONS. EACH UNIT IN A HYPOTHETICAL POPULATION CORRESPONDS TO A PARTICULAR UNIT IN THE REAL POPULATIONS (PRETREATMENT OR POSTTREATMENT).

THAT IS, BOTH HYPOTHETICAL POPULATIONS (OR “POTENTIAL OUTCOME” POPULATIONS) CONTAIN ALL UNITS OF THE REAL POPULATIONS, WHETHER TREATED OR UNTREATED, AND THE VALUES OF Y₀ AND Y₁ FOR A PARTICULAR UNIT HAVE ABSOLUTELY NOTHING TO DO WITH WHETHER THE UNIT ACTUALLY RECEIVES TREATMENT.

THE POPULATION ATE (I.E., “TRUE VALUE” OF THE ATE) IS THE DIFFERENCE IN MEANS OF THE TWO HYPOTHETICAL (POTENTIAL OUTCOME) POPULATIONS. AN UNBIASED ESTIMATE OF THE ATE MAY BE OBTAINED BY SELECTING A RANDOM SAMPLE OF EACH POPULATION, AND FORMING THE DIFFERENCE. THIS MAY BE DONE BY SELECTING A RANDOM SAMPLE FROM THE REAL POPULATION, RANDOMLY ASSIGNING EACH SELECTED UNIT TO TREATMENT, AND THEN SELECTING A UNIT FROM THE RESPECTIVE HYPOTHETICAL POPULATION, ACCORDING TO WHETHER THE UNIT IS TREATED OR UNTREATED. CONDUCTING AN EXPERIMENTAL DESIGN DOES EXACTLY THIS, AND SO THE ESTIMATED (OBSERVED) TREATMENT EFFECT IN AN ED IS A VALID ESTIMATE OF THE ATE.

FOR A QED, THE SITUATION IS QUITE DIFFERENT. ASSIGNMENT TO TREATMENT IS NOT DETERMINED BY RANDOMIZATION. THE POOLS OF TREATED AND UNTREATED UNITS ARE NOT RANDOM SAMPLES FROM THE TWO HYPOTHETICAL POPULATIONS, SAMPLES SELECTED FROM THESE TWO POOLS ARE NOT RANDOM SAMPLES FROM THE TWO HYPOTHETICAL POPULATIONS, AND THE OBSERVED TREATMENT EFFECT IN A QED IS NOT A VALID ESTIMATE OF THE ATE.

[END OF DISCUSSION OF HYPOTHETICAL DISTRIBUTIONS]

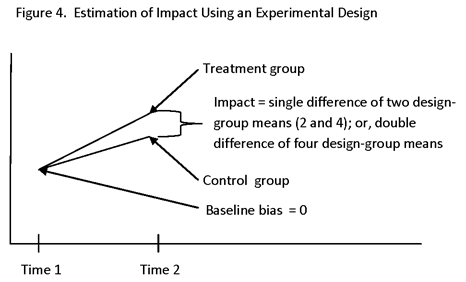
THE REASON WHY THE DD ESTIMATOR IS AN UNBIASED ESTIMATE OF THE ATE FOR AN EXPERIMENTAL DESIGN IS THAT THE FOUR GROUPS ARE FORMED BY USING A KNOWN RANDOMIZATION PROCESS TO SELECT UNITS FROM THE PROGRAM-ELIGIBLE POPULATION AND TO ASSIGN TREATMENT.

THE REASON WHY THE DD ESTIMATOR MAY BE A BIASED ESTIMATE OF THE ATE FOR A QUASI-EXPERIMENTAL DESIGN IS THAT THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS NOT KNOWN, E.G., IT MAY DEPEND ON UNOBSERVED VARIABLES THAT ARE CAUSALLY RELATED TO RESPONSE (OUTCOME). FOR EXAMPLE, IN A TRAINING PROGRAM, ELIGIBLE CANDIDATES WHO ARE MORE ABLE MAY BE MORE LIKELY TO BE SELECTED BY THE PROGRAM STAFF, OR BE MORE LIKELY TO AGREE TO PARTICIPATE. IN THIS CASE, MEMBERS OF THE TREATED POPULATION MAY BE LIKELY TO RESPOND MUCH BETTER TO PROGRAM SERVICES THAN WOULD A RANDOMLY SELECTED MEMBER OF THE POPULATION (WHICH IS THE BASIS FOR THE ATE MEASURE). IN THIS CASE, THE COMPLETE PROBABILITY DISTRIBUTION OF OUTCOME IS NOT KNOWN, AND IT IS NOT POSSIBLE (WITHOUT MAKING ADDITIONAL ASSUMPTIONS) TO OBTAIN AN UNBIASED ESTIMATE OF THE ATE. IN OTHER WORDS, IN THE ABSENCE OF RANDOM ASSIGNMENT TO TREATMENT, THE MEAN RESPONSE OF THE TREATED GROUP MAY BE QUITE DIFFERENT FROM THE MEAN RESPONSE OF RANDOMLY SELECTED INDIVIDUALS. THE MEAN OF THE “PROGRAM-ELIGIBLE POPULATION IF TREATED” IS NOT EQUAL TO THE MEAN OF THE ACTUALLY TREATED POPULATION (μ₂) AND THE MEAN OF THE “PROGRAM-ELIGIBLE POPULATION IF NOT TREATED” IS NOT EQUAL TO THE MEAN OF THE COMPARISON POPULATION (μ₄).

NOTE THAT FOR AN EXPERIMENTAL DESIGN, A PRETEST (BASELINE) SURVEY IS NOT NECESSARY, SINCE TREATMENT AND CONTROL GROUPS ARE STOCHASTICALLY EQUIVALENT AT PRETEST. HENCE, FOR AN ED, TWO MEASURES OF IMPACT MAY BE CONSIDERED: A (SINGLE) DIFFERENCE IN MEANS OF THE TREATED AND UNTREATED UNITS, AFTER TREATMENT; AND A DOUBLE DIFFERENCE IN MEANS: THE DIFFERENCE, BETWEEN THE TREATMENT AND CONTROL GROUPS, OF THE DIFFERENCE IN MEANS BEFORE AND AFTER TREATMENT.

FOR AN ED:

MEASURES OF IMPACT:

IMPACT MEASURE = AVERAGE TREATMENT EFFECT (ATE)

= (SINGLE) DIFFERENCE IN PROGRAM-ELIGIBLE POPULATION IF TREATED AND PROGRAM-ELIGIBLE POPULATION IF UNTREATED = SINGLE DIFFERENCE IN POPULATION MEANS OF TREATMENT AND CONTROL POPULATIONS AT TIME 2, SD = μ₂ – μ₄

= INTERACTION EFFECT (DOUBLE DIFFERENCE) OF TREATMENT AND TIME = (μ₂ – μ₁) – (μ₄ – μ₃) = µ₂ - µ₄ SINCE THE BASELINE BIAS = µ₃ - µ₁.

ESTIMATORS OF IMPACT (BASED ON SAMPLE DATA):

IMPACT ESTIMATOR = ESTIMATED AVERAGE TREATMENT EFFECT

= SAMPLE SINGLE DIFFERENCE AT TIME 2 =

= SAMPLE DOUBLE DIFFERENCE = .

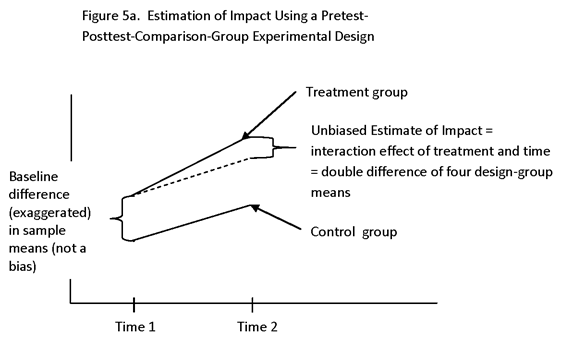
FOR AN ED, THE SAMPLE DOUBLE-DIFFERENCE ESTIMATOR IS AN UNBIASED ESTIMATE OF THE POPULATION DOUBLE-DIFFERENCE MEASURE (WHICH, IN THIS CASE (AN ED), IS THE ATE). FOR INDEPENDENT DESIGN GROUPS (NO MATCHING), THE DOUBLE-DIFFERENCE ESTIMATOR WILL BE LESS PRECISE THAN THE SINGLE-DIFFERENCE ESTIMATOR. IF THE FOUR DESIGN GROUPS ARE RANDOMLY SELECTED (NO MATCHING OR PAIRING), THE DOUBLE-DIFFERENCE ESTIMATOR WILL HAVE TWICE THE VARIANCE, FOR THE SAME TOTAL (ALL-GROUP) SAMPLE SIZE. IF THE DESIGN GROUPS (TREATMENT BEFORE, TREATMENT AFTER, CONTROL BEFORE, CONTROL AFTER) ARE MATCHED, THE DOUBLE-DIFFERENCE ESTIMATOR MAY BE MORE PRECISE. (MORE WILL BE SAID ON THIS LATER.)

THE DOUBLE-DIFFERENCE ESTIMATOR IS LESS PRECISE (THAN THE SINGLE-DIFFERENCE ESTIMATE) IN CERTAIN CASES AND MORE PRECISE IN OTHERS. IF USED WITH PANEL SAMPLING, IT GUARDS AGAINST THE THREAT THAT THE BASELINE OR ENDLINE SAMPLES MIGHT BE “BAD” (I.E., HAVE AN UNUSUALLY LOW OR HIGH SAMPLE MEAN, EVEN THOUGH RANDOMLY SELECTED – AN UNUSUALLY LOW SAMPLE MEAN IS DEPICTED IN FIGURE 5a). BECAUSE OF RANDOMIZED SELECTION OF THE EXPERIMENTAL UNITS, THE BIASES (EXPECTED DIFFERENCES BETWEEN SAMPLE MEANS AND THEIR RESPECTIVE POPULATION MEANS, IN REPEATED SAMPLING) OF THE BASELINE AND ENDLINE ESTIMATED MEANS ARE ZERO, BUT, BECAUSE OF (UNBIASED) SAMPLING VARIATION, THE SAMPLE MEANS OF A PARTICULAR BASELINE OR ENDLINE SAMPLE, FOR SMALL SAMPLES, MAY BE SOMEWHAT DIFFERENT FROM THE POPULATION MEANS. (BIAS IS AN “EXPECTED-VALUE” QUANTITY ASSOCIATED WITH REPEATED SAMPLING, IN ANY PARTICULAR STUDY WE HAVE ONE PARTICULAR SAMPLE, AND THE SAMPLE MEAN WILL DIFFER FROM THE POPULATION MEAN BECAUSE OF SAMPLING VARIATION, EVEN IF THE BIAS IS ZERO.) THE USE OF LARGE SAMPLES ASSURES THAT THESE BIASES WILL BE SMALL. FOR SMALLER SAMPLES, THE USE OF A LONGITUDINALLY MATCHED SAMPLE (PANEL SAMPLE), ALONG WITH THE USE OF THE DOUBLE-DIFFERENCE ESTIMATOR, REDUCES THIS SOURCE OF VARIATION (IT IS A COVARIATE-ADJUSTED ESTIMATE, WHICH REMOVES THE EFFECT OF TIME-INVARIANT COVARIATES).

FOR A QED, THE DOUBLE-DIFFERENCE ESTIMATOR IS, AS IN THE CASE OF AN ED, AN UNBIASED ESTIMATE OF THE POPULATION DOUBLE-DIFFERENCE MEASURE (INTERACTION EFFECT OF TREATMENT AND TIME, (μ₂ – μ₁) - (μ₄ – μ₃)), BUT THE POPULATION DOUBLE-DIFFERENCE MEASURE (THE “OBSERVED TREATMENT EFFECT”) IS NOT A VALID MEASURE OF THE CAUSAL EFFECT OF TREATMENT (THE “AVERAGE TREATMENT EFFECT”), AND THE DOUBLE-DIFFERENCE ESTIMATOR IS HENCE NOT AN UNBIASED ESTIMATE OF THE CAUSAL EFFECT OF TREATMENT (I.E., OF THE AVERAGE EFFECT OF TREATMENT ON A RANDOMLY SELECTED MEMBER OF THE POPULATION). (THE DOUBLE-DIFFERENCE ESTIMATOR IS AN UNBIASED ESTIMATE OF THE OBSERVED TREATMENT EFFECT (OTE) AND OF THE AVERAGE TREATMENT EFFECT ON THE TREATED (ATT).)

IT IS HERE THAT THE DISTINCTION BETWEEN POPULATION CHARACTERISTICS AND PROCESS CHARACTERISTICS BECOMES VERY IMPORTANT AND THE DISTINCTION BETWEEN AN ED AND A QED BECOMES VERY EVIDENT. IF TREATMENT IS NOT RANDOMLY ASSIGNED, THEN THE MEANS OF THE TREATED AND UNTREATED UNITS IN THE POPULATION AT HAND ARE NOT VALID ESTIMATES OF THE MEANS OF TREATED AND UNTREATED IF TREATMENT IS RANDOMLY ASSIGNED. THAT IS, THE POPULATION MEANS ARE NOT EQUAL TO THE PROCESS MEANS. IN PROGRAM EVALUATION, WE ARE (USUALLY) INTERESTED IN ESTIMATING THE AVERAGE TREATMENT EFFECT (ATE) OF THE PROGRAM INTERVENTION, I.E., IN ESTIMATING THE AVERAGE EFFECT OF ASSIGNING PROGRAM SERVICES TO A RANDOMLY SELECTED PROGRAM-ELIGIBLE INDIVIDUAL. FOR AN ED, BECAUSE OF RANDOMIZED ASSIGNMENT, THE POPULATION MEANS AND PROCESS MEANS ARE THE SAME. FOR AN ED, IF TREATMENT WAS ASSIGNED TO A VERY SPECIAL GROUP (E.G., THE DISABLED, OR HIGHLY MOTIVATED AND HIGHLY CAPABLE INDIVIDUALS), THE DIFFERENCE IN MEANS BETWEEN TREATED AND UNTREATED UNITS IN THE POPULATION AT HAND MAY BE A VERY BIASED ESTIMATE OF THE ATE.

USING THE OBSERVED TREATMENT EFFECT (INTERACTION EFFECT OF TREATMENT AND TIME) AS AN ESTIMATE OF THE AVERAGE TREATMENT EFFECT IS FINE FOR AN EXPERIMENTAL DESIGN (SEE FIGURE 5a), BUT NOT AT ALL APPROPRIATE FOR ESTIMATING THE ATE IN A QED. (IT IS QUITE APPROPRIATE FOR ESTIMATING THE OTE.)

IN A QED, THERE ARE TWO SOURCES OF BIAS, RELATIVE TO THE GOAL OF USING THE DOUBLE-DIFFERENCE ESTIMATOR TO ESTIMATE THE AVERAGE TREATMENT EFFECT: (1) BASELINE BIAS, WHICH IS THE DIFFERENCE IN MEANS BETWEEN THE TREATED AND UNTREATED POPULATIONS AT BASELINE; AND (2) DIFFERENTIAL-TREATMENT-EFFECT (DTE) BIAS, WHICH IS THE DIFFERENCE IN TREATMENT RESPONSE FOR THE TREATED AND UNTREATED POPULATIONS IF BOTH WERE TREATED. (THE TERM “SELECTION BIAS” MAY REFER TO EITHER SOURCE OF BIAS, OR TO BOTH COMBINED.) FIGURE 5b ILLUSTRATES THE SITUATION. MATCHING MAY REDUCE EITHER SOURCE OF BIAS, AND ITS EFFECTIVENESS DEPENDS ON THE RELATIONSHIP OF OUTCOME TO THE MATCH VARIABLES. MORE WILL BE SAID ABOUT THE DTE LATER.

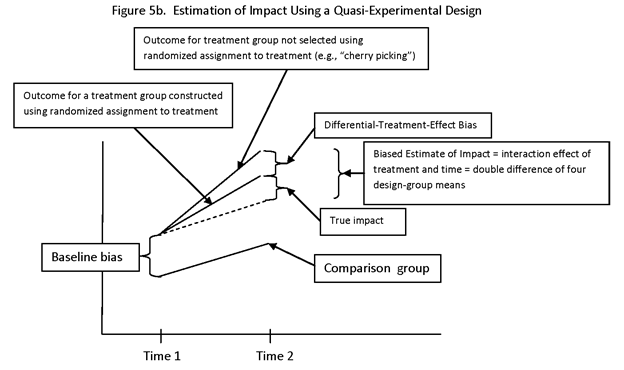
FOR A QED, THE DOUBLE DIFFERENCE ESTIMATOR IS NOT AN UNBIASED ESTIMATE OF THE ATE (I.E., OF IMPACT). THE DOUBLE-DIFFERENCE ESTIMATOR REMOVES THE BASELINE BIAS AND THE EFFECT OF ALL TIME-INVARIANT HIDDEN (UNOBSERVED) VARIABLES. IT DOES NOT REMOVE DTE BIAS.

THIS PRESENTATION CONSIDERS THE USE OF MATCHING TO REDUCE SELECTION BIAS (BOTH BASELINE BIAS AND DTE BIAS).

IN WHAT FOLLOWS WE WILL ADDRESS THE ISSUE OF REDUCING SELECTION BIAS APART FROM THAT INTRODUCED BY FAILING TO SELECT EXPERIMENTAL UNITS USING PROBABILITY SAMPLING FROM A WELL-DEFINED POPULATION. THAT IS, WE ADDRESS THE ISSUE OF REDUCING BIAS ASSOCIATED WITH NON-RANDOM ASSIGNMENT TO TREATMENT.

FOR QEDs, MATCHING ADDRESSES BOTH (1) INCREASING PRECISION AND POWER AND (2) DECREASING BIAS.

NOTE THAT IT IS NOT ADVISABLE TO MATCH ON A PREMEASURE OF OUTCOME, AS THIS MAY INTRODUCE A REGRESSION-EFFECT BIAS (BECAUSE A PREMEASURE OF OUTCOME IS LIKELY TO BE CORRELATED WITH OUTCOME). MATCHING IS DONE ON VARIABLES THAT MAY HAVE A SUBSTANTIAL EFFECT ON OUTCOMES OF INTEREST, BUT NOT ON AN IMPRECISE PREMEASURE OF THE OUTCOME OF INTEREST ITSELF. (THIS IS THE SAME ISSUE AS DECIDING WHETHER TO CONDITION ON A PRETEST OUTCOME, IN ANALYSIS OF PANEL DATA. WHETHER TO DO SO OFTEN REPRESENTS A QUANDARY FOR ANALYSTS. THE PROBLEM MAY BE RESOLVED USING PEARL’S DAG-BASED ESTIMABILITY CRITERIA.)

A NOTE ON TERMINOLOGY: DISPERSION-RELATED PROPERTIES OF AN ESTIMATOR: PRECISION (RELIABILITY), BIAS (VALIDITY), AND ACCURACY (BOTH)

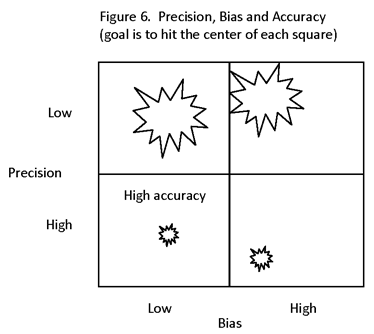
MEASURE OF PRECISION = VARIANCE = E(X-E(X))² (OR ITS SQUARE ROOT, THE STANDARD DEVIATION)

MEASURE OF BIAS = E(X) - μ

MEASURE OF ACCURACY = MEAN SQUARED ERROR (MSE) = VARIANCE + BIAS² (OR ITS SQUARE ROOT, THE ROOT-MEAN-SQUARED ERROR)

THESE MEASURES ARE EXPECTATIONS. THE ESTIMATE (E.G., A MEAN) FOR A PARTICULAR SAMPLE WILL (IN GENERAL) NOT EQUAL THE POPULATION VALUE, EVEN IF THE ESTIMATOR IS UNBIASED. IF THE ESTIMATOR IS UNBIASED, THAT THAT DIFFERENCE IS CALLED SAMPLING VARIATION, NOT BIAS. THE SAMPLING VARIATION OF AN ESTIMATOR (GENERALLY) DECREASES AS THE SAMPLE SIZE INCREASES, WHILE THE BIAS DOES NOT.

A DESCRIPTION OF HOW MATCHING REDUCES BIAS IS COMPLICATED, INVOLVING CONSIDERATION OF CAUSAL MODELING (NEYMAN-FISHER-COX-RUBIN CAUSAL MODEL / COUNTERFACTUALS MODEL / POTENTIAL-OUTCOMES MODEL).

A DESCRIPTION OF HOW MATCHING INCREASES PRECISION AND POWER IS SIMPLER, AND WILL BE ADDRESSED FIRST. FOR THIS, THE DISCUSSION FOCUSES ON THE VARIANCE AND INTERCORRELATIONS (NOT ON BIAS).

4.2. THE USE OF MATCHING TO INCREASE PRECISION AND POWER

SYMBOLIC REPRESENTATION OF A SINGLE-ROUND TWO-GROUP EXPERIMENTAL OR QUASI-EXPERIMENTAL DESIGN.

SINGLE ROUND (CROSS-SECTIONAL DATA), TWO DESIGN GROUPS: (1) TREATMENT AND (2) COMPARISON (CONTROL).

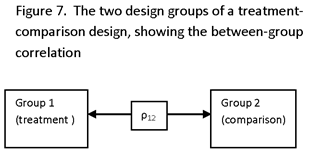
FOR AN ED, THE SINGLE-DIFFERENCE ESTIMATE IS AN UNBIASED ESTIMATE OF THE DIFFERENCE IN MEANS OF THE PROGRAM-ELIGIBLE POPULATION IF TREATED AND THE PROGRAM-ELIGIBLE POPULATION IF UNTREATED, WHICH, IN THIS CASE, IS THE AVERAGE TREATMENT EFFECT (ATE).

IMPACT MEASURE = AVERAGE TREATMENT EFFECT = DIFFERENCE IN MEANS BETWEEN THE PROGRAM-ELIGIBLE POPULATION IF TREATED AND THE PROGRAM-ELIGIBLE POPULATION IF UNTREATED = μ₁ – μ₂

SIMPLE, DESIGN-BASED ESTIMATOR OF IMPACT:

IMPACT ESTIMATOR = DIFFERENCE IN SAMPLE MEANS = SAMPLE SINGLE DIFFERENCE =

PAIRED (MATCHED-PAIRS) DESIGN. POPULATION UNITS ARE FORMED INTO MATCHED PAIRS AND ONE MEMBER OF EACH PAIR IS RANDOMLY ASSIGNED TO TREATMENT. THE CORRELATION BETWEEN UNITS IN THE SAME PAIR IS DENOTED BY ρ.

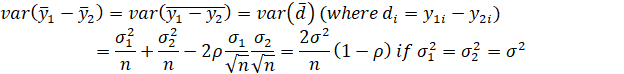
UNPAIRED (UNMATCHED, INDEPENDENT GROUPS) DESIGN (ρ = 0):

FOR AN ED, THE SINGLE DIFFERENCE IN MEANS IS AN UNBIASED ESTIMATE OF THE AVERAGE TREATMENT EFFECT, AND THE PRECEDING PRECISION ESTIMATES APPLY. FOR A QED, THE SINGLE DIFFERENCE IN MEANS IS NOT AN UNBIASED ESTIMATE OF THE AVERAGE TREATMENT EFFECT. IT IS BIASED, AND THE BIAS IS REMOVED BY MEANS OF CAUSAL MODELING AND ANALYSIS, TO BE DISCUSSED LATER.

SYMBOLIC REPRESENTATION OF A TWO-ROUND FOUR-GROUP ED OR QED

TWO SURVEY ROUNDS (LONGITUDINAL DATA, PANEL DATA), FOUR DESIGN GROUPS: (1) TREATMENT BEFORE; (2) TREATMENT AFTER; (3) COMPARISON BEFORE; (4) COMPARISON AFTER.

NOTE: FOR AN ED, THE COMPARISON GROUP IS CALLED A CONTROL GROUP. FOR A QED, THE COMPARISON GROUP IS GENERALLY CALLED A COMPARISON GROUP, BUT IS OFTEN REFERRED TO AS A CONTROL GROUP.

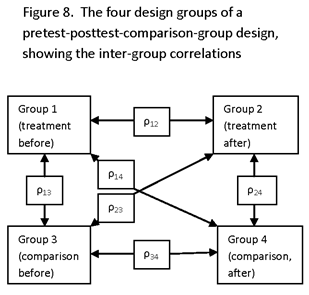
WITH TWO TREATMENT LEVELS (TREATMENT AND COMPARISON) AND TWO SURVEY ROUNDS, THERE ARE SIX INTERGROUP CORRELATIONS, NOT JUST ONE (AS IN THE CASE OF THE TWO-GROUP (TREATMENT AND COMPARISON) DESIGN)).

THERE ARE TWO TYPES OF MATCHING:

LONGITUDINAL MATCHING, E.G., INTERVIEW THE SAME HOUSEHOLDS IN BOTH SURVEY ROUNDS, E.G., ρ₁₂ = ρ₃₄ = .5.

CROSS-SECTIONAL MATCHING, E.G., MATCH VILLAGES, DISTRICTS, SCHOOLS, HOSPITALS (THE LOWEST LEVEL OF SAMPLING FOR WHICH PRE-SURVEY DATA ARE AVAILABLE FOR USE IN SURVEY DESIGN), E.G., ρ₁₃ = ρ₂₄ = .3.

IF THE DESIGN CONSISTS OF TWO SURVEY ROUNDS AND UNITS ARE MATCHED LONGITUDINALLY (AT ANY LEVEL OF SAMPLING), THE SURVEY IS CALLED A PANEL SURVEY.

NOTE THAT THERE ARE TWO “ARTIFACTUAL” CORRELATIONS, ρ₁₄ AND ρ₂₃. THE VALUES OF THESE ARE CONSTRAINED SO THAT THE CORRELATION MATRIX OF THE VECTOR (y₁, y₂, y₃, y₄) IS POSITIVE DEFINITE, E.G., ρ₁₄ = ρ₁ ρ₄ AND ρ₂₃ = ρ₂ ρ₃.

(THE TERM “ARTIFACTUAL” IS USED TO CONNOTE THAT THESE CORRELATIONS ARE NOT DIRECTLY CONTROLLED IN THE DESIGN, IN CONTRAST TO THE OTHER CORRELATIONS (ρ₁₂ AND ρ₃₄, WHICH ARE CONTROLLED BY LONGITUDINAL MATCHING, AND ρ₁₃ AND ρ₂₄, WHICH ARE CONTROLLED BY CROSS-SECTIONAL MATCHING.)

THE DOUBLE-DIFFERENCE ESTIMATOR IS AN UNBIASED ESTIMATE OF THE POPULATION DOUBLE-DIFFERENCE MEASURE. FOR AN ED, THIS EQUALS THE AVERAGE TREATMENT EFFECT. FOR A QED, IT DOES NOT.

FOR AN ED:

IMPACT MEASURE = POPULATION ATE

= DOUBLE DIFFERENCE OF POPULATION MEANS = (μ₂ – μ₁) – (μ₄ – μ₃).

SIMPLE, DESIGN-BASED ESTIMATOR OF IMPACT:

IMPACT ESTIMATOR = SAMPLE ESTIMATE OF ATE

= DOUBLE DIFFERENCE OF SAMPLE MEANS = .

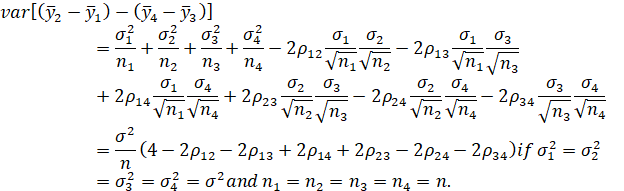
IF ALL INTERGROUP CORRELATIONS ARE ZERO, THEN THIS VARIANCE IS EQUAL TO 4σ²/n (THE FORMULA FOR THE VARIANCE OF A SUM OR DIFFERENCE OF MEANS OF FOUR INDEPENDENT SAMPLES).

(IN THE CASE OF ZERO CORRELATIONS, THE VARIANCE OF THE SINGLE-DIFFERENCE ESTIMATOR FOR A SINGLE-ROUND SURVEY IS 2σ²/n AND THE VARIANCE OF THE DOUBLE-DIFFERENCE ESTIMATOR FOR A TWO-ROUND SURVEY IS 4σ²/n, FOR THE SAME SAMPLE SIZE, n, IN EACH DESIGN GROUP. FOR THE SAME TOTAL SAMPLE SIZE n*, THE SINGLE-DIFFERENCE ESTIMATOR VARIANCE IS 2σ²/(n*/2) = 4σ²/n*, AND THE DOUBLE-DIFFERENCE ESTIMATOR VARIANCE IS 4σ²/(n*/4) = 16σ²/n*. HENCE, IN THE CASE OF ZERO CORRELATIONS (NO MATCHING) THE EFFICIENCY OF THE DOUBLE-DIFFERENCE ESTIMATOR (RELATIVE TO THE VARIANCE) IS HENCE ¼ THAT OF THE SINGLE-DIFFERENCE ESTIMATOR.

FOR QEDs, TO REDUCE SELECTION BIAS IT IS ESSENTIAL TO USE A PRETEST-POSTTEST-COMPARISON-GROUP DESIGN EVEN THOUGH IT MAY BE LESS EFFICIENT (THIS WILL BE DISCUSSED AT LENGTH LATER) AND ESTIMATORS THAT ARE SIMILAR TO THE DOUBLE-DIFFERENCE ESTIMATOR (BUT SUITABLY MODIFIED TO REDUCE SELECTION BIAS). THE EFFICIENCY OF THE DOUBLE-DIFFERENCE ESTIMATOR CAN BE IMPROVED MARKEDLY BY MEANS OF MATCHING (TO INTRODUCE CORRELATIONS AMONG THE DESIGN GROUPS).

NOTE THAT THE INTERGROUP CORRELATIONS ARE DIFFERENT FROM THE INTRA-GROUP CORRELATIONS, DENOTED BY icc_i. (E.G., IF THE FOUR GROUPS ARE INDEPENDENT, THE ρ_ijWILL BE ZERO, YET EACH GROUP COULD (AND TYPICALLY WOULD) HAVE A NONZERO icc_i.)

FOR AN EXPERIMENTAL DESIGN, THE SAMPLE DOUBLE DIFFERENCE IS AN UNBIASED ESTIMATE OF THE POPULATION DOUBLE DIFFERENCE AND THE ATE. FOR A QUASI-EXPERIMENTAL DESIGN, THE SAMPLE DOUBLE DIFFERENCE IS AN UNBIASED ESTIMATE OF THE POPULATION DOUBLE DIFFERENCE, BUT IT IS A BIASED ESTIMATE OF THE ATE. THE BIAS MAY BE REMOVED OR REDUCED IN TWO WAYS, BOTH USING CAUSAL MODELING AND ANALYSIS. THE FIRST WAY IS TO STRATIFY THE SAMPLE SUCH THAT UNBIASED ESTIMATES ARE AVAILABLE FOR EACH STRATUM, AND FORM A STRATUM-WEIGHTED ESTIMATE. THE SECOND WAY IS TO CONSTRUCT A CORRECTLY IDENTIFIED REGRESSION MODEL, AND DERIVE AN UNBIASED ESTIMATE FROM THE REGRESSION MODEL.

BOTH APPROACHES REQUIRE THE IDENTIFICATION OF A CAUSAL MODEL THAT IDENTIFIES VARIABLES AFFECTING SELECTION FOR TREATMENT. FOR THE REGRESSION APPROACH THE RESULTING ESTIMATE, USUALLY (FOR A BINARY TREATMENT VARIABLE) A COEFFICIENT IN A REGRESSION EQUATION, IS CALLED A “COVARIATE ADJUSTED” OR “REGRESSION ADJUSTED” DOUBLE-DIFFERENCE ESTIMATE.

WE SHALL INVESTIGATE THE TOPIC OF CAUSAL MODELING AS IT RELATES TO MATCHING, AFTER CONSIDERING THE RELATIONSHIP OF MATCHING TO PRECISION AND POWER IN SOMEWHAT GREATER DETAIL.

NUMERICAL EXAMPLE.

WE SHALL NOW PRESENT A DETAILED EXAMPLE OF ANALYSIS OF A FOUR-GROUP DESIGN IN THE CASE OF AN EXPERIMENTAL DESIGN, USING REGRESSION ANALYSIS AND ANALYSIS OF VARIANCE (BOTH ARE EXAMPLES OF A GENERAL LINEAR STATISTICAL MODEL).

THE PURPOSE OF THIS EXAMPLE IS TO ILLUSTRATE IN DETAIL THE PRECISION BENEFITS ASSOCIATED WITH MATCHING.

WE WILL SIMULATE A DATA SET USING THE MODEL

T = μ + P + δtT + E

WHERE

Y = response (e.g., a test score)

μ = population mean

t = treatment (0 = control, 1 = treatment)

T = time (survey round; 0 = baseline, 1 = endline)

P = pair effect (random)

δ = treatment effect (coefficient of interaction of treatment and time)

E = model error (residual random variation).

SET μ = 50, P~N(0,10), E~N(0,5), and δ=5. WITH THESE VALUES FOR P AND E, THE INTRA-PAIR CORRELATION COEFFICIENT IS icc = var(P)/(var(P) + var(E)) = 10²/(10² + 5²) = .8.

WE WILL USE THE DATA TO EXEMPLIFY BOTH THE SINGLE-ROUND DESIGN AND THE TWO-ROUND DESIGN. WE WILL USE THE SECOND-ROUND DATA TO ILLUSTRATE THE SINGLE-ROUND CASE.

THE DATA SET WILL BE ANALYZED USING REGRESSION ANALYSIS AND ANALYSIS OF VARIANCE (ANOVA), TO ILLUSTRATE THE SIMILARITIES AND DIFFERENCES OF THESE METHODS. (ANOVA AND REGRESSION ANALYSIS ARE SPECIAL CASES OF THE GENERAL LINEAR STATISTICAL MODEL. IN ANOVA, THE VALUES OF THE EXPLANATORY VARIABLES ARE DISCRETE (OFTEN ZERO AND ONE). IN REGRESSION ANALYSIS, THE COVARIANCE MATRIX OF THE DATA IS NONSINGULAR (INVERTIBLE)).

NOTE THAT THIS DATA SET CORRESPONDS TO AN EXPERIMENTAL DESIGN, NOT A QUASI-EXPERIMENTAL DESIGN.

SAMPLE DATA (2 TREATMENTS, 2 ROUNDS, 12 PAIRS, 48 OBSERVATIONS TOTAL)

+--------------------------------------------------------+

| Pair e1 Tre~t Time e2 Score |

|--------------------------------------------------------|

1. | 1 -.08535 0 0 1.221592 55.25446 |

2. | 1 -.08535 0 1 -.8195791 45.0486 |

3. | 1 -.08535 1 1 .7226272 57.75964 |

4. | 1 -.08535 1 0 -.3747932 47.27253 |

5. | 2 .2892469 0 1 -.3125347 51.3298 |

|--------------------------------------------------------|

6. | 2 .2892469 0 0 -.5035399 50.37477 |

7. | 2 .2892469 1 1 -1.157536 52.10479 |

8. | 2 .2892469 1 0 -.1820993 51.98197 |

9. | 3 1.689594 0 0 1.032842 72.06014 |

10. | 3 1.689594 0 1 1.458244 74.18716 |

|--------------------------------------------------------|

11. | 3 1.689594 1 1 -.6816902 68.48749 |

12. | 3 1.689594 1 0 -.1588628 66.10162 |

13. | 4 .0809735 0 0 1.088992 56.2547 |

14. | 4 .0809735 0 1 .2972595 52.29603 |

15. | 4 .0809735 1 1 1.791799 64.76873 |

|--------------------------------------------------------|

16. | 4 .0809735 1 0 -.7534142 47.04266 |

17. | 5 .9282094 0 0 -.4368788 57.0977 |

18. | 5 .9282094 0 1 -1.37336 52.41529 |

19. | 5 .9282094 1 1 -1.782762 55.36828 |

20. | 5 .9282094 1 0 -1.243684 53.06367 |

|--------------------------------------------------------|

21. | 6 .5659719 0 0 -1.255076 49.38434 |

22. | 6 .5659719 0 1 -.1299917 55.00976 |

23. | 6 .5659719 1 1 .0704919 61.01218 |

24. | 6 .5659719 1 0 .2342806 56.83112 |

25. | 7 .1425843 0 0 .9349558 56.10062 |

|--------------------------------------------------------|

26. | 7 .1425843 0 1 -.893132 46.96018 |

27. | 7 .1425843 1 1 .6154595 59.50314 |

28. | 7 .1425843 1 0 -2.046756 41.19207 |

29. | 8 .8164383 0 1 -1.098096 52.6739 |

30. | 8 .8164383 0 0 -.8821722 53.75352 |

|--------------------------------------------------------|

31. | 8 .8164383 1 1 -.9302391 58.51319 |

32. | 8 .8164383 1 0 -1.231853 52.00512 |

33. | 9 1.408515 0 1 .5346485 66.75839 |

34. | 9 1.408515 0 0 -1.646716 55.85157 |

35. | 9 1.408515 1 1 -.3373884 67.39821 |

|--------------------------------------------------------|

36. | 9 1.408515 1 0 .0017994 64.09415 |

37. | 10 -.0036408 0 0 -2.932731 35.29993 |

38. | 10 -.0036408 0 1 .1540828 50.734 |

39. | 10 -.0036408 1 0 -.1800493 49.06335 |

40. | 10 -.0036408 1 1 1.4293 62.11009 |

|--------------------------------------------------------|

41. | 11 -.391012 0 1 -.5365699 43.40703 |

42. | 11 -.391012 0 0 -.3613488 44.28313 |

43. | 11 -.391012 1 1 .0606523 51.39314 |

44. | 11 -.391012 1 0 .1947535 47.06365 |

45. | 12 -2.471484 0 0 -.4403474 23.08342 |

|--------------------------------------------------------|

46. | 12 -2.471484 0 1 -.4068243 23.25104 |

47. | 12 -2.471484 1 0 -.3710693 23.42981 |

48. | 12 -2.471484 1 1 1.565848 38.1144 |

+--------------------------------------------------------+

SINGLE-ROUND RESULTS

ANOVA, IGNORING PAIRING

Number of obs = 24 R-squared = 0.1040

Root MSE = 10.5339 Adj R-squared = 0.0633

Source | Partial SS df MS F Prob > F

-----------+----------------------------------------------------

Model | 283.333057 1 283.333057 2.55 0.1243

Treatment | 283.333057 1 283.333057 2.55 0.1243

Residual | 2441.17282 22 110.962401

-----------+----------------------------------------------------

Total | 2724.50588 23 118.456777

ANOVA, TAKING PAIRING INTO ACCOUNT

Number of obs = 24 R-squared = 0.9203

Root MSE = 4.44284 Adj R-squared = 0.8334

Source | Partial SS df MS F Prob > F

-----------+----------------------------------------------------

Model | 2507.3791 12 208.948259 10.59 0.0002

Pair | 2224.04605 11 202.186004 10.24 0.0003

Treatment | 283.333057 1 283.333057 14.35 0.0030

Residual | 217.126774 11 19.7387976

-----------+----------------------------------------------------

Total | 2724.50588 23 118.456777

REGRESSION ANALYSIS

Source | SS df MS Number of obs = 24

-------------+------------------------------ F( 12, 11) = 10.59

Model | 2507.3791 12 208.948259 Prob > F = 0.0002

Residual | 217.126774 11 19.7387976 R-squared = 0.9203

-------------+------------------------------ Adj R-squared = 0.8334

Total | 2724.50588 23 118.456777 Root MSE = 4.4428

------------------------------------------------------------------------------

Score | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

Treatment | 6.871839 1.81378 3.79 0.003 2.879735 10.86394

Pair1 | 20.7214 4.442837 4.66 0.001 10.94278 30.50002

Pair2 | 21.03457 4.442837 4.73 0.001 11.25596 30.81319

Pair3 | 40.6546 4.442837 9.15 0.000 30.87599 50.43322

Pair4 | 27.84966 4.442837 6.27 0.000 18.07104 37.62828

Pair5 | 23.20907 4.442837 5.22 0.000 13.43045 32.98769

Pair6 | 27.32825 4.442837 6.15 0.000 17.54963 37.10687

Pair7 | 22.54894 4.442837 5.08 0.000 12.77032 32.32756

Pair8 | 24.91083 4.442837 5.61 0.000 15.13221 34.68944

Pair9 | 36.39558 4.442837 8.19 0.000 26.61696 46.1742

Pair10 | 25.73933 4.442837 5.79 0.000 15.96071 35.51795

Pair11 | 16.71737 4.442837 3.76 0.003 6.938751 26.49599

_cons | 27.2468 3.269839 8.33 0.000 20.04993 34.44367

------------------------------------------------------------------------------

NOTE THE EQUIVALENCE OF THE ANOVA AND REGRESSION ANALYSIS: Residual sum of squares = 217.13. Statistical significance of the treatment effect is the same (t² = 3.79² = 14.35 = F), but the regression model provides the estimate of the impact (treatment effect, 6.87).

TWO-ROUND RESULTS

ANOVA, IGNORING PAIRING

Number of obs = 48 R-squared = 0.0854

Root MSE = 11.1078 Adj R-squared = 0.0230

Source | Partial SS df MS F Prob > F

---------------+----------------------------------------------------

Model | 506.801533 3 168.933844 1.37 0.2646

Treatment*Time | 506.801533 3 168.933844 1.37 0.2646

Residual | 5428.90692 44 123.384248

---------------+----------------------------------------------------

Total | 5935.70845 47 126.291669

ANOVA, TAKING PAIRING INTO ACCOUNT

Number of obs = 48 R-squared = 0.8659

Root MSE = 4.7681 Adj R-squared = 0.8200

Source | Partial SS df MS F Prob > F

-----------+----------------------------------------------------

Model | 5139.99048 12 428.33254 18.84 0.0000

TrtTim | 497.247582 1 497.247582 21.87 0.0000

Pair | 4642.7429 11 422.067536 18.56 0.0000

Residual | 795.71797 35 22.7347991

-----------+----------------------------------------------------

Total | 5935.70845 47 126.291669

REGRESSION ANALYSIS

Source | SS df MS Number of obs = 48

-------------+------------------------------ F( 12, 35) = 18.84

Model | 5139.99048 12 428.33254 Prob > F = 0.0000

Residual | 795.71797 35 22.7347991 R-squared = 0.8659

-------------+------------------------------ Adj R-squared = 0.8200

Total | 5935.70845 47 126.291669 Root MSE = 4.7681

------------------------------------------------------------------------------

Score | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

TrtTim | 7.433016 1.589367 4.68 0.000 4.206429 10.6596

Pair1 | 24.36414 3.371557 7.23 0.000 17.51951 31.20876

Pair2 | 24.47816 3.371557 7.26 0.000 17.63354 31.32279

Pair3 | 43.23943 3.371557 12.82 0.000 36.39481 50.08406

Pair4 | 28.12086 3.371557 8.34 0.000 21.27624 34.96549

Pair5 | 27.51657 3.371557 8.16 0.000 20.67194 34.36119

Pair6 | 28.58968 3.371557 8.48 0.000 21.74506 35.43431

Pair7 | 23.96933 3.371557 7.11 0.000 17.12471 30.81396

Pair8 | 27.26676 3.371557 8.09 0.000 20.42214 34.11139

Pair9 | 36.55591 3.371557 10.84 0.000 29.71128 43.40054

Pair10 | 22.33218 3.371557 6.62 0.000 15.48755 29.1768

Pair11 | 19.56707 3.371557 5.80 0.000 12.72244 26.4117

_cons | 25.11141 2.416936 10.39 0.000 20.20477 30.01806

------------------------------------------------------------------------------

NOTE THE EQUIVALENCE OF THE ANOVA AND REGRESSION ANALYSIS: Residual sum of squares = 795.92. The statistical significance of the treatment-by-time interaction effect is the same (t² = 4.68² = 21.87 = F), but the regression model provides the estimate of the impact (treatment-by-time interaction effect, 7.43).

NOTE THAT THE USE OF A STRAIGHTFORWARD REGRESSION ANALYSIS (OR ANOVA) IS APPROPRIATE FOR DATA GENERATED BY THE PRECEDING MODEL, SINCE IT CORRESPONDS TO RANDOMIZED ASSIGNMENT TO TREATMENT (I.E., TO AN EXPERIMENTAL DESIGN). THIS ANALYSIS WOULD NOT BE APPROPRIATE FOR A QED (SINCE, WITHOUT RANDOMIZED ASSIGNMENT OF TREATMENT, THE MODEL ERROR TERM FOR Y WOULD NOT BE INDEPENDENT OF TREATMENT). IT IS PRESENTED TO ILLUSTRATE ANALYSIS USING ONE ROUND OF DATA VERSUS TWO ROUNDS OF DATA, ANOVA VS. REGRESSION ANALYSIS, AND THE INCREASE IN PRECISION THAT RESULTS IF THE MATCHED-PAIRS FEATURE OF THE DATA IS TAKEN INTO ACCOUNT.

OBSERVATION: USING MATCHING CAN MAKE A BIG DIFFERENCE IN PRECISION. THE ESTIMATED EFFECT WAS HIGHLY STATISTICALLY SIGNIFICANT WHEN THE PAIRING WAS TAKEN INTO ACCOUNT, BUT NOT SIGNIFICANT IF THE PAIRING WAS NOT DONE (OR INCORRECTLY IGNORED!).

NOTE: MANY RESEARCHERS DO NOT TAKE MATCHING INTO ACCOUNT WHEN DOING THE ANALYSIS. REFERENCE: Peter C. Austin, “A critical appraisal of propensity-score matching in the medical literature between 1996 and 2003,” Statistics in Medicine, Vol. 27, pp. 2037-2049, 2008. “However, the analysis of propensity-score-matched samples requires statistical methods appropriate for matched-pairs data. We critically evaluated 47 articles that were published between 1996 and 2003 in the medical literature and that employed propensity-score matching. We found that only two of the articles reported the balance of baseline characteristics between treated and untreated subjects in the matched sample and used the correct statistical methods appropriate for the analysis of matched data when estimating the treatment effect and its statistical significance.”

4.3. ESTIMATION OF SAMPLE SIZE

A DIVERSION: ESTIMATION OF SAMPLE SIZE (NEEDED TO ASSESS DESIGN EFFICIENCY (PRECISION RELATIVE TO SAMPLE SIZE) AND CAPABILITY (POWER TO DETECT EFFECTS OF ANTICIPATED MAGNITUDE))

ESTIMATION OF SAMPLE SIZE FOR DESCRIPTIVE SURVEYS

A DESCRIPTIVE SURVEY IS ONE INTENDED TO PRODUCE ESTIMATES OF CHARACTERISTICS (E.G., MEANS, PROPORTIONS) OF A POPULATION OR SUBPOPULATION. THE SAMPLE DESIGN AND SAMPLE SIZE FOR THE SURVEY ARE DETERMINED BY MEANS OF A STATISTICAL PRECISION ANALYSIS.

THERE ARE TWO TYPES OF ESTIMATES: POINT ESTIMATES AND INTERVAL ESTIMATES. THE PRECISION OF A POINT ESTIMATE IS INDICATED BY ITS STANDARD ERROR (SQUARE ROOT OF THE VARIANCE OF THE ESTIMATE, IN REPEATED SAMPLING). THE PRECISION OF AN INTERVAL ESTIMATE IS INDICATED BY THE WIDTH OF A CONFIDENCE INTERVAL (OF A SPECIFIED CONFIDENCE COEFFICIENT).

(AN ESTIMATE IS A RANDOM VARIABLE. WHEN SPEAKING OF THE RANDOM VARIABLE AS A CONCEPT (OR A FORMULA OR A PROCEDURE), WE SHALL GENERALLY USE THE TERM “ESTIMATOR,” AND WHEN SPEAKING OF A REALIZATION OF THE RANDOM VARIABLE (I.E., A PARTICULAR NUMERICAL VALUE CALCULATED FROM A SAMPLE) WE SHALL GENERALLY USE THE TERM “ESTIMATE.”)

THE ESTIMATES ARE DERIVED FROM A MATHEMATICAL MODEL OF THE SURVEY DESIGN, AND ARE CALLED DESIGN-BASED ESTIMATES.

STATISTICAL PRECISION ANALYSIS: ESTIMATE THE SAMPLE SIZE REQUIRED TO PRODUCE A CONFIDENCE INTERVAL OF SPECIFIED SIZE (WIDTH) FOR A MEASURE OF INTEREST (E.G., A POPULATION MEAN OR A DOUBLE DIFFERENCE) OR GIVEN A SAMPLE SIZE, ESTIMATE THE SIZE OF THE CONFIDENCE INTERVAL.

THE FOLLOWING SAMPLE SIZE ESTIMATES REFER TO THE CASE OF AN EXPERIMENTAL DESIGN OR A SAMPLE SURVEY BASED ON PROBABILITY SAMPLING.

THE BASIC FORMULA FOR DETERMINING SAMPLE SIZE IS:

WHERE

n = sample size (of second-stage sample units (or of ultimate sample units, called elements))

μ = population mean

σ² = population variance

= design-based sample estimate (e.g., when estimating the population mean with a simple random sample, this is the sample mean, )

1 – α = confidence coefficient (e.g., .95 for α = .05), is the probability that the confidence interval includes the true value μ

z_1-α = normal deviate for which Prob(z < z_1-α) = 1-α (e.g., z_1-α

= 1.96 for α = .05)

E = error bound (half-width of confidence interval having confidence coefficient 1 – α)

deff = Kish’s design effect (ratio of the variance of the mean (of elements) for the design to the variance of the mean for a simple random sample of the same size).

TO DETERMINE THE SAMPLE SIZE, n, GIVEN VALUES FOR THE OTHER PARAMETERS, SOLVE THE PRECEDING EQUATION FOR n. IGNORING THE FINITE POPULATION CORRECTION (FPC), THIS YIELDS:

NOTE THAT THIS QUANTITY DEPENDS ON THE VARIANCE, NOT ON THE MEAN.

TO DETERMINE SAMPLE SIZE FOR A SURVEY INVOLVING A NUMBER OF OUTCOMES OF INTEREST, ESTIMATE n FOR VARYING σ², E AND deff FOR OUTCOMES OF INTEREST, AND SELECT A VALUE OF n THAT ACCOMMODATES THE PRECISION DESIRES AND THE AVAILABLE BUDGET. FOR TWO-STAGE SAMPLING, deff = 1 + (m-1)icc, WHERE m DENOTES THE (CONSTANT) NUMBER OF SECOND-STAGE UNITS SELECTED FROM EACH SELECTED FIRST-STAGE SAMPLE UNIT AND icc DENOTES THE FIRST-STAGE INTRA-UNIT CORRELATION COEFFICIENT.

NOTE THAT FOR TWO-STAGE SAMPLING, n IN THE PRECEDING FORMULA IS THE NUMBER OF SECOND-STAGE SAMPLE UNITS. (IN SAMPLING WITH MORE THAN TWO STAGES, IT IS THE NUMBER OF FINAL-STAGE (OR ULTIMATE) SAMPLE UNITS.)

THIS EXAMPLE ASSUMES THAT THE VALUE OF m IS CONSTANT. IN GENERAL, IT DOES NOT HAVE TO BE, BUT FOR MANY SURVEYS IT IS. AN OPTIMAL VALUE OF m MAY BE OBTAINED BY TAKING INTO ACCOUNT THE RELATIVE COST OF SAMPLING FIRST- AND SECOND-STAGE SAMPLE UNITS AND THE INTRA-GROUP CORRELATION COEFFICIENT. THE FORMULA IS

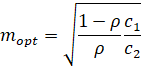
WHERE c₁ DENOTES THE COST OF SAMPLING A FIRST-STAGE UNIT AND c₂ DENOTES THE COST OF SAMPLING A SECOND-STAGE UNIT (SO THAT THE TOTAL SAMPLING COST IS C = c₁n + c₂nm). IN MANY PRACTICAL SITUATIONS, THE VALUE OF m IS RATHER SMALL, E.G., IN THE RANGE 5 – 15. (IF TRAVEL COSTS ARE SUBSTANTIAL, THE MINIMUM VALUE OF m WOULD BE THE NUMBER OF INTERVIEWS AN INTERVIEWER COULD CONDUCT IN A DAY.)

EXAMPLE

CONSIDER THE CASE OF SAMPLING FOR PROPORTIONS, IN WHICH IT IS DESIRED TO ESTIMATE THE SAMPLE SIZE REQUIRED TO OBTAIN A CONFIDENCE INTERVAL OF HALF-WIDTH E = .05. IN THIS CASE THE VALUE OF THE STANDARD DEVIATION IS ASSUMED TO BE σ = .5 (IN SAMPLING FOR PROPORTIONS THE MAXIMUM VALUE OF σ = SQRT(p(1-p)) OCCURS FOR p = .5). LET US ASSUME THAT WE ARE USING TWO-STAGE SAMPLING WITH A SECOND-STAGE SAMPLE OF m = 10 TAKEN FROM EACH SAMPLED FIRST-STAGE UNIT. FOR THE VALUE IF THE INTRA-UNIT CORRELATION OF icc = .1, THIS CORRESPONDS TO A VALUE OF deff = 1 + (m-1)icc = 1.9. WE ASSUME A STANDARD VALUE OF α = .05 (CONFIDENCE COEFFICIENT = .95). FOR THESE VALUES WE OBTAIN A VALUE OF n = 729 SECOND-STAGE UNITS AS THE REQUIRED SAMPLE SIZE (SO THE NUMBER OF FIRST-STAGE UNITS = 729/m = 729/10 = 73).

ESTIMATION OF SAMPLE SIZE FOR ANALYTICAL SURVEYS

AN ANALYTICAL SURVEY IS INTENDED TO PROVIDE INFORMATION ABOUT A PROCESS, SUCH AS THE IMPACT OF A PROGRAM INTERVENTION. THIS IS DONE BY USING SURVEY DATA TO ESTIMATE CHARACTERISTICS OF A MODEL OF THE PROCESS (WHICH IS CONCEIVED TO HAVE GENERATED THE PHYSICAL POPULATION AT HAND). THE SAMPLE DESIGN AND SAMPLE SIZE IS DETERMINED BY MEANS OF A STATISTICAL POWER ANALYSIS.

ESTIMATES BASED ON AN ANALYTICAL SURVEY MAY BE DESIGN-BASED ESTIMATES (BASED ON A MATHEMATICAL MODEL OF THE SURVEY DESIGN), MODEL-BASED OR MODEL-DEPENDENT ESTIMATES (BASED ON THE MODEL OF A PROCESS) OR MODEL-ASSISTED ESTIMATES (BASED ON BOTH THE SURVEY DESIGN AND THE PROCESS MODEL).

STATISTICAL POWER ANALYSIS: ESTIMATE THE SAMPLE SIZE REQUIRED TO PRODUCE A SPECIFIED LEVEL OF POWER FOR A TEST OF HYPOTHESIS ABOUT A MEASURE OF INTEREST (E.G., WHETHER A TREATMENT EFFECT IS ZERO) OR GIVEN A SAMPLE SIZE, ESTIMATE THE POWER OF SUCH A TEST. THE POWER OF A TEST IS THE PROBABILITY OF (CORRECTLY) REJECTING A NULL HYPOTHESIS WHEN IT IS FALSE. (NOTE THAT THE POWER DEPENDS ON WHAT THE ALTERNATIVE IS.)

THE FORMULAS PRESENTED BELOW REFER TO THE CASE OF AN EXPERIMENTAL DESIGN OR A SAMPLE SURVEY BASED ON PROBABILITY SAMPLING. THE FORMULAS DO NOT INCLUDE A FINITE POPULATION CORRECTION (FPC), SINCE THE GOAL IS TO MAKE INFERENCES ABOUT A HYPOTHETICAL PROCESS THAT GENERATES THE PARTICULAR FINITE POPULATION ON HAND, AND NOT INFERENCES ABOUT THIS PARTICULAR POPULATION.

STATISTICAL POWER ANALYSIS

THE FORMULA FOR DETERMINING SAMPLE SIZE FOR A PRETEST-POSTTEST-COMPARISON-GROUP EXPERIMENTAL DESIGN IS:

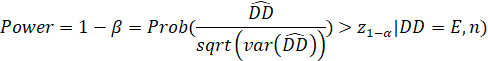
WHERE

n = sample size (for second-stage units)

DD = true (population) value of the double difference

= design-based estimate of the population double difference (e.g., if simple random sampling is used in the four design groups, then this would be the sample double difference)

α = probability of a type 1 error of deciding that the true effect exceeds zero when it is in fact zero (i.e., the significance level of the test of hypothesis that DD equals zero); a standard value is α = .05.

E = minimum detectable effect (the minimum effect magnitude it is desired to detect with high power);

β = probability of a type 2 error of deciding that the true effect does not exceed E when it in fact equals E. Power = 1 – β; a standard value is β = .1 (power 90%).

z_1-α, z_1-β and deff as before; e.g., z_1-α = 1.6449 for α = .05 (one-sided test), z_1-β = 1.2816 for β = .1.

intergroup correlations ρ_ij defined earlier.

NOTE THAT FOR STATISTICAL POWER ANALYSIS, ONE-SIDED TESTS OF HYPOTHESIS ARE GENERALLY USED, SINCE THE DIRECTION OF CHANGE IS GENERALLY KNOWN.

THE EXPRESSION FOR IS

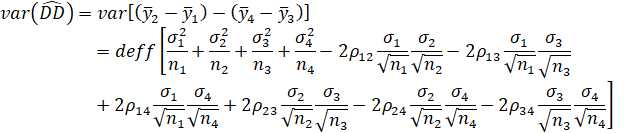
WHERE, AS BEFORE, deff, KISH’S DESIGN EFFECT, IS THE RATIO OF THE VARIANCE OF THE SAMPLE MEAN FOR A DESIGN GROUP UNDER THE SAMPLE DESIGN TO THE VARIANCE OF THE SAMPLE MEAN FOR A DESIGN GROUP FOR A SIMPLE RANDOM SAMPLE OF THE SAME (ELEMENT) SAMPLE SIZE.

IF AND , THIS EXPRESSION REDUCES TO

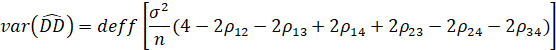
SOLVING THE “POWER” EQUATION FOR n (ASSUMING THE SAME SAMPLE SIZE FOR EACH OF THE FOUR DESIGN GROUPS) YIELDS:

FOR EACH OF THE FOUR DESIGN GROUPS.

NOTE THAT THE PRECEDING FORMULA DEPENDS (AMONG OTHER THINGS) ON THE DESIGN AND THE ESTIMATOR. FOR MULTI-STAGE SURVEYS, THE SAMPLE SIZE MUST BE DETERMINED FOR EACH LEVEL OF SAMPLING. THIS IS DONE BY DETERMINING AN OPTIMAL VALUE OF THE WITHIN-FIRST-STAGE-UNIT SAMPLE SIZE, GIVEN THE RELATIVE COSTS OF SAMPLING THE FIRST- AND SECOND-STAGE SAMPLE UNITS, AND THE INTRA-UNIT CORRELATION COEFFICIENT, AS DESCRIBED EARLIER.

IN GENERAL, WE NEED TO SPECIFY A MINIMUM DETECTABLE EFFECT, E, THE STANDARD DEVIATION OF THE VARIABLE OF INTEREST, THE INTRA-GROUP CORRELATIONS AND THE DESIGN EFFECT, deff. THEN, SELECT A VALUE FOR n SUCH THAT THE MINIMUM DETECTABLE EFFECT, E, CAN BE DETECTED WITH ADEQUATE POWER, WITHIN THE AVAILABLE BUDGET.

THE SAMPLE SIZE MAY DIFFER FOR EACH OUTCOME VARIABLE (OR ESTIMATOR) OF INTEREST (SINCE ITS STATISTICAL PROPERTIES (VARIANCE, CORRELATIONS) MAY DIFFER, AND THE VALUE OF E MAY ALSO DIFFER).

SINCE THE MDE, E, WILL DIFFER FOR DIFFERENT OUTCOME VARIABLES, THE DESIGN SHOULD ASSURE ADEQUATE POWER FOR DETECTING THE MDE FOR ALL IMPORTANT OUTCOME VARIABLES. THERE IS NO POINT TO CONDUCTING A SURVEY THAT HAS A LOW PROBABILITY (POWER) FOR DETECTING AN IMPACT OF A REASONABLY ANTICIPATED SIZE.

THE PRECEDING SAMPLE-SIZE FORMULAS ARE APPROPRIATE FOR DETERMINING IMPACT USING A DOUBLE-DIFFERENCE ESTIMATE OF IMPACT IN AN EXPERIMENTAL DESIGN OR SAMPLE SURVEY BASED ON PROBABILITY SAMPLING. FOR A QUASI-EXPERIMENTAL DESIGN OF THE SAME STRUCTURE, THE ESTIMATE OF IMPACT WILL DIFFER FROM THE “RAW” DOUBLE-DIFFERENCE ESTIMATE (IT WILL BE BASED ON A PROPERLY STRATIFIED DESIGN OR REGRESSION MODEL), AND THE POWER AND SAMPLE SIZE ESTIMATES WILL BE DIFFERENT. THE STANDARD APPROACH IS TO USE THE SAMPLE-SIZE ESTIMATE CORRESPONDING TO THE ED USING THE PRECEDING FORMULA (SINCE THE STRATIFICATION OR REGRESSION MODEL USED TO ANALYZE THE QED DATA WILL NOT BE KNOWN UNTIL AFTER THE SURVEY DATA HAVE BEEN COLLECTED AND ANALYZED).

FOR A QED BASED ON A REGRESSION MODEL INCLUDING VARIABLES (“COVARIATES”) THAT AFFECT THE PRECISION OF A DOUBLE-DIFFERENCE ESTIMATE, THE REQUIRED SAMPLE SIZE MAY BE LESS THAN THE ESTIMATE PRODUCED BY THE PRECEDING FORMULA (SINCE, WHEN ADDITIONAL VARIABLES ARE INCLUDED IN A MODEL, THE VARIANCE OF THE DOUBLE-DIFFERENCE ESTIMATE MAY DECREASE). THIS DOES NOT HAVE TO BE THE CASE, HOWEVER, SINCE THE QED ANALYSIS WILL TYPICALLY INVOLVE INTERCORRELATED (MULTICOLLINEAR) EXPLANATORY VARIABLES, AND IT IS DIFFICULT TO PREDICT HOW THE INCLUSION OF ADDITIONAL VARIABLES WILL AFFECT THE PRECISION OF A PARTICULAR COEFFICIENT. (ALSO, FOR A QED, THE RESPONSE MODEL IS RATHER COMPLEX, TYPICALLY CONSISTING OF A FIRST-STEP SELECTION MODEL AND A SECOND-STEP OUTCOME MODEL.)

EXAMPLE:

FOR SAMPLING FOR PROPORTIONS, WE MAY SPECIFY “WORST CASE” OF p= .5 AND E.G., E AS .1. ASSUME 2-STAGE SAMPLING WITH m=10 2^ND-STAGE UNITS SELECTED PER SELECTED 1^ST-STAGE UNIT, AND INTRA-UNIT CLUSTER CORRELATION COEFFICIENT icc = .1, SO deff = 1 + (m – 1) icc = 1.9. ASSUME α = .05 AND β = .1 (POWER = 1 – β = 90%).

IF THE SAME HOUSEHOLDS ARE INTERVIEWED IN BOTH SURVEY ROUNDS, E.G., ρ₁₂ = ρ₃₄ = .5. IF MATCHING IS DONE AT THE VILLAGE LEVEL, E.G., ρ₁₃ = ρ₂₄ = .3. FOR THESE CASES, REASONABLE VALUES FOR THE REMAINING CORRELATIONS ARE ρ₁₄ = ρ₂₃ = ( .5)( .3) = .15.

FOR A 1-ROUND, 2-GROUP DESIGN, ESTIMATING THE DIFFERENCE IN MEANS OF TREATMENT AND CONTROL GROUPS, n (per design group) = 570 2^ND-STAGE UNIT, OR 570/m = 570/10 = 57 1^ST-STAGE UNITS.

FOR A 2-ROUND, 4-GROUP DESIGN (PRETEST-POSTTEST-MATCHED-COMPARISON-GROUP DESIGN) USING A DOUBLE-DIFFERENCE ESTIMATOR, n = 570 2^ND-STAGE UNITS, OR 570/m = 570/10 = 57 1^ST-STAGE UNITS.

IF THE FOUR DESIGN-GROUP SAMPLES ARE INDEPENDENT AND THERE IS NO MATCHING (SO ZERO INTER-GROUP CORRELATIONS): n = 1627 2^ND STAGE UNITS, OR 1627/m = 1627/10 = 163 1^ST STAGE UNITS.

NOTE THE BIG DIFFERENCE IN SAMPLE SIZE, DEPENDING ON WHETHER MATCHING IS USED.

KEY POINT: FOR CORRECT SAMPLE SIZE ESTIMATION, THE SAMPLE SIZE FORMULA MUST BE DERIVED FROM THE SAMPLE DESIGN. (EXAMPLES ABOUND WHERE RESEARCHERS USE THE POWER FORMULA FOR A SINGLE-DIFFERENCE ESTIMATE BASED ON A SINGLE-STAGE SURVEY TO ESTIMATE THE POWER FOR A DOUBLE-DIFFERENCE ESTIMATOR BASED ON A TWO-ROUND SURVEY.)

THE PRECEDING EXAMPLES ILLUSTRATE HOW MATCHING CAN INCREASE PRECISION AND POWER IN AN ED OR QED.

WE SHALL NOW ADDRESS IN DETAIL THE ISSUE OF USING MATCHING TO REDUCE BIAS IN A QED.

4.4. THE USE OF MATCHING TO REDUCE BIAS (IN A QED)

MATCHING IS DONE WITH RESPECT TO VARIABLES THAT ARE KNOWN PRIOR TO SAMPLING, FOR USE IN SAMPLE DESIGN. THESE ARE KNOWN AS DESIGN VARIABLES, COVARIATES, CORRELATES, OR OBSERVABLES. THE PRECEDING DISCUSSION FOCUSED ON THE ROLE OF MATCHING RELATIVE TO INCREASING PRECISION AND POWER, IN BOTH EDs AND QEDs. WE SHALL NOW DISCUSS HOW MATCHING MAY BE USED TO REDUCE BIAS IN A QED. TO ACCOMPLISH THIS WE WILL DISCUSS SOME ASPECTS OF CAUSAL MODELING AND CAUSAL ANALYSIS.

A COVARIATE IS AN EXPLANATORY VARIABLE, OTHER THAN TREATMENT (THE PRINCIPAL EXPLANATORY VARIABLE OF INTEREST), THAT MAY AFFECT OUTCOME (BUT IS NOT AFFECTED BY IT) ACCORDING TO A CAUSAL MODEL. THIS DEFINITION (IN WHICH THE OUTCOME VARIABLE DOES NOT AFFECT THE COVARIATES) APPLIES TO A SPECIAL CASE – A RECURSIVE MODEL. A MORE GENERAL CASE, THE NONRECURSIVE MODEL (OR SIMULTANEOUS MODEL), ALLOWS FOR THE OUTCOME AND EXPLANATORY VARIABLES TO INFLUENCE EACH OTHER. THIS PRESENTATION IS LIMITED TO RECURSIVE MODELS. (WITH RESPECT TO MATCHING AND SURVEY DESIGN (THE TOPIC OF THIS PRESENTATION), THE CONCLUSIONS ARE THE SAME IN BOTH CASES. IN ANALYSIS, THE RECURSIVE AND NONRECURSIVE CASES ARE QUITE DIFFERENT.)

IN THIS PRESENTATION WE ARE CONCERNED HERE WITH MATCHING IN DESIGN, NOT WITH MATCHING IN ANALYSIS. MATCHING IN THE ANALYSIS PHASE (EX POST) DIFFERS SOMEWHAT FROM MATCHING IN THE DESIGN PHASE (EX ANTE).

· IN THE DESIGN PHASE, MATCHING IS OFTEN DONE AT A HIGH LEVEL OF SAMPLING (E.G., VILLAGE, SCHOOL, HOSPITAL), FOR WHICH PRE-SURVEY DATA ARE AVAILABLE (FOR USE IN DESIGN)

· IN THE ANALYSIS PHASE, THERE ARE MANY MORE VARIABLES (COVARIATES) THAT MAY BE USED IN “MATCHING ESTIMATORS”

· IN THE DESIGN PHASE, WE EXAMINE PRIMARILY A SINGLE, SIMPLE ESTIMATOR (E.G., THE DOUBLE-DIFFERENCE ESTIMATOR NOT BASED ON COVARIATES), WHEREAS IN ANALYSIS PHASE, WE ARE CONCERNED WITH A NUMBER OF DIFFERENT AND MORE COMPLEX ESTIMATORS OF IMPACT

· MATCHING IN EITHER THE DESIGN OR THE ANALYSIS PHASE MAY INCLUDE CONSIDERATION OF THE PROPENSITY SCORE (PROBABILITY OF SELECTION FOR TREATMENT, GIVEN OBSERVED COVARIATES AFFECTING SELECTION FOR TREATMENT). IN THE DESIGN PHASE, WITH MANY FEWER VARIABLES AT HAND, THE PROPENSITY SCORE MAY BE ESTIMATED WITH MUCH LESS ACCURACY THAN IN THE ANALYSIS PHASE, WHEN ALL OF THE VARIABLES OF THE QUESTIONNAIRE ARE AVAILABLE.

TO SHOW HOW MATCHING MAY REDUCE BIAS, WE NEED TO CONSIDER A CAUSAL MODEL THAT RELATES BIAS TO THE COVARIATES (DENOTED BY X (A VECTOR)).

NOTATION: USE CAPITAL LETTERS FOR RANDOM VARIABLES, LOWER-CASE FOR REALIZATIONS (OBSERVATIONS). (THIS WILL NOT ALWAYS BE DONE CONSISTENTLY IN THIS PRESENTATION, SINCE AUTHORS ARE NOT CONSISTENT IN THEIR NOTATION (EVEN THE SAME AUTHOR IN DIFFERENT ARTICLES), AND EXAMPLES PRESENTED HERE TEND TO USE THE SAME NOTATION AS IN THE ORIGINAL SOURCES (TO FACILITATE COMPARISON OF THIS MATERIAL TO THE ORIGINAL SOURCES).)

4.5. CAUSAL MODELING

A CAUSAL MODEL IS A MATHEMATICAL MODEL THAT DESCRIBES CAUSAL RELATIONSHIPS AMONG VARIABLES. THERE ARE A NUMBER OF CAUSAL THEORIES AND DEFINITIONS OF CAUSAL RELATIONSHIPS. IT APPEARS IMPOSSIBLE TO CONSTRUCT A UNIVERSALLY ACCEPTABLE DEFINITION OF WHAT A “CAUSE” IS, AND AS A RESULT THERE ARE A NUMBER OF THEORIES OF CAUSATION.

CAUSAL MODELING FALLS MAINLY INTO TWO CATEGORIES – DETERMINISTIC OR “LOGICAL” CAUSAL MODELS, AND PROBABILITY-BASED MODELS, WHICH INVOLVE CONSIDERATION OF STOCHASTIC OUTCOMES AND THE USE OF STATISTICAL ANALYSIS TO ESTIMATE THE MAGNITUDE OF CAUSAL EFFECTS. THIS PRESENTATION IS CONCERNED WITH THE LATTER CATEGORY OF CAUSAL MODELING.

A STANDARD APPROACH IS TO DEFINE CAUSES AND CAUSATION IN TERMS OF PROBABILITY DISTRIBUTIONS. THESE THEORIES ARE KNOWN UNDER THE RUBRIC OF “PROBABILISTIC CAUSATION.” A SIMPLE DEFINITION OF CAUSATION IS THAT AN EVENT C IS A CAUSE OF AN EVENT E IF AND ONLY IF P(E|C)>P(E|~C), WHERE THE TILDE (~) REPRESENTS COMPLEMENTATION (NEGATION, “NOT”). (THAT IS, THE OCCURRENCE/PRESENCE OF ONE EVENT “RAISES THE PROBABILITY” OF ANOTHER.) THIS SIMPLE DEFINITION ENCOUNTERS DIFFICULTIES. FIRST, IT IS SYMMETRIC. THAT IS, IF P(E|C)>P(E|~C) THEN P(C|E)>P(C|~E), I.E., IF C IS A CAUSE OF E THEN E IS A CAUSE OF C. ANOTHER PROBLEM IS THAT OF “SPURIOUS CAUSES”: IF C AND E ARE BOTH CAUSED BY A THIRD FACTOR, A, THEN IT IS POSSIBLE THAT P(E|C)>P(E|~C) EVEN THOUGH C DOES NOT CAUSE E. THE VARIABLE A, WHICH AFFECTS BOTH THE CAUSE C AND THE RESULT E IS CALLED A CONFOUNDING FACTOR, OR “CONFOUNDER.”

ANOTHER PROBLEM WITH THE PRECEDING DEFINITION IS “SIMPSON’S PARADOX”: FOR ANY DATA SET, IT IS POSSIBLE TO REVERSE ANY CONDITIONAL PROBABILISTIC RELATIONSHIP BETWEEN TWO VARIABLES WITH THE ADDITION OF ANOTHER VARIABLE TO THE DATA SET. FOR EXAMPLE, THE EXPECTED GRADES FOR MALES AT A SCHOOL MAY BE HIGHER THAN THOSE FOR FEMALES OVERALL, BUT IF CONDITIONED ON COURSE SUBJECT, THE EXPECTED GRADES FOR FEMALES MAY BE HIGHER IN EVERY COURSE SUBJECT THAN FOR MALES (E.G., IF MALES TEND TO TAKE EASIER COURSES). (IN SYMBOLS, P(E|C)<P(E|~C), BUT P(E|C&B)>P(E|~C&B) AND P(E|C&~B)>P(E|~C&~B).) ADDITIONAL REVERSALS MAY BE CAUSED BY ADDITIONAL VARIABLES. WHILE SIMPSON’S PARADOX MAY NOT OCCUR VERY OFTEN, IT IS NOT AT ALL SURPRISING. IT ILLUSTRATES THE FACT THAT IT I S NOT POSSIBLE TO INFER CAUSAL RELATIONSHIPS FROM ANALYSIS OF DATA ALONE (OR FROM PROBABILISTIC RELATIONSHIPS). ONCE A CAUSAL MODEL IS SPECIFIED, SIMPSON’S SO-CALLED “PARADOX” IS RESOLVED.

IT MAY BE THOUGHT THAT THE PRECEDING ISSUE OF THE SYMMETRY OF A PROBABILISTIC RELATIONSHIP CAN BE RESOLVED BY PLACING AN EXTERNAL CONSTRAINT (OUTSIDE OF THE PROBABILITY RELATIONSHIP) THAT ONE VARIABLE MAY BE A CAUSE OF ANOTHER VARIABLE ONLY IF IT IS TEMPORALLY PRECEDENT. EVEN TEMPORAL PRECEDENCE IS NOT SUFFICIENT TO ESTABLISH A CAUSAL RELATIONSHIP. FOR EXAMPLE, A BAROMETER READING FALLS PRIOR TO A STORM, BUT THE BAROMETER READING DOES NOT CAUSE THE STORM. (FOR ADDITIONAL INFORMATION ON PROBABILISTIC DEFINITIONS OF CAUSALITY, SEE THE WIKIPEDIA ARTICLE ON GRANGER CAUSALITY, OR THE TIME-SERIES TEXTS BY LUTKEPOHL (NEW INTRODUCTION TO MULTIPLE TIME SERIES ANALYSIS) OR HAMILTON (TIME SERIES ANALYSIS).)

IT MAY BE SAID THAT A CAUSAL RELATIONSHIP EXISTS BETWEEN TWO VARIABLES IF THEY ARE PROBABILISTICALLY DEPENDENT WHEN RANDOMIZATION-BASED REALIZATIONS (FORCED CHANGES, SELECTIONS) ARE MADE IN ONE OF THEM. THIS DEFINITION WORKS AFTER A FASHION, BUT IT HAS DRAWBACKS: IT INVOLVES AN EXPERIMENT, AND IT DOES NOT UNEQUIVOCALLY ESTABLISH CAUSALITY (SINCE AN HYPOTHESIZED CAUSAL RELATIONSHIP MAY BE ESTABLISHED ONLY AS THE RESULT OF A STATISTICAL DECISION). SOME WOULD REQUIRE THAT FORCED CHANGES (CONTROLLED MANIPULATIONS), NOT JUST RANDOM SELECTIONS, BE MADE TO ESTABLISH A CAUSAL RELATIONSHIP. SOME OBJECT TO THIS DEFINITION SINCE IT CONFLATES THE CONCEPT OF CAUSALITY WITH A MEANS FOR MEASURING IT. UNFORTUNATELY, NO BETTER DEFINITION OF CAUSALITY IS AVAILABLE.

IN CAUSAL ANALYSIS, THE DIFFICULTY IN DEFINING A (REAL) CAUSE AND A (REAL) CAUSAL RELATIONSHIP ARE RESOLVED – OR SIDESTEPPED – BY DEFINING THESE TERMS IN THE CONTEXT OF A MODEL. THE SITUATION IS SIMILAR TO THE DIFFICULTY OF DEFINING A PROBABILITY IN TERMS OF THE RESULT OF A SERIES OF EXPERIMENTS (SUCH AS REPEATED TOSSING OF COIN, AND DEFINING THE PROBABILITY OF A HEAD AS THE RATIO OF HEADS TO TOTAL TOSSES, IN A VERY LONG SERIES OF TOSSES), VS. DEFINING IT IN TERMS OF SET AND MEASURE THEORY. IN THIS PRESENTATION, A CAUSAL RELATIONSHIP WILL BE CONSIDERED TO BE A “PRIMITIVE,” I.E., IT IS NOT DEFINED IN TERMS OF MORE ELEMENTARY CONCEPTS.

(THE ISSUE OF FORCED CHANGES VS. RANDOM SELECTIONS SHOULD BE ADDRESSED. LOOSELY SPEAKING, IT MAY BE SAID THAT RACE IS NOT A “CAUSE” AND SOME OTHER VARIABLE (SINCE RACE CANNOT BE FORCIBLY SET), BUT THAT THERE MAY BE A “CAUSAL RELATIONSHIP” BETWEEN RACE AND A VARIABLE (IF THERE IS A RELATIONSHIP OF THE VARIABLE TO RACE WHEN RACE IS RANDOMLY SELECTED). IN THIS CASE, RACE IS A SURROGATE FOR A COLLECTION OF OTHER VARIABLES THAT MAY BE VIEWED AS CAUSES FROM THE “FORCED-CHANGE” POINT OF VIEW.)

A CAUSAL RELATIONSHIP IS ALWAYS RELATIVE TO ALL OTHER VARIABLES THAT MAY AFFECT THE CAUSAL VARIABLE OR THE EFFECT VARIABLE, I.E., THE VARIABLES THAT DEFINE THE “SETTING” OR “ENVIRONMENT” IN WHICH THE CAUSE-EFFECT RELATIONSHIP IS BEING STUDIED. THE “CAUSAL EFFECT” OF ONE VARIABLE ON ANOTHER MAY BE VIEWED EITHER IN THE CONTEXT OF HOLDING ALL OTHER VARIABLES CONSTANT (A CONDITIONAL CAUSAL EFFECT), OR AVERAGING OVER THEM IN SOME POPULATION (AN AVERAGE CAUSAL EFFECT).

SINCE THE 1970s, MUCH WORK HAS BEEN DONE IN THE FIELD OF CAUSAL MODELING AND ANALYSIS. IN THIS PRESENTATION, WE ARE CONCERNED ONLY WITH THEORIES OF PROBABILISTIC CAUSATION THAT LEND THEMSELVES TO THE USE OF STATISTICAL METHODS TO ASSESS THE MAGNITUDES OF CAUSAL EFFECTS. THE MOST SIGNIFICANT EARLY WORK WAS THAT OF ROSENBAUM AND RUBIN (R&R, 1983), WHO EXTENDED NEYMAN’S THEORY OF POTENTIAL OUTCOMES (“COUNTERFACTUALS”) FROM THE REALM OF DESIGNED EXPERIMENTS TO THE ANALYSIS OF OBSERVATIONAL DATA (PASSIVELY OBSERVED DATA).

THERE ARE TWO SIGNIFICANT PROBLEMS ASSOCIATED WITH THE ROSENBAUM-RUBIN APPROACH. FIRST, IT IS FOUNDED ON ASSUMPTIONS ABOUT POTENTIAL OUTCOMES; SOME PEOPLE HAVE DIFFICULTY IN ACCEPTING THIS FRAMEWORK, AND PREFER A THEORY THAT IS EXPRESSED IN TERMS OF ACTUAL OBSERVATIONS (AND DOES NOT INVOLVE EXPLICIT CONSIDERATION OF HYPOTHETICAL COUNTERFACTUAL OBSERVATIONS). THE SECOND PROBLEM IS THAT THE THEORY DOES NOT LEND ITSELF TO DETAILED SPECIFICATION AND ANALYSIS OF CAUSAL RELATIONSHIPS, I.E., OF INCORPORATING DETAILED (VARIABLE-TO-VARIABLE) PRIOR KNOWLEDGE OR BELIEFS ABOUT THE NATURE OF THE CAUSAL RELATIONSHIPS IN THE SYSTEM UNDER STUDY. WITH THE ROSENBAUM-RUBIN THEORY, IT IS NECESSARY TO MAKE AN ASSUMPTION ABOUT CONDITIONAL INDEPENDENCE OF POTENTIAL OUTCOMES AND TREATMENT GIVEN COVARIATES, BUT THE THEORY DOES NOT INCLUDE A MEANS FOR INVESTIGATION OF CONDITIONS UNDER WHICH THE CONDITIONAL INDEPENDENCE MAY HOLD. MANY RESEARCHERS WOULD PREFER TO MAKE A DETAILED SPECIFICATION OF CAUSAL RELATIONSHIPS (SUCH AS A PATH DIAGRAM OR A SET OF STRUCTURAL EQUATIONS), AND HAVE THE THEORY PROVIDE A MEANS FOR ASSESSING WHETHER CONDITIONAL INDEPENDENCE HOLDS, GIVEN THEIR SPECIFICATION.

IF ONE VARIABLE IS CAUSALLY RELATED TO ANOTHER, WE USE THE EXPRESSION THAT IT “AFFECTS” (OR “IS AFFECTED BY”) THE OTHER VARIABLE. IF THERE IS AN APPARENT RELATIONSHIP BETWEEN THE TWO VARIABLES (E.G., THEY ARE CORRELATED), BUT IT IS NOT CLEAR THAT IT IS A CAUSAL RELATIONSHIP, WE USE THE EXPRESSION THAT ONE VARIABLE “IS RELATED TO” OR “IS ASSOCIATED WITH” OR “IS CORRELATED WITH” THE OTHER.

MUCH OF STATISTICS IS DESCRIPTIVE OR ASSOCIATIVE INFERENCE, WHERE IT IS OF INTEREST TO ESTIMATE THE STRENGTH OF ASSOCIATIVE RELATIONSHIPS. IN MANY TECHNICAL DISCUSSIONS, REFERENCE IS MADE TO “EFFECTS,” WITHOUT MENTIONING WHETHER THEY ARE ASSOCIATIVE OR CAUSAL. OFTEN, THE TERM “TREATMENT” AND “CAUSE” ARE USED INTERCHANGEABLY. HOLLAND (OP. CIT.) ASSERTS THAT ATTRIBUTES MAY NOT BE CAUSES IF THEY CANNOT BE MANIPULATED. (AS REMARKED EARLIER, THIS POSITION APPEARS TO BE A LITTLE EXTREME, IN VIEW OF THE EXAMPLE THAT THE DIURNAL MOTION OF THE SUN IS A DIRECT CAUSE OF MANY THINGS, BUT IT CANNOT BE MANIPULATED.) IN THIS PRESENTATION, WE FOCUS ON ESTIMATION OF THE EFFECTS OF CAUSES THAT ARE IDENTIFIED IN A CAUSAL MODEL, NOT ON THE PROBLEM OF DECIDING WHETHER A VARIABLE IS A CAUSE OF A SPECIFIED EFFECT (E.G., WHETHER SMOKING IS A CAUSE OF LUNG CANCER). THAT IS, WE FOCUS ON THE ESTIMATION OF THE EFFECTS OF CAUSES, NOT ON DECIDING ON THE CAUSES OF EFFECTS.

THE TERMS “CAUSAL MODELING” AND “CAUSAL ANALYSIS” ARE OFTEN USED INTERCHANGEABLY. “CAUSAL MODELING” TENDS TO REFER TO THE ACTIVITY OF SPECIFICATION AND DESCRIPTION OF CAUSAL MODELS (E.G., BY MEANS OF DIRECTED GRAPHS AND DESCRIPTIONS OF CONDITIONAL PROBABILITY DISTRIBUTIONS (SUCH AS MODEL EQUATIONS)) AND TO DETERMINATION OF WHICH CAUSAL EFFECTS ARE ESTIMABLE, WHEREAS “CAUSAL ANALYSIS” TENDS TO REFER TO THE USE OF STATISTICAL METHODOLOGY (DESIGN AND ANALYSIS) TO ESTIMATE THE STRENGTH OF ESTIMABLE CAUSAL RELATIONSHIPS (E.G., THE MAGNITUDE OF AN EFFECT IN A RESPONSE VARIABLE CAUSED BY (ASSOCIATED WITH, FOLLOWING IN TIME) A SPECIFIED CHANGE IN AN EXPLANATORY VARIABLE).

IN 2000, JUDEA PEARL PUBLISHED A BOOK (CAUSALITY: MODELS, REASONING, AND INFERENCE, 2^ND EDITION, CAMBRIDGE UNIVERSITY PRESS, 2009 (1^ST ED. 2000)) IN WHICH HE PRESENTED A COMPREHENSIVE DESCRIPTION OF A PROBABILISTIC CAUSALITY THEORY THAT IS OF BROAD APPLICABILITY AND RELATIVELY EASY TO APPLY. THE THEORY ALLOWS THE ANALYST TO SPECIFY CAUSAL KNOWLEDGE AND BELIEFS IN DETAIL USING A FAMILY OF MODELS (BAYESIAN NETWORKS) BASED ON DIRECTED ACYCLIC GRAPHS (DAGs). PEARL IDENTIFIES TWO CRITERIA THAT CAN BE USED TO QUICKLY DETERMINE, FROM THE CAUSAL MODEL’S DAG, WHETHER A SPECIFIED CAUSAL EFFECT IS ESTIMABLE.

OF THE TWO MAIN ASPECTS TO CAUSAL MODELING AND ANALYSIS, THE FIRST ASPECT, OR “QUALITATIVE ASPECT,” IS CONCERNED WITH THE DESCRIPTION OF CAUSAL MODELS AND THE DETERMINATION OF WHETHER CONSISTENT ESTIMATES OF CAUSAL EFFECTS CAN BE DERIVED FROM DATA, GIVEN A CAUSAL MODEL. THE SECOND ASPECT, OR “QUANTITATIVE ASPECT,” IS CONCERNED WITH STATISTICAL PROCEDURES FOR ESTIMATING THE MAGNITUDE OF CAUSAL EFFECTS. TOGETHER, THESE TWO ASPECTS ARE REFERRED TO AS “CAUSAL MODELING AND ANALYSIS.” PEARL’S THEORY AND BOOK ADDRESSES THE FIRST ASPECT OF CAUSAL MODELING ANALYSIS (THE QUALITATIVE ASPECT: DESCRIPTION OF CAUSAL MODELS; ASSESSMENT OF ESTIMABILITY).

ALTHOUGH PEARL’S APPROACH TO CAUSAL MODELING DOES NOT EXPLICITLY DISCUSS COUNTERFACTUALS OR POTENTIAL OUTCOMES, IT CERTAINLY INVOLVES DISTRIBUTIONS OF OUTCOMES UNDER ALTERNATIVE ASSUMPTIONS, AND IT CERTAINLY INVOLVES ASSUMPTIONS ABOUT CONDITIONAL INDEPENDENCE. WITH RESPECT TO THESE TWO FUNDAMENTAL ASPECTS OF PROBABILISTIC CAUSALITY, IT IS SIMILAR TO THE SO-CALLED POTENTIAL-OUTCOMES APPROACH. THE SALIENT FEATURE OF PEARL’S APPROACH IS ITS IDENTIFICATION OF A COMPLETE CAUSAL MODEL, USE OF A GRAPHICAL FRAMEWORK FOR DESCRIBING THE CAUSAL MODEL, AND USE OF THE GRAPHICAL FRAMEWORK FOR MAKING DECISIONS ABOUT IDENTIFIABILITY OF CAUSAL ESTIMATES. THIS PRESENTATION WILL SUMMARIZE BOTH PEARL’S APPROACH AND THE POTENTIAL-OUTCOMES APPROACH TO CAUSAL MODELING.

AS DISCUSSED EARLIER, G. E. P. BOX OBSERVED THAT FOR A MODEL TO ESTIMATE THE EFFECTS OF FORCED CHANGES TO A SYSTEM, THE MODEL MUST BE BASED ON DATA FOR WHICH FORCED CHANGES WERE MADE TO THE SYSTEM. WITHOUT MAKING STRONG ASSUMPTIONS ABOUT A CAUSAL MODEL (E.G., SPECIFYING THE MODEL EXPLICITLY AND MAKING ASSUMPTIONS ABOUT CONDITIONAL INDEPENDENCE AND STABILITY), THAT ASSERTION HOLDS. THAT ASSERTION IS A STATEMENT THAT THE SCOPE OF INFERENCE DEPENDS ON THE WAY (SELECTION METHOD) IN WHICH THE DATA WERE GENERATED (I.E., THAT THE ESTIMATES APPLY TO SETTINGS (EXPERIMENTAL OR OBSERVATIONAL CONDITIONS) SIMILAR TO THOSE FOR THE ANALYZED DATA SET), OR ON ASSUMPTIONS ABOUT A CAUSAL MODEL UNDERLYING THE DATA (E.G., THAT THERE ARE NO HIDDEN VARIABLES OMITTED FROM THE MODEL). IT SHOULD NOT BE TAKEN AS AN ASSERTION THAT CAUSAL ANALYSIS MAY NOT BE DONE USING OBSERVATIONAL DATA – OTHERWISE, IT WOULD IMPLY THAT CAUSAL ANALYSIS COULD BE REASONABLY DONE ONLY USING EXPERIMENTAL DESIGNS, AND WOULD REJECT ALL THE CAUSAL-MODELING THEORY OF NEYMAN-RUBIN, PEARL, HECKMAN AND OTHERS. TO CONDUCT CAUSAL ANALYSIS USING OBSERVATIONAL DATA IT IS NECESSARY TO CONSTRUCT A MORE COMPLICATED CAUSAL MODEL THAN FOR A RANDOMIZED EXPERIMENT, AND TO MAKE CERTAIN ASSUMPTIONS ABOUT CONDITIONAL INDEPENDENCE AND STABILITY. THE ROSENBAUM-RUBIN APPROACH MAKES SUCH ASSUMPTIONS ONE WAY, AND THE PEARL APPROACH MAKES THEM A DIFFERENT WAY. WITHOUT MAKING SUCH ASSUMPTIONS, IT WOULD NOT BE POSSIBLE TO MAKE CAUSAL INFERENCES FROM OBSERVATIONAL DATA, AND THE ONLY AVAILABLE OPTION WOULD BE TO USE AN EXPERIMENT INVOLVING RANDOMIZED ASSIGNMENT TO TREATMENT. (WE HAVE NOT DEFINED THE CONCEPT OF “STABILITY.” SEE PEARL AND CARTWRIGHT FOR DISCUSSION OF THIS CONCEPT. IT REFERS TO THE FACT THAT EFFECTS MUST ALWAYS BE PROBABILISTICALLY LINKED TO CAUSES, AND THAT CAUSAL RELATIONSHIPS REMAIN UNCHANGED AS LONG AS THERE IS NO CHANGE IN THE ENVIRONMENT. PROBABILISTIC RELATIONSHIPS DEPEND ON WHAT INFORMATION IS KNOWN OR CONDITIONED ON; CAUSAL RELATIONSHIPS DO NOT.)

PEARL’S THEORY OF CAUSALITY WILL NOW BE SUMMARIZED VERY BRIEFLY. THIS SUMMARY DRAWS FROM PEARL’S BOOK, CAUSALITY (OP. CIT.). THE DEFINITIONS PRESENTED BELOW ARE ALMOST VERBATIM FROM PEARL’S BOOK. THE MATERIAL PRESENTED HERE IS AN EXCERPT OF BASIC CONCEPTS OF PEARL'S THEORY. MORE ADVANCED CONCEPTS, SUCH AS MODULARITY AND STABILITY, (NECESSARY TO AN UNDERSTANDING OF THE MATHEMATICAL FOUNDATIONS OF THE THEORY) ARE NOT ADDRESSED HERE.

A CAUSAL STRUCTURE (OR CAUSAL DIAGRAM) OF A SET OF VARIABLES V IS A DIRECTED ACYCLIC GRAPH (DAG) IN WHICH EACH NODE CORRESPONDS TO A DISTINCT ELEMENT OF V, AND EACH LINK REPRESENTS A DIRECT FUNCTIONAL RELATIONSHIP AMONG THE CORRESPONDING VARIABLES.

A CAUSAL MODEL IS A PAIR M = (D, Θ_D) CONSISTING OF A CAUSAL STRUCTURE D AND A SET OF PARAMETERS Θ_D COMPATIBLE WITH D. THE PARAMETERS Θ_D ASSIGN A FUNCTION X_i = f(PA_i, U_i), i = 1,…,n, TO EACH X_i IN V AND A PROBABILITY MEASURE (OR DISTRIBUTION) P(U_i) TO EACH U_i, WHERE PA_i ARE THE PARENTS OF X_i IN D AND WHERE EACH U_i IS A RANDOM DISTURBANCE DISTRIBUTED ACCORDING TO P(U_i) INDEPENDENT OF ALL OTHER U. (THE PARENTS OF A VARIABLE, X, ARE THE VARIABLES, PA(X), FOR WHICH ARROWS LEAD FROM THOSE VARIABLES DIRECTLY INTO THE VARIABLE X. PARENTS OF PA(X) ARE NOT ALSO PARENTS OF X, UNLESS THIS CONDITION HOLDS.)

THE CAUSAL STRUCTURE (REPRESENTED BY THE GRAPH) AND THE PROBABILITY DISTRIBUTION ARE DISTINCT. THEY REFLECT DIFFERENT KINDS OF INFORMATION. THE CAUSAL STRUCTURE SPECIFIES CAUSAL RELATIONSHIPS AMONG VARIABLES, I.E., WHICH VARIABLES MAY BE AFFECTED BY FORCED CHANGES IN OTHER VARIABLES. THE PROBABILITY MEASURE DEFINES THE ASSOCIATIONAL RELATIONSHIP AMONG VARIABLES (I.E., THE DEGREE TO WHICH ONE VARIABLE IS LIKELY TO CHANGE, ASSOCIATED WITH CHANGES (FORCED OR NOT) IN OTHER VARIABLES (TO WHICH IT MAY OR MAY NOT BE CAUSAL RELATED)). NO INFORMATION ABOUT CAUSAL RELATIONSHIPS MAY BE OBTAINED FROM THE PROBABILITY DISTRIBUTION ALONE.

FIGURE 9 PRESENTS EXAMPLES OF CAUSAL DIAGRAMS. (WE USE THE TERMS “CAUSAL DIAGRAM” AND “CAUSAL MODEL” SOMEWHAT INTERCHANGEABLY. TECHNICALLY, THE TWO TERMS ARE NOT EQUIVALENT: THE CAUSAL MODEL IS A BROADER CONCEPT THAT INCLUDES THE CAUSAL DIAGRAM.)

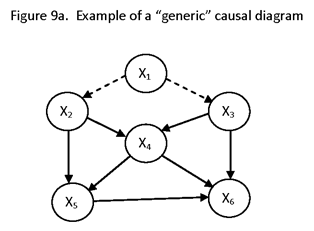
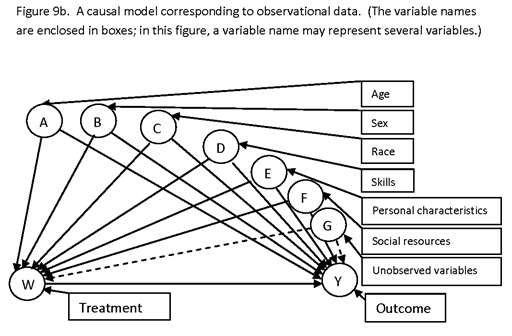
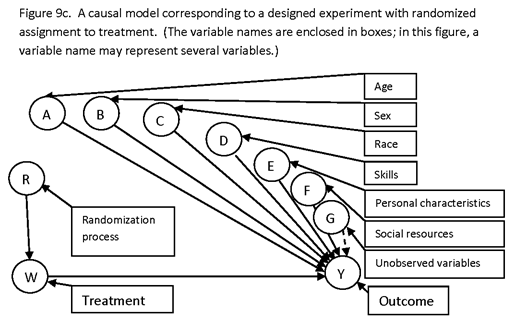
EACH VARIABLE OR SET OF VARIABLES IS REPRESENTED BY A CAPITAL LETTER. IF A VARIABLE (OR SET OF VARIABLES) EXERTS A CAUSAL INFLUENCE ON ANOTHER VARIABLE (OR SET OF VARIABLES), THEN A SOLID DIRECTED LINE (LINE WITH AN ARROWHEAD ON ONE END AND NOT ON THE OTHER) IS DRAWN FROM THE FORMER TO THE LATTER (WITH THE ARROWHEAD POINTING TOWARD THE VARIABLE THAT IS ACTED ON). A VARIABLE THAT IS CAUSING AN EFFECT ON ANOTHER IS CALLED A CAUSAL VARIABLE, EXPLANATORY VARIABLE, INDEPENDENT VARIABLE, INPUT VARIABLE, OR CONTROL VARIABLE. A VARIABLE THAT IS INFLUENCED BY A CAUSAL VARIABLE IS CALLED AN EFFECT VARIABLE, EXPLAINED VARIABLE, AFFECTED VARIABLE, RESPONSE VARIABLE, OUTCOME VARIABLE, DEPENDENT VARIABLE OR OUTPUT VARIABLE.

IN THIS PRESENTATION, WE WILL CONSIDER ONLY CAUSAL MODELS THAT MAY BE REPRESENTED BY DIRECTED ACYCLIC GRAPHS (DAGs), IN WHICH THERE ARE NO MUTUAL (SIMULTANEOUS) CAUSAL RELATIONSHIPS (DOUBLE-HEADED ARROWS BETWEEN TWO VARIABLES) OR CYCLES (LOOPS, FEEDBACK LOOPS). MODELS SUCH AS THIS ARE HIERARCHICAL: FOR EVERY SET OF TWO MODEL VARIABLES, ONLY ONE OF THEM (THE "ANCESTOR"; AN IMMEDIATELY DIRECT ANCESTOR IS CALLED A "PARENT") MAY AFFECT THE OTHER (THE "DESCENDENT"; AN IMMEDIATELY DIRECT DESCENDENT IS CALLED A "CHILD"). THEY ARE CALLED "RECURSIVE" MODELS (BECAUSE EACH MODEL VARIABLE MAY BE DEFINED RECURSIVELY IN TERMS OF ANCESTOR VARIABLES). A DASHED LINE INDICATES THAT A NUMBER OF UNOBSERVED VARIABLES MAY HAVE AN INFLUENCE ON THE VARIABLES AT THE ARROW ENDS OF THE LINE.

IN FIGURE 9a, THE MODEL VARIABLES ARE X₁,…,X₆. X₁ REPRESENTS UNOBSERVED VARIABLES AFFECTING X₂ AND X₃. X₆ MIGHT BE AN OUTCOME VARIABLE OF INTEREST, AND X₅ MIGHT BE A TREATMENT VARIABLE, AND X₂, X₃ AND X₄ OBSERVED COVARIATES.

IN THE FIGURE, OUR NOTATION DEPARTS SLIGHTLY FROM THAT OF PEARL (BECAUSE OF LIMITATIONS IN THE MICROSOFT WORD EQUATION SOFTWARE USED TO PREPARE THIS DOCUMENT). PEARL SIGNIFIES AN UNOBSERVED VARIABLE BY AN OPEN CIRCLE AND AN OBSERVED VARIABLE BY A CLOSED CIRCLE, AND DRAWS DASHED ARROWS FROM ALL UNOBSERVED VARIABLES. WE SHALL USE OPEN CIRCLES FOR ALL VARIABLES, AND INSERT THE VARIABLE NAME INSIDE THE CIRCLE (BUT INDICATE LONGER VARIABLE NAMES USING TEXT BOXES POINTING TO THE CIRCLES). AS PEARL, WE DRAW DASHED ARROWS FROM ALL UNOBSERVED VARIABLES. IN OUR DIAGRAMS, A VARIABLE LABEL MAY REPRESENT A SCALAR, A VECTOR, OR A SET OF VARIABLES.

A CAUSAL MODEL DIAGRAM (SUCH AS THOSE IN FIGURE 9) INCLUDES VARIABLES THAT ARE CAUSALLY RELATED TO EACH OTHER. (THE TERM “CAUSALLY RELATED” INCLUDES BOTH EXPLANATORY VARIABLES IN WHICH FORCED CHANGES MAY BE MADE, SUCH AS A PROGRAM INTERVENTION, AS WELL AS VARIABLES SUCH AS RACE, THAT MAY BE SELECTED BUT NOT FORCIBLY CHANGED.) IT DOES NOT INCLUDE VARIABLES THAT ARE SIMPLY ASSOCIATED (E.G., LINEARLY CORRELATED), BUT HAVE NO CAUSAL RELATIONSHIP. (TO BE CLEAR, RACE IS CLASSIFIED AS A “CAUSAL VARIABLE,” EVEN THOUGH FORCED CHANGES CANNOT BE MADE IN IT. RACE IS AN ATTRIBUTE THAT CANNOT BE MANIPULATED, AND SOME WOULD ARGUE THAT IT THEREFORE CANNOT BE A CAUSE (OR A “CAUSAL VARIABLE”). WE WISH TO AVOID AN ARGUMENT ON SEMANTICS (VIEWING IT AS A WASTE OF TIME AND EFFORT THAT MAY BE AVOIDED BY MORE SPECIFIC DEFINITIONS). PERHAPS WE COULD REFER TO “ALL CAUSAL VARIABLES AND COVARIATES,” AND AVOID THIS CONTROVERSY. THE POINT IS THAT RACE CAN BE SELECTED, IS A “SURROGATE VARIABLE” FOR MANY UNOBSERVED MANIPULABLE VARIABLES, AND TO OMIT IT FROM THE MODEL WOULD BE WRONG – IT WOULD INTRODUCE BIASES AND REDUCE PRECISION. THE ARGUMENT IS OBVIATED BY REFERRING TO THE DEFINITION OF “CAUSAL EFFECT” – IT IS DEFINED WITH RESPECT TO AN ABSTRACT MODEL, NOT TO REALITY. MODEL VARIABLES ARE “CAUSAL VARIABLES” IF THEY ARE PARENTS (PRECEDENT VARIABLES, ANTECEDENT VARIABLES, EXPLANATORY VARIABLES) OF OTHER VARIABLES IN THE MODEL DIAGRAM (I.E., HAVE ARROWS LEADING FROM THEM TO OTHER VARIABLES) AND THE CONDITIONAL-PROBABILITY EQUATION ASSOCIATED WITH THEM.

IN THIS PRESENTATION, CAUSAL RELATIONSHIPS AND CAUSAL EFFECTS ARE DEFINED IN A THEORETICAL MODEL. THE MODEL IS DERIVED FROM EXPERIENCE, BELIEFS, AND THOUGHT EXPERIMENTS ABOUT THE SUPPOSED NATURE OF THINGS. AS DISCUSSED EARLIER, A CAUSAL RELATIONSHIP EXISTS BETWEEN TWO VARIABLES IF THERE IS A PROBABILISTIC DEPENDENCE BETWEEN THEM WHEN RANDOMIZATION-BASED REALIZATIONS (MANIPULATIONS, FORCED SETTINGS) ARE MADE IN ONE OF THEM.

THE KEY ASSUMPTION IN PEARL’S REPRESENTATION OF A CAUSAL MODEL IS THAT THE MODEL DISTURBANCES, U, ARE INDEPENDENT. (THE MODEL DISTURBANCES ARE THE ERROR TERMS IN THE MODEL THAT DEFINES THE CONDITIONAL DISTRIBUTIONS FOR EACH MODEL VARIABLE, GIVEN ITS PARENTS.) THIS IS A VERY STRONG ASSUMPTION, AND MAY BE JUSTIFIED ONLY WHEN THE DAG INCLUDES ALL OF THE MAJOR VARIABLES HAVING A SUBSTANTIAL EFFECT ON THE OUTCOME VARIABLE OF INTEREST. EVEN WHEN THEY ARE ALL REPRESENTED, THAT IS NOT SUFFICIENT – THE MODEL DISTURBANCES (ERROR TERMS) MUST BE INDEPENDENT. CORRELATIONS BETWEEN SEVERAL CAUSAL VARIABLES MAY BE REPRESENTED BY A THIRD CAUSAL VARIABLE (OBSERVED OR UNOBSERVED) THAT AFFECTS ALL OF THEM.

THE JOINT PROBABILITY OF THE VARIABLES, X_i, REPRESENTED IN A (RECURSIVE, HIERARCHICAL, BAYESIAN, MARKOVIAN, DAG-BASED) CAUSAL MODEL IS GIVEN BY (USING THE CHAIN RULE OF PROBABILITY):

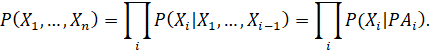
FOR THE CAUSAL MODEL DEPICTED IN FIGURE 9a, THE JOINT PROBABILITY IS

(OUR NOTATION DIFFERS FROM PEARL’S IN THAT HE MAINLY PRESENTS PROBABILITY STATEMENTS USING LOWER-CASE LETTERS FOR RANDOM VARIABLES, AND WE SHALL MAINLY USE UPPER-CASE LETTERS. FOR EXAMPLE, PEARL USUALLY WRITES P(Y=y|X=x) AS P(y|x).)

THE ASSUMPTION OF INDEPENDENCE OF THE Us IMPLIES THAT THE JOINT DISTRIBUTION OF THE MODEL VARIABLES X₁,…,X_n TAKES THE PRECEDING SIMPLE FORM. ALL OF THE DEPENDENCIES AMONG THE MODEL VARIABLES ARE REPRESENTED BY THE PARENT VARIABLES OF EACH MODEL VARIABLE. THIS CONDITION IS CALLED A “MARKOV” CONDITION. IF THERE IS AN INTERACTION BETWEEN TWO MODEL VARIABLES, THEN THAT INTERACTION MUST BE REPRESENTED AS ANOTHER VARIABLE IN THE MODEL. THE RESULTING JOINT DISTRIBUTION HAS THE SIMPLE FORM SHOWN ABOVE. THE PEARL MODEL IS REFERRED TO AS A “MARKOV MODEL” OR A “BAYESIAN NETWORK” OR A "BAYES NET."

PEARL’S FRAMEWORK IS A VERY SPECIAL, IDEALIZED, MODEL. IT IS SIMILAR TO THE STANDARD STRUCTURAL EQUATION MODEL (SEM) OF ECONOMETRICS, BUT SIMPLER – A “TOPOLOGICAL” REPRESENTATION OF CAUSAL RELATIONSHIPS, INSTEAD OF A “STRUCTURAL-EQUATION” REPRESENTATION. THE SEM APPROACH ALLOWS FOR MORE GENERAL JOINT DISTRIBUTIONS (E.G., ONE INVOLVING A COVARIANCE MATRIX THAT SPECIFIES COVARIANCES AMONG MODEL VARIABLES – IN THE PEARL MODEL EVERY MODEL VARIABLE, CONDITIONAL ON ITS PARENTS, IS INDEPENDENT OF ALL OTHER MODEL VARIABLES).

THE PRECEDING DEFINES THE CAUSAL MODEL. THE NEXT ISSUE TO ADDRESS IS HOW TO DEFINE A “CAUSAL EFFECT.” PEARL DEFINES A CAUSAL EFFECT TO BE A CERTAIN PROBABILITY DISTRIBUTION OF THE OUTCOME (Y), WHICH WE SHALL DEFINE SHORTLY. THIS APPROACH IS STANDARD IN EVALUATION RESEARCH WHEN DEALING WITH A CONTINUOUS TREATMENT VARIABLE. WHEN DEALING WITH SIMPLER DISTRIBUTIONAL ASPECTS, SUCH AS MEANS, THE CAUSAL EFFECT MAY BE DEFINED DIFFERENTLY. FOR EXAMPLE, IN THE CASE OF A BINARY TREATMENT VARIABLE, THE CAUSAL EFFECT IS USUALLY DEFINED AS A CERTAIN DIFFERENCE IN MEANS. FOR ESTIMATION OF SIMPLER QUANTITIES, IT IS NOT NECESSARY TO ESTIMATE THE FULL DISTRIBUTION. (THE DESIGN OF THE EXPERIMENT OR SURVEY TO COLLECT DATA FOR ANALYSIS CAN ALSO BE SIMPLER (SINCE IT IS FOCUSED ON SPECIALIZED MEASURES, NOT ON THE COMPLETE OUTCOME DISTRIBUTION), SUCH AS THE USE OF RANDOMIZATION TO SELECT BETWEEN JUST TWO TREATMENT LEVELS, TREATED AND UNTREATED.)

GIVEN THE PRECEDING DEFINITION OF A CAUSAL MODEL, PEARL DEFINES A CAUSAL EFFECT AS WILL SOON BE DESCRIBED. BEFORE DESCRIBING HIS APPROACH, SOME BASIC CONCEPTS STATISTICAL THEORY RELATING TO ESTIMATION OF EFFECTS WILL BE SUMMARIZED, AND ILLUSTRATIVE EXAMPLES PRESENTED. THESE CONCEPTS UNDERLIE ALL OF THE BASIC APPROACHES TO ESTIMATION OF CAUSAL EFFECTS (PEARL, R&R, HECKMAN).

PROBABILISTIC CONCEPTS RELATING TO ESTIMATION OF CAUSAL EFFECTS

THIS SECTION WILL PRESENT A NUMBER OF EXAMPLES TO MOTIVATE THE VARIOUS APPROACHES USED IN CAUSAL ANALYSIS.

FOR THIS SECTION, THE DISCUSSION WILL BE IN TERMS OF CONDITIONAL EXPECTATIONS, RATHER THAN OF PROBABILITY DISTRIBUTIONS (PEARL DOES THE LATTER). ONE REASON FOR THIS MORE SPECIFIC APPROACH IN THE EXAMPLES IS THAT EXPECTATIONS ARE EASIER TO WORK WITH AND TO COMPREHEND THAN PROBABILITY DISTRIBUTIONS. THE MAJOR DIFFERENCE ASSOCIATED WITH WORKING WITH EXPECTATIONS RATHER THAN DISTRIBUTIONS IS THAT CONDITIONS ARE STATED IN TERMS OF CONDITIONAL INDEPENDENCE OF MEANS RATHER THAN CONDITIONAL INDEPENDENCE OF RANDOM VARIABLES. ANOTHER REASON FOR WORKING WITH EXPECTATIONS IS THAT MOST OF THE STATISTICAL THEORY FOR ESTIMATION OF CAUSAL EFFECTS (TO BE DISCUSSED LATER) DEALS WITH EXPECTATIONS, NOT WITH DISTRIBUTIONS OR OTHER FUNCTIONALS OF DISTRIBUTIONS. (A “FUNCTIONAL” IS A MAPPING FROM A VECTOR SPACE, SUCH AS A SPACE OF FUNCTIONS, TO A FIELD, SUCH AS THE FIELD OF REAL OR COMPLEX NUMBERS. COMMONLY, A FUNCTIONAL IS A FUNCTION OF FUNCTIONS. A “STATISTICAL FUNCTIONAL” T(F) OF A DISTRIBUTION FUNCTION F IS ANY FUNCTION OF F, SUCH AS THE MEAN OR VARIANCE.)

WE SHALL GENERALLY PRESENT EXAMPLES ASSUMING THAT THE RANDOM VARIABLES INVOLVED ARE DISCRETE, IN WHICH CASE THE EXPECTED VALUES INVOLVED ARE SIMPLY SUMS (INSTEAD OF INTEGRALS), SUCH AS AVERAGES OVER THE CATEGORIES OF A ONE-DIMENSIONAL TABLE OR THE CELLS OF A CROSS-TABULATION. NO PROOFS ARE GIVEN HERE, SIMPLY RESULTS AND EXAMPLES.

WOOLDRIDGE (OP. CIT.) GIVES A GOOD SUMMARY OF USEFUL RESULTS ABOUT CONDITIONAL EXPECTATIONS (PP. 18-22, 30-32, 397-405). THE DISCUSSION THAT FOLLOWS DRAWS FROM THIS REFERENCE. (WOOLDRIDGE USES LOWER-CASE LETTERS TO REPRESENT RANDOM VARIABLES, AND THIS SECTION FOLLOWS HIS USAGE IN THE MATERIAL DRAWN FROM HIS BOOK. OTHERWISE, RANDOM VARIABLES IN THE ABSTRACT ARE DENOTED USING CAPITAL LETTERS AND REALIZED VALUES USING SMALL LETTERS.)

PEARL'S APPROACH TO CAUSAL MODELING IS TO DETERMINE CONDITIONS FOR IDENTIFIABILITY OF ANY QUANTITY COMPUTABLE FROM THE PROBABILITY DISTRIBUTION FUNCTION ASSOCIATED WITH A SPECIFIED CAUSAL MODEL (SUCH AS A MEAN OR MEDIAN). HE DOES THIS FOR BAYESIAN NETWORKS, FOR WHICH THE CALCULATIONS INVOLVED ARE PARTICULARLY EASY. FOR THIS CLASS OF CAUSAL MODELS, PEARL'S APPROACH IS A VERY GENERAL NONPARAMETRIC APPROACH. TO SIMPLIFY THE DISCUSSION, WE SHALL ADDRESS THE ISSUE OF IDENTIFIABILITY OF A PARAMETER, θ (A VECTOR), THAT DEFINES A PROBABILITY DISTRIBUTION. THE PARAMETER θ COULD BE, FOR EXAMPLE, THE MEAN AND VARIANCE OF A DISTRIBUTION, OR IT COULD BE THE SET OF REGRESSION COEFFICIENTS OF A REGRESSION-EQUATION MODEL. IN FACT, THE PARAMETER θ CAN DESCRIBE ANY FEATURE OF THE DISTRIBUTION, SUCH AS A CONDITIONAL MEAN, A CONDITIONAL MEAN AND CONDITIONAL VARIANCE, A CONDITIONAL MEDIAN – EVEN A CONDITIONAL DISTRIBUTION OR A COMPLETE DISTRIBUTION.

WITH THIS APPROACH, IT IS ASSUMED THAT THE CAUSAL MODEL FOR THE MEAN OF A VARIABLE y, CONDITIONAL ON VARIABLES x, IS

E(y|x) = m(x, θ).

THE VARIABLE y IS THE EXPLAINED (RESPONSE) VARIABLE AND THE VARIABLE x IS THE EXPLANATORY VARIABLE (IN GENERAL, A VECTOR). THIS MODEL IS CALLED A REGRESSION MODEL, AND THE FUNCTION m(x, θ) IS CALLED A REGRESSION FUNCTION.

RELATING BACK TO THE EARLIER DEFINITION OF A CAUSAL MODEL, y REPRESENTS ONE OF THE MODEL VARIABLES (SAY, x₁), AND x REPRESENTS ONE OR MORE OF THE OTHER MODEL VARIABLES (x₂,...,x_n). NOTE, HOWEVER, THAT THE u's INTRODUCED IN THE JUST-PRECEDING MODEL DEFINITION ARE NOT THE SAME AS THE u's SPECIFIED IN PEARL'S DEFINITION OF A CAUSAL MODEL. IN THE JUST-PRECEDING MODEL, THE u's ARE ASSUMED TO BE ADDITIVE (I.E., ADDED TO THE EXPECTED VALUE); NO SUCH ASSUMPTION IS MADE IN PEARL'S DEFINITION. (THIS IS ONE MORE WAY IN WHICH THE EXAMPLES PRESENTED HERE ARE SIMPLIFIED SPECIAL CASES.)

THE JOINT PROBABILITY FUNCTION CORRESPONDING TO A BAYESIAN NETWORK WAS SHOWN EARLIER. BECAUSE OF THE HIERARCHICAL STRUCTURE OF A BAYESIAN NETWORK (NO LOOPS), THAT PROBABILITY FUNCTION HAS A VERY SIMPLE FORM. AN ALTERNATIVE REPRESENTATION OF THE MODEL MAY BE GIVEN IN TERMS OF A SET OF HIERARCHICAL EQUATIONS:

E(X_i) = m(X₁,...,X_i-1), i=1,...n.

THIS REPRESENTATION IS NOT AS GENERAL AS THE PROBABILITY-DISTRIBUTION REPRESENTATION USED BY PEARL, BUT WILL BE USED IN THE DISCUSSION AND EXAMPLES THAT FOLLOWS, FOR THE REASONS EXPLAINED EARLIER. WE MAY DROP REFERENCE TO THE PARAMETER θ, BUT IT IS IMPLICIT. (PEARL'S APPROACH IS NONPARAMETRIC, BUT MOST APPLICATIONS USE PARAMETRIC REPRESENTATIONS.)

THE PRECEDING MODEL IS STATISTICALLY EQUIVALENT TO THE MODEL

y = m(x,θ) + u, E(u|x)=0.

IN THIS MODEL, THE MODEL ERROR TERM, u, IS SIMPLY DEFINED TO BE u = y – m(x,θ). THAT THE MODEL E(y|x) = m(x, θ) IMPLIES THE JUST-PRECEDING ONE (y = m(x,θ) + u, E(u|x)=0) IS DEFINITIONAL. THAT THE MODEL y = m(x,θ) + u, E(u|x)=0 IMPLIES E(y|x) = m(u|x, θ) IS OBVIOUS (BY THE LAW OF ITERATED EXPECTATIONS, E(u) = E_x(E(u|x)) = E_x(0) = 0).

THE REQUIREMENT E(u|x)=0 IMPLIES E(u)=0, BUT NOT VICE VERSA.

THE ASSUMPTION THAT E(u)=0 IS RATHER TRIVIAL – IT HOLDS FOR ANY MODEL THAT ALLOWS FOR A MEAN. (NOT ALL MODELS REQUIRE MEANS – FOR EXAMPLE, SUBSTANTIVE THEORY MAY REQUIRE THE MODEL TO PASS THROUGH THE ORIGIN, AS IN THE MODEL E(y) = ax.)

THE ASSUMPTION E(u|x)=0 IS A VERY STRONG ONE. IT MEANS THAT THE MEAN OF THE MODEL RESIDUALS (u) IS INDEPENDENT OF THE EXPLANATORY VARIABLES (x). THIS CONDITION IS CALLED A CONDITION OF "MEAN INDEPENDENCE." IT REQUIRES THAT THE MEAN OF THE MODEL ERROR TERMS BE ZERO FOR EVERY VALUE OF x. WITHOUT THIS ASSUMPTION, THE EXPECTATION OF y GIVEN x (I.E., THE CONDITIONAL MEAN FUNCTION) IS NOT NECESSARILY EQUAL TO m(x,θ) (RATHER, IT IS EQUAL TO m(x,θ) + E(u|x), AND, WITHOUT THE ASSUMPTION E(u|x)=0, THE SECOND TERM IS NOT NECESSARILY EQUAL TO ZERO). THE ASSUMPTION E(u|x)=0 IS A CRUCIAL ASSUMPTION OF A REGRESSION MODEL.

IN HIS THEORY, PEARL ASSUMES THAT THE ERROR TERMS (THE u's – ONE FOR EACH MODEL VARIABLE) ARE INDEPENDENT. THIS IS A VERY STRONG REQUIREMENT, THAT REQUIRES A VERY DETAILED DESCRIPTION OF THE MODEL. THE PRECEDING REQUIREMENT, THAT OF MEAN INDEPENDENCE OF THE MODEL RESIDUALS, E(y|x)=0, IS MUCH WEAKER.

FOR A RANDOM SAMPLE OF OBSERVATIONS, FOR EACH MODEL VARIABLE THERE IS A SET OF u's, ONE FOR EACH MEMBER OF THE SAMPLE. FOR A RANDOM SAMPLE, THE u's (FOR THE SAMPLE OBSERVATIONS OF EACH MODEL VARIABLE) ARE INDEPENDENT AND IDENTICALLY DISTRIBUTED, NO MATTER HOW THEY ARE RELATED TO x. IN GENERAL, HOWEVER, THE u's MAY NOT BE INDEPENDENT OF x. FOR EXAMPLE, IF y ≥ 0, THEN u ≥ -m(x,θ), SO u AND x CANNOT BE INDEPENDENT. THIS SITUATION OFTEN ARISES WHEN THE RANGE OF y IS RESTRICTED. BECAUSE OF THIS SITUATION, IT IS IN GENERAL NOT POSSIBLE TO REQUIRE THAT THE MODEL ERROR TERMS (u's) OF THE PRECEDING MODEL (y = m(x,θ) + u, E(u|x)=0) ARE INDEPENDENTLY DISTRIBUTED, CONDITIONAL ON x.

THE FIRST ASSUMPTION WE SHALL MAKE ABOUT THE PRECEDING (PARAMETRIC) MODEL IS THAT THERE DOES EXIST SOME VALUE OF θ (SAY θ₀) FOR WHICH THE MODEL IS TRUE. THIS MEANS THAT THE MODEL IS CORRECTLY SPECIFIED. (THIS MEANS THAT THE ASSUMED MODEL IS OF THE CORRECT FUNCTIONAL FORM. FOR EXAMPLE, IF THE TRUE MODEL IS E(y|x) = a exp(-bx) (HERE, θ = (a,b)), BUT IT IS ASSUMED THAT E(y|x) = a + bx, THEN THE MODEL IS NOT CORRECTLY SPECIFIED, SINCE THERE IS NO WAY THAT A LINEAR FUNCTION CAN REPRESENT AN EXPONENTIAL FUNCTION.) (THIS ASSUMPTION ABOUT SPECIFICATION RELATES TO PARAMETRIC MODELS, NOT TO NONPARAMETRIC MODELS.)

UNDER THE ASSUMPTION THAT E(u|x) = 0, IT CAN BE PROVED THAT THE VALUE OF θ MUST SATISFY

THE MAXIMIZING VALUE OF θ (= θ₀, SAY) IS CALLED THE "TRUE VALUE OF θ".

(THE PRECEDING FACT IS GENERALIZATION OF A PROPERTY OF CONDITIONAL EXPECTATIONS. SEE P. 32 OF WOOLDRIDGE OP. CIT. THAT IS, IF μ(x) = E(y|x), THEN μ IS A SOLUTION TO

THAT IS, μ(x) IS THE BEST MEAN-SQUARED PREDICTOR BASED ON x. THE PROOF OF THIS RESULT (WOOLDRIDGE, P. 400) USES THE FACT THAT THE CONDITION E(u|x)=0 IMPLIES THAT u IS UNCORRELATED WITH ANY FUNCTION OF x.)

THE PRECEDING STATES THAT, IF E(u|x)=0, THEN THE PARAMETER θ IS A SOLUTION TO A MINIMIZATION PROBLEM. DEPENDING ON THE NATURE OF THE POPULATION AND THE REGRESSION FUNCTION m(x,θ), HOWEVER, THIS SOLUTION MAY OR MAY NOT BE UNIQUE. TO ASSURE IDENTIFIABILITY OF θ₀ (I.E., THERE NOT ONLY EXISTS A SOLUTION FOR θ, BUT IT IS UNIQUE), IT IS NECESSARY TO ASSUME

THAT IS, IF WE MAKE THE PRECEDING ASSUMPTION, THE MODEL (OR MORE SPECIFICALLY, THE PARAMETER THAT SPECIFIES THE MODEL) IS IDENTIFIABLE (OR "IDENTIFIED"). THIS ASSUMPTION RULES OUT THE CASE, FOR EXAMPLE, WHERE THE CROSS-PRODUCTS MATRIX IN A REGRESSION MODEL IS SINGULAR (E.G., IF A LINEARLY DEPENDENT SET OF INDICATOR VARIABLES IS INCLUDED IN THE MODEL), IN WHICH CASE THERE ARE MULTIPLE SOLUTIONS.

WHAT THE PRECEDING RESULTS IMPLY IS THAT IF THE EXPLANATORY VARIABLE x IS INDEPENDENT OF THE MODEL ERROR TERM (u(x)), THEN THE EXPECTED VALUE OF THE OBSERVED RANDOM VARIABLE y IS EQUAL TO THE FUNCTION m(x,θ₀) DEFINING THE MODEL. FOR AN EXPERIMENTAL DESIGN, THE DESIGN MAY BE SET UP SO THAT THIS CONDITION HOLDS (E.G., IF x IS SELECTED USING RANDOMIZATION, IT IS INDEPENDENT OF ALL OTHER MODEL VARIABLES). FOR OBSERVATIONAL DATA, THE EXPLANATORY VARIABLE x MAY VERY WELL BE RELATED TO OTHER MODEL VARIABLES, AND THE ESTIMATION PROCESS BECOMES MORE COMPLICATED (SINCE THE SAMPLE MEAN (TAKING INTO ACCOUNT THE SURVEY DESIGN, BUT NOT THE DISTRIBUTION OF x) IS NOT AN UNBIASED ESTIMATE OF THE MODEL MEAN FUNCTION).

IN THE DEFINITION OF A CAUSAL MODEL, THERE ARE n EXPECTATION EQUATIONS (ONE FOR EACH MODEL VARIABLE). IF ALL MODEL VARIABLES COULD BE OBSERVED, THESE EXPECTATIONS COULD BE ESTIMATED BY TAKING A RANDOM SAMPLE FROM THE POPULATION. IN THE PRESENT CONTEXT, THE TERM "RANDOM SAMPLE" SHALL BE INTERPRETED TO MEAN THAT EACH MEMBER OF THE POPULATION HAS AN EQUAL CHANCE OF SELECTION, AND THAT ASSIGNMENT TO TREATMENT IS DONE INDEPENDENTLY AT RANDOM. TWO PROBLEMS THAT ARISE IN MOST SOCIO-ECONOMIC INVESTIGATIONS ARE THAT NOT ALL MODEL VARIABLES MAY BE OBSERVED, AND ASSIGNMENT TO TREATMENT IS OFTEN NOT DONE INDEPENDENTLY AT RANDOM.

(THE TERM "AT RANDOM" MEANS SIMPLY THAT PROBABILITY SAMPLING IS USED. THE PROBABILITY OF SELECTION OR ASSIGNMENT MAY OR MAY NOT DEPEND ON OTHER MODEL VARIABLES (OBSERVED OR UNOBSERVED). THE TERM "INDEPENDENTLY AT RANDOM" MEANS THAT PROBABILITY SAMPLING IS USED, BUT THE PROBABILITY OF SELECTION DOES NOT DEPEND ON ANY OTHER RANDOM VARIABLES (IT DOES NOT HAVE TO BE SIMPLE RANDOM SAMPLING; IT CAN OBEY ANY PROBABILITY DISTRIBUTION THAT DOES NOT DEPEND ON OTHER MODEL VARIABLES).

(THE TERMS "SELECTION FOR TREATMENT" AND "ASSIGNMENT TO TREATMENT" ARE USED FOR THE SITUATION IN WHICH TREATMENT IS A BINARY RANDOM VARIABLE (0 = UNTREATED, 1 = TREATED). IN GENERAL, WHEN THE TREATMENT VARIABLE HAS MORE THAN TWO LEVELS OR IS CONTINUOUS, WE REFER SIMPLY TO "TREATMENT" OR "TREATMENT LEVEL," AND DO NOT USE THE PRECEDING TERMS. IN THE CONTINUOUS CASE, FOR EXAMPLE, WE MIGHT SAY THAT A VARIABLE MAY BE "CORRELATED WITH TREATMENT," AND NOT "CORRELATED WITH SELECTION FOR TREATMENT" OR "CORRELATED WITH ASSIGNMENT TO TREATMENT.")

(IN PRACTICAL APPLICATIONS, A SAMPLE OF INDIVIDUALS (OR OTHER POPULATION UNITS) IS USUALLY NOT SELECTED FROM THE POPULATION USING SIMPLE RANDOM SAMPLING, BUT INSTEAD BY USING A COMPLEX SURVEY DESIGN, SUCH AS STRATIFIED MULTISTAGE SAMPLING. WE ARE NOT CONCERNED HERE WITH THIS TYPE OF NOT-INDEPENDENTLY-AT-RANDOM SAMPLING OF POPULATION UNITS. WHAT WE ARE CONCERNED WITH IS THE SITUATION IN WHICH THE ASSIGNMENT TO TREATMENT (OR TREATMENT LEVEL) IS NOT INDEPENDENTLY AT RANDOM. FOR SIMPLICITY, IN THE EXAMPLES THAT FOLLOW, WE SHALL IGNORE THE FACT THAT IN MOST PRACTICAL APPLICATIONS THE SURVEY DESIGN FOR SELECTION OF UNITS IS NOT SIMPLE RANDOM SAMPLING, AND FOCUS SOLELY ON THE ISSUE OF THE TREATMENT ASSIGNMENT BEING NOT-INDEPENDENTLY-AT-RANDOM. THE ASSUMPTION OF SIMPLE RANDOM SAMPLING OF THE SURVEY DESIGN USED FOR SELECTION OF UNITS FROM THE POPULATION IS MADE HERE TO KEEP THE EXAMPLES SIMPLE, AND TO FOCUS ON THE ISSUE OF SELECTION FOR TREATMENT. IN GENERAL, THE PROBABILITIES OF SELECTION ARE KNOWN FOR THE SURVEY DESIGN, AND MAY BE TAKEN INTO ACCOUNT USING THE STANDARD ESTIMATION PROCEDURES OF SAMPLE SURVEY. (NOTE THAT THE WORD "INDEPENDENTLY" HERE REFERS TO INDEPENDENCE AMONG THE MODEL VARIABLES. IT DOES NOT REFER TO INDEPENDENCE AMONG SAMPLE UNITS; THE SAMPLE UNITS ARE ALWAYS ASSUMED TO BE INDEPENDENT OF EACH OTHER.))

WE SHALL NOW DISCUSS ASPECTS OF THE TWO MAIN PROBLEMS FACING SOCIO-ECONOMIC STUDIES (VIZ., THAT NOT ALL MODEL VARIABLES MAY BE OBSERVED, AND ASSIGNMENT TO TREATMENT IS OFTEN NOT DONE INDEPENDENTLY AT RANDOM). ALTHOUGH SOME ASPECTS OF THESE TWO ISSUES WILL BE DISCUSSED SEPARATELY, IN PRACTICE ESTIMATORS ARE USED THAT ADDRESS BOTH ASPECTS SIMULTANEOUSLY.

PROBLEM 1: NOT ALL MODEL VARIABLES MAY BE OBSERVED, OR USED

IN GENERAL, GIVEN A CAUSAL MODEL, THE APPROACH TO DETERMINING CONSISTENT OR UNBIASED ESTIMATES OF CAUSAL EFFECTS IS TO DETERMINE A DATA MODEL FOR WHICH THE ASSUMPTION E(u|x)=0 IS SATISFIED IN SOME WAY (I.E., UNDER CERTAIN CONDITIONS SPECIFIED BY MODEL VARIABLES). IF THE DATA MODEL (ESTIMATION MODEL) IS A CORRECT SPECIFICATION OF THE CAUSAL MODEL AND THE CONDITION E(u|x)=0 HOLDS, THEN THE MODEL ESTIMATES WILL BE UNBIASED CAUSAL ESTIMATES. NOTE THAT THE DATA MODEL DOES NOT NECESSARILY INCLUDE ALL OF THE VARIABLES OF THE CAUSAL MODEL. IF THE DATA MODEL INCLUDES ALL CAUSAL-MODEL VARIABLES, THIS CONDITION IS SATISFIED (BY THE ASSUMPTION MADE FOR THE CAUSAL MODEL, THAT THE MODEL RESIDUALS (GIVEN ALL THE MODEL VARIABLES) ARE INDEPENDENT).

A PROBLEM THAT ARISES IN PRACTICE IS THAT NOT ALL MODEL VARIABLES ARE OBSERVABLE. IN THIS CASE, THE STATISTICAL MODEL BASED ON THE OBSERVED VARIABLES MUST BE A SPECIFICATION SUCH THAT THE CAUSAL QUANTITIES OF INTEREST ARE IDENTIFIABLE (ESTIMABLE). (ESTIMABILITY OF A QUANTITY MEANS THAT A GOOD ESTIMATE (E.G., AN UNBIASED OR CONSISTENT) OF THE QUANTITY MAY BE DETERMINED FROM SAMPLE DATA.) THE PROBLEM IS TO FIND SUCH MODEL SPECIFICATIONS. FOR SOME SETS OF OBSERVED MODEL VARIABLES, UNDER VARIOUS ASSUMPTIONS ABOUT CONDITIONAL INDEPENDENCE, THIS WILL BE POSSIBLE. FOR OTHERS, IT WILL NOT BE. JUDEA PEARL'S CONTRIBUTION TO CAUSAL MODELING AND ANALYSIS IS THAT, FOR A USEFUL CLASS OF CAUSAL MODELS (BAYESIAN NETWORKS) HE IDENTIFIES SIMPLE GRAPHICAL PROCEDURES FOR IDENTIFYING SETS OF CONDITIONING VARIABLES THAT WILL RESULT IN IDENTIFIABILITY OF CAUSAL ENTITIES OF INTEREST.

LATER, WE WILL PROVIDE A SUMMARY DESCRIPTION OF PEARL'S METHODOLOGY FOR DETERMINING IDENTIFIABILITY (ESTIMABILITY). FOR THE MOMENT, WE SHALL PRESENT SOME ADDITIONAL GENERAL COMMENTS ON THE ISSUE OF ESTIMATION WHEN NOT ALL MODEL VARIABLES ARE AVAILABLE OR OF INTEREST.

IT IS IMPORTANT TO DISTINGUISH BETWEEN THE SPECIFICATION OF THE CAUSAL MODEL AND THE SPECIFICATION OF THE STATISTICAL MODEL DESCRIBING THE POPULATION AND SAMPLING PROCEDURES, AND USED AS A BASIS FOR ESTIMATION. THE CAUSAL MODEL IS

y = m(x,θ) + u, E(u|x)=0.

WHAT LEADS TO CONFUSION IS THE FACT THAT THIS IS EXACTLY THE SAME NOTATION USED FOR THE STATISTICAL MODEL!

WHAT IS IMPORTANT TO RECOGNIZE IS THAT IN THE STATISTICAL MODEL, E(y|x) = m(x,θ), THE VECTOR x MAY CONTAIN MANY FEWER VARIABLES THAN ARE AVAILABLE IN THE CAUSAL MODEL E(y|x) = m(x,θ). BECAUSE OF THE NOTATION, THE MODELS APPEAR TO BE IDENTICAL, BUT THEY ARE NOT AT ALL, IF THE OBSERVED x HAS FEWER COMPONENTS THAN THE CAUSAL-MODEL x. FOR EXAMPLE, IT MAY BE DESIRED TO ESTIMATE A REGRESSION MODEL E(y|x) WITH A SINGLE (SCALAR) EXPLANATORY VARIABLE, x, (E.G., TREATMENT), OMITTING ALL OTHER CAUSAL-MODEL VARIABLES FROM THE REGRESSION MODEL. AS LONG AS x IS INDEPENDENT OF ALL OTHER MODEL VARIABLES, THIS IS A CORRECT REPRESENTATION (SPECIFICATION) OF THE DATA, EVEN THOUGH IT IS A SIMPLER MODEL THAN THE CAUSAL MODEL.

THE STATISTICAL MODEL (USED FOR ESTIMATION) MAY DIFFER FROM THE CAUSAL MODEL FOR TWO MAIN REASONS: SOME OF THE VARIABLES IN THE CAUSAL MODEL MAY BE UNOBSERVABLE, AND IT MAY BE OF INTEREST TO ESTIMATE THE EXPECTED VALUE OF THE OUTCOME VARIABLE CONDITIONAL ON FEWER EXPLANATORY VARIABLES THAN ARE REPRESENTED IN THE CAUSAL MODEL. ALTHOUGH THE STATISTICAL MODEL MAY DIFFER FROM THE CAUSAL MODEL, IT MUST BE CONSISTENT WITH THE CAUSAL MODEL (SINCE IT DERIVES FROM THE CAUSAL MODEL).

PROBLEM 2: SELECTION FOR TREATMENT NOT INDEPENDENTLY AT RANDOM

THE SECOND MAJOR PROBLEM FACING MANY SOCIO-ECONOMIC STUDIES IS THAT TREATMENT IS NOT ASSIGNED INDEPENDENTLY. THE GOAL OF CAUSAL ESTIMATION IS TO OBTAIN AN ESTIMATOR THAT IS AN UNBIASED OR CONSISTENT ESTIMATOR OF THE MODEL MEAN FUNCTION (m(x,θ)). THE SAMPLE MEAN IS A CONSISTENT ESTIMATE OF THE MODEL MEAN ASSUMING RANDOM SAMPLING OF SAMPLE UNITS FROM A POPULATION (INCLUDING SAMPLING ACCORDING TO A KNOWN SURVEY DESIGN, SUCH AS A STRATIFIED TWO-STAGE SAMPLE DESIGN), AND ALLOCATION OF TREATMENT ACCORDING TO A DESIRED DISTRIBUTION (E.G., RANDOM ASSIGNMENT TO "TREATED" AND "UNTREATED"). A PROBLEM THAT ARISES IS THAT IN MANY SITUATIONS (INVOLVING OBSERVATIONAL DATA, NOT EXPERIMENTAL-DESIGN DATA) THE ALLOCATION OF TREATMENT MAY NOT BE RANDOM – THAT IS, IT MAY BE ACCORDING TO A PROBABILITY DISTRIBUTION THAT MAY DEPEND ON ONE OR MORE (OTHER) MODEL VARIABLES. WHEN THIS HAPPENS, THE EXPECTED VALUE OF THE SAMPLE MEAN (TAKING INTO ACCOUNT THE SURVEY DESIGN) WILL REPRESENT THE EXPECTED VALUE IF TREATMENT IS ALLOCATED AS IT WAS, NOT IF ALLOCATED AT RANDOM. THE ISSUE IS HOW TO OBTAIN AN UNBIASED ESTIMATE WHEN THE TREATMENT VARIABLE IS NOT SELECTED INDEPENDENTLY OF OTHER MODEL VARIABLES.

WE ASSUME THAT, ALTHOUGH TREATMENT IS NOT ASSIGNED INDEPENDENTLY, IT IS ASSIGNED AT RANDOM, I.E., USING PROBABILITY SAMPLING. IN PRACTICE, TWO ISSUES MAY ARISE. FIRST, THE PROBABILITY OF ASSIGNMENT MAY VARY OVER THE POPULATION. SECOND, THE PROBABILITY OF ASSIGNMENT MAY DEPEND ON OTHER MODEL VARIABLES, I.E., NOT BE INDEPENDENT. OF THESE TWO PROBLEMS, THE FIRST IS EASY TO ADDRESS (SINCE, IN PROBABILITY SAMPLING, IT IS ASSUMED THAT THE SELECTION PROBABILITIES ARE KNOWN), BUT THE SECOND MAY BE VERY DIFFICULT TO ADDRESS.

IN ORDER TO DISCUSS THIS PROBLEM, IT IS NECESSARY TO REVIEW SOME BASIC RESULTS ABOUT EXPECTATIONS AND CONDITIONAL EXPECTATIONS.

BY THE LAW OF ITERATED EXPECTATIONS, IT IS TRUE THAT

E(Y) = E_X(E(Y|X)).

(THE RIGHT-HAND-SIDE OF THIS EXPRESSION IS USUALLY WRITTEN SIMPLY AS EE(Y|X), SINCE THE VARIABLE INVOLVED IN EACH EXPECTATION IS USUALLY OBVIOUS.)

FOR CONDITIONAL EXPECTATIONS, THE CORRESPONDING RESULT IS

E(Y|X) = E_ZE(Y|X,Z).

IN TERMS OF PROBABILITY DISTRIBUTIONS, THIS IS EQUIVALENT TO

E(Y|X) = ∑_Z E(Y|X,Z) P(Z|X).

THE ESSENTIAL THING TO NOTE HERE IS THAT THE PROBABILITY DISTRIBUTION INVOLVING THE CONDITIONING VARIABLE Z IS THE CONDITIONAL DISTRIBUTION P(Z|X), NOT THE MARGINAL DISTRIBUTION P(Z).

THE SECOND ESSENTIAL THING TO REALIZE IS THAT E(Y|X,Z) IS NOT NECESSARILY AN UNBIASED ESTIMATOR OF m(x,z,θ) (SINCE IT IS NOT NECESSARILY TRUE THAT E(U|X,Z)=0).

IF E(Y|X,Z) IS AN UNBIASED ESTIMATOR OF m(x,z,θ),THE SUM ∑_Z E(Y|X,Z) P(Z) IS AN UNBIASED ESTIMATOR OF m(x,θ), WHERE THE RANDOM VARIABLE Z HAS POSITIVE PROBABILITY OVER THE POPULATION. (NOTE THAT THE LAST TERM IN THIS EXPRESSION IS P(Z), NOT P(Z|X), AS IN THE LAW OF ITERATED EXPECTATIONS.) BY DEFINITION, IF Z HAS PROBABILITY DENSITY P(Z), THEN r(Z) IS AN UNBIASED ESTIMATOR OF θ IF ITS EXPECTATION IS θ, I.E., E(r(Z)) = ∑_Zr(Z)P(Z) = θ. BUT THERE IS NO REASON WHY ∑_Zr(Z)P(Z|X) SHOULD EQUAL θ FOR SOME OTHER DISTRIBUTION, SUCH AS P(Z|X). IF r(Z) IS UNBIASED CONDITIONAL ON X, I.E., E(r(Z|X))=θ, THEN ∑_Xr(Z|X)P(X) UNBIASED, I.E., E∑_Xr(Z|X)P(X) = ∑_XE(r(Z|X))P(X) = ∑_XθP(X) = θ∑_XP(X) = θ.

IN VIEW OF THE PRECEDING RESULTS, AN APPROACH TO FINDING AN UNBIASED ESTIMATE OF m(x,θ) IS TO IDENTIFY COVARIATES (z) SUCH THAT, CONDITIONAL ON THOSE COVARIATES, THE EXPLANATORY VARIABLE x IS INDEPENDENT OF THE MODEL ERROR TERM, I.E., IS INDEPENDENT OF ALL MODEL VARIABLES (OBSERVED OR UNOBSERVED) OTHER THAN y. (MORE SPECIFICALLY, WE ASSUME THAT E(u|x,z)=0, I.E., THAT THE MODEL, CONDITIONAL ON z, INCLUDES A MEAN TERM, SO E(u|z) = E_XE(u|x,z) = E_XE0 = 0.) UNDER THESE CONDITIONS, E(u|x,z) = E(u|z) = 0. (THE POPULATION VALUE OF m(x,θ) IS THEN SIMPLY THE EXPECTED VALUE OF THE CONDITIONAL EXPECTATION OF m(x,θ) GIVEN THE COVARIATES z, AVERAGED OVER THE COVARIATES.

THE CHALLENGE, THEN, IS TO FIND A SET OF COVARIATES z SUCH THAT, CONDITIONAL ON z, x IS INDEPENDENT OF ALL MODEL VARIABLES OTHER THAN y. WHAT PEARL DOES IS IDENTIFY STRAIGHTFORWARD GRAPHIC CRITERIA FOR IDENTIFYING SUCH VARIABLES.

THE CONDITION E(U|X,Z)=0 IS SATISFIED BY IDENTIFYING POPULATION GROUPS (DEFINED, E.G., BY A VECTOR MODEL VARIABLE Z) SUCH THAT WITHIN EACH GROUP THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS INDEPENDENTLY AT RANDOM. THIS IS ACCOMPLISHED BY USING SUBSTANTIVE KNOWLEDGE ABOUT THE SELECTION PROCESS AND USING AN APPROPRIATE SAMPLE DESIGN. THE POPULATION MEAN IS THEN ESTIMATED AS THE POPULATION-WEIGHTED AVERAGE OF THESE MEANS (I.E., AVERAGE USING THE MARGINAL DISTRIBUTION OF Z).

AN EXPERIMENTAL DESIGN CAN BE STRUCTURED SO THAT THIS CONDITION HOLDS (FOR HOWEVER MANY EXPLANATORY VARIABLES ARE INCLUDED IN THE MODEL), AND THE USUAL ESTIMATES ARE UNBIASED ESTIMATES OF CAUSAL EFFECTS. FOR OBSERVATIONAL DATA, THE STATISTICAL MODEL OF THE DATA MAY OR MAY NOT SATISFY THE ASSUMPTION THAT E(u|x)=0. IF IT DOES NOT, THEN THE USUAL ESTIMATES OF MEANS WILL NOT BE UNBIASED ESTIMATES OF CAUSAL EFFECTS (I.E., THEY WILL NOT BE UNBIASED ESTIMATES OF m(x,θ)). THE GOAL IN ANALYSIS OF OBSERVATIONAL DATA IS TO FIND A CONDITIONING VARIABLE, z, FOR WHICH THE CONDITION E(u|x,z)=0 HOLDS.

TWO BASIC PROCEDURES FOR CONDITIONING

THERE ARE TWO MAIN WAYS OF OBTAINING AN UNBIASED ESTIMATE OF θ. THE FIRST IS TO STRATIFY (PARTITION) THE POPULATION INTO GROUPS SUCH THAT WITHIN EACH GROUP TREATMENT IS INDEPENDENTLY ASSIGNED (I.E., INDEPENDENTLY OF ALL MODEL VARIABLES EXCEPT FOR THOSE DEFINING THE STRATA). AN UNBIASED ESTIMATE OF THE CAUSAL EFFECT MAY BE OBTAINED FOR EACH STRATUM (SINCE, WITHIN EACH STRATUM, TREATMENT IS INDEPENDENTLY ASSIGNED). A POPULATION ESTIMATE IS THEN OBTAINED BY CONSTRUCTING THE USUAL STRATIFIED ESTIMATE (I.E., A WEIGHTED ESTIMATE OF THE STRATUM ESTIMATES, WHERE EACH STRATUM ESTIMATE IS WEIGHTED IN PROPORTION TO THE TOTAL POPULATION IN THAT STRATUM).

TO BE MORE SPECIFIC, TO OBTAIN AN UNBIASED ESTIMATE OF m(x,θ) BY THE STRATIFICATION METHOD, IT IS NECESSARY TO DO TWO THINGS. FIRST, DETERMINE A VARIABLE (OR VARIABLES) Z SUCH THAT WITHIN EACH SUBGROUP THE CONDITION E(U|X,Z)=0 HOLDS (I.E., CONDITIONAL ON Z, X IS INDEPENDENT OF U, I.E., OF ALL OTHER MODEL VARIABLES). SECOND, CONSTRUCT THE AVERAGE ∑_Z E(Y|X,Z) P(Z) (I.E., AVERAGE THE SUBGROUP ESTIMATES USING THE MARGINAL DISTRIBUTION P(Z), NOT THE CONDITIONAL DISTRIBUTION P(Z|X)).

THE SECOND MAIN METHOD OF OBTAINING AN UNBIASED ESTIMATE OF θ IS TO USE INVERSE-PROBABILITY WEIGHTING (IPW). WITH THIS APPROACH, THE ESTIMATE IS THE WEIGHTED AVERAGE OF THE SAMPLE OBSERVATIONS, WHERE EACH OBSERVATION IS WEIGHTED BY THE INVERSE OF THE PROBABILITY OF ASSIGNMENT TO TREATMENT LEVEL. NOTE THAT THIS ESTIMATOR USES THE INVERSES OF THE SURVEY DESIGN UNIT-SELECTION PROBABILITIES, NOT THE INVERSES OF THE PROBABILITY OF ALLOCATION TO TREATMENT, GIVEN SELECTION IN THE SAMPLE). THIS IS THE SAME AS THE HORVITZ-THOMPSON ESTIMATE OF SAMPLE SURVEY. WITH THIS APPROACH, AN UNBIASED ESTIMATE IS OBTAINED BY FORMING A WEIGHTED AVERAGE OF THE SAMPLE OBSERVATIONS, WITH THE SAMPLE WEIGHTS PROPORTIONAL TO THE INVERSES OF THE SELECTION PROBABILITIES(ALL OF WHICH MUST BE GREATER THAN ZERO). THE RATIONALE FOR THIS APPROACH IF THAT IS A RANDOM VARIABLE x IS SELECTED WITH PROBABILITY P(x), THEN THE IPW ESTIMATOR x_i/P(x_i) IS AN UNBIASED ESTIMATE OF THE POPULATION TOTAL, SINCE, E(x_i/P(x_i)) = ∑P(x_j)x_j/P(x_j)=∑x_j. GIVEN A SAMPLE OF x_i, i = 1,...,n, AN UNBIASED ESTIMATE OF THE TOTAL IS n^-1∑_i x_i/P(x_i), AND AN UNBIASED ESTIMATE OF THE SAMPLE MEAN IS N^-1 TIMES THIS.

IT IS ESSENTIAL TO REALIZE THAT IPW PRODUCES AN UNBIASED ESTIMATE OF m(x,θ) ONLY IF IT IS BASED ON A COVARIATE z SUCH THAT CONDITIONAL ON z, E(u|x,z) = 0. OTHERWISE, THE IPW ESTIMATOR WILL BE AN UNBIASED ESTIMATOR OF E(y|x), NOT OF m(x,θ).

(NOTE: IF x IS A BINARY (0-1) RANDOM VARIABLE, THEN P(x), THE PROBABILITY OF ALLOCATION TO TREATMENT LEVEL (OR SELECTION FOR TREATMENT) IS CALLED THE PROPENSITY SCORE. THE PROPENSITY SCORE IS OFTEN CALCULATED CONDITIONAL ON A RANDOM VARIABLE, z, SUCH THAT, CONDITIONAL ON z, x IS INDEPENDENT OF OTHER RANDOM VARIABLES. IN THAT CASE, THE OVERALL ESTIMATE IS THE CONDITIONAL ESTIMATE AVERAGED OVER z. IF X DENOTES THE TREATMENT VARIABLE, AND PA_X DENOTES ALL VARIABLES ON WHICH IT DEPENDS (I.E., THE PARENTS OF X), THEN THIS QUANTITY IS DENOTED AS P(X|PA_X).)

PEARL'S APPROACH TO CAUSAL MODELING

THE STANDARD APPROACH IN STATISTICS IS TO CONSTRUCT AN ESTIMATOR THAT HAS DESIRABLE PROPERTIES (E.G., UNBIASEDNESS OR CONSISTENCY FOR THE ESTIMAND (QUANTITY BEING ESTIMATED)), GIVEN THE PROBABILITY DISTRIBUTION FUNCTION OF THE OBSERVATIONS. PEARL'S APPROACH IS A LITTLE DIFFERENT. WHAT HE DOES IS TO MODIFY THE JOINT PROBABILITY DISTRIBUTION FOR THE MODEL BY DIVIDING IT BY THE PROBABILITY, P(X|PA_X), OF THE TREATMENT VARIABLE (X) GIVEN THE VARIABLES ON WHICH IT DEPENDS (THE PARENTS OF X, DENOTED PA_X), AND CALL THIS THE JOINT PROBABILITY DISTRIBUTION OF THE MODEL, CONDITIONAL ON "SETTING" OR "DOING" OR "FORCING" THE VALUE OF X. IN OTHER WORDS, HE PERFORMS THE DIVISION BY P(X|PA_X) IN THE DISTRIBUTION FUNCTION, RATHER THAN IN THE ESTIMATOR.

THE INVERSE-PROBABILITY-WEIGHTING HAS THE EFFECT OF REMOVING THE SELECTION PROBABILITY P(X|Z) FROM THE SAMPLE LIKELIHOOD FUNCTION (PROPORTIONAL TO THE PROBABILITY DISTRIBUTION), AND REPLACING IT WITH A CONSTANT (REPRESENTING ASSIGNMENT TO TREATMENT INDEPENDENTLY AT RANDOM (I.E., INDEPENDENTLY OF OTHER VARIABLES)). THE IPW ESTIMATOR IS THE MOTIVATION FOR PEARL'S REMOVING THE FACTOR P(X|Z) FROM THE CAUSAL-MODEL JOINT DISTRIBUTION FUNCTION, WHEN CONSTRUCTING AN ESTIMATE OF THE CAUSAL EFFECT.

AS MOTIVATION FOR HIS APPROACH, WE SHALL PRESENT SEVERAL SIMPLE EXAMPLES. THESE EXAMPLES WILL ILLUSTRATE THE DEVICES OF STRATIFYING (OR CONDITIONING) SO THAT IDENTIFIED (UNBIASED, CONSISTENT) MODELS ARE OBTAINED WITHIN EACH STRATUM (OR CONDITION), OR WEIGHTING BY THE INVERSE OF THE PROPENSITY SCORE. (WHAT IS PRESENTED IS SIMPLY RESULTS, NOT PROOFS. FOR PROOFS, SEE WOOLDRIDGE OR PEARL.) AFTER PRESENTING THESE EXAMPLES, WE WILL PROCEED TO DISCUSS PEARL'S GENERAL THEORY.

(NOTE: THERE IS A POTENTIAL FOR CONFUSION WITH RESPECT TO THE TERMS, "PROPENSITY SCORE" AND "PROBABILITY OF ASSIGNMENT TO TREATMENT." AS MENTIONED, A PROPENSITY SCORE MAY BE DEFINED RELATIVE TO THE TOTAL POPULATION, OR IT MAY BE DEFINED CONDITIONAL ON COVARIATES (E.G., TO POPULATION SUBGROUPS, SUCH AS STRATA). IF ASSIGNMENT TO TREATMENT IS DONE BY SELECTING A SAMPLE OF UNITS FROM THE POPULATION FOR TREATMENT, AND A SECOND (INDEPENDENT) SAMPLE OF UNITS FOR CONTROL, THEN THE PROPENSITY SCORE IS THE SAME AS THE SAMPLE INCLUSION PROBABILITY, I.E., AS THE PROBABILITY OF SELECTION FOR TREATMENT. BY CONTRAST, ASSIGNMENT TO TREATMENT IS OFTEN DONE IN TWO STAGES, BY FIRST SELECTING UNITS FROM THE POPULATION AND THEN RANDOMLY ASSIGNING THEM TO TREATMENT. IF THIS PROCEDURE IS FOLLOWED, THE PROPENSITY SCORE IS THE PROBABILITY OF INCLUSION IN THE SAMPLE (I.E., IN THE FIRST STAGE) TIMES THE PROBABILITY OF ASSIGNMENT TO TREATMENT, GIVEN SELECTION INTO THE SAMPLE (I.E., THE SECOND STAGE). (THE INCLUSION PROBABILITIES ARE THE PROBABILITIES USED IN THE HORVITZ-THOMPSON ESTIMATOR. THE SAMPLE "WEIGHTS" ARE THE INVERSES OF THE INCLUSION PROBABILITIES.

(THE POINT HERE IS THAT IF THIS TWO-STAGE SAMPLING PROCEDURE IS USED, THE PROPENSITY SCORE AND THE PROBABILITY OF ASSIGNMENT TO TREATMENT ARE NOT IDENTICAL (I.E., THEY DIFFER BY THE PROBABILITY OF INCLUSION IN THE SAMPLE, PRIOR TO ASSIGNMENT TO TREATMENT). THE PROPENSITY SCORE IS ALWAYS P(x) OR P(x|z). IF THE SAMPLING IS DONE IN TWO STAGES, THEN P(x) = P(x|inclusion in sample)P(inclusion in sample) or P(x|z, inclusion in sample)P(inclusion in sample | z). IN DATA SUMMARIES, THE FIRST TERM IN THESE EXPRESSIONS MAY (LOOSELY) BE REFERRED TO AS THE PROPENSITY SCORE, PARTICULARLY IF THE SECOND TERM IS A CONSTANT. IN CALCULATING ESTIMATES, IT IS IMPORTANT TO USE THE CORRECT QUANTITY, EVEN IF THE SECOND TERM IS A CONSTANT (IN ORDER TO OBTAIN CORRECT ESTIMATES OF POPULATION TOTALS. (OMISSION OF THE SECOND TERM, IF IT IS A CONSTANT OVER THE SAMPLE, WILL RESULT IN CORRECT ESTIMATES IN MANY INSTANCES; IT IS EQUIVALENT TO USING ARBITRARILY NORMALIZED SURVEY WEIGHTS IN DATA ANALYSIS, INSTEAD OF WEIGHTS THAT SUM TO POPULATION TOTALS. THE ARBITRARILY NORMALIZED WEIGHTS WORK CORRECTLY FOR SOME ESTIMATES, BUT NOT FOR OTHERS. FOR CONDITIONING AND FOR ESTIMATION OF MEANS, IT DOES NOT MATTER WHAT NORMALIZATION IS USED. IN CONSTRUCTING EXPANSION ESTIMATES OF POPULATION TOTALS, IT MATTERS A GREAT DEAL.))

FOR THE EXAMPLES THAT FOLLOW, WE ASSUME THAT THE EXPLANATORY VARIABLE (THE VECTOR x) IS A SCALAR, x. LET y DENOTE A RESPONSE VARIABLE OF INTEREST. LET z BE A VECTOR OF VARIABLES THAT ARE CONDITIONED ON, AND v BE A VECTOR OF ALL OTHER MODEL VARIABLES. IN GENERAL, THE ERROR VARIABLE u MAY DEPEND ON x, z AND v, UNLESS ASSUMED OR SHOWN OTHERWISE. WE SHALL DROP THE PARAMETER θ FROM THE NOTATION, SINCE IT IS NOT NECESSARY TO MAKE IT EXPLICIT HERE.

TO AVOID CONFUSION, NOTE THAT THE VARIABLES y, x, z AND v ARE ALL OF THE VARIABLES OF AN UNDERLYING CAUSAL MODEL, BUT NOT ALL OF THESE VARIABLES MAY BE INCLUDED IN A PARTICULAR STATISTICAL MODEL. FOR THESE EXAMPLES, WE SHALL NOT EXPLICITLY IDENTIFY THE CAUSAL MODEL, OTHER THAN BY SPECIFYING CAUSAL RELATIONSHIPS THAT AFFECT STATISTICAL DEPENDENCIES.

EXAMPLE 1. CAUSAL VARIABLE (TREATMENT VARIABLE, x) RANDOMIZED OVER THE ENTIRE POPULATION

SUPPOSE THAT x IS SPECIFIED BY A RANDOMIZATION PROCESS INDEPENDENT OF ALL OTHER MODEL VARIABLES.

IN THIS CASE THE CAUSAL MODEL IS

E(y|x) = m(x), E(u|x)=0.

THE STATISTICAL MODEL FOR THE DATA IS, IN GENERAL,

E(y|x) = m(x), E(u)=0.

THE ISSUE TO ADDRESS IS WHETHER THE ERROR TERM IN FACT SATISFIES E(u|x)=0, UNDER THE SAMPLING ASSUMPTION (OF RANDOMIZED x). NOW E(u)=0 IS MAINTAINED BY THE DEFINITION OF u (= y – m(x)). CONCEIVABLY, THE MODEL ERROR TERM, u, COULD DEPEND ON ANY OF THE MODEL VARIABLES OTHER THAN y, THAT IS, ON x, z OR v. BUT SINCE x IS DETERMINED BY A RANDOMIZATION PROCESS INDEPENDENT OF ALL OTHER MODEL VARIABLES, u CANNOT DEPEND ON x. HENCE E(u|x) = E(u) = 0. HENCE, UNDER THE ASSUMPTION OF RANDOM SELECTION OF x INDEPENDENTLY OF ALL OTHER MODEL VARIABLES, THE ESSENTIAL MODEL ASSUMPTION OF E(u|x)=0 HOLDS, THE STATISTICAL MODEL FOR THE SAMPLE DATA IS THE SAME AS THE CAUSAL MODEL, AND THE SAMPLE MEAN OF y IS AN UNBIASED ESTIMATE OF m(x).

EXAMPLE 2. x RANDOMIZED WITHIN STRATA

SUPPOSE THAT THE POPULATION IS DIVIDED INTO STRATA DEFINED BY z, AND THAT THE VARIABLE x IS RANDOMIZED WITHIN EACH STRATUM. WITHIN EACH STRATUM, THE MODEL IS E_z(y|x) = E(y|x,z) WITH E_z(u|x) = 0. HENCE, WITHIN EACH STRATUM, E(y|x,z) IS UNBIASED. BY THE LAW OF ITERATED EXPECTATIONS, THE STRATUM ESTIMATE E_zE_y(y|x,z) IS THE OVERALL POPULATION ESTIMATE, E(y|x). IT IS TRUE THAT A WEIGHTED AVERAGE OF UNBIASED ESTIMATES IS ALSO UNBIASED. HENCE THE STRATUM ESTIMATE E_zE_y(y|x,z) IS UNBIASED.

EXAMPLE 3. CONDITION ON ALL VARIABLES AFFECTING TREATMENT

FOR THIS EXAMPLE AND THE FOLLOWING TWO EXAMPLES, REFER TO FIGURE 11c. (THE NOTATION OF THE FIGURE DIFFERS FROM THAT USED IN THE EXAMPLES.)

SUPPOSE THAT z REPRESENTS ALL VARIABLES AFFECTING TREATMENT (x). AS IN THE PREVIOUS CASE, CONSIDER THE MODEL CONDITIONED ON z. THEN, GIVEN z, THE MODEL IS

y|z = m_y|z(x,θ) + u_y|z.

EXAMPLE 4. CONDITION ON ALL VARIABLES AFFECTING OUTCOME

LET z DENOTE ALL MODEL VARIABLES OTHER THAN y AND x. THE DATA MODEL IS

y|x,z = m_y(x,z) + u_y(x,z).

THE ISSUE TO ADDRESS IS WHETHER E(u_y|x,z) IS EQUAL TO ZERO. WITHOUT LOSS OF GENERALITY, WE ASSUME, AS BEFORE, THAT E(u_y)=0.

BUT (BY THE DEFINITION OF THE CAUSAL MODEL) EVERY MODEL VARIABLE, CONDITIONAL ON ALL OTHER MODEL VARIABLES, DEPENDS ONLY ON RANDOM VARIATION THAT IS INDEPENDENT OF ALL OTHER MODEL VARIABLES. SO u_y(x,z) IS IN FACT INDEPENDENT OF x AND z. SO E(u_y(x,z)) = E(u_y) = 0. SO E(y|x,z) = m_y(x,z) + E(u_y(x,z)) = m_y(x,z).

EXAMPLE 5. CONDITION ON ALL VARIABLES AFFECTING BOTH OUTCOME AND TREATMENT

LET

z_xy = ALL VARIABLES AFFECTING BOTH OUTCOME AND TREATMENT

z_x = ALL VARIABLES AFFECTING TREATMENT BUT NOT OUTCOME

z_y = ALL VARIABLES AFFECTING OUTCOME BUT NOT TREATMENT.

SINCE z_x DOES NOT AFFECT OUTCOME, WE HAVE E(y|x, z_xy) = E(y|x, z_xy, z_x) = E(y|x and all other variables affecting treatment). BUT THIS IS THE SITUATION CONSIDERED IN EXAMPLE 3. THIS CONDITIONAL MEAN IS UNBIASED. SIMPLY AVERAGE OVER ALL OF THE VARIABLES AFFECTING TREATMENT TO OBTAIN AN UNBIASED ESTIMATE FOR THE POPULATION.

EXAMPLE 6. EXAMPLE ILLUSTRATING THE DIFFERENCE BETWEEN THE CAUSAL EFFECT AND THE OBSERVED EFFECT

IN THE FIELD OF EVALUATION, INTEREST FOCUSES ON ESTIMATION OF THE AVERAGE TREATMENT EFFECT (ATE), OR THE AVERAGE EFFECT OF TREATMENT ON AN INDIVIDUAL RANDOMLY SELECTED FROM THE POPULATION, AND RANDOMLY ASSIGNED TO TREATMENT. THE ATE IS THE CAUSAL EFFECT OF TREATMENT. THE MAJOR PROBLEM THAT ARISES IN PRACTICE IS THAT THE DATA AVAILABLE FOR ESTIMATION OF THE ATE INVOLVE DATA IN WHICH TREATMENT IS NOT RANDOMLY ASSIGNED. THE STANDARD PROCEDURES OF SAMPLE SURVEY ANALYSIS PRODUCE ESTIMATES OF THE OBSERVED TREATMENT EFFECT, WHICH IS THE AVERAGE ACCEPTING WHATEVER PROCESS WAS USED TO ASSIGN TREATMENT.

THIS EXAMPLE IS A VERY SIMPLE ONE CONTRIVED TO ILLUSTRATE THE DIFFERENCE BETWEEN THE AVERAGE TREATMENT EFFECT AND THE OBSERVED TREATMENT EFFECT. IT ILLUSTRATES EXAMPLE 5 PRESENTED ABOVE. IN THIS EXAMPLE, THERE IS A SINGLE INPUT VARIABLE (x), A SINGLE OUTPUT VARIABLE (y), AND A SINGLE VARIABLE (z) THAT AFFECTS BOTH OF THEM. (THIS EXAMPLE IS CONTRIVED TO ILLUSTRATE A SPECIFIC POINT; IT IS NOT REALISTIC.)

WE SHALL DESCRIBE THE SITUATION USING A TABLE AND A GRAPH.

THE FOLLOWING TABLE SUMMARIZES THE POPULATION AND SAMPLE DATA. THE POPULATION CONSISTS OF N = 10,000 INDIVIDUALS IN CERTAIN REGION. SIMPLE RANDOM SAMPLING IS USED TO SELECT SAMPLES OF 500 INDIVIDUALS TO BE PROVIDED WITH TRAINING AND 500 INDIVIDUALS TO COMPRISE A COMPARISON GROUP. AFTER EACH INDIVIDUAL IS SELECTED, THAT INDIVIDUAL IS INFORMED ABOUT THE NATURE OF THE PROGRAM AND MAKES A DECISION ABOUT WHETHER TO PARTICIPATE. RANDOM SAMPLING CONTINUES UNTIL THE DESIRED SAMPLE SIZES OF 500 TREATMENT UNITS AND 500 COMPARISON UNITS ARE REACHED.

FOR VARIOUS REASONS, IT TURNS OUT THAT INDIVIDUALS WITH MORE SCHOOLING ARE THE TREATMENT SAMPLE IS COMPRISED MUCH MORE HEAVILY WITH INDIVIDUALS WITH HIGH SCHOOL EDUCATION ("HS") THAN WITH INDIVIDUALS WITHOUT HIGH SCHOOL EDUCATION ("NHS").

THE FOLLOWING TABLE SUMMARIZES THE DATA. THE LABEL y WILL BE USED TO DENOTE OUTCOME, THE LABEL x WILL BE USED TO DENOTE TREATMENT (x = T FOR TREATED, UT FOR UNTREATED), AND THE LABEL z WILL BE USED TO DENOTE EDUCATIONAL LEVEL (z = HS FOR HIGH SCHOOL, NHS FOR NO HIGH SCHOOL).

		Treatment (x)
		x = T	x = UT	Row summaries
Covariate, Education (z)	z = HS	E_HS,T(y)=100 n_HS,T=300 P(x=T\|z=HS) =300/400=.75 P(z=HS\|x=T) =300/500=.6	E_HS,UT(y)=40 n_HS,UT=100 P(x=UT\|z=HS) =100/400=.25 P(z=HS\|x=UT) =100/500=.2	n_HS.=400 N_HS.=1,000 P(z=HS)=1000/10000=.1 P(in sample\|z=HS) =400/1000=.4
Covariate, Education (z)	z = NHS	E_NHS,T(y)=50 n_NHS,T=200 P(x=T\|z=NHS) =200/600=1/3 P(z=NHS\|x=T) =200/500=.4	E_NHS,UT(y)=30 n_NHS,UT=400 P(x=UT\|z=NHS) =400/600=2/3 P(z=NHS\|x=UT) =400/500=.8	n_NHS.=600 N_NHS.=9,000 P(z=HS)=9000/10000=.9 P(in sample\|z=NHS) =600/9000=2/30=.0667
	Column summaries	n_.T=500	n_.NT=500	n=1,000 N=10,000

OBSERVED TREATMENT EFFECT:

OTE_x=T = ∑_zE(y|x=T,z)P(z|x=T) = 100(.6) + 50(.4) = 80

OTE_x=UT = ∑_zE(y|x=UT,z)P(z|x=UT) = 40(.2) + 30(.8) = 32

OTE = OTE_x=T - OTE_x=UT = 80 – 32 = 48

CAUSAL EFFECT ("AVERAGE TREATMENT EFFECT"), STRATIFIED ESTIMATE:

CE_x=T = ∑_zE(y|x=T,z)P(z) = 100(.1) + 50(.9) = 55

CE_x=UT = ∑_zE(y|x=UT,z)P(z) = 40(.1) + 30(.9) = 31

CE = CE_x=T - CE_x=UT = 55 – 31 = 24

CAUSAL EFFECT, INVERSE-PROBABILITY-WEIGHTED (IPW) ESTIMATE:

CE_x=T = [∑_zn_x=T,zE(y|x=T,z)/(P(x=T|z,in sample)P(in sample|z))]

/[∑_zn_x=T,z/(P(x=T|z,in sample)P(in sample|z))] = [(300)(100)/(.75)(.4) + (200)(50)/(.333)(.0667)]/ [300/(.75)(.4) + 200/(.333)(.0667)] = 55

CE_x=UT = [∑_zn_x=UT,zE(y|x=UT,z)/(P(x=UT|z,in sample)P(in sample|z))]

/[∑_zn_x=UT,z/(P(x=UT|z,in sample)P(in sample|z))] = [(100)(40)/(.25)(.4) + (400)(30)/(.667(.0667)]/ [100/(.25)(.4) + 400/(.667)(.0667)] = 31

CE = CE_x=T - CE_x=UT = 55 – 31 = 24 (the same as the stratified estimate)

(THE FACTORS n_x=T,z AND n_x=UT,z APPEAR IN THE ABOVE EXPRESSIONS INSTEAD OF SUMS OVER SAMPLE UNITS BECAUSE THE SUMMARY TABLE INCLUDES THE MEANS FOR THE VARIOUS GROUPS, NOT THE INDIVIDUAL SAMPLE UNITS.)

WE SEE THAT THE OBSERVED TREATMENT EFFECT, 48, IS A SUBSTANTIALLY BIASED ESTIMATE OF THE CAUSAL EFFECT, 24.

THE FOLLOWING FIGURE DISPLAYS THE PRECEDING RESULTS IN THE FORM OF A GRAPH.

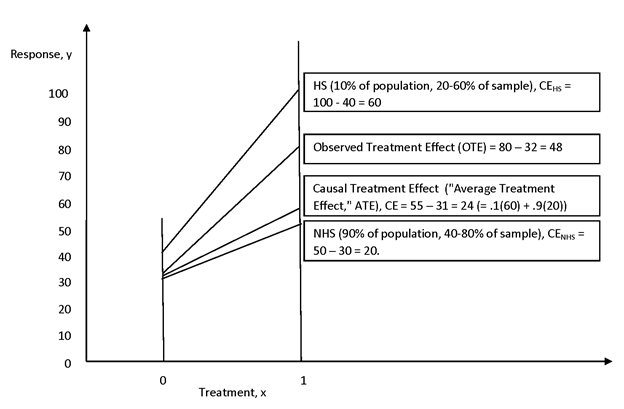
A FEW OBSERVATIONS ABOUT THE FIGURE ARE THE FOLLOWING.

THE OTE LINE IS THE (INVALID) REGRESSION LINE THAT WOULD BE ESTIMATED IF THE EDUCATION VARIABLE WERE NOT INCLUDED IN THE MODEL. THE CE LINES ARE THE REGRESSION LINES THAT WOULD BE ESTIMATED IF THE EDUCATION VARIABLE IS INCLUDED IN THE MODEL.

THE OBSERVED TREATMENT EFFECT (OTE) A SUBSTANTIALLY BIASED ESTIMATE OF THE CAUSAL EFFECT FOR TWO REASONS. FIRST, THE SAMPLE IS HEAVILY WEIGHTED TO THE HS POPULATION, WHOSE RESPONSE TO TREATMENT IS MUCH HIGHER THAN THE NHS POPULATION. SECOND, THE OTE MEAN IS CLOSER TO THE HS MEAN FOR x=1 AND CLOSER TO THE NHS MEAN FOR x=0 SINCE THE HS SAMPLE IS HEAVILY WEIGHTED TO T (x=1) AND THE NHS SAMPLE IS HEAVILY WEIGHTED TO UT (x=0).

THE NAMES "OBSERVED TREATMENT EFFECT" (OTE) AND "AVERAGE TREATMENT EFFECT" (ATE) ARE VERY CONFUSING. THE OTE IS IN FACT AN "AVERAGE TREATMENT EFFECT" – IT IS AN AVERAGE OVER THE TREATMENT DISTRIBUTION THAT OCCURRED FOR THE STUDY POPULATION, GIVEN WHATEVER TREATMENT SELECTION PROCESS OPERATED. THE ATE, OR CAUSAL EFFECT, IS THE AVERAGE FOR A TREATMENT DISTRIBUTION THAT IS INDEPENDENT OF ALL OTHER VARIABLES. THE OTE IS IN FACT A "CAUSAL EFFECT," WHEN THE SYSTEM CONTINUES TO OPERATE AS IT DID FOR THE SAMPLE DATA. THE USUAL "CAUSAL EFFECT" IS THE CAUSAL EFFECT WHEN IT IS ASSUMED THAT UNITS ARE SELECTED FROM THE POPULATION AT RANDOM AND TREATMENT IS ASSIGNED INDEPENDENTLY (AND IT IS ASSUMED THAT WHEN TREATMENT IS ASSIGNED INDEPENDENTLY, THE REST OF THE SYSTEM CONTINUES TO OPERATE AS IT DID BEFORE (I.E., THE ASSUMPTION OF STABILITY, FAITHFULNESS, MODULARITY, AUTONOMY, INVARIANCE)).

ONE IMPORTANT THING TO REALIZE ABOUT CAUSAL ESTIMATES IS THAT THEY ARE ALWAYS AVERAGES (EXPECTED VALUES). THE PRIMARY REASON FOR THIS IS THAT CAUSALITY CANNOT BE OBSERVED AT THE UNIT (INDIVIDUAL) LEVEL, SINCE THE UNIT CANNOT BE REPLICATED – OBSERVED WITH AND WITHOUT TREATMENT OR AT DIFFERENT TREATMENT LEVELS. A SECONDARY REASON IS THAT, IN GENERAL, NOT ALL OF THE VARIABLES OF A CAUSAL MODEL CAN BE OBSERVED, AND ESTIMATES OF IMPACT MUST BE FOUND CONDITIONAL ON OBSERVED VARIABLES, AVERAGED OVER UNOBSERVED VARIABLES. THE ISSUE TO ADDRESS IS TO DETERMINE WHICH AVERAGES REPRESENT UNBIASED OR CONSISTENT CAUSAL ESTIMATES. WE CAN ESTIMATE DISTRIBUTIONS AND EXPECTED VALUES (AND OTHER DISTRIBUTIONAL PROPERTIES) OF CAUSAL EFFECTS, BUT NOT CAUSAL EFFECTS AT THE LEVEL OF THE INDIVIDUAL UNIT.

THE PRECEDING EXAMPLES ILLUSTRATE THE BASIC APPROACH TO CAUSAL ANALYSIS, OF CONDITIONING OVER SETS OF VARIABLES SUCH THAT, GIVEN THOSE VARIABLES, THE MODEL ERROR TERM IS INDEPENDENT OF OTHER MODEL VARIABLES. (THESE CONDITIONS ARE CALLED "CONDITIONAL INDEPENDENCE" ASSUMPTIONS.) IN THE PRECEDING EXAMPLES, IT WAS ASSUMED THAT ALL VARIABLES WERE OBSERVED. THE ISSUE THAT ARISES IN PRACTICE IS THAT IN GENERAL, NOT ALL MODEL VARIABLES ARE OBSERVED. THE PROBLEM IS TO DETERMINE A SET OF OBSERVED MODEL VARIABLES THAT CAN BE CONDITIONED ON, TO PROVIDE UNBIASED ESTIMATES OF CAUSAL EFFECTS. THAT IS EXACTLY THE PROBLEM THAT PEARL ADDRESSES.

PEARL’S DEFINITION OF CAUSAL EFFECT

DEFINITION OF PEARL CAUSAL EFFECT: GIVEN TWO DISJOINT SETS OF VARIABLES, X AND Y, THE (PEARL) CAUSAL EFFECT OF X ON Y, DENOTED EITHER AS P(y|) OR P(y|do(x)), IS A FUNCTION FROM X TO THE SPACE OF PROBABILITY DISTRIBUTIONS ON Y. FOR EACH REALIZATION x OF X, P(y|) GIVES THE PROBABILITY OF Y = y INDUCED BY DELETING FROM THE MODEL x_i = f_i(pa_i, u_i), i=1,…,n, ALL EQUATIONS CORRESPONDING TO VARIABLES IN X AND SUBSTITUTING X = x IN THE REMAINING EQUATIONS.

IT IS NOTED THAT SOME AUTHORS TAKE ISSUE WITH PEARL'S APPROACH, MAINTAINING THAT IT IS NOT REALISTIC TO ASSUME THAT PART OF A CAUSAL SYSTEM CAN BE HELD FIXED (OR "SURGICALLY REMOVED FROM," TO USE PEARL'S TERMINOLOGY) WITHOUT CHANGES OCCURRING IN THE REST OF THE SYSTEM. WHILE THAT OBSERVATION IS REASONABLE, IT IS APPROPRIATE IN THIS CONTEXT TO RECALL BOX'S REMARK THAT "ESSENTIALLY, ALL MODELS ARE WRONG, BUT SOME ARE USEFUL."

FROM THE EXPRESSION GIVEN ABOVE FOR THE JOINT PROBABILITY OF THE MODEL VARIABLES, THE PEARL CAUSAL EFFECT OF x_i ON ALL MODEL VARIABLES OTHER THAN x_i IS GIVEN BY

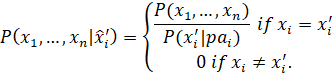
PEARL ALSO DENOTES THIS AS OR .

(NOTE THE AMBIGUITY IN THE PRECEDING NOTATION. AS IN THE CASE OF THE NOTATION FOR ORDINARY CONDITIONAL DISTRIBUTIONS, IN THE EXPRESSION ALL OF THE x_i ARE PRESENT IN x₁,…,x_n, WHEREAS IN THE EXPRESSION THE VARIABLE x_i IS OMITTED FROM x₁,…,x_n. SOME AUTHORS USE THE BACKSLASH (\) TO INDICATE EXCLUSION (E.G., P(X₁,...X_n\X₂) = P(X₁, X₃, ...,X_n)), BUT WE SHALL NOT DO THIS.)

THE ESSENTIAL POINT TO REALIZE ABOUT THIS DEFINITION IS THAT IT IS DIFFERENT FROM THE DEFINITION OF THE CONDITIONAL PROBABILITY OF y GIVEN x. IT IS A CONDITIONAL PROBABILITY, BUT IT CONDITIONS ON THE RANDOM VARIABLE x|pa RATHER THAN x, IN THE STANDARD DEFINITION OF CONDITIONAL PROBABILITY.

THE JOINT CONDITIONAL PROBABILITY OF ALL MODEL VARIABLES OTHER THAN x_i GIVEN x_i = x_i’ IS GIVEN BY

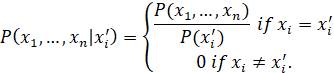
THIS COULD ALSO BE DENOTED AS .

WHEN MAKING COMPARISONS OF THE JOINT CONDITIONAL PROBABILITY TO THE PEARL CAUSAL EFFECT, WE MAY REFER TO THE PRECEDING EXPRESSION (THE JOINT CONDITIONAL PROBABILITY) AS THE OBSERVED EFFECT OF x_i ON ALL MODEL VARIABLES OTHER THAN x_i.

AN IMPORTANT THING TO KEEP IN MIND ABOUT THE TWO PRECEDING QUANTITIES (THE PEARL CAUSAL EFFECT AND THE OBSERVED EFFECT) IS THAT THEY ARE PROBABILITY DISTRIBUTIONS, NOT EXPECTED VALUES. THEY DEFINE THE CAUSAL EFFECT AT THE LEVEL OF THE EXPERIMENTAL UNIT. MORE DESCRIPTIVELY, THESE QUANTITIES MIGHT BE REFERRED TO AS THE UNIT-LEVEL PEARL CAUSAL EFFECT AND THE UNIT-LEVEL OBSERVED EFFECT. THESE QUANTITIES ARE JOINT PROBABILITIES AT THE LEVEL OF THE INDIVIDUAL UNIT (OR "CELL" OF A DISCRETE MULTIVARIATE DISTRIBUTION). THEY ARE NOT MARGINAL PROBABILITIES, BUT CONDITIONAL PROBABILITIES.

COMPARING THESE EXPRESSIONS, WE SEE THAT THE OBSERVED EFFECT DIFFERS FROM THE PEARL CAUSAL EFFECT BY THE FACTOR . THE OBSERVED EFFECT (ORDINARY JOINT CONDITIONAL PROBABILITY) INFLATES THE PROBABILITY OF EACH POINT IN THE FULL JOINT PROBABILITY DISTRIBUTION THAT IS ASSOCIATED WITH BY THE FACTOR . THE PEARL CAUSAL EFFECT INFLATES THE PROBABILITY OF EACH POINT IN THE FULL JOINT PROBABILITY DISTRIBUTION THAT IS ASSOCIATED WITH AND pa_i BY THE FACTOR .

IF x_i IS INDEPENDENT OF ALL OTHER VARIABLES IN THE MODEL (I.E., HAS NO PARENT VARIABLES), THEN ), AND THE PEARL CAUSAL EFFECT IS EQUAL TO THE OBSERVED EFFECT.

WE SHALL NOW DISCUSS IN FURTHER DETAIL THE DIFFERENCES BETWEEN THE PEARL CAUSAL EFFECT AND THE OBSERVED EFFECT.

MARGINAL CAUSAL EFFECTS

THE PRECEDING DEFINITION OF CAUSAL EFFECT WAS STATED IN TERMS OF THE EFFECT OF ONE VARIABLE ON ALL OTHERS OF THE MODEL, I.E., THE EFFECT OF ONE VARIABLE ON THE SYSTEM UNDER CONSIDERATION. WE SHALL NOW ADDRESS THE ISSUE OF DEFINING THE CAUSAL EFFECT OF ONE VARIABLE ON ONE OTHER VARIABLE.

LET US SUPPOSE THAT WE ARE INTERESTED IN THE EFFECT OF ONE VARIABLE, SAY, x_i, ON ANOTHER, SAY x_k. TO FACILITATE KEEPING THE ROLES OF THESE TWO VARIABLES STRAIGHT, WE SHALL RELABEL x_k AS y. THAT IS, y IS THE RESPONSE VARIABLE (OUTCOME VARIABLE, DEPENDENT VARIABLE, EFFECT VARIABLE) AND x_i IS THE EXPLANATORY VARIABLE (CAUSAL VARIABLE). THIS IS THE NOTATION USED BY PEARL IN OP. CIT.

WE HAVE DEFINED THE PEARL CAUSAL EFFECT OF x_i ON ALL OTHER MODEL VARIABLES AS

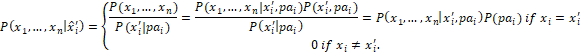
THIS IS A UNIT-LEVEL CAUSAL EFFECT. TO OBTAIN THE DISTRIBUTION (I.E., THE PEARL CAUSAL EFFECT OF x_i ON ANOTHER VARIABLE x_k, WHICH WE SHALL DENOTE AS y) WE SUM THE PRECEDING EXPRESSION OVER ALL VARIABLES OTHER THAN y AND x_i. SUMMING OVER VARIABLES OTHER THAN pa_iREMOVES THOSE VARIABLES FROM THE EXPRESSION. THE SUMMATION OVER pa_i REMAINS:

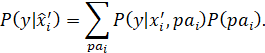
BY SUMMING OVER ONE OR MORE OF THE RANDOM VARIABLES OF THE JOINT DISTRIBUTION WE OBTAIN A MARGINAL DISTRIBUTION (IN THIS CASE, A CONDITIONAL MARGINAL DISTRIBUTION).

SIMILARLY, FOR THE DISTRIBUTION (I.E., THE OBSERVED EFFECT OF x_i ON A SINGLE VARIABLE y) WE OBTAIN:

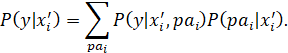
FROM THESE TWO EXPRESSIONS, WE SEE THAT THE COMMON FACTOR IN EACH IS THE CONDITIONAL PROBABILITY . ALL THAT DIFFERS IN THE TWO EXPRESSIONS ARE THE “WEIGHTING FACTORS,” AND . LET US WRITE THE OBSERVED EFFECT AS:

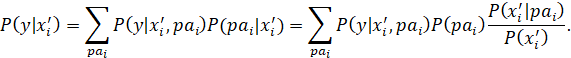
THIS EXPRESSION HIGHLIGHTS THE FACT, MENTIONED EARLIER, THAT THE PEARL CAUSAL EFFECT AND THE OBSERVED EFFECT DIFFER BY THE FACTOR .

NOTE THAT THE TWO PRECEDING EFFECTS ARE MARGINAL DISTRIBUTIONS, I.E., THEY ARE SUMMED OVER VARIABLES OTHER THAN y AND x_i.

FROM THIS EXPRESSION, IT IS CLEAR THAT THE FACTOR INTRODUCES THE SELECTION BIAS ASSOCIATED WITH USING THE OBSERVED EFFECT AS AN ESTIMATE OF THE PEARL CAUSAL EFFECT. IF P(x_i|pa_i) IS NOT INDEPENDENT OF pa_i, THEN THE SAMPLE OBSERVED EFFECT IS A BIASED ESTIMATE OF THE CAUSAL EFFECT. IF P(x_i|pa_i) IS INDEPENDENT OF pa_i (I.E., P(x_i|pa_i) = P(x_i)), THEN THE SAMPLE OBSERVED EFFECT IS AN UNBIASED ESTIMATE OF THE PEARL CAUSAL EFFECT. THE NUMERATOR OF THIS FACTOR, THE PROBABILITY OF ASSIGNMENT TO TREATMENT GIVEN THE VARIABLES ON WHICH IT DEPENDS (I.E., GIVEN THE PARENTS OF x_i IN THE DAG) IS CALLED THE PROPENSITY SCORE OF x_i BASED ON THOSE VARIABLES (WHICH ARE USUALLY CALLED “COVARIATES”). IF THIS PROBABILITY WERE INDEPENDENT OF pa_i, THEN THE NUMERATOR AND DENOMINATOR OF THE FACTOR WOULD BE IDENTICAL, MAKING THE FACTOR EQUAL TO 1.

SO, WHAT INTRODUCES A BIAS INTO THE OBSERVED EFFECT (CONSIDERED AS AN ESTIMATE OF THE CAUSAL EFFECT) IS THE DEPENDENCE OF THE DISTRIBUTION OF x_i ON OTHER VARIABLES (I.E., ON ITS PARENTS).

IN WORDS, THE PEARL CAUSAL EFFECT OF x_i ON y, , IS OBTAINED BY ESTIMATING THE PROBABILITY DISTRIBUTION OF OUTCOME y CONDITIONAL ON THE CAUSAL VARIABLE (x_i) AND ALL ITS PARENT VARIABLES (I.E., THE VARIABLES (pa_i) ON WHICH THE CAUSAL VARIABLE DEPENDS DIRECTLY), AND THEN TAKING THE EXPECTATION OF THIS CONDITIONAL OUTCOME OVER THE (UNCONDITIONAL) POPULATION DISTRIBUTION OF pa_i. SYMBOLICALLY, WE MAY WRITE:

WHERE P(pa_i) DENOTES THE (UNCONDITIONAL) PROBABILITY DISTRIBUTION OF pa_i OVER THE POPULATION. NOTE THAT THE PEARL CAUSAL EFFECT IS IN FACT AN AVERAGE CAUSAL EFFECT – IT IS THE EXPECTED CAUSAL EFFECT ON AN INDIVIDUAL THAT IS RANDOMLY SELECTED FROM THE POPULATION UNDER STUDY. (THE EXPECTATION IS TAKEN OVER (“CONDITIONED OVER”) ALL VARIABLES ON WHICH THE CONDITIONAL DISTRIBUTION OF y GIVEN x_i DEPENDS, WHICH IS JUST THE PARENTS OF x_i (pa_i).) WE HAVE ADDED THE TERM “AVERAGE” IN PARENTHESES TO EMPHASIZE THIS FACT.

THE ESSENTIAL THING TO KEEP IN MIND IN THIS DEFINITION OF THE PEARL CAUSAL EFFECT OF ONE VARIABLE (x_i) ON ANOTHER (y) IS THAT IT IS AN AVERAGE OVER THE DISTRIBUTION P(pa_i) FOR THE POPULATION. THAT IS, WHILE PEARL DEFINES THE CAUSAL EFFECT OF x_i ON THE SYSTEM (ALL OTHER MODEL VARIABLES) AS A UNIT-LEVEL EFFECT, HE DEFINES THE CAUSAL EFFECT OF x_i ON y AS AN AVERAGE (RELATIVE TO THE DISTRIBUTION P(pa_i)).

THE OBSERVED EFFECT TAKES THIS EXPECTATION USING THE (OBSERVED) CONDITIONAL DISTRIBUTION OF pa_i GIVEN x_i:

WHERE P(pa_i|x_i) DENOTES THE CONDITIONAL PROBABILITY DISTRIBUTION OF pa_i GIVEN x_i. AGAIN, AN ESSENTIAL THING TO OBSERVE IS THAT THE OBSERVED EFFECT IS AN AVERAGE, TAKEN OVER THE POPULATION DISTRIBUTION P(pa_i|x_i).

WE HAVE ADDED THE PARENTHETIC “AVERAGE” TO EMPHASIZE THAT THE OBSERVED EFFECT IS THE AVERAGE (EXPECTED VALUE) OF THE CAUSAL EFFECT (OVER pa_i).

THE PRECEDING FORMULAS ILLUSTRATE THE THEORETICAL NATURE OF THE PEARL CAUSAL EFFECT CORRESPONDING TO A CAUSAL MODEL DESCRIBED AS A DAG (AND THE ASSOCIATED CONDITIONAL-PROBABILITY FORMULAS). IN PRACTICE, THE PRECEDING FORMULAS ARE NOT USED TO ESTIMATE THE PEARL CAUSAL EFFECT. A PRINCIPAL REASON IS THAT IN MANY APPLICATIONS, NOT ALL OF THE PARENTS OF A CAUSAL VARIABLE MAY BE OBSERVED, AND IT IS NECESSARY TO USE ESTIMATION FORMULAS THAT TAKE THIS INTO ACCOUNT (DESCRIBED IN PEARL OP. CIT.). ANOTHER IS THE “CURSE OF DIMENSIONALITY” – WITH SEVERAL PARENTS (COVARIATES AFFECTING THE PROBABILITY DISTRIBUTION OF THE CAUSAL VARIABLE), IT IS NOT POSSIBLE (EVEN IF THEY ARE ALL OBSERVABLE) TO USE A STRAIGHTFORWARD “STRATIFICATION” APPROACH TO CALCULATING THE SUMS (EXPECTATIONS) INVOLVED IN THE FORMULAS (SINCE THERE ARE USUALLY A VAST NUMBER OF CROSS-STRATIFIED STRATA, MANY CONTAINING NO OBSERVATIONS (SO THAT NO STRATUM ESTIMATE IS AVAILABLE)). THE ROLE OF PEARL’S APPROACH IS TO DESCRIBE CAUSAL MODELS AND DETERMINE ESTIMABILITY OF CAUSAL EFFECTS (BY DERIVING FORMULAS FOR THE PROBABILITY DISTRIBUTION OF OUTCOME GIVEN OBSERVABLES), NOT TO ESTIMATE CAUSAL EFFECTS – THAT IS DONE BY A VARIETY OF STATISTICAL PROCEDURES, AND IS NOT ADDRESSED BY PEARL’S (PROBABILISTIC) METHODOLOGY.

THE PRECEDING DISCUSSION SHOWED HOW A PEARL CAUSAL EFFECT COULD BE ESTIMATED, BY CONDITIONING ON (AVERAGING OVER) ALL OF THE PARENTS OF A CAUSAL VARIABLE IN A DAG. IN PRACTICE, NOT ALL OF THE PARENTS ARE OBSERVED. IN THIS CASE, IT MAY NOT BE OBVIOUS WHETHER A PARTICULAR CAUSAL EFFECT IS ESTIMABLE, AND, IF SO, HOW IT MAY BE ESTIMATED. THE SIGNIFICANT POWER OF PEARL’S METHODOLOGY IS THAT IT CAN BE READILY DETERMINED FROM A DAG WHETHER A PARTICULAR CAUSAL EFFECT IS ESTIMABLE, AND WHAT VARIABLES MAY BE CONDITIONED ON TO ESTIMATE IT. HOW THIS IS DONE WILL BE DESCRIBED LATER.

AN IMPROVED NOTATION FOR THE AVERAGE CAUSAL EFFECT

IN CAUSAL ANALYSIS, WE ARE INTERESTED IN THE EXPECTED VALUE OF THE UNIT-LEVEL CAUSAL EFFECT RELATIVE TO DIFFERENT DISTRIBUTIONS OF THE PARENTS OF x_i. THESE DIFFERENT DISTRIBUTIONS REPRESENT DIFFERENT SETTINGS IN WHICH THE (AVERAGE) CAUSAL EFFECT IS ESTIMATED. WE SHALL DENOTE THE AVERAGE CAUSAL EFFECT RELATIVE TO A SPECIFIC DISTRIBUTION P* FOR THE PARENTS OF x_i AS

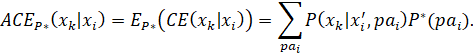
TO AVOID LONG EXPRESSIONS IN SUBSCRIPTS, WE SHALL ALSO DENOTE

THIS NOTATION MAKES IT VERY CLEAR THAT THE AVERAGE CAUSAL EFFECT IS CONDITIONAL NOT ONLY ON x_i, BUT ALSO ON THE DISTRIBUTION P* OF THE PARENTS OF x_i, pa_i.

THE DISTRIBUTION P* IS ARBITRARY. IT IS THE DISTRIBUTION OF pa_i FOR WHICH THE AVERAGE CAUSAL EFFECT IS DESIRED. IN MOST APPLICATIONS, IT IS DESIRED TO ESTIMATE THE CAUSAL EFFECT AVERAGED OVER THE ENTIRE POPULATION FROM WHICH THE DATA WERE SAMPLED. OTHER POPULATIONS COULD BE OF SUBSTANTIAL INTEREST, SUCH AS THE POPULATION OF THOSE TREATED, OR THOSE IN A PARTICULAR DEMOGRAPHIC GROUP (E.G., FEMALES, OR POORLY EDUCATED). PEARL DISCUSSES THIS PROCESS (P. 74 OF OP. CIT.).

THE AVERAGE OBSERVED EFFECT (OR EXPECTED OBSERVED EFFECT) OF x_i ON x_k (DENOTED BY AOE(x_k|x_i’;P(pa_i|x_i’)) IS THE EXPECTATION OF THIS EXPRESSION, I.E., USING THE WEIGHTING DISTRIBUTION P* = P(pa_i|x_i) – THIS IS THE ORDINARY CONDITIONAL DISTRIBUTION OF x_k GIVEN x_i:

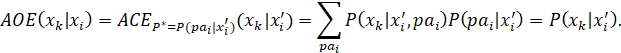
(IN THE EARLIER DISCUSSION OF PEARL’S APPROACH, THIS IS SIMPLY CALLED THE “OBSERVED EFFECT,” NOT THE “AVERAGE OBSERVED EFFECT.”)

THE AVERAGE CAUSAL EFFECT OF x_i ON x_k IS THE EXPECTATION OF THIS EXPRESSION USING THE WEIGHTING DISTRIBUTION P* = P(pa_i):

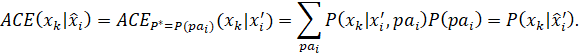
THIS EXPRESSION IS WHAT IS REFERRED TO AS THE “CAUSAL EFFECT” OR "AVERAGE CAUSAL EFFECT." THE PEARL CAUSAL EFFECT IS IN FACT AN AVERAGE (EXPECTED VALUE) OF THE UNAVERAGED CONDITIONAL UNIT-LEVEL CAUSAL EFFECT OVER THE DISTRIBUTION OF pa_i FOR THE POPULATION OF INTEREST (USUALLY THE ENTIRE POPULATION UNDER STUDY). IN THE NEW NOTATION, THE FACT THAT IT IS AN AVERAGE (RELATIVE TO A DISTRIBUTION P* OF pa_i) IS EXPLICIT. TO EMPHASIZE THIS, WE INDICATE THE DISTRIBUTION P* OF pa_i IN THE NOTATION (SYMBOLOGY).

THE AVERAGE TREATMENT EFFECT IS USUALLY DEFINED AS THE DIFFERENCE IN THE AVERAGE CAUSAL EFFECT FOR TWO DIFFERENT VALUES OF THE CAUSAL VARIABLE (I.E., TREATED AND UNTREATED). SOME PEOPLE MAY HAVE DIFFICULTY WITH THE DEFINITION OF “AVERAGE TREATMENT EFFECT” AS THE EXPECTATION OF THE EFFECT OF TREATMENT. WITHOUT ELABORATION, THIS EXPRESSION COULD REASONABLY REFER EITHER TO THE AVERAGE OBSERVED TREATMENT EFFECT (OVER THE POPULATION UNDER STUDY) OR THE AVERAGE EFFECT OF TREATMENT FOR A RANDOMLY SELECTED INDIVIDUAL. WHAT IS NOT CLEAR FROM THE EXPRESSION IS THAT THESE TWO QUANTITIES ARE SIMPLY EXPECTATIONS (OF THE EFFECT OF TREATMENT) OVER TWO DIFFERENT DISTRIBUTIONS OF pa_i (THAT IS, THEY REPRESENT THE AVERAGE CAUSAL EFFECT IN DIFFERENT SETTINGS). THE LABELS “AVERAGE TREATMENT EFFECT” OR (THE EQUIVALENT) “EXPECTED TREATMENT EFFECT” DO NOT MAKE THIS DISTINCTION CLEAR AT ALL. THE SO-CALLED “OBSERVED TREATMENT EFFECT” IS THE EXPECTED VALUE OF THE DIFFERENCE BETWEEN TREATED AND UNTREATED UNITS FROM THE STUDY POPULATION (GIVEN WHATEVER MECHANISM WAS USED TO ASSIGN TREATMENT, AND THEREBY DETERMINE THE DISTRIBUTION OF pa_i), AND THE SO-CALLED (BUT AMBIGUOUS) “AVERAGE TREATMENT EFFECT” IS THE EXPECTED VALUE OF THE DIFFERENCE BETWEEN TREATED AND UNTREATED UNITS, IF UNITS ARE RANDOMLY SELECTED FROM THE POPULATION AND TREATMENT IS RANDOMLY ASSIGNED. BOTH OF THESE QUANTITIES ARE “AVERAGE TREATMENT EFFECTS” OR “EXPECTED TREATMENT EFFECTS,” AND THIS AMBIGUOUS TERMINOLOGY HAS LED TO MUCH MISUNDERSTANDING AND CONFUSION.

NOTE THAT THE PRIMES ARE A NOTATIONAL CONVENIENCE. THE EXPRESSION P(x_k|x_i’) IS SHORTHAND FOR P(x_k|X_i=x_i’) OR P(x_k|x_i=x_i’). THE NOTATION IMPLIES THAT THE CONDITIONAL DISTRIBUTION P(x_k|x_i) = P(x_k,x_i)/P(x_i) IS FORMED, AND THEN x_i’ IS SUBSTITUTED FOR x_i. SOME AUTHORS WOULD DEPICT THIS DISTRIBUTION AS P(X_k|X_i=x_i) = P(X_k,X_i)/P(X_i)|_Xi=xi OR P(X_k|X_i=x_i’) = P(X_k,X_i)/P(X_i)|_Xi=xi’ (USING CAPITAL LETTERS FOR ABSTRACT RANDOM VARIABLES AND LOWER-CASE LETTERS FOR REALIZATIONS). FOR THIS PRESENTATION WE ARE USING PEARL’S NOTATION (LOWER-CASE LETTERS, WITH A PRIME INDICATING A PARTICULAR VALUE OF THE VARIABLE BEING CONDITIONED ON), TO PERMIT EASY COMPARISON TO HIS FORMULAS.

IF WE RELABEL x_k AS y, THIS BECOMES:

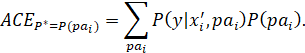
THIS IS EXACTLY THE FORMULA 3.13 ON PAGE 73 OF PEARL OP. CIT. (2^ND ED.) (IN PEARL’S NOTATION, THIS QUANTITY IS DENOTED AS .

AT THIS POINT, IT IS OBSERVED THAT PEARL’S DEVICE OF MODIFYING THE SYMBOL USED FOR THE CONDITIONING VARIABLE (I.E., CHANGING x_i TO OR TO do(x_i)) MAY LEAD TO AMBIGUITY AND CONFUSION. WHAT DIFFERS IN THE EXPRESSION FOR THE AVERAGE OBSERVED EFFECT AND THE (AVERAGE) PEARL CAUSAL EFFECT IS NOT THE VARIABLE x_i OR THE DEFINITION OF THE INDIVIDUAL-UNIT CAUSAL EFFECT, BUT THE DISTRIBUTION P* OF pa_i. FOR THE AVERAGE OBSERVED EFFECT, THE WEIGHTING DISTRIBUTION OF pa_i IS P(pa_i|x_i). FOR THE AVERAGE CAUSAL EFFECT (OVER THE STUDY POPULATION (FROM WHICH THE DATA ARE SAMPLED)), THE WEIGHTING DISTRIBUTION OF pa_i IS P(pa_i). TO MAKE THIS DISTINCTION CLEAR IS THE REASON WHY WE INCLUDED THE WEIGHTING DISTRIBUTION (P*) IN THE NOTATION OF THE FORMULA FOR THE AVERAGE CAUSAL EFFECT.

FROM THIS DEFINITION/NOTATION, IT IS CLEAR THAT THE AVERAGE CAUSAL EFFECT IS ALWAYS RELATIVE TO AN ASSUMED DISTRIBUTION (P*) FOR pa_i. THIS ESSENTIAL FACT IS NOT EVIDENT FROM PEARL’S NOTATION, WHICH IMPLICITLY ASSUMES THAT THE DISTRIBUTION P*(pa_i) IS THAT FOR THE STUDY POPULATION. THERE ARE AN INFINITE NUMBER OF AVERAGE CAUSAL EFFECTS – ONE FOR EVERY DISTRIBUTION OF P*. IF INTEREST FOCUSES ON THE EFFECT OF A PROGRAM UNDER THE SAME CONDITIONS AS WERE PRESENT FOR THE SAMPLE (RATHER THAN FOR A RANDOMLY SAMPLED INDIVIDUAL), THEN THE "AVERAGE CAUSAL EFFECT" OF THE PROGRAM WOULD IN FACT BE THE OBSERVED CAUSAL EFFECT.

IT IS EMPHASIZED THAT THE DISTRIBUTION P* USED TO CALCULATE THE AVERAGE CAUSAL EFFECT IS ARBITRARY. IT IS WHATEVER DISTRIBUTION IS DESIRED TO BE AVERAGED OVER, TO DETERMINE THE AVERAGE CAUSAL EFFECT RELATIVE TO THAT DISTRIBUTION. IT MAY BE THE CONDITIONAL DISTRIBUTION OF pa_i GIVEN x_i, P(pa_i|x_i) FOR THE POPULATION UNDER STUDY (TO ESTIMATE THE AVERAGE OBSERVED EFFECT), OR IT MAY BE SOME OTHER DISTRIBUTION (E.G., A SPECIAL POPULATION OF INTEREST, SUCH AS A POPULATION WHOSE DEMOGRAPHIC CHARACTERISTICS DIFFER FROM THOSE OF THE STUDY POPULATION). IT MAY REFER TO ANY OTHER POPULATION OF INTEREST, SUCH AS THE DISTRIBUTION OF FEMALES, OR THE POPULATION OF PERSONS RECEIVING TREATMENT (I.E., THE AVERAGE EFFECT OF TREATMENT ON THE TREATED, ATT).

AN IMMEDIATE ADVANTAGE OF THE PRECEDING NOTATION FOR AN AVERAGE CAUSAL EFFECT – ALWAYS RELATIVE TO AN EXPLICITLY SPECIFIED DISTRIBUTION FOR pa_i – IS THAT IT IS VERY CLEAR THAT THAT DISTRIBUTION MAY BE VARIED AT WILL. A DISADVANTAGE OF PEARL’S NOTATION, WHICH FOCUSES SOLELY ON x_i, NOT ON pa_i, IS THAT IT IS NOT EVIDENT WHAT THE DISTRIBUTION OF pa_i IS. IN PEARL’S FRAMEWORK, THE (AVERAGE) PEARL CAUSAL EFFECT IS DEFINED RELATIVE TO THE DISTRIBUTION OF pa_i OVER THE POPULATION UNDER STUDY. IT MAY BE, HOWEVER, THAT IT IS DESIRED TO KNOW THE AVERAGE CAUSAL EFFECT RELATIVE TO SOME OTHER DISTRIBUTION OF pa_i. FOR EXAMPLE, IF IT IS DESIRED TO ESTIMATE THE AVERAGE CAUSAL EFFECT, THE UNCONDITIONAL DISTRIBUTION OF pai (NOT OF pai|xi); OR, IF IT IS DESIRED TO KNOW THE ACE OF pa FOR FEMALES, THE VARIABLE P* IS SIMPLY SET EQUAL TO THE DISTRIBUTION OF FEMALES. IN PEARL’S FRAMEWORK, THE MARGINAL DISTRIBUTION OF pa_i (FOR THE POPULATION AND DATA SET UNDER STUDY) IS AN INTEGRAL PART OF THE DEFINITION OF THE CAUSAL EFFECT, AND THE CONCEPT OF CAUSALITY BECOMES VERY CONVOLUTED. IN PEARL’S APPROACH THE CAUSAL EFFECT IS DEFINED AS THE AVERAGE CAUSAL EFFECT RELATIVE TO A SPECIFIC DISTRIBUTION FOR THE PARENTS OF THE CAUSAL VARIABLE(VIZ., THE DISTRIBUTION OBSERVED IN THE STUDY POPULATION).

NOTE THAT EVEN IN THE NEW NOTATION, THERE IS NO INDICATION OF THE PARENTS, pa, OF x. THAT SET OF VARIABLES REMAINS THE SAME, EVEN THOUGH THE DISTRIBUTION OVER IT MAY VARY. IT IS SPECIFIED IN THE CAUSAL MODEL.

NOTE THAT THE PRECEDING CHANGE IN NOTATION DOES NOT MODIFY PEARL’S THEORY FOR DETERMINING ESTIMABILITY (IDENTIFIABILITY) FROM DAGs IN ANY WAY (EXCEPT FOR NOTATION). (PEARL’S METHODOLOGY FOR ASSESSING ESTIMABILITY WILL BE DESCRIBED LATER.) HIS CAUSAL DIAGRAMS REMAIN UNCHANGED, AND HIS CRITERIA FOR ESTABLISHING ESTIMABILITY ARE EXACTLY THE SAME. ALL THAT DIFFERS IS THAT INSTEAD OF WRITING THE PEARL CAUSAL EFFECT AS

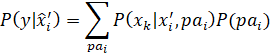
(WHERE y = x_k) WE WRITE THE (IDENTICAL) AVERAGE CAUSAL EFFECT AS

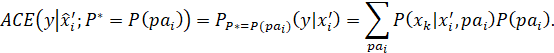
IT HAS BEEN CONJECTURED THAT THE FIELD OF PROBABILISTIC CAUSALITY MIGHT BENEFIT FROM INTRODUCTION OF THE NOTION OF “DIRECTIONAL” PROBABILITIES, THAT ALLOW FOR THE PROBABILITY OF Y GIVEN A TEMPORALLY PRECEDENT X TO DEPEND ON X, BUT FOR X TO BE INDEPENDENT OF Y IN THIS CASE. THE VERY SUBSTANTIAL PROBLEM THAT THIS WOULD INTRODUCE IS THAT THE ENTIRE PROBABILITY CALCULUS OF ASSOCIATIVE PROBABILITY WOULD NO LONGER APPLY. IT WOULD BE TRUE THAT P(Y|X) = P(Y,X)/P(X), BUT NOT THAT P(X|Y) = P(Y,X)/P(Y) (SINCE P(X|Y) WOULD IN FACT BE INDEPENDENT OF Y IN THIS FRAMEWORK. IT WOULD APPEAR THAT THERE IS NO NEED FOR THE INTRODUCTION OF DIRECTIONAL PROBABILITIES, SINCE EXISTING CAUSAL MODELS (E.G., PEARL, R&R) ARE QUITE ADEQUATE. THE PREFERRED APPROACH IS TO CONTINUE TO REPRESENT ASSOCIATIONAL RELATIONSHIPS USING PROBABILITY DISTRIBUTIONS AND CAUSAL RELATIONSHIPS, SEPARATELY, USING GRAPHIC CAUSAL DIAGRAMS.

WE SHALL NOW DESCRIBE HOW PEARL’S METHODOLOGY IS APPLIED TO DETERMINE WHETHER AND HOW A CAUSAL EFFECT IS ESTIMABLE FROM A CAUSAL MODEL.

PEARL’S ESTIMABILITY CRITERIA ARE ESSENTIALLY AN ELABORATION OF THE CONCEPT THAT A CAUSAL EFFECT MAY BE ESTIMATED BY CONDITIONING ON ALL VARIABLES THAT AFFECT BOTH THE CAUSAL VARIABLE AND THE EFFECT VARIABLE.

DETERMINATION OF ESTIMABILITY (IDENTIFIABILITY) USING DIRECTED ACYCLIC GRAPHS

[OPTIONAL SECTION]

AS DISCUSSED, THE CONDITIONAL DISTRIBUTION OF A RESPONSE VARIABLE GIVEN AN EXPLANATORY VARIABLE AND ITS PARENTS IS CALLED THE “CAUSAL EFFECT” OR “IMPACT” OF THE EXPLANATORY VARIABLE. A PRINCIPAL USE OF CAUSAL DIAGRAMS IS TO ESTABLISH WHETHER A CAUSAL EFFECT CAN BE ESTIMATED (I.E., AN UNBIASED ESTIMATE DETERMINED). (IF ALL MODEL PARAMETERS ARE ESTIMABLE, THEN THE MODEL IS SAID TO BE IDENTIFIABLE. IN CAUSAL ANALYSIS, ATTENTION OFTEN FOCUSES ON A SINGLE PARAMETER (NOT ON THE ENTIRE DISTRIBUTION). THE OTHER PARAMETERS MAY OR MAY NOT BE OF INTEREST, BUT IN ORDER FOR ONE OF THEM TO BE ESTIMABLE, IT IS OFTEN NECESSARY (E.G., IN A REGRESSION MODEL WITH NON-ORTHOGONAL EXPLANATORY VARIABLES) FOR ALL OF THEM TO BE ESTIMATED. IN THIS CASE, ATTENTION FOCUSES ON IDENTIFIABILITY OF THE MODEL (I.E., ESTIMATION OF ALL OF THE MODEL PARAMETERS), NOT JUST ON ESTIMATING ONE OF THEM.)

PREVIOUSLY, ANALYSTS TENDED TO ESTABLISH ESTIMABILITY BY SPECIFYING A SET OF SIMULTANEOUS EQUATIONS RELATING THE INPUT AND OUTPUT VARIABLES, AND DETERMINING WHETHER THEY COULD BE SOLVED (FOR ONE OR MORE PARAMETERS OF INTEREST). ALTERNATIVELY, A SET OF ESTIMATING EQUATIONS COULD BE DEVELOPED, AND A DETERMINATION MADE CONCERNING WHETHER THEY COULD BE SOLVED. THIS APPROACH WORKS IN MANY CASES, BUT IT MAY BE COMPLICATED. AN ALTERNATIVE APPROACH, BASED ON DIRECTED ACYCLIC GRAPHS, IS AVAILABLE AND WILL NOW BE DESCRIBED.

NOTE THAT PEARL’S APPROACH IS NONPARAMETRIC. HE FOCUSES ON ESTIMATING THE ENTIRE PROBABILITY DISTRIBUTION OF OUTCOME CONDITIONAL ON THE CAUSAL VARIABLE, IRRESPECTIVE OF WHETHER THE DISTRIBUTION IS PARAMETERIZED.

PEARL’S METHODOLOGY FOR DESCRIBING CAUSAL MODELS AND DETERMINING THE ESTIMABILITY OF CAUSAL EFFECTS USES DIRECTED ACYCLIC GRAPHS. OTHER SIMILAR METHODS HAVE BEEN USED IN THE PAST. THE TWO PRINCIPAL METHODS ARE PATH DIAGRAMS AND SYSTEMS OF LINEAR EQUATIONS.

PATH DIAGRAMS WERE POPULARIZED BY SEWALL WRIGHT ABOUT 1923. REFERENCES ON PATH ANALYSIS INCLUDE THE FOLLOWING:

1. LI, C. C., PATH ANALYSIS – A PRIMER (THE BOXWOOD PRESS, 1975)

2. OLOBATUYI, MOSES E., A USER’S GUIDE TO PATH ANALYSIS (UNIVERSITY PRESS OF AMERICA, 2006).

(PATH ANALYSIS IS USED MAINLY IN CONJUNCTION WITH LINEAR MODELS HAVING NORMALLY DISTRIBUTED ERROR TERMS, WHEREAS PEARL’S THEORY IS COMPLETELY NONPARAMETRIC.)

SIMULTANEOUS EQUATION MODELS (SEMs) ARE DESCRIBED IN THE FOLLOWING REFERENCES:

1. MULAIK, STANLEY A., LINEAR CAUSAL MODELING WITH STRUCTURAL EQUATIONS (CRC PRESS, 2009)

2. SCHUMAKER, RANDALL E. AND RICHARD G. LOMAX, A BEGINNER’S GUIDE TO STRUCTURAL EQUATION MODELING 3^RD EDITION (ROUTLEDGE, 2010)

3. KLINE, REX B., PRINCIPLES AND PRACTICE OF STRUCTURAL EQUATION MODELING 3^RD EDITION (THE GUILFORD PRESS, 2011)

4. GOLDBERGER, ARTHUR S. AND OTIS DUDLEY DUNCAN, STRUCTURAL EQUATION MODELING IN THE SOCIAL SCIENCES (SEMINAR PRESS, 1973)

5. DUNCAN, OTIS DUDLEY, INTRODUCTION TO STRUCTURAL EQUATION MODELS (ACADEMIC PRESS, 1975).

FOR ADDITIONAL DISCUSSION OF IDENTIFICATION, SEE THE FOLLOWING:

1. AHSER, HERBERT B., CAUSAL MODELING 2^ND EDITION, SAGE PUBLICATIONS, 1983

2. FINKEL, STEVEN E., CAUSAL ANALYSIS WITH PANEL DATA, SAGE PUBLICATIONS, 1995

3. DAVIS, JAMES A., THE LOGIC OF CAUSAL ORDER, SAGE PUBLICATIONS, 1985

4. SAS/STAT 9.2 USER’S GUIDE: THE FOUR TYPES OF ESTIMABLE FUNCTIONS (BOOK EXCERPT), SAS INSTITUTE, 2008

5. ELSWICK, R. K. JR., CHRIS GENNINGS, VERNON M. CHINCHILLI AND KATHRYN S. DAWSON, A SIMPLE APPROACH FOR FINDING ESTIMABLE FUNCTIONS IN LINEAR MODELS, THE AMERICAN STATISTICIAN, VOL. 45, NO. 1 (FEB. 1991), PP. 51-53.

SOLVING EQUATIONS AS A METHOD OF ESTABLISHING ESTIMABILITY HAS SHORTCOMINGS. FIRST, IT IS NOT AS RAPID OR AS TRANSPARENT AS PEARL’S GRAPHICAL METHODS. SECOND, IT DOES NOT SHOW DIRECTION OF CAUSAL EFFECTS. THIRD, IT DOES NOT RELIABLY SHOW WHICH VARIABLES MAY BE SAFELY CONDITIONED ON (WITHOUT INTRODUCING BIASES) (THAT IS, IT DOES NOT TAKE INTO ACCOUNT STOCHASTIC RELATIONSHIPS SUCH AS THE CORRELATION OF EXPLANATORY VARIABLES WITH MODEL ERROR TERMS.)

FOR OUR PURPOSES IN THIS PRESENTATION, WE SHALL DEFINE A CAUSAL MODEL GRAPHICALLY TO ESTABLISH ESTIMABILITY (ACCORDING TO PEARL’S CRITERIA), AND AS A SET OF EQUATIONS (THAT DEFINES THE PROBABILITY FUNCTION OF ONE VARIABLE, Y, IN TERMS OF ANOTHER VARIABLE, X (A VECTOR)) FOR PURPOSES OF ESTIMATING THE MAGNITUDES OF CAUSAL RELATIONSHIPS (VIA STATISTICAL METHODS).

THE SIMULATION MODEL PRESENTED EARLIER IS AN EXAMPLE OF A CAUSAL MODEL SPECIFIED BY EQUATIONS.

THIS PRESENTATION IS RESTRICTED TO CAUSAL MODELS IN WHICH CAUSAL INFLUENCES PROCEED IN ONE DIRECTION FROM ONE VARIABLE TO ANOTHER BUT NOT IN BOTH DIRECTIONS, AND DO NOT FOLLOW A PATH FROM ONE VARIABLE BACK TO ITSELF VIA OTHER VARIABLES. AS MENTIONED EARLIER, SUCH MODELS ARE CALLED RECURSIVE MODELS, AND THEY MAY BE REPRESENTED BY DIRECTED ACYCLIC GRAPHS (DAGs). MODELS THAT ARE NOT RECURSIVE ARE CALLED NONRECURSIVE OR SIMULTANEOUS MODELS, AND THEY MAY BE REPRESENTED BY DIRECTED CYCLIC GRAPHS (DCGs).

THE DESCRIPTION PRESENTED HERE IS VERY BRIEF. SEE PEARL OP. CIT. FOR MORE DETAILED DESCRIPTION, INCLUDING MOTIVATION, RATIONALE, PROOFS AND EXAMPLES. TO FACILITATE COMPARISON TO PEARL’S BOOK, WE SHALL USE HIS “HAT” NOTATION.

BY DEFINITION, A CAUSAL EFFECT IS ESTIMABLE IF THE QUANTITY

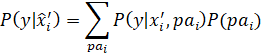
CAN BE ESTIMATED. IF y, x_i AND pa_i ARE ALL OBSERVABLE, THEN THERE IS NO PROBLEM. A PROBLEM ARISES WHEN SOME OF THE pa_i ARE NOT OBSERVABLE. IN THAT CASE THE AVERAGE CAUSAL EFFECT MUST BE ESTIMATED FROM DATA ON THE VARIABLES THAT ARE OBSERVED. PEARL DETERMINES CONDITIONS UNDER WHICH THIS CAN BE DONE.

PEARL PRESENTS TWO CRITERIA FOR ESTABLISHING ESTIMABILITY – THE “BACK-DOOR” CRITERION AND THE “FRONT-DOOR” CRITERION. THESE CRITERIA ARE STATED IN TERMS OF PROPERTIES OF THE CAUSAL MODEL DIAGRAM (THE DAG).

PEARL’S ESTIMABILITY CRITERIA ARE SPECIFIED IN TERMS OF A CONCEPT OF “BLOCKAGE” OR “d-SEPARABILITY” (WHERE “d” DENOTES “DIRECTIONAL), DEFINED AS FOLLOWS:

d-SEPARATION, OR “BLOCKAGE”. A PATH p IN A DAG IS SAID TO BE d-SEPARATED (OR BLOCKED) BY A SET OF NODES Z IF AND ONLY IF

(1) p CONTAINS A CHAIN i→ m → j OR A FORK i ← m → j SUCH THAT THE MIDDLE NODE m IS IN Z; OR

(2) p CONTAINS AN INVERTED FORK (OR “COLLIDER”) i → m ← j SUCH THAT THE MIDDLE NODE m IS NOT IN Z AND SUCH THAT NO DESCENDENT OF m IS IN Z.

A SET Z IS SAID TO d-SEPARATE X FROM Y IF AND ONLY IF Z BLOCKS EVERY PATH FROM A NODE IN X TO A NODE IN Y.

THE CONCEPT OF d-SEPARATION OR BLOCKING IS USEFUL SINCE IT IDENTIFIES VARIABLES THAT AFFECT BOTH THE CAUSAL VARIABLE AND THE EFFECT VARIABLE – THESE ARE THE ONES THAT INTRODUCE SELECTION BIAS. IT IS OBVIOUS THAT BLOCKING A CHAIN ELIMINATES THE RELATIONSHIP BETWEEN VARIABLES ON OPPOSITE SIDES OF THE CHAIN. WHAT IS NOT OBVIOUS IS THAT BLOCKING A COLLIDER DOES NOT ACCOMPLISH THIS. IN FACT, IT ACCOMPLISHES EXACTLY THE OPPOSITE. CONDITIONING ON A COLLIDER MAY INTRODUCE A RELATIONSHIP BETWEEN VARIABLES ON ITS TWO SIDES, EVEN THOUGH THEY MAY BE UNCONDITIONALLY INDEPENDENT.

FIGURE 10 PRESENTS AN ILLUSTRATION OF A RELATIONSHIP INTRODUCED BETWEEN INDEPENDENT VARIABLES BY CONDITIONING. WITHOUT CONDITIONING THE TWO VARIABLES ARE INDEPENDENT. CONDITIONAL ON THE VALUE OF A VARIABLE THAT THEY BOTH AFFECT, THERE IS A STRONG NEGATIVE CORRELATION BETWEEN THEM. FOR EXAMPLE, X AND Y MIGHT REPRESENT SCORES FOR TWO INDEPENDENT CRITERIA FOR ADMITTANCE TO AN ORGANIZATION. AN INDIVIDUAL IS ADMITTED IF THE SUM OF THE TWO SCORES EXCEEDS THE VALUE C. IN THIS CASE, A STRONG NEGATIVE CORRELATION IS INTRODUCED INTO THE DISTRIBUTIONS OF X AND Y FOR ADMITTED INDIVIDUALS. IF ADMITTANCE IS NOT CONDITIONED ON, X AND Y ARE INDEPENDENT (AND BLOCK THE PATH ON WHICH THEY ARE LOCATED). IF ADMITTANCE IS CONDITIONED ON, X AND Y ARE HIGHLY NEGATIVELY CORRELATED (AND DO NOT BLOCK THE PATH ALONG WHICH THEY ARE LOCATED). NOT CONDITIONING ON ADMITTANCE BLOCKS THE PATH ON WHICH IT IS LOCATED (SINCE X AND Y ARE THEN INDEPENDENT). CONDITIONING ON ADMITTANCE DOES NOT HOLD EITHER OF THESE VARIABLES CONSTANT, AND DOES NOT BLOCK THE PATH ON WHICH IT IS LOCATED.

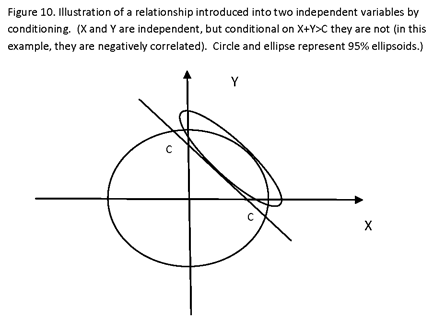
THE “BACK-DOOR” CRITERION IS DEFINED AS FOLLOWS.

BACK-DOOR CRITERION (PEARL). A SET OF VARIABLES Z SATISFIES THE BACK-DOOR CRITERION RELATIVE TO AN ORDERED PAIR OF VARIABLES (X_i, X_j) IN A DAG G IF:

(1) NO NODE IN Z IS A DESCENDENT OF X_j; AND

(2) Z BLOCKS EVERY PATH BETWEEN X_i AND X_j THAT CONTAINS AN ARROW INTO X_i.

SIMILARLY, IF X AND Y ARE TWO DISJOINT SUBSETS OF NODES IN G, THEN Z IS SAID TO SATISFY THE BACK-DOOR CRITERION RELATIVE TO (X,Y) IF IT SATISFIES THE CRITERION RELATIVE TO ANY PAIR (X_i, X_j) SUCH THAT X_i ε X AND X_j ε Y.

PEARL PROVES THAT IF ALL PATHS LEADING BACKWARDS FROM X_i TOWARD X_j ARE BLOCKED, THEN THE PEARL CAUSAL EFFECT (I.E., THE AVERAGE CAUSAL EFFECT RELATIVE TO THE POPULATION UNDER STUDY) IS ESTIMABLE.

BACK-DOOR ADJUSTMENT (OR CONDITIONING) (PEARL). IF A SET OF VARIABLES Z SATISFIES THE BACK-DOOR CRITERION RELATIVE TO (X,Y), THEN THE CAUSAL EFFECT OF X ON Y IS IDENTIFIABLE AND IS GIVEN BY THE FORMULA

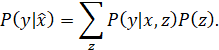
THE BACK-DOOR CRITERION APPLIES TO SITUATIONS IN WHICH THERE ARE NO DESCENDENTS OF X BETWEEN X AND Y. IF THERE ARE, THEN A DIFFERENT CRITERION APPLIES – THE FRONT-DOOR CRITERION.

FRONT-DOOR CRITERION (PEARL). A SET OF VARIABLES Z IS SAID TO SATISFY THE FRONT-DOOR CRITERION RELATIVE TO AN ORDERED PAIR OF VARIABLES (X,Y) IF:

(1) Z INTERCEPTS ALL DIRECTED PATHS FROM X TO Y;

(2) THERE IS NO UNBLOCKED BACK-DOOR PATH FROM X TO Z; AND

(3) ALL BACK-DOOR PATHS FROM Z TO Y ARE BLOCKED BY X.

PEARL PROVES THAT THE AVERAGE CAUSAL EFFECT IS ESTIMABLE UNDER THE FOLLOWING CONDITION.

FRONT-DOOR ADJUSTMENT (OR CONDITIONING) (PEARL). IF Z SATISFIES THE FRONT-DOOR CRITERION RELATIVE TO (X,Y) AND IF P(x,z)>0, THEN THE (AVERAGE) CAUSAL EFFECT OF X ON Y IS IDENTIFIABLE AND IS GIVEN BY THE FORMULA

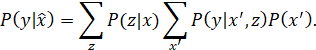
APPLICATION OF THE FRONT-DOOR CRITERION IS MUCH LESS FREQUENT THAN THE BACK-DOOR CRITERION. THE REASON IS THAT IT IS COMMON PRACTICE TO AVOID CONDITIONING ON VARIABLES THAT MAY BE AFFECTED BY TREATMENT (SEE THE PLANNING OF EXPERIMENTS BY D. R. COX (WILEY, 1958)). AS THE FRONT-DOOR CRITERION SHOWS, IT IS IN FACT POSSIBLE TO CONDITION ON SUCH VARIABLES, BUT THE ESTIMATION IS MORE COMPLICATED.

THE MOST COMPREHENSIVE BOOK ON PEARL'S APPROACH TO CAUSAL MODELING IS HIS BOOK, CAUSALITY: MODELS, REASONING, AND INFERENCE, 2^ND EDITION, CAMBRIDGE UNIVERSITY PRESS, 2009 (1^ST ED. 2000). A SUMMARY DESCRIPTION OF PEARL'S APPROACH IS PRESENTED IN COUNTERFACTUALS AND CAUSAL INFERENCE: METHODS AND PRINCIPLES FOR SOCIAL RESEARCH BY STEPHEN L. MORGAN AND CHRISTOPHER WINSHIP (CAMBRIDGE UNIVERSITY PRESS, 2007).

SOME IMPLICATIONS OF PEARL’S BACK-DOOR CRITERION

CAUSAL EFFECTS MAY BE ESTIMATED IF ALL VARIABLES AFFECTING SELECTION FOR TREATMENT ARE KNOWN, OR IF ALL VARIABLES AFFECTING OUTCOME ARE KNOWN. IT IS NOT NECESSARY TO KNOW BOTH SETS OF VARIABLES. IF ONE OF THEM IS KNOWN THEN THE OTHER NEED NOT BE KNOWN. THIS FACT IS DISCUSSED IN A CONSIDERATION OF CAUSAL MODELING, E.G., AS IN MORGAN AND WINSHIP, OP. CIT., P. 74-84.)

FIGURE 11 ILLUSTRATES TWO CAUSAL MODEL DIAGRAMS. FIGURE 11a DEPICTS A SITUATION IN WHICH IMPACT IS ESTIMABLE. FIGURE 11b DEPICTS A SITUATION IN WHICH IMPACT IS NOT ESTIMABLE.

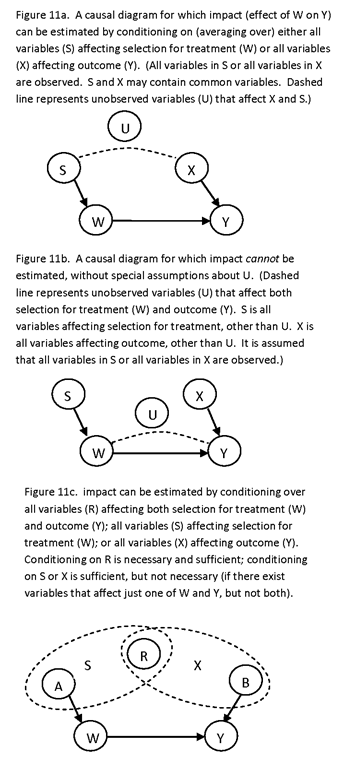
NOTE THAT IN THE FIGURES, ESTIMABILITY MAY BE ACHIEVED EVEN THOUGH THERE ARE UNOBSERVED VARIABLES (THE SET U) THAT AFFECT BOTH S AND X. WHAT IS NOT ALLOWED (FOR ESTIMABILITY) IS UNOBSERVED VARIABLES THAT AFFECT BOTH W AND Y DIRECTLY (AS DEPICTED IN FIGURE 11b). THAT SITUATION MAY BE ADDRESSED ONLY BY MAKING SPECIAL ASSUMPTIONS ABOUT THE UNOBSERVABLES (E.G., THAT THEY ARE TIME-INVARIANT AND A PANEL SURVEY IS USED).

[END OF SECTION ON ESTIMABILITY USING PEARL’S CRITERIA]

CONDITIONING

IN ORDER TO ESTIMATE THE EFFECT OF ONE VARIABLE ON ANOTHER VARIABLE (OR OTHER QUANTITY OF INTEREST), IT IS OFTEN DESIRABLE TO DO THE ESTIMATION CONDITIONAL ON VALUES OF OTHER VARIABLES (“COVARIATES”), AND AVERAGE THE CONDITIONAL ESTIMATES (I.E., CONSTRUCT A WEIGHTED AVERAGE, OVER THE DISTRIBUTION OF THE OTHER VARIABLES). CONSTRUCTING AN ESTIMATE CONDITIONAL ON ONE OR MORE OTHER VARIABLES IS CALLED “CONDITIONING” ON THE OTHER VARIABLE(S). AMBIGUOUSLY, THE PROCESS OF AVERAGING THE CONDITIONAL VALUES IS ALSO CALLED “CONDITIONING” ON THE OTHER VARIABLES. AVERAGING A QUANTITY WITH RESPECT TO (OR “OVER”) ONE OR MORE VARIABLES IS MORE SPECIFICALLY REFERRED TO AS TAKING THE EXPECTED VALUE OF THE QUANTITY WITH RESPECT TO (OR “OVER”) THE OTHER VARIABLES.

THE PROCESS OF CALCULATING A QUANTITY (A DISTRIBUTION OR AN EXPECTED VALUE) BY CONDITIONING OVER (AVERAGING OVER) A VARIABLE (OR VARIABLES) IS ALSO REFERRED TO AS “ADJUSTING FOR” THE VARIABLE (OR VARIABLES).

THE VARIABLE FOR WHICH THE EXPECTED VALUE IS TAKEN IS CALLED THE “CONDITIONED VARIABLE.” THE “OTHER” VARIABLES WITH RESPECT TO WHICH THE EXPECTED VALUE IS TAKEN ARE CALLED THE “CONDITIONING VARIABLES.” THE CONDITIONING VALUES MAY BE ANY VARIABLES – COVARIATES, “FORCED-CHANGE” CAUSAL VARIABLES, VARIABLES THAT AFFECT THE CONDITIONED VARIABLE, OR VARIABLES THAT IT AFFECTS. (THE REASON FOR THIS IS THAT JOINT PROBABILITIES ARE SYMMETRIC: IF P(X,Y) IS DEFINED, SO ARE BOTH P(Y|X) AND P(X|Y) (AS LONG AS THE PROBABILITY OF THE CONDITIONED VARIABLE IS NOT EQUAL TO ZERO). THEY ARE RELATED BY THE RELATIONSHIP P(X,Y) = P(Y|X)P(X)=P(X|Y)P(Y).)

THE EXPECTED VALUE MAY BE CALCULATED, FOR EXAMPLE, BY FORMING A NUMBER OF STRATA BASED ON VALUES OF THE VARIABLE, CALCULATING THE MEAN VALUE WITHIN EACH STRATUM, AND FORMING THE WEIGHTED AVERAGE OF THE STRATUM MEANS (WEIGHTED BY THE NUMBER OF POPULATION UNITS IN EACH STRATUM). (THIS IS CALLED A “STRATIFIED ESTIMATE.”) OR, IT MAY BE ACCOMPLISHED BY WEIGHTING SAMPLE UNITS BY THE INVERSES OF THE PROBABILITIES OF SELECTION. (THIS IS CALLED AN “INVERSE PROBABILITY” OR “HORVITZ-THOMPSON TYPE” ESTIMATOR.) CONDITIONING MAY BE DONE WITH RESPECT TO (OR “OVER”) A VARIABLE FOR WHICH FORCED CHANGES HAVE BEEN MADE (AS IN A DESIGNED EXPERIMENT INVOLVING RANDOMIZED ASSIGNMENT TO TREATMENT), OR OVER A VARIABLE IN A POPULATION THAT IS SIMPLY PASSIVELY OBSERVED, WITH NO INTERVENTION AT ALL (I.E., IT IS AN ASSOCIATIONAL OPERATION THAT DOES NOT DEPEND ON THE CAUSAL NATURE OF THE VARIABLES INVOLVED).

IN ORDINARY STRATIFICATION, SAMPLE SIZES ARE SPECIFIED FOR EACH STRATUM. IN GENERAL, THE STRATUM SAMPLE SIZES DO NOT HAVE TO BE FIXED. FOR EXAMPLE, IF STRATIFICATION IS DONE USING VARIABLE SELECTION PROBABILITIES (VSP), AS IN MARGINAL STRATIFICATION, THE STRATUM SAMPLE SIZES ARE RANDOM VARIABLES.

CONDITIONING MAY BE DONE TO TAKE INTO ACCOUNT VARIABLES (“COVARIATES”) THAT CANNOT BE CONTROLLED. IT IS OF GREATER APPLICABILITY IN QUASI-EXPERIMENTAL DESIGNS THAN IN EXPERIMENTAL DESIGNS (WHERE EXPLANATORY VARIABLES ARE OFTEN ORTHOGONALIZED). IN A DESIGNED EXPERIMENT, CONDITIONING MAY BE DONE TO INCREASE PRECISION (E.G., AS IN AN ANALYSIS OF COVARIANCE); FOR OBSERVATIONAL DATA, CONDITIONING IS DONE ALSO TO REDUCE BIAS.

MORE ON CONDITIONING, CONFOUNDING AND ESTIMABILITY

THE PRIMARY USE OF PEARL’S ESTIMABILITY CRITERIA (BACK-DOOR CRITERION, FRONT-DOOR CRITERION) IS THE DETERMINATION OF A SET OF VARIABLES THAT MAY BE CONDITIONED ON TO OBTAIN AN UNBIASED OR CONSISTENT ESTIMATE OF THE AVERAGE CAUSAL EFFECT. THE MAIN PROBLEM THAT ARISES IN ANALYSIS OF OBSERVATIONAL DATA IS CONFOUNDING. CONFOUNDING MAY BE A CONCERN IN DESIGNED EXPERIMENTS, BUT IT IS USUALLY CONTROLLED (E.G., AS IN THE USE OF DELIBERATE CONFOUNDING OF EFFECTS IN A FRACTIONAL FACTORIAL DESIGN). IT IS MORE DIFFICULT TO ADDRESS IN ANALYSIS OF PASSIVELY OBSERVED DATA. THERE ARE ALTERNATIVE DEFINITIONS OF CONFOUNDING. IN CAUSAL MODELING, TWO CAUSAL VARIABLES ARE SAID TO BE CONFOUNDED IF THEY BOTH HAVE AN EFFECT ON AN OUTCOME VARIABLE AND ONE OF THEM AFFECTS THE OTHER (SO THAT IT IS NOT CLEAR WHICH ONE IS CAUSING AN OBSERVED EFFECT OF INTEREST). IN DESCRIPTIVE STATISTICS, TWO EFFECTS ARE SAID TO BE CONFOUNDED IF THEY ARE ASSOCIATED (E.G., CORRELATED OR COLLINEAR). (IN STATISTICS, IT IS SAID THAT EFFECTS, NOT EXPLANATORY VARIABLES, ARE CONFOUNDED. THE CONCEPT IS SIMILAR, BUT THE DEFINITIONS ARE NOT EQUIVALENT. THE STATISTICAL DEFINITIONS ARE NOT NECESSARY OR SUFFICIENT; IT IS NOT POSSIBLE TO DEFINE CONFOUNDING UNEQUIVOCALLY BASED SOLELY ON ASSOCIATIONAL STATISTICS – A CAUSAL DEFINITION IS REQUIRED.)

IN ORDER TO OBTAIN AN UNBIASED OR CONSISTENT ESTIMATE OF THE CAUSAL EFFECT OF AN EXPLANATORY VARIABLE W ON AN OUTCOME VARIABLE Y, IT IS NECESSARY TO MAKE FORCED CHANGES IN W (IN AN EXPERIMENT) OR MAKE CERTAIN ASSUMPTIONS IN A CAUSAL MODEL (FOR OBSERVATIONAL DATA). THE PROBLEM THAT ARISES IS WHAT TO DO ABOUT ALL OF THE OTHER VARIABLES THAT ALSO AFFECT Y. IF FORCED CHANGES ARE MADE IN W BY MEANS OF A RANDOMIZATION PROCESS, THE DISTRIBUTIONS OF ALL OTHER VARIABLES (“COVARIATES,” X) ARE (ON AVERAGE) THE SAME FOR THE TREATED AND UNTREATED UNITS, AND THE OBSERVED EFFECT OF W ON Y IS THE AVERAGE TREATMENT EFFECT. RANDOMIZED ASSIGNMENT TO TREATMENT ELIMINATES CONFOUNDING WITH ALL OTHER VARIABLES. IF THE FORCED CHANGES ARE NOT MADE BY A RANDOMIZATION PROCESS, THE OBSERVED EFFECT IS THE AVERAGE TREATMENT EFFECT (ATE) CONDITIONAL ON THE VALUES OF THE COVARIATES. TO OBTAIN AN ESTIMATE OF THE AVERAGE TREATMENT EFFECT IN THIS CASE, IT IS NECESSARY TO “CONDITION” ON THE COVARIATES (X), I.E., TO ESTIMATE THE ATE FOR EACH COMBINATION OF VALUES OF THEM (I.E., ATE(X)), AND AVERAGE THIS CONDITIONAL VALUE OVER X (USING THE JOINT PROBABILITY DISTRIBUTION OF X). WHAT COVARIATES SHOULD BE CONDITIONED ON IS DETERMINED BY ANALYSIS OF THE CAUSAL MODEL’S DAG, USING PEARL’S ESTIMABILITY CRITERIA.

THIS PROCESS IS ILLUSTRATED IN FIGURE 12, IN THE CASE OF A SINGLE COVARIATE, X. IN THE FIGURE, Y IS THE OUTCOME VARIABLE, W IS THE TREATMENT INDICATOR VARIABLE, AND X IS A COVARIATE. IF FORCED CHANGES WERE MADE IN W, THAT WOULD “BLOCK” THE BACK-DOOR PATH TO Y, AND IT WOULD NOT BE NECESSARY TO CONDITION ON X. IF FORCED CHANGES ARE NOT MADE IN W, THERE IS A PROBLEM: X ALSO AFFECTS Y (I.E., IT IS A “CONFOUNDER”). UNLESS THE FACT THAT BOTH X AND W MAY AFFECT Y IS TAKEN INTO ACCOUNT, THE EFFECT OF X ON Y AND THE EFFECT OF W ON Y ARE CONFOUNDED. THE CONFOUNDING IS ELIMINATED BY CONDITIONING ON X. IN THIS SIMPLE EXAMPLE, X IS THE ONLY VARIABLE ALONG A BACK-DOOR PATH FROM W TO Y.

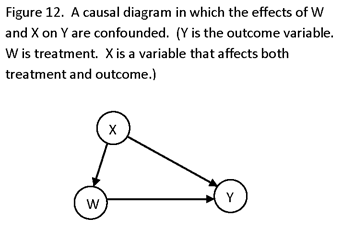
IN A DESIGNED EXPERIMENT, W AND X MAY BE ORTHOGONALIZED, SO THAT THE EFFECTS OF W AND X ARE NOT CONFOUNDED.

FIGURES 13 AND 14 (ADAPTED FROM MORGAN & WINSHIP OP. CIT.) ILLUSTRATE TWO APPLICATIONS OF PEARL’S METHOD FOR DETERMINING ESTIMABILITY, AND DETERMINING WHICH VARIABLES SHOULD BE CONDITIONED ON.

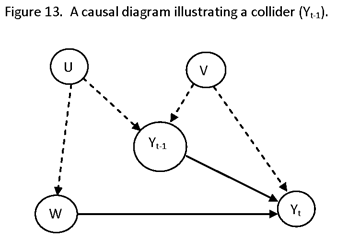
FIGURE 13 ILLUSTRATES THE PROBLEM OF DECIDING WHETHER TO CONDITION ON THE VALUE OF AN OUTPUT VARIABLE FROM A PREVIOUS SURVEY ROUND. THERE IS MUCH CONFLICTING ADVICE CONCERNING WHETHER THIS SHOULD BE DONE. THE REASON FOR THE CONFLICT IS THAT THE ANSWER IS “IT DEPENDS” – IT DEPENDS ON THE CAUSAL MODEL. AS THE FIGURE ILLUSTRATES, IF THERE ARE VARIABLES THAT AFFECT OUTCOME IN BOTH ROUNDS (I.E., BOTH Y_t AND Y_t-1), THEN Y_t IS A COLLIDER VARIABLE. IT CANNOT BE CONDITIONED ON WITHOUT INTRODUCING A BIAS INTO THE ESTIMATE OF THE DISTRIBUTION OF Y_t (FOR THE REASONS EXPLAINED RELATIVE TO FIGURE 10). IF THE VARIABLES U AND V AFFECTING Y_t-1 WERE OBSERVED, THE PROBLEM COULD BE RESOLVED BY CONDITIONING ON ONE OF THEM AND ON Y_t-1 (SINCE THAT WOULD BLOCK ALL BACK-DOOR PATHS). BUT IN THIS EXAMPLE, THE VARIABLES U AND V ARE UNOBSERVED. IN THIS CASE, THE DESIGN MUST BE STRUCTURED SO THAT THESE VARIABLES DROP OUT OF THE MODEL (E.G., IF THESE VARIABLES ARE TIME-INVARIANT, BY USING FIRST-DIFFERENCES IN Y AS THE BASIS FOR ESTIMATING (IN WHICH CASE THEY DROP OUT OF THE MODEL)).

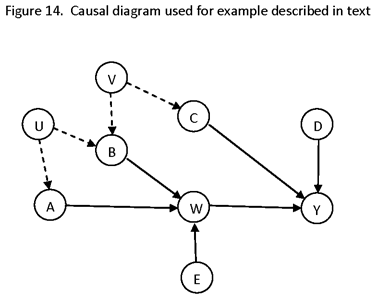
FIGURE 14 ILLUSTRATES A MORE COMPLICATED EXAMPLE. THIS EXAMPLE IS TAKEN FROM MORGAN AND WINSHIP OP. CIT. (PP. 69-73; SEE PP. 61-86 FOR GENERAL DISCUSSION). MORGAN AND WINSHIP SUMMARIZE THE BACK-DOOR CRITERION AS FOLLOWS (COMBINING THE DEFINITION OF BLOCKING AND THE CRITERION AS GIVEN BY PEARL OP. CIT.):

ALL BACK-DOOR PATHS ARE BLOCKED BY Z IF AND ONLY IF EACH BACK-DOOR PATH:

(1) CONTAINS A CHAIN OF MEDIATION A→C→B, WHERE THE MIDDLE VARIABLE C IS IN Z, OR

(2) CONTAINS A FORK OF MUTUAL DEPENDENCE A←C→B, WHERE THE MIDDLE VARIABLE C IS IN Z, OR

(3) CONTAINS AN INVERTED FORK OF MUTUAL CAUSATION A→C←B, WHERE THE MIDDLE VARIABLE C AND ALL OF C’s DESCENDENTS ARE NOT IN Z.

APPLYING THIS CRITERION, WE SEE THAT THE CAUSAL EFFECT OF W ON Y MAY BE ESTIMATED BY CONDITIONING ON C OR BY CONDITIONING ON BOTH A AND B. CONDITIONING ON B ALONE DOES NOT SATISFY THE BACK-DOOR CRITERION, SINCE B IS A COLLIDER (CONDITIONING ON IT WOULD CREATE AN ASSOCIATION BETWEEN W AND Y).

THERE ARE OTHER SETS OF VARIABLES THAT MAY BE CONDITIONED ON (I.E., AS C AND A, C AND B, AND C AND A AND B). THERE IS NO NEED TO INCLUDE THESE ADDITIONAL VARIABLES IN THE CONDITIONING SET. THE DAG SHOWS CLEARLY WHAT ARE “MINIMAL SETS” OF CONDITIONING VARIABLES.

NOTE THAT EFFECTS MAY BE CONFOUNDED EVEN IF THE VARIABLES WITH WHICH THEY ARE ASSOCIATED ARE SUBJECT TO FORCED CHANGES, AND EVEN IF THEIR LEVELS ARE RANDOMIZED BY ASSIGNMENT. AN EXAMPLE OF THIS IS A FRACTIONAL FACTORIAL EXPERIMENTAL DESIGN IN WHICH HIGHER-ORDER INTERACTIONS ARE DELIBERATELY CONFOUNDED WITH LOWER-ORDER INTERACTIONS. THE CONFOUNDING IS ELIMINATED WITH RANDOMIZATION ONLY IF THE VARIABLES ARE ORTHOGONAL (UNCORRELATED). FOR A SMALL NUMBER OF DESIGN VARIABLES HAVING A SMALL NUMBER OF LEVELS, ALL DESIGN VARIABLES MAY BE ORTHOGONALIZED. FOR SEVERAL DESIGN VARIABLES AT SEVERAL LEVELS, IT IS USUALLY NOT FEASIBLE (FOR A REASONABLE SAMPLE SIZE) TO ORTHOGONALIZE ALL OF THE DESIGN VARIABLES. IN THIS CASE, THE DESIGN IS CONFIGURED (E.G., AS IN A FRACTIONAL FACTORIAL DESIGN) SO THAT MAIN EFFECTS AND INTERACTIONS OF INTEREST ARE NOT CONFOUNDED WITH EACH OTHER, BUT ARE CONFOUNDED WITH HIGH-LEVEL INTERACTIONS THAT ARE NOT OF INTEREST (AND UNLIKELY TO BE SIGNIFICANT).

ESTIMATION OF THE MAGNITUDE OF CAUSAL EFFECTS – THEORETICAL CONSIDERATIONS

THE PRECEDING DISCUSSION ON ASSESSING THE ESTIMABILITY OF CAUSAL EFFECTS DEALT ONLY WITH THE ISSUE OF WHETHER AN EFFECT COULD BE ESTIMATED, NOT WITH THE ISSUE OF HOW TO ESTIMATE IT. THIS SECTION AND THE NEXT ADDRESS THE LATTER ISSUE.

THEORETICALLY, THE MAGNITUDE OF CAUSAL EFFECTS IS ESTIMATED BY CONDITIONING ON (AVERAGING OVER) COVARIATES. FROM A PRACTICAL POINT OF VIEW, THIS MAY BE DIFFICULT TO DO (SINCE SOME OF THE RELEVANT COVARIATES MAY BE UNOBSERVED, OR INSUFFICIENT DATA MAY BE AVAILABLE (E.G., TO ALLOW CROSS-STRATIFICATION OVER A LARGE NUMBER OF VARIABLES, WITH TREATED AND UNTREATED UNITS IN EACH CELL OF THE CROSS-STRATIFICATION). THIS SECTION WILL DISCUSS SOME BASIC ASPECTS OF CONDITIONING. A LATER SECTION WILL DISCUSS PRACTICAL APPROACHES TO ESTIMATION.

AS DISCUSSED EARLIER, CAUSALITY CANNOT BE UNEQUIVOCALLY ESTABLISHED FROM ANALYSIS OF DATA ALONE. STATISTICAL DECISION THEORY MAY BE APPLIED TO TEST AN HYPOTHESIS ABOUT WHETHER ONE VARIABLE HAS A CAUSAL EFFECT ON ANOTHER, SUCH AS A TEST OF GRANGER CAUSALITY. AS MENTIONED, THAT SUBJECT IS NOT A CONCERN OF THIS PRESENTATION. THIS PRESENTATION IS CONCERNED WITH ESTIMATION OR TESTING HYPOTHESES ABOUT THE MAGNITUDE OF A CAUSAL EFFECT, GIVEN A CAUSAL MODEL.

FOR ESTIMATION OF THE MAGNITUDE OF CAUSAL RELATIONSHIPS (STATISTICAL CAUSAL ANALYSIS), THERE ARE TWO APPROACHES: (1) (EXPERIMENTAL DATA), MAKE RANDOMIZATION-BASED FORCED CHANGES IN AN EXPLANATORY VARIABLE AND OBSERVE THE ASSOCIATED CHANGES (EFFECTS) IN THE OUTCOME (AFFECTED) VARIABLE; (2) (OBSERVATIONAL DATA): SPECIFY A CAUSAL MODEL AND ANALYZE THE DATA IN A MANNER THAT IS CONSISTENT WITH THE CAUSAL MODEL. (A CAUSAL MODEL IS ACTUALLY ASSOCIATED WITH THE FIRST APPROACH, BUT IT IS SO STRAIGHTFORWARD THAT IT IS USUALLY NOT DEPICTED GRAPHICALLY. USING RANDOMIZED ASSIGNMENT TO TREATMENT, THE DISTRIBUTIONS OF ALL VARIABLES OTHER THAN TREATMENT ARE THE SAME FOR THE TREATED AND UNTREATED GROUPS. THE CAUSAL MODEL IN THIS CASE SIMPLY HAS A RANDOMIZATION PROCESS AS THE PARENT OF THE TREATMENT SELECTION VARIABLE.)

IF NO CAUSAL MODEL IS SPECIFIED, THE STATISTICAL ANALYSIS WILL SIMPLY MEASURE THE MAGNITUDE OF THE ASSOCIATIONS IN THE DATA, NOT THE MAGNITUDES OF CAUSAL EFFECTS. IF NO FORCED CHANGES ARE MADE IN AN EXPLANATORY VARIABLE, SOME CLAIM THAT CAUSAL ANALYSIS MAY NOT BE DONE.

SOME AUTHORS CONFLATE THE THEORETICAL CONCEPT OF A CAUSAL RELATIONSHIP (SPECIFIED IN A THEORETICAL MODEL) AND THE PROCESS USED TO ESTIMATE IT, SUCH AS IN DEFINING A CAUSAL EFFECT TO BE THE RESULT OF A RANDOMIZATION-BASED DESIGNED EXPERIMENT. THE REASON FOR THIS APPROACH IS THERE IS NO UNIVERSALLY ACCEPTED DEFINITION OF WHAT A “CAUSE” IS. THIS PROBLEM IS OBVIATED IF CAUSAL EFFECTS ARE DEFINED SIMPLY AS EFFECTS ASSOCIATED WITH A RANDOMIZATION-BASED DESIGNED EXPERIMENT. THE MAJOR DIFFICULTY THAT THIS APPROACH CAUSES IS THAT IT DOES NOT SHED LIGHT ON HOW TO CONDUCT CAUSAL ANALYSIS OF OBSERVATIONAL DATA – A VERY COMMON REQUIREMENT IN EVALUATION OF SOCIAL AND ECONOMIC PROGRAMS.

THREE APPROACHES FOR CONDITIONING ARE ILLUSTRATED IN FIGURE 11. ONE OF THEM IS TO CONDITION ON ALL VARIABLES AFFECTING ASSIGNMENT TO TREATMENT (I.E., TO CONDITION ON S IN THE FIGURE). THIS IS CALLED “CONDITIONING TO BALANCE”). ANOTHER IS TO CONDITION ON ALL VARIABLES AFFECTING OUTCOME, OTHER THAN TREATMENT (I.E., TO CONDITION ON X IN THE FIGURE). THIS IS CALLED “CONDITIONING TO ADJUST”). IT IS POSSIBLE ALSO TO CONDITION ON VARIABLES THAT AFFECT BOTH ASSIGNMENT TO TREATMENT AND OUTCOME (I.E., TO CONDITION ON SET R IN THE FIGURE). ANALYSIS OF THE CAUSAL DIAGRAM REVEALS EACH SET.

PEARL'S METHODOLOGY IS AN EFFICIENT METHOD FOR DETERMINING WHICH VARIABLES MAY BE CONDITIONED ON TO OBTAIN AN UNBIASED ESTIMATE OF THE CAUSAL EFFECT. THE THREE CONDITIONING APPROACHES ILLUSTRATED IN FIGURE 11 ARE SIMPLY THREE POSSIBLE CONDITIONING METHODS, ASSUMING THAT ALL VARIABLES IN THE CONDITIONING SETS ARE OBSERVABLE. PEARL'S METHODOLOGY MAY BE USED TO DETERMINE A MINIMAL CONDITIONING SET FROM OBSERVABLE VARIABLES (USING THE BACK-DOOR OR FRONT-DOOR CRITERIA). CONDITIONING IS DONE OVER MORE VARIABLES THAN A MINIMAL SET IN ORDER TO IMPROVE THE PRECISION OF ESTIMATES (E.G., BY STRATIFICATION OR REGRESSION) OR TO ESTIMATE CONDITIONAL EFFECTS OF INTEREST.

MORGAN AND WINSHIP DESCRIBE CONDITIONING TO BALANCE AND CONDITIONING TO ADJUST (P. 84 OP. CIT.). (THESE APPROACHES WERE PRESENTED IN THE EXAMPLES GIVEN EARLIER, PRIOR TO DISCUSSING PEARL'S APPROACH. AT RISK OF REPETITION, THE APPROACH WILL BE SUMMARIZED ONCE MORE.) IF CONDITIONING IS PERFORMED WITH RESPECT TO S, THEN ESTIMATE E(Y|W=1, S=s) – E(Y|W=0, S=s) FOR ALL VALUES OF s IN S. (THE FIRST TERM IS E(Y₁) BECAUSE, GIVEN S, THE SET OF ALL MODEL VARIABLES, THE MODEL ERROR TERM INCLUDES NO OTHER VARIABLES, SO THE EXPLANATORY VARIABLE W IS UNCORRELATED WITH U, E(U|W,S)=E(U)=0, AND HENCE E(Y|W=1) IS AN UNBIASED ESTIMATE OF E(Y₁). THE FIRST TERM IS THE AVERAGE TREATMENT EFFECT ON THE TREATED, E(Y₁). SIMILARLY, THE SECOND TERM IS E(Y₀), THE AVERAGE TREATMENT EFFECT ON THE UNTREATED. THE KEY POINT IS THAT, GIVEN THE CONDITIONING VARIABLE (IN THIS CASE, S), W IS UNCORRELATED WITH THE RESPONSE (Y₁, Y₀). THIS ARGUMENT HAS BEEN PRESENTED EARLIER, AND WILL NOT BE REPEATED AGAIN FOR THE OTHER SIMILAR EXPRESSIONS IN THIS AND THE NEXT PARAGRAPH. NOTE THAT THESE TWO EXPECTED VALUES WILL BE OVER DIFFERENT UNITS, SINCE AN INDIVIDUAL UNIT MAY NOT BE BOTH TREATED AND UNTREATED. THE TWO SAMPLES (OF TREATED AND UNTREATED UNITS) ARE INDEPENDENT. FOR A STRATIFIED ESTIMATE, IT IS NECESSARY TO HAVE OBSERVATIONS IN EACH STRATUM CELL, BUT THE STRATIFICATION NEED NOT BE THE SAME FOR THE TREATED AND UNTREATED UNITS.

IF CONDITIONING IS PERFORMED WITH RESPECT TO X, THEN ESTIMATE E(Y|W=1,X=x) – E(Y|W=0, X=x) FOR ALL VALUES OF x IN X. (AS BEFORE, THIS EXPRESSION IS E(Y₁) – E(Y₀) (THE ATT MINUS THE ATU) SINCE, GIVEN X (ALL VARIABLES AFFECTING W, W IS UNCORRELATED WITH THE MODEL ERROR TERM, AND SO THE RESPONSE (Y₁, Y₀) IS UNCORRELATED WITH W. NOTE THAT THESE TWO EXPECTED VALUES WILL BE OVER DIFFERENT UNITS, SINCE AN INDIVIDUAL UNIT MAY NOT BE BOTH TREATED AND UNTREATED. (THIS APPROACH WOULD NOT BE USED DIRECTLY BECAUSE OF THE "CURSE OF DIMENSIONALITY"; INSTEAD, CONDITIONING WOULD BE ON THE PROPENSITY SCORE BASED ON X.)

THE TWO PRECEDING APPROACHES TO ESTIMATING THE ATE MAY PRODUCE DIFFERENT ESTIMATES OF ATT, ATU AND ATE FOR SMALL SAMPLES, BUT THEY ARE CONSISTENT ESTIMATES AND WILL PRODUCE SIMILAR RESULTS FOR LARGE SAMPLES.

A THIRD APPROACH TO CONDITIONING IS TO AVERAGE OVER ALL VARIABLES THAT AFFECT BOTH SELECTION FOR TREATMENT AND OUTCOME (SET R IN FIGURE 11). FOR EXAMPLE, IN FIGURE 12, WE MAY CONDITION ON THE VARIABLE X, WHICH AFFECTS BOTH SELECTION (W) AND OUTCOME (Y). (THIS FACT IS THE MOTIVATION FOR PEARL’S “BACK DOOR” CRITERION – CONDITIONING MAY BE DONE ON ALL VARIABLES THAT AFFECT BOTH SELECTION AND OUTCOME.)

SINCE THE ESTIMATES ARE BASED ON INDEPENDENT SAMPLES (SINCE NO UNIT MAY BE BOTH TREATED AND UNTREATED), CLOSED-FORM FORMULAS COULD BE DETERMINED FOR THE VARIANCE OF THE ESTIMATES. IT IS SIMPLER TO CALCULATE THE STANDARD ERRORS BY RESAMPLING (SIMULATION, BOOTSTRAPPING).

AS LONG AS THE VARIABLES S AND X SATISFY THE BACK-DOOR CRITERION (WHICH THE SETS S, X AND R DO), IT DOES NOT MATTER AT ALL HOW TREATMENT IS ASSIGNED (I.E., RANDOMLY OR OTHERWISE) – THE IMPACT ESTIMATE IS ESTIMABLE (MODEL-UNBIASED OR MODEL-CONSISTENT). THIS FACT FOLLOWS DIRECTLY FROM THE BACK-DOOR ASSUMPTION AND THE FACT THAT IN CONDITIONING, THE EXPECTATION (AVERAGING) IS DONE OVER EVERY VALUE OF s IN S (OR x IN X). RANDOMIZED ASSIGNMENT TO TREATMENT ASSURES THAT THESE CONDITIONS HOLD. WITHOUT RANDOMIZED ASSIGNMENT TO TREATMENT, THE BACK-DOOR CRITERION DOES NOT NECESSARILY HOLD, AND MUST BE ASSUMED FOR THE ESTIMATES TO BE CONSISTENT.

NOTE THAT AS LONG AS CONDITIONING IS APPLIED TO ALL OF S OR TO ALL OF X (TO REMOVE SELECTION BIAS), IT IS ACCEPTABLE TO INCLUDE VARIABLES FROM THE OTHER SET (AS ADDITIONAL COVARIATES, TO INCREASE PRECISION).

THE EXAMPLES JUST PRESENTED INVOLVE "BRUTE FORCE" ESTIMATES, INTENDED SIMPLY TO DESCRIBE THE CONCEPTS OF CONDITIONING TO ADJUST AND CONDITIONING TO BALANCE. IT IS UNLIKELY THAT THESE ESTIMATORS WOULD BE USED IN PRACTICE. IN CONDITIONING, IT IS NECESSARY TO TAKE THE EXPECTATION OVER THE ENTIRE JOINT DISTRIBUTION OF THE CONDITIONING VARIABLES, E.G., BY STRATIFICATION (A FULL CROSS-STRATIFICATION OVER ALL VARIABLES IN S OR ALL VARIABLES IN X). IN MOST APPLICATIONS INVOLVING MULTIDIMENSIONAL S OR X, THIS IS NOT FEASIBLE TO DO (AN INCIDENCE OF THE SO-CALLED “CURSE OF DIMENSIONALITY” – THERE ARE FAR TOO MANY STRATUM CELLS IN A CROSS-STRATIFICATION, MANY WITH NO OBSERVATIONS). WHAT MAY BE DONE AS A PRACTICAL ALTERNATIVE IS TO CALCULATE THE MEAN OVER THE DATA, WHICH IS A PROBABILITY SAMPLE FROM THE JOINT DISTRIBUTION. THIS AND OTHER METHODS FOR ADDRESSING THE CURSE OF DIMENSIONALITY WILL BE DISCUSSED LATER.

4.6. STATISTICAL CAUSAL ANALYSIS (ESTIMATION OF THE MAGNITUDE OF CAUSAL EFFECTS)

THE PRECEDING DISCUSSION DESCRIBED THE FIRST CATEGORY OF CAUSAL MODELING AND ANALYSIS, CONCERNED WITH DESCRIBING CAUSAL RELATIONSHIPS AND DETERMINING WHETHER CERTAIN CAUSAL EFFECTS ARE ESTIMABLE. THAT DISCUSSION INCLUDED A LIMITED AMOUNT OF MATERIAL ON THE ESTIMATION OF EFFECTS BY CONDITIONING. THE SECOND CATEGORY OF CAUSAL MODELING AND ANALYSIS IS CONCERNED WITH PRACTICAL METHODS FOR ESTIMATION OF THE STRENGTH OF CAUSAL RELATIONSHIPS (MAGNITUDE OF CAUSAL EFFECTS) FROM DATA, ONCE IT IS ESTABLISHED THAT THEY ARE ESTIMABLE. THIS IS DONE USING STATISTICAL ANALYSIS, SPECIFICALLY ESTIMATION AND TESTS OF HYPOTHESIS. IT IS THIS ASPECT OF CAUSAL MODELING THAT IS THE FOCUS OF THIS PRESENTATION, WITH PARTICULAR REFERENCE TO MATCHING USED IN EXPERIMENTAL DESIGN AND QUASI-EXPERIMENTAL DESIGN. REFERENCES FOR THIS ASPECT OF CAUSAL MODELING INCLUDE THE FOLLOWING:

1. ROSENBAUM, PAUL R. AND DONALD B. RUBIN, “THE CENTRAL ROLE OF THE PROPENSITY SCORE IN OBSERVATIONAL STUDIES FOR CAUSAL EFFECTS,” BIOMETRIKA, (1983), VOL. 70, NO. 1, PP. 41-55.

2. HOLLAND, PAUL W., “STATISTICS AND CAUSAL INFERENCE,” JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, DEC. 1986, VOL. 81, NO. 396, PP. 945 – 960. (THIS ARTICLE IS LIMITED TO CONSIDERATION OF EXPERIMENTAL DATA, NOT OBSERVATIONAL DATA.)

3. HECKMAN, JAMES J. AND EDWARD J. VYTLACIL, “ECONOMETRIC EVALUATION OF SOCIAL PROGRAMS, PART I: CAUSAL MODELS, STRUCTURAL MODELS AND ECONOMETRIC POLICY EVALUATION,” HANDBOOK OF ECONOMETRICS, VOL. 6B, CHAPTER 70, PP. 4779 – 4874, (SEE ALSO PART II (CHAPTER 71, PP. 4875 – 5143) AND PART III, PP. 5145 – 5303), ELSEVIER, 2007. AN EXTRACT OF PART I IS ECONOMETRIC CAUSALITY BY JAMES J. HECKMAN, NATIONAL BUREAU OF ECONOMIC RESEARCH WORKING PAPER 13934, APRIL 2008, POSTED AT INTERNET WEBSITE http://www.nber.org/papers/w13934 .

4. COCHRAN, WILLIAM G., AND GERTRUDE M. COX, EXPERIMENTAL DESIGNS, 2^ND ED., JOHN WILEY & SONS, 1957 (1^ST ED. 1950).

5. COCHRAN, WILLIAM G., SAMPLING TECHNIQUES, 3^RD ED., JOHN WILEY & SONS, 1977

6. WOOLDRIDGE, JEFFREY M., ECONOMETRIC ANALYSIS OF CROSS SECTION AND PANEL DATA, 2^ND ED., THE MIT PRESS, 2010 (1^ST ED. 2002).

7. GREENE, WILLIAM H., ECONOMETRIC ANALYSIS, 7^TH EDITION, PRENTICE HALL, 2012

THE PEARL AND WINSHIP & MORGAN BOOKS ARE NOT INCLUDED IN THIS LIST, SINCE THEY DEAL WITH PROBABILISTIC MODELING OF CAUSALITY, NOT WITH STATISTICAL ANALYSIS AND ESTIMATION OF CAUSAL EFFECTS (EXCEPT FOR ASSESSMENT OF ESTIMABILITY).

THE STATISTICAL THEORY OF CAUSAL MODELING AND ANALYSIS STEMS FROM THE WORK OF NEYMAN AND FISHER, AND IS OFTEN REFERRED TO AS THE NEYMAN-RUBIN THEORY OF CAUSALITY. NEYMAN PROPOSED THE POTENTIAL OUTCOMES APPROACH IN THE FIELD OF DESIGNED EXPERIMENTS (CONTROL OF VARIABLES BY RANDOMIZATION). RUBIN EXTENDED THE APPROACH TO THE CASE OF OBSERVATIONAL DATA (PASSIVELY OBSERVED DATA). SOME AUTHORS (E.G., WOOLDRIDGE) REFER TO IT AS THE RUBIN CAUSAL MODEL (RCM), IN RECOGNITION OF RUBIN’S ACCOMPLISHMENT IN EXTENDING THE CONCEPTS TO THE CASE OF OBSERVATIONAL DATA AND POPULARIZING THE POTENTIAL-OUTCOMES APPROACH FOR ANALYSIS OF OBSERVATIONAL DATA. WE SHALL USE THE TERM NEYMAN-RUBIN TO DESCRIBE THE APPROACH, IN RECOGNITION OF NEYMAN’S ORIGINAL CONTRIBUTION (IN DESIGNED EXPERIMENTS) AND RUBIN’S SIGNIFICANT EXTENSION OF THE METHOD TO PERFORM CAUSAL ANALYSIS OF OBSERVATIONAL DATA.

A NUMBER OF RESEARCHERS WORKED IN THE FIELD FOLLOWING NEYMAN, AND A MORE COMPLETE ATTRIBUTION OF THE APPROACH IS THE “NEYMAN-FISHER-COX-RUBIN CAUSAL MODEL.” APPELLATIONS NOT INVOLVING INDIVIDUALS’ NAMES INCLUDE THE “POTENTIAL-OUTCOMES MODEL” OR THE “COUNTERFACTUALS MODEL.”

IN DISCUSSING PEARL’S APPROACH TO CAUSAL MODELING, THE CAUSAL EFFECT WAS THE COMPLETE DISTRIBUTION OF OUTCOME, GIVEN THE CAUSAL VARIABLE. IN THIS SECTION (AND MOST OF THIS PRESENTATION), WE WILL RESTRICT ATTENTION TO THE BINARY-OUTCOME CASE. THE TWO OUTCOMES ARE “TREATED” AND “UNTREATED.” THE THEORY MAY BE EXTENDED BUT THAT IS NOT DONE HERE.

IN THIS PRESENTATION, WE WILL DESCRIBE TWO BASIC APPROACHES TO STATISTICAL CAUSAL ANALYSIS (ESTIMATION OF THE MAGNITUDES OF CAUSAL RELATIONSHIPS SPECIFIED IN A CAUSAL MODEL DIAGRAM). WE SHALL REFER TO THESE TWO APPROACHES AS THE ROSENBAUM-RUBIN (R&R) APPROACH AND THE HECKMAN APPROACH. THE R&R APPROACH FOCUSES ON VARIABLES THAT AFFECT SELECTION FOR TREATMENT. THE HECKMAN APPROACH FOCUSES ON VARIABLES THAT AFFECT BOTH SELECTION FOR TREATMENT AND OUTCOMES OF INTEREST.

BOTH THE R&R AND HECKMAN APPROACHES MAY USE MATCHING, AND BOTH MAY USE REGRESSION ADJUSTMENT. MATCHING IS MORE IMPORTANT, HOWEVER, IN THE R&R APPROACH, SINCE IT MAKES LESS USE OF REGRESSION ADJUSTMENT. IF BOTH MATCHING AND REGRESSION ADJUSTMENT ARE USED, A CORRECT (UNBIASED) ESTIMATE OF IMPACT CAN BE DETERMINED IF THE MATCHING MODEL IS CORRECT OR IF THE REGRESSION (OUTCOME) MODEL IS CORRECT, BUT NOT NECESSARILY BOTH (I.E., THE APPROACH USING BOTH TECHNIQUES IS “DOUBLY ROBUST.” SINCE THE R&R APPROACH TYPICALLY MAKES LIMITED USED OF REGRESSION ADJUSTMENT, MORE IMPORTANCE FALLS ON THE EFFECTIVENESS OF THE MATCHING. IT IS SOMETIMES SAID THAT STATISTICIANS PREFER MATCHING AND ECONOMISTS PREFER REGRESSION MODELS. THIS MAY BE SO. THE REASON FOR THIS IS PROBABLY THAT ECONOMISTS ARE MORE FAMILIAR WITH AND KNOWLEDGEABLE ABOUT ECONOMIC MODELS, AND SO PREFER AN APPROACH TO IMPACT ESTIMATION THAT TAKES FULL ADVANTAGE OF THAT FAMILIARITY AND KNOWLEDGE.

THE TERMINOLOGY “R&R APPROACH” AND “HECKMAN APPROACH” ARE NOT STANDARD DESCRIPTORS. THESE DESCRIPTORS ARE USED IN THIS PRESENTATION SIMPLY AS EXAMPLES OF TWO METHODS FOR ESTIMATING CAUSAL EFFECTS, USING THE CONCEPTS OF THE NEYMAN-RUBIN CAUSAL MODEL. THERE IS A WIDE VARIETY OF TECHNIQUES AVAILABLE, AND RESEARCH IN THE FIELD OF STATISTICAL CAUSAL MODELING HAS BEEN DONE BY MANY RESEARCHERS. THESE TWO PARTICULAR APPROACHES ARE USED SIMPLY AS ILLUSTRATIVE EXAMPLES TO CONSTRUCT RECOMMENDATIONS CONCERNING MATCHING.

BEFORE DESCRIBING THE R&R AND HECKMAN APPROACHES, WE SHALL FIRST DESCRIBE THE BASIC THEORY OF POTENTIAL-OUTCOMES STATISTICAL CAUSAL MODELING THAT IS COMMON TO BOTH APPROACHES. THESE APPROACHES ARE GENERALLY DESCRIBED IN TERMS OF THE CONCEPT OF POTENTIAL OUTCOMES AND THE NOTION OF CONDITIONAL INDEPENDENCE. POTENTIAL OUTCOMES ARE ALL OF THE POSSIBLE OUTCOMES OF AN EXPERIMENT, WHETHER OBSERVED OR UNOBSERVED. IN THE CASE OF BINARY TREATMENT VARIABLES, THERE ARE JUST TWO POTENTIAL OUTCOMES, USUALLY CALLED "TREATED" AND "UNTREATED"; FOR WHICHEVER OUTCOME HAPPENS TO BE OBSERVED, THE OTHER (UNOBSERVED) OUTCOME IS CALLED THE COUNTERFACTUAL.

RUBIN POINTS OUT THE TERM “POTENTIAL OUTCOMES” IS TO BE PREFERRED TO “COUNTERFACTUAL OUTCOMES” (WHEN REFERRING TO BOTH OUTCOMES), SINCE POTENTIAL OUTCOMES ARE ALWAYS WELL DEFINED (IN THOUGHT), BUT A COUNTERFACTUAL DOES NOT EXIST (EVEN IN THOUGHT) UNTIL ONE OF THE TWO POTENTIAL OUTCOMES HAS BEEN REALIZED (I.E., BECOMES “ACTUAL” AS THE RESULT OF A PHYSICAL EXPERIMENT). A COUNTERFACTUAL NEVER EXISTS IN REALITY – IT IS THE OBSERVATION THAT NEVER OCCURS. RUBIN'S POINT IS WELL-TAKEN.

IT IS NOTED THAT THE R&R AND HECKMAN APPROACHES, AND THE PEARL APPROACH, ARE COMPLEMENTARY. PEARL’S METHOD MAY BE USED TO DETERMINE ESTIMABILITY (IDENTIFIABILITY) FOR MEASURES IN BOTH THE R&R AND HECKMAN APPROACHES. IN THE CASE OF THE R&R METHOD, THE DAG WILL SPECIFY CONDITIONS FOR WHICH CONDITIONAL INDEPENDENCE OF RESPONSE AND ASSIGNMENT TO TREATMENT GIVEN COVARIATES WILL HOLD. IN THE CASE OF THE HECKMAN METHOD, THE DAG WILL INDICATE WHETHER CONSISTENT ESTIMATES ARE AVAILABLE IN A JOINT SELECTION / OUTCOME MODEL.

A CRITICISM THAT HAS BEEN LEVELED AGAINST THE R&R APPROACH IS THAT AN ASSUMPTION OF CONDITIONAL INDEPENDENCE MAY BE MADE WITHOUT JUSTIFICATION SUPPORTED BY A COMPLETELY SPECIFIED CAUSAL MODEL. USE OF THE PEARL APPROACH TO ASSESSING IDENTIFIABILITY REQUIRES SPECIFICATION OF A COMPLETE CAUSAL MODEL.

ALL APPROACHES TO PROBABILISTIC CAUSALITY INCLUDE THE NOTION OF POTENTIAL OUTCOMES. IN SOME APPROACHES, THE POTENTIAL OUTCOMES FOR INDIVIDUAL UNITS ARE EXPLICITLY CONSIDERED IN THEORETICAL FORMULAS (BUT NOT IN ESTIMATION FORMULAS, SINCE THE COUNTERFACTUAL VALUES ARE NOT OBSERVED). IN OTHER APPROACHES ONLY THE MARGINAL DISTRIBUTIONS OF THE POTENTIAL OUTCOMES ARE EXPLICITLY CONSIDERED. IN THIS PRESENTATION, WE SHALL EXPLICITLY CONSIDER INDIVIDUAL COUNTERFACTUAL VALUES (IN THEORETICAL FORMULAS) TO PROMOTE UNDERSTANDING. THE ESTIMATION FORMULAS INVOLVE ONLY MARGINAL DISTRIBUTIONS OF POTENTIAL OUTCOMES, WHICH (DISTRIBUTIONS) ARE ESTIMABLE, AND MAKE NO REFERENCE TO THE USE OF COUNTERFACTUAL VALUES FOR INDIVIDUAL UNITS (WHICH ARE NOT OBSERVABLE, AND ESTIMABLE ONLY BY MAKING ASSUMPTIONS ABOUT THE JOINT DISTRIBUTION OF THE POTENTIAL OUTCOMES). (ONCE A POTENTIAL-OUTCOMES MODEL HAS BEEN SPECIFIED, IT IS POSSIBLE TO ESTIMATE THE VALUE OF A COUNTERFACTUAL, UNDER ASSUMPTIONS ABOUT THE JOINT DISTRIBUTION OF THE POTENTIAL OUTCOMES (SUCH AS CONDITIONAL INDEPENDENCE).) IN THIS PRESENTATION, WE DO NOT ADDRESS THE ISSUE OF PREDICTING INDIVIDUAL COUNTERFACTUAL VALUES. ALL THAT IS ADDRESSED IS ESTIMATION OF AVERAGE TREATMENT EFFECTS.

WE ARE GOING TO PRESENT A FEW SIMPLE MODELS IN CONSIDERABLE DETAIL, TO MAKE SURE THAT THE BASIC CONCEPT OF POTENTIAL OUTCOMES IS CLEAR.

SOME EXAMPLES OF POTENTIAL-OUTCOMES MODELS

THE NOTION OF POTENTIAL OUTCOMES AND COUNTERFACTUALS HAS BEEN USED TO DESCRIBE EXPERIMENTS FROM THE TIME OF JERZY NEYMAN AND R. A. FISHER. IT IS EMBEDDED IN THE MATHEMATICAL REPRESENTATION THAT DESCRIBES THE OUTCOME OF AN EXPERIMENT, E.G.,

Y_i = μ + θW_i + E_i

WHERE

Y_i = observed outcome for experimental unit i

μ = population grand mean

θ = average treatment effect

W_i = treatment indicator variable (= 0 if the i-th unit is untreated, = 1 if the i-th unit is treated)

E_i = model error term (zero mean, mutually independent and identically distributed (IID)

It is assumed that E_i is independent of all other explanatory variables in the model. For this model, this implies either that W_i is a non-stochastic (deterministic) variable or is a random variable independent of E_i.

THE INDEX i MAY REFER TO THE i-th UNIT OF A SAMPLE, OR THE i-th UNIT OF THE POPULATION, DEPENDING ON CONTEXT.

(RECALL THAT WE ARE USING UPPER-CASE (CAPITAL) LETTERS TO REPRESENT ABSTRACT RANDOM VARIABLES, AND LOWER-CASE (SMALL) LETTERS TO REPRESENT ACTUAL REALIZATIONS OF THOSE RANDOM VARIABLES (I.E., THE RESULT OF AN EXPERIMENT (A THOUGHT EXPERIMENT OR A REAL, PHYSICAL EXPERIMENT).)

A STATISTICAL MODEL SUCH AS THE PRECEDING ONE IS DEFINED BY A NUMBER OF ASSUMPTIONS ABOUT THE STOCHASTIC (PROBABILISTIC) NATURE OF THE MODEL VARIABLES, AND THE STOCHASTIC RELATIONSHIPS AMONG THEM. FOR CAUSAL ANALYSIS, THE MODEL SHOULD CORRESPOND TO A CAUSAL DIAGRAM (OR OTHER DESCRIPTION) THAT SPECIFIES THE CAUSAL RELATIONSHIPS AMONG THE MODEL VARIABLES. (THE EQUATION ALONE DOES NOT SPECIFY THE CAUSAL MODEL. IT SIMPLY DESCRIBES PROBABILISTIC RELATIONSHIPS AMONG THE VARIABLES. THESE PROBABILISTIC RELATIONSHIPS MAY DESCRIBE ASSOCIATIVE RELATIONSHIPS OR CAUSAL RELATIONSHIPS. IF CAUSAL RELATIONSHIPS ARE SPECIFIED IN THE MODEL, IT IS A “CAUSAL MODEL.” OTHERWISE, IT IS A “DESCRIPTIVE” OR “ASSOCIATIVE” MODEL.)

IN THE PRECEDING EXAMPLE, Y IS AN OUTCOME VARIABLE THAT IS AFFECTED BY THE TREATMENT VARIABLE. μ AND θ ARE CONSTANTS. IN THIS PRESENTATION WE SHALL OFTEN ASSUME THAT W_i IS A RANDOM VARIABLE. IF IT IS, THEN AN ESSENTIAL MODEL ASSUMPTION (IF THE ORDINARY-LEAST-SQUARES ESTIMATION PROCEDURE IS USED TO ESTIMATE THE MODEL PARAMETERS IN A GENERAL LINEAR MODEL) IS THAT W_i AND THE MODEL ERROR TERMS ARE UNCORRELATED.

NOTE THAT THE PRECEDING MODEL IS AN ABSTRACT IDEALIZATION OF REALITY. THE MODEL IS HYPOTHETICAL – IT EXISTS IN THE MIND. IT IS A MATHEMATICAL APPROXIMATION TO REALITY. PRIOR TO CONDUCTING AN EXPERIMENT, THERE ARE NO PHYSICAL DATA ASSOCIATED WITH THE MODEL. SOME WRITERS (E.G., DAWID) REFER TO CONSIDERATIONS OF AN ABSTRACT MODEL AS “METAPHYSICAL,” AND PREFER TO SPEAK ONLY OF REALIZED OUTCOMES OF THE MODEL, I.E., THE DATA. MORE WILL BE SAID ON THIS LATER.

IN THE (PEARL) THEORY OF CAUSAL MODELING THAT WAS PRESENTED EARLIER, THE CAUSAL EFFECT WAS DEFINED AS THE ENTIRE OUTCOME DISTRIBUTION OF THE EFFECT VARIABLE GIVEN A CAUSAL VARIABLE. A VARIETY OF AVERAGE CAUSAL EFFECTS (SUCH AS THE ATE AND ATT) CAN BE DERIVED FROM SUCH A MODEL. HERE, WE ARE FOCUSING ON THE CASE IN WHICH THERE ARE JUST TWO POSSIBLE OUTCOMES, AND THE AVERAGE CAUSAL EFFECTS OF INTEREST (THE ATE AND ATT) WILL BE BASED ON THOSE. IN THIS SETTING, THERE ARE JUST TWO POTENTIAL OUTCOMES, Y₀ AND Y₁.

FOR THE i-th EXPERIMENTAL UNIT, THE TWO POTENTIAL OUTCOMES, Y_i0 AND Y_i1, CORRESPOND TO WHETHER THE UNIT IS TREATED (W_i = 1) OR UNTREATED (W_i = 0):

Y_i0 = μ + θ x 0 + E_i = μ + E_i (THE OUTCOME ASSOCIATED WITH W_i = 0)

Y_i1 = μ + θ x 1 + E_i = μ + θ + E_i (THE OUTCOME ASSOCIATED WITH W_i = 1).

PRIOR TO CONDUCTING AN EXPERIMENT, NO REAL (ACTUAL, EXISTING) VALUES EXIST FOR Y_i, Y_0i AND Y_1i. AFTER THE EXPERIMENT, REAL VALUES (OBSERVED DATA) EXIST FOR Y_i AND ONE OF Y_0i AND Y_1i. IF W_i = 0, THEN Y_0i IS OBSERVED. IF W_i = 1, THEN Y_1i IS OBSERVED. THE MODEL IS ALWAYS “METAPHYSICAL” (HYPOTHETICAL, ABSTRACT, CONCEPTUAL, EXISTING IN THOUGHT). HOW THE DATA SHOULD BE ANALYZED DEPENDS ON THE MODEL SPECIFICATION. DATA WITHOUT A MODEL ARE USELESS – NOTHING MORE THAN A MEANINGLESS SET OF NUMBERS.

THE PRECEDING MODEL IS REFERRED TO AS AN “ADDITIVE” MODEL, SINCE THE DIFFERENCE BETWEEN THE TWO POTENTIAL OUTCOMES FOR EVERY UNIT IS A CONSTANT, T (ADDED TO Y₀ TO OBTAIN Y₁). IN THIS INSTANCE, THE ADDITIVE CONSTANT OCCURS AT THE LEVEL OF THE INDIVIDUAL TREATMENT, AND THIS MODEL FEATURE IS REFERRED TO SPECIFICALLY AS TREATMENT-UNIT ADDITIVITY (TUA). MORE GENERAL MODELS ALLOW FOR TREATMENT-UNIT HETEROGENEITY.

THE TERM “FIXED EFFECTS MODEL” IS USED TO REFER TO A LINEAR STATISTICAL MODEL IN WHICH ALL OF THE EXPLANATORY VARIABLES OF THE MODEL (I.E., ALL VARIABLES EXCEPT THE MODEL ERROR TERM) ARE “FIXED” (NON-STOCHASTIC, DETERMINISTIC). IF ALL OF THE EXPLANATORY VARIABLES ARE RANDOM, THE MODEL IS CALLED A “RANDOM EFFECTS” MODEL. IF SOME EXPLANATORY VARIABLES ARE FIXED AND SOME ARE RANDOM, THEN THE MODEL IS CALLED A “MIXED” MODEL. THERE IS AN EASY SOURCE OF CONFUSION IN THIS DISCUSSION, SINCE THERE ARE TWO VARIABLES WITH SIMILAR NAMES BUT QUITE DIFFERENT MEANINGS: THE TREATMENT EFFECT (T) AND THE TREATMENT-SELECTION INDICATOR VARIABLE (W_i). EITHER OF THESE MAY BE FIXED OR RANDOM. THE CONFUSION THAT ARISES IS THAT THE TERM “RANDOM TREATMENT EFFECT” IS USED TO REFER TO EITHER OF THESE VARIABLES. TO AVOID CONFUSION, WE SHALL GENERALLY REFER TO A SPECIFIC VARIABLE OR PARAMETER (SUCH AS T OR W_i) WHEN USING THE TERMS RANDOM OR FIXED, RATHER THAN TO A MODEL. MOST OF THE MODELS CONSIDERED IN THIS PRESENTATION ARE NOT GENERAL LINEAR STATISTICAL MODELS, BUT EXTENSIONS (GENERALIZED LINEAR MODELS) SUCH AS A “SWITCHING” REGRESSION MODEL (E.G., TOBIT MODEL, LOGISTIC REGRESSION MODEL, LATENT-VARIABLE MODEL, OR A TWO-STEP MODEL INCLUDING A FIRST-STEP SELECTION (LOGISTIC REGRESSION) MODEL AND A SECOND-STEP (GLM) OUTCOME MODEL).

IN MUCH OF THE DISCUSSION IN THIS PRESENTATION, THE TREATMENT SELECTION INDICATOR VARIABLE (W_i) IS A RANDOM VARIABLE, SINCE THAT IS THE SITUATION IN WHICH “SELECTION EFFECTS” MAY OCCUR TO BIAS THE IMPACT ESTIMATES.

THE PRECEDING EQUATIONS THAT INCLUDED THE INDEX i REFER TO A SPECIFIC POPULATION UNIT OR TO A SPECIFIC EXPERIMENTAL UNIT (TEST UNIT, SAMPLE UNIT), OF INDEX i. THE NOTION OF POTENTIAL OUTCOMES EXTENDS TO THE ENTIRE POPULATION, NOT JUST THE SAMPLE. THE SETS OF POTENTIAL OUTCOMES CORRESPONDING TO W=0 AND W=1 CORRESPOND TO THE TWO HYPOTHETICAL POPULATIONS, THE “PROGRAM-ELIGIBLE POPULATION IF TREATED” AND THE “PROGRAM-ELIGIBLE POPULATION IF UNTREATED.”

IF WE DROP THE UNIT INDEX i, THE MODEL FOR THE OBSERVED OUTCOME BECOMES (NOW REFERRING TO AN ARBITRARY UNIT OF THE POPULATION OR SAMPLE):

Y = μ + θW + E

AND THE MODEL FOR THE POTENTIAL OUTCOMES BECOMES:

Y₀ = μ + E (FOR W=0)

Y₁ = μ + θ + E (FOR W=1).

FOR PURPOSES OF THIS DISCUSSION, IT IS HELPFUL TO KEEP EXPLICITLY IN MIND THE INDIVIDUAL UNIT, AND FOR THIS REASON WE SHALL RETAIN THE INDEX i (EXCEPT FOR CONVENIENCE WHEN REFERRING TO A “GENERIC” UNIT OR WHEN DESCRIBING MODEL ASSUMPTIONS).

IN THE PRECEDING VERY SIMPLE MODEL, IT IS ASSUMED THAT THE TREATMENT EFFECT IS IDENTICAL FOR ALL UNITS – IT IS THE VALUE θ. THE VARIABILITY REPRESENTED BY THE MODEL ERROR TERM, E, REPRESENTS VARIABILITY FROM ALL OTHER SOURCES. THIS ASSUMPTION OF CONSTANT TREATMENT EFFECT (TUA) IS RATHER STRICT. THE ASSUMPTION OF A CONSTANT TREATMENT EFFECT IS REFERRED TO AS A HOMOGENEOUS TREATMENT EFFECT, OR TREATMENT HOMOGENEITY.

THE PRECEDING MODEL IS PERHAPS THE SIMPLEST ONE FOR REPRESENTING THE EFFECT OF A BINARY TREATMENT ON MEMBERS OF A POPULATION. IT IS ALSO VERY UNREALISTIC FOR SOCIAL AND ECONOMIC APPLICATIONS. WITH THIS MODEL, THE RESPONSE IS CONSTANT: APART FROM UNIT-TO-UNIT VARIABILITY REPRESENTED BY E, EVERY UNIT THAT IS TREATED IS ASSUMED TO REALIZE EXACTLY THE SAME ADDITIONAL RESPONSE (θ) AS IF IT HAD NOT BEEN TREATED. WITH THIS MODEL, THERE CAN NEVER BE ANY “SELECTION EFFECTS,” SINCE NO MATTER HOW UNITS ARE SELECTED FOR TREATMENT, THE RESPONSE TO TREATMENT IS IDENTICAL.

A MUCH MORE REALISTIC MODEL IS ONE THAT ALLOWS FOR THE RESPONSE TO TREATMENT TO BE A RANDOM VARIABLE. THIS ALLOWS FOR HETEROGENEITY OF THE INDIVIDUAL RESPONSE TO TREATMENT. WHEN THE RESPONSE TO TREATMENT MAY VARY, THERE IS THE POSSIBILITY THAT THE MAGNITUDE OF THE RESPONSE MAY BE RELATED TO OTHER VARIABLES (SUCH AS SEX OR RACE). IN THIS SITUATION, SELECTION EFFECTS ARE POSSIBLE – UNITS MAY BE SELECTED FOR TREATMENT BASED ON THOSE OTHER VARIABLES, SO THAT THE MEAN RESPONSE OF THE TREATED IS DIFFERENT FROM THE RESPONSE EXPECTED FOR A RANDOMLY SELECTED INDIVIDUAL. WHEN ASSIGNMENT TO TREATMENT IS NOT RANDOM, THE FORMULAS THAT ARE APPROPRIATE FOR ESTIMATING IMPACT FROM A RANDOMIZED EXPERIMENT DO NOT APPLY – IF THOSE FORMULAS ARE USED, THE IMPACT ESTIMATE MAY BE BIASED.

IN MANY APPLICATIONS, IT IS REASONABLE TO ASSUME THAT THE RESPONSE TO TREATMENT IS NOT EXACTLY THE SAME FOR ALL UNITS, I.E., IS HETEROGENEOUS. INSTEAD, WE MAY ENTERTAIN THE NOTION THAT THE TREATMENT EFFECT MAY VARY FROM INDIVIDUAL TO INDIVIDUAL, I.E., VIEW IT AS A RANDOM EFFECT. IN THIS CASE, THE MODEL IS:

Y_i = μ + T_iW_i + E_i

WHERE T_i IS NOW A RANDOM VARIABLE HAVING MEAN θ. WE MAY REPRESENT THIS RANDOM VARIABLE AS

T_i = θ + U_i

WHERE θ DENOTES THE MEAN TREATMENT EFFECT (A CONSTANT) AND U_i DENOTES A RANDOM VARIABLE HAVING ZERO MEAN. IT IS ASSUMED THAT U_i AND E_i ARE INDEPENDENT. IN THIS NOTATION, THE MODEL BECOMES:

Y_i = μ + T_iW_i + E_i = μ + θW_i + U_iW_i + E_i

WHERE θ IS THE MEAN TREATMENT EFFECT AND W_i IS THE TREATMENT-SELECTION INDICATOR VARIABLE FOR THE i-th UNIT. CONSIDERING THE TREATED AND UNTREATED UNITS SEPARATELY, THE MODEL IS

Y_0i = μ + E_i (FOR W_i=0 (UNTREATED))

Y_1i = μ + θ + U_i + E_i (FOR W_i=1 (TREATED)).

(THESE TWO EQUATIONS REPRESENT THE “SWITCHING” REGRESSION MODEL REFERRED TO EARLIER.)

IF TREATMENT IS RANDOMLY ASSIGNED, W_i AND E_i ARE UNCORRELATED, AND THE IMPACT, E(Y₁ – Y₀) MAY BE ESTIMATED SIMPLY BY ESTIMATING THE MEAN OF Y₀ USING THE FIRST MODEL (FOR Y_0i) AND THE MEAN OF Y₁ USING THE SECOND MODEL (FOR Y_1i) AND TAKING THE DIFFERENCE IN THE MEANS. SINCE THE SAMPLES OF TREATED AND UNTREATED UNITS ARE INDEPENDENT, THE VARIANCE OF THIS ESTIMATOR IS SIMPLY THE SUM OF THE VARIANCES OF THE TWO ESTIMATED MEANS.

IF TREATMENT IS NOT RANDOMLY ASSIGNED, THE CORRECT APPROACH TO ESTIMATION IS QUITE DIFFERENT.

NOTE THAT THE TREATED AND UNTREATED SAMPLES ARE EXCLUSIVE (NONOVERLAPPING, CONTAINING DIFFERENT OBSERVATIONS). FOR THIS REASON, IT DOES NOT MATTER WHETHER WE REPRESENT THE MODEL ERROR TERM AS E_i FOR BOTH POTENTIAL OUTCOMES, OR AS E_0i AND E_1i FOR THE TREATED AND UNTREATED UNITS, RESPECTIVELY.

NOTE THAT WHEN THE TREATMENT EFFECT (T = θ + U) IS RANDOM, A CORRELATION EXISTS BETWEEN Y₀ AND Y₁, OVER THE TOTAL POPULATION. THIS CORRELATION IS GIVEN BY ρ = σ²_U/(σ²_U+ σ²_E). THIS CORRELATION IS PRESENT EVEN IF TREATMENT (W_i) IS RANDOMLY ASSIGNED.

ANOTHER FEATURE OF THE MODEL (IN SOCIO-ECONOMIC STUDIES) IS THAT SINCE Y₀ AND Y₁ ARE NEVER OBSERVED ON THE SAME UNIT (I.E., REPLICATION IS NOT POSSIBLE FOR UNITS SUCH AS INDIVIDUAL PERSONS OR FAMILIES), IT IS NOT POSSIBLE TO MAKE ANY STATISTICAL (DATA-BASED) INFERENCES ABOUT THE JOINT DISTRIBUTION OF Y₀ AND Y₁. IN WHAT FOLLOWS, WE MAY MAKE AN ASSUMPTION ABOUT THE JOINT DISTRIBUTION, SUCH AS CONDITIONAL INDEPENDENCE OF THE PAIR (Y₀, Y₁) GIVEN COVARIATES, BUT THIS ASSUMPTION IS NOT TESTABLE FROM THE DATA.

THE POTENTIAL-OUTCOMES APPROACH IS SOMETIMES CRITICIZED ON THE BASIS OF THE FACT THAT IT MAKES AN ASSUMPTION ABOUT THE JOINT DISTRIBUTION OF THE POTENTIAL OUTCOMES, I.E., ABOUT THE JOINT DISTRIBUTION (Y₀, Y₁). ONE WAY OR ANOTHER, ALL APPROACHES MAKE SOME SORT OF SIMILAR ASSUMPTION. FOR EXAMPLE, IN PEARL’S APPROACH, IT IS ASSUMED THAT THE MODEL DISTURBANCES (Us) OF THE CAUSAL MODEL ARE INDEPENDENT.

A FEATURE OF THE PRECEDING MODEL IS THAT FOR THE TREATED UNITS IT IS NOT POSSIBLE TO DISTINGUISH BETWEEN U_i AND E_i (BECAUSE THERE IS NO REPLICATION OF INDIVIDUALS). THIS FACT LIMITS THE USEFULNESS OF THE MODEL IN DESCRIBING FEATURES OF THE POPULATION OR PROCESS REPRESENTING THE DATA. THIS PROBLEM DID NOT ARISE FOR THE TUA (CONSTANT TREATMENT EFFECT) MODEL: THE EFFECT OF THE TREATMENT WAS ASSUMED TO BE THE SAME IN ALL INSTANCES, SO THAT THE ONLY VARIATION IN THE MODEL WAS THE UNIT-TO-UNIT VARIATION (E_i). FOR THE RANDOM-EFFECTS MODEL, HOWEVER, THE UNIT-TO-UNIT VARIATION (E_i) IS CONFOUNDED WITH THE TREATMENT-TO-TREATMENT VARIATION (U_i). IT IS ALSO CONFOUNDED WITH UNIT-TREATMENT INTERACTION (NOT SHOWN IN THE PRECEDING MODEL).

NOTE THAT THE PROBLEM OF CONFOUNDING OF THE TREATMENT EFFECT WITH A UNIT EFFECT OR WITH A UNIT-TREATMENT INTERACTION HAS NOTHING TO DO WITH THE POTENTIAL-OUTCOMES APPROACH. THIS PROBLEM ARISES SINCE THE DATA DESIGN IS NOT ADEQUATE TO ALLOW FOR SEPARATION OF THESE EFFECTS. TO DO SO WOULD REQUIRE DATA HAVING VARIATION OF TREATMENTS AND REPLICATION WITHIN UNITS. THIS LIMITATION OF THE MODEL IS ASSOCIATED WITH INABILITY TO REPLICATE INDIVIDUAL UNITS; IT IS NOT A LIMITATION OF THE POTENTIAL-OUTCOMES FRAMEWORK.

AN EXAMPLE OF A DESIGN THAT WOULD OVERCOME THIS LIMITATION IS AN AGRICULTURAL EXPERIMENT IN WHICH VARIOUS FERTILIZER LEVELS (E.G., TWO AS IN THE PREVIOUS EXAMPLE – TREATED AND UNTREATED) ARE APPLIED TO SUBPLOTS LOCATED WITHIN PLOTS, AND THERE ARE MULTIPLE APPLICATIONS OF EACH FERTILIZER LEVEL ON SEVERAL SUBPLOTS WITHIN EACH PLOT. THE PLOTS VARY IN FERTILITY, BUT ARE RELATIVELY UNIFORM WITHIN, WITH EXPERIMENTAL ERROR REPRESENTED BY SUBPLOT-TO-SUBPLOT VARIATION WITHIN PLOTS. THIS TYPE OF DESIGN IS NOT FEASIBLE IN MANY SOCIO-ECONOMIC STUDIES, SINCE THE “PLOT” CORRESPONDS TO THE FAMILY OR INDIVIDUAL RECEIVING TREATMENT, AND THERE IS PHYSICALLY NO WAY TO REPLICATE THE FAMILY OR INDIVIDUAL. A MODEL CORRESPONDING TO THIS DESIGN IS:

Y_kji = μ + θ_k + ϒ_kj + U_k + V_kj + E_kji

WHERE θ_k DENOTES THE TREATMENT (FERTILIZER) EFFECT, ϒ_kj DENOTES THE PLOT-TREATMENT INTERACTION EFFECT, U_k DENOTES THE TREATMENT VARIATION, V_kj DENOTES THE PLOT-TREATMENT VARIATION, AND E_kji DENOTES SUBPLOT (WITHIN-PLOT) VARIATION (EXPERIMENTAL ERROR, MODEL ERROR). (IN THIS MODEL REPRESENTATION, THE TREATMENT EFFECT IS REPRESENTED BY TWO PARAMETERS, θ₀ AND θ₁, RATHER THAN BY A SINGLE PARAMETER, θ, AS USED EARLIER (θ = θ₁ – θ₀).)

WITH SUFFICIENT DATA CORRESPONDING TO THIS MODEL, IT IS POSSIBLE TO ESTIMATE THE MODEL PARAMETERS θ_k AND ϒ_kj AND THE VARIANCES σ²_k, σ²_kj AND σ²_E. THE ϒ_kj PARAMETERS (PLOT-TREATMENT INTERACTION EFFECTS) MAY OR MAY NOT BE OF INTEREST, DEPENDING ON THE APPLICATION. THEY MAY REPRESENT UNOBSERVED VARIABLES RELATED TO OUTCOME. FOR EXAMPLE, IN THIS AGRICULTURAL EXAMPLE, IT MAY BE THAT THE FERTILIZER EFFECT IS VERY SENSITIVE TO THE SOIL ACIDITY (pH LEVEL), AND THAT THE SOIL ACIDITY VARIES SUBSTANTIALLY BETWEEN THE PLOTS BUT NOT MUCH WITHIN PLOTS. ON SEEING A STRONG PLOT-TREATMENT INTERACTION, FURTHER INVESTIGATION MAY BE WARRANTED TO DISCOVER THE PHYSICAL SOURCE OF THE HIGH PLOT-TREATMENT INTERACTION (CAUSE OF THE VARIATION, SUCH AS, pH). IN A SOCIO-ECONOMIC PROGRAM, UNOBSERVED VARIABLES THAT CONTRIBUTE TO SUBSTANTIAL TREATMENT-EFFECT VARIATION MIGHT BE PERSONAL CHARACTERISTICS SUCH AS INTELLIGENCE, AMBITION, DISCIPLINE AND INTEGRITY.

WITHOUT ADEQUATE DATA, IT MAY NOT BE POSSIBLE TO ESTIMATE ALL OF THE MODEL PARAMETERS. IN THIS CASE, A SIMPLER MODEL IS USED. WHAT IS IMPORTANT IS THAT, FOR WHATEVER MODEL IS USED, THE EFFECT OF INTEREST IS ESTIMABLE.

THE PRECEDING MODEL INCLUDES BUT A SINGLE EXPLANATORY VARIABLE – THE TREATMENT VARIABLE (W_i). THE MODEL MAY BE EXTENDED TO INCLUDE COVARIATES, OR EXPLANATORY VARIABLES ADDITIONAL TO THE TREATMENT VARIABLE (THE VARIABLE OF PRIMARY INTEREST). FOR EXAMPLE (DROPPING THE UNIT OBSERVATION INDEX i):

Y = μ + TW + X’β + E

where

X = vector of explanatory variables

β = vector of parameters (“main effects”)

Y = μ + TW + X’β + W(X - )’ϒ + E

where

ϒ= vector of parameters (“interaction-with-treatment effects”).

THE COVARIATES ARE DEMEANED IN THE W(X - ) INTERACTION TERM SO THAT THE PRINCIPAL EFFECT OF INTEREST (THE AVERAGE EFFECT OF TREATMENT) IS THE COEFFICIENT OF THE W TERM. IN THE PRECEDING MODEL, THE TREATMENT EFFECT, T, MAY BE CONSTANT OR RANDOM, AS IN THE SIMPLER VERSION OF THE MODEL DISCUSSED EARLIER. EVEN THOUGH THIS MODEL CONTAINS MANY MORE VARIABLES THAN THE ORIGINAL, THE TWO POTENTIAL OUTCOMES ARE STILL EQUAL TO Y EVALUATED FOR W = 0 AND W = 1, AND THE TREATMENT EFFECT MAY BE CONSTANT (ADDITIVE) OR RANDOM).

LIMITATIONS OF THE POTENTIAL-OUTCOMES APPROACH

IT IS IMPORTANT TO REALIZE, AS STATED EARLIER, THAT THE POTENTIAL OUTCOMES (COUNTERFACTUALS) APPROACH CANNOT REASONABLY BE USED TO ESTIMATE COUNTERFACTUAL VALUES FOR INDIVIDUAL UNITS (EXCEPT UNDER ADDITIONAL ASSUMPTIONS ABOUT THE JOINT DISTRIBUTION OF THE POTENTIAL OUTCOMES). FOR A DETAILED DISCUSSION OF THIS LIMITATION SEE “CAUSAL INFERENCE WITHOUT COUNTERFACTUALS” BY A. P. DAWID, JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, JUNE 2000, VOL. 95, NO. 450, PP. 407-448. (ALSO, SEE THE REVIEWERS’ COMMENTS FOLLOWING DAWID’S ARTICLE, FOR DISCUSSION OF SPECIFIC PROBLEMS ASSOCIATED WITH THE APPROACH. MORE WILL BE SAID ON THIS LATER.)

THE CONCEPT OF CAUSALITY IS DIFFICULT, AND THERE ARE A NUMBER OF THEORIES OF CAUSALITY. UNIDIRECTIONAL CAUSALITY DOES NOT APPEAR TO EXIST AT THE QUANTUM LEVEL, BUT IT IS A QUINTESSENTIAL FEATURE OF EXISTENCE AT THE MACRO LEVEL, WHERE BIOLOGICAL LIFE EXISTS.

IT IS DIFFICULT TO DISCUSS CAUSALITY WITHOUT THE NOTION OF COUNTERFACTUALS. IF CONSIDERATION IS RESTRICTED TO EXPERIMENTAL DESIGNS, THIS DIFFICULTY DISAPPEARS, SINCE, WITHOUT SELECTION BIAS, THE OBSERVED POPULATION TREATMENT EFFECT CORRESPONDS TO THE AVERAGE TREATMENT EFFECT. THAT IS, AS LONG AS WE RESTRICT ATTENTION TO EXPERIMENTAL DESIGNS (RANDOMIZED ASSIGNMENT TO TREATMENT), THERE IS NO NEED TO EXPLICITLY CONSIDER COUNTERFACTUALS.

THE NOTION OF COUNTERFACTUALS PERVADES THE STUDY OF CAUSALITY. IT IS NOT JUST THE BINARY-TREATMENT POTENTIAL OUTCOMES MODEL THAT INVOLVES COUNTERFACTUALS. FOR EXAMPLE, IN PEARL’S THEORY, THE CAUSAL EFFECT IS DEFINED AS THE CONDITIONAL DISTRIBUTION OF OUTCOME, GIVEN THE VALUE OF THE CAUSAL VARIABLE. SINCE IT IS ONLY OBSERVATIONS, NOT DISTRIBUTIONS, THAT MAY BE OBSERVED, IN THIS FRAMEWORK EVERY ASPECT OF THE CAUSAL EFFECT IS UNOBSERVABLE AND HENCE “METAPHYSICAL.”

PEARL (OP. CIT. P 79) CITES THE FOLLOWING DEFINITION OF IGNORABILITY (CONDITIONAL INDEPENDENCE) AS AN EXAMPLE OF THE OBTUSENESS OF THE CONCEPT OF COUNTERFACTUALS, AND THE DIFFICULTY OF KNOWING HOW TO TEST FOR CONDITIONAL INDEPENDENCE: “IGNORABILITY READS: ‘Z IS AN ADMISSIBLE SET OF COVARIATES IF, GIVEN Z, THE VALUE THAT Y WOULD OBTAIN HAD X BEEN x IS INDEPENDENT OF X.’” THIS CONCEPT IS COMPLEX, AND PEARL IS ABSOLUTELY CORRECT THAT IT IS NOT APPARENT HOW TO TEST THIS CRITERION. THE ADVANTAGE OF PEARL’S CRITERIA FOR ASSESSING ESTIMABILITY IS THAT THE RESEARCHER CAN SPECIFY HIS BELIEFS ABOUT VARIABLE INTERRELATIONSHIPS IN A CAUSAL MODEL IN SUBSTANTIAL DETAIL. THERE ARE STILL ASPECTS OF PEARL’S MODEL THAT ARE NOT TESTABLE, BUT IT IS SUBSTANTIALLY EASIER TO ASSESS WHETHER CONDITIONAL INDEPENDENCE GIVEN X HOLDS IF DETAILED DESCRIPTION OF HOW THE VARIABLES IN X INTERACT AMONG THEMSELVES AND WITH THE OUTCOME VARIABLE.

PEARL’S FRAMEWORK PROVIDES A VERY USABLE METHODOLOGY FOR DISPLAYING SUBJECTIVE BELIEFS ABOUT A CAUSAL MODEL AND IDENTIFYING A SET OF VARIABLES THAT MAY BE CONDITIONED ON TO ACHIEVE CONDITIONAL INDEPENDENCE. ALTHOUGH COUNTERFACTUALS ARE NOT EXPLICIT IN PEARL’S FRAMEWORK, PEARL’S THEORY IS EQUIVALENT TO THE POTENTIAL-OUTCOMES FRAMEWORK, IN THE SENSE THAT EVERY THEOREM IN PEARL’S THEORY HAS A COUNTERPART IN THE POTENTIAL-OUTCOMES THEORY (PEARL OP. CIT. P. 98). AS PEARL IMPLIES (P. 244), HIS APPROACH IS SUBSTANTIALLY EASIER TO CONCEPTUALIZE AND USE. IN HIS APPROACH, SIMPLE CAUSAL STATEMENTS ARE THE PRIMITIVES OF THE FRAMEWORK. IN THE COUNTERFACTUALS APPROACH, THE MUCH MORE COMPLEX CONCEPT OF CONDITIONAL INDEPENDENCE IS THE PRIMITIVE. ON THE OTHER HAND, THE POTENTIAL-OUTCOMES APPROACH IS HELPFUL FOR SHOWING THE NATURE OF SELECTION BIAS. IT OFFERS NO INSIGHT ON HOW TO ESTABLISH CONDITIONAL INDEPENDENCE. WITH PEARL’S APPROACH IT IS STILL NECESSARY TO MAKE ASSUMPTIONS ABOUT CONDITIONAL INDEPENDENCE – THIS IS EASIER TO DO AFTER EXAMINING A DETAILED DAG THAT INCORPORATES BELIEFS ABOUT CAUSAL INTERRELATIONSHIPS.

FOR QEDs, IT IS AWKWARD AND COUNTERPRODUCTIVE TO AVOID THE CONCEPT OF COUNTERFACTUALS. WHILE THE MATHEMATICAL MODEL DESCRIBING THE DATA MAY INCLUDE THE NOTION OF POTENTIAL OUTCOMES AND COUNTERFACTUAL RESPONSES, THE ESTIMATION FORMULAS REFER TO OBSERVED DATA AND ESTIMABLE QUANTITIES.

ONE SOMETIMES HEARS THE EXPRESSION “ESTIMATE THE COUNTERFACTUAL.” THAT IS NOT REALLY THE POINT (AND, WITHOUT ASSUMPTIONS ABOUT THE JOINT DISTRIBUTION OF Y₀ AND Y₁, NOT POSSIBLE AT THE LEVEL OF THE INDIVIDUAL). (IT IS RARELY DONE, OR DESIRED TO BE DONE, EXCEPT PERHAPS IN LEGAL PROCEEDINGS – E.G., WHAT WOULD THE FUTURE EARNINGS OF A PERSON BE IF HE HAD NOT BEEN KILLED.) THE POINT (IN EVALUATION STUDIES) IS TO ESTIMATE IMPACT – THE MEAN DIFFERENCE BETWEEN THE FACTUAL AND COUNTERFACTUAL OUTCOMES FOR SOME GROUP.

THE TERM “COUNTERFACTUAL” IS OFTEN USED TO REFER TO A COMPARISON GROUP (RATHER THAN, AS ABOVE, TO REFER TO AN OUTCOME UNDER ALTERNATIVE CONDITIONS (TREATED VS. UNTREATED)). THE EXPRESSION “CONSTRUCT COMPARISON GROUPS TO ENABLE ESTIMATION OF THE COUNTERFACTUAL” IS ALSO SEEN. THESE USAGES ARE DIFFERENT FROM (ALTHOUGH RELATED TO AND DERIVED FROM) THE PRECEDING USAGE. FROM A TECHNICAL POINT OF VIEW, THEY ARE DIFFICULT TO FATHOM, SINCE A COUNTERFACTUAL CAN NEVER BE OBSERVED FOR AN INDIVIDUAL UNIT, AND IT IS RARELY THE INTENTION IN EVALUATION RESEARCH TO ESTIMATE THE COUNTERFACTUAL FOR AN INDIVIDUAL UNIT, BUT RATHER TO ESTIMATE CHARACTERISTICS OF THE MARGINAL DISTRIBUTIONS OF THE TWO POTENTIAL OUTCOMES (FOR TREATED AND UNTREATED UNITS). FURTHERMORE, A COMPARISON (CONTROL) GROUP IS NOT A “COUNTERFACTUAL” IN ANY SENSE – IT IS QUITE REAL! (THE TWO MARGINAL POTENTIAL-OUTCOME DISTRIBUTIONS ARE METAPHYSICAL, BUT THEY ARE IN NO SENSE “COUNTERFACTUAL” – NEITHER ONE IS OBSERVED, BUT THEY MAY BOTH BE ESTIMATED. ASSUMPTIONS MAY BE MADE ABOUT THE JOINT DISTRIBUTION OF POTENTIAL OUTCOMES FOR AN INDIVIDUAL UNIT, SUCH AS CONDITIONAL INDEPENDENCE OF THE POTENTIAL OUTCOMES (Y₀, Y₁) AND W GIVEN CERTAIN COVARIATES. THE PURPOSE OF THESE ASSUMPTIONS IS TO ENABLE ESTIMATION OF CHARACTERISTICS OF THE MARGINAL DISTRIBUTIONS. THERE IS RARELY AN ATTEMPT TO ESTIMATE AN INDIVIDUAL COUNTERFACTUAL, AND A COMPARISON GROUP IS NOT COUNTERFACTUAL.)

THIS PRESENTATION USES THE NOTION OF COUNTERFACTUALS TO ASSIST UNDERSTANDING OF CONCEPTS. CONCEPTUAL DIFFICULTIES ARISE IN THE COUNTERFACTUAL FRAMEWORK ONLY WHEN IT IS ATTEMPTED TO ESTIMATE PROPERTIES OF THE JOINT DISTRIBUTION OF Y₀ AND Y₁ (SINCE THE TWO POTENTIAL OUTCOMES CANNOT BE OBSERVED ON THE SAME UNIT (OR, REPLICATION OF INDIVIDUAL UNITS IN NOT POSSIBLE)). IT WORKS FINE FOR ILLUSTRATING CONCEPTS BASED ON THE MARGINAL DISTRIBUTIONS OF THE TWO POTENTIAL OUTCOMES (Y₀ AND Y₁), SUCH AS THEIR MEANS. IT WOULD BE DIFFICULT TO SPEAK IN TERMS OF THE TWO MARGINAL POTENTIAL-OUTCOME DISTRIBUTIONS WITHOUT STATING, AT LEAST CONCEPTUALLY, WHAT THE POTENTIAL OUTCOMES ARE (E.G., OUTCOME IF TREATED VS. OUTCOME IF UNTREATED). THEY CERTAINLY EXIST IN THE THEORETICAL FORMULATION OF THE MODEL: THE TWO POTENTIAL OUTCOMES ARE ALWAYS AN EXPLICIT FEATURE OF THE MODEL (BY SUBSTITUTING W=0 OR W=1).

THE FUNDAMENTAL ISSUE IN CAUSAL MODELING IS ESTIMABILITY (IDENTIFIABILITY) OF EFFECTS OF INTEREST. ESTIMABILITY RESTS ON THE VALIDITY OF THE CONDITIONAL INDEPENDENCE ASSUMPTION. THIS IS ESTABLISHED BY EXAMINING THE DAG AND APPLYING PEARL’S CRITERIA. THE POTENTIAL-OUTCOMES APPROACH PROCEEDS FROM THE POINT OF ACCEPTING CONDITIONAL INDEPENDENCE. A KEY POINT THAT IS EMPHASIZED IS THAT WE WILL NOT BE MAKING AN ASSUMPTION OF CONDITIONAL INDEPENDENCE OF TREATMENT W AND RESPONSE (Y₀, Y₁) GIVEN COVARIATES, X, EXCEPT AS A RESULT OF ANALYSIS OF A CAUSAL DIAGRAM AND ESTABLISHMENT OF PEARL’S ESTIMABILITY CRITERIA. IT IS DIFFICULT TO ASSERT CONDITIONAL INDEPENDENCE WITHOUT FIRST SPECIFYING AND THEN ANALYZING CAUSAL DIAGRAMS. (IT IS A LIMITATION OF THE R&R APPROACH THAT IT REQUIRES THAT AN ASSUMPTION ABOUT CONDITIONAL INDEPENDENCE BE MADE WITHOUT DETAILED AND EXPLICIT REPRESENTATION OF ALL THAT IS BELIEVED ABOUT THE CAUSAL RELATIONSHIPS INVOLVED IN AN INVESTIGATION.)

ALTHOUGH THE TWO POTENTIAL OUTCOMES CANNOT BE OBSERVED FOR A PARTICULAR UNIT, THE MARGINAL DISTRIBUTIONS OF THE POTENTIAL OUTCOMES CAN CERTAINLY BE ESTIMATED. THE INFERENCES THAT WE MAKE HERE WILL BE BASED ON THESE MARGINAL DISTRIBUTIONS, NOT ON THE JOINT DISTRIBUTION OF THE POTENTIAL OUTCOMES FOR AN INDIVIDUAL UNIT. THE ONLY ASSUMPTION THAT WE WILL MAKE ABOUT THE JOINT DISTRIBUTION IS ONE OF CONDITIONAL INDEPENDENCE OF THE JOINT DISTRIBUTION OF (Y₀, Y₁) AND W, GIVEN CERTAIN COVARIATES (IN WHICH CASE ALL OF THE INFORMATION AVAILABLE ABOUT THE POTENTIAL OUTCOMES IS CONTAINED IN THE TWO MARGINAL DISTRIBUTIONS).

STATISTICAL INFERENCE WILL BE RESTRICTED TO ESTIMATION OF THE ATE, NOT TO ESTIMATION OF INDIVIDUAL COUNTERFACTUAL VALUES. DAWID EXPRESSES NO OBJECTION TO THIS USE OF THE COUNTERFACTUAL FRAMEWORK.

THE STATISTICAL CAUSAL ANALYSIS DISCUSSED IN THIS PRESENTATION IS CONCERNED WITH ESTIMATION OF THE EFFECTS OF CAUSES (I.E., ESTIMATING THE EFFECT CAUSED IN AN OUTCOME VARIABLE BY CHANGES IN EXPLANATORY VARIABLES), RATHER THAN WITH THE DETERMINATION OF THE CAUSES OF EFFECTS (I.E., DECIDING WHICH VARIABLE CAUSED A PARTICULAR OUTCOME). (PEARL’S THEORY ADDRESSES THE ISSUE OF ESTIMATING THE EFFECTS OF CAUSES THAT ARE SPECIFIED IN A DAG.) QUITE APART FROM THIS FUNDAMENTAL ISSUE, IN OBSERVATIONAL DATA, EXPLANATORY VARIABLES ARE USUALLY CORRELATED, SO THAT THE EFFECTS ASSOCIATED WITH CHANGES ARE CONFOUNDED, MAKING IT DIFFICULT TO ASSOCIATE EFFECTS WITH SPECIFIC EXPLANATORY VARIABLES. THIS PROBLEM IS DRAMATICALLY REDUCED IN EXPERIMENTAL DESIGN, IN WHICH THE EXPLANATORY VARIABLES MAY BE CONTROLLED AND ORTHOGONALIZED (SET SUCH THAT THEY ARE UNCORRELATED). THE SEVERITY OF THIS PROBLEM IS REDUCED IN THE R&R APPROACH, WHICH FOCUSES ON A SINGLE EXPLANATORY VARIABLE. IT IS MORE AN ISSUE WITH THE HECKMAN APPROACH, WHICH FOCUSES ON MODELS CONTAINING MULTIPLE EXPLANATORY VARIABLES.

(IN THIS PRESENTATION, NO ATTEMPT IS MADE TO DETERMINE THE CAUSES OF EFFECTS. IT IS CONCERNED WITH ESTIMATION OF THE EFFECTS OF CAUSES. THE CAUSES OF EFFECTS WILL BE IDENTIFIED (BASED ON SUBJECTIVE VIEWS ABOUT NATURE) IN THE CAUSAL MODELS. THE STATISTICAL ANALYSIS IS USED SOLELY TO ESTIMATE THE MAGNITUDE OF CAUSAL EFFECTS IDENTIFIED IN THE CAUSAL MODEL. (SEE DAWID’S ARTICLE FOR DISCUSSION OF THE STATISTICAL DECISION PROBLEM OF DECIDING THE CAUSE (“TREATED” OR “UNTREATED”) OF A PARTICULAR OUTCOME, GIVEN THE OBSERVED VALUE FOR THAT OUTCOME. THE APPROACH CENTERS ON ESTIMATING THE PROBABILITY DISTRIBUTION OF THE INDIVIDUAL TREATMENT EFFECT, GIVEN THE OBSERVED OUTCOME. THE DIFFICULTY IS THAT THIS DISTRIBUTION DEPENDS ON THE PARAMETER ρ THAT WAS MENTIONED EARLIER (ρ = σ²_U/(σ²_U+ σ²_E)), AND THE VALUE OF ρ DEPENDS ON THE VARIANCE OF THE TREATMENT EFFECT, WHICH, FOR OBSERVATIONAL DATA, IS NOT ESTIMABLE. DAWID CONSIDERS A DECISION RULE CORRESPONDING TO ALTERNATIVE VALUES OF ρ.)

(NOTE THAT ρ CAN BE ESTIMATED FOR AN EXPERIMENTAL DESIGN. THE VARIANCE OF E MAY BE ESTIMATED FROM THE UNTREATED SAMPLE, AND THE VARIANCE OF U+E MAY BE ESTIMATED FROM THE TREATED SAMPLE. THE VARIANCE OF U IS ESTIMATED AS THE DIFFERENCE IN THESE VARIANCES. ρ MAY THEN BE ESTIMATED. THE PROBLEM THAT ARISES WITH OBSERVATIONAL DATA IS THAT TREATMENT MAY BE CORRELATED WITH THE MODEL ERROR TERM, SO THAT THE VARIANCE OF E MAY NOT BE THE SAME FOR THE TREATED AND UNTREATED SAMPLE. HENCE, UNLIKE THE CASE OF A RANDOMIZED EXPERIMENT, IT IS NOT POSSIBLE TO OBTAIN AN UNBIASED ESTIMATE OF THE VARIANCE OF E FOR UNTREATED SAMPLE, USING OBSERVATIONAL DATA.)

IN WHAT FOLLOWS, ASSUMPTIONS WILL BE MADE ABOUT CONDITIONAL INDEPENDENCE OF (Y₀, Y₁) AND W, GIVEN COVARIATES. (NOTE THAT THIS IS NOT SAYING THAT Y₀ AND Y₁ ARE CONDITIONALLY INDEPENDENT: IT IS SAYING THAT THE JOINT DISTRIBUTION OF (Y₀, Y₁) AND W ARE CONDITIONALLY INDEPENDENT, GIVEN X – WHATEVER THE JOINT DISTRIBUTION OF (Y₀, Y₁) MAY BE FOR THAT VALUE OF X.) AS MENTIONED ABOVE, WITH RANDOM TREATMENT EFFECTS, THERE IS ALWAYS A CORRELATION BETWEEN Y₀ AND Y₁ OVER THE ENTIRE POPULATION, EVEN WITH RANDOM ASSIGNMENT TO TREATMENT. EVEN CONDITIONAL ON X, Y₀ AND Y₁ ARE CORRELATED, IF THE TREATMENT EFFECT IS RANDOM. (NOTE THAT IF (Y₀,Y₁) IS INDEPENDENT OF W GIVEN COVARIATES X, THEN EACH OF Y₀ AND Y₁ IS SEPARATELY INDEPENDENT OF W GIVEN COVARIATES X.)

IN ORDER TO HAVE CONDITIONAL INDEPENDENCE OF Y₀ AND Y₁ (WHICH WE ARE NOT ASSERTING), IT WOULD BE NECESSARY TO CONDITION NOT ONLY ON ALL VARIABLES THAT AFFECT ASSIGNMENT TO TREATMENT OR ON ALL VARIABLES OTHER THAN TREATMENT THAT AFFECT OUTCOME, BUT ALSO ON THE RANDOM COMPONENT OF TREATMENT (I.E., ON U) AS WELL – AND U IS UNOBSERVED! UNLESS THIS IS DONE, THERE WILL ALWAYS BE A CORRELATION BETWEEN Y₀ AND Y₁ (WITH A (NONZERO) RANDOM TREATMENT EFFECT) – THEY WILL NOT BE CONDITIONALLY INDEPENDENT.

SOME ADDITIONAL REMARKS COMPARING THE R&R APPROACH TO THE PEARL APPROACH

THE TERMINOLOGY USED BY PEARL IS DIFFERENT FROM THAT USED BY R&R. R&R SIMPLY DEFINE THE CAUSAL EFFECT RELATIVE TO THE STATISTICAL MODEL THAT DESCRIBES THE OBSERVED DATA. THEY DO NOT SPECIFY A COMPLETE CAUSAL MODEL. THEY IDENTIFY CAUSAL EFFECTS IN TERMS OF CONDITIONAL-INDEPENDENCE ASSUMPTIONS IMPOSED ON THIS MODEL. PEARL IDENTIFIES AN EXPLICIT CAUSAL MODEL AND DEFINES THE CAUSAL EFFECTS RELATIVE TO THIS MODEL.

A MAJOR PROBLEM ASSOCIATED WITH THE R&R APPROACH IS THE FOLLOWING: IF THE CAUSAL MODEL IS NOT EXPLICITLY IDENTIFIED, HOW IS IT POSSIBLE TO JUSTIFY THE CONDITIONAL-INDEPENDENCE ASSUMPTIONS REQUIRED TO INSURE THAT CERTAIN ESTIMATES ARE IN FACT CAUSAL ESTIMATES? PEARL EXPLICITLY IDENTIFIES A CAUSAL MODEL, AND IT IS POSSIBLE TO DEDUCE WHETHER CONDITIONAL INDEPENDENCE HOLDS FROM THE MODEL.

AN ESSENTIAL REQUIREMENT OF THE R&R APPROACH TO ESTIMATE E(Y₁) – E(Y₀) IS THAT THE JOINT DISTRIBUTION OF (Y₀, Y₁) BE INDEPENDENT OF TREATMENT (W), GIVEN COVARIATES X. THIS IS THE ESSENTIAL CONDITIONAL INDEPENDENCE ASSUMPTION. FOR THE PEARL APPROACH, THE CORRESPONDING REQUIREMENT IS THAT THE ERROR TERM OF THE DISTRIBUTION OF Y|X BE INDEPENDENT OF X (AND ALL OTHER MODEL VARIABLES).

IN THE R&R APPROACH TO CAUSAL MODELING, THE POTENTIAL OUTCOMES FOR AN EXPERIMENTAL UNIT ARE USUALLY DENOTE BY SUBSCRIPTS (OR SUPERSCRIPTS), SUCH AS Y_0i AND Y_1i FOR THE i-th UNIT. IN THE PEARL APPROACH, THE POTENTIAL OUTCOMES ARE DERIVED FROM THE SYMBOLIC REPRESENTATION OF THE CAUSAL MODEL:

P(Y₀) = P(Y|do(X=0))

P(Y₁) = P(Y|do(X=1)).

OF COURSE, PEARL DOES NOT RESTRICT THE MODEL TO THE BINARY CASE, AND IN GENERAL, WE WOULD WRITE

P(Y_x) = P(Y|do(X=x)).

THE R&R COUNTERFACTUAL MODEL IS EQUIVALENT TO A SPECIAL CASE OF PEARL'S CAUSAL MODEL. THE R&R CAUSAL MODEL FOCUSES ON A BINARY CAUSAL (EXPLANATORY) VARIABLE – TREATED AND UNTREATED – AND CAN EASILY BE EXTENDED TO THE CASE OF MORE THAN TWO DISCRETE RESPONSES. IN THE PEARL MODEL, THE EXPLANATORY VARIABLE MAY BE CONTINUOUS OR DISCRETE. THE CAUSAL EFFECT IS DEFINED AS A PROBABILITY DISTRIBUTION, NOT AS THE EXPECTED VALUE OF A DIFFERENCE BETWEEN EXPECTED VALUES FOR TWO DIFFERENT VALUES OF THE CONDITIONING VARIABLE.

IN BOTH MODELS, THERE IS ONE FACTUAL (OBSERVED) VALUE FOR EACH EXPERIMENTAL UNIT, AND ALL OTHER POTENTIAL VALUES ARE COUNTERFACTUAL (UNOBSERVED). IN THE (BINARY) R&R APPROACH, THE CAUSAL EFFECT IS DEFINED AS THE DIFFERENCE BETWEEN THE EXPECTED VALUES OF THE TREATED (W=1) AND UNTREATED (W=0) POTENTIAL OUTCOMES:

E(Y₁) – E(Y₀).

IN THE PEARL APPROACH, THE CAUSAL EFFECT IS DEFINED AS THE ENTIRE RESPONSE DISTRIBUTION, P(Y|do(X=x)). IN PEARL'S NOTATION, THE PRECEDING QUANTITY IS

E(Y₁) – E(Y₀) = E(Y|do(X=1)) – E(Y|do(X=0)).

4.7. THE NEYMAN-RUBIN CAUSAL MODEL / POTENTIAL OUTCOMES MODEL / COUNTERFACTUALS MODEL

WE “DEFINED” THE ATE EARLIER AS THE EXPECTED EFFECT OF TREATMENT FOR A UNIT RANDOMLY SELECTED FROM THE POPULATION (A MORE USEFUL DEFINITION, WHICH DOES NOT CONFLATE THE CONCEPT OF EFFECT WITH A PROCESS FOR ESTIMATING IT, WILL SOON BE PRESENTED). THAT IS, IT IS THE AVERAGE DIFFERENCE IN OUTCOME BETWEEN TREATED AND UNTREATED UNITS, IF THE UNITS ARE RANDOMLY SELECTED FROM THE POPULATION OF INTEREST AND TREATMENT IS ASSIGNED AT RANDOM TO THE SELECTED UNITS. FOR EXPERIMENTAL DESIGNS, THESE CONDITIONS HOLD, AND SO THE ATE IS THE OBSERVED MEAN EFFECT OF TREATMENT. (FOR A COMPLEX DESIGN, THE FORMULAS MAY BE COMPLICATED, BUT, FOR AN APPROPRIATE DESIGN THE EFFECT IS ESTIMABLE.) AS DISCUSSED EARLIER, THE KEY REQUIREMENT (FOR “RANDOM ASSIGNMENT TO TREATMENT”) IS THAT THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS KNOWN OR IS A CONSTANT, I.E., IT DOES NOT DEPEND ON UNOBSERVED VARIABLES (IT MAY DEPEND ON OBSERVED VARIABLES, SUCH AS IN THE CASE IN WHICH THE ASSIGNMENT PROBABILITY DIFFERS BY STRATUM, LEADING TO DIFFERING PROPORTIONS OF TREATED AND UNTREATED UNITS IN DIFFERENT STRATA).

FOR SIMPLICITY, IN PRESENTING THE BASIC CONCEPTS OF THE NEYMAN-RUBIN APPROACH, WE SHALL CONSIDER THE SINGLE-ROUND SITUATION. THIS IS ADMITTEDLY ARTIFICIAL, BECAUSE FOR THE APPROACH TO WORK WELL IN PRACTICE IT IS NECESSARY TO HAVE TWO ROUNDS OF DATA (TO ELIMINATE BASELINE BIAS AND THE EFFECT OF TIME-INVARIANT UNOBSERVED VARIABLES).

THE SINGLE-ROUND CASE

RESPONSE MODEL:

For each experimental unit (suppressing the observation index i):

OR, IF

Y₀ AND Y₁ ARE CALLED POTENTIAL OUTCOMES. FOR EACH EXPERIMENTAL UNIT, ONLY ONE OF THEM MAY BE OBSERVED. THE UNOBSERVED ONE IS CALLED A COUNTERFACTUAL FOR THE OBSERVED ONE, AND VICE-VERSA.

THE INDIVIDUAL-LEVEL CAUSAL EFFECT IS δ_i = Y_1i – Y_0i. THIS INDIVIDUAL-LEVEL EFFECT MAY NEVER BE OBSERVED, SINCE ONLY ONE OF THE TWO OUTCOMES Y_1i OR Y_0i MAY BE OBSERVED.

NOTE THAT THIS MODEL IS MORE GENERAL THAN THE LINEAR MODEL USED IN THE EARLIER SIMULATION EXAMPLE (SINCE IT ALLOWS FOR COMPLETE HETEROGENEITY OF EFFECT AT THE ULTIMATE SAMPLING UNIT).

A STANDARD GOAL IN AN EVALUATION STUDY IS TO ESTIMATE THE AVERAGE TREATMENT EFFECT (ATE):

ATE = δ = E(Y₁ – Y₀) = E(Y₁) – E(Y₀) = μ₁ – μ₀ (RECALL, CAPITAL LETTERS INDICATE RANDOM VARIABLES)

OR THE AVERAGE TREATMENT EFFECT ON THE TREATED (ATT):

ATT = E(Y₁ – Y₀ | W=1)

OR THE AVERAGE TREATMENT EFFECT ON THE UNTREATED (ATU):

ATU = E(Y₁ – Y₀ | W=0).

THE DEFINITIONS OF ATE, ATT AND ATU PRESENTED ABOVE ARE THE TECHNICAL DEFINITIONS OF ATE, ATT AND ATU. THESE DEFINITIONS ARE SPECIFIED IN TERMS OF EXPECTATIONS OF THE MODEL OF POTENTIAL OUTCOMES (NOT IN TERMS OF A RANDOMIZATION PROCESS FOR ESTIMATING THEM).

IMPACT MAY BE MEASURED IN A NUMBER OF WAYS, INCLUDING THE ATE, ATT, ATU, THE PARTIAL TREATMENT EFFECT, THE MARGINAL TREATMENT EFFECT, AND THE LOCAL AVERAGE TREATMENT EFFECT (LATE). WHILE THOSE OTHER MEASURES ARE OF INTEREST IN ANALYSIS, THEY ARE NOT OF INTEREST IN THIS PRESENTATION ON MATCHING AND DESIGN (SINCE THEY WOULD NOT CHANGE THE ESSENCE OF THE PRESENTATION). (FOR A DISCUSSION OF THE MARGINAL TREATMENT EFFECT, SEE HECKMAN (OP. CIT. 2007). FOR A DISCUSSION OF THE LATE, SEE ANGRIST AND PISCHKE (OP. CIT.) OR LEE (OP. CIT.). ADDITIONALLY, SEE “SIMPLE ESTIMATORS FOR TREATMENT PARAMETERS IN A LATENT-VARIABLE FRAMEWORK” BY JAMES HECKMAN, JUSTIN L. TOBIAS AND EDWARD VYTLACIL, THE REVIEW OF ECONOMICS AND STATISTICS, AUGUST 2003, 85(3), PP. 748-755.)

PEARL DEFINES THE CAUSAL EFFECT AS THE PROBABILITY DISTRIBUTION OF AN OUTCOME VARIABLE, y, GIVEN AN INPUT VARIABLE, x, WHERE x IS INDEPENDENTLY SAMPLED. R&R DEFINE THE CAUSAL EFFECT AS THE DIFFERENCE IN THE EXPECTED VALUES OF THE TREATED AND UNTREATED UNITS (I.E., FOR TWO DIFFERENT VALUES OF x), WHEN TREATMENT IS INDEPENDENTLY ASSIGNED.

THERE ARE STRONG REASONS TO PREFER THE DIFFERENCE AS A MEASURE OF IMPACT IN COUNTERFACTUAL INFERENCE, RATHER THAN SOME OTHER MEASURE, SUCH AS A RATIO (Y₁/Y₀). THE REASON IS THAT IN THIS CASE THE ANALYSIS MAY FOCUS ON THE MARGINAL DISTRIBUTIONS OF THE TWO COUNTERFACTUAL OUTCOMES, AND QUANTITIES OF INTEREST ARE ESTIMABLE. EVEN THOUGH BOTH POTENTIAL OUTCOMES CANNOT BE OBSERVED ON THE SAME UNIT, THE PROPERTIES OF THE TWO MARGINAL DISTRIBUTIONS (SUCH AS THEIR MEANS) ARE ESTIMABLE. FOR SOME IMPACT MEASURES, SUCH AS RATIOS (Y₁/Y₀), THE JOINT DISTRIBUTION OF THE POTENTIAL OUTCOMES BECOMES INVOLVED, AND IT IS NECESSARY TO MAKE ASSUMPTIONS ABOUT THE JOINT DISTRIBUTION, BEYOND CONDITIONAL INDEPENDENCE OF THAT DISTRIBUTION AND W GIVEN X.

THE PROBLEM IN ESTIMATING THE ATE IS THAT FOR ANY PARTICULAR SAMPLE UNIT WE CAN OBSERVE ONLY ONE OF THE TWO RESPONSES (VALUES Y₀ AND Y₁), SINCE WE MAY OBSERVE THE UNIT EITHER UNDER TREATMENT CONDITIONS OR UNDER NON-TREATMENT CONDITIONS, BUT NOT BOTH. THAT IS, WE CANNOT OBSERVE Y_0i AND Y_1i FOR THE i-th INDIVIDUAL, AND, FOR EXAMPLE, CALCULATE THE MEAN OF THE INDIVIDUAL DIFFERENCES δ_i = Y_1i – Y_0i.

NOTE THAT IT IS EASY TO ESTIMATE THE OBSERVED TREATMENT EFFECT, OTE:

OTE = E(Y | W = 1) – E(Y | W=0) =

IF WE HAVE RANDOMIZED ASSIGNMENT TO TREATMENT, THEN IS AN UNBIASED ESTIMATE OF μ₁ AND IS AN UNBIASED ESTIMATE OF μ₀, SO THAT THE OBSERVED OTE IS AN UNBIASED ESTIMATE OF THE POPULATION OTE, µ₁ - µ₀.

OTHERWISE:

SINCE, WHERE p = P(W=1),

FROM WHICH

OTE – E(δ) = E(Y | W=1) – E(Y | W=0) – E(δ)

= E(Y₁ | W=1) – E(Y₀ | W=0) – E(δ)

= E(_Y1| W=1) – E(Y₀ | W=0) – pE(Y₁ | W=1) – (1-p)E(Y₁ | W=0) + pE(Y₀ | W=1) + (1-p)E(Y₀ | W=0)

= p[E(Y₀ | W=1) – E(Y₀ | W=0)] (BASELINE BIAS)

+ (1-p)[E(Y₁ | W=1) – E(Y₁ | W=0)] (DIFFERENTIAL-TREATMENT-EFFECT BIAS)

OTE = ATE + BASELINE BIAS + DTE BIAS.

THE COMBINED BIAS (BASELINE + DTE) IS CALLED THE SELECTION BIAS. IT IS THE BIAS OF THE OTE RELATIVE TO ESTIMATING THE ATE.

WE CAN ALSO SHOW:

OTE = E(Y | W=1) – E(Y | W=0)

= E(Y₁ | W=1) – E(Y₀ | W=1) + E(Y₀ | W=1) – E(Y₀ | W=0)

OTE = ATT + BASELINE BIAS.

THIS BIAS (BASELINE ONLY) IS ALSO CALLED THE SELECTION BIAS, BUT IT IS DIFFERENT FROM THE ABOVE DEFINITION OF SELECTION BIAS. IT IS THE BIAS OF THE OTE RELATIVE TO ESTIMATING THE ATT. (RECALL THAT THE BIAS OF AN ESTIMATOR IS ALWAYS RELATIVE TO WHAT IS BEING ESTIMATED. HENCE THE SELECTION BIAS OF THE OTE VARIES, DEPENDING ON WHETHER IT IS CONSIDERED AN ESTIMATE OF THE ATE OR OF THE ATT.)

THE PRECEDING EXPRESSION SHOWS HOW TO ESTIMATE THE ATT: IT IS SIMPLY THE OTE MINUS THE BASELINE BIAS (WHICH CAN BE ESTIMATED – IT IS SIMPLY THE DIFFERENCE IN MEANS BETWEEN THOSE SELECTED FOR TREATMENT AND THOSE NOT SELECTED FOR TREATMENT, PRIOR TO TREATMENT). THIS RESULT SHOWS THAT THE SINGLE-ROUND ESTIMATE OF THE ATT IS USELESS, SINCE IT INCLUDES THE BASELINE BIAS, BUT THAT THE ATT MAY IN GENERAL BE ESTIMATED BY THE OTE FROM A PANEL DESIGN, USING THE DD ESTIMATOR TO REMOVE THE BASELINE BIAS. (BY THE DD ESTIMATOR, WE MEAN THE DOUBLE DIFFERENCE IN THE ESTIMATED MEANS OF THE FOUR DESIGN GROUPS, APPROPRIATELY ESTIMATED, TAKING INTO CORRECT ACCOUNT THE NATURE OF THE SAMPLE DESIGN, SUCH AS STRATIFICATION AND MULTISTAGE SAMPLING.)

NOTE THAT FOR UNBIASED ESTIMATION OF ATT, WE NEED ONLY TO ASSUME THAT THE BASELINE BIAS IS ZERO (I.E., Y₁ – Y₀ MAY BE CORRELATED WITH X). (THIS IS OBVIOUS – WE ARE ESTIMATING IMPACT FOR THOSE SELECTED FOR TREATMENT, HOWEVER THEY WERE SELECTED.)

IF WE HAVE RANDOMIZED ASSIGNMENT TO TREATMENT (I.E., AN EXPERIMENTAL DESIGN), THE RESPONSE (Y₀, Y₁) (I.E., THE ACTUAL AND COUNTERFACTUAL RESPONSES) IS INDEPENDENT OF TREATMENT, W, AND SO

BASELINE BIAS = E(Y₀ | W=1) – E(Y₀ | W=0) = E(Y₀) – E(Y₀) = 0

AND SO, SINCE δ = Y₁ – Y₀ IS ALSO INDEPENDENT OF W,

DTE BIAS = E(δ | W=1) – E(δ | W=0) = E(δ) – E(δ) = 0.

IN THIS CASE ALL THE BIAS COMPONENTS EQUAL ZERO, SO

OTE = ATE = ATT (FOR RANDOMIZED ASSIGNMENT TO TREATMENT).

THE PRECEDING RESULTS SHOW THAT, FOR A QUASI-EXPERIMENTAL DESIGN (ANALYSIS OF OBSERVATIONAL DATA), THE KEY PROBLEM IS TO REDUCE OR ELIMINATE THE DTE BIAS (SINCE THE BASELINE BIAS IS EASILY REMOVED BY DOUBLE DIFFERENCING (IN A PANEL DESIGN)).

THE DTE BIAS IS

(1-p) E(Y₁ | W = 1) – E(Y₁ | W = 0).

IN WORDS, IT IS THE AVERAGE DIFFERENCE BETWEEN THE RESPONSE WHEN TREATED (Y₁) BETWEEN THE TREATED POPULATION UNITS AND THE UNTREATED POPULATION UNITS (TIMES A CONSTANT, 1 – p). (THIS, OF COURSE, WOULD BE EQUAL TO ZERO IF THE UNITS HAD BEEN RANDOMLY ASSIGNED TO TREATMENT, AS IN AN EXPERIMENTAL DESIGN.) THE TERM 1 – p IS THE FRACTION OF UNITS NOT TREATED (SINCE p = P(W = 1)).

THE PROBLEM WITH THE PRECEDING EXPRESSION IS THAT SINCE Y₁ IS OBSERVABLE WHEN W = 1 BUT NOT WHEN W = 0, THE FIRST TERM IS KNOWN, BUT THE SECOND TERM IS NOT. SO THE BIAS IS NOT KNOWN.

THE TWO-ROUND CASE

WE SHALL NOW ILLUSTRATE THE TWO-ROUND SITUATION.

WE SHALL NOT DESCRIBE THIS TO THE LEVEL OF DETAIL USED FOR THE SINGLE-ROUND CASE JUST DESCRIBED, EVEN THOUGH THE TWO-ROUND CASE IS THE ONE THAT OCCURS MORE IN PRACTICE (TWO ROUNDS ARE NECESSARY TO REMOVE THE BASELINE BIAS, AS WELL AS THE EFFECT OF TIME-INVARIANT UNOBSERVED VARIABLES (WHICH ARE OFTEN PRESENT IN PROGRAM EVALUATIONS)). THE REASON WHY THE SINGLE-ROUND CASE IS EXAMINED IN DETAIL IS THAT IT IS SUBSTANTIALLY SIMPLER, AND AN EASIER CONTEXT IN WHICH TO DESCRIBE BASIC CONCEPTS. THE TWO-ROUND CASE IS DESCRIBED IN GREATER DETAIL IN A PRESENTATION ON ANALYSIS FOR EVALUATION.

EXAMPLE (SELECTION FOR TREATMENT BASED ON SEX):

SUPPOSE THAT SELECTION FOR TREATMENT IS MADE BASED ON SEX, AND THAT THE DISTRIBUTION OF RESPONSE (Y₀, Y₁) DIFFERS FOR MALES AND FEMALES. (IN THIS CASE, X IS A SCALAR RANDOM VARIABLE, X, E.G., SEX CODED AS X = 0 FOR MALES AND X = 1 FOR FEMALES.) THE SITUATION IS ILLUSTRATED IN FIGURE 15.

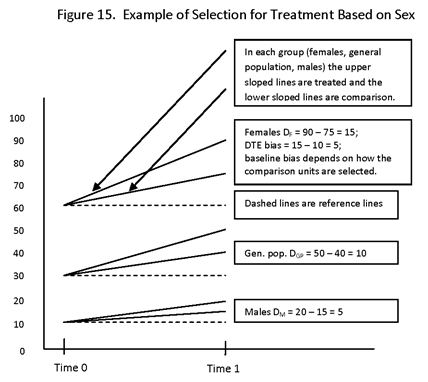
CLEARLY, IF SELECTION FOR TREATMENT IS BASED ON SEX AND SEX IS NOT TAKEN INTO ACCOUNT, THE IMPACT ESTIMATE FOR THE ENTIRE POPULATION WILL BE SERIOUSLY BIASED.

IN THE ILLUSTRATION, IT IS DEPICTED THAT SELECTION IS BIASED IN THE EXTREME (FOR ESTIMATING THE ATE OVER THE GENERAL POPULATION) BY SELECTING ONLY FEMALES FOR TREATMENT. THE SIZE OF THE BASELINE BIAS DEPENDS ON HOW THE COMPARISON SAMPLE IS SELECTED. IF ONLY FEMALES ARE SELECTED AND THEN SOME OF THESE ARE RANDOMLY ASSIGNED TO TREATMENT, THE BASELINE BIAS WOULD BE ZERO. IF THE CONTROLS WERE SELECTED FROM THE GENERAL POPULATION, THEN THE BASELINE BIAS WOULD BE EQUAL TO THE BASELINE DIFFERENCE BETWEEN THE TREATED AND GENERAL POPULATIONS (60 – 30 = 30 IN THE EXAMPLE IN THE FIGURE). IN EITHER CASE, THE DOUBLE-DIFFERENCE ESTIMATOR WOULD REMOVE THE BASELINE BIAS, BUT NOT THE DIFFERENTIAL-TREATMENT-EFFECT (DTE) BIAS.

THE DTE BIAS IS THE BIAS RESULTING FROM THE POSSIBILITY THAT THE RESPONSE TO TREATMENT (Y₁ OR Y₀) MAY HAVE A DIFFERENT DISTRIBUTION FOR TREATED AND UNTREATED UNITS (I.E., IN THE FIGURE, THE SLOPES OF THE LINES DIFFER FOR TREATED AND UNTREATED UNITS). IN THIS EXAMPLE, THE AVERAGE FEMALE RESPONSE TO TREATMENT IS 15, THE AVERAGE MALE RESPONSE IS 5, AND THE AVERAGE GENERAL-POPULATION RESPONSE IS 10. IF ONLY FEMALES ARE SELECTED FOR TREATMENT, THE RESPONSE TO TREATMENT WILL BE ESTIMATED TO BE 15 RATHER THAN 10 (FOR THE GENERAL POPULATION). HENCE, IN THIS EXAMPLE (WHERE ONLY FEMALES ARE SELECTED), THE DTE IS 15 – 10 = 5.

SUPPOSE THAT SELECTION FOR TREATMENT IS BASED (SOLELY) ON SEX, BUT THAT WITHIN EACH SEX CATEGORY, ASSIGNMENT TO TREATMENT IS RANDOM (I.E., WITHIN EACH SEX GROUP THE PROBABILITY OF SELECTION IS UNIFORM FOR THE TREATMENT AND COMPARISON GROUPS). IN THIS CASE, WE HAVE CONDITIONAL INDEPENDENCE OF RESPONSE, (Y₀, Y₁), AND TREATMENT, W, GIVEN SEX (X), AND WE CAN THEREFORE CONSTRUCT AN UNBIASED ESTIMATE OF IMPACT (ATE) WITHIN EACH SEX CATEGORY (I.E., FOR EACH SEX CATEGORY), E.G., USING THE DOUBLE-DIFFERENCE ESTIMATE. WE MAY THEN CONSTRUCT AN UNBIASED ESTIMATE OF THE POPULATION IMPACT BY FORMING A WEIGHTED AVERAGE OF THE TWO SEX-CATEGORY ESTIMATES.

THE PRECEDING ILLUSTRATION IS EXTREME IN THAT IT DEPICTS SELECTING ALL FEMALES AND NO MALES. IT WOULD NOT BE POSSIBLE TO ESTIMATE IMPACT OVER THE ENTIRE POPULATION (OF MALES AND FEMALES) IN THIS SITUATION, WHERE NO MALES ARE TREATED. IN ORDER THAT THE MEANS MAY BE ESTIMATED FOR ALL DESIGN GROUPS (MALES BEFORE, MALES AFTER, FEMALES BEFORE, FEMALES AFTER) IT IS ASSUMED THAT AT LEAST A SMALL PERCENTAGE OF MALES IS SELECTED. THIS MAY BE IMPLEMENTED IN TWO WAYS: (1) SELECT A RANDOM SAMPLE FROM EACH OF THE TWO SEX POPULATIONS; OR (2) SELECT A RANDOM SAMPLE OF INDIVIDUALS FROM THE POPULATION, AND ASSIGN EACH TO TREATMENT WITH A PROBABILITY THAT DEPENDS ONLY ON SEX. THEN WE MAY CONSTRUCT AN UNBIASED ESTIMATE OF THE ATE FOR THE ENTIRE POPULATION BY CALCULATING THE WEIGHTED AVERAGE OF THE ATEs FOR THE TWO SEX CATEGORIES, WEIGHTED BY THE PROPORTION OF THE POPULATION IN THE TWO CATEGORIES.

FOR EXAMPLE, LET US SUPPOSE THAT FOR RANDOMLY SELECTED INDIVIDUALS THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS .8 FOR FEMALES AND .2 FOR MALES.

SYMBOLICALLY:

WHERE

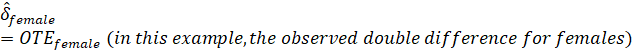
AND P(male) AND P(female) DENOTE THE PROPORTIONS OF MALES AND FEMALES IN THE POPULATION.

IN GENERAL, IF WE CAN STRATIFY SO THAT, WITHIN EACH STRATUM, ANY OF THE FOLLOWING CONDITIONS HOLD:

· SELECTION FOR TREATMENT IS RANDOM (AS IN THE PRECEDING EXAMPLE)

· THE POTENTIAL OUTCOMES (Y₀, Y₁) ARE INDEPENDENT OF TREATMENT (W)

· THE MEAN OUTCOMES (E(Y₀) AND E(Y₁), FOR TREATED AND UNTREATED UNITS) ARE INDEPENDENT OF W,

THEN WE CAN CONSTRUCT AN UNBIASED ESTIMATE OF IMPACT (ATE) FOR EACH STRATUM, AND WE CAN CONSTRUCT AN UNBIASED ESTIMATE OF ATE OVERALL BY FORMING A WEIGHTED AVERAGE OF THE STRATUM ATEs:

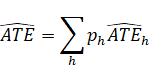
WHERE p_h DENOTES THE PROPORTION OF THE POPULATION IN STRATUM h. IN GENERAL, IT IS DIFFICULT TO TEST ANY OF THE THREE CONDITIONS DIRECTLY. (IN THIS EXAMPLE, THEY WERE FORMED BY CONSTRUCTION.)

EARLIER IN THIS PRESENTATION, WE PRESENTED EXAMPLES OF ESTIMATING ATE BY CONDITIONING EITHER ON THE PROBABILITY OF SELECTION OR ON VARIABLES THAT AFFECT OUTCOME. WE CONSTRUCTED THE PRECEDING EXAMPLE SO THAT THE PROBABILITY OF ASSIGNMENT TO TREATMENT DEPENDED ONLY ON SEX, AND THE OUTCOME DEPENDED ONLY ON SEX, SO, FOR THIS PARTICULAR EXAMPLE, BOTH APPROACHES ARE IDENTICAL.

TWO SPECIFIC APPROACHES TO ESTIMATION OF THE ATE AND ATT FOR QEDs

IF IT IS KNOWN THAT SELECTION IS ON OBSERVABLES, THEN THE PRECEDING METHODOLOGY APPLIES (BY STRATIFYING ON THE OBSERVABLES AFFECTING SELECTION, FORMING THE DIFFERENCE FOR EACH STRATUM, AND FORMING THE WEIGHTED AVERAGE OF THE DIFFERENCE (WHERE THE STRATUM WEIGHTS ARE THE PROPORTION OF THE POPULATION IN EACH STRATUM)). IN MANY SITUATIONS, HOWEVER, IT IS NOT CLEAR EXACTLY HOW UNITS WERE SELECTED FROM THE POPULATION OF INTEREST, OR HOW THEY WERE ASSIGNED TO TREATMENT.

ONE APPROACH TO SOLUTION IS TO ASSUME THAT (Y₀, Y₁) IS INDEPENDENT OF W GIVEN A SET OF COVARIATES, X, AND THEN FIND A PRACTICAL METHOD OF STRATIFYING ON X OR ON A (SIMPLER, LOW DIMENSIONAL) FUNCTION OF X. NEEDLESS TO SAY, IT IS NOT ACCEPTABLE TO SIMPLY MAKE THIS ASSUMPTION OF CONDITIONAL INDEPENDENCE WITHOUT CONSIDERATION OF AN EXPLICIT CAUSAL MODEL. THERE ARE A NUMBER OF STATISTICAL APPROACHES TO CAUSAL ANALYSIS (SEVERAL OF THESE WILL BE LISTED, LATER). FOR THE PURPOSES OF THIS PRESENTATION ON MATCHING (TO CONSTRUCT GENERAL GUIDELINES FOR DESIGN AND MATCHING FOR IMPACT EVALUATION STUDIES), IT IS SUFFICIENT TO FOCUS ON JUST TWO OF THEM: THE ROSENBAUM-RUBIN (R&R) APPROACH AND THE HECKMAN APPROACH.

THE ROSENBAUM-RUBIN (R&R) APPROACH RELIES ON SPECIFICATION OF THE VARIABLES (COVARIATES) THAT AFFECT SELECTION FOR TREATMENT. THESE VARIABLES MUST ALL BE OBSERVED. THE HECKMAN APPROACH RELIES ON SPECIFICATION OF VARIABLES THAT AFFECT BOTH SELECTION AND OUTCOME. A PRINCIPAL ADVANTAGE OF THE HECKMAN APPROACH IS THAT IT MAKES ALLOWANCE FOR SELECTION ON UNOBSERVED VARIABLES UNDER CERTAIN CONDITIONS. (IT MAY ALSO APPLY TO THE CASE OF MUTUAL (SIMULTANEOUS) CAUSATION.) IF SELECTION FOR TREATMENT IS BASED ON OBSERVABLES, THEN EITHER APPROACH IS APPLICABLE AND BOTH ARE SIMILAR. IF SELECTION FOR TREATMENT IS BASED ON UNOBSERVABLES, THEN THE R&R APPROACH DOES NOT APPLY, BUT THE HECKMAN APPROACH MAY.

THE HECKMAN APPROACH FOCUSES MORE ON REGRESSION ADJUSTMENT THAN THE R&R APPROACH. AS DISCUSSED EARLIER, IMPACT ESTIMATION IS FACILITATED BY MATCHING AND BY REGRESSION ADJUSTMENT, OR BOTH, BUT IT IS NOT REQUIRED TO DO BOTH. BECAUSE THE R&R APPROACH PLACES LESS EMPHASIS ON REGRESSION ADJUSTMENT, IT USUALLY PLACES MORE EMPHASIS ON MATCHING. (AS DISCUSSED, IF THE MATCHING MODEL IS CORRECT, THERE IS NO NEED FOR REGRESSION ADJUSTMENT (TO PRODUCE UNBIASED ESTIMATES OF IMPACT), AND VICE VERSA.)

ALTHOUGH SIMILAR IN ESSENTIAL ASPECTS, THESE TWO APPROACHES REPRESENT DIFFERENT QUITE DIFFERENT APPROACHES TO THE PROBLEM OF ESTIMATING IMPACT. (THE HECKMAN APPROACH IS MORE SIMILAR TO THE PEARL APPROACH, SINCE IT IS MORE DETAILED AND EXPLICIT IN SPECIFYING A CAUSAL MODEL.) THE PURPOSE OF THIS PRESENTATION IS TO DISCUSS MATCHING IN EVALUATION DESIGN. BY USING TWO RATHER DIFFERENT APPROACHES TO IMPACT ESTIMATION, IT IS INTENDED TO ACHIEVE BROAD-BASED RECOMMENDATIONS ON MATCHING.

BOTH APPROACHES ARE BASED ON ESTIMATING THE PROBABILITY OF ASSIGNMENT TO TREATMENT. IF THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS 0 OR 1 FOR SOME SAMPLE UNITS, THEN THESE APPROACHES DO NOT APPLY.

THE DEVELOPMENT OF AN ANALYTICAL SURVEY DESIGN (FOR ASSESSMENT OF IMPACT) REQUIRES CONSIDERATION OF A CAUSAL MODEL. THE DESIGN SHOULD BE CONFIGURED TO INCREASE THE PRECISION AND POWER, AND DECREASE THE BIAS, OF THE IMPACT ESTIMATES THAT WILL BE BASED ON THE COLLECTED DATA. THE DISCUSSION THAT FOLLOWS WILL INDICATE HOW CONSIDERATION OF THE APPROACH TO CAUSAL MODELING (R&R AND HECKMAN) AFFECTS THE DESIGN OF SURVEYS FOR IMPACT EVALUATION.

FOR ESTIMATING THE ATE BOTH THE R&R AND HECKMAN APPROACHES MAKE USE OF DATA FOR WHICH THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS NOT EQUAL TO 0 OR 1 (FOR ESTIMATION OF ATT, NOT EQUAL TO 1). IF THE PROBABILITY OF ASSIGNMENT TO TREATMENT IS EQUAL TO 0 OR 1 JUST FOR A SMALL PORTION OF THE SAMPLE, A MODEL-BASED ESTIMATE OF THE METHODS MAY REASONABLY APPLY. IF A LARGE PORTION OF THE DATA HAVE PROBABILITIES EQUAL TO 0 OR 1 (E.G., IN A CONDITIONAL CASH TRANSFER PROGRAM, IN WHICH UNITS ARE ASSIGNED TO TREATMENT BY A DETERMINISTIC ELIGIBILITY CRITERION (SCORE)), THESE METHODS DO NOT APPLY. IN SUCH CASES, MODEL-BASED ESTIMATES (EMPLOYING ADDITIONAL ASSUMPTIONS) ARE USED (SUCH AS REGRESSION-DISCONTINUITY DESIGN).

ESTIMATION OF THE ATE BY AVERAGING OVER COVARIATES AFFECTING SELECTION FOR TREATMENT

IN THE PRECEDING, WE HAVE DISCUSSED ESTIMATING CAUSAL EFFECTS BY CONDITIONING OVER A VARIETY OF SETS OF VARIABLES. IN MUCH OF THE DISCUSSION THAT FOLLOWS, WE WILL RESTRICT THE DISCUSSION TO ESTIMATORS THAT CONDITION ON VARIABLES THAT AFFECT SELECTION FOR TREATMENT.

THE R&R APPROACH TO CAUSAL MODELING FOR OBSERVATIONAL DATA IS TO IDENTIFY COVARIATES, X, FOR WHICH SELECTION FOR TREATMENT (W) DEPENDS, AND TO ESTIMATE THE IMPACT AS

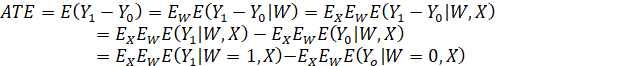
THAT IS, AS LONG AS WE CONDITION ON X, THE DIFFERENCE BETWEEN THE MEANS OF THE TREATED AND UNTREATED UNITS AT THAT VALUE OF X IS AN UNBIASED ESTIMATE OF ATE AT THAT POINT (VALUE OF X). WE SIMPLY AVERAGE THE OBSERVED VALUES, Y, OVER X TO OBTAIN THE IMPACT FOR THE ENTIRE POPULATION. (NOTE THAT THE Y₁ – Y₀ TERMS IN THE FIRST SEVERAL TERMS OF THE ABOVE ARE NOT OBSERVABLE ON INDIVIDUAL UNIT (SINCE BOTH Y₁ AND Y₀ MAY NOT BE OBSERVED ON THE SAME UNIT – THIS DOES NOT MATTER, SINCE THE EXPECTATIONS CAN BE SPLIT APART AND ESTIMATED SEPARATELY.)

(THE PRECEDING FORMULA WAS PRESENTED EARLIER, IN SLIGHTLY DIFFERENT NOTATION, IN THE DISCUSSION OF CONDITIONING ON THE SET S OF ALL VARIABLES THAT AFFECT ASSIGNMENT TO TREATMENT.)

THE ONLY REQUIREMENT FOR THIS APPROACH IS THAT THE PROBABILITY OF W = 0 OR W = 1 CANNOT BE ZERO OR ONE, IN WHICH CASE THE CONDITIONAL EXPECTATION WOULD BE UNDEFINED (SINCE THE DENOMINATORS P(W) ARE EQUAL TO ZERO FOR THOSE CASES).

TO CALCULATE THE EXPRESSION THERE ARE TWO APPROACHES, THE STRATIFICATION APPROACH AND THE REGRESSION OR “ADJUSTMENT” APPROACH. IN THE STRATIFICATION APPROACH, WE SIMPLY STRATIFY OVER X, CALCULATE THE DIFFERENCE IN MEANS WITHIN THE TREATED AND UNTREATED UNITS WITHIN EACH STRATUM, AND CALCULATE THE STRATUM-WEIGHTED ESTIMATE OF THE DIFFERENCES, WHICH IS THE ATE.

FOR THE STRATIFICATION APPROACH, TREATED AND UNTREATED OBSERVATIONS MUST BE PRESENT IN EVERY STRATUM CELL (ALTHOUGH THE STRATA MAY BE DEFINED DIFFERENTLY FOR THE TREATED AND UNTREATED UNITS). FOR THE REGRESSION APPROACH, WE CONSTRUCT TWO REGRESSION MODELS DESCRIBING THE OUTCOME FOR TREATED AND UNTREATED UNITS, ESTIMATE THE DIFFERENCE IN OUTCOME FOR EACH SAMPLE UNIT FROM THESE TWO REGRESSION EQUATIONS, AND AVERAGE OVER THE SAMPLE UNITS. THESE PROCEDURES WERE DESCRIBED EARLIER.

THE FIRST TASK IN APPLYING THE R&R APPROACH IS TO IDENTIFY THE COVARIATES X ON WHICH ASSIGNMENT TO TREATMENT DEPENDS. THIS IS DONE VIA CAUSAL MODELING. THE SECOND TASK IS A COMPUTATIONAL ONE – CONDITIONING OVER X. AS JUST MENTIONED, THERE ARE ALTERNATIVE APPROACHES FOR DOING THIS (STRATIFYING OVER X OR DEVELOPING A REGRESSION MODEL OVER THE VARIABLES OF STRATIFICATION (AND AVERAGING OVER THE SAMPLE)).

THE STRATIFICATION APPROACH ENCOUNTERS SERIOUS DIFFICULTIES. FOR MULTIDIMENSIONAL X, IF WE CROSS-STRATIFY THERE MAY BE MANY STRATA FOR WHICH THERE ARE NO SAMPLE UNITS AT ALL (EITHER TREATED OR UNTREATED), OR SOME OF ONE BUT NOT THE OTHER, IN WHICH CASE THE DIFFERENCE IN STRATIFIED MEANS CANNOT BE CALCULATED. THIS IS AN INSTANCE OF THE “CURSE OF DIMENSIONALITY.”

CONSTRUCTION OF THE REGRESSION MODEL IS ONE WAY OF REDUCING THE DIMENSIONALITY OF THE PROBLEM. WE SHALL NOW DISCUSS ANOTHER METHOD FOR REDUCING THE DIMENSIONALITY OF THE PROBLEM. R&R SHOWED A WAY TO DRAMATICALLY REDUCE THE DIMENSIONALITY OF THE PROBLEM (TO A ONE-DIMENSIONAL PROBLEM). THE REGRESSION APPROACH DISCUSSED EARLIER FOCUSES ON DEVELOPING A REGRESSION MODEL OF OUTPUT. THE R&R APPROACH FOCUSES ON DEVELOPING A REGRESSION MODEL OF THE PROBABILITY OF SELECTION. (WE SHALL LATER DISCUSS AN APPROACH (HECKMAN) THAT DEVELOPS MODELS OF BOTH SELECTION AND OUTPUT.)

[OPTIONAL SECTION ON CONDITIONAL INDEPENDENCE]

THE FOLLOWING PARAGRAPHS PRESENT SOME ADDITIONAL DISCUSSION OF THE TOPIC OF CONDITIONAL INDEPENDENCE.

DEFINITION OF CONDITIONAL INDEPENDENCE OF RESPONSE AND TREATMENT, GIVEN COVARIATES. THE OBSERVED RESPONSE Y = (1-W)Y₀ + WY₁ IS A FUNCTION OF TREATMENT, W, AND SO THE (PROBABILITY) DISTRIBUTION OF THE OBSERVED OUTCOME Y CLEARLY DEPENDS ON W. THE DISTRIBUTION OF THE JOINT POTENTIAL-OUTCOME RESPONSES (Y₀, Y₁) MAY OR MAY NOT BE DEPENDENT ON TREATMENT. FOR EXAMPLE, IF TREATMENT IS RANDOMLY ASSIGNED TO UNITS, THEN THE DISTRIBUTION OF THE POTENTIAL-OUTCOME RESPONSE (Y₀, Y₁) IS INDEPENDENT OF TREATMENT (W). OTHERWISE, WITHOUT RANDOMIZED ASSIGNMENT TO TREATMENT, THE POTENTIAL-OUTCOME RESPONSE (Y₀, Y₁) MAY BE DEPENDENT ON TREATMENT. IT IS POSSIBLE, HOWEVER, THAT EVEN IF THE JOINT DISTRIBUTION OF RESPONSE (Y₀, Y₁) DEPENDS ON TREATMENT (W), IT MAY BE CONDITIONALLY INDEPENDENT OF TREATMENT GIVEN A COVARIATE, X.

NOTE THAT IN MAKING THE STATEMENT THAT THE RESPONSE (Y₀, Y₁) IS INDEPENDENT OF W GIVEN X WE ARE NOT MAKING ANY ASSERTION ABOUT THE JOINT DISTRIBUTION OF (Y₀, Y₁) GIVEN X OTHER THAN IT IS INDEPENDENT OF W, GIVEN X. THE VALUES OF Y₀ AND Y₁ COULD BE VERY CLOSE TOGETHER (SIMILAR) FOR ALL UNITS IN A STRATUM WITH X = x₁, OR THEY COULD BE VERY FAR APART (DIFFERENT) IN ANOTHER STRATUM, X = x₂. THE POINT IS THAT THE JOINT DISTRIBUTION (Y₀, Y₁) IS THE SAME FOR ALL UNITS HAVING THE SAME (PARTICULAR) VALUE OF X (E.G., ALL THE UNITS IN A STRATUM DEFINED BY A PARTICULAR VALUE OF X). (AS MENTIONED EARLIER, IF (Y₀,Y₁) IS INDEPENDENT OF W, THEN Y₀ AND Y₁ ARE EACH, SEPARATELY, INDEPENDENT OF W.)

IN THIS PRESENTATION THE EXPRESSION THAT “THE RESPONSE (Y₀, Y₁) IS INDEPENDENT OF TREATMENT, W, GIVEN OBSERVED COVARIATE X” WILL BE USED A LOT. AT FIRST LOOK, THIS EXPRESSION SEEMS INCORRECT, SINCE IT WOULD SEEM THAT THE RESPONSE IS SURELY DEPENDENT ON TREATMENT. YES, THE OBSERVED RESPONSE, Y (WHICH IS EITHER Y₀ OR Y₁), IS GENERALLY DEPENDENT ON TREATMENT (IF THE INTERVENTION (TREATMENT) HAS ANY EFFECT AT ALL), BUT THE POTENTIAL OUTCOMES, (Y₀, Y₁) MAY OR MAY NOT BE DEPENDENT ON TREATMENT (DEPENDING ON WHAT WE CONDITION ON), EVEN IF THE OBSERVED RESPONSE TO TREATMENT IS STRONG.

INDEPENDENCE OF RESPONSE, (Y₀, Y₁), AND TREATMENT, W, IS DENOTED (Y₀, Y₁) W. CONDITIONAL INDEPENDENCE OF RESPONSE (Y₀, Y₁), AND TREATMENT, W, GIVEN COVARIATE X, IS DENOTED (Y₀, Y₁) W |X. EITHER ONE OF THESE CONDITIONS (INDEPENDENCE OR CONDITIONAL INDEPENDENCE) IS CALLED “UNCONFOUNDEDNESS” OR “IGNORABILITY OF TREATMENT.” THE TERM “IGNORABILITY OF TREATMENT” IS DECLINING IN USE.

(NOTE ON NOTATION: USE OF THE SYMBOL TO SIGNIFY INDEPENDENCE IS PROBLEMATIC. IN JOURNAL ARTICLES AND BOOKS, THE SYMBOL USED TO SIGNIFY INDEPENDENCE IS SIMILAR TO THE SYMBOL , BUT WITH TWO NARROW VERTICAL BARS INSTEAD OF A SINGLE VERTICAL BAR. THAT SYMBOL IS NOT AVAILABLE IN MICROSOFT OFFICE WORD EQUATION (THE PROGRAM USED TO PREPARE THIS PRESENTATION DOCUMENT). THE PROBLEM THAT THIS PRESENTS IS THAT THE SYMBOL IS GENERALLY USED TO DENOTE ORTHOGONALITY (ZERO CROSS PRODUCT, ZERO INNER PRODUCT, ZERO COVARIANCE, ZERO CORRELATION), NOT INDEPENDENCE (WHICH IS A MUCH STRONGER CONDITION). IN THIS PRESENTATION, THE SYMBOL IS ALWAYS USED TO DENOTE INDEPENDENCE, NOT ZERO CORRELATION (ORTHOGONALITY).)

NOTE THAT THE RESPONSE (Y₀,Y₁) MAY DEPEND ON ANY COVARIATE X. WITH RANDOMIZED ASSIGNMENT TO TREATMENT SUCH DEPENDENCE DOES NOT BIAS THE RESULTS (SINCE RANDOMIZED ASSIGNMENT TO TREATMENT ASSURES THAT THE DISTRIBUTION OF ALL COVARIATES IS THE SAME FOR THE TREATMENT AND COMPARISON GROUPS). IT IS WHEN SELECTION DEPENDS ON COVARIATES THAT PROBLEMS ARISE.

NOTE TWO KEY ASPECTS (CONSEQUENCES) OF RANDOMIZED SELECTION FOR TREATMENT (ASSIGNMENT TO TREATMENT):

1. THE PROBABILITY OF SELECTION FOR TREATMENT IS CONSTANT (UNIFORM) WITHIN THE TREATMENT AND CONTROL GROUPS (BUT THE CONSTANT MAY DIFFER FOR THE TWO GROUPS, I.E., THE PROPORTION OF TREATED AND UNTREATED UNITS MAY DIFFER).

2. THE PROBABILITY DISTRIBUTION OF ALL COVARIATES, X, IS THE SAME FOR THE TREATMENT AND CONTROL GROUPS.

THESE TWO FEATURES WILL PLAY A PROMINENT ROLE IN WHAT FOLLOWS.

THE ESSENTIAL PROBLEM WHEN USING QEDs (ANALYSIS OF OBSERVATIONAL DATA) IS WHAT TO DO ABOUT THE ABSENCE OF RANDOMIZED ASSIGNMENT, IN WHICH CASE THE SELECTION BIAS MAY NOT BE ZERO.

WITHOUT RANDOMIZED ASSIGNMENT TO TREATMENT (OR, MORE PRECISELY, LACKING KNOWLEDGE ABOUT ITS PROBABILISTIC NATURE), ASSIGNMENT TO TREATMENT (OR “SELECTION FOR TREATMENT”) MAY DEPEND ON VARIABLES THAT MAY AFFECT OUTCOME. FOR EXAMPLE, A PREFERENCE MAY BE GIVEN TO SELECTION OF FEMALES, AND THE RESPONSE OF FEMALES TO TREATMENT MAY DIFFER FROM THAT OF RANDOMLY SELECTED INDIVIDUALS. IF THE VARIABLES THAT AFFECT SELECTION ARE RELATED TO OUTCOMES OF INTEREST, THEN THE OTE MAY BE A BIASED ESTIMATE OF THE ATE OR THE ATT. IN THIS CASE, THE SINGLE-DIFFERENCE OR DOUBLE-DIFFERENCE ESTIMATORS ARE STILL UNBIASED ESTIMATORS OF THE POPULATION SINGLE-DIFFERENCE OR DOUBLE-DIFFERENCE MEASURES, BUT THESE POPULATION DIFFERENCES ARE NOT UNBIASED ESTIMATORS OF THE AVERAGE TREATMENT EFFECT (THE AVERAGE EFFECT OF TREATMENT ON AN INDIVIDUAL RANDOMLY SELECTED FROM THE POPULATION).

[END OF OPTIONAL SECTION ON CONDITIONAL INDEPENDENCE]

4.8. ALTERNATIVE APPROACHES TO STATISTICAL CAUSAL MODELING AND ANALYSIS

THE PRECEDING DISCUSSION PRESENTED GENERAL THEORY ABOUT ESTIMATION OF CAUSAL EFFECTS, AND PRESENTED EXAMPLES BASED ON AVERAGING OVER (CONDITIONING ON) VARIABLES THAT AFFECT EITHER SELECTION FOR TREATMENT OR OUTCOME. THE FORMULAS PRESENTED WERE “THEORETICAL,” AND ARE NOT USEFUL AS PRACTICAL ESTIMATION PROCEDURES. THIS SECTION WILL DISCUSS TWO PRACTICAL METHODS FOR ESTIMATING CAUSAL EFFECTS.

THERE ARE SEVERAL APPROACHES TO THE NEYMAN-RUBIN METHODOLOGY, WHICH ARE REFERRED TO BY VARIOUS NAMES. THESE APPROACHES DIFFER WITH RESPECT TO THE LEVEL OF DETAIL WITH WHICH CAUSAL RELATIONSHIPS ARE REPRESENTED, AND WITH RESPECT TO THE ASSUMPTIONS MADE. WE SHALL DISCUSS THESE APPROACHES IN THREE MAIN CATEGORIES. THE FIRST APPROACH IS REFERRED TO AS THE BALANCING APPROACH, THE STATISTICAL APPROACH, OR THE ROSENBAUM-RUBIN (R&R) APPROACH. THE SECOND APPROACH IS REFERRED TO AS THE ECONOMETRIC APPROACH, OR THE HECKMAN APPROACH. THE THIRD APPROACH WILL BE ALL OTHER APPROACHES, SUCH AS THE REGRESSION-DISCONTINUITY APPROACH, THE USE OF INSTRUMENTAL VARIABLES, AND TREATMENT OF IMPACT ANALYSIS USING POTENTIAL OUTCOMES AS A “MISSING DATA” PROBLEM.

THE CLASSIFICATION OF STATISTICAL CAUSAL MODELING INTO THESE THREE CATEGORIES IS CONVENIENT FOR THE PURPOSES OF THIS PRESENTATION (DISCUSSING MATCHING). IT IS NOT A CLEAR-CUT CATEGORIZATION. THE THREE CATEGORIES OVERLAP, AND CONTAIN SIMILAR ESTIMATES. THIS CATEGORIZATION IS NOT MUCH USED ANY MORE. IT IS USED IN THIS PRESENTATION SIMPLY FOR CONVENIENCE. WHILE RUBIN, ROSENBAUM AND HECKMAN WERE “PIONEERS” IN STATISTICAL CAUSAL MODELING FOR OBSERVATIONAL DATA, MANY OTHER PEOPLE HAVE WORKED IN THE FIELD SINCE THEY PUBLISHED THEIR SEMINAL WORKS, AND A VARIETY OF APPROACHES TO ESTIMATION OF IMPACT (ALL BASED ON THE NEYMAN-RUBIN MODEL, SOME IMPLEMENTED USING PEARL’S DAG-BASED THEORY TO ESTABLISH ESTIMABILITY) ARE NOW AVAILABLE. MORE COMMON CATEGORIZATIONS ARE MODEL-BASED VERSUS DESIGN-BASED (ALTHOUGH IT COULD BE SAID THAT ALL CAUSAL ESTIMATION IS MODEL-BASED), OR CONDITIONING TO BALANCE VS. CONDITIONING TO ADJUST, OR MATCHING VS. NONMATCHING, OR REGRESSION BASED VS. NON-REGRESSION BASED, OR PARAMETRIC VS. NONPARAMETRIC OR SEMIPARAMETRIC. THERE ARE NOW SO MANY SPECIFIC APPROACHES THAT THEY ARE NO LONGER MUCH PLACED INTO BROAD CATEGORIES.

A DISTINGUISHING FEATURE OF THE R&R AND HECKMAN APPROACHES IS THAT THEY DEPEND ON ESTIMATING THE PROBABILITY OF ASSIGNMENT TO (OR SELECTION FOR) TREATMENT (WHICH IS NOT KNOWN FOR OBSERVATIONAL DATA) AS A FUNCTION OF OBSERVABLES, AND THEY APPLY TO SITUATIONS IN WHICH THIS PROBABILITY IS NOT EQUAL TO ZERO OR ONE. THE REGRESSION-DISCONTINUITY DESIGN IS AN EXAMPLE OF AN APPROACH THAT DOES NOT REQUIRE THE PROBABILITY OF ASSIGNMENT TO TREATMENT TO BE DIFFERENT FROM 0 OR 1.

WE SHALL DESCRIBE EACH APPROACH AT A SUMMARY LEVEL OF DETAIL, AND THEN DISCUSS THE IMPLICATIONS OF THE APPROACH FOR SURVEY DESIGN, WITH PARTICULAR REFERENCE TO MATCHING. THE DESCRIPTION PRESENTED HERE ABOUT THE R&R AND HECKMAN APPROACHES IS SOMEWHAT DETAILED. (THIS LEVEL OF DETAIL IS USED BECAUSE THE PRESENTATION ON ANALYSIS FOR PROGRAM EVALUATION WAS NOT YET AVAILABLE WHEN THIS PRESENTATION WAS WRITTEN.)

A REFERENCE FOR THE R&R APPROACH IS “THE CENTRAL ROLE OF THE PROPENSITY SCORE IN OBSERVATIONAL STUDIES FOR CAUSAL EFFECTS” BY PAUL R. ROSENBAUM AND DONALD B. RUBIN, BIOMETRIKA (1983), VOL. 70, NO. 1, PP. 41-55. FOR MORE DISCUSSION OF THE ROSENBAUM-RUBIN APPROACH, SEE “STATISTICS AND CAUSAL INFERENCE” BY PAUL W. HOLLAND, JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, VOL. 81, NO. 396 (DEC. 1986), PP. 945-960).

A REFERENCE FOR THE HECKMAN APPROACH IS “CHOOSING AMONG ALTERNATIVE NONEXPERIMENTAL METHODS FOR ESTIMATING THE IMPACT OF SOCIAL PROGRAMS: THE CASE OF MANPOWER TRAINING” BY JAMES J. HECKMAN AND V. JOSEPH HOTZ, JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, VOL. 84, NO. 408 (DEC. 1989), PP. 862-874. FOR ADDITIONAL REFERENCES ON THE ECONOMETRIC APPROACH, SEE ALSO COUNTERFACTUALS AND CAUSAL INFERENCE: METHODS AND PRINCIPLES FOR SOCIAL RESEARCH BY STEPHEN L. MORGAN AND CHRISTOPHER WINSHIP (CAMBRIDGE UNIVERSITY PRESS, 2007); MOSTLY HARMLESS ECONOMETRICS: AN EMPIRICIST’S COMPANION BY JOSHUA D. ANGRIST AND JÖRN-STEFFEN PISCHKE (PRINCETON UNIVERSITY PRESS, 2009); MICRO-ECONOMICS FOR POLICY, PROGRAM AND TREATMENT EFFECTS BY MYOUNG-JAE LEE (OXFORD UNIVERSITY PRESS, 2005); AND ECONOMETRIC ANALYSIS 7^TH EDITION, BY WILLIAM H. GREENE (PRENTICE HALL, 2012).

THE R&R APPROACH IS AN EXAMPLE OF “CONDITIONING TO BALANCE.” THE HECKMAN APPROACH IS AN EXAMPLE OF “CONDITIONING TO ADJUST.”

FROM A PRACTICAL VIEWPOINT, A MAJOR PROBLEM FACING THE CONSTRUCTION OF ESTIMATES OF CAUSAL EFFECTS IS THE "CURSE OF DIMENSIONALITY" – IT IS NOT PRACTICAL TO CONDITION DIRECTLY OVER A LARGE NUMBER OF VARIABLES. THE R&R AND HECKMAN APPROACHES OFFER PRACTICAL SOLUTIONS TO THIS PROBLEM. IN THE R&R APPROACH, A METHOD IS SHOWN FOR REDUCING THE PROBLEM OF MATCHING OR STRATIFICATION ON A MULTIDIMENSIONAL VARIABLE TO THE MUCH SIMPLER PROBLEM OF MATCHING OR STRATIFICATION ON A SCALAR VARIABLE. IN THE HECKMAN APPROACH, THE PROBLEM IS RESOLVED BY USING REGRESSION MODELS. WE SHALL FIRST DISCUSS THE R&R APPROACH, AND THEN THE HECKMAN APPROACH.

4.9. THE ROSENBAUM-RUBIN (“STATISTICAL,” BALANCING) APPROACH TO STATISTICAL CAUSAL MODELING AND ANALYSIS

[OPTIONAL MATERIAL]

FROM THE PRECEDING DISCUSSION, AN APPROACH THAT COMES TO MIND TO OBTAIN AN UNBIASED ESTIMATE OF IMPACT – ASSUMING CONDITIONAL INDEPENDENCE OF RESPONSE (POTENTIAL OUTCOMES (Y₀, Y₁)) AND TREATMENT (W) GIVEN X – IS TO CROSS-STRATIFY ON ALL COMPONENTS OF X, ESTIMATE IMPACT WITHIN EACH STRATUM AS THE DIFFERENCE IN (APPROPRIATELY ESTIMATED) MEANS BETWEEN THE TREATED AND UNTREATED UNITS, AND FORM A STRATUM-WEIGHTED ESTIMATE OF THE WITHIN-STRATUM DIFFERENCES.

THAT APPROACH – CROSS-STRATIFYING ON ALL COMPONENTS OF X – IS SIMPLE IN CONCEPT BUT DIFFICULT TO IMPLEMENT. THIS TYPE OF MATCHING TO REDUCE SELECTION BIAS IS CALLED “SUBCLASSIFICATION” OR “MULTIVARIATE MATCHING.” THE PRACTICAL PROBLEM THAT ARISES HERE IS THE “CURSE OF DIMENSIONALITY”: IF THERE ARE MANY DESIGN VARIABLES AND LEVELS, THE NUMBER OF STRATA (COMBINATIONS OF VARIABLES BY LEVELS IN A CROSS-STRATIFIED DESIGN) IS VERY LARGE, AND THERE MAY BE MANY STRATA (OR, AS THEY ARE USUALLY CALLED IN A CROSS-STRATIFIED DESIGN, “STRATUM CELLS” OR “CELLS”) THAT DO NOT CONTAIN BOTH TREATMENT AND COMPARISON UNITS (SO THAT IT IS NOT POSSIBLE TO ESTIMATE THE STRATIFIED MEANS FOR THESE TWO GROUPS (AND HENCE THE DIFFERENCE IN MEANS)). IN GENERAL, MULTIDIMENSIONAL STRATIFICATION BY X IS NOT PRACTICAL IN MOST APPLICATIONS (SINCE, WITH THE READY AVAILABILITY OF DEMOGRAPHIC AND GEOGRAPHIC DATA, THERE IS A LARGE NUMBER OF DESIGN VARIABLES AVAILABLE FOR CONSIDERATION).

A PRACTICAL SOLUTION TO THIS CALCULATION PROBLEM, INVOLVING STRATIFICATION ON A SCALAR (A FUNCTION OF X), WAS PRESENTED BY PAUL ROSENBAUM AND DONALD RUBIN IN THE FOLLOWING ARTICLE:

REFERENCE (“R&R”): PAUL R. ROSENBAUM AND DONALD B. RUBIN, “THE CENTRAL ROLE OF THE PROPENSITY SCORE IN OBSERVATIONAL STUDIES FOR CAUSAL EFFECTS,” BIOMETRIKA, VOL. 70, NO. 1, PP. 41-55, 1983.

SUMMARY OF THE R&R APPROACH

FROM PEARL'S THEORY, IT IS CLEAR THAT THE CAUSAL EFFECT MAY BE ESTIMATED BY CONDITIONING ON ALL VARIABLES AFFECTING SELECTION FOR TREATMENT. THE FUNDAMENTAL PROBLEM ASSOCIATED WITH THIS FACT IS THAT IT IS DIFFICULT TO CONDITION OVER MULTIPLE VARIABLES. WHAT R&R PROVE IS THAT THE PROBLEM OF CONDITIONING OVER A VECTOR RANDOM VARIABLE MAY BE REDUCED TO THE PROBLEM OF CONDITIONING OVER A SCALAR – THE PROPENSITY SCORE, OR PROBABILITY OF SELECTION FOR TREATMENT, GIVEN THE COVARIATES ON WHICH SELECTION DEPENDS.

HERE FOLLOWS A SIMPLE PROOF OF THE R&R APPROACH (FROM WOOLDRIDGE, 2^ND ED., OP. CIT., P. 925).

THE SIGNIFICANCE OF THIS THEOREM IS THAT IT ELIMINATES THE “CURSE OF DIMENSIONALITY” PROBLEM FOR ESTIMATING IMPACT FROM THE SET OF VARIABLES (X) THAT AFFECT ASSIGNMENT TO TREATMENT. INSTEAD OF CONDITIONING ON A MULTIDIMENSIONAL X, WE MAY SIMPLY CONDITION ON A SCALAR, P(X). THE SIGNIFICANT PROBLEM THAT REMAINS, HOWEVER, IT TO IDENTIFY A SET OF COVARIATES, X, SUCH THAT (Y₀,Y₁) AND W ARE INDEPENDENT CONDITIONAL ON X.

PROOF: WE WISH TO SHOW (GIVEN THAT W AND (Y₀, Y₁) ARE INDEPENDENT CONDITIONAL ON X) THAT W AND (Y₀, Y₁) ARE INDEPENDENT CONDITIONAL ON THE PROPENSITY SCORE, P(X). SINCE W IS A BINARY VARIABLE, THE LATTER IS TRUE IF P(W=1|Y₀, Y₁,P(X) = P(W=1|P(X).

ACCORDING TO THE LAW OF ITERATED EXPECTATIONS, E(Y|Z) = E_X(E_Y(Y|X)|Z) WHERE Y IS A RANDOM VARIABLE, X IS A RANDOM VECTOR, AND Z IS A RANDOM VECTOR THAT IS A FUNCTION OF X. HENCE

E(W|Y₀, Y₁, P(X)) = E_X(E(W|Y₀, Y₁, X)|Y₀, Y₁, P(X)) = E_X(E(W|X))|Y₀, Y₁, P(X)) = E(P(X) | Y₀, Y₁, P(X)) = P(X).

THAT IS, E(W|Y₀,Y₁,P(X)) IS INDEPENDENT OF Y₀, Y₁. SINCE W IS BINARY, THIS IMPLIES P(W|Y₀, Y₁,P(X)) IS INDEPENDENT OF Y₀, Y₁, I.E., P(W=1|Y₀, Y₁,P(X) = P(W=1|P(X)), WHICH WAS TO BE PROVED.

SINCE Y = (1-W)Y₀ + WY₁,

INSERTING W=0 AND W=1 GIVES THE CONDITIONAL MEANS.

[END OF PROOF]

WE SHALL NOW DESCRIBE THE R&R APPROACH TO CAUSAL ANALYSIS IN SOMEWHAT GREATER DETAIL. (THE FOLLOWING SECTION PROVIDES INFORMATION ABOUT THE CONCEPTUAL FOUNDATIONS OF THE R&R APPROACH. IT DRAWS HEAVILY ON THE JUST-REFERENCED ARTICLE. IF IT IS DESIRED TO SKIP OVER THIS MATERIAL, PROCEED TO THE MARKER “[END OF DESCRIPTION OF THE R&R METHODOLOGY]”.

[OPTIONAL DESCRIPTION OF THE R&R METHODOLOGY]

LET X DENOTE ANY SET OF OBSERVED COVARIATES. FOR THE FIRST PART OF THE DISCUSSION THAT FOLLOWS, DEALING WITH BALANCING SCORES (I.E., ABOUT CONDITIONAL INDEPENDENCE OF COVARIATES AND TREATMENT, GIVEN A BALANCING SCORE), THIS SET OF OBSERVED COVARIATES DOES NOT NEED TO INCLUDE ALL VARIABLES AFFECTING TREATMENT ASSIGNMENT OR OUTCOME. WHEN THE DISCUSSION MOVES TO THE ISSUE OF CONDITIONAL INDEPENDENCE OF RESPONSE AND TREATMENT, GIVEN THE COVARIATES, THIS ASSUMPTION WILL CHANGE (TO INCLUDE ALL COVARIATES AFFECTING TREATMENT ASSIGNMENT).

DEFINITION: ANY (VECTOR-VALUED) FUNCTION b(X) SUCH THAT, GIVEN b(X), THE DISTRIBUTION OF X IS THE SAME FOR THE TREATMENT AND COMPARISON GROUPS IS CALLED A BALANCING SCORE.

THAT IS, X AND W ARE CONDITIONALLY INDEPENDENT GIVEN THE BALANCING SCORE: X W | b(X). AS MENTIONED, IN THIS DEFINITION X IS ANY SET OF OBSERVED VARIATES – NOT JUST ONES AFFECTING TREATMENT OR OUTCOME. THIS IS SIMPLY A DEFINITION, NOT A "RESULT."

(NOTE THAT IN THE DEFINITION WE ARE MAKING AN ASSERTION ABOUT THE CONDITIONAL INDEPENDENCE OF ANY VARIABLES X AND W GIVEN THE BALANCING SCORE, NOT ON THE CONDITIONAL INDEPENDENCE OF THE RESPONSE (Y₀,Y₁) AND W GIVEN THE BALANCING SCORE.)

THE SIMPLEST (“FINEST”) BALANCING SCORE BASED ON X IS THE VECTOR X ITSELF, SINCE X W | X. THAT IS, IF X IS GIVEN, THEN IT IS A FIXED VALUE, AND ITS (DEGENERATE) PROBABILITY DISTRIBUTION IS OBVIOUSLY THE SAME FOR THE TREATMENT AND COMPARISON GROUPS. THIS MEANS THAT ANY OBSERVED VECTOR X IS A (MULTIDIMENSIONAL) BALANCING SCORE. (NOTE THAT X IS STILL ANY COVARIATE, AND NEED NOT INCLUDE ALL VARIABLES AFFECTING SELECTION FOR TREATMENT.)

(A SCORE b(X) IS FINER THAN ANOTHER SCORE e(X) IF THERE EXISTS A FUNCTION f SUCH THAT e(X) = f(b(X)). NOTE THAT BY THIS DEFINITION, A SCORE IS FINER THAN ITSELF.)

R&R PROVE THAT THE COARSEST BALANCING SCORE BASED ON X IS THE PROPENSITY SCORE (THE PROBABILITY OF SELECTION FOR TREATMENT, GIVEN X), e(X) = P(W=1 | X).

THE VERY USEFUL ASPECT OF THE PROPENSITY SCORE IS THAT IT IS A SCALAR (A SINGLE-DIMENSIONAL NUMBER, NOT A MULTIDIMENSIONAL VECTOR, SUCH AS X MAY BE). THE PRECEDING RESULT SPECIFIES THAT X AND W ARE CONDITIONALLY INDEPENDENT GIVEN THE PROPENSITY SCORE BASED ON X (A SCALAR), NO MATTER HOW MANY OR WHICH COVARIATES ARE INCLUDED IN X.

IN GENERAL, THE TERM “PROPENSITY SCORE” MAY REFER TO THE UNCONDITIONAL PROPENSITY SCORE, P(W=1), OR TO THE CONDITIONAL PROPENSITY SCORE, P(W=1 | X). IN THIS DISCUSSION, THE PROPENSITY SCORE WILL GENERALLY BE CONDITIONAL ON A COVARIATE, X. (AT THE PRESENT POINT IN THIS DISCUSSION, X MAY BE ANY COVARIATE AT ALL, NOT NECESSARILY ALL THOSE AFFECTING SELECTION FOR TREATMENT OR OUTCOME.) THE TERM “PROPENSITY SCORE” MAY REFER TO THE TRUE VALUE OF THE PROPENSITY SCORE GIVEN X, OR TO A SAMPLE ESTIMATE OF THIS QUANTITY. THE TERM “TRUE VALUE OF THE PROPENSITY SCORE” IS AMBIGUOUS – IT MAY REFER EITHER TO THE TRUE VALUE OF THE SCORE GIVEN X, OR TO THE UNCONDITIONAL PROPENSITY SCORE, P(W=1).

SOME AUTHORS DO NOT MAKE CLEAR WHICH “TRUE VALUE” THEY ARE REFERRING TO, LEADING TO SUBSTANTIAL CONFUSION. THEY ATTRIBUTE POOR RESULTS ASSOCIATED WITH NOT KNOWING THE “TRUE VALUE” OF THE PROPENSITY SCORE, WITHOUT MAKING CLEAR WHETHER THE PROBLEM IS THE SAMPLING VARIABILITY IN AND ESTIMATE OF P(W=1|X), OR THE FACT THAT P(W=1|X) IS CONDITIONED ON X AND X MAY NOT INCLUDE ALL OF THE VARIABLES ON WHICH P(W) DEPENDS (BECAUSE OF THE PRESENCE OF UNOBSERVED VARIABLES). MORE WILL BE SAID ON THIS TOPIC LATER.

IT IS EASY TO SHOW THAT THE PROPENSITY SCORE IS A BALANCING SCORE FOR ANY X: GIVEN e(X), THE PROBABILITY THAT W IS EQUAL TO ONE IS SPECIFIED AND INDEPENDENT OF X, I.E., THE PROBABILITY FUNCTION OF W IS SPECIFIED AND INDEPENDENT OF X. (STOCHASTIC INDEPENDENCE IS A SYMMETRICAL PROPERTY: IF W IS INDEPENDENT OF X, THEN X IS INDEPENDENT OF W.)

R&R PROVE THAT A FUNCTION b(X) IS A BALANCING SCORE IF AND ONLY IF IT IS FINER THAN e(X). (NOTE THAT BY DEFINITION, e(X) IS FINER THAN e(X).)

UP TO NOW, X HAS BEEN ANY COVARIATE. THE PRECEDING DISCUSSION IS SIMPLY ABOUT BALANCING SCORES BASED ON X AND CONDITIONAL INDEPENDENCE OF THE COVARIATES X AND W. WHAT WE ARE REALLY INTERESTED IN, HOWEVER, IS CONDITIONS UNDER WHICH THE RESPONSE (Y₀, Y₁) (THE RESPONSE, NOT ARBITRARY COVARIATES) IS INDEPENDENT OF W.

A NOTE ON TERMINOLOGY. AT FIRST GLANCE, THE EXPRESSION THAT THE RESPONSE IS INDEPENDENT OF TREATMENT W GIVEN X SOUNDS ABSURD. THE REASON FOR THIS REACTION IS THAT THE OBSERVED RESPONSE IS MOST ASSUREDLY NOT INDEPENDENT OF TREATMENT – THE REASON FOR APPLYING THE TREATMENT IS TO AFFECT THE OBSERVED RESPONSE. THE CONFUSION RESULTS FROM THE FACT THAT, IN THIS EXPRESSION, “RESPONSE” REFERS TO THE JOINT POTENTIAL-OUTCOME (OR JOINT COUNTERFACTUAL) RESPONSE, (Y₀, Y₁), NOT THE OBSERVED RESPONSE Y. THE EXPRESSION MEANS THAT THE JOINT DISTRIBUTION OF VALUES OF Y₀ – THE POTENTIAL RESPONSE IF A UNIT IS TREATED – AND Y₁ – THE POTENTIAL RESPONSE IF A UNIT IS UNTREATED – IS NOT DEPENDENT ON TREATMENT (W), I.E., ARE THE SAME WHETHER THE UNIT IS SELECTED FOR TREATMENT OR NOT (THE OBSERVED RESPONSE, Y, MAY CERTAINLY DEPEND ON W). IF RANDOMIZATION IS USED TO ASSIGN UNITS TO TREATMENT, THIS IS SURELY THE CASE. (TO AVOID CONFUSION, IT IS IMPORTANT TO MAKE CLEAR WHEN USING THE WORD "RESPONSE" WHETHER ONE IS REFERRING TO THE OBSERVED RESPONSE OR THE POTENTIAL-OUTCOME RESPONSE.)

(NOTE, AS MENTIONED EARLIER, THAT IF (Y₀,Y₁) IS INDEPENDENT OF TREATMENT (W), THE Y₀ AND Y₁ ARE INDIVIDUALLY INDEPENDENT OF TREATMENT (THE CONVERSE OF THIS STATEMENT IS NOT TRUE: SEPARATE INDEPENDENCE OF W AND Y₀ AND W AND Y₁ DOES NOT IMPLY INDEPENDENCE OF W AND (Y₀,Y₁) JOINTLY.))

IF THE JOINT DISTRIBUTION OF (Y₀,Y₁) IS NOT INDEPENDENT OF W, IT IS POSSIBLE THAT THE UNITS SELECTED FOR TREATMENT MAY RESPOND DIFFERENTLY TO TREATMENT THAN THOSE THAT ARE NOT (I.E., THE MEAN VALUES OF Y₀ AND Y₁ ARE DIFFERENT, E.G., IF “CREAMING” OR “CHERRY-PICKING” IS USED TO SELECT HIGH-MOTIVATION / HIGH-ABILITY CLIENTS FOR A PROGRAM).

(THE PRECEDING COMMENT ABOUT “CHERRY PICKING” IS NOT MEANT TO DISPARAGE THE PRACTICE. IN AN OPERATIONAL PROGRAM WITH LIMITED RESOURCES, IT MAY BE EFFICIENT AND DESIRED TO ALLOCATE PROGRAM RESOURCES TO THOSE WHO WILL MAKE THE MOST OF THEM, OR FOR INDIVIDUALS WHO PERCEIVE GREATER BENEFIT FROM THE PROGRAM TO BE MORE LIKELY TO PARTICIPATE. IN THAT CONTEXT, "CHERRY PICKING" CAN BE A VERY DESIRABLE WAY OF MAXIMIZING THE RETURN ON INVESTMENT OF PROGRAM RESOURCES. IN AN EVALUATION STUDY, HOWEVER, WHERE IT IS DESIRED TO ESTIMATE THE RELATIONSHIP OF PROGRAM IMPACT TO COVARIATES, OR TO ESTIMATE THE PROGRAM IMPACT FOR A LARGE POPULATION (I.E., AVERAGE IMPACT FOR A RANDOMLY SELECTED INDIVIDUAL), THIS PRACTICE BIASES THE DESIRED ESTIMATES. RELATIVE TO THE PERSONS TREATED, THE IMPACT MEASURE OF INTEREST IS THE AVERAGE TREATMENT EFFECT ON THE TREATED (ATT). DEPENDING ON THE POLICY ISSUES TO BE ADDRESSED, THE ATT COULD BE OF JUST AS MUCH INTEREST AS (OR MORE INTEREST THAN) THAN THE ATT).

WE SHALL NOW CONSIDER THE IMPLICATIONS OF ASSUMING THAT X IS A SET OF COVARIATES SUCH THAT RESPONSE AND TREATMENT ARE CONDITIONALLY INDEPENDENT, GIVEN X. (THAT IS, X IS NO LONGER ANY OBSERVED COVARIATE (AS WAS ASSUMED FOR THE PRECEDING DISCUSSION OF BALANCING SCORES), BUT ONE FOR WHICH RESPONSE AND TREATMENT ARE CONDITIONALLY INDEPENDENT, GIVEN X.)

R&R REFER TO CONDITIONAL INDEPENDENCE OF RESPONSE AND TREATMENT GIVEN THE COVARIATES X AS “IGNORABILITY OF TREATMENT.” IF THE ADDITIONAL CONDITION 0 < P(W=1 | X) < 1 (I.E., 0 < e(X) < 1) IS IMPOSED, THE CONDITION IS CALLED “STRONG IGNORABILITY OF TREATMENT.” (THE TERM “IGNORABLE” REFERS TO THE FACT THAT IF RESPONSE (Y₀, Y₁) IS CONDITIONALLY INDEPENDENT OF W GIVEN X, THEN THE TREATMENT STATUS (OR THE ASSIGNMENT MECHANISM) MAY BE IGNORED IN ESTIMATING E(Y₀) AND E(Y₁). AS NOTED EARLIER, THE TERM “IGNORABILITY OF TREATMENT” IS DECLINING IN USE, BEING REPLACED BY “UNCONFOUNDEDNESS” OR “CONDITIONAL INDEPENDENCE.”)

IF TREATMENT IS STRONGLY IGNORABLE GIVEN X, THEN THE ATE MAY BE ESTIMATED FOR ANY VALUE OF X (SINCE 0 < P(W = 1 |X) < 1 FOR ALL X, THERE EXIST (IN THE POPULATION) TREATED AND UNTREATED UNITS FOR EVERY X, SO THE DIFFERENCE IS ESTIMABLE FOR EVERY X (AS LONG AS THERE ARE TREATED AND UNTREATED UNITS IN THE SAMPLE FOR EACH VALUE OF X)). WE HAVE

E(Y₁ | X, W=1) – E(Y₀ | X, W=0) = E(Y₁ | X) – E(Y₀ | X) (SINCE Y₁ AND Y₀ ARE INDEPENDENT OF W, GIVEN X)

= ATE(X).

TAKING THE EXPECTATION OVER X, WE HAVE

E_X[E(Y₁ | X) – E(Y₀ | X)] = E(Y₁) – E(Y₀) = ATE.

IN ORDER FOR THIS EXPECTATION TO BE ESTIMABLE OVER THE ENTIRE POPULATION OF X, ALL X IN THE DOMAIN OF X MUST HAVE POSITIVE PROBABILITY OF BEING SAMPLED.

R&R SHOW THAT IF TREATMENT IS STRONGLY IGNORABLE GIVEN X, THEN IT IS STRONGLY IGNORABLE GIVEN ANY BALANCING SCORE b(X) BASED ON X (IN PARTICULAR, e(X)). (IN SYMBOLS, IF IT IS TRUE THAT (Y₀, Y₁) W | X AND 0 < p(W = 1 | X) < 1, IT IS TRUE THAT (Y₀, Y₁) W | e(X) AND 0 < p(W = 1 | e(X)) < 1.)

(THE CONDITION 0 < p(W = 1 | e(X)) < 1 IS CALLED THE “OVERLAP” CONDITION, SINCE IT ASSURES THAT BOTH TREATED AND UNTREATED UNITS WILL BE AVAILABLE FOR ALL VALUES OF X.)

IT FOLLOWS THAT IF TREATMENT IS STRONGLY IGNORABLE GIVEN e(X), THEN WE CAN ESTIMATE THE ATE, SINCE WE CAN ESTIMATE ATE(e(X)), AND THEN AVERAGE OVER e(X). THAT IS,

E_e(X)[E(Y₁ | e(X)) – E(Y₀ | e(X))] = E(Y₁) – E(Y₀) = ATE.

THIS EXPECTATION MUST BE TAKEN OVER THE ENTIRE DOMAIN OF e(X) (EXCEPT FOR SETS OF PROBABILITY ZERO, SINCE A CONDITIONAL EXPECTATION IS NOT DEFINED FOR SUCH SETS).

THE REASON WHY WE NEED STRONG IGNORABILITY (I.E., DISALLOW e(X) = P(W=1 | X) = 0 and e(X) = 1 (or p(W = 1 | e(X)) = 0 AND p(W = 1 | e(X)) = 1)) IS THAT IF P(W=1 | e(X)) = 0 THEN Y₁ (THE OUTCOME IF A UNIT IS TREATED (W=1)) IS NEVER OBSERVED FOR THAT VALUE OF e(X) AND SO E(Y₁ | e(X)) CANNOT BE ESTIMATED, AND IF P(W=1 | e(X)) = 1 THEN P(W=0 | e(X)) = 0 THEN Y₀ (THE OUTCOME IF A UNIT IS NOT TREATED (W=0)) IS NEVER OBSERVED FOR THAT VALUE OF e(X) AND SO E(Y₀ | e(X)) CANNOT BE ESTIMATED.

THIS IS THE SAME REQUIREMENT AS FOR EXPERIMENTAL DESIGNS OR SAMPLE SURVEYS – IN ORDER TO ESTIMATE A QUANTITY (FOR THE ENTIRE POPULATION OF INTEREST), EVERY UNIT OF THE POPULATION MUST HAVE A KNOWN (OR EQUAL) POSITIVE PROBABILITY (OR PROBABILITY DENSITY) OF BEING SELECTED.

THIS RESULT ASSURES THAT IF (Y₀, Y₁) W | X AND WE MATCH ON THE PROPENSITY SCORE, e(X), THEN, AS LONG AS 0 < e(X) < 1, WE CAN OBTAIN AN UNBIASED ESTIMATE OF ATE BY STRATIFYING BY THE PROPENSITY SCORE. THE TREMENDOUS SIGNIFICANCE OF THIS RESULT IS THAT IT OVERCOMES THE CURSE OF DIMENSIONALITY, SINCE THE PROPENSITY SCORE IS A SCALAR.

THE KEY ASSUMPTION HERE IS THAT THE RESPONSE (Y₀, Y₁) IS INDEPENDENT OF TREATMENT W GIVEN X. THE PRECEDING RESULT IS USEFUL IN DESIGN TO THE EXTENT THAT (Y₀, Y₁) IS INDEPENDENT OF W GIVEN THE AVAILABLE COVARIATES. FOR THE R&R APPROACH TO WORK, IT IS NOT SUFFICIENT SIMPLY TO STRATIFY ON THE PROPENSITY SCORE GIVEN OBSERVED X – IT MUST BE A PROPENSITY SCORE BASED ON AN X THAT ASSURES CONDITIONAL INDEPENDENCE OF RESPONSE AND TREATMENT, I.E., ONE THAT INCLUDES ALL VARIABLES THAT AFFECT TREATMENT. (THIS IS WHAT IS MEANT BY THE TERM “SELECTION ON OBSERVABLES.”)

THE PRECEDING POINT IS VERY IMPORTANT, AND OFTEN OVERLOOKED. IT IS NOT MATCHING ON THE PROPENSITY SCORE THAT REDUCES BIAS OF THE ATE. THE KEY POINT IS MATCHING ON VARIABLES THAT AFFECT SELECTION FOR TREATMENT, WHETHER THIS MATCHING IS BASED ON THE PROPENSITY SCORE OR NOT. THE PROPENSITY SCORE IS USED TO MITIGATE THE CURSE OF DIMENSIONALITY, BY ENABLING MATCHING ON ONE VARIABLE RATHER THAN A CROSS-STRATIFICATION OF VARIABLES AFFECTING TREATMENT (EITHER ALL OF THEM, OR ALL OF THEM THAT AFFECT BOTH SELECTION FOR TREATMENT AND OUTCOME). THE CRUCIAL ASPECT OF PROPENSITY-SCORE MATCHING IS IDENTIFICATION OF A COMPLETE SET OF COVARIATES THAT AFFECT SELECTION FOR TREATMENT. MATCHING ON THE PROPENSITY SCORE IS SIMPLY A MECHANICAL PROCESS TO COPE WITH THE CURSE OF DIMENSIONALITY. IDENTIFICATION AND JUSTIFICATION OF SUCH A SET CANNOT BE REASONABLY DONE WITHOUT FIRST IDENTIFYING A CAUSAL MODEL. SIMPLY MAKING A CLAIM OF "STRONG IGNORABILITY," WITHOUT JUSTIFICATION BASED ON A COMPLETE CAUSAL MODEL, IS INADEQUATE. (PEARL DISCUSSES THIS POINT ON PP. 348-352 OF CAUSALITY (OP. CIT., 2ND ED.).)

NOTE ALSO THAT A KEY ASSUMPTION IS THAT THE PROPENSITY SCORE IS NOT EQUAL TO ZERO OR ONE. DATA FOR WHICH THE PROPENSITY SCORE IS ZERO OR ONE CANNOT BE USED (FOR DESIGN-BASED ESTIMATES OF ATE), SINCE THE DIFFERENCE IN MEANS OF THE TREATED AND UNTREATED CANNOT BE CALCULATED (SINCE IF THE PROPENSITY SCORE IS ZERO OR ONE ALL OF THE UNITS ARE TREATED OR ALL ARE UNTREATED). MORE SIGNIFICANTLY, SINCE BOTH TREATED AND UNTREATED UNITS ARE NOT OBSERVABLE IF e(X) = 0 OR 1, THEN ATE(e(X)) CANNOT BE AVERAGED OVER THE ENTIRE POPULATION OF e(X). (THIS FOLLOWS FROM THE FACT THAT THE CONDITIONAL EXPECTATION IS NOT DEFINED FOR e(X) = 0 OR 1.) THAT IS, IF e(X) = 0 OR 1 FOR SOME UNITS, THE ATE CANNOT BE ESTIMATED (OVER THE ENTIRE POPULATION).

STRONG IGNORABILITY (FULL OVERLAP) IS NOT REQUIRED FOR ESTIMATION OF ATT. ALL THAT IS REQUIRED IS THAT P(W=1|X)<1. ALTHOUGH THIS PRESENTATION HAS FOCUSED ON THE ATE, THE ATT IS ALSO OF INTEREST. FOR EXAMPLE, IF A PROGRAM IS UNDER CONSIDERATION FOR TERMINATION OR REDUCTION IN SIZE, IT MAY BE OF PARTICULAR INTEREST TO ASSESS THE BENEFIT TO THOSE BEING TREATED, EVEN THOUGH INTEREST NO LONGER CENTERS ON BENEFIT TO RANDOMLY SELECTED MEMBERS OF THE POPULATION.

TO SUMMARIZE: WHAT R&R PROVE IS THAT A PROPENSITY SCORE BALANCES THE DISTRIBUTION OF ALL VARIABLES ON WHICH IT IS BASED, AND IF THESE VARIABLES INCLUDE ALL VARIABLES AFFECTING SELECTION FOR TREATMENT, THEN AN UNBIASED ESTIMATE OF THE ATE CAN BE OBTAINED, AS LONG AS THE PROPENSITY SCORE (GIVEN X) IS NOT EQUAL TO ZERO OR ONE.

IF THE PROPENSITY SCORE (BASED ON ALL VARIABLES AFFECTING SELECTION FOR TREATMENT) EQUALS ZERO OR ONE FOR SOME UNITS OF THE POPULATION, THE ESTIMATED ATE CALCULATED FROM SAMPLE UNITS FOR WHICH THE PROPENSITY SCORE IS NOT EQUAL TO ZERO OR ONE WOULD APPLY TO THE POPULATION FOR WHICH THE PROPENSITY SCORE IS NOT EQUAL TO ZERO OR ONE. IF THIS POPULATION IS OF INTEREST, SUCH AN ESTIMATE COULD BE OF VALUE.

THE RESTRICTION THAT THE PROPENSITY SCORE NOT BE EQUAL TO ZERO OR ONE MAY BE RELAXED FOR ESTIMATION OF THE ATT. FOR ESTIMATION OF ATT, THERE IS NO REQUIREMENT THAT P(W=0|X) NEVER EQUAL ZERO, JUST THAT IT NEVER EQUAL ONE. IT IS NOT CORRECT TO INCLUDE ALL OF THE TREATED UNITS IN THE ESTIMATOR – JUST THE ONES THAT WERE SELECTED FOR TREATMENT WITH PROBABILITY LESS THAN ONE.

NOTE THAT IF THERE ARE UNOBSERVED VARIABLES THAT AFFECT SELECTION FOR TREATMENT AND RESPONSE (OUTCOME), THE BASIC R&R METHOD DOES NOT APPLY (SINCE THERE IS NO OBSERVED X FOR WHICH THE RESPONSE (Y₀, Y₁) IS INDEPENDENT OF TREATMENT, W, GIVEN X). BY INCLUDING AN ESTIMATE THAT USES A MODEL-BASED PROPENSITY SCORE, THESE CASES MAY BE ADDRESSED IF THE PROPORTION OF SUCH CASES IS SMALL.

IDENTIFICATION OF THE VARIABLES THAT AFFECT SELECTION FOR TREATMENT REQUIRES CAREFUL CONSIDERATION OF A CAUSAL MODEL INVOLVING OUTCOME VARIABLES AND VARIABLES THAT AFFECT THEM. IT IS NOT APPROPRIATE TO APPLY THE R&R METHODOLOGY TO WHATEVER OBSERVED COVARIATES HAPPEN TO BE AVAILABLE – THE METHODOLOGY APPLIES WHEN THE PROPENSITY SCORE ESTIMATE IS BASED ON ALL VARIABLES AFFECTING SELECTION FOR TREATMENT. TO SIMPLY ASSUME THAT WHATEVER OBSERVED COVARIATES ARE AVAILABLE ARE ALL THOSE AFFECTING SELECTION FOR TREATMENT WOULD BE A “HEROIC” ASSUMPTION OF CONVENIENCE, AND NOT JUSTIFIED. IF THERE ARE UNOBSERVED VARIABLES THAT HAVE A SUBSTANTIAL EFFECT ON SELECTION FOR TREATMENT AND THE APPROACH DOES NOT ADDRESS THEM, APPLICATION OF THE R&R METHODOLOGY CANNOT BE JUSTIFIED.

NOTE THAT WE MAY MATCH ON ANY BALANCING SCORE, E.G., ONE THAT IS FINER THAN THE PROPENSITY SCORE, AND ACHIEVE THE SAME RESULT OF REDUCING BIAS AS IF WE HAD MATCHED ON THE PROPENSITY SCORE ALONE. FOR EXAMPLE, WE COULD MATCH ON THE PROPENSITY SCORE AND A VARIABLE, X, THAT HAS AN IMPORTANT EFFECT ON OUTCOME (TO IMPROVE PRECISION, OR TO EXPLORE ATE FOR SUBPOPULATIONS OF INTEREST, SUCH AS MALES AND FEMALES). IN THIS CASE, MATCHING IS DONE ON A BIVARIATE VECTOR (PS, X), WHERE “PS” DENOTES THE PROPENSITY SCORE. THE PROBLEM, OF COURSE, IS THAT THIS IS NO LONGER MATCHING ON A SCALAR (I.E., ON THE PROPENSITY SCORE ALONE), SO THAT MATCHING BECOMES MORE DIFFICULT.

[END OF DESCRIPTION OF THE R&R METHODOLOGY]

ESTIMATION OF THE PROPENSITY SCORE

THE R&R METHODOLOGY IS BASED ON USE OF THE PROPENSITY SCORE. IN OBSERVATIONAL STUDIES (QEDs), THE UNCONDITIONAL PROPENSITY SCORE IS IN GENERAL UNKNOWN, AND MUST BE ESTIMATED FROM DATA. THE STANDARD PROCEDURE FOR ESTIMATING THE PROPENSITY SCORE IS TO DEVELOP A LOGISTIC REGRESSION MODEL FROM THE OBSERVED COVARIATES. ANOTHER IS TO DEVELOP A PROBIT MODEL.

THE PROCEDURE FOR DEVELOPING A LOGISTIC-REGRESSION MODEL OF THE PROPENSITY SCORE IS AS FOLLOWS.

Let w denote the binary treatment indicator random variable, which has the value 1 if a unit is treated and 0 otherwise. We define a binary response model:

P(w=1|x) = g(x’β) ≡ p(x)

where x denotes a (column) vector of explanatory variables, P(w=1|x) denotes the probability that w=1 (i.e., is treated) conditional on x, β is a vector of parameters and g(.) is a the logistic link function:

g(z) = exp(z)/(1 + exp(z)).

If we define z as

z = x’β + e,

where e denotes a random error term uncorrelated with x and with mean zero, then

w = 1 if g(z)>.5 and 0 otherwise.

The expression x’β is referred to as an index. The parameters β are estimated by the method of maximum likelihood. The expression x’β does not have any substantive (economic, physical) meaning (or units) – it is simply a modeling artifact. The individual parameters (components of β) are of no particular interest. The model is often referred to as a “latent variable” model, since the variable z is unobserved.

For use in design, the propensity-score model is estimated from variables that are available in the design phase of the study. For use in analysis, the model is estimated from variables that are available from the survey questionnaire. The identification of the explanatory variables to include in the selection model is guided by an underlying causal model. Variables are selected from the questionnaire that are considered likely to have an effect on selection. The questionnaire variables are correlated, and it is attempted to make a selection that is not highly intercorrelated, yet reflects the underlying factors that may affect selection. The selection model uses data only from the first survey round (baseline).

THE PROBIT MODEL IS SIMILAR IN FORM TO THE LOGISTIC MODEL, BUT THE LINK FUNCTION g(z) IS REPLACED BY THE LINK FUNCTION FOR A NORMAL DISTRIBUTION:

g(z) = φ(z) =

WHERE φ(z) DENOTES THE CUMULATIVE NORMAL PROBABILITY DISTRIBUTION FUNCTION (INTEGRAL) FROM MINUS INFINITY TO z.

THE PROBIT MODEL ARISES IN THEORETICAL DISCUSSIONS, WHERE MODEL ERROR TERMS ARE OFTEN ASSUMED TO BE NORMALLY DISTRIBUTED. IN PRACTICAL APPLICATIONS, THE LOGISTIC MODEL IS MORE FREQUENTLY USED.

IF MATCH DATA ARE AVAILABLE ONLY FOR HIGHER-LEVEL SAMPLE UNITS, THE NUMBER OF VARIABLES AND THE SAMPLE SIZE FOR DEVELOPING A PROPENSITY-SCORE MODEL MAY BE SMALL. IN THIS CASE THE USEFULNESS OF MATCHING IS CONSTRAINED. WITH LIMITED DATA, THE ACCURACY OF THE PROPENSITY-SCORE MODEL MAY BE LOW. IT MAY BE DIFFICULT TO CONSTRUCT A MODEL FOR WHICH THE RESPONSE (POTENTIAL OUTCOMES – ACTUAL AND COUNTERFACTUAL) IS INDEPENDENT OF TREATMENT, GIVEN THE PROPENSITY SCORE . THE MODEL MAY BE MIS-SPECIFIED, E.G., BECAUSE OF UNOBSERVED VARIABLES THAT ARE CORRELATED WITH EXPLANATORY VARIABLES IN THE MODEL.

ALTERNATIVE PROCEDURES FOR IMPLEMENTING THE R&R METHODOLOGY

THE PRECEDING DISCUSSION PRESENTS GENERAL CONDITIONS FOR DETERMINING THE ATE, BASED ON THE CONCEPT OF CONDITIONAL INDEPENDENCE. WE SHALL NOW DISCUSS SOME MORE DETAILED ASPECTS OF ESTIMATION OF THE ATE. THE PRECEDING THEORY MAY BE APPLIED IN SEVERAL WAYS, SOME OF WHICH WILL NOW BE SUMMARIZED. IN EVERY CASE, IT IS ASSUMED THAT THE PROPENSITY SCORE IS BASED ON ALL VARIABLES AFFECTING SELECTION FOR TREATMENT (SO THAT RESPONSE (Y₀, Y₁) IS INDEPENDENT OF TREATMENT W GIVEN COVARIATES X).

1. PAIR MATCHING. TREATED AND UNTREATED UNITS ARE MATCHED BASED ON THE PROPENSITY SCORE (PS). THE DIFFERENCE IN OUTCOMES IS AN UNBIASED ESTIMATE OF THE ATE FOR THE MATCH VALUE OF THE PS. BY AVERAGING THESE DIFFERENCES OVER THE SAMPLE, AN UNBIASED ESTIMATE OF THE ATE IS OBTAINED.

2. STRATIFICATION. THE SAMPLE IS STRATIFIED BY VALUES OF THE PS, E.G., 0-.1, .1-.2, .2-.3,…,.8-.9, .9-1.0. FOR EACH STRATUM, THE ATE IS ESTIMATED BY THE DIFFERENCE IN MEANS (APPROPRIATELY ESTIMATED, GIVEN THE SURVEY DESIGN) BETWEEN THE TREATED AND UNTREATED UNITS IN THE STRATUM. AN UNBIASED ESTIMATE OF THE ATE IS OBTAINED BY WEIGHTING THE STRATUM ATE ESTIMATES BY THE PROPORTION OF THE POPULATION IN EACH STRATUM.

HERE FOLLOWS A MORE DETAILED DESCRIPTION OF THE STRATIFICATION METHOD.

IF WE CAN DETERMINE A FUNCTION FOR THE PROBABILITY OF SELECTION FOR TREATMENT AS A FUNCTION OF THE OBSERVABLES, e(X) = P(selection for treatment | X), THEN WE CAN FORM AN UNBIASED ESTIMATE OF IMPACT BY AVERAGING OVER e (I.E., STRATIFYING OVER e):

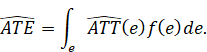
IN PRACTICE, WE ESTIMATE e(X) (E.G., VIA A LOGISTIC REGRESSION MODEL) AND STRATIFY BY CATEGORIES OF e:

|0-.1|.1-.2|…|.9-1.0|.

IF p_h DENOTES THE PROPORTION OF THE SAMPLE IN EACH STRATUM, THEN

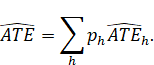
(THIS IS COROLLARY 4.2 OF R&R OP. CIT.)

NOTE: WE CANNOT STRATIFY SO THAT ANY STRATUM h HAS p_h = 0 OR p_h = 1 SINCE IN THESE INSTANCES WE WOULD NOT HAVE BOTH TREATMENT AND COMPARISON UNITS TO COMPARE IN SUCH A STRATUM. AS MENTIONED, THIS ADDITIONAL CONSTRAINT, COMBINED WITH CONDITIONAL INDEPENDENCE OF (Y₀, Y₁) AND W, IS CALLED “STRONG IGNORABILITY OF TREATMENT” BY R&R.

THIS IS THE SAME CONDITION AS HOLDS IN AN EXPERIMENTAL DESIGN – SELECT FROM THE POPULATION OF INTEREST WITH POSITIVE PROBABILITY AND RANDOMLY ASSIGN TO TREATMENT WITH A KNOWN PROBABILITY NOT EQUAL TO ZERO OR ONE.

NOTE THAT WE ARE NOT SIMPLY EXCLUDING THE OBSERVATIONS FOR WHICH THE PROPENSITY SCORE IS ZERO OR ONE FROM THE CALCULATION OF THE ESTIMATE OF ATE. THE POINT IS THAT THE ESTIMATE OF ATE OVER THE ENTIRE POPULATION CANNOT BE DETERMINED, IF THERE ARE PORTIONS OF IT FOR WHICH THE PROPENSITY SCORE IS ZERO OR ONE.

THE PRECEDING RESULT HOLDS FOR SUBPOPULATIONS, E.G. ATT (R&R COROLLARY 4.3).

3. COVARIATE ADJUSTMENT. SUPPOSE THAT IT IS POSSIBLE TO CONSTRUCT A REGRESSION MODEL OF THE RELATIONSHIP OF THE OUTCOMES Y₀ AND Y₁ TO COVARIATES:

E(Y₀(X)) = α₀ + β₀ e(X)

E(Y₁(X)) = α₁ + β₁ e(X).

THEN WE CAN ESTIMATE

WHERE THE ESTIMATES ARE CONDITIONALLY UNBIASED, GIVEN X, AND

WHERE

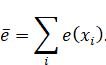
THIS RESULT IS APPLICABLE ONLY IF THERE ARE NO UNOBSERVED VARIABLES CORRELATED WITH THE PROPENSITY SCORE (OR THE VARIABLES INCLUDED IN IT, IF IT IS A LINEAR COMBINATION OF EXPLANATORY VARIABLES). IF THERE ARE, THEN THE ESTIMATES OF WILL BE BIASED, AND THE RESULT DOES NOT HOLD.

THE METHOD OF COVARIATE ADJUSTMENT DOES NOT WORK VERY WELL IF THE VARIANCE WITHIN THE TREATMENT AND COMPARISON GROUPS DIFFERS SUBSTANTIALLY. IN MANY APPLICATIONS, THIS IS THE CASE, SINCE TREATMENT GROUPS TEND TO BE MORE HOMOGENEOUS THAN COMPARISON GROUPS, WHICH TEND TO CONTAIN EXTREME VALUES OF COVARIATES.

THE METHOD OF COVARIATE ADJUSTMENT MAY BE USED TO EXTEND THE BASIC R&R METHODOLOGY TO INCLUDE CASES IN WHICH A FEW OBSERVATIONS MAY HAVE THE PROPENSITY SCORE EQUAL TO 0 OR 1. THIS IS POSSIBLE SINCE THE ESTIMATE OF ATE IS A FUNCTION OF THE EXPECTATION COMPUTED FROM THE REGRESSION EQUATION (REPLACING THE ESTIMATED REGRESSION EQUATION PARAMETERS AND THE MEAN VALUE OF THE PROPENSITY SCORE ()). THE ZERO AND ONE VALUES ARE USED IN DETERMINING THE REGRESSION EQUATION, BUT NO STRATIFICATION IS INVOLVED, AND UNLIKE THE STRATIFICATION APPROACH MEANS MAY STILL BE CALCULATED FOR THE TREATED AND UNTREATED GROUPS (USING THE FITTED REGRESSION MODEL). THIS IS A MODEL-BASED ESTIMATE, AND THE RESULTS ARE CORRECT ONLY IF THE MODEL IS CORRECT.

A NUMBER OF ALTERNATIVE PROPENSITY-SCORE-BASED ESTIMATORS ARE DESCRIBED IN Econometric Analysis of Cross Section and Panel Data 2^nd ed. by Jeffrey M. Wooldridge (MIT Press, 2010, 2002), INCLUDING A MODEL-BASED BASED ON INVERSE-PROBABILITY WEIGHTING (SIMILAR TO THE HORVITZ-THOMPSON ESTIMATOR OF SAMPLE SURVEY) AND TWO REGRESSION ESTIMATORS. THESE WILL BE DISCUSSED IN THE NEXT SECTION.

ADVANTAGES (STRENGTHS, USES) OF THE R&R APPROACH

SIGNIFICANT FEATURES / BENEFITS / ADVANTAGES OF THE R&R APPROACH INCLUDE THE FOLLOWING (SEE R&R OP. CIT. FOR DETAILS):

1. TO OBTAIN THE BENEFITS OF PROPENSITY SCORE MATCHING, WE MAY MATCH ON THE PROPENSITY SCORE PLUS ANY COMPONENTS OF X. FOR EXAMPLE, IF SEX IS ONE OF THE COMPONENTS OF X, WE MAY MATCH ON THE PS AND SEX, AND OBTAIN UNBIASED ESTIMATES OF ATE WITH EACH SEX CATEGORY. WE MAY STRATIFY / MATCH ON THE PS AND ANYTHING FINER (I.E., ON (PS,X)). WE CAN MATCH ON THE PS PLUS ADDITIONAL VARIABLES TO ESTIMATE IMPACT ON SUBPOPULATIONS, OR TO STRATIFY TO IMPROVE PRECISION AND POWER.

2. IT IS EASIER TO PRESENT AND EXPLAIN RESULTS IN TERMS OF MATCHED TREATMENT AND CONTROL GROUPS, THAN TO PRESENT AND EXPLAIN MORE COMPLEX MODELS, SUCH AS REGRESSION MODELS.

3. MATCHING CAN BE USED BOTH TO REDUCE BIAS AND TO INCREASE PRECISION. THE PRECISION INCREASES AS THE DIFFERENCE BETWEEN THE TREATMENT AND CONTROL GROUPS MATCHED ON X DECREASES.

4. MATCHING CAN BE USED TO REDUCE MODEL DEPENDENCE ON THE CHARACTERISTICS OF THE EXPLANATORY VARIABLES. MODEL-BASED ADJUSTMENT (REGRESSION ADJUSTMENT) ON MATCHED SAMPLES IS LESS AFFECTED BY MODEL SPECIFICATION ERRORS THAN MODEL-BASED ADJUSTMENT ON RANDOM SAMPLES.

5. IN STUDIES WITH A LARGE POOL OF POTENTIAL CONTROLS AND MANY CONFOUNDING VARIABLES, BUT A LIMITED SAMPLE SIZE FOR ANALYSIS, IT IS FEASIBLE TO REDUCE CONFOUNDING OF VARIABLES BY MULTIVARIATE MATCHING, WHEREAS IT MAY BE DIFFICULT TO CONTROL FOR CONFOUNDING IN ANALYSIS BECAUSE OF A SMALL SAMPLE SIZE, AND LIMITED OPPORTUNITY FOR CULLING, PRUNING OR TRIMMING THE COVARIATES.

(NOTE. IT IS QUITE ACCEPTABLE TO CULL, PRUNE OR TRIM THE EXPLANATORY VARIABLES ON WHICH A MODEL IS BASED. (THIS IS MATCHING TO REDUCE MODEL DEPENDENCE (DISCUSSED IN A PRESENTATION ON ANALYSIS).) IT IS NOT ACCEPTABLE TO DO THIS FOR THE DEPENDENT (RESPONSE, EXPLAINED) VARIABLE. AS NOTED EARLIER, THE PROCESS OF MATCHING AND COVARIATE ADJUSTMENT (REGRESSION ANALYSIS) TO REDUCE MODEL DEPENDENCE ARE DOUBLY ROBUST, IN THE SENSE THAT IF THE MATCHING IS CORRECT OR IF THE REGRESSION MODEL IS CORRECT (BUT NOT NECESSARILY BOTH) THEN THE ESTIMATE OF ATE WILL BE CORRECT.)

THE STRATIFICATION AND COVARIATE-ADJUSTMENT APPROACHES TO IMPACT ESTIMATION ARE NOT FUNDAMENTALLY DIFFERENT. BOTH INVOLVE THE USE OF THE GENERAL LINEAR STATISTICAL MODEL OR STANDARD SAMPLE-SURVEY ESTIMATION PROCEDURES. THE STRATIFICATION METHOD WOULD TYPICALLY INVOLVE DESIGN-BASED ESTIMATES, AND THE COVARIATE-ADJUSTMENT METHOD WOULD TYPICALLY INVOLVE MODEL-BASED ESTIMATES.

RECALL THAT IN ORDER TO MAKE VALID INFERENCES ABOUT THE EFFECT OF FORCED CHANGES IN VARIABLES ON OUTCOME, IT IS NECESSARY TO ESTIMATE THE EFFECTS FROM DATA IN WHICH FORCED CHANGES HAVE BEEN MADE.

THE R&R APPROACH TO CAUSAL MODELING IS ON A STRONG FOOTING IN THIS REGARD. THE ONLY EXPLANATORY VARIABLES IN THE MODEL ARE TREATMENT AND THE ESTIMATED PROPENSITY SCORE. BY DEFINITION, THESE TWO ARE UNCORRELATED, SO THERE IS NO CONFOUNDING. BY ASSUMPTION, THERE ARE NO UNOBSERVED VARIABLES AFFECTING TREATMENT AND RESPONSE. THE ONLY POLICY-RELEVANT VARIABLE IN THE MODEL IS THE TREATMENT VARIABLE, WHICH REPRESENTS THE PROGRAM INTERVENTION. THAT IS, FOR THE EXPLANATORY VARIABLE, FORCED CHANGES ARE BEING MADE. (AS WE WILL SEE, THIS SITUATION DIFFERS MARKEDLY FOR THE HECKMAN APPROACH, WHERE THERE MAY BE EXPLANATORY VARIABLES IN THE MODEL, WITH CONFOUNDING AND FOR MANY OF THEM, IT MAY BE DIFFICULT TO ESTIMATE THE EFFECT OF MAKING FORCED CHANGES FROM PASSIVELY OBSERVED DATA, YET IT IS DESIRED TO PREDICT THE EFFECT OF MAKING FORCED CHANGES.)

WEAKNESSES AND LIMITATIONS OF THE R&R APPROACH

THE CITED REFERENCE BY HECKMAN (“ECONOMETRIC EVALUATION OF SOCIAL PROGRAMS”) PRESENTS A LIST AND DISCUSSION OF THE LIMITATIONS AND WEAKNESSES OF THE R&R APPROACH. THESE ARE SUMMARIZED AS FOLLOWS:

ASSUMPTIONS OF THE R&R APPROACH:

1. THE R&R APPROACH IS INTENDED FOR EX POST ESTIMATION OF IMPACT OF A SPECIFIC PROGRAM INTERVENTION USING HISTORICAL DATA, NOT FOR PREDICTION OF THE EFFECT OF MAKING CHANGES IN POLICY VARIABLES EITHER IN THE ENVIRONMENT FROM WHICH THE DATA CAME OR FOR OTHER ENVIRONMENTS.

2. THE MECHANISM FOR ASSIGNMENT TO TREATMENT IS NOT EXPLICITLY IDENTIFIED, BEYOND IDENTIFICATION OF THE COVARIATES ON WHICH ASSIGNMENT DEPENDS.

3. NO GENERAL EQUILIBRIUM EFFECTS (NO “MACRO-LEVEL” EFFECTS, I.E., THE STABLE UNIT-TREATMENT-VALUE ASSUMPTION (SUTVA)).

4. NO SIMULTANEOUS CAUSAL RELATIONSHIPS.

THE REFERENCE CITES THE FOLLOWING ADVANTAGES OF THE HECKMAN APPROACH.

ADVANTAGES OF THE HECKMAN APPROACH:

1. A MORE DETAILED FRAMEWORK FOR REPRESENTING SELECTION FOR TREATMENT, AND FOR ASSESSING ESTIMABILITY.

2. ALLOWS FOR ANALYSIS OF SUBJECTIVE EVALUATIONS OF OUTCOMES IN SELECTION FOR TREATMENT.

3. MAY BE USED TO EVALUATE BOTH EX POST AND EX ANTE EVALUATION OF TREATMENT. MAY BE USED TO PREDICT THE EFFECT OF NEW POLICIES, OR OF OLD POLICIES ON NEW ENVIRONMENTS.

4. ALLOWS FOR ESTIMATION OF THE DISTRIBUTION OF TREATMENT EFFECTS, NOT JUST THE MEAN TREATMENT EFFECT.

5. ALLOWS FOR IDENTIFICATION OF DISTRIBUTIONAL CRITERIA FOR ANALYSIS OF ALTERNATIVE FUNCTIONS OF OUTCOME DISTRIBUTIONS.

6. ALLOWS FOR SIMULTANEOUS CAUSAL RELATIONSHIPS.

7. PARAMETERS ARE DEFINED WITHOUT REFERENCE TO EXPERIMENTAL MANIPULATIONS (E.G., DEFINING A CAUSAL EFFECT AS THE EFFECT ON A RANDOMLY SELECTED INDIVIDUAL).

8. RECOGNITION THAT THE ANALYSIS FRAMEWORK SHOULD BE TAILORED TO THE EVALUATION GOALS (E.G., IF ALL THAT IS DESIRED IS AN ESTIMATE OF THE MEAN EFFECT OF TREATMENT, IT IS NOT NECESSARY TO DEVELOP A FULLY SPECIFIED ECONOMETRIC MODEL; “MARSCHAK’S MAXIM”).

IMPLICATIONS OF THE R&R APPROACH FOR SAMPLE SURVEY DESIGN AND MATCHING

THE PRECEDING DISCUSSION HAS SHOWN THAT TO REDUCE BIAS AND INCREASE PRECISION IT IS IMPORTANT TO MATCH ON VARIABLES THAT AFFECT SELECTION FOR TREATMENT. MATCHING HELPS ASSURE A “COMMON SUPPORT,” OR “OVERLAP” IN THE DISTRIBUTIONS OF MATCH VARIABLES FOR THE TREATED AND UNTREATED SAMPLES. MATCHING ON THE PROPENSITY SCORE ASSISTS REDUCTION OF BIAS BUT MAY OR MAY NOT INCREASE PRECISION, AND MATCHING ON COVARIATES GENERALLY INCREASES PRECISION.

IF THE GOAL IS TO IMPLEMENT THE R&R APPROACH, THEN MATCHING ON THE PROPENSITY SCORE ESTIMATED FROM OBSERVABLES IS ACCEPTABLE, BUT IT IS RECOMMENDED ALSO TO MATCH AND STRATIFY ON VARIABLES THAT ARE CONSIDERED, BASED ON A CAUSAL MODEL, TO HAVE AN IMPORTANT RELATIONSHIP TO OUTCOMES OF INTEREST. THIS MAY IMPROVE PRECISION OF IMPORTANT ESTIMATES (VIA RATIO OR REGRESSION ESTIMATES). ALSO, STRATIFY ON ANY VARIABLES THAT ARE DESIRED TO BE USED TO ESTIMATE IMPACT OVER SUBPOPULATIONS OF INTEREST, SUCH AS MALES AND FEMALES, AGE, EDUCATION, REGION AND TREATMENT MODALITIES, IF IT IS DESIRED TO COMPARE THEM.

TO SUMMARIZE:

CONSIDERATION OF THE R&R APPROACH TO CAUSAL ANALYSIS SUGGESTS THAT FOR THE DESIGN:

1. STRATIFY ON THE PROPENSITY SCORE TO REDUCE BIAS.

2. STRATIFY ALSO ON OTHER VARIABLES (I.E., ON A FINER BALANCING SCORE) TO IMPROVE PRECISION AND POWER, EITHER FOR ESTIMATES OVER THE FULL POPULATION OR FOR SUBPOPULATIONS OF INTEREST.

PRECISION AND POWER ARE INCREASED BY USING ESTIMATES SUCH AS RATIO AND REGRESSION ESTIMATES. THESE ESTIMATES MAY BE CONSTRUCTED WITHIN EACH PROPENSITY-SCORE STRATUM, OR OUTSIDE OF THEM (E.G., IN A REGRESSION MODEL THAT INCLUDES THE PROPENSITY SCORE AND OTHER COVARIATES).

4.10. THE HECKMAN (ECONOMETRIC) APPROACH TO STATISTICAL CAUSAL MODELING AND ANALYSIS

IN THE PRECEDING (APPLYING THE R&R METHODOLOGY TO PERFORM STATISTICAL CAUSAL ANALYSIS OF PASSIVELY OBSERVED DATA), THE PROPENSITY SCORE IS ALWAYS CONDITIONAL ON A PARTICULAR SET OF COVARIATES X. (IF THE PROPENSITY SCORE IS KNOWN UNCONDITIONALLY (I.E., P(W = 1) IS KNOWN FOR EACH OBSERVATION, AS IN AN EXPERIMENTAL DESIGN), THEN AN UNBIASED ESTIMATE MAY BE DETERMINED BY AVERAGING DIFFERENCES (SUITABLY ESTIMATED) BETWEEN THE TREATED AND UNTREATED MEANS OVER IT (THE SAME AS FOR THE CONDITIONAL PROPENSITY SCORE, e(X) = P(W=1 | X).) IF (Y₀, Y₁) W |X (I.E., X INCLUDES ALL VARIABLES AFFECTING THE RELATIONSHIP OF THE DISTRIBUTION OF (Y₀, Y₁) TO W), MATCHING ON THE PROPENSITY SCORE CAN REDUCE BIAS SUBSTANTIALLY.

IF THERE ARE UNOBSERVED (HIDDEN) VARIABLES THAT AFFECT SELECTION AND OUTCOME, SO THAT (Y₀, Y₁) IS NOT CONDITIONALLY INDEPENDENT OF W GIVEN ALL OBSERVABLE COVARIATES, THEN MATCHING ON THE PROPENSITY SCORE (WHICH IS BASED ON OBSERVED COVARIATES) WILL HAVE A CORRESPONDINGLY LIMITED EFFECT ON REDUCING SELECTION BIAS.

THE R&R APPROACH DOES NOT ADDRESS WHAT TO DO ABOUT THE ISSUE OF UNOBSERVED VARIABLES. IF THE ASSUMPTION OF CONDITIONAL INDEPENDENCE OF (Y₀, Y₁) AND W GIVEN X IS NOT JUSTIFIED, THE APPROACH IS NOT APPLICABLE. THE HECKMAN APPROACH FOCUSES ATTENTION ON THE ISSUE OF UNOBSERVED VARIABLES, AND ADDRESSES MEANS OF ACCOMMODATING THEM IN CERTAIN CASES.

EXAMPLES OF OBSERVED VARIABLES (FOR DESIGN, PRIOR TO SURVEY): EDUCATION, EXPERIENCE, YEARS OF EMPLOYMENT, AGE, SEX, ASSETS, DEMOGRAPHIC CHARACTERISTICS, GEOGRAPHIC CHARACTERISTICS.

EXAMPLES OF UNOBSERVED (HIDDEN) VARIABLES: MOTIVATION, AMBITION, INTELLIGENCE, CRAFTINESS, PERSISTENCE, DISCIPLINE, TRUSTWORTHINESS, AFFABILITY, ARTICULATENESS, INNATE ABILITIES, FAMILY OR SOCIAL CONTACTS. (PERHAPS “UNRECORDED” WOULD BE A MORE APT DESCRIPTOR THAN “UNOBSERVED.”)

NOTE THAT UNOBSERVED CHARACTERISTICS MAY BE REFLECTED IN (CORRELATED WITH) OBSERVED VARIABLES. FOR EXAMPLE, ACHIEVEMENT OF A HIGH LEVEL OF EDUCATION REQUIRES SOME MEASURE OF ALL OF THE PRECEDING PERSONAL CHARACTERISTICS. SIMPLY BECAUSE A DIRECT MEANS OF OBSERVATION IS NOT AVAILABLE DOES NOT PRECLUDE USEFUL ANALYSIS USING THE R&R APPROACH. IT THE VARIABLE IS REFLECTED IN OBSERVED COVARIATES, THE FACT THAT IT IS UNOBSERVED MAY BE OVERCOME (E.G., THE METHOD OF INSTRUMENTAL VARIABLES).

THE HECKMAN APPROACH TO IMPACT ESTIMATION ADDRESSES THE ISSUE OF UNOBSERVED VARIABLES (IN CERTAIN CASES).

ANOTHER IMPORTANT ADVANTAGE OF THE HECKMAN APPROACH IS THAT IT PROVIDES A FRAMEWORK TO ESTIMATE THE RELATIONSHIP OF OUTCOME TO EXPLANATORY VARIABLES, SUCH AS POLICY-RELEVANT VARIABLES. THE R&R APPROACH IS ORIENTED MAINLY TO ESTIMATING IMPACT (AVERAGE TREATMENT EFFECT) OVER THE POPULATION OR SUBPOPULATIONS. THE HECKMAN APPROACH IS TO ESTIMATE THE RELATIONSHIP OF IMPACT TO POLICY-RELEVANT EXPLANATORY VARIABLES. RECALL THAT IN ORDER TO MAKE VALID INFERENCES ABOUT THE EFFECT OF MAKING FORCED CHANGES IN EXPLANATORY VARIABLES, SUCH AS POLICY-RELEVANT VARIABLES, IT IS NECESSARY TO USE DATA IN WHICH FORCED CHANGES HAVE BEEN MADE IN THOSE VARIABLES. (THIS POINT HAS BEEN MADE A NUMBER OF TIMES, BUT IT BEARS REPEATING, IN VIEW OF THE FACT THAT IT IS FREQUENTLY IGNORED.)

BOTH THE R&R (BALANCING) APPROACH AND THE HECKMAN (ECONOMETRIC) APPROACHES TO CAUSAL MODELING FOCUS ON THE ISSUE OF CONDITIONAL INDEPENDENCE OF RESPONSE AND TREATMENT, GIVEN COVARIATES. THEY ARE BOTH “POTENTIAL OUTCOMES” OR “COUNTERFACTUALS” APPROACHES. THE MAIN DIFFERENCES LIE IN THE FACTS THAT (1) THE HECKMAN APPROACH ADDRESSES THE ISSUE OF UNOBSERVED VARIABLES THAT MAY AFFECT SELECTION FOR TREATMENT, AND THE R&R APPROACH DOES NOT; (2) THE HECKMAN APPROACH CONSIDERS THE DISTRIBUTION OF OUTCOME, NOT JUST THE MEAN IMPACT; AND (3) THE HECKMAN APPROACH CONSIDERS THE RELATIONSHIP OF OUTCOME TO COVARIATES (IN ADDITION TO THE PROPENSITY SCORE).

BOTH APPROACHES ARE VALID ONLY IF AN ASSUMPTION OF CONDITIONAL INDEPENDENCE CAN BE MADE. THE FUNDAMENTAL ISSUE IS WHETHER THE IMPACT (E.G., ATE) IS ESTIMABLE. THE TWO APPROACHES MAKE DIFFERENT ASSUMPTIONS TO ACHIEVE THIS. THE R&R APPROACH ASSUMES THAT THERE ARE NO UNOBSERVED VARIABLES AFFECTING SELECTION FOR TREATMENT. THE HECKMAN APPROACH ALLOWS FOR UNOBSERVED VARIABLES, BY STRUCTURING THE DESIGN (E.G., AS A PANEL SURVEY) SO THAT THEIR PRESENCE DOES NOT INTRODUCE BIAS (E.G., IF THEY ARE TIME-INVARIANT).

BOTH THE BASIC HECKMAN AND R&R APPROACHES ASSUME THAT THE PROBABILITY OF ASSIGNMENT TO TREATMENT NOT BE EQUAL TO 0 OR 1. IF THE ASSUMED REGRESSION MODEL (FOR THE PROPENSITY SCORE) CAN REASONABLY BE ASSUMED TO HOLD FOR OBSERVATIONS HAVING THESE VALUES, THEN THE METHODS MAY BE EXTENDED TO APPLY TO THESE VALUES AS WELL. IF THIS ASSUMPTION CANNOT BE REASONABLY MADE (E.G., A LARGE PROPORTION OF THE SAMPLE HAS VALUES OF THE PROPENSITY SCORE EQUAL TO ZERO OR ONE (FOR ESTIMATION OF ATE, EQUAL TO 1 FOR ESTIMATION OF ATT)), THEN OTHER APPROACHES MUST BE USED (E.G., A REGRESSION DISCONTINUITY DESIGN).

SUMMARY DESCRIPTION OF THE HECKMAN APPROACH TO CAUSAL MODELING

THE R&R APPROACH DESCRIBES A CAUSAL MODEL IN VERY SIMPLE TERMS. IT SIMPLY IDENTIFIES THE COVARIATES X ON WHICH SELECTION DEPENDS (I.E., FOR WHICH CONDITIONAL INDEPENDENCE OF (Y₀, Y₁) AND W HOLDS, GIVEN X), AND THEN AVERAGES (STRATIFIES, REGRESSES OR AVERAGES OVER THE SAMPLE) OVER THOSE VARIABLES (OR A SUITABLE FUNCTION, SUCH AS THE PROPENSITY SCORE) TO OBTAIN AN UNBIASED ESTIMATE OF IMPACT. THE R&R APPROACH MAKES A MINIMAL NUMBER OF ASSUMPTIONS ABOUT COVARIATES. THE KEY ASSUMPTION IS THAT CONDITIONAL INDEPENDENCE HOLDS. IF THIS ASSUMPTION IS NOT VALID – IT THERE ARE VARIABLES IN THE MODEL ERROR TERM CORRELATED WITH W AFTER TAKING INTO ACCOUNT X, THEN THE METHOD DOES NOT APPLY, AND THE ATE ESTIMATE WOULD NOT BE UNBIASED (EITHER FOR THE STRATIFICATION APPROACH OR THE COVARIATE-ADJUSTMENT APPROACH).

THE HECKMAN APPROACH DESCRIBES THE CAUSAL MODEL IN MORE DETAIL THAN THE R&R APPROACH. WHILE BOTH THE R&R AND HECKMAN APPROACHES ARE BASED ON SELECTION MODELS (E.G., LOGISTIC OR PROBIT MODELS OF SELECTION), THE HECKMAN APPROACH ALSO USES AN EXPLICIT (ECONOMETRIC) OUTCOME MODEL. IT DOES NOT RESTRICT ATTENTION TO OBSERVED COVARIATES THAT AFFECT SELECTION FOR TREATMENT. IT POSITS COMPLETE, ALL-CAUSES SELECTION AND OUTCOME MODELS, WHICH MAY OR MAY NOT INCLUDE UNOBSERVED VARIABLES, AND SEEKS CONDITIONS ON THE MODEL FOR WHICH A SPECIFIED IMPACT MEASURE (E.G., ATE) IS ESTIMABLE, EVEN IF UNOBSERVED VARIABLES ARE PRESENT. THE WAY THAT IT DOES THIS IS AS FOLLOWS.

IN CONTRAST TO THE R&R APPROACH, WHICH IS COMPACTLY DESCRIBED IN A SINGLE ARTICLE, THE HECKMAN APPROACH IS DESCRIBED IN MANY DIFFERENT ARTICLES, WHICH ADDRESS A VARIETY OF SPECIFIC APPLICATIONS. THE BASIC THEORY IS PRESENTED IN HANDBOOK OF ECONOMETRICS (OP. CIT.). FOR A DISCUSSION OF A MODEL VERSION THAT IS BASED ON THE ASSUMPTION THAT MODEL RESIDUALS ARE NORMALLY DISTRIBUTED, SEE GREENE OP. CIT. FOR AN EXAMPLE OF A PARTICULAR APPLICATION, SEE “CHOOSING AMONG ALTERNATIVE NONEXPERIMENTAL METHODS FOR ESTIMATING THE IMPACT OF SOCIAL PROGRAMS: THE CASE OF MANPOWER TRAINING,” BY JAMES J. HECKMAN AND V. JOSEPH HOTZ, JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, VOL. 84, NO. 408 (DEC. 1989), PP. 862-874; OR “ESTIMATING TREATMENT EFFECTS FOR DISCRETE OUTCOMES WHEN RESPONSES TO TREATMENT VARY; AN APPLICATION TO NORWEGIAN VOCATIONAL REHABILITATION PROGRAMS” BY ARILD AAKVIK, JAMES J. HECKMAN AND EDWARD J. VYTLACIL, JOURNAL OF ECONOMETRICS 125 (2005), PP. 15-51.

BEFORE DESCRIBING THE HECKMAN APPROACH, WE SHALL SUMMARIZE SOME FEATURES OF THE R&R APPROACH, DEALING WITH REGRESSION ESTIMATES.

THE R&R STATEMENT OF CONDITIONAL INDEPENDENCE OF RESPONSE GIVEN THE COVARIATES X, (Y₀, Y₁) W | X, MAY BE WRITTEN AS

Y₀ = f₀(X, E₀)

Y₁ = f₁(X, E₁)

WHERE X IS A VECTOR OF OBSERVED COVARIATES AND E₀ E₁. MORE SPECIFICALLY, WE MAY WRITE

Y₀ = f₀(g(X), E₀)

Y₁ = f₁(g(X), E₁)

WHERE g(X) IS THE PROPENSITY SCORE GIVEN X (AND E₀ E₁).

THE BASIC VERSION OF THE R&R MODEL IS TO STRATIFY OVER THE PROPENSITY SCORE, AND ESTIMATE ATE AS A STRATUM-WEIGHTED AVERAGE OF THE ATEs IN EACH STRATUM. ANOTHER VERSION OF THIS MODEL (THE “COVARIATE ADJUSTED” VERSION) CONSISTS OF A REGRESSION EQUATION INCLUDING THE PROPENSITY SCORE AS AN EXPLANATORY VARIABLE:

Y₀ = α₀₁ + α₀₂ g(X) + E₀

Y₁ = α₁₁ + α₁₂ g(X) + E₁.

IN THIS FORM, AS A REGRESSION EQUATION, ONE IS REMINDED OF THE FACT THAT FOR ORDINARY-LEAST-SQUARES ESTIMATES OF THE MODEL PARAMETERS (REGRESSION COEFFICIENTS) TO BE UNBIASED, THE EXPLANATORY VARIABLES IN THE MODEL MUST BE UNCORRELATED WITH THE MODEL ERROR TERMS (E_i), I.E., THERE MUST BE NO UNOBSERVED VARIABLES CORRELATED WITH THE EXPLANATORY VARIABLES OF THE MODEL. THE ONLY TWO EXPLANATORY VARIABLES OF THIS MODEL ARE TREATMENT (REPRESENTED BY THE TWO EQUATIONS) AND THE PROPENSITY SCORE g(X), AND IT IS ASSUMED THAT (Y₀, Y₁) ARE INDEPENDENT OF TREATMENT, GIVEN g(X), SO THE ASSUMPTION HOLDS.

AS DESCRIBED EARLIER, SOME OF THE OBSERVED COVARIATES, DENOTED BY X₁, MAY BE INCLUDED AS EXPLANATORY VARIABLES, SEPARATE FROM THE PROPENSITY SCORE. THIS FOLLOWS SINCE MATCHING MAY BE DONE ON ANY BALANCING SCORE FINER THAN THE PROPENSITY SCORE. THAT IS, MATCHING MAY BE DONE BY SUBCLASSIFICATION (STRATIFICATION) ON THE PROPENSITY SCORE AND THE COVARIATE X₁, OR IT MAY BE DONE AS A REGRESSION MODEL:

Y₀ = X₁’β₀ + α₀₁ + α₀₂ g(X) + E₀

Y₁ = X₁’β₁ + α₁₁ + α₁₂ g(X) + E₁

WHERE β₀ AND β₁DENOTE VECTORS OF PARAMETERS. IF X₁ IS A SUBSET OF X THEN, TO AVOID MULTICOLLINEARITY, THIS MUST BE DONE IN SUCH A WAY THAT X₁ AND g(X) ARE NOT LINEARLY DEPENDENT (E.G., X CONTAINS A COVARIATE NOT INCLUDED IN X₁, OR g(X) IS A NONLINEAR FUNCTION OF X). (SEE R&R, OP. CIT.)

ALTHOUGH THE R&R MODEL MAY BE REPRESENTED AS A REGRESSION MODEL INCLUDING THE PROPENSITY SCORE AND OTHER COVARIATES, THAT IS NOT THE FOCUS OF THE APPROACH. IN THE ORIGINAL R&R MODEL, THE ONLY EXPLANATORY VARIABLE INCLUDED IN THE REGRESSION MODEL WAS THE PROPENSITY SCORE.

THE R&R APPROACH FOCUSES ON A MODEL OF THE PROBABILITY OF SELECTION (ASSIGNMENT TO TREATMENT). IN CONTRAST, THE HECKMAN APPROACH FOCUSES EQUALLY ON MODELS OF BOTH THE PROBABILITY OF SELECTION AND THE OUTCOME. THE SELECTION MODEL IS THE SAME AS THAT USED IN THE R&R APPROACH – A GENERALIZED LINEAR MODEL (LOGIT OR PROBIT “LATENT VARIABLE” MODEL). A SIMPLE VERSION OF THE HECKMAN APPROACH IS AS FOLLOWS.

WE SHALL DESCRIBE TWO VERSIONS OF THE HECKMAN APPROACH: ONE THAT ASSUMES THAT THE MODEL ERROR TERMS IN BOTH THE SELECTION MODEL AND THE OUTCOME MODEL ARE NORMALLY DISTRIBUTED, AND ONE IN WHICH THIS ASSUMPTION IS NOT MADE.

THE HECKMAN APPROACH, ASSUMING NORMALITY

IF NORMALITY OF THE MODEL ERRORS IS ASSUMED, THE STRAIGHTFORWARD APPROACH TO ESTIMATING IMPACT WOULD BE TO WRITE DOWN THE FULL LIKELIHOOD FOR THE OBSERVATIONS (INCLUDING THE PROBABILITY OF SELECTION, AND THE PROBABILITY OF OUTCOME GIVEN SELECTION), AND ESTIMATE THE MODEL PARAMETERS BY THE METHOD OF MAXIMUM LIKELIHOOD. THE SOLUTION TO THIS OPTIMIZATION PROBLEM WOULD REQUIRE NUMERICAL ANALYSIS. THE MAXIMUM-LIKELIHOOD ESTIMATOR IS CONSISTENT. THIS APPROACH OF WORKING WITH THE COMPLETE LIKELIHOOD FUNCTION IS CALLED THE FULL-INFORMATION MAXIMUM LIKELIHOOD (OR FIML) APPROACH.

FOR REASONS THAT ARE NOT ENTIRELY CLEAR, STATISTICAL ANALYSTS TEND TO AVOID ESTIMATION PROCEDURES THAT INVOLVE NUMERICAL METHODS, SUCH AS MAXIMUM LIKELIHOOD AND THE EXPECTATION-MAXIMIZATION (EM) METHOD, AND PREFER ESTIMATION APPROACHES THAT INCLUDE THE GENERAL LINEAR STATISTICAL MODEL AND EXTENSIONS, EVEN THOUGH THE NUMERICAL METHODS MAY BE SUPERIOR. AS AN ALTERNATIVE TO THE MAXIMUM LIKELIHOOD ESTIMATION PROCEDURE, HECKMAN DETERMINED A “TWO-STEP” ESTIMATION PROCEDURE FOR THE PRECEDING MODEL. IN THE FIRST STEP, THE PARAMETERS OF THE SELECTION MODEL ARE ESTIMATED USING A GENERALIZED LINEAR STATISTICAL MODEL, AND THEN, IN THE SECOND STEP, THE PARAMETERS OF THE OUTCOME MODEL ARE ESTIMATED USING A GENERAL LINEAR STATISTICAL MODEL, GIVEN THE PARAMETER ESTIMATES OBTAINED IN THE FIRST STEP. GREENE (OP. CIT., PP. 872-878) DESCRIBES THIS MODEL. IT IS SUMMARIZED AS FOLLOWS:

Selection model:

z_i* = w_i’ϒ + u_i, z_i =1 if z_i* > 0 and 0 otherwise;

P(z_i = 1 | w_i) = Φ(w_i’ϒ); and

P(z_i = 0 | w_i) = 1 – Φ(w_i’ ϒ).

Outcome model:

y_i = x_i’ β + є_i observed only if z_i = 1,

(u_i, є_i) ~bivariate normal (0,0,1,σ_є,ρ).

Φ denotes the cumulative normal distribution function. z_i and w_i are observed for a random sample of units, and y_i is observed only when z_i =1. The parameter ϒ is estimated by the method of maximum likelihood. For each observation in the sample calculate and , where φ denotes the normal density function. Estimate β and β_λ = ρσ_є by least-squares regression of y on x and . (The quantities are involved in the estimation of σ_є² and ρ separately.)

THE TWO-STEP APPROACH (A “SWITCHING REGRESSION MODEL”) IS A STANDARD APPROACH IN ESTIMATION (IT IS A SPECIAL CASE OF M-ESTIMATION – SEE WOOLDRIDGE OP. CIT. FOR DETAILS). THE ESTIMATES ARE NOT AS EFFICIENT AS THE FULL-INFORMATION MAXIMUM LIKELIHOOD ESTIMATES. THE PRECEDING TWO-STEP HECKMAN MODEL IS CALLED THE “HECKIT” MODEL (IT IS AN INSTANCE OF A TOBIN TYPE II MODEL, REFERRED TO AS A “TOBIT” MODEL, HENCE THE “HECKIT” DIMINUTIVE.) IT IS ALSO CALLED THE “HECKMAN CORRECTION” METHOD. EITHER THE FIML OR THE TWO-STEP ESTIMATE MAY BE OBTAINED IN STANDARD STATISTICAL COMPUTER SOFTWARE PROGRAMS, SUCH AS STATA.

IT IS WELL KNOWN THAT THE NORMALITY ASSUMPTION IS A CRUCIAL ONE IN THE PRECEDING MODEL. THE RESULTS ARE VERY SENSITIVE TO DEPARTURES FROM NORMALITY. THE REASON FOR THIS IS THAT ATTENTION FOCUSES ON THE TAILS OF THE ERROR DISTRIBUTION (I.E., ON PROBABILITIES CALCULATED UNDER THE NORMAL DISTRIBUTION).

WE SHALL NOW DESCRIBE A MORE GENERAL VERSION OF THE HECKMAN APPROACH, WHICH DOES NOT ASSUME NORMALITY, AND WHICH IN SOME CASES ALLOWS FOR UNOBSERVED VARIABLES THAT AFFECT BOTH SELECTION AND OUTCOME.

THE HECKMAN APPROACH, NOT ASSUMING NORMALITY

SUPPOSE THAT THE PROPENSITY SCORE (PROBABILITY OF SELECTION FOR TREATMENT) IS A FUNCTION OF OBSERVED VARIABLES Z AND UNOBSERVED VARIABLES U, I.E., THE PROPENSITY SCORE IS DENOTED AS g(Z, U). THE PROPENSITY SCORE MAY BE ESTIMATED USING A LOGISTIC REGRESSION OR A TOBIT MODEL (AS DONE FOR THE HECKMAN TWO-STEP MODEL). SUPPOSE THAT THE OUTCOME (Y₀(X,U), Y₁(X,U)) DEPENDS ON OBSERVED VARIABLES X AND UNOBSERVED VARIABLES U. THE VECTORS Z AND X MAY OVERLAP, I.E., CONTAIN SOME (OR ALL) OF THE SAME COMPONENT VARIABLES.

FOR SIMPLICITY, WE ASSUME AN OUTCOME MODEL OF THE FORM

Y₀ = X’β₀ + f₀(g(Z, U)) + h₁(U) + E₀

Y₁ = X’β₁ + f₁(g(Z, U)) + h₂(U) + E₁

WHERE THE ERROR TERMS E₀AND E₁ ARE INDEPENDENT (GIVEN Z, U). THAT IS, THIS REPRESENTATION ASSUMES INDEPENDENCE OF Y₀ AND Y₁, GIVEN THE PROPENSITY SCORE AND THE UNOBSERVED VARIABLES U. THE TERMS f₀ AND f₁ REPRESENT “FLEXIBLE” REGRESSION MODELS USING THE PROPENSITY SCORE. IT IS REQUIRED THAT THESE TERMS NOT BE CORRELATED WITH X (OR ELSE THE RIGHT-HAND SIDE OF THE EQUATION WILL INVOLVE COLLINEAR REGRESSORS). (THIS REQUIREMENT MAY BE SATISFIED IF THE FUNCTIONS h_i ARE NONLINEAR OR IF THE PROPENSITY SCORE MODEL DOES NOT CONTAIN ALL OF THE VARIABLES USED IN THE OUTCOME MODEL.)

THE ADDITIONAL COMPLEXITY THAT THE HECKMAN APPROACH ALLOWS (OVER THE R&R APPROACH) IS THE UNOBSERVED VARIABLES, U THAT AFFECT BOTH SELECTION (g) AND OUTCOME (Y₀, Y₁). BUT FOR THEM, THIS WOULD BE THE SAME MODEL AS USED BY R&R (EXCEPT THAT THE STRATIFICATION IS REPRESENTED BY THE INITIAL TERMS IN THE REGRESSION MODEL).

THE ISSUE IS HOW TO ESTIMATE Y₀ AND Y₁ GIVEN THE UNOBSERVED VARIABLES, THE Us. THE FIRST STEP IS TO REPLACE g(Z,U) BY AN ESTIMATE , THAT IS BASED SOLELY ON OBSERVABLES. THE MODEL THEN BECOMES:

Y₀ = X’β₀ + f₀() + h₁(U) + E₀

Y₁ = X’β₁ + f₁()) + h₂(U) + E₁.

THE TERMS INVOLVING ARE NOT CORRELATED WITH THE MODEL ERROR TERMS (E_i), SINCE THE MODEL ERROR TERMS ARE INDEPENDENT GIVEN (Z, U). THE VARIABLE AS , MAY BE VIEWED AS AN INSTRUMENTAL VARIABLE FOR g(Z, U) (I.E., IT IS A VARIABLE THAT IS CORRELATED WITH THE RESPONSE VARIABLES Y_i BUT NOT CORRELATED WITH THE MODEL ERROR TERMS, GIVEN Z).

WHAT REMAINS IS TO ADDRESS THE h_i(U) TERMS, WHICH DEPEND ON UNOBSERVABLES (Us). TO ADDRESS THIS PROBLEM, THE HECKMAN APPROACH UTILIZES (FOR EXAMPLE) A SURVEY DESIGN AND MODEL ESTIMATORS (ESTIMATING EQUATION) SUCH THAT THE h(.) TERMS DROP OUT. WE SHALL ILLUSTRATE THIS IN THE CASE OF A TWO-ROUND PANEL SURVEY (IN WHICH THE SAME UNITS ARE INTERVIEWED IN BOTH SURVEY ROUNDS).

FOR A TWO-ROUND PANEL SURVEY, A SIMPLE LINEAR MODEL OF OUTCOME IS THE FOLLOWING:

Y_0t = X_t’β₀ + f₀() + t f₃() + h₁(U) + E₀

Y_1t = X_t’β₁ + f₁()) + t f₄() + h₂(U) + E₁.

IN THIS CASE, THE β PARAMETERS MAY BE ESTIMATED FROM AN ESTIMATING EQUATION FORMED BY TAKING DIFFERENCES OF MATCHING UNITS BETWEEN THE TWO SURVEY ROUNDS:

ΔY₀ = ΔX’β₀ + f₃() + ΔE₀

ΔY₁ = ΔX’β₁ + f₄()) + ΔE₁.

NOTE THAT THE TERMS INVOLVING U DROP OUT (SINCE U IS ASSUMED TO BE TIME-INVARIANT), AND THE TERMS INVOLVING f₀ AND f₁ DROP OUT (SINCE THE PROPENSITY SCORE IS ESTIMATED FROM DATA FOR THE FIRST SURVEY ROUND).

A REMAINING PROBLEM IS THAT SINCE AND Y_i (i = 0, 1) BOTH DEPEND ON SOME OF THE SAME VARIABLES, THE EXPLANATORY VARIABLES OF THE RESPONSE VARIABLES Y_i MAY BE LINEARLY DEPENDENT. THIS PROBLEM IS RESOLVED UNDER THE (EXCLUSION) RESTRICTION THAT BE BASED ON AT LEAST ONE VARIABLE NOT INCLUDED IN X. THE ESTIMATED PROPENSITY SCORE IS HENCE A SO-CALLED “INSTRUMENTAL VARIABLE” – A VARIABLE CORRELATED WITH Y_i GIVEN Z, BUT INDEPENDENT OF THE ERROR TERM E_i. (IF f₃ AND f₄ ARE NONLINEAR FUNCTIONS, IT MAY NOT BE NECESSARY TO INVOKE THE EXCLUSION RESTRICTION.)

IF IT CANNOT BE REASONABLY ASSUMED THAT THE UNOBSERVED VARIABLES, U, THAT AFFECT BOTH SELECTION FOR TREATMENT AND OUTCOME ARE TIME-INVARIANT, THEN THE FIRST-DIFFERENCE METHOD DOES NOT APPLY. IN THAT CASE, THE HECKMAN APPROACH IS BASED ON “SELECTION ON OBSERVABLES,” NOT “SELECTION ON UNOBSERVABLES.” THE MODEL IN THAT CASE IS

Y_0t = X_t’β₀ + f₀() + t f₃() + E₀

Y_1t = X_t’β₁ + f₁()) + t f₄() + E₁

(I.E., THE h(U) TERMS ARE NOT PRESENT).

THE IMPACT (ATE) IS ESTIMATED BY FORMING THE SAMPLE AVERAGE OF ΔY₀ AND ΔY₁, AND TAKING THE DIFFERENCE. THE ATT IS ESTIMATED BY FORMING THESE AVERAGES OVER THE TREATED (W=1) SUBSAMPLE. NOTE THAT W DOES NOT EXPLICITLY APPEAR IN THE PRECEDING EQUATION: IT IS REPRESENTED BY TAKING THE MEAN OVER THE TWO SAMPLES, W = 0 AND W = 1. FOR THIS APPROACH TO WORK, IT IS ESSENTIAL THAT THE SAMPLE OF UNITS BE A PROBABILITY SAMPLE OVER THE ENTIRE POPULATION OF INTEREST.

THE PRECEDING LINEAR-MODEL REPRESENTATION MAY SEEM A LITTLE FORMIDABLE. A STANDARD IMPLEMENTATION OF THE APPROACH FOR A SINGLE ROUND OF DATA (NO TIME-INVARIANT UNOBSERVED (U) VARIABLES) IS TO REGRESS OUTCOME, Y, ON 1, W, PS OR ON 1, W, PS, W(PS-). FOR A PANEL SURVEY (TIME-INVARIANT U VARIABLES ALLOWED IN FIRST DIFFERENCE MODELS), THE IMPACT IS THE COEFFICIENT ON THE INTERACTION OF TREATMENT AND TIME (SURVEY ROUND), I.E., THE REGRESSION OF Y IS ON 1, W, PS, R x W, R x (PS-), R x W x (PS-) OR ON 1, W, PS, R x W, R x (PS-), R x W x PS, W(PS-). THE INTERACTION TERMS WITH PS ARE DEMEANED SO THAT THE IMPACT IS THE COEFFICIENT ON THE R x W TERM. FOR A FIRST-DIFFERENCE (“FIXED-EFFECTS”) MODEL, ALL TIME-INVARIANT VARIABLES DROP OUT (I.E., 1, W, AND PS DROP OUT, WHERE W IS DEFINED IN THE FIRST ROUND (AND HAS THE SAME VALUE IN THE SECOND ROUND). THESE MODELS MAY BE ESTIMATED, FOR EXAMPLE, USING THE STATA xtreg PANEL-REGRESSION PROGRAM. (SEE WOOLDRIDGE OP. CIT. FOR A DISCUSSION OF THESE APPROACHES.)

ADVANTAGES (STRENGTHS, USES) OF THE HECKMAN APPROACH

IN SUMMARY, THE HECKMAN APPROACH ALLOWS UNOBSERVED VARIABLES ONLY IN SPECIAL CASES IN WHICH THEY “DROP OUT” OF THE MODEL ESTIMATING EQUATION, SO THAT Y₀ AND Y₁ CAN BE ESTIMATED. WHILE THIS MAY APPEAR TO BE A TRIVIAL EXTENSION OF THE R&R APPROACH, IT IN FACT REPRESENTS A RATHER SIGNIFICANT EXTENSION, SINCE IN MANY PROGRAM-EVALUATION APPLICATIONS THE UNOBSERVED VARIABLES ARE TIME-INVARIANT.

THE MODEL IS HENCE “IDENTIFIED,” (Y₀, Y₁) ARE INDEPENDENT GIVEN X AND Z, AND THE IMPACT IS ESTIMABLE AS THE DIFFERENCE BETWEEN Δ AND Δ. THE PROPENSITY SCORE EXPLANATORY VARIABLE IS AN ESTIMATE. FOR LARGE SAMPLES, ITS SAMPLING ERROR WILL BE SMALL, SO THIS PRESENTS NO PROBLEM. FOR SMALL SAMPLES, THIS IS AN “ERRORS IN VARIABLES” SITUATION, WHICH INTRODUCES BIAS (AN “INSTRUMENTAL-VARIABLES” BIAS).

THE HECKMAN APPROACH IS MORE GENERAL THAN THE R&R APPROACH IN SEVERAL WAYS. IT ALLOWS FOR, IN CERTAIN SITUATIONS, THE POSSIBILITY OF UNOBSERVED VARIABLES THAT AFFECT BOTH SELECTION FOR TREATMENT AND OUTCOME. (TO BE PROBLEMATIC, THE UNOBSERVED VARIABLES MUST BE RELATED TO BOTH SELECTION FOR TREATMENT AND TO OUTCOME.) THE PROBLEM IS THAT THE APPROACH REQUIRES ADDITIONAL ASSUMPTIONS. IF THERE ARE IN FACT UNOBSERVED VARIABLES AFFECTING BOTH SELECTION FOR TREATMENT AND OUTCOME, THEN THIS MAY BE A VIABLE SOLUTION (IF THE CHOICE OF DESIGN / MODEL / ESTIMATOR OVERCOME THE PROBLEM, AND ENABLE ESTIMABILITY OF IMPACT).

IF THERE ARE NO UNOBSERVED COVARIATES, AND NO EXPLANATORY VARIABLES OTHER THAN TREATMENT, THIS FORMULATION IS ESSENTIALLY THE SAME AS THE R&R APPROACH – IT SIMPLY USES A REGRESSION MODEL AS A SURROGATE FOR STRATIFICATION / SUBCLASSIFICATION. WHERE THE HECKMAN APPROACH DEPARTS FROM THE R&R APPROACH IS THAT THERE MAY BE UNOBSERVED COVARIATES THAT AFFECT BOTH SELECTION AND OUTCOME. IF THE UNOBSERVED VARIABLES ARE NOT TAKEN INTO ACCOUNT, THE ERROR TERMS E₀ AND E₁ MAY NOT BE INDEPENDENT, AND THEY MAY NOT BE INDEPENDENT OF THE PROPENSITY SCORE ESTIMATE (WHICH IS AN EXPLANATORY VARIABLE IN THE OUTCOME EQUATION). THE HECKMAN APPROACH SEEKS SITUATIONS IN WHICH THERE MAY BE UNOBSERVED COVARIATES THAT AFFECT BOTH SELECTION AND OUTCOME, AND YET THE CONDITIONAL INDEPENDENCE ASSUMPTION IS STILL JUSTIFIED. FOR EXAMPLE, IF THE UNOBSERVED COVARIATES IN THE OUTCOME MODEL ARE TIME-INVARIANT AND A PANEL SURVEY IS USED, THEN THESE VARIABLES WILL DROP OUT OF A MODEL OF THE OUTCOME DIFFERENCES BETWEEN THE TWO SURVEY ROUNDS.

THE R&R APPROACH CONSIDERS ONLY A VERY SIMPLE MODEL OF COVARIATE (REGRESSION) ADJUSTMENT INVOLVING PROPENSITY SCORES AS COVARIATES, WHEREAS THE HECKMAN APPROACH CONSIDERS MORE DETAILED MODELS.

THE HECKMAN APPROACH ALLOWS FOR THE FULL USE OF ECONOMETRIC MODELING. THE R&R APPROACH IS RESTRICTED TO THE CASE OF RECURSIVE CAUSAL MODELS, IN WHICH CAUSAL INFLUENCE PROCEEDS IN ONLY ONE DIRECTION (I.E., THE EXPLANATORY VARIABLES MAY HAVE A CAUSAL EFFECT ON THE OUTCOME VARIABLE, BUT NOT VICE VERSA). ECONOMETRIC MODELS, ON THE OTHER HAND, ALLOW FOR NONRECURSIVE (SIMULTANEOUS) MODELS, IN WHICH THE EXPLANATORY AND EXPLAINED VARIABLES MAY AFFECT EACH OTHER. THIS IS AN EXTENSION OF THE R&R METHODOLOGY.

WEAKNESSES AND LIMITATIONS OF THE HECKMAN APPROACH

FOR THE R&R APPROACH TO WORK, ALL THAT IS REQUIRED IS CONDITIONAL INDEPENDENCE OF RESPONSE ((Y₀, Y₁)) AND TREATMENT (W) GIVEN OBSERVED COVARIATES (X). FOR THE HECKMAN APPROACH TO WORK, THERE ARE STRONG CONDITIONS THAT MUST BE SPECIFIED ON ALL OF THE ADDITIONAL EXPLANATORY VARIABLES INCLUDE IN THE MODEL. THESE INCLUDE:

1. THE ADDITIONAL VARIABLES MUST BE UNCORRELATED WITH THE MODEL ERROR TERMS (AFTER DIFFERENCING, IF DIFFERENCING IS USED).

2. IN ORDER TO PREDICT THE EFFECT OF MAKING FORCED CHANGES IN POLICY VARIABLES, THE MODEL MUST BE DEVELOPED FROM DATA IN WHICH FORCED CHANGES WERE MADE IN THOSE VARIABLES.

3. THE CORRELATION OF THE ADDITIONAL (POLICY-RELEVANT) VARIABLES WITH THE TREATMENT SHOULD BE VERY LOW, OR ELSE THE EFFECTS OF TREATMENT AND OF THE ADDITIONAL VARIABLES WILL BE CONFOUNDED.

4. THE SELECTION MODEL MUST INCLUDE AN EXPLANATORY VARIABLE THAT IS NOT INCLUDED IN THE OUTCOME MODEL.

THE INSIGHT THAT TIME-INVARIANT UNOBSERVED VARIABLES MAY BE ADDRESSED BY USING A PANEL SURVEY IS A SIGNIFICANT EXTENSION OF THE R&R METHODOLOGY. THE INCLUSION OF POLICY-RELEVANT VARIABLES AND NONRECURSIVE MODELS IS NOT SO SIGNIFICANT. THE CONSTRUCTION OF ELABORATE ECONOMETRIC MODELS FROM OBSERVATIONAL DATA HAS NOT PROVED TO BE OF MUCH VALUE, OVER MORE THAN A HALF CENTURY OF WORK IN THIS AREA. THE PREPONDERANCE OF EVIDENCE IS THAT MANY-VARIABLE ECONOMETRIC MODELS DEVELOPED FROM OBSERVATIONAL DATA SIMPLY DON’T WORK FOR PREDICTION OR CONTROL. THAT IS THE REASON WHY RECESSIONS COME AND GO, WITHOUT THE GOVERNMENT'S BEING ABLE TO ANTICIPATE THEM, AVOID THEM, CONTROL THEM, OR EVEN MODERATE THEM VERY WELL.

THE MAIN REASON FOR THE FAILURE OF ECONOMETRIC MODELS IS THE FACT THAT THE MODELS ARE DEVELOPED FROM DATA IN WHICH THE EXPLANATORY VARIABLES ARE PASSIVELY OBSERVED, NOT ACTIVELY CONTROLLED. G. E. P. BOX’S ADVICE ON THIS TOPIC SHOULD BE TAKEN MORE SERIOUSLY.

ALTHOUGH DEVELOPMENT OF A MODEL WITH MANY COVARIATES MAY INCREASE PRECISION SOMEWHAT, THE BENEFIT OF THE INCREASED PRECISION IS ILLUSORY. AS A GUIDE TO CONTROL, AN ELABORATE ECONOMETRIC MODEL DEVELOPED FROM PASSIVELY-OBSERVED DATA IS A “HOUSE OF CARDS.” SUCH A MODEL IS A POOR GUIDE FOR PREDICTING WHAT WILL HAPPEN IF FORCED CHANGES ARE MADE IN POLICY-RELEVANT VARIABLES THAT ARE SIMPLY OBSERVED, NOT CONTROLLED. THE R&R APPROACH IS MUCH LESS SANGUINE ABOUT THE APPLICATION OF COVARIATE ADJUSTMENT, EXCEPT AS A MEANS OF INCREASING ESTIMATE PRECISION (NOT FOR MAKING PREDICTIONS).

IMPLICATIONS OF THE HECKMAN APPROACH FOR SAMPLE DESIGN AND MATCHING

WITH RESPECT TO DESIGN AND MATCHING, CONSIDERATION OF THE HECKMAN APPROACH TO CAUSAL MODELING LEADS TO THE FOLLOWING CONCLUSIONS. IN WHAT FOLLOWS, THE “PROPENSITY SCORE” IS THE PROPENSITY SCORE BASED ON VARIABLES THAT ARE OBSERVED IN THE DESIGN PHASE (THESE WILL TYPICALLY DIFFER FROM THOSE IN THE ANALYSIS PHASE).

1. TO PROMOTE BIAS REDUCTION, INCLUDE THE PROPENSITY SCORE AS A MATCH VARIABLE.

2. STRATIFY TO ENSURE VARIATION IN VARIABLES THAT WILL BE USED AS EXPLANATORY VARIABLES, AND LOW CORRELATION AMONG THEM. THESE VARIABLES INCLUDE BOTH VARIABLES THAT HAVE AN EFFECT ON SELECTION FOR TREATMENT AND OUTCOMES OF INTEREST. (THE DESIRE FOR LOW CORRELATION IS MORE IMPORTANT FOR THE OUTCOME MODELS THAN FOR SELECTION MODELS, SINCE IN A STRUCTURAL MODEL IT IS DESIRED TO ESTIMATE INDIVIDUAL COEFFICIENTS, WHEREAS IN THE SELECTION MODEL IT IS NOT.) THE STRATIFICATION SHOULD BE SO AS TO PROMOTE ADEQUATE VARIATION IN EXPLANATORY VARIABLES CONSIDERED TO HAVE A SUBSTANTIAL EFFECT ON SELECTION FOR TREATMENT OR OUTCOMES OF INTEREST, AND A HIGH DEGREE OF ORTHOGONALITY AMONG THEM. (IN THE R&R APPROACH, STRATIFICATION IS DONE OVER THE PROPENSITY SCORE AND ANY SUBPOPULATIONS OF INTEREST.) (LOW CORRELATION AMONG VARIABLES OF STRATIFICATION MAY BE ACHIEVED BY USING THE METHOD OF MARGINAL STRATIFICATION WITH VARIABLE PROBABILITIES OF SELECTION (OF THE SAMPLE UNITS).

THESE ARE ESSENTIALLY THE SAME CONCLUSIONS AS RESULTED FROM CONSIDERATION OF THE R&R APPROACH.

4.11. COMPARISON OF THE R&R AND HECKMAN APPROACHES TO STATISTICAL CAUSAL MODELING AND ANALYSIS

[THIS SECTION IS OPTIONAL. IT SIMPLY SUMMARIZES, IN ONE PLACE, THE RELATIVE ADVANTAGES AND DISADVANTAGES OF THE R&R AND HECKMAN APPROACHES.]

NOTE ON TERMINOLOGY. MANY DESCRIPTORS HAVE BEEN USED TO CONTRAST THE R&R APPROACH AND THE HECKMAN APPROACH. THE R&R APPROACH IS SOMETIMES CALLED THE “STATISTICAL” APPROACH. “STATISTICAL” IS NOT A VERY GOOD CHOICE OF DESCRIPTOR FOR THE R&R APPROACH, SINCE THE ECONOMETRIC APPROACH IS CERTAINLY A STATISTICAL APPROACH. A DISTINGUISHING FEATURE IS THE FACT THAT THE HECKMAN APPROACH ADDRESSES THE ISSUE OF MODEL IDENTIFICATION MORE THOROUGHLY THAN THE R&R APPROACH, INCLUDING CONSIDERATION OF UNOBSERVED VARIABLES THAT AFFECT SELECTION AND OUTCOME, IDENTIFICATION OF A PARTICULAR CAUSAL MODEL (INCLUDING THE RELATIONSHIPS AMONG THE CAUSAL VARIABLES THAT AFFECT SELECTION FOR TREATMENT AND OUTCOME), AND THE ASSESSMENT OF THE APPROPRIATENESS OF THE MODEL (ESTIMABILITY OF IMPACT).

THE TERMS “DESIGN-BASED” AND “MODEL-BASED” ARE ALSO NOT VERY GOOD DIFFERENTIATORS, SINCE BOTH APPROACHES TAKE INTO ACCOUNT THE SURVEY DESIGN, BOTH APPROACHES CONSIDER CAUSAL MODELS (AT DIFFERENT LEVELS OF DETAIL), AND BOTH APPROACHES INCLUDE A PROPENSITY-SCORE MODEL. SOMETIMES THE R&R APPROACH IS REFERRED TO AS THE “PROPENSITY-SCORE” APPROACH, BUT THIS IS VERY MISLEADING, SINCE THE HECKMAN APPROACH ALSO INCLUDES A PROPENSITY-SCORE MODEL. THE R&R APPROACH IS SOMETIMES REFERRED TO AS A “BALANCING” APPROACH, SINCE IT “BALANCES” (MAKES SIMILAR) THE DISTRIBUTION OF OBSERVABLES WITHIN STRATA. IT MAY ALSO BE REFERRED TO AS A “STRATIFICATION” APPROACH OR A “MATCHING” APPROACH. THIS IS IN CONTRAST TO THE HECKMAN APPROACH, WHICH MAY BE CHARACTERIZED AS A “COVARIATE ADJUSTMENT” APPROACH. THIS, TOO, PRESENTS DIFFICULTIES, SINCE THE R&R APPROACH ALSO INCLUDES COVARIATE ADJUSTMENT. THE R&R APPROACH MAY BE CHARACTERIZED AS “CONDITIONING TO BALANCE,” AND THE HECKMAN (ECONOMETRIC) APPROACH AS “CONDITIONING TO ADJUST.” THE FACT IS, BOTH APPROACHES ARE BASED ON THE SAME FUNDAMENTAL CONCEPT (CONDITIONAL INDEPENDENCE GIVEN THE PROPENSITY SCORE), AND SIMPLY USE TWO DIFFERENT TYPES OF ESTIMATES (I.E., BASED PRIMARILY ON MATCHING FOR THE R&R APPROACH AND ON REGRESSION ANALYSIS FOR THE HECKMAN APPROACH).

A SUMMARY OF THE RELATIVE ADVANTAGES AND DISADVANTAGES OF THE R&R AND HECKMAN APPROACHES TO STATISTICAL CAUSAL ANALYSIS FOLLOWS.

GENERAL CHARACTERISTICS OF THE TWO APPROACHES

THE R&R AND HECKMAN APPROACHES ARE BOTH POTENTIAL-OUTCOMES MODELS, BASED ON THE CONCEPT OF CONDITIONAL INDEPENDENCE OF THE POTENTIAL-OUTCOMES RESPONSE (Y₀, Y₁) AND W GIVEN OBSERVED COVARIATES X. BOTH APPROACHES ESTIMATE THE PROPENSITY SCORE, AND BOTH MAKE THE ASSUMPTION THAT THE PROPENSITY SCORE IS NEVER EQUAL TO ZERO OR ONE (STRONG IGNORABILITY). THE TWO APPROACHES ARE VERY SIMILAR (I.E., BOTH ARE “POTENTIAL OUTCOMES” MODELS, DEPENDENT ON AN ASSUMPTION OF CONDITIONAL INDEPENDENCE OF OUTCOME AND TREATMENT, GIVEN COVARIATES), EXCEPT FOR THE FACT THAT THE HECKMAN APPROACH CONSIDERS THE CAUSAL MODEL IN GREATER DETAIL (AND IN DOING SO MAKES ADDITIONAL ASSUMPTIONS). WITH BOTH APPROACHES, THE ATE IS USUALLY ESTIMATED OVER THE ENTIRE POPULATION (FOR THE R&R APPROACH IT ALWAYS IS; FOR THE (MODEL-BASED) HECKMAN APPROACH IT MAY NOT BE). BY USING REGRESSION ANALYSIS, THE HECKMAN APPROACH MAKES ESTIMATES OF THE DISTRIBUTIONAL ASPECTS OF IMPACT, WHILE THE R&R APPROACH SIMPLY ESTIMATES THE MEAN OVERALL IMPACT FOR THE WHOLE POPULATION OR SUBPOPULATIONS OF INTEREST.

THE R&R (BALANCING) APPROACH AND THE HECKMAN (ECONOMETRIC) APPROACH FOCUS ON ANALYSIS, NOT ON DESIGN. THEY ARE DESCRIBED HERE (IN THIS PRESENTATION ON MATCHING IN DESIGN) BECAUSE THE CAUSAL MODEL SHOULD BE TAKEN INTO ACCOUNT IN THE DESIGN OF AN ANALYTICAL SURVEY (I.E., A SURVEY TO ASSESS CAUSAL EFFECTS, SUCH AS PROGRAM IMPACT). BY UNDERSTANDING THE NATURE OF THESE TWO APPROACHES TO CAUSAL ANALYSIS, IT IS POSSIBLE TO DRAW CONCLUSIONS ABOUT GOOD APPROACHES TO THE DESIGN OF SURVEYS IN SUPPORT OF CAUSAL ANALYSIS (IMPACT ANALYSIS).

BOTH THE R&R AND HECKMAN APPROACHES ARE BASED ON CAUSAL MODELS. BOTH APPROACHES ARE CORRECT IF THE RESPECTIVE ASSUMPTIONS ARE JUSTIFIED. THE R&R APPROACH IS SIMPLER, SINCE IT SIMPLY IDENTIFIES THE OBSERVED VARIABLES THAT AFFECT SELECTION (“SELECTION ON OBSERVABLES”) AND THEN STRATIFIES ON THEM (OR REGRESSES) ON THE PROPENSITY SCORE. THE HECKMAN APPROACH IS MORE GENERAL SINCE IT ADDRESSES THE ISSUE OF UNOBSERVED VARIABLES THAT AFFECT SELECTION (THAT IS, IT ENCOMPASSES BOTH “SELECTION ON OBSERVABLES” AND “SELECTION ON UNOBSERVABLES”). IT IS ALSO MORE GENERAL, IN THAT IT

- ASSESSES DISTRIBUTIONAL ASPECTS OF IMPACT

- ESTIMATES THE EFFECTS OF POLICY-RELEVANT VARIABLES OTHER THAN A SINGLE PROGRAM INTERVENTION INDICATOR (TREATMENT) VARIABLE

- ALLOWS FOR MUTUALLY CAUSAL VARIABLES (NONRECURSIVE, OR SIMULTANEOUS, CAUSAL MODELS).

THE TWO APPROACHES ARE TECHNICALLY SIMILAR, BUT USE RATHER DIFFERENT ESTIMATION APPROACHES IN IMPLEMENTATION. IN ESSENCE, MATCHING AND REGRESSION ADJUSTMENT ARE JUST TWO DIFFERENT WAYS OF ACHIEVING THE SAME GOAL (I.E., OF OBTAINING AN UNBIASED ESTIMATE OF IMPACT).

MAJOR DISTINCTIONS BETWEEN THE R&R AND HECKMAN APPROACHES

THE GOAL OF ESTIMATING THE ATE OVER THE ENTIRE POPULATION (I.E., THE GOAL OF THE R&R APPROACH) IS LESS AMBITIOUS THAN THE GOAL (OF THE HECKMAN APPROACH) OF ESTIMATING THE CAUSAL EFFECTS OF MULTIPLE VARIABLES THAT ARE NOT SUBJECT TO EXPERIMENTAL CONTROL (AS TREATMENT MAY BE, AT LEAST TO SOME EXTENT, PARTICULARLY IF CLIENT CHOICE IS A MAJOR FACTOR IN SELECTION FOR TREATMENT).

ON THE SURFACE, IT MAY APPEAR THAT IF ALL THAT IS DESIRED IS AN ESTIMATE OF THE ATE OR ATT OVER THE ENTIRE POPULATION OR SUBPOPULATIONS, THE R&R APPROACH IS PREFERRED TO THE HECKMAN APPROACH. THIS IS NOT REALLY SO. THE ESSENTIAL REQUIREMENT FOR BOTH THE R&R AND HECKMAN APPROACHES IS CONDITIONAL INDEPENDENCE OF RESPONSE (Y₀, Y₁) AND W GIVEN COVARIATES X. THE ISSUE FACED BY BOTH APPROACHES IS THE ISSUE OF UNOBSERVED VARIABLES THAT MAY AFFECT SELECTION FOR TREATMENT AND OUTCOME. THE HECKMAN APPROACH EMPHASIZES THE USE OF AN “ALL CAUSES” CAUSAL MODEL, AND PLACES MUCH MORE EMPHASIS ON THE ISSUE OF IDENTIFYING A REASONABLE CAUSAL MODEL AND MATCHING THE ESTIMATION PROCEDURE TO IT. BY CONSIDERATION OF IT WE ARE LED DIRECTLY TO DESIGNS SUCH AS PANEL SAMPLING (TO REMOVE THE EFFECT OF UNOBSERVED TIME-INVARIANT VARIABLES). THOSE IMPLICATIONS ARE MUCH LESS APPARENT FOR THE R&R APPROACH (SINCE IT IS LESS DETAILED).

ON THE OTHER HAND, THE HECKMAN APPROACH IS PRESUMPTIVE TO IMPLY THAT THE CAUSAL EFFECT OF POLICY-RELEVANT VARIABLES MAY BE ESTIMATED FROM OBSERVATIONAL DATA IN WHICH FORCED CHANGES WERE NOT MADE IN THOSE VARIABLES. AS G. E. P. BOX NOTED, TO PREDICT THE EFFECT OF MAKING FORCED CHANGES IN A SYSTEM, IT IS NECESSARY TO CONSTRUCT A MODEL FROM DATA FOR WHICH FORCED CHANGES HAVE BEEN MADE, I.E., FROM EXPERIMENTAL, NOT OBSERVATIONAL, DATA. AS OBSERVED EARLIER, THE HIGH LEVEL OF DETAIL OF AN ECONOMETRIC MODEL BASED ON OBSERVATIONAL DATA IS ILLUSORY.

ALSO, FOR OBSERVATIONAL DATA, CONFOUNDING OF EFFECTS MAY REPRESENT A SUBSTANTIAL PROBLEM. THIS MAY BE REMOVED TO SOME EXTENT IN THE DATA SET BY MARGINAL STRATIFICATION, BUT EVEN IF THIS IS DONE THE RESULTING ORTHOGONALITY IS RELATIVE TO PASSIVELY OBSERVED DATA, NOT TO DATA IN WHICH FORCED CHANGES HAVE BEEN MADE.

REGARDLESS OF WHICH APPROACH IS USED, THE SELECTION METHOD (FORCED CHANGES, RANDOM SELECTION, PASSIVE OBSERVATION) IS THE WAY IT IS, AND IT LIMITS THE SCOPE OF INFERENCE ACCORDINGLY.

THERE IS, IN FACT, NOTHING FUNDAMENTALLY DIFFERENT IN THE HECKMAN APPROACH BEYOND THE CONCEPTS EMBODIED IN THE R&R APPROACH (COUNTERFACTUALS, CONDITIONAL INDEPENDENCE, STRONG IGNORABILITY). THE ALLOWANCE FOR UNOBSERVED VARIABLES IN CERTAIN SPECIAL SITUATIONS IS CONVENIENT AND INSIGHTFUL. THE INCORPORATION OF POLICY-RELEVANT VARIABLES IS USEFUL, BUT FOR PREDICTIONS OF THE IMPACT OF MAKING CHANGES TO EXPLANATORY VARIABLES IT IS NECESSARY TO DEVELOP THE MODEL FROM DATA IN WHICH SUCH CHANGES WERE MADE. THIS REQUIREMENT IMPOSES A REQUIREMENT FOR RESEARCH DESIGN AND EXPERIMENTAL CONTROL, AND WOULD NOT CORRESPOND TO “OBSERVATIONAL DATA.” THE ALLOWANCE FOR NONRECURSIVE MODELS IS HARDLY WORTH MENTION, SINCE THE PROCEDURES FOR HANDLING THIS SITUATION ARE STRAIGHTFORWARD MODIFICATIONS OF THE RECURSIVE CASE (E.G., TRANSFORMING TO REDUCED-FORM EQUATIONS).

IN MANY SAMPLE SURVEYS USED FOR EVALUATION, THE UNOBSERVED VARIABLES ARE PERSONAL CHARACTERISTICS. THE EFFECT OF ALL OF THESE HIDDEN VARIABLES ARE REMOVED IN A PANEL SURVEY THAT INTERVIEWS THE SAME INDIVIDUALS IN BOTH SURVEY ROUNDS. BY CONSIDERING THE HECKMAN APPROACH, WE SEE THAT IT IS VERY NECESSARY IN EVALUATION STUDIES TO EMPLOY A PANEL DESIGN THAT REMOVES THE EFFECT OF UNOBSERVED VARIABLES THAT MAY AFFECT SELECTION FOR TREATMENT. THE R&R APPROACH PROVIDES NO SUCH INSIGHT.

COMMENTS ON HECKMAN’S CRITICISM OF THE R&R APPROACH

HECKMAN HAS CRITICIZED THE R&R APPROACH ON THE BASIS THAT IT REQUIRES THE USER TO MAKE AN “ASSUMPTION OF CONVENIENCE” THAT SELECTION IS BASED ON OBSERVABLES (I.E., THAT (Y₀, Y₁) IS INDEPENDENT OF W GIVEN X), WHETHER IT IS TRUE OR NOT. THIS IS AN UNJUSTIFIED CRITICISM. IF THE ASSUMPTION CANNOT BE JUSTIFIED, THEN THE R&R APPROACH IS NOT APPROPRIATE. THE ASSUMPTION SHOULD NEVER BE AN “ASSUMPTION OF CONVENIENCE.” WHILE THIS ASSUMPTION MAY BE A LIMITATION ON THE USEFULNESS (BREADTH OF APPLICATION) OF THE METHOD, IT IS BY NO MEANS A CRITICISM OF THE CORRECTNESS OF THE METHOD WHEN THE ASSUMPTION HOLDS. (MAKING THIS ASSUMPTION WITHOUT JUSTIFICATION MAY BE CRITICIZED, BUT NOT THE APPROACH.) THE HECKMAN APPROACH REQUIRES A SIMILAR CONDITIONAL INDEPENDENCE ASSUMPTION, FOR A MORE DETAILED MODEL SPECIFICATION.

BOTH THE R&R AND HECKMAN METHODS ARE CORRECT, IF THE RESPECTIVE ASSUMPTIONS ON WHICH THEY ARE BASED ARE VALID (JUSTIFIED). THE HECKMAN APPROACH IS MORE GENERAL. IN ORDER TO ACHIEVE THE GREATER GENERALITY IT MAKES ADDITIONAL ASSUMPTIONS ABOUT THE CAUSAL MODEL.

THE HECKMAN APPROACH MAKES ASSUMPTIONS ABOUT THE CAUSAL EFFECT OF OTHER EXPLANATORY VARIABLES INCLUDED IN THE MODEL, E.G., POLICY-RELEVANT VARIABLES. IF THE MODEL IS TO BE USED TO PREDICT CHANGES IN OUTCOME AS A FUNCTION OF CERTAIN EXPLANATORY VARIABLES, THEN IT IS NECESSARY THAT THE DATA INCLUDE OBSERVATIONS FOR WHICH FORCED CHANGES HAVE BEEN MADE IN THESE VARIABLES. IF IT IS DESIRED TO PREDICT CHANGES IN SEVERAL VARIABLES, THEN THE DATA SHOULD INCLUDE OBSERVATIONS FOR WHICH INDEPENDENT CHANGES HAVE BEEN MADE IN THESE VARIABLES (TO ORTHOGONALIZE THESE VARIABLES AND THEREBY AVOID CONFOUNDING OF EFFECTS).

THE R&R APPROACH ASSUMES THAT THE OBSERVED COVARIATES ARE ALL THE VARIABLES THAT AFFECT SELECTION FOR TREATMENT. IT MAKES THE ASSUMPTION THAT THERE ARE NO UNOBSERVED VARIABLES THAT AFFECT SELECTION FOR TREATMENT. IN CONTRAST, THE HECKMAN APPROACH SPECIFIES AN EXPLICIT CAUSAL MODEL RELATING OUTCOMES OF INTEREST TO ALL IDENTIFIABLE CAUSAL VARIABLES (OBSERVED OR UNOBSERVED) THAT MAY HAVE A SIGNIFICANT EFFECT ON SELECTION OR OUTCOME, AND MAKES THE CONDITIONAL INDEPENDENCE ASSUMPTION ONLY AFTER THOROUGH CONSIDERATION AND ANALYSIS OF THE SPECIFIED CAUSAL MODEL. FURTHERMORE, IT EXPLICITLY ADDRESSES THE ISSUE OF UNOBSERVED VARIABLES THAT AFFECT SELECTION OR OUTCOME, BY IDENTIFYING DESIGN / MODEL / ESTIMATOR STRUCTURES THAT ARE NOT AFFECTED BY THE UNOBSERVED VARIABLES.

IN ONE ARTICLE (“THE SCIENTIFIC MODEL OF CAUSALITY,” SOCIOLOGICAL METHODOLOGY, VOL. 35 (2005), PP. 1-97), IN COMPARING HIS APPROACH TO THAT OF ROSENBAUM AND RUBIN, HECKMAN CHARACTERIZES HIS APPROACH AS THE “SCIENTIFIC MODEL OF CAUSALITY,” AND CONTRASTS “THE SCIENTIFIC METHOD VERSUS THE NEYMAN-RUBIN MODEL.” THIS COMPARISON IS ILL-FOUNDED. BOTH METHODS ARE, IN FACT, “SCIENTIFIC” APPROACHES. THE ESSENCE OF BOTH APPROACHES IS THE CONCEPT OF POTENTIAL OUTCOMES (Y₀, Y₁) AND CONDITIONAL INDEPENDENCE OF RESPONSE (Y₀, Y₁) AND TREATMENT, W, GIVEN OBSERVED COVARIATES, X. THE CONCEPT OF POTENTIAL OUTCOMES DATES BACK TO J. NEYMAN AND R. A. FISHER (WITH REFERENCE TO RANDOMIZED DESIGNED EXPERIMENTS). THE CONCEPT OF CONDITIONAL INDEPENDENCE OF THE POTENTIAL OUTCOMES AND TREATMENT, GIVEN COVARIATES, TO ADDRESS ANALYSIS OF OBSERVATIONAL DATA, WAS FORMALIZED BY ROSENBAUM AND RUBIN IN 1983.

HECKMAN MADE THE SIGNIFICANT EXTENSION TO INCLUDE UNOBSERVED VARIABLES. ALTHOUGH HIS INSIGHT CONCERNING UNOBSERVED VARIABLES IS SIGNIFICANT, IT IS SIMPLY AN EXTENSION OF THE BASIC NEYMAN-RUBIN METHODOLOGY.

HECKMAN HAS CRITICIZED THE R&R APPROACH (WHICH HE REFERS TO AS THE “NEYMAN-RUBIN” APPROACH, WHEN IT IS REALLY JUST THE R&R APPROACH) AS MAKING AN “ASSUMPTION OF CONVENIENCE” THAT RESPONSE IS INDEPENDENT OF TREATMENT GIVEN THE OBSERVED COVARIATES. IN FACT, THE HECKMAN APPROACH MAKES THIS SAME ASSUMPTION PLUS ADDITIONAL ASSUMPTIONS THAT ARE OFTEN VERY TENUOUS, SUCH AS

- SCOPE OF INFERENCE. FORCED-CHANGES IN THE MANY POLICY-RELEVANT EXPLANATORY VARIABLES ARE REQUIRED TO PREDICT THE EFFECT OF MAKING CHANGES IN THOSE VARIABLES. (THE R&R APPROACH CONDITIONS ON COVARIATES TO INCREASE PRECISION OF “HISTORICAL” ESTIMATES, AND MAKES NO CLAIMS ABOUT PREDICTIONS IF THE COVARIATES ARE MANIPULATED. THE R&R APPROACH REPRESENTS THE IMPACT ESTIMATE AS PERTAINING TO THE MODEL AND DATA SET ANALYZED. THE HECKMAN APPROACH PURPORTS TO USE THE ANALYSIS AS THE BASIS FOR PREDICTION RESULTS FOR DIFFERENT SYSTEMS OTHER THAN THE ONE FOR WHICH THE DATA WAS OBTAINED. THIS IS A RATHER “HEROIC” ASSUMPTION. IT IS IN THE REALM OF SPECULATION, NOT THAT OF INFERENCE FROM OBSERVED DATA.)

- CONFOUNDING. WITH MANY PASSIVELY OBSERVED EXPLANATORY VARIABLES, THERE IS LIKELY TO BE SUBSTANTIAL CONFOUNDING. (IN THE R&R APPROACH, THERE ARE FEW EXPLANATORY VARIABLES, USED MAINLY ONE AT A TIME (AS VARIABLES OF STRATIFICATION / SUBCLASSIFICATION TO REPRESENT SUBPOPULATIONS OF INTEREST). CONFOUNDING IS LESS AN ISSUE. MULTIPLE COVARIATES USUALLY DO NOT APPEAR IN THE SAME MODEL (EXCEPT FOR ESTIMATION OF THE PROPENSITY SCORE, AND THERE THE ISSUE IS SIMPLY OBTAINING AN UNBIASED ESTIMATE OF THE PS, NOT OF THE COEFFICIENTS OF VARIABLES IN THE PS MODEL). THIS POINT IS VERY IMPORTANT. CONFOUNDING OF EXPLANATORY VARIABLES IS NOT A CONCERN IN SELECTION MODELS (I.E., ESTIMATING THE PROPENSITY SCORE), SINCE ALL WE ARE INTERESTED IN IS THE ESTIMATED PROPENSITY SCORE, NOT THE INDIVIDUAL REGRESSION COEFFICIENTS OF THE EXPLANATORY VARIABLES. CONFOUNDING ("MULTICOLLINEARITY") IS A SERIOUS CONCERN IN OUTCOME MODELS, WHERE IT CAN EASILY AFFECT THE PRECISION OF REGRESSION-COEFFICIENT ESTIMATES.

4.12. OTHER APPROACHES TO STATISTICAL CAUSAL MODELING AND ANALYSIS

CONSIDERATION OF OTHER APPROACHES TO CAUSAL MODELING DOES NOT PRODUCE ADDITIONAL INSIGHTS FOR SURVEY DESIGN AND MATCHING, BEYOND THOSE PRODUCED BY CONSIDERATION OF THE R&R AND HECKMAN APPROACHES (WHICH, CONSIDERED TOGETHER, PROVIDE A GOOD REPRESENTATION OF THE MATCHING AND REGRESSION-ANALYSIS APPROACHES TO IMPACT ESTIMATION). FOR COMPLETENESS, A FEW COMMENTS WILL BE MADE ABOUT ADDITIONAL APPROACHES TO CAUSAL ANALYSIS. THESE APPROACHES INCLUDE ADDITIONAL ESTIMATORS FOR IGNORABILITY, THE REGRESSION DISCONTINUITY APPROACH, INSTRUMENTAL VARIABLES, LOCAL AVERAGE TREATMENT EFFECT, MARGINAL TREATMENT EFFECT AND THE CONSIDERATION OF CAUSAL ANALYSIS AS A PROBLEM OF MISSING DATA.

ADDITIONAL ESTIMATORS ASSOCIATED WITH R&R (I.E., ASSUMING IGNORABILITY OF TREATMENT (UNCONFOUNDEDNESS))

THERE ARE A VARIETY OF ESTIMATORS THAT MAY BE USED IN APPLYING THE R&R APPROACH. TWO OF THESE WERE DESCRIBED EARLIER. A LIST OF SEVERAL FOLLOWS. IN WHAT FOLLOWS, THE VARIABLE X DENOTES THE COVARIATES FOR WHICH UNCONFOUNDEDNESS HOLDS (I.E., CONDITIONAL INDEPENDENCE OF RESPONSE (Y₀, Y₁) AND TREATMENT (W), GIVEN X). THESE ESTIMATORS ARE DESCRIBED IN DETAIL IN WOOLDRIDGE OP. CIT. (THEY ARE NOT DESCRIBED IN DETAIL HERE, BECAUSE THIS PRESENTATION FOCUSES ON DESIGN, NOT ON ANALYSIS.)

1. INVERSE-PROPENSITY-SCORE WEIGHTING.

2. REGRESSION ADJUSTMENT: EXPECTED DIFFERENCE IN MEANS OF TREATED AND UNTREATED UNITS, GIVEN X.

3. REGRESSION ADJUSTMENT USING PROPENSITY SCORES (REGRESS y ON 1, w, ; ESTIMATE OF IMPACT IS COEFFICIENT OF w; OR, REGRESS y ON 1, w, , w( - ) WHERE IS A CONSISTENT ESTIMATE OF ρ = E(P(x)) = P(w=1)). THE ESTIMATE OF IMPACT IS STILL THE COEFFICIENT OF W (SINCE THE INTERACTION TERM IS DEMEANED.

4. TWO-STEP ESTIMATOR: IN THE FIRST STEP, ESTIMATE THE PROPENSITY SCORE (E.G., USING A LOGISTIC REGRESSION MODEL), AND IN THE SECOND STEP, USE A REGRESSION ESTIMATOR WEIGHTED BY THE INVERSE PROPENSITY SCORE. THE ESTIMATED IMPACT IS THE AVERAGE OF THE DIFFERENCE IN PREDICTED VALUES FOR TREATMENT AND NO-TREATMENT (OVER THE FULL SAMPLE). (THIS APPROACH IS “DOUBLY ROBUST” IN THE SENSE THAT IF EITHER THE SELECTION MODEL IS CORRECTLY SPECIFIED OR THE OUTCOME MODEL IS CORRECTLY SPECIFIED (BUT NOT NECESSARILY BOTH), THEN THE ESTIMATE OF IMPACT IS CORRECT (CONSISTENT).)

5. MATCHING ESTIMATORS. MATCH EACH TREATED UNIT WITH A SIMILAR UNTREATED UNIT, AND ESTIMATE THE EXPECTED DIFFERENCE IN OUTCOME OVER THE SAMPLE.

TWO EXAMPLES WILL BE SHOWN OF THE PRECEDING ESTIMATORS.

EXAMPLE 1. SAMPLE-BASED AVERAGING (CONDITIONING) OVER S

(SEE WOOLDRIDGE OP. CIT. (ED. 1 OR 2) FOR DETAILS.)

USING THE LAW OF ITERATED EXPECTATIONS, IT CAN BE SHOWN THAT UNDER THE ASSUMPTION OF IGNORABILITY IN MEAN (E(Y₀|X,W)=E(Y₀|X)) AND OVERLAP (FOR ALL X, P(W=1|X)<1)),

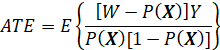
AND

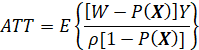
WHERE ρ DENOTES THE UNCONDITIONAL PROBABILITY OF TREATMENT, ρ = P(W=1).

HENCE THE FOLLOWING MAY BE USED AS “SAMPLE AVERAGE” ESTIMATES OF ATE AND ATE:

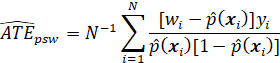
AND

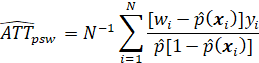
WHERE =N₁/N IS THE FRACTION OF TREATED UNITS IN THE SAMPLE.

IN ORDER TO USE THE PRECEDING ESTIMATES, IT IS NECESSARY TO ESTIMATE THE PROPENSITY SCORE, P(W=1|X). THIS IS USUALLY DONE USING A LOGISTIC REGRESSION MODEL. THIS MODEL MAY BE “FLEXIBLE,” INCLUDING ANY VARIABLES AND FUNCTIONAL FORMS THAT WORK WELL. THERE IS NO NEED FOR THE INDIVIDUAL COEFFICIENTS OF THE MODEL TO BE ESTIMABLE.

IT MAY APPEAR THAT USING AN ESTIMATE (THE ESTIMATED PROPENSITY SCORE) IN THE ESTIMATOR WOULD CAUSE THE ESTIMATOR TO BE INEFFICIENT. WOOLDRIDGE POINT OUT THE “SURPRISING” RESULT THAT, BECAUSE THIS ESTIMATOR IS A TWO-STEP “M” ESTIMATOR IN WHICH THE FIRST-STEP ESTIMATOR (THE PROPENSITY SCORE) IS A CONDITIONAL MAXIMUM-LIKELIHOOD ESTIMATOR, THE ESTIMATE IS ASYMPTOTICALLY EFFICIENT (I.E., HAS SMALLER VARIANCE THAN OTHER ESTIMATORS, FOR LARGE SAMPLES).

THE PRECEDING RESULT SHOWS, AS DISCUSSED EARLIER, THAT THE PROBLEM OF MULTIDIMENSIONAL STRATIFICATION MAY BE COUNTERED SIMPLY BY AVERAGING OVER THE SAMPLE, E.G., USING A HORVITZ-THOMPSON-TYPE (INVERSE-PROBABILITY-WEIGHTED) ESTIMATOR (AS LONG AS BOTH THE TREATED AND UNTREATED UNITS ARE A PROBABILITY SAMPLE OVER THE COMPLETE POPULATION). THE DIFFICULTIES ASSOCIATED WITH THE STRATIFICATION APPROACH ARE OBVIATED BY OBSERVING THAT WHAT IS REQUIRED IN THE FORMULAS GIVEN ABOVE IS THE EXPECTED VALUE OF Y GIVEN X, CONDITIONAL ON W=0 OR W=1 (AND THEN DIFFERENCED).

A PROBLEM WITH THIS APPROACH IS THAT THE DENOMINATOR OF SOME TERMS MAY BE SMALL, SO THAT THE PRECISION OF THE ESTIMATE MAY BE VERY LOW. (THIS PROBLEM IS ADDRESSED BY TRUNCATING HIGH AND LOW VALUES OF THE PROPENSITY SCORE. THIS INCREASES PRECISION AT THE COST OF INTRODUCING SOME BIAS.) ANOTHER APPROACH IS THE REGRESSION APPROACH MENTIONED EARLIER (AND TO BE DISCUSSED FURTHER IN THE NEXT EXAMPLE). THAT APPROACH DOES NOT INCLUDE THE PROBABILITIES IN THE DENOMINATORS OF THE SUM OVER THE SAMPLE UNITS.

EXAMPLE 2. SAMPLE-BASED AVERAGING (CONDITIONING) OVER X

RATHER THAN STRATIFY, SIMPLY CONSTRUCT A REGRESSION ESTIMATE OF Y GIVEN THE VALUE OF X. DO THIS FOR THE TREATED SAMPLE (W=1) AND UNTREATED SAMPLE (W=0). THEN, SIMPLY FORM THE DIFFERENCE OF THESE ESTIMATED MEANS (OF Y CONDITIONAL ON X) FOR EACH OF THE TWO SAMPLES (TREATED AND UNTREATED) (FOR A PARTICULAR VALUE OF X, SAY THE MEAN). THESE EXPECTATIONS ARE NONPARAMETRICALLY IDENTIFIED. AS WOOLDRIDGE POINT OUT, AS LONG AS WE HAVE AVAILABLE A PROBABILITY SAMPLE, WE MAY SIMPLY AVERAGE THE REGRESSION ESTIMATES OVER THE AVAILABLE SAMPLE (TO OBTAIN AN ESTIMATE OF THE POPULATION MEANS). THIS PROCEDURE IS AS FOLLOWS (SEE WOOLDRIDGE OP. CIT. (ED. 1 OR 2) FOR DETAILS.)

LET AND DENOTE THE TWO REGRESSION ESTIMATES, I.E.,

AND

THEN, UNDER THE ASSUMPTION OF INDEPENDENCE OF Y₀ AND W GIVEN X, AND THE “OVERLAP” ASSUMPTION 0<P(W=1|X)<1 (OR SIMPLY P(W=1|X)<1),

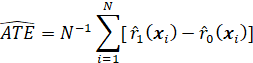
AND

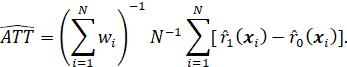
THE CRUCIAL ASSUMPTION IS CONDITIONAL INDEPENDENCE OF RESPONSE (Y₀, Y₁) AND W GIVEN X (ACTUALLY, THIS REQUIREMENT MAY BE WEAKENED TO CONDITIONAL MEAN INDEPENDENCE OF Y₀ AND W GIVEN X). THE AVERAGING HAS TO BE DONE OVER A COVARIATE, X, FOR WHICH (Y₀, Y₁) IS CONDITIONALLY INDEPENDENT OF W, GIVEN X.

NOTE THAT THE PRECEDING METHOD AND THE FORMULAS ASSOCIATED WITH IT ARE INDEPENDENT OF HOW MANY OR WHICH UNITS ARE TREATED. IT SIMPLY ESTIMATES THE RELATIONSHIP OF OUTCOME TO X FOR WHICHEVER UNITS ARE TREATED AND UNTREATED. IT DOES ASSUME THAT ALL X HAVE A NONZERO PROBABILITY (OR PROBABILITY DENSITY) OF OCCURRING IN THE SAMPLE (OR ELSE THE CONDITIONAL EXPECTATION CANNOT BE CALCULATED). UNLIKE THE STRATIFICATION APPROACH, THERE IS NO NEED TO ASSUME THAT SOME Y₁ AND Y₀ ARE OBSERVED FOR EACH VALUE OF X – ONCE THE REGRESSION EQUATION IS ESTIMATED, THE TWO VALUES AND ARE AVAILABLE FOR EVERY OBSERVATION.

THE MEANS ARE CALCULATED BY “SAMPLE AVERAGING,” SINCE A RANDOM SAMPLE OF X IS PROVIDED BY THE PROBABILITY SAMPLE. A CRUCIAL ASSUMPTION IS THE “OVERLAP” ASSUMPTION, THAT FOR ALL X, 0<P(W=1|X)<1. IF THERE ARE UNITS FOR WHICH THE PROBABILITY OF TREATMENT IS 0 OR 1, THE METHOD DOES NOT APPLY.

NOTE THAT THE QUANTITIES E(Y|X,W=1) AND E(Y|X, W=0) ON WHICH THE PRECEDING RESULT DEPENDS ARE “NONPARAMETRICALLY IDENTIFIED.” THEY ARE CONDITIONAL EXPECTATIONS THAT DEPEND ON OBSERVABLES, SO THEY ARE ESTIMABLE. THERE IS NO REQUIREMENT TO OBTAIN INDIVIDUAL ESTIMATES FOR ANY OF THE COEFFICIENTS IN THE REGRESSION EQUATIONS. ALL THAT MATTERS IS THE UNBIASED ESTIMATE OF THE ESTIMANDS ( AND ), NOT THE INDIVIDUAL COEFFICIENTS.

THE PRECEDING ESTIMATORS ARE CALLED “REGRESSION ADJUSTMENT” ESTIMATORS.

SYMBOLICALLY, WE MAY WRITE

WHERE, IN THIS CASE,

(RECALL THAT ATE(X) = E(Y₁ – Y₀ |X) = E(Y₁ |X) – E(Y₀ | X) AND OTE(X) = E(Y | W=1, X) – E(Y | W=0, X) = E(Y₁ |X) – E(Y₀ | X).)

THE CRUCIAL DIFFERENCE BETWEEN THE OVERALL OTE AND THIS ESTIMATE IS THAT THE OVERALL OTE IS INFLUENCED BY THE ASSIGNMENT TO TREATMENT (W), WHEREAS THIS ESTIMATE, AVERAGED OVER THE DISTRIBUTION OF X IN THE POPULATION (NOT IN THE SAMPLE), IS NOT.

IF WE HAVE A SIMPLE RANDOM SAMPLE FROM THE POPULATION WE CAN SIMPLY AVERAGE OVER THE SAMPLE. IF THE SAMPLE IS NOT A SIMPLE RANDOM SAMPLE THEN THE AVERAGE MUST BE CALCULATED TAKING THE SAMPLE SELECTION PROBABILITIES INTO ACCOUNT.

THE SIGNIFICANT ASPECT OF THE PRECEDING IS THAT THE AVERAGING IS DONE SEPARATELY FOR W=0 AND W=1 OVER THE DISTRIBUTION OF X (SINCE THE AVERAGES ARE DONE SEPARATELY FOR W=0 AND W=1 (I.E., ARE CONDITIONAL ON W), IT IS IRRELEVANT HOW W IS DISTRIBUTED OVER THE POPULATION, OR IS RELATED TO X)).

IF THE IGNORABILITY (UNCONFOUNDEDNESS) ASSUMPTION IS NOT JUSTIFIED, THEN THE PRECEDING ESTIMATORS ARE NOT APPROPRIATE. SEVERAL ALTERNATIVES ARE THE INSTRUMENTAL-VARIABLES METHOD, THE LOCAL AVERAGE TREATMENT EFFECT (LATE) AND THE REGRESSION-DISCONTINUITY METHOD.

INSTRUMENTAL VARIABLES METHODS

THE ESSENTIAL PROBLEM IN THE OUTCOME MODEL IS THAT SELECTION FOR TREATMENT MAY BE CORRELATED WITH THE MODEL ERROR TERM, I.E., WITH UNOBSERVED VARIABLES (SO THAT ALL REGRESSION COEFFICIENTS, OF WHICH THE TREATMENT EFFECT IS ONE, MAY BE BIASED). A STANDARD APPROACH TO ADDRESS THIS PROBLEM IS THE “INSTRUMENTAL VARIABLES” METHOD: FIND A VARIABLE THAT UNCORRELATED WITH THE MODEL ERROR TERM BUT PARTIALLY CORRELATED WITH TREATMENT, GIVEN THE OTHER EXPLANATORY VARIABLES IN THE MODEL.

ANOTHER INSTRUMENTAL-VARIABLE APPROACH IS THE LOCAL AVERAGE TREATMENT EFFECT (LATE) APPROACH. IN A SIMPLE CASE OF A BINARY INSTRUMENTAL VARIABLE, THE LATE IS THE AVERAGE TREATMENT EFFECT FOR PERSONS WHO WOULD BE INDUCED TO PARTICIPATE IF THE VALUE OF THE INSTRUMENTAL VARIABLE (AN INCENTIVE) WERE CHANGED FROM 0 TO 1.

(THE MOTIVATION FOR THIS APPROACH IS THAT THE MECHANISM FOR SELECTION FOR TREATMENT – THE INDUCEMENT – IS KNOWN, AND INCLUDED IN THE MODEL AS A VARIABLE AFFECTING TREATMENT.)

WE SHALL NOT PROVIDE DETAILS ON THE INSTRUMENTAL-VARIABLES APPROACH TO IMPACT ESTIMATION. FROM THE VIEWPOINT OF MATCHING, POTENTIAL INSTRUMENTAL VARIABLES SHOULD BE INCLUDED IN DESIGN CONSIDERATIONS.

REGRESSION DISCONTINUITY

BOTH THE R&R AND HECKMAN APPROACHES STRIVE TO ESTIMATE THE ATE OVER THE ENTIRE POPULATION OF INTEREST. THAT IS THE REASON FOR THE FOCUS ON STRONG IGNORABILITY, I.E., NOT ALLOWING THE PROPENSITY SCORE TO BE ZERO OR ONE. IN SOME APPLICATIONS, HOWEVER, THIS ASSUMPTION CANNOT POSSIBLY BE MADE. FOR EXAMPLE, IN A CONDITIONAL CASH TRANSFER (CCT) PROGRAM, AN ELIGIBILITY SCORE, BASED ON ASSETS, IS CALCULATED FOR EACH POTENTIALLY ELIGIBLE HOUSEHOLD, AND HOUSEHOLDS THAT EXCEED THE SCORE ARE NOT ALLOWED TO PARTICIPATE. THAT IS, THE PROBABILITY OF SELECTION IS EITHER ZERO OR ONE FOR ALL UNITS IN THE POPULATION. FOR THIS TYPE OF PROBLEM, A DIFFERENT APPROACH IS REQUIRED.

THE REGRESSION-DISCONTINUITY MODEL IS A USEFUL APPROACH IN SOME APPLICATIONS. THE REGRESSION-DISCONTINUITY APPROACH ESTIMATES THE REGRESSION OF OUTCOME ON THE SCORE, FOR BOTH PARTICIPANTS AND NONPARTICIPANTS. THE “JUMP” IN REGRESSION LINES AT THE ELIGIBILITY CUT-OFF POINT IS A MEASURE OF THE PROGRAM IMPACT. SEE FIGURE 16 FOR AN ILLUSTRATION.

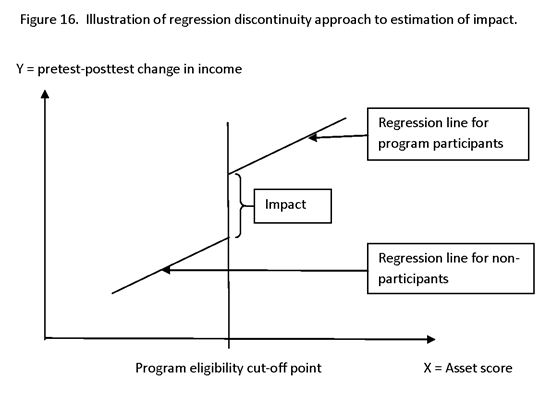
SOME RESEARCHERS RECOMMEND RESTRICTING THE SAMPLE TO UNITS JUST ABOVE AND JUST BELOW THE CUT-OFF POINT. I RECOMMEND SELECTING A SAMPLE OVER THE RANGE OF VARIATION OF THE SCORE VARIABLE (TO ENABLE ESTIMATE OF A MORE ACCURATE REGRESSION MODEL BY HAVING GREATER VARIATION IN THE REGRESSORS).

TREATMENT OF COUNTERFACTUALS ANALYSIS AS A PROBLEM OF MISSING DATA

THE PROBLEM OF ESTIMATING A TREATMENT EFFECT MAY BE APPROACHED AS A PROBLEM WITH MISSING DATA. FOR EACH OBSERVATION, ONLY ONE OF THE COUNTERFACTUAL OUTCOME – IS UNKNOWN, OR “MISSING.”

REFERENCES ON TREATMENT OF MISSING VALUES INCLUDE THE FOLLOWING:

1. LITTLE, RODERICK J. A. AND DONALD B. RUBIN, STATISTICAL ANALYSIS WITH MISSING DATA, 2^ND EDITION, WILEY, 2002

2. KIM, JAE KWANG AND JUN SHAO, STATISTICAL METHODS FOR HANDLING INCOMPLETE DATA, CRC PRESS, 2014

3. LONGFORD, NICHOLAS T., MISSING DATA AND SMALL-AREA ESTIMATION: MODERN ANALYTICAL EQUIPMENT FOR THE SURVEY STATISTICIAN, SPRINGER, 2005

MULTIPLE OUTCOME VARIABLES

THIS PRESENTATION IS RESTRICTED TO THE CASE IN WHICH THE OUTCOME VARIABLE, Y, IS A SCALAR. THE THEORY MAY BE EXTENDED FROM THIS UNIVARIATE CASE TO A MULTIVARIATE SETTING. A FRAMEWORK FOR THIS IS DISCUSSED IN “FORMAL MODES OF STATISTICAL INFERENCE FOR CAUSAL EFFECTS” BY DONALD B. RUBIN (JOURNAL OF STATISTICAL PLANNING AND INFERENCE, VOL. 25 (1990), PP. 279-292.

THE NOTION OF UNCONFOUNDEDNESS IS EXPRESSED IN THE ASSUMPTION THAT P(W|X,Y)=P(W|X), WHERE BOTH X AND Y ARE VECTORS. THE NOTION OF OVERLAP IS EXPRESSED AS 1>P(W|X,Y)>0 FOR ALL X AND Y.

MULTIPLE TREATMENT LEVELS, CONTINUOUS TREATMENT VARIABLES

MOST OF THIS PRESENTATION HAS ADDRESSED THE CASE OF A BINARY TREATMENT VARIABLE. THE PEARL THEORY ON CAUSAL MODELING (WHICH FOCUSED ON ASSESSMENT OF ESTIMABILITY, NOT ON ESTIMATION) WAS COMPLETELY GENERAL, SINCE IT DEFINED THE CAUSAL EFFECT AS THE ENTIRE OUTCOME DISTRIBUTION CONDITIONAL ON THE CAUSAL VARIABLE. THE OUTCOME VARIABLE COULD TAKE ON MANY DISCRETE LEVELS, OR BE CONTINUOUS. ON THE OTHER HAND, MOST OF THE ESTIMATION PROCEDURES CONSIDERED ADDRESSED THE BINARY-TREATMENT-LEVEL CASE.

THE R&R METHODOLOGY IS DESIGNED FOR APPLICATION TO THE BINARY-TREATMENT-VARIABLE CASE. THE HECKMAN APPROACH WAS PRESENTED FOR THE BINARY CASE, BUT MAY BE EXTENDED TO THE MORE GENERAL CASE.

WOOLDRIDGE PRESENTS DISCUSSION OF THE CASE OF MULTIPLE TREATMENT LEVELS AND CONTINUOUS TREATMENT VARIABLES. FOR MULTIPLE TREATMENT LEVELS, TWO DIFFERENT LEVELS MAY BE COMPARED USING EXACTLY THE SAME METHODOLOGY AS FOR THE BINARY-TREATMENT CASE.

THE CASE OF MULTIPLE TREATMENT VARIABLES IS MORE COMPLICATED. IN THIS CASE, THE SCALAR TREATMENT VARIABLE W BECOMES A VECTOR W. WOOLDRIDGE CONSIDERS SOME SPECIAL CASES.

MULTIPLE TREATMENTS

THE PRECEDING DISCUSSION HAS CONSIDERED APPLICATIONS IN WHICH THERE IS A SINGLE (UNIVARIATE) TREATMENT VARIABLE. EXTENSIONS TO THE CASE OF MULTIPLE TREATMENTS ARE AVAILABLE (SEE WOOLDRIDGE OP. CIT.). WITH RESPECT TO MATCHING, THE CONCLUSIONS REACHED FOR THE SINGLE-VARIABLE CASE APPLY – MATCHING SHOULD BE DONE ON ALL VARIABLES IMPORTANT TO THE ANALYSIS, EITHER AS RESPONSE VARIABLES OR AS EXPLANATORY VARIABLES.

PANEL DATA

MUCH OF THE DISCUSSION HAS CONSIDERED EXAMPLES FOR A SINGLE SURVEY ROUND. IN EVALUATION RESEARCH INVOLVING ANALYSIS OF OBSERVATIONAL DATA, HAVING MORE THAN ONE SURVEY ROUND IS ESSENTIAL. THERE ARE USUALLY MANY UNOBSERVED VARIABLES AFFECTING SELECTION AND OUTCOME, AND IT IS OFTEN THE CASE THAT MANY OF THESE ARE TIME-INVARIANT OVER THE TIME-FRAME OF THE STUDY. IN THIS CASE, THEY DROP OUT OF SINGLE-DIFFERENCE MODELS. AS UNOBSERVED VARIABLES, THEY ARE NOT SUBJECT TO MATCHING IN DESIGN.

5. A PROBLEM WITH PROPENSITY SCORE MATCHING (PSM) IN DESIGN

IN ORDER TO REDUCE SELECTION BIAS, ONE MAY CONSIDER A SURVEY DESIGN IN WHICH UNITS ARE MATCHED ON THE PROPENSITY SCORE. PRIOR TO THE SURVEY, IN THE DESIGN PHASE, THE PROPENSITY SCORE IS ESTIMATED FROM DATA THAT ARE AVAILABLE AT THAT TIME. THE AVAILABLE DATA MAY OR MAY NOT INCLUDE ALL VARIABLES AFFECTING SELECTION FOR TREATMENT. IT IS OBVIOUS THAT PROPENSITY SCORE MATCHING IS FOR USE ONLY FOR MATCHING IN A QED, NOT AN ED (IN WHICH A KNOWN RANDOMIZATION PROCESS IS USED TO ASSIGN UNITS TO TREATMENT, SO THAT THE PS IS KNOWN). TWO PROBLEMS ARISE:

1. THE CONDITIONAL PROPENSITY SCORE BASED ON OBSERVED COVARIATES MAY NOT BE A VERY ACCURATE ESTIMATE OF THE UNCONDITIONAL PROPENSITY SCORE.

2. THE VARIATION WITHIN PS-MATCHED PAIRS OR WITHIN PS-MATCHED COMPARISON GROUPS MAY BE VERY HIGH ON VARIABLES OTHER THAN THE PS.

IF SUFFICIENT DATA ARE AVAILABLE IN THE DESIGN PHASE OF A STUDY (PRE-SURVEY), IT MAY BE POSSIBLE TO CONSTRUCT A REASONABLE (PRE-SURVEY) ESTIMATE OF THE PROPENSITY SCORE. IN THAT CASE, IT MAY BE USED AS A BASIS FOR STRATIFICATION.

A MAJOR PROBLEM WITH PROPENSITY SCORE MATCHING (PSM) IS THAT, ALTHOUGH THE SAMPLE UNITS MAY MATCH WITH RESPECT TO THE PROPENSITY SCORE (PS), THEY MAY NOT MATCH WITH RESPECT TO INDIVIDUAL COMPONENTS (COVARIATES X) OF THE PS. IF SOME OF THESE COMPONENTS HAVE A SUBSTANTIAL EFFECT ON OUTCOMES OF INTEREST, THE PRECISION OF THE IMPACT ESTIMATOR (ATE) WILL BE LOW.

AS RUBIN POINTS OUT (R&R OP. CIT.), CONTROL GROUPS ARE OFTEN MUCH MORE VARIABLE THAN TREATMENT GROUPS, E.G., CONTAINING EXTREME VALUES OF THE COVARIATES. ALSO, COVARIATE ADJUSTMENT MAY BE POOR IF THE MODEL IS MISSPECIFIED. THESE CONDITIONS CAUSE PROBLEMS IN TWO WAYS. FIRST, IT IS DIFFICULT TO CONSTRUCT COVARIATE-ADJUSTED ESTIMATES – STRATIFYING ON THE PS OR ON THE PS PLUS ONE OR TWO IMPORTANT COVARIATES IS MUCH SIMPLER. SECOND, IF THE PS IS USED AS A DESIGN VARIABLE, THE RESULTING DESIGN MAY HAVE SUBSTANTIALLY LESS PRECISION THAN IF MATCHING IS DONE USING THE COMPONENT VARIABLES.

PS MATCHING FOCUSES ON VARIABLES THAT AFFECT THE PROBABILITY OF SELECTION. THESE ARE IMPORTANT WITH RESPECT TO BIAS. WITH RESPECT TO POWER AND PRECISION, HOWEVER, WHAT MATTERS ALSO IS VARIABLES THAT HAVE SUBSTANTIAL EFFECTS ON OUTCOMES OF INTEREST. (WE ARE TRYING TO FIND CONDITIONS UNDER WHICH THE OUTCOME, (Y₀, Y₁) IS INDEPENDENT OF TREATMENT, W. FOCUSING ON THE PROBABILITY OF SELECTION IS ONE WAY OF ACHIEVING THIS OBJECTIVE.) FOR CAUSAL ANALYSIS, IT IS IMPORTANT TO TAKE INTO ACCOUNT CAUSAL RELATIONSHIPS AMONG CAUSAL VARIABLES, NOT EXTRANEOUS ONES. ATTENTION SHOULD FOCUS ON CAUSAL VARIABLES THAT AFFECT BOTH SELECTION AND OUTCOME. IF, E.G., EYE COLOR HAS NO EFFECT ON OUTCOMES OF INTEREST, AND SELECTION IS BASED ON EYE COLOR, THE PS MODEL WILL SHOW A STRONG RELATIONSHIP TO EYE COLOR. MATCHING ON THIS WILL NOT INCREASE THE PRECISION OF THE IMPACT ESTIMATE (AND THE POWER OF TESTS OF HYPOTHESIS ABOUT IMPACT) AND WILL HAVE NO EFFECT ON REDUCING BIAS.

WHAT WE WOULD PREFER TO DO FROM THE POINT OF VIEW OF PRECISION IS MATCH THE TREATMENT AND CONTROL GROUPS WITH RESPECT TO VARIABLES THAT HAVE AN IMPORTANT EFFECT ON OUTCOMES OF INTEREST. IF WE DO THIS, WE WILL BOTH REDUCE BIAS AND INCREASE PRECISION. THE PROBLEM, AS DISCUSSED, IS THE DIFFICULTY OF DOING MULTIDIMENSIONAL MATCHING.

PSM FOCUSES MATCHING ON VARIABLES THAT REFLECT SELECTION FOR TREATMENT. IT DOES NOT EXPLICITLY TAKE INTO ACCOUNT THE RELATIONSHIP OF OUTCOMES OF INTEREST TO EXPLANATORY VARIABLES, OR THE RELATIVE IMPORTANCE OF EXPLANATORY VARIABLES TO OUTCOMES OF INTEREST – IT FOCUSES SOLELY ON THE PROBABILITY OF SELECTION FOR TREATMENT. (THIS STATEMENT MAY BE MISINTERPRETED. PSM IMPLICITLY TAKES INTO ACCOUNT OUTCOME IN THAT THE GOAL IS TO USE A PS FOR WHICH OUTCOME (RESPONSE (Y₀, Y₁)) IS CONDITIONALLY INDEPENDENT OF TREATMENT GIVEN X.) WHILE THIS ADDRESSES THE GOAL OF REDUCING BIAS (TO THE EXTENT THAT OBSERVABLE VARIABLES AFFECT THE PROBABILITY OF SELECTION), IT DOES NOT ADDRESS THE ISSUE OF INCREASING POWER OR PRECISION. THIS PROBLEM MAY PERSIST EVEN IF THE VARIABLES X ON WHICH THE PS IS BASED HAVE A STRONG EFFECT ON OUTCOMES OF INTEREST (E.G., IF THE CONTROL GROUPS ARE HIGHLY INTERNALLY VARIABLE).

IN FACT, THIS ASPECT OF PSM TURNS OUT TO BE A SIGNIFICANT PROBLEM. DESIGNS BASED ON PSM MAY HAVE LOW PRECISION. THIS PROBLEM IS MANIFEST TO THE EXTENT THAT THE VARIABLES AFFECTING SELECTION DO NOT HAVE A STRONG EFFECT ON OUTCOMES OF INTEREST AND THE VARIATION IS HIGH WITHIN SOME CONSTANT-PROPENSITY-SCORE STRATA.

EXAMPLE

THE FOLLOWING IS A “CONTRIVED” EXAMPLE THAT ILLUSTRATES A SITUATION IN WHICH PRECISION MAY BE SUBSTANTIALLY REDUCED BY MATCHING ON THE PROPENSITY SCORE. IN THIS EXAMPLE, THE OUTCOME OF INTEREST IS JUMPING HEIGHT. SUPPOSE THAT WE MATCH ON WHETHER OR NOT AN INDIVIDUAL IS IN THE ARMED FORCES. THIS VARIABLE HAS A STRONG EFFECT ON FITNESS, AND THEREFORE ON JUMPING ABILITY.

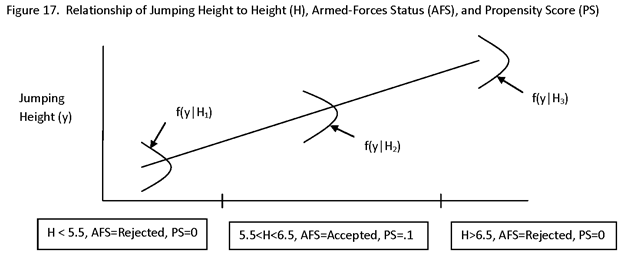
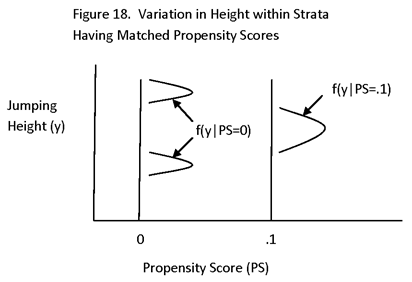
FOR THE PURPOSES OF THIS EXAMPLE, SUPPOSE THAT STRATIFICATION IS DONE ON THE PROPENSITY SCORE, AND THAT THERE ARE JUST TWO VALUES OF IT, VIZ., 0 AND .1. THIS EXAMPLE IS ADMITTEDLY EXTREME, BUT IS BEING USED TO ILLUSTRATE A POINT. FURTHERMORE, LET US ASSUME THAT INDIVIDUALS ARE FORMED INTO MATCHED PAIRS BY MATCHING ON THE PS.

PEOPLE ARE REJECTED FROM THE ARMED FORCES BECAUSE THEY ARE TOO SHORT OR TOO TALL. SINCE JUMPING ABILITY DEPENDS ON HEIGHT, THE DISTRIBUTION OF GROUP ABILITY WILL BE VERY VARIABLE FOR THE NON-SERVICE GROUP. (THIS IS A GOOD EXAMPLE OF RUBIN’S POINT THAT CONTROL GROUPS MAY CONTAIN EXTREME VALUES OF COVARIATES, AND BE INTERNALLY MUCH MORE VARIABLE THAN TREATMENT GROUPS.)

FOR THIS EXAMPLE, IT IS ASSUMED THAT WE ARE CONSTRUCTING A STRATIFIED SAMPLE SURVEY IN WHICH THERE ARE TWO STRATA – PERSONS WHO ARE IN THE ARMED FORCES, AND PERSONS WHO ARE NOT IN THE ARMED FORCES. IN THIS EXAMPLE, IT IS CLEAR THAT THE STRATUM OF PERSONS WHO ARE NOT IN THE ARMED FORCES WILL BE HIGHLY VARIABLE, CONSISTING OF INDIVIDUALS OF EXTREME HEIGHTS, BOTH VERY SHORT AND VERY TALL. SINCE PEOPLE IN THE 0-PS STRATUM WILL VARY CONSIDERABLY WITH RESPECT TO JUMPING ABILITY, USE OF THIS STRATIFICATION WILL LIKELY PRODUCE ESTIMATES OF LOWER PRECISION THAN HAD THE STRATIFICATION NOT BEEN USED AT ALL.

PRECISION OF THE ESTIMATE WILL BE LOW, SINCE MATCHING ON THE PS HAS INTRODUCED MUCH VARIABILITY IN JUMPING ABILITY IN THE NON-SERVICE CATEGORY. PEOPLE WITH LOW PS (LOW LIKELIHOOD OF BEING IN THE SAMPLE) WILL HAVE MUCH VARIATION IN HEIGHT AND VERY LARGE AND VERY SMALL JUMPING SCORES. (THE PRECISION OF STRATIFIED ESTIMATES IS INCREASED WHEN THE STRATA ARE INTERNALLY HOMOGENEOUS.)

PSM ASSURES THAT THE DISTRIBUTION OF X WILL BE THE SAME FOR THE TREATMENT AND COMPARISON GROUPS, GIVEN e(X), NOT THAT MEMBERS OF THE TREATMENT AND COMPARISON GROUPS WILL BE SIMILAR WITH RESPECT TO EVERY X OR ANY X ON WHICH THE PS IS BASED.

WHILE THE PRECEDING EXAMPLE IS EXTREME, THE GENERAL PROBLEM THAT IT ILLUSTRATES IS NOT UNCOMMON. AS OBSERVED BY R&R, TREATMENT GROUPS TEND TO BE MORE HOMOGENEOUS THAN COMPARISON GROUPS.

6. MATCHING METHODS AND COMPUTER SOFTWARE

6.1. STATISTICAL MATCHING PROCEDURES

TO IMPLEMENT EITHER THE R&R OR HECKMAN APPROACHES, WE NEED PRACTICAL METHODS FOR MULTIDIMENSIONAL MATCHING. METHODS OF MULTIDIMENSIONAL MODELING ARE DISCUSSED ON GARY KING’S WEBSITE, http://gking.harvard.edu/category/research-interests/methods/causal-inference .

THE FOLLOWING ARTICLE DISCUSSES THE USE OF MATCHING TO REDUCE MODEL DEPENDENCE: Ho, Daniel, Kosuke Imai, Gary King, and Elizabeth Stuart. 2007. Matching as Nonparametric Preprocessing for Reducing Model Dependence in Parametric Causal Inference, Political Analysis 15: 199–236.

SOFTWARE FOR PERFORMING MATCHING IS POSTED AT THE FOLLOWING WEBSITE: http://gking.harvard.edu/gking/matchit, AND DESCRIBED IN THE ARTICLE: Ho, Daniel E, Kosuke Imai, Gary King, and Elizabeth A Stuart. 2011. MatchIt: Nonparametric Preprocessing for Parametric Causal Inference, Journal of Statistical Software 42, no. 8.

THE PRECEDING ARTICLES IDENTIFY AND DISCUSS THE FOLLOWING MATCHING METHODS:

1. EXACT MATCHING: EACH TREATMENT UNIT IS MATCHED TO ALL POSSIBLE COMPARISON UNITS WITH EXACTLY THE SAME VALUE ON ALL COVARIATES, FORMING GROUPS SUCH THAT WITHIN EACH GROUP ALL UNITS (BOTH TREATMENT AND COMPARISON) HAVE THE SAME COVARIATE VALUES.

2. SUBCLASSIFICATION: GROUPS ARE FORMED SUCH THAT IN EACH GROUP THE DISTRIBUTION OF THE COVARIATES IS AS SIMILAR AS POSSIBLE. THIS IS ACCOMPLISHED IN VARIOUS WAYS, SUCH AS BY MATCHING ON THE PROPENSITY SCORE.

3. NEAREST-NEIGHBOR MATCHING: FOR EACH TREATMENT UNIT, SELECT THE r NEAREST COMPARISON-UNIT MATCHES, WHERE “NEAREST” IS DEFINED ACCORDING TO A PARTICULAR SCALAR DISTANCE MEASURE. ONCE A COMPARISON UNIT HAS BEEN MATCHED, IT IS NO LONGER AVAILABLE FOR MATCHING. (THIS IS REFERRED TO AS “GREEDY” MATCHING. DISTANCE MEASURES INCLUDE MAHALANOBIS, BINOMIAL GENERALIZED LINEAR STATISTICAL MODELS (E.G., LOGIT, PROBIT, AND COMPLEMENTARY LOG-LOG).

4. OPTIMAL MATCHING. FIND MATCHED SAMPLES HAVING THE MINIMUM AVERAGE ABSOLUTE DISTANCE ACROSS ALL MATCHED PAIRS. (THIS IS USEFUL WHEN THE POOL OF COMPARISON UNITS IS NOT VERY LARGE.)

5. FULL MATCHING: A TYPE OF SUBCLASSIFICATION MATCHING THAT USES ALL TREATED AND COMPARISON UNITS, OPTIONALLY DISCARDING THOSE OUTSIDE THE RANGE OF COMMON SUPPORT.

6. GENETIC MATCHING: DETERMINE A SET OF WEIGHTS FOR EACH COVARIATE SUCH THAT OPTIMAL BALANCE IS ACHIEVED.

7. SUMMARY OPTION “interactions”: SHOW THE BALANCE OF ALL SQUARES AND INTERACTIONS OF COVARIATES USED IN THE MATCHING PROCEDURE.

8. SUMMARY OPTION “addlvariables”: PROVIDE BALANCE MEASURES ON ADDITIONAL VARIABLES NOT INCLUDED IN THE ORIGINAL MATCHING PROCEDURE.

6.2. MATCHING FOR STATISTICAL CAUSAL MODELING AND ANALYSIS: IMPORTANCE-WEIGHTED MATCHING AND MARGINAL STRATIFICATION

THE PRECEDING MATCHING TECHNIQUES ARE APPROPRIATE IN THE APPLICATION FOR WHICH THEY WERE INTENDED, VIZ., FOR MATCHING TO REDUCE MODEL DEPENDENCE. FOR THE APPLICATION OF MATCHING IN DESIGN, HOWEVER, THESE METHODS HAVE A SERIOUS SHORTCOMING: THEY DO NOT TAKE INTO ACCOUNT A CAUSAL MODEL. THEY CONSTRUCT MATCHES BY TAKING INTO ACCOUNT THE VARIATION IN VARIABLES, WITH NO REGARD TO THE IMPORTANCE OF CAUSAL RELATIONSHIPS. FOR EXAMPLE, MATCHING USING THE “NEAREST NEIGHBOR” CRITERION AND MAHALANOBIS DISTANCE WOULD PLACE MORE IMPORTANCE ON A VARIABLE THAT REPRESENTS A SUBSTANTIAL PROPORTION OF THE TOTAL VARIATION (E.G., A MAJOR PRINCIPAL COMPONENT) EVEN THOUGH IT MAY BE OF LITTLE IMPORTANCE EITHER TO SELECTION OR OUTCOME.

FOR ANALYTICAL SURVEY DESIGN IN SUPPORT OF ESTIMATION OF CAUSAL IMPACT, IT IS ESSENTIAL TO CONSIDER A CAUSAL MODEL. A MATCHING METHOD (“IMPORTANCE-WEIGHTED MATCHING”) THAT DOES SO IS DESCRIBED IN THE FOLLOWING REFERENCE, POSTED AT INTERNET WEBSITE http://www.foundationwebsite.org/SampleSurveyDesignForEvaluation.pdf .

THE MATCHING METHOD DESCRIBED IN THIS REFERENCE IS PART OF A MORE GENERAL DESIGN PROCEDURE THAT INVOLVES BOTH MATCHING AND MARGINAL STRATIFICATION. MARGINAL STRATIFICATION IS USED TO ADDRESS THE “CURSE OF DIMENSIONALITY” THAT ORDINARY STRATIFICATION (CROSS-STRATIFICATION) ENCOUNTERS IN APPLICATIONS HAVING NUMEROUS DESIGN (EXPLANATORY) VARIABLES. THE MARGINAL STRATIFICATION IS IMPLEMENTED BY SPECIFYING VARIABLE PROBABILITIES OF SELECTION. IN MOST DESIGNS, BOTH PROCEDURES (IMPORTANCE-WEIGHTED MATCHING AND MARGINAL STRATIFICATION) WOULD BE EMPLOYED, AND THE SAME OBSERVED VARIABLES WOULD BE USED FOR BOTH MATCHING AND STRATIFICATION. THE CITED REFERENCE DESCRIBES THE PROCEDURE FOR BOTH MATCHING AND MARGINAL STRATIFICATION. HERE FOLLOWS A DESCRIPTION OF THE MATCHING PROCEDURE.

THE MATCHING PROCEDURE IS AN EXAMPLE OF THE “NEAREST-NEIGHBOR” METHOD OF HO ET AL., IN WHICH THE SCALAR DISTANCE FUNCTION INVOLVES THE IMPORTANCE-WEIGHTED SUM OF INDIVIDUAL COVARIATE DISTANCES.

THE METHOD OF IMPORTANCE-WEIGHTED MATCHING SHOULD BE TAILORED TO THE NATURE OF THE PLANNED ANALYSIS. IF IT IS PLANNED TO USE AN R&R-TYPE ANALYSIS BASED MAINLY ON MATCHING, THEN “IMPORTANCE” REFERS TO VARIABLES THAT HAVE A SUBSTANTIAL RELATIONSHIP TO SELECTION FOR TREATMENT. IF IT IS PLANNED TO USE A HECKMAN-TYPE ANALYSIS BASED BOTH ON A SELECTION MODEL AND AN OUTCOME MODEL, THEN “IMPORTANCE” REFERS TO VARIABLES THAT HAVE A SUBSTANTIAL RELATIONSHIP TO BOTH SELECTION FOR TREATMENT AND OUTCOME.

THE DISTANCE FUNCTION IS CALCULATED AS FOLLOWS. FOR INTERVAL-LEVEL COVARIATES, STRATIFY ON A SMALL NUMBER (E.G., 3-5) OF CATEGORIES. DEFINE THE STRATUM VALUES AS 0, 1, 2,…. DEFINE THE STRATUM BOUNDARIES SUCH THAT OUTCOMES OF INTEREST BEAR AN APPROXIMATELY LINEAR RELATIONSHIP TO THEM, BASED ON A CAUSAL MODEL. FOR CATEGORICAL VARIABLES, STRATIFY ON NATURAL CATEGORIES. FOR THE INTERVAL-LEVEL VARIABLES, NORMALIZE THE VARIABLES TO THE RANGE 0-1. FOR EACH COVARIATE, DEFINE A MATCHING IMPORTANCE WEIGHT THAT REFLECTS THE STRENGTH OF THE RELATIONSHIP OF THE VARIABLE TO OUTCOME VARIABLES OF INTEREST OR TO SELECTION FOR TREATMENT, BASED ON A CAUSAL MODEL.

FOR EACH PAIR OF TREATED AND UNTREATED SAMPLE UNITS, CALCULATE THE INDIVIDUAL COVARIATE DISTANCE AS FOLLOWS: FOR INTERVAL VARIABLES, THE DISTANCE IS THE DIFFERENCE BETWEEN THE STRATUM VALUES; FOR CATEGORICAL VARIABLES, THE DISTANCE IS ZERO IF THE TREATED AND UNTREATED SAMPLE UNITS ARE IN THE SAME STRATUM, AND ONE OTHERWISE. THE DISTANCE BETWEEN THE TWO UNITS IS THE WEIGHTED SUM OF THE COVARIATE DISTANCES, USING THE IMPORTANCE WEIGHTS.

HERE FOLLOWS AN EXAMPLE OF MATCHING IMPORTANCE WEIGHTS, FOR A SURVEY TO COLLECT DATA IN SUPPORT OF AN IMPACT EVALUATION OF A WELFARE PROGRAM INVOLVING CONDITIONAL CASH TRANSFERS. IN THIS EXAMPLE, THERE ARE A TOTAL OF 30 OBSERVED VARIABLES USED FOR MATCHING AND MARGINAL STRATIFICATION. THE 30 VARIABLES WERE ASSEMBLED INTO FIVE MAJOR CATEGORIES (“GROUPS”), ECONOMIC STATUS, FAMILY DEMOGRAPHICS, GEOGRAPHIC LOCATION / URBANICITY, INDICATORS OF INTEREST, AND PROGRAM RELATED. (THE WEIGHTS ARE THE NUMBERS FOLLOWING THE VARIABLE NAMES.)

Group Importances:

Economic status (wealth):16

ScoreCode: 16 (Program participants are selected based on Score, so these will never match well.)

Family demographics: 16

AgeCode: 4

FamilySize: 4

NumChildren: 4

NumStudents: 4

Geographic location / urbanicity: 16

Urban: 4

ParishCode: 12 (Make weight for ParishCode high for efficient survey administration, not just a desire for blocking. Want replacements for control units) to be likely to be in same parish as the treatment unit. This is not a major consideration, however, since the sample would likely be sorted by the survey' field staff prior to going to the field (as part of planning for efficient travel).)

Indicators of interest: 22

Child0to5months: 1

Child6to11months: 1

Child0to5years: 1

Child6to17years: 1

StudentGrade1to6Code: 1

StudentGrade7to9Code: 1

StudentGrade10to11Code: 1

StudentGrade12to13Code: 1

HeadResident: 1

HeadFemale: 1

HeadMarriedOrCL: 1

HeadDisabled: 1

FemaleMbr: 1

PregJune30Mbr: 1

LactJune30Mbr: 1

ElderlyMbr: 1

DisabledMbr: 1

ChronicIllMbr: 1

MentallyIllMbr: 1

SpecialEdMbr: 1

ShutInMbr: 1

OutOfSchoolMbr: 1

Program related: 5

YearCode: 5

THEORETICALLY, WE NEED ONLY TO MATCH ON EXPLANATORY VARIABLES THAT AFFECT OUTCOMES OF INTEREST OR VARIABLES THAT AFFECT SELECTION FOR TREATMENT, BUT NOT NECESSARILY BOTH. THE PROBLEM IS THAT WE DO NOT KNOW ALL SUCH VARIABLES. IN ORDER TO SUPPORT A WIDE RANGE OF ESTIMATION TECHNIQUES (E.G., R&R-TYPE ESTIMATORS BASED ON MATCHING AND SELECTION FOR TREATMENT, AND HECKMAN-TYPE ESTIMATORS BASED ON BOTH SELECTION FOR TREATMENT AND OUTCOME), IT IS DESIRABLE TO MATCH ON VARIABLES THAT HAVE SUBSTANTIAL RELATIONSHIPS EITHER TO OUTCOMES OF INTEREST OR TO SELECTION FOR TREATMENT.

USE OF THE PROPENSITY SCORE REDUCES THE MULTIDIMENSIONAL MATCHING PROBLEM FOR VARIABLES RELATED TO SELECTION FOR TREATMENT TO MATCHING ON A SCALAR (I.E., THE PROPENSITY SCORE). IT IS BEST SUITED FOR APPLICATIONS IN WHICH THE PROPENSITY SCORE MODEL CAN BE ESTIMATED WELL. USE OF THE IMPORTANCE-WEIGHTED MATCHING METHOD (BASED ON MARGINAL STRATIFICATION) REDUCES THE MULTIDIMENSIONAL MATCHING PROBLEM TO MATCHING ON A SCALAR (I.E., THE IMPORTANCE SCORE) FOR VARIABLES RELATED TO OUTCOME. THIS IS USEFUL FOR APPLICATIONS IN WHICH IT IS DIFFICULT TO ESTIMATE THE PROPENSITY SCORE, AND THE OUTCOME MODEL BECOMES MORE IMPORTANT.

NOTE THAT IN DESIGN, IN MANY APPLICATIONS MATCHING IS DONE AT A HIGH LEVEL (E.G., AT THE PRIMARY SAMPLE UNIT (PSU) LEVEL). IN SUCH CASES, IT MAY NOT BE FEASIBLE TO DEVELOP A USEFUL PROPENSITY SCORE MODEL, AND THE DESIGN WOULD BE CONSTRUCTED USING MARGINAL STRATIFICATION FOR VARIABLES THAT ARE CONSIDERED TO HAVE AN IMPORTANT EFFECT ON OUTCOMES OF INTEREST, NOT ON THE PROPENSITY SCORE (PS). IN SUCH CASES, USE PS FOR MATCHING IN ANALYSIS, WHEN MUCH DATA (OBSERVATIONS, VARIABLES) ARE AVAILABLE (AT THE LEVEL OF THE ULTIMATE UNIT OF SAMPLING) FOR DEVELOPMENT OF THE PS MODEL.

7. RECOMMENDED APPROACH TO MATCHING IN EVALUATION DESIGN

MATCHING IMPROVES PRECISION AND POWER IN EDs AND QEDs. MATCHING ON THE PROPENSITY SCORE (PS) REDUCES BIAS IN QEDs, BUT MATCHING ON THE PS ALONE MAY REDUCE PRECISION.

THE TERM “MATCHING” REFERS NOT ONLY TO CROSS-SECTIONAL MATCHING, BUT ALSO TO LONGITUDINAL MATCHING. FOR EXAMPLE, A PRETEST-POSTTEST-COMPARISON-GROUP DESIGN MAY BE “DOUBLY MATCHED,” IN THE SENSE THAT TREATMENT AND COMPARISON GROUPS MAY BE MATCHED IN A PARTICULAR SURVEY ROUND, AND PRETEST AND POSTTEST GROUPS MAY BE MATCHED BY USING A PANEL-SURVEY DESIGN.

BASED ON CONSIDERATION OF THE RESULTS DISCUSSED IN THIS PRESENTATION, THE FOLLOWING ALTERNATIVE APPROACHES TO MATCHING MAY REASONABLY BE CONSIDERED. WHEN THE TERM “EFFECT” IS USED, IT REFERS TO A CAUSAL EFFECT BASED ON A CAUSAL MODEL.

ALTERNATIVE APPROACHES TO MATCHING

1. MATCH ON VARIABLES THAT ARE CONSIDERED TO HAVE A SUBSTANTIAL EFFECT ON OUTCOMES OF INTEREST OR SELECTION FOR TREATMENT, AND THEN USE THE PROPENSITY SCORE (PS) FOR CHECKING.

2. MATCH ON THE PS AND VARIABLES THAT ARE CONSIDERED TO HAVE AN IMPORTANT EFFECT ON OUTCOMES OF INTEREST. THE MATCHING IS FINER THAN PROPENSITY-SCORE MATCHING (PSM), AND IT ADDRESSES NOT ONLY BIAS (THROUGH THE PS) BUT ALSO PRECISION (THROUGH THE OTHER VARIABLES).

3. MATCH ONLY ON VARIABLES THAT ARE CONSIDERED TO HAVE AN IMPORTANT EFFECT ON OUTCOMES OF INTEREST OR SELECTION FOR TREATMENT. IGNORE THE PROPENSITY SCORE.

DISCUSSION

IN APPROACH 1, IF THE INDIVIDUAL VARIABLES (“COVARIATES”) USED FOR MATCHING ARE IMPORTANT ONES IN THE PS, THEN INCLUSION OF THE PS IN THE MATCHING IS UNNECESSARY (SINCE MATCHING DIRECTLY ON THE VARIABLES WILL ASSURE THAT THE PS MATCHES, ALSO).

THE R&R ARTICLE IDENTIFIES APPROACH 2.

APPROACH 3 IS APPROPRIATE IF MATCHING IS DONE AT HIGH LEVELS, E.G., AT THE PRIMARY SAMPLING UNIT LEVEL, WHEN IT IS POSSIBLE THAT VARIABLES AFFECTING SELECTION FOR TREATMENT ARE NOT KNOWN, AND WHEN THE SAMPLE SIZE FOR DETERMINING A PS MODEL IS SMALL.

THE GOAL IN MATCHING IS TO ACHIEVE, TO THE DEGREE POSSIBLE, CONDITIONAL INDEPENDENCE OF RESPONSE (Y₀, Y₁) AND TREATMENT, W, GIVEN THE COVARIATES, X. THIS CAN BE ACHIEVED BY MATCHING EITHER ON ALL VARIABLES AFFECTING SELECTION FOR TREATMENT, OR ON ALL VARIABLES AFFECTING OUTCOMES OF INTEREST, OR ON ALL VARIABLES AFFECTING BOTH SELECTION FOR TREATMENT AND OUTCOMES OF INTEREST. THE “CURSE OF DIMENSIONALITY” PROBLEM ASSOCIATED WITH MATCHING ON A LARGE NUMBER OF VARIABLES IS ADDRESSED IN THE FIRST INSTANCE BY MATCHING ON THE PROPENSITY SCORE, AND IN THE SECOND AND THIRD INSTANCES THROUGH THE USE OF MARGINAL STRATIFICATION AND MATCHING ON AN IMPORTANCE-WEIGHTED SCORE (AS DISCUSSED IN AN EARLIER SECTION).

IN MANY APPLICATIONS, SELECTION FOR TREATMENT MAY BE DONE AT THE LEVEL OF THE ULTIMATE SAMPLE UNIT, E.G., AT THE LEVEL OF AN INDIVIDUAL OR HOUSEHOLD. IN SUCH APPLICATIONS, IT MAY NOT BE POSSIBLE TO CONSTRUCT A GOOD ESTIMATE OF THE PROPENSITY SCORE IN THE DESIGN PHASE. IN THIS CASE, MATCHING IN DESIGN WILL BE BASED ON VARIABLES HAVING AN IMPORTANT RELATIONSHIP TO OUTCOMES OF INTEREST OR TO SELECTION FOR TREATMENT, BUT NOT TO THE PROPENSITY SCORE.

IT IS RECOMMENDED TO INCLUDE THE PS AS A MATCH VARIABLE ONLY IF A REASONABLE ESTIMATE OF THE PS IS AVAILABLE. OTHERWISE, MATCH ON INDIVIDUAL COVARIATES (AFFECTING EITHER SELECTION FOR TREATMENT OR OUTCOMES OF INTEREST), NOT ON THE PS. IN DESIGN, USE BOTH IMPORTANCE-WEIGHTED MATCHING AND MARGINAL STRATIFICATION AS DESIGN TOOLS. USE MARGINAL STRATIFICATION WITH VARIABLE SELECTION PROBABILITIES TO ADDRESS THE “CURSE OF DIMENSIONALITY” PROBLEM ASSOCIATED WITH STRATIFICATION ON NUMEROUS VARIABLES. (MARGINAL STRATIFICATION CAN BE IMPLEMENTED FOR ANY NUMBER OF VARIABLES. UNLIKE CROSS STRATIFICATION, IT DOES NOT RESULT IN STRATUM CELLS CONTAINING NO SAMPLE UNITS.) USE THE SAME VARIABLES AND STRATUM DEFINITIONS FOR BOTH IMPORTANCE-WEIGHTED MATCHING AND MARGINAL STRATIFICATION.

SOME FINAL NOTES:

THIS PRESENTATION HAS ADDRESSED MAINLY THE ISSUE OF MATCHING IN DESIGN, NOT MATCHING IN ANALYSIS. MATCHING MAY BE DONE BOTH IN DESIGN AND IN ANALYSIS. THE TOPIC OF MATCHING IN ANALYSIS (MATCHING ESTIMATORS, PROPENSITY-SCORE-BASED ESTIMATORS) IS SUBSTANTIAL – THE ISSUE OF MATCHING DOES NOT END WITH THE DESIGN. MATCHING IN DESIGN AFFECTS BOTH THE QUALITY (PRECISION, BIAS) OF THE ANALYSIS AND THE PROCEDURES USED IN THE ANALYSIS. ADDITIONAL MATCHING MAY BE DONE IN THE ANALYSIS PHASE, USING SEVERAL DIFFERENT ESTIMATORS.

IN MANY APPLICATIONS, MATCHING IN DESIGN MAY BE DONE ONLY FOR HIGHER LEVELS OF SAMPLING (E.G., AT THE LEVEL OF A PRIMARY SAMPLING UNIT), SINCE DATA FOR MATCHING IN THE DESIGN PHASE ARE USUALLY AVAILABLE ONLY FOR HIGHER LEVELS. THE SAMPLE SIZE OF FIRST-STAGE SAMPLE UNITS IS USUALLY MODEST. FOR THESE TWO REASONS, IT MAY NOT BE POSSIBLE TO CONSTRUCT A GOOD ESTIMATE OF THE PS IN THE DESIGN PHASE. IN THIS CASE, IMPORTANCE-WEIGHTED MATCHING AND MARGINAL STRATIFICATION ARE BETTER APPROACHES TO BIAS REDUCTION THAN PSM. (THEY ARE UNQUESTIONABLY BETTER APPROACHES TO PRECISION ENHANCEMENT, BECAUSE PSM DOES NOT ADDRESS PRECISION, AND MAY IN FACT DECREASE IT.)

IMPORTANCE-WEIGHTED MATCHING AND MARGINAL STRATIFICATION ARE BETTER APPROACHES THAN PSM IF IT IS PLANNED TO USE THE HECKMAN APPROACH TO ANALYSIS (SINCE THEY PROMOTE VARIATION IN AND LOW CORRELATION AMONG IMPORTANT EXPLANATORY VARIABLES).

PSM IS APPROPRIATE FOR MATCHING ON OBSERVABLES IN APPLICATIONS IN WHICH SELECTION FOR TREATMENT IS A MAJOR FACTOR, BUT IT IS NOT ORIENTED TO SUPPORT IMPROVED ESTIMATION OF OUTCOME MODELS. IF THERE ARE UNOBSERVED VARIABLES IMPORTANT TO SELECTION OR OUTCOME, THE DESIGN MUST BE SET UP SO THAT THE EFFECT OF THESE VARIABLES IS REMOVED (E.G., IN THE CASE OF TIME-INVARIANT VARIABLES BY USING A PANEL DESIGN). IF THE ASSUMPTION OF CONDITIONAL INDEPENDENCE ((Y₀, Y₁) W GIVEN X) IS NOT JUSTIFIED, THEN THE DESIGN WILL BE WEAK FOR MODELS REQUIRING THIS ASSUMPTION.

EX POST MATCHING (TRIMMING, CULLING, PRUNING OF THE COLLECTED SURVEY DATA TO REDUCE MODEL DEPENDENCY) IS INEFFICIENT. IT LOSES DATA. IT IS NOT VERY USEFUL IF SAMPLE SIZES ARE SMALL. IF POSSIBLE, IT IS VERY DESIRABLE TO CONSTRUCT THE SURVEY DESIGN TO REDUCE THE AMOUNT OF DATA LOSS FROM DATA CULLING TO REDUCE MODEL DEPENDENCE. THAT IS, TO THE EXTENT POSSIBLE, PERFORM MATCHING IN DESIGN, TO AVOID DATA LOSS FROM MATCHING IN ANALYSIS.

AFTER THE SURVEY DATA ARE COLLECTED, IMPACT ESTIMATION MAY INVOLVE BOTH MATCHING AND COVARIATE ADJUSTMENT (REGRESSION ADJUSTMENT). MATCHING HAS THE ADVANTAGE THAT IT IS EASIER TO UNDERSTAND THAN COVARIATE ADJUSTMENT. COVARIATE ADJUSTMENT HAS THE ADVANTAGE THAT IT IS GENERALLY MORE EFFICIENT (DOES NOT LOSE DATA). USE OF BOTH PROCEDURES IS DOUBLY ROBUST, IN THE SENSE THAT IF EITHER THE MATCHING MODEL IS CORRECT OR THE COVARIATE-ADJUSTMENT MODEL IS CORRECT (CORRECTLY SPECIFIED, IDENTIFIED), THE SELECTION BIAS WILL BE ELIMINATED.

FndID(211)

FndTitle(CAUSAL INFERENCE AND MATCHING: LECTURE NOTES (PREVIOUS TITLE: MATCHING IN EVALUATION DESIGN: CONCEPTS, PRACTICES AND PITFALLS, USE AND ABUSE: LECTURE NOTES))

FndDescription(CAUSAL INFERENCE AND MATCHING: LECTURE NOTES (PREVIOUS TITLE: MATCHING IN EVALUATION DESIGN: CONCEPTS, PRACTICES AND PITFALLS, USE AND ABUSE: LECTURE NOTES))

FndKeywords(statistical methods; monitoring and evaluation; statistics course; short course; sample survey; causal inference; statistical design and analysis; matching)