STATISTICAL INFERENCE: REVIEW OF THEORY NEEDED AS BACKGROUND FOR OTHER TOPICS (CAUSAL ANALYSIS, ANALYSIS OF MISSING DATA, AND ANALYSIS OF PANEL DATA), LECTURE NOTES
Joseph George Caldwell, PhD (Statistics)
1432 N Camino Mateo, Tucson, AZ 85745-3311 USA
Tel. (001)(520)222-3446, E-mail jcaldwell9@yahoo.com
Version without figures
May 9, 2016
Revised November 14, 2017
Copyright © 2016, 2017 Joseph George Caldwell. All rights reserved.
Contents
4. CUMULATIVE DISTRIBUTION FUNCTIONS AND PROBABILITY DENSITY FUNCTIONS. 13
7. CLASSICAL PARAMETRIC ESTIMATION.. 38
9. NUMERICAL METHODS (OPTIMIZATION, SIMULATION), PART 1 (SIMPLE MODELS; ESTIMATION OF VARIANCES) 52
10. CLASSICAL HYPOTHESIS TESTING.. 58
12. STANDARD STATISTICAL MODELS. 69
13. TRUNCATED, CENSORED, AND LATENT-VARIABLE MODELS. 101
14. TREATMENT OF MISSING DATA; SMALL-AREA ESTIMATION; CAUSAL MODELS. 109
15. NUMERICAL METHODS PART 2 (COMPLEX MODELS). 112
16. TESTS OF GOODNESS OF FIT, MODEL ADEQUACY, VALIDITY AND QUALITY. 116
19. EXPERIMENTAL DESIGN; QUASI-EXPERIMENTAL DESIGNS. 133
1. OVERVIEW
THIS PRESENTATION SUMMARIZES THE THEORY OF STATISTICAL INFERENCE CONSIDERED NECESSARY AS BACKGROUND FOR A NUMBER OF PRESENTATIONS ON OTHER TOPICS, INCLUDING PRESENTATIONS ON CAUSAL ANALYSIS, ANALYSIS OF MISSING DATA, AND ANALYSIS OF PANEL DATA.
THE PRESENTATION GENERALLY FOLLOWS THE TEXTBOOK, ALL OF STATISTICS BY LARRY WASSERMAN (SPRINGER, 2004). THE REASONS FOR USING WASSERMAN AS A REFERENCE TEXT ARE TWO: IT IS A COMPACT AND COMPREHENSIVE SUMMARY OF BASIC STATISTICS, AND IT IS ONE OF THE FEW STATISTICS TEXTS THAT INCLUDES A DISCUSSION OF CAUSAL ANALYSIS. OTHER TEXTS REFERRED TO INCLUDE:
MOOD, ALEXANDER M., FRANKLIN A. GRAYBILL AND DUANE C. BOES, INTRODUCTION TO THE THEORY OF STATISTICS, 3RD ED, MCGRAW-HILL, 1974
JOHNSTON, J., ECONOMETRIC METHODS, 3RD ED., MCGRAW-HILL, 1984
WOOLDRIDGE, JEFFREY, ECONOMETRIC ANALYSIS OF CROSS SECTION AND PANEL DATA, 2ND ED., THE MIT PRESS, 2010
GREENE, WILLIAM H., ECONOMETRIC ANALYSIS, 7TH ED., PRENTICE HALL, 2012
OTHER TEXTS WILL BE REFERENCED, IN DISCUSSION OF SPECIALIZED TOPICS.
THE INTENDED AUDIENCE FOR THIS PRESENTATION IS THOSE WHO WISH TO ATTEND THE AUTHOR'S PRESENTATIONS FOR WHICH THIS MATERIAL IS ASSUMED AS A PREREQUISITE. THOSE PRESENTATIONS DEAL WITH SAMPLE SURVEY AND STATISTICAL METHODS IN EVALUATION RESEARCH. THE INTENDED AUDIENCE FOR MOST OF THE PRESENTATIONS IS PEOPLE WITH SOME RELEVANT TECHNICAL BACKGROUND (SUCH AS A FIRST COURSE IN STATISTICS) WHO WISH TO UNDERSTAND THE BASIC CONCEPTS INVOLVED IN THE TOPICS. WHILE SOME OF THE MATERIAL IS SUFFICIENTLY DETAILED TO SUPPORT APPLICATION, SUBSTANTIAL ADDITIONAL STUDY WOULD BE REQUIRED TO ACHIEVE A REASONABLE LEVEL OF COMPETENCE IN APPLYING THE DISCUSSED METHODOLOGY (SUCH AS A MASTER'S DEGREE IN STATISTICS).
SOME MATERIAL ON THIS TOPIC IS PRESENTED IN DAY ONE OF THE COURSE, "SAMPLE SURVEY DESIGN AND ANALYSIS: A COMPREHENSIVE THREE-DAY COURSE WITH APPLICATION TO MONITORING AND EVALUATION." THAT MATERIAL IS ORIENTED TOWARD STATISTICAL INFERENCE IN SAMPLE SURVEYS, I.E., WITH COMPLEX SAMPLE DESIGNS USED IN SAMPLING FROM FINITE POPULATIONS. THE MATERIAL PRESENTED HERE IS BASED LARGELY ON THE ASSUMPTION OF RANDOM SAMPLING FROM INFINITE POPULATIONS (OR SAMPLING FROM FINITE POPULATIONS WITH REPLACEMENT).
IN THIS PRESENTATION IT IS ASSUMED THAT SAMPLE SIZES ARE SUFFICIENTLY LARGE THAT THE LAW OF LARGE NUMBERS AND THE CENTRAL LIMIT THEORY MAY BE INVOKED.
THE MATERIAL PRESENTED HERE APPLIES TO GENERAL SAMPLE DESIGNS, NOT NECESSARILY HIGHLY STRUCTURED EXPERIMENTAL DESIGNS.
INFERENCE IS COMPRISED OF TWO PARTS, ESTIMATION AND HYPOTHESIS TESTING. THE PURPOSE OF ESTIMATION IS TO INFER CHARACTERISTICS ABOUT A POPULATION, BASED ON A SUBSET OF THE POPULATION. THE PURPOSE OF HYPOTHESIS TESTING IS TO MAKE DECISIONS ABOUT THE POPULATION, BASED ON A SUBSET OF THE POPULATION. IN STATISTICAL INFERENCE, THE SUBSET OF DATA ON WHICH THE ESTIMATION OR HYPOTHESIS TESTING IS BASED IS A PROBABILITY SAMPLE.
IN STATISTICAL INFERENCE, THE PURPOSE OF ESTIMATION IS TO INFER, FROM A PROBABILITY SAMPLE, THE PROBABILITY DISTRIBUTION OF A VARIABLE OF INTEREST OR SOME CHARACTERISTIC OF IT, SUCH AS THE MEAN, THE VARIANCE OR A PARAMETER VALUE; AND THE PURPOSE OF HYPOTHESIS TESTING IS TO MAKE A DECISION ABOUT THE PROBABILITY DISTRIBUTION OR SOME CHARACTERISTIC OF IT.
THE KEY POINT HERE IS THAT STATISTICAL INFERENCE IS BASED ON PROBABILITY THEORY. IT MAKES INFERENCES FROM DATA OBTAINED BY PROBABILITY SAMPLING.
BOTH OF THE PRECEDING DEFINITIONS INVOLVE TERMS THAT ARE NOT YET DEFINED, SUCH AS PROBABILITY, DISTRIBUTION, MEAN AND VARIANCE. THESE TERMS WILL BE DEFINED SHORTLY.
ONE OF THE GOALS OF THIS PRESENTATION IS TO DESCRIBE TWO GENERAL METHODS OF STATISTICAL ESTIMATION THAT ARE USED IN ANALYSIS OF MISSING DATA. THESE TWO METHODS ARE THE MAXIMUM LIKELIHOOD METHOD AND BAYESIAN ANALYSIS. THEY ARE BOTH BASED ON THE PROBABILITY DISTRIBUTION OF THE OBSERVED DATA. THESE TWO METHODS WILL BE DESCRIBED IN SUMMARY FASHION, SUFFICIENT TO CONVEY A CONCEPTUAL UNDERSTANDING OF THEM. BASIC CONCEPTS OF PROBABILITY AND STATISTICS WILL BE SUMMARIZED BEFORE PRESENTING THE MATERIAL ON THE TWO TOPICS OF PRIMARY INTEREST.
IT IS EMPHASIZED THAT THIS PRESENTATION FOCUSES ON JUST TWO OF THE MANY METHODS OF STATISTICAL INFERENCE. IN THE TOPIC OF ESTIMATION, THERE ARE MANY OTHER APPROACHES TO ESTIMATION, INVOLVING CONCEPTS SUCH AS MINIMUM-VARIANCE ESTIMATORS, UNBIASED ESTIMATORS, BEST LINEAR UNBIASED ESTIMATORS, AND SUFFICIENT STATISTICS. IN THE TOPIC OF HYPOTHESIS TESTING, WE WILL FOCUS MAINLY ON POWER, MAKING LITTLE MENTION OF THE MANY OTHER APPROACHES SUCH AS UNBIASEDNESS AND STATISTICAL DECISION THEORY.
AS BACKGROUND FOR THIS PRESENTATION, IT IS ASSUMED THAT THE READER HAS KNOWLEDGE OF THE BASIC CONCEPTS OF PROBABILITY AND STATISTICS, AS WOULD BE PRESENTED IN ANY FIRST COURSE ON THESE TOPICS. THESE BASIC CONCEPTS WILL NOW BE IDENTIFIED AND DISCUSSED BRIEFLY, PRIOR TO PROCEEDING TO DISCUSS THE TWO MAIN TOPICS OF INTEREST.
THE METHODS OF STATISTICS ARE FOUNDED IN THE THEORY OF PROBABILITY. THE BASIC CONCEPTS OF PROBABILITY THEORY WILL NOW BE SUMMARIZED.
2. PROBABILITY
THE THEORY OF PROBABILITY IS BASED ON THE THEORY OF SETS (AND FIELDS). BASIC CONCEPTS IN SET THEORY WILL NOW BE SUMMARIZED (DEFINED, LISTED, BUT NOT DISCUSSED IN DETAIL).
A KNOWLEDGE OF THE BASIC CONCEPTS OF SET THEORY IS ASSUMED FOR THIS PRESENTATION. A STANDARD REFERENCE IS NAIVE SET THEORY BY PAUL R. HALMOS (SPRINGER, 1960).
A SET IS A COLLECTION OF WELL-DEFINED OBJECTS, CALLED ELEMENTS, OR MEMBERS.
EXAMPLES: ALL 1955 CHEVROLET AUTOMOBILES; ALL INTEGERS; ALL FRACTIONS; ALL AMERICAN FEMALES BORN IN 1950; ALL GRADUATES OF A PARTICULAR UNIVERSITY IN THE YEAR 2000; ALL PARTICIPANTS IN A JOB TRAINING PROGRAM; ALL PATIENTS TREATED BY A PARTICULAR CLINIC IN A PARTICULAR MONTH.
NOTATION:
LET SETS BE DENOTED BY UPPER-CASE (CAPITAL) LETTERS, A, B,... AND ELEMENTS OF SETS BE DENOTED BY LOWER-CASE LETTERS, a, b,....
IF a, b, c,... ARE MEMBERS OF A SET S, THEN WE WRITE S = {a, b, c,...} (USING BRACES, NOT BRACKETS)
IF ELEMENT a IS A MEMBER OF SET A THEN WE WRITE aєA.
IF ALL OF THE ELEMENTS OF
A ARE IN B, THEN WE SAY THAT A IS A SUBSET OF B, OR A IS CONTAINED IN B, DENOTED
BY A![]() B.
B.
NOTE THAT THE RELATION є
(BELONGING) IS CONCEPTUALLY DIFFERENT FROM THE RELATION ![]() (INCLUSION). THE RELATION
(INCLUSION). THE RELATION ![]() IS REFLEXIVE (A
IS REFLEXIVE (A![]() A), WHEREAS THE RELATION є IS NOT. (AєA DOES NOT
APPEAR EVER TO BE TRUE; INCLUSION IS TRANSITIVE, WHEREAS BELONGING IS NOT.)
A), WHEREAS THE RELATION є IS NOT. (AєA DOES NOT
APPEAR EVER TO BE TRUE; INCLUSION IS TRANSITIVE, WHEREAS BELONGING IS NOT.)
THE UNION OF A AND B, DENOTED BY AUB, IS THE SET OF ELEMENTS IN EITHER A OR B. ALSO WRITTEN A OR B.
THE INTERSECTION OF A AND B, DENOTED BY A∩B, IS THE SET OF ELEMENTS IN BOTH A AND B. ALSO WRITTEN A AND B OR AB OR A,B.
IF A AND B ARE SETS, THE DIFFERENCE BETWEEN A AND B, OR THE RELATIVE COMPLEMENT OF A IN B, IS THE SET B – A DEFINED AS B – A = {xєB : x є'A} (WHERE є' MEANS "IS NOT A MEMBER OF")
THAT IS, THE COMPLEMENT OF A SET A RELATIVE TO A SET B IS THE SET OF ELEMENTS IN B THAT ARE NOT IN A. THE COMPLEMENT OF A IS DENOTED AS Ac (OR A'). IN A PARTICULAR DISCUSSION, COMPLEMENTATION IS USUALLY WITH RESPECT TO THE SAME SET, E.G., THE SET E CONTAINING ALL ELEMENTS OF INTEREST, AND MENTION OF E IS SUPPRESSED IN THE NOTATION. IN THIS CASE, A U A' = E.
THE SET CONSISTING OF NO ELEMENTS IS THE EMPTY SET, DENOTED BY Ø.
AN EXPERIMENT IS A WELL-DEFINED, CONTROLLED PROCEDURE USED TO PRODUCE (GENERATE, CREATE, IDENTIFY) WELL-DEFINED ENTITIES, CALLED THE OUTCOMES OF THE EXPERIMENT. A SPECIFIC PROCEDURE USED TO PRODUCE OUTCOMES IS CALLED A TREATMENT. IF THE TREATMENT IS APPLIED TO PHYSICAL OBJECTS, THEY ARE CALLED EXPERIMENTAL UNITS.
EXAMPLES: ALL BRICKS PRODUCED BY A PARTICULAR KILN SET AT A SPECIFIC TEMPERATURE AND BAKED FOR A SPECIFIC LENGTH OF TIME; ALL FISH COLLECTED AT A PARTICULAR LOCATION OF A LAKE AT A PARTICULAR HOUR ON A PARTICULAR DATE, USING A PARTICULAR FISHING METHOD; ALL GRADUATES OF A JOB-TRAINING PROGRAM; ALL SUBJECTS OF A CLINICAL TRIAL.
A SAMPLE SPACE IS THE SET, S, OF ALL POSSIBLE OUTCOMES OF A PARTICULAR EXPERIMENT.
EXAMPLES:
THE EXPERIMENT IS A SINGLE TOSS OF A COIN. THE OUTCOMES ARE EITHER HEAD, H, OR TAIL, T. THE SAMPLE SPACE IS S = {H, T}. (RECALL THAT IN SPECIFYING A SET, THE LISTED ORDER OF THE ELEMENTS IS OF NO SIGNIFICANCE. SO WE COULD ALSO WRITE S = {T, H}.)
THE EXPERIMENT IS TOSSING A COIN TWICE. THE OUTCOMES ARE:
TOSS 1: H, TOSS 2: H; DENOTE OUTCOME AS HH
TOSS 1: H, TOSS 2: T; DENOTE OUTCOME AS HT
TOSS 1: T, TOSS 2: H; DENOTE OUTCOME AS TH
TOSS 1: T, TOSS 2: T; DENOTE OUTCOME AS TT
SO S = {HH, HT, TH, TT}.
IN A SET, SUCH AS S, THE ORDERING OF THE MEMBERS OF THE SET IS OF NO SIGNIFICANCE. (NOTE THAT WHILE THE ORDERING OF HH, HT, TH AND TT WITHIN S IS IRRELEVANT, THE ORDERING OF H AND T WITHIN EACH OUTCOME LABEL (HH, ETC.) IS SIGNIFICANT – IT IS ESSENTIAL TO DESCRIBING THE OUTCOME OF THE EXPERIMENT COMPLETELY (I.E., THE RESULT OF EACH OF THE TWO TOSSES).)
AN EVENT, E, IS ANY COLLECTION OF OUTCOMES OF AN EXPERIMENT. THAT IS, AN EVENT IS A SUBSET OF THE SAMPLE SPACE, INCLUDING THE SAMPLE SPACE ITSELF.
IN ANY DISCUSSION RELATING TO A PARTICULAR SAMPLE SPACE, THE COMPLEMENT OF A SET IS ASSUMED, UNLESS STATED OTHERWISE, TO BE WITH RESPECT TO THE SAMPLE SPACE.
EXAMPLE: IN THE EXPERIMENT OF TOSSING A COIN TWICE, CONSIDER THE EVENT THAT A SINGLE TAIL OCCURS IN THE TWO TOSSES. THEN E = {TH, HT}.
SINCE A SAMPLE SPACE IS A SET, AND AN EVENT IS A SUBSET OF THE SAMPLE SPACE, ELEMENTARY SET OPERATIONS (UNION, INTERSECTION, COMPLEMENTATION) MAY BE APPLIED TO EVENTS.
EXAMPLE: IF E1 = {TH, HT} AND E2 = {TT, HH}, THEN E1 U E2 = {TH, HT, TT, HH} = S; E1 ∩ E2 = Ø; E1c = {TT, HH} = E2. (RECALL: U DENOTES UNION, ∩ DENOTES INTERSECTION, Ec DENOTES THE COMPLEMENT OF E (I.E., ALL EVENTS IN THE SAMPLE SPACE THAT ARE NOT IN E), AND Ø DENOTES THE EMPTY SET (A SET CONSISTING OF NO ELEMENTS). INTERSECTION OF TWO EVENTS A AND B IS DENOTED EITHER AS A∩B OR AB OR A,B.)
WE SHALL NOW DEFINE PROBABILITIES OF EVENTS. FOR FINITE OR COUNTABLY INFINITE SAMPLE SPACES, PROBABILITIES CAN BE SUITABLY DEFINED FOR ALL SUBSETS OF THE SAMPLE SPACE. FOR UNCOUNTABLY INFINITE SAMPLE SPACES, SUCH AS THE UNIT INTERVAL OR THE REAL LINE, IT IS NOT POSSIBLE TO SPECIFY A REASONABLE DEFINITION OF PROBABILITY FOR ALL SUBSETS OF THE SAMPLE SPACE. IF CONSIDERATION IS RESTRICTED TO A COLLECTION OF SUBSETS KNOWN AS A σ-FIELD (OR σ-ALGEBRA OR BOREL FIELD), A SUITABLE DEFINITION IS POSSIBLE.
A σ-FIELD, F, IS A COLLECTION OF SUBSETS THAT SATISFIES THE FOLLOWING PROPERTIES:
1. Ø є S (I.E., THE EMPTY SET IS CONTAINED IN F)
2. IF A є S THEN Ac є S (I.E., F IS CLOSED UNDER COMPLEMENTATION)
3.
IFA1, A2,... є S THEN ![]() є S (I.E., F IS CLOSED UNDER COUNTABLE UNIONS)
є S (I.E., F IS CLOSED UNDER COUNTABLE UNIONS)
EXAMPLE: LET S = THE REAL LINE, R = (-∞, ∞). THE SET OF ALL INTERVALS OF THE FORM [a,b], (a,b], [a,b), (a,b) FOR ANY REAL NUMBERS a AND b (b≥a) COMPRISE A σ-FIELD. THE SMALLEST σ-FIELD THAT CONTAINS ALL OPEN SUBSETS OF THE REAL LINE IS CALLED THE BOREL σ-FIELD (OR BOREL σ-ALGEBRA).
GIVEN A SAMPLE SPACE S AND A σ-FIELD F DEFINED ON IT, A PROBABILITY FUNCTION (PROBABILITY DISTRIBUTION, PROBABILITY MEASURE) IS ANY FUNCTION, P, WITH DOMAIN F THAT SATISFIES:
1. P(A) ≥ 0 FOR ALL A є S
2. P(S) = 1
3.
IF A1, A2,... є F ARE PAIRWISE DISJOINT, THEN ![]()
FOR ANY GIVEN SAMPLE SPACE, MANY DIFFERENT PROBABILITY FUNCTIONS MAY BE DEFINED. WHICH ONES ARE OF INTEREST DEPENDS ON THE APPLICATION.
THE TRIPLET (S, F, P) (I.E., A SAMPLE SPACE, S; A σ-FIELD ,F, OF EVENTS IN S; AND A PROBABILITY FUNCTION, P, DEFINED ON F) IS CALLED A PROBABILITY SPACE.
FROM THE DEFINITION OF PROBABILITY, A NUMBER OF RESULTS CAN BE DERIVED, SUCH AS (WHERE A AND B ARE EVENTS IN S):
P(Ø) = 0
A
![]() B
B ![]() P(A) ≤ P(B)
P(A) ≤ P(B)
0 ≤ P(A) ≤ 1
P(Ac) = 1 – P(A)
P(A U B) = P(A) + P(B) – P(A∩B).
EXAMPLE: IN THE EXPERIMENT CONSISTING OF A SINGLE TOSS OF A COIN, IT IS REASONABLE TO ASSIGN THE PROBABILITY .5 TO EACH OF THE OUTCOMES OF A SINGLE TOSS (BY SYMMETRY – SINCE THE COIN IS SYMMETRIC, RELABELING THE OUTCOMES T AS H AND H AS T SHOULD RESULT IN THE SAME OUTCOME PROBABILITIES). ALSO, IT IS REASONABLE TO ASSIGN ZERO AS THE PROBABILITY THAT NEITHER A HEAD NOR A TAIL OCCURS, I.E., P(Ø) = 0, AND ONE AS THE PROBABILITY THAT EITHER A HEAD OR TAIL OCCURS, I.E., P(S) = 1.
TO VERIFY THAT THIS ASSIGNMENT IS A PROBABILITY FUNCTION, IT IS NECESSARY TO SHOW THAT THE REQUIREMENTS OF THE DEFINITION OF A PROBABILITY FUNCTION ARE SATISFIED.
FOR THIS EXAMPLE, P(H) = P(T) = .5, P(Ø)= 0 AND P(S) = 1 (ALL BY ASSIGNMENT). THE ONLY NONTRIVIAL COLLECTION OF DISJOINT EVENTS (I.E., COLLECTION CONTAINING MORE THAN ONE EVENT) IS {{H}, {T}}. FOR THIS COLLECTION, P({H} U {T}) = P(S) = 1 AND P({H}) + P({T}) = .5 + .5 = 1. HENCE P({H} U {T}) = P({H}) + P({T}). SO ALL REQUIREMENTS ARE SATISFIED, AND P(.) AS DEFINED IS A PROBABILITY FUNCTION. [END OF EXAMPLE.]
CONDITIONAL PROBABILITY AND INDEPENDENCE
IN THE FOLLOWING, IT IS ASSUMED THAT ALL MENTIONED EVENTS ARE IN A PROBABILITY SPACE (S, F, P).
THE CONDITIONAL PROBABILITY OF AN EVENT A GIVEN AN EVENT B (OR OF AN EVENT "CONDITIONAL ON AN EVENT B") IS DEFINED BY:
P(A|B) = P(AB)/P(B) IF P(B)>0
P(A|B) IS UNDEFINED IF P(B) = 0.
(NOTE THAT CONDITIONAL PROBABILITY IS DEFINED, NOT DERIVED.)
EXAMPLE: IN THE EXPERIMENT CONSISTING OF TWO TOSSES OF A COIN, ASSUME THAT EACH OF THE FOUR EVENTS HH, HT, TH, TT IS EQUALLY LIKELY. THEN THE PROBABILITY OF A1 = {A HEAD ON THE SECOND TOSS} GIVEN A2 = {A HEAD ON THE FIRST TOSS} IS:
P(A1|A2) = P(A1 A2)/P(A2) = P(HH)/P(TH OR HH) = (¼)/(¼ + ¼) = ½.
IT CAN BE SHOWN THAT THE CONDITIONAL PROBABILITY FUNCTION DEFINED ABOVE IS A PROBABILITY FUNCTION FOR EVERY CONDITIONING EVENT B FOR WHICH P(B)>0.
THE THEOREM OF TOTAL PROBABILITIES. FOR A PROBABILITY SPACE (S,F,P), IF B1, B2,...,Bn IS A COLLECTION OF MUTUALLY DISJOINT EVENTS IN S SATISFYING
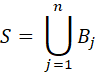
AND P(Bj)>0 FOR j=1,...n, THEN FOR EVERY AєS,
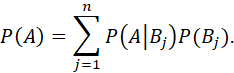
FOR n=2, THE RESULT IS P(A) = P(A|B)P(B) + P(A|Bc)P(Bc).
THE RESULT HOLDS FOR n=∞.
BAYES' FORMULA (BAYES' RULE, BAYES' THEOREM).
FOR A PROBABILITY SPACE (S,F,P), IF B1, B2,...,Bn IS A COLLECTION OF MUTUALLY DISJOINT EVENTS IN S SATISFYING
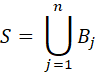
AND P(Bj)>0 FOR j=1,...n, THEN FOR EVERY AєS FOR WHICH P(A)>0,
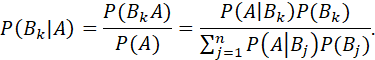
MULTIPLICATION RULE: FOR A PROBABILITY SPACE (S,F,P), LET A1, A2,...,An BE EVENTS IN S FOR WHICH P(A1A2...An)>0. THEN
P(A1A2...An) = P(A1)P(A2|A1)P(A3|A1A2)...P(An|A1...An-1).
INDEPENDENCE OF EVENTS
DEFINITION OF
INDEPENDENCE OF TWO EVENTS: FOR A
PROBABILITY SPACE (S,F,P), TWO EVENTS A AND B ARE DEFINED TO BE INDEPENDENT ("STOCHASTICALLY
INDEPENDENT," "STATISTICALLY INDEPENDENT"; DENOTED BY A![]() IF AND ONLY IF ANY ONE OF THE FOLLOWING CONDITIONS
HOLDS:
IF AND ONLY IF ANY ONE OF THE FOLLOWING CONDITIONS
HOLDS:
1. P(AB) = P(A)P(B)
2. P(A|B) = P(A) IF P(B)>0
3. P(B|A) = P(B) IF P(A)>0.
INDEPENDENCE OF TWO EVENTS IMPLIES INDEPENDENCE OF THEIR COMPLEMENTS.
DEFINITION OF INDEPENDENCE OF SEVERAL EVENTS: FOR A PROBABILITY SPACE (S,F,P), THE EVENTS A1, A2,...,An ARE DEFINED TO BE INDEPENDENT IF AND ONLY IF:
P(AiAj) = P(Ai)P(Aj) FOR i≠J
P(AiAjAk) = P(Ai)P(Aj)P(Ak) FOR i≠j, j≠k, i≠k
![]()
ALL OF THE CONDITIONS MUST BE SATISFIED, AND PAIRWISE INDEPENDENCE DOES NOT IMPLY INDEPENDENCE OF SEVERAL (I.E., MORE THAN TWO) EVENTS.
3. RANDOM VARIABLES
FOR A PROBABILITY SPACE (S,F,P), A RANDOM VARIABLE (RV), X, IS A REAL-VALUED FUNCTION DEFINED ON S (I.E., THE DOMAIN OF THE FUNCTION IS S AND THE COUNTERDOMAIN (RANGE, IMAGE, CODOMAIN) IS THE REAL LINE). THE FUNCTION X(.) MUST BE SUCH THAT THE SETS {ω:X(ω)≤r} ARE EVENTS IN F FOR EVERY r, I.E., THE FUNCTION IS MEASURABLE.
THE NAME "RANDOM VARIABLE" IS MISLEADING. A RANDOM VARIABLE IS NOT RANDOM AND NOT A VARIABLE. IT IS A FUNCTION – A REAL-VALUED SET FUNCTION.
FOR A GIVEN RANDOM VARIABLE, X, AND A SUBSET, A, OF THE REAL LINE, THE PREIMAGE (OR INVERSE IMAGE) OF A IS THE SET X-1(A) = {ωєS : X(ω)єA)}. THE PROBABILITY FUNCTION OF A PROBABILITY SPACE (S,F,P) INDUCES A PROBABILITY FUNCTION ON THE RANDOM VARIABLE:
DEFINITION: P(X є A) = P(X-1(A)) = P({ωєS : X(ω) є A})
DEFINITION: P(X = x) = P(X-1(x)) = P({ωєS : X(ω) = x}).
A RANDOM VARIABLE X DEFINED ON A PROBABILITY SPACE INDUCES ANOTHER PROBABILITY SPACE ON THE SET OF REAL NUMBERS. IN THIS PROBABILITY SPACE, INTERVALS ARE EVENTS.
NOTE THAT THE UPPER-CASE LETTER X DENOTES THE RANDOM VARIABLE AND THE LOWER-CASE LETTER x DENOTES A SPECIFIC VALUE OF X (I.E., VALUE OF X CORRESPONDING TO THE OUTCOME OF A PARTICULAR EXPERIMENT). FOR THE PRECEDING DEFINITION TO BE VALID, THE SET A AND THE POINT x MUST BE MEMBERS OF F.
EXAMPLE: CONSIDER THE EXPERIMENT IN WHICH A COIN IS TOSSED TWICE, WITH OUTCOMES HH, TH, HT, TT. DEFINE THE RANDOM VARIABLE X TO BE THE NUMBER OF HEADS IN THE TOSS. THEN, FOR THE FOUR OUTCOMES (ω) OF THE SAMPLE SPACE, THE VALUES OF X, AND THE PROBABILITY DISTRIBUTION OF X ARE
ω X(ω) P({ω}) x P(X=x)
HH 0 ¼ 0 ¼
TH 1 ¼ 1 ½
HT 1 ¼ 2 ¼
TT 2 ¼ .
WHILE THE PROBABILITY DISTRIBUTION DEFINED ABOVE IS USEFUL FOR FINITE OR COUNTABLY INFINITE SAMPLE SPACES, IT IS AWKWARD FOR USE WITH UNCOUNTABLE SAMPLE SPACES, SINCE IT MAY NOT BE DEFINED FOR EVERY VALUE OF x, OR MAY BE EQUAL TO ZERO FOR ALL VALUES OF x. A MORE USEFUL CONCEPT IS THAT OF THE CUMULATIVE DISTRIBUTION FUNCTION (CDF), TO BE DEFINED NOW.
4. CUMULATIVE DISTRIBUTION FUNCTIONS AND PROBABILITY DENSITY FUNCTIONS
THE CUMULATIVE DISTRIBUTION FUNCTION (CDF) (OR DISTRIBUTION FUNCTION) OF A RANDOM VARIABLE X, DENOTED BY FX(.) (OR F(.)), IS THE FUNCTION WITH DOMAIN THE REAL LINE AND COUNTERDOMAIN THE INTERVAL [0,1] DEFINED AS
FX(x) = P(X≤x) = P(ω: X(ω)≤x) FOR EVERY REAL NUMBER x.
IF A RANDOM VARIABLE X HAS DISTRIBUTION FUNCTION F, WE DENOTE X~F.
EXAMPLE:
FOR THE EXPERIMENT IN WHICH A COIN IS TOSSED TWICE, THE CDF OF THE RANDOM VARIABLE X DEFINED EARLIER IS:
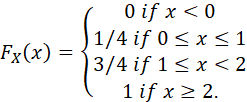
IN GENERAL, A CDF IS RIGHT-CONTINUOUS, NONDECREASING, DEFINED FOR ALL VALUES OF X, F(-∞)=0, AND F(∞) = 1.
A RANDOM VARIABLE IS DISCRETE IF IT TAKES ON COUNTABLY MANY VALUES (I.E., ITS COUNTERDOMAIN (RANGE) IS COUNTABLE). IF A RANDOM VARIABLE IS DISCRETE, WE SAY THAT ITS CDF IS DISCRETE.
FOR A DISCRETE RANDOM VARIABLE, THE PROBABILITY FUNCTION (OR PROBABILITY MASS FUNCTION OR DISCRETE DENSITY FUNCTION), fX(.) (OR f(.)) OF X IS DEFINED AS
fX(x) = P(X=x).
THE CDF FOR A DISCRETE RANDOM VARIABLE IS RELATED TO f BY:
FX(x)
= P(X≤x) = ![]() (
(![]()
NOTE THAT A DENSITY FUNCTION MAY BE DEFINED WITHOUT REFERENCE TO A RANDOM VARIABLE: ANY FUNCTION f(.) WITH DOMAIN THE REAL LINE AND COUNTERDOMAIN [0,1] IS A DISCRETE DENSITY FUNCTION IF FOR SOME COUNTABLE SET x1, x2,... (FINITE OR COUNTABLY INFINITE)
f(xi) > 0 for all i
f(x) = 0 for x≠xi for all i
Σ f(xi) =1 where the summation is over the specified set of points xi.
EXAMPLE: GRAPHS OF THE PROBABILITY FUNCTION AND CUMULATIVE DISTRIBUTION FUNCTION OF THE RANDOM VARIABLE OF THE COIN-TOSSING EXPERIMENT.
FIGURE 1. PROBABILITY FUNCTION FOR THE EXPERIMENT OF TOSSING A COIN TWICE
FIGURE 2. CUMULATIVE DISTRIBUTION FUNCTION FOR THE EXPERIMENT OF TOSSING A COIN TWICE
A RANDOM VARIABLE IS CONTINUOUS
IF THERE EXISTS A FUNCTION fX SUCH THAT fX(x) ≥0 FOR ALL
X, ![]() AND FOR EVERY A≤B
AND FOR EVERY A≤B
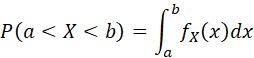
THE FUNCTION fX IS CALLED THE PROBABILITY DENSITY FUNCTION (PDF). THE CUMULATIVE DISTRIBUTION FUNCTION IS
![]()
AND WE HAVE
![]()
AT ALL POINTS x AT WHICH FX IS DIFFERENTIABLE (WHERE THE PRIME (') INDICATES DIFFERENTIATION, I.E., F' IS THE DERIVATIVE OF F).
NOTE THAT WE MAY DEFINE A PROBABILITY DENSITY FUNCTION WITHOUT REFERENCE TO A DISTRIBUTION FUNCTION OR A RANDOM VARIABLE: ANY FUNCTION f(.) WITH DOMAIN THE REAL LINE AND COUNTERDOMAIN [0,∞) IS DEFINED TO BE A PROBABILITY DENSITY FUNCTION IF AND ONLY IF
f(x)≥0 for all x
![]() .
.
EXAMPLE. A RANDOM VARIABLE HAVING THE PROBABILITY DENSITY FUNCTION
![]()
IS SAID TO BE RANDOMLY DISTRIBUTED OVER THE INTERVAL [0,1], OR TO HAVE A UNIFORM DISTRIBUTION OVER [0,1]. THE CUMULATIVE DISTRIBUTION FUNCTION FOR THIS RANDOM VARIABLE IS
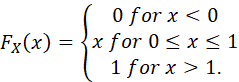
FIGURE 3. PROBABILITY FUNCTION OF UNIFORM [0,1]
FIGURE 4. CDF OF UNIFORM [0,1]
PROPERTIES OF A CDF:
1.
P(X=x) = F(x) – F(x-) WHERE F(x-) = ![]()
2. P(x<X≤y) = F(y) – F(x)
3. P(X>x) = 1 – F(x)
THE INVERSE CDF (OR QUANTILE FUNCTION) OF A CDF, F, IS DEFINED AS
F-1(q) = inf{x: F(x)>q} for 0≤q≤1
IF F IS CONTINUOUS, THEN F-1(q) IS ANY VALUE OF x FOR WHICH F(x) =q. IF F IS STRICTLY INCREASING AND CONTINUOUS, THEN THIS VALUE OF x IS UNIQUE.
SOME DISCRETE PROBABILITY DISTRIBUTIONS / RANDOM VARIABLES
THE FORMULAS DEFINING A NUMBER OF BASIC PROBABILITY DISTRIBUTIONS WILL NOW BE PRESENTED, ALONG WITH GRAPHS OF PROBABILITY MASS/DENSITY FUNCTIONS AND CUMULATIVE DISTRIBUTION FUNCTIONS. THE FORMULAS ARE USED TO CALCULATE DISTRIBUTION CHARACTERISTICS, SUCH AS MEANS AND VARIANCES. THEY WILL BE USED, IN PARTICULAR, IN DISCUSSION OF THE MAXIMUM LIKELIHOOD METHOD AND BAYESIAN ESTIMATION.
[PROVIDE DISCUSSION OF APPLICATIONS OF EACH DISTRIBUTION.]
1. THE POINT MASS DISTRIBUTION
A RANDOM VARIABLE X HAS A POINT MASS DISTRIBUTION AT a IF P(X=a)=1.
PROBABILITY MASS FUNCTION
![]()
FIGURE 5. PROBABILITY MASS FUNCTION FOR POINT MASS DISTRIBUTION.
CUMULATIVE DISTRIBUTION FUNCTION
![]()
FIGURE 6. CUMULATIVE DISTRIBUTION FUNCTION FOR POINT MASS DISTRIBUTION.
2. THE DISCRETE UNIFORM DISTRIBUTION
PROBABILITY MASS FUNCTION
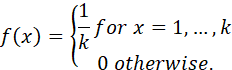
FIGURE 7. PROBABILITY MASS FUNCTION FOR THE DISCRETE UNIFORM DISTRIBUTION.
CUMULATIVE DISTRIBUTION FUNCTION
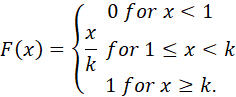
FIGURE 8. CUMULATIVE DISTRIBUTION FUNCTION FOR THE DISCRETE . DISTRIBUTION
3. THE BERNOULLI DISTRIBUTION
PROBABILITY MASS FUNCTION
![]()
IF RV X HAS A BERNOULLI DISTRIBUTION, WE WRITE X ~ Bernoulli (p). A BERNOULLI RV IS ALSO REFERRED TO AS A "BINARY" RV OR A "0,1" RV.
FIGURE 9. PROBABILITY MASS FUNCTION FOR THE BERNOULLI DISTRIBUTION.
CUMULATIVE DISTRIBUTION FUNCTION
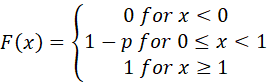
FIGURE 10. PROBABILITY MASS FUNCTION FOR THE BERNOULLI DISTRIBUTION.
4. THE BINOMIAL DISTRIBUTION
PROBABILITY MASS FUNCTION
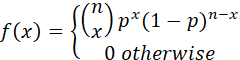
NOTATION X ~ Binomial(n,p).
FIGURE 11. PROBABILTY MASS FUNCTION FOR THE BINOMIAL DISTRIBUTION.
CUMULATIVE DISTRIBUTION FUNCTION
![]()
FIGURE 12. CUMULATIVE DISTRIBUTION FOR THE BINOMIAL DISTRIBUTION.
5. THE POISSON DISTRIBUTION
PROBABILITY MASS FUNCTION
![]()
NOTATION X ~ Poisson(λ).
FIGURE 13. PROBABILITY MASS FUNCTION FOR THE POISSON DISTRIBUTION.
CUMULATIVE DISTRIBUTION FUNCTION
![]()
FIGURE 14. CUMULATIVE DISTRIBUTION FUNCTION FOR THE POISSON DISTRIBUTION.
SOME CONTINUOUS DISTRIBUTIONS / RANDOM VARIABLES
1. THE UNIFORM DISTRIBUTION
PROBABILITY DENSITY FUNCTION
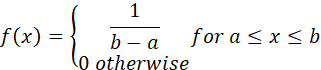
FIGURE 15. PROBABILITY DENSITY FUNCTION FOR THE UNIFORM DISTRIBUTION.
CUMULATIVE DISTRIBUTION FUNCTION
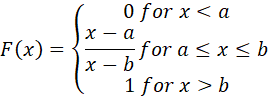
FIGURE 16. CUMULATIVE DISTRIBUTION FUNCTION FOR THE UNIFORM DISTRIBUTION.
2. THE NORMAL (GAUSSIAN) DISTRIBUTION
![]()
NOTATION X ~ N(μ, σ2).
FIGURE 17. PROBABILITY DENSITY FUNCTION FOR THE NORMAL DISTRIBUTION.
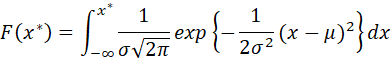
THIS DISTRIBUTION IS DENOTED AS N(μ,σ2) (I.E., IF X HAS A NORMAL DISTRIBUTION WITH PARAMETERS μ AND σ, X~N(μ,σ2)). THERE IS NO CLOSED-FORM EXPRESSION FOR F(x*). THE MEAN OF THE DISTRIBUTION IS μ AND THE VARIANCE IS σ2. IF μ=0 AND σ2=1, THE DISTRIBUTION IS CALLED A STANDARD NORMAL DISTRIBUTION. IF x~N(μ,σ2) THEN Z = (X – μ)/σ ~N(0,1).
THE PROBABILITY DENSITY FUNCTION OF A STANDARDIZED NORMAL RANDOM VARIABLE z IS DENOTED BY φ(z) AND THE CDF IS DENOTED BY Φ(z). TABLES OF φ(z) AND Φ(z) ARE INCLUDED IN MOST STATISTICS TEXTS.
FIGURE 18. CUMULATIVE DISTRIBUTION FUNCTION OF THE NORMAL DISTRIBUTION.
3. THE EXPONENTIAL DISTRIBUTION
![]()
NOTATION X ~ Exp(β).
THE EXPONENTIAL DISTRIBUTION REPRESENTS LIFETIMES OF ITEMS HAVING A CONSTANT FAILURE RATE, AND TIMES BETWEEN EVENTS THAT OCCUR WITH LOW PROBABILITY.
THE FOLLOWING DISTRIBUTIONS OCCUR FREQUENTLY IN STATISTICS. THEIR DENSITY FUNCTIONS ARE A LITTLE COMPLICATED, AND WILL NOT BE PRESENTED HERE. SOME OF THEM OCCUR AS THE DISTRIBUTION OF TEST STATISTICS, AND OTHERS ARE USEFUL AS PRIOR DISTRIBUTIONS IN BAYESIAN ANALYSIS. A PRINCIPAL APPLICATION WILL BE MENTIONED FOR EACH.
4. THE GAMMA (γ) DISTRIBUTION. A FLEXIBLE TWO-PARAMETER FAMILY OF CONTINUOUS DISTRIBUTIONS DEFINED FOR POSITIVE VALUES. SPECIAL CASES INCLUDE THE CHI-SQUARE AND EXPONENTIAL DISTRIBUTIONS.
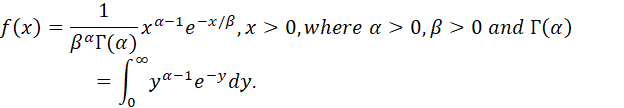
NOTATION: X ~ Gamma(α,β).
5. THE BETA (β) DISTRIBUTION. A FLEXIBLE TWO-PARAMETER FAMILY OF CONTINUOUS DISTRIBUTIONS OVER THE INTERVAL (0,1). IN BAYESIAN INFERENCE, THE BETA DISTRIBUTION IS THE CONJUGATE PRIOR PROBABILITY DISTRIBUTION FOR THE BERNOULLI, BINOMIAL, NEGATIVE BINOMIAL AND GEOMETRIC DISTRIBUTIONS. APPROACHES A BERNOULLI DISTRIBUTION AS THE TWO PARAMETERS APPROACH ZERO.
![]()
NOTATION: X ~ Beta(α,β).
6. THE t DISTRIBUTION: THE DISTRIBUTION OF A SAMPLE MEAN DIVIDED BY ITS ESTIMATED STANDARD DEVIATION.
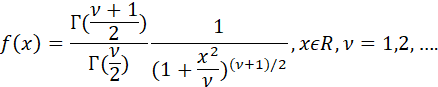
NOTATION: X ~ tν.
7. THE CHI-SQUARE (χ2) DISTRIBUTION: THE DISTRIBUTION OF THE SQUARE OF A NORMAL VARIABLE, AND OF A SAMPLE VARIANCE.
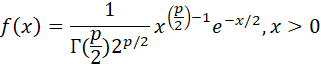
NOTATION: X ~ χ2p.
8. THE F DISTRIBUTION: THE DISTRIBUTION OF THE RATIO OF TWO CHI-SQUARE DISTRIBUTIONS (OR TWO SAMPLE VARIANCES).
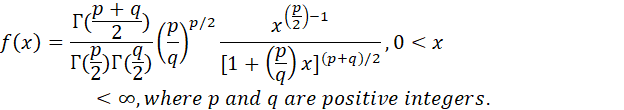
NOTATION: X ~ F(p,q).
9. THE EXPONENTIAL FAMILY OF DISTRIBUTIONS: THE DISTRIBUTION OF FAILURE TIMES.
DEFINITION (MOOD, GRAYBILL AND BOES). A ONE-PARAMETER (UNIDIMENSIONAL PARAMETER, θ) FAMILY (OR CLASS) OF DENSITIES THAT CAN BE EXPRESSED AS
f(x;θ) = a(θ)b(x) exp [c(θ)d(x)]
FOR -∞ < x < ∞, FOR ALL θєΘ AND FOR A SUITABLE CHOICE OF FUNCTIONS a(.), b(.), c(.) AND d(.) IS DEFINED TO BE THE EXPONENTIAL FAMILY OR EXPONENTIAL CLASS.
THE EXPONENTIAL CLASS OF DISTRIBUTIONS IS A VERY FLEXIBLE CLASS OF DISTRIBUTIONS, CAPABLE OF REPRESENTING A WIDE ARRAY OF PHENOMENA. THE EXPONENTIAL CLASS OF DISTRIBUTIONS IS OF INTEREST BECAUSE A NUMBER OF VERY IMPORTANT RESULTS CAN BE SHOWN TO APPLY TO ALL MEMBERS OF THE EXPONENTIAL CLASS. FOR EXAMPLE, A NUMERICAL ALGORITHM USED TO FIND MAXIMUM-LIKELIHOOD ESTIMATORS MAY BE SHOWN TO WORK WELL FOR ALL MEMBERS OF THE EXPONENTIAL CLASS.
AN ALTERNATIVE DEFINITION OF THE EXPONENTIAL CLASS IS AS FOLLOWS.
DEFINITION (HILBE AND ROBINSON): THE CLASS OF PROBABILITY FUNCTIONS OF THE FORM
![]()
WHERE θ IS THE CANONICAL PARAMETER OR LINK FUNCTION, α(θ) IS THE SCALE, b(θ) IS THE CUMULANT, AND c(y,Ф) IS THE NORMALIZATION FUNCTION THAT GUARANTEES THAT THE PDF SUMS OR INTEGRATES TO ONE. THE DERIVATIVE OF THE CUMULANT WITH RESPECT TO θ IS THE MEAN AND THE SECOND DERIVATIVE IS THE VARIANCE OF THE DISTRIBUTION. (ADDITIONAL DISCUSSION OF THE LINK FUNCTION WILL BE PRESENTED LATER, IN DISCUSSION OF GENERALIZED LINEAR MODELS.)
THE FOLLOWING DISTRIBUTIONS ARE MEMBERS OF THE EXPONENTIAL CLASS: NORMAL (GAUSSIAN), BERNOULLI (INCLUDES BINOMIAL), GAMMA, INVERSE GAUSSIAN, POISSON, GEOMETRIC AND NEGATIVE BINOMIAL.
BIVARIATE DISTRIBUTIONS
GIVEN TWO DISCRETE RANDOM VARIABLES X AND Y, THE JOINT PROBABILITY FUNCTION IS DEFINED AS
fX,Y(x,y) = f(x,y) = P(X=x and Y=y) = P(X=x,Y=y).
GIVEN TWO CONTINUOUS RANDOM VARIABLES X AND Y, A FUNCTION f(x,y) IS A JOINT PROBABILITY DENSITY FUNCTION (PDF) IF
f(x,y)≥0 for all (x,y)
![]() and
and
for
any set A![]() R x R, P((X,Y)єA =
R x R, P((X,Y)єA = ![]()
(RECALL THAT R DENOTES THE REAL LINE.)
IN BOTH THE DISCRETE AND CONTINUOUS CASES, THE JOINT CDF IS DEFINED AS
FX,Y(x,y) = P(X≤x, Y≤Y)
EXAMPLE:
THE UNIFORM DISTRIBUTION ON THE UNIT SQUARE:
![]()
P(X≤.5,
Y≤.5) = ![]() = .25.
= .25.
FIGURE 21. THE UNIFORM DISTRIBUTION ON THE UNIT SQUARE.
EXAMPLE:
THE BIVARIATE NORMAL DISTRIBUTION:
LET -∞ < μX < ∞, -∞ < μY < ∞, 0 < σX, 0 < σY AND -1 < ρ <1 BE FIVE REAL NUMBERS. THE BIVARIATE NORMAL PDF WITH MEANS μX AND μY, VARIANCS σX2 AND σY2 AND CORRELATION ρ IS
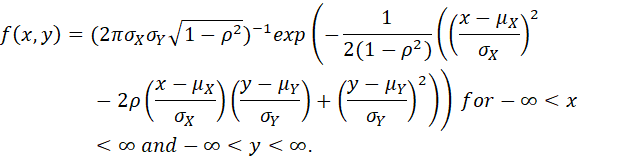
FIGURE 22: THE BIVARIATE NORMAL DISTRIBUTION.
JOINT DISTRIBUTIONS FOR MORE THAN TWO VARIABLES (THE k-DIMENSIONAL CASE, WHERE k>2) ARE DEFINED ANALOGOUSLY TO THE CASE OF TWO VARIABLES JUST CONSIDERED.
MARGINAL DISTRIBUTIONS (BIVARIATE CASE)
FOR DISCRETE RANDOM VARIABLES X AND Y HAVING JOINT DISTRIBUTION FUNCTION fXY, THE MARGINAL MASS FUNCTION FOR X IS DEFINED AS
fX(x)
= P(X=x) = ![]()
AND THE MARGINAL MASS FUNCTION FOR Y IS DEFINED AS
fY(y)
= P(Y=y) = ![]() .
.
EXAMPLE:
fXY IS SPECIFIED IN THE FOLLOWING TABLE. THE MARGINAL DISTRIBUTION FOR X IS GIVEN BY THE ROW TOTALS AND THE MARGINAL DISTRIBUTION FOR Y IS GIVEN BY THE COLUMN TOTALS.
|
Y=0 |
Y=1 |
fX(x) |
|
|
X=0 |
.1 |
.3 |
.4 |
|
X=1 |
.2 |
.4 |
.6 |
|
fY(y) |
.3 |
.7 |
FOR CONTINUOUS RANDOM VARIABLES X AND Y HAVING PDF f(x,y), THE MARGINAL DENSITIES FOR X AND Y ARE DEFINED AS
fX(x) = ∫f(x,y)dy
AND
fY(y) = ∫f(x,y)dx.
EXAMPLE:
JOINT NORMAL DISTRIBUTION.
EXAMPLE:
fXY(x,y) = e-(x+y) for x,y≥0.
THEN
fX(x) = ∫ e-(x+y)dy = e-x∫0∞e-ydy = e-x.
FIGURE 23. MARGINAL DISTRIBUTIONS.
LET X AND Y BE DISCRETE RANDOM VARIABLES WITH JOINT PROBABILITY FUNCTION fXY(x,y). THE CONDITIONAL PROBABILITY FUNCTION (OR CONDITIONAL DISCRETE DENSITY FUNCTION) OF Y GIVEN X IS DEFINED AS
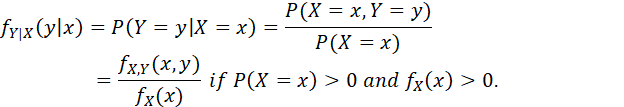
LET X AND Y BE CONTINUOUS RANDOM VARIABLES WITH JOINT PROBABILITY DENSITY FUNCTION fXY(x,y). THE CONDITIONAL PROBABILITY DENSITY FUNCTION OF Y GIVEN X IS DEFINED AS
![]()
IF P(X=x)>0, WE DEFINE FOR INTERVALS A
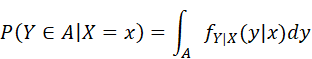
NOTE THAT fX,Y(x,y) = fX|Y(x|y)fY(y) = fY|X(y|x)fX(x).
EXAMPLE: BIVARIATE NORMAL RANDOM VARIABLES.
FIGURE 24. BIVARIATE NORMAL RANDOM DENSITY.
STOCHASTIC INDEPENDENCE OF RANDOM VARIABLES
STOCHASTIC INDEPENDENCE MAY BE DEFINED EITHER IN TERMS OF CUMULATIVE DISTRIBUTION FUNCTIONS OR DENSITY FUNCTIONS. WE SHALL DO THE LATTER.
LET X AND Y BE RANDOM VARIABLES WITH JOINT PROBABILITY FUNCTION OR JOINT PROBABILITY DENSITY FUNCTION fX,Y. X AND Y ARE STOCHASTICALLY INDEPENDENT (OR SIMPLY INDEPENDENT) IF AND ONLY IF
fX,Y(x,y) = fX(x)fY(y) for all x and y.
SINCE
fX,Y(x,y) = fY|X(y|x)fX(x) = fX|Y(x|y)fY(y)
INDEPENDENCE HOLDS IF AND ONLY IF
fY|X(y|x) = fY(y)
AND
fX|Y(x|y) = fX(x).
IF RANDOM VARIABLES X AND
Y ARE INDEPENDENT, WE DENOTE X![]() Y.
Y.
FIGURE 25. INDEPENDENT BIVARIATE NORMAL DISTRIBUTION.
THE RESULTS PRESENTED ABOVE FOR TWO RANDOM VARIABLES CONCERNING JOINT DISTRIBUTIONS, CONDITIONAL DISTRIBUTIONS AND INDEPENDENCE CAN BE EXTENDED FROM THE CASE OF TWO RANDOM VARIABLES TO MORE THAN TWO. THE TERM "MULTIVARIATE" REFERS EITHER TO THE BIVARIATE CASE OR THE CASE OF MORE THAN TWO RANDOM VARIABLE. THE CASE OF A SINGLE RANDOM VARIABLE IS CALLED "UNIVARIATE."
LET X1,...,Xk DENOTE k RANDOM VARIABLES. THE VECTOR (X1,...,Xk) IS CALLED A RANDOM VECTOR. WE SHALL DENOTE VECTORS IN BOLDFACE, E.G., X = (X1,...,Xk) AND x = (x1,...,xk).
THE JOINT PROBABILITY FUNCTION OR JOINT PROBABILITY DENSITY FUNCTION IS DENOTED AS f(X1,...,Xk). THE RANDOM VARIABLES X1,...,Xk ARE DEFINED TO BE INDEPENDENT IF AND ONLY IF
![]()
IF X1,..., Xn ARE INDEPENDENT AND HAVE THE SAME CUMULATIVE DISTRIBUTION FUNCTION, F, (OR DENSITY f,) THEY ARE SAID TO BE INDEPENDENT AND IDENTICALLY DISTRIBUTED (IID), AND THEY ARE SAID TO BE A RANDOM SAMPLE OF SIZE n FROM F (OR FROM f). WE WRITE X1,...,Xn ~ F (OR X1,...,Xn ~ f).
THE TERM RANDOM SAMPLE MAY REFER EITHER TO THE VECTOR RANDOM VARIABLE (X1,...,Xn) OR TO A REALIZED VALUE OF IT, (x1,...,xn). (THE PARENTHESES MAY OR MAY NOT BE INCLUDED.) AS STATED EARLIER, UPPER-CASE LETTERS ARE USED TO REFER TO RANDOM VARIABLES AND LOWER-CASE LETTERS TO REALIZED VALUES OF RANDOM VARIABLES. THE RANDOM VARIABLE IS A (REAL-VALUED) FUNCTION (A RATHER ABSTRACT MATHEMATICAL CONCEPT); THE REALIZED VALUE IS A VECTOR OF NUMBERS. (ACTUALLY, NUMBERS ARE ABSTRACT CONCEPTS, TOO, BUT MOST PEOPLE ARE VERY COMFORTABLE WITH THEM. THE POINT IS THAT X (A VECTOR OF RANDOM VARIABLES) AND x (A VECTOR OF NUMBER) ARE CONCEPTUALLY DIFFERENT.) THE REALIZED VALUE OF A RANDOM SAMPLE MAY BE REFERRED TO AS THE DATA.
MULTIVARIATE DISTRIBUTIONS
MULTINOMIAL DISTRIBUTION
THE BINOMIAL DISTRIBUTION IS THE DISTRIBUTION OF THE NUMBER OF OCCURRENCES IN EACH OF TWO CATEGORIES, WHERE THE TOTAL SAMPLE SIZE IS FIXED (n). THE EXTENSION TO MORE THAN TWO CATEGORIES IS DESCRIBED BY THE MULTINOMIAL DISTRIBUTION.
MULTINOMIAL DISTRIBUTION (CASELLA AND BURGER): LET n AND m BE POSITIVE INTEGERS AND LET p1,..., pn BE NUMBERS SATISFYING 0 ≤ pi ≤1, i = 1,...,n AND ∑pi = 1. A RANDOM VECTOR (X1,...Xn) HAS A MULTINOMIAL DISTRIBUTION WITH m TRIALS AND CELL PROBABILITIES p1,..., pn IF ITS JOINT PROBABILITY MASS FUNCTION IS
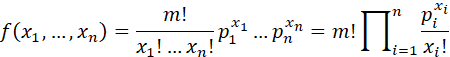
ON THE SET OF (x1,...,xn) SUCH THAT EACH xi IS A NONNEGATIVE INTEGER AND ∑xi = m.
AN EXAMPLE OF A MULTINOMIAL DISTRIBUTION IS THE NUMBER OF COUNTS IN EACH CELL OF A CROSSTABULATION, WHERE m IS THE TOTAL NUMBER OF COUNTS.
MULTIVARIATE NORMAL DISTRIBUTION
EARLIER WAS GIVEN THE BIVARIATE NORMAL DISTRIBUTION. THE NORMAL DISTRIBUTION MAY BE EXTENDED TO AN ARBITRARY NUMBER OF JOINTLY DISTRIBUTED RVs. FOR MORE THAN TWO RVs, MATRIX NOTATION IS USED.
A VECTOR X = (X1,...,Xk) HAS A MULTIVARIATE NORMAL DISTRIBUTION, DENOTED AS X ~ N(μ,∑), IF ITS DENSITY FUNCTION IS
![]()
WHERE μ IS A VECTOR OF LENGTH k AND ∑ IS A k x k SYMMETRIC POSITIVE DEFINITE MATRIX.
EXPECTATION, VARIANCE AND COVARIANCE
THE EXPECTATION, MEAN, OR FIRST CENTRAL MOMENT, OF A RANDOM VARIABLE X IS THE VALUE

AND

THE VARIANCE OF A RANDOM VARIABLE IS THE SECOND CENTRAL MOMENT:
![]()
THE COVARIANCE OF TWO RANDOM VARIABLES X AND Y IS:
![]()
THE CORRELATION OF TWO RANDOM VARIABLES X AND Y IS:
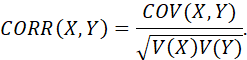
THE MEAN IS OFTEN DENOTED AS μ, THE VARIANCE AS σ2, AND THE CORRELATION AS ρ.
THE PRECEDING DEFINITIONS APPLY BOTH TO UNIVARIATE RANDOM VARIABLES AND VECTOR RANDOM VARIABLES.
FOR THE MULTIVARIATE NORMAL DISTRIBUTION DEFINED EARLIER, THE EXPECTATION OF X IS E(X) = μ AND THE COVARIANCE (MATRIX) OF X IS V(X) = ∑.
A USEFUL RESULT IS
V(X) = EY(V(X|Y)) + VY(E(X|Y)).
FUNCTIONS AND TRANSFORMATIONS OF RANDOM VARIABLES
IN MANY APPLICATIONS, IT IS OF INTEREST TO DETERMINE THE PROPERTIES OF FUNCTIONS OF RANDOM VARIABLES, SUCH AS THE MEAN AND VARIANCE OF A FUNCTION OF THE RANDOM VARIABLE. THERE ARE THREE MAIN WAYS TO FIND MOMENTS (MEANS, VARIANCES) OF FUNCTIONS OF RANDOM VARIABLES: (1) BY INTEGRATION (OR SUMMATION) OF THE FUNCTION OF INTEREST WITH RESPECT TO THE PROBABILITY FUNCTION OF THE ORIGINAL (NONTRANSFORMED) RANDOM VARIABLE; (2) BY FINDING THE PROBABILITY FUNCTION OF THE FUNCTION OF INTEREST, AND FINDING QUANTITIES OF INTEREST WITH RESPECT TO THAT PROBABILITY FUNCTION; (3) BY USING A LINEAR APPROXIMATION (THE DELTA METHOD). THIS SECTION DISCUSSES PROCEDURES FOR FINDING THE DISTRIBUTION OF A FUNCTION OF A RANDOM VARIABLE.
UNIVARIATE CASE
LET X BE A RANDOM VARIABLE WITH PDF fX AND CDF FX. LET Y = r(X) BE A FUNCTION OF X. THE OBJECTIVE IS TO DETERMINE THE PDF AND CDF OF Y.
FOR A DISCRETE RV, THE SOLUTION IS
fY(y) = P(Y=y) = P(r(X) = P({x: r(x)=y}.
FOR A CONTINUOUS RANDOM VARIABLE, THE SOLUTION IS
1. FOR EACH y, DETERMINE THE SET Ay = {x: r(x) ≤ y}
2. THE CDF OF Y IS
FY(y) = P(Y ≤ y) = P(r(X) ≤ y) = P({x: r(x) ≤ y}).
3. IF F IS DIFFERENTIABLE, THE PDF OF Y IS
fY(y) = FY'(y).
IF r IS A DIFFERENTIABLE FUNCTION THE SOLUTION IS
FX(x) = ∫fX(x)dx = ∫fY(r-1(y) (dx/dy) dy = FY(y).
EXAMPLE:
SUPPOSE THAT fX(x) = 1 OVER THE UNIT INTERVAL (0,1) AND THAT Y = r(X) = X2.
THEN
FX(x) = ∫dx = ∫ (1/(2sqrt(y)) dy, 0 ≤ y ≤ 1.
THE EXPECTED VALUE OF X2 MAY BE FOUND BY TAKING THE EXPECTATION OF X2 WITH RESPECT TO THE DISTRIBUTION OF X OR BY TAKING THE EXPECTATION OF Y= X2 WITH RESPECT TO THE DISTRIBUTION OF Y.
E(X2) = ∫x2dx = 1/3.
E(Y) = ∫y/(2sqrt(y))dy = ∫sqrt(y)/2 dy = 1/3.
MULTIVARIATE CASE
TRANSFORMATIONS IN THE MULTIVARIATE CASE ARE A LOGICAL EXTENSION OF THE PROCEDURE IN THE UNIVARIATE CASE.
WITHOUT PROVIDING ALL OF THE DETAILS, THE PROCEDURE SIMPLY CORRESPONDS TO A TRANSFORMATION OF VARIABLES IN MULTIPLE INTEGRATION, SUCH AS, IN THE BIVARIATE CASE:
![]()
WHERE J IS THE JACOBEAN
(MATRIX OF PARTIAL DERIVATIVES) AND ![]() IS THE SUPPORT
OF THE DISTRIBUTION IN THE (y1,y2) PLANE.
IS THE SUPPORT
OF THE DISTRIBUTION IN THE (y1,y2) PLANE.
INEQUALITIES
MANY INEQUALITIES ARISE IN STATISTICS, BUT MORESO IN PROOFS THAN IN DATA-ANALYSIS APPLICATIONS. THESE INCLUDE INEQUALITIES SUCH AS CHEBYCHEV'S INEQUALITY AND JENSEN'S INEQUALITY. THEY ARE IMPORTANT, BUT BECAUSE OF THEIR LOW FREQUENCY OF OCCURRENCE IN APPLICATIONS, THEY ARE NOT DISCUSSED HERE.
5. LARGE SAMPLE THEORY (LIMIT THEOREMS; LAW OF LARGE NUMBERS, CENTRAL LIMIT THEOREM; THE DELTA METHOD)
TWO VERY IMPORTANT RESULTS IN THE THEORY OF STATISTICS ARE THE LAW OF LARGE NUMBERS AND THE CENTRAL LIMIT THEOREM. THERE IS MORE THAN ONE VERSION OF THE LAW OF LARGE NUMBERS, BUT THEY ALL ASSERT THAT AS THE SAMPLE SIZE INCREASES, THE SAMPLE MEAN (OF A RANDOM SAMPLE) GETS CLOSER AND CLOSER TO THE DISTRIBUTION MEAN (FOR ANY RANDOM VARIABLE HAVING A FINITE VARIANCE, WHICH HOLDS FOR ALL PRACTICAL PURPOSES), I.E., THE SAMPLE MEAN IS A CONSISTENT ESTIMATOR OF THE POPULATION (DISTRIBUTION) MEAN.
THE CENTRAL LIMIT THEOREM STATES THAT FOR ANY RANDOM VARIABLE WITH FINITE VARIANCE THE DISTRIBUTION OF THE SAMPLE MEAN (OF A RANDOM SAMPLE) TENDS TO A NORMAL DISTRIBUTION. THAT IS, IF μ DENOTES THE MEAN AND σ2 DENOTES THE VARIANCE OF THE DISTRIBUTION, THEN
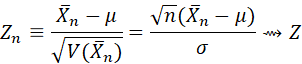
WHERE Z ~ N(0,1). THE THEOREM HOLDS IF THE STANDARD DEVIATION σ IS REPLACED BY THE USUAL SAMPLE ESTIMATE (Sn).
A PRECISE STATEMENT OF THESE TWO LAWS MAY BE FOUND IN MOST STATISTICS TEXTS (INCLUDING WASSERMAN).
THESE THEOREMS ARE VERY GENERAL, APPLYING TO ANY RANDOM VARIABLE HAVING FINITE VARIANCE. THEY PROVIDE THE BASIS FOR MAKING APPROXIMATE PROBABILITY STATEMENTS ABOUT THE SAMPLE MEAN. FOR LARGE SAMPLES. HOW LARGE IS LARGE? IT IS GENERALLY STATED THAT FOR A SAMPLE OF SIZE 30 OR MORE THE APPROXIMATION OF THE SAMPLING DISTRIBUTION OF THE SAMPLE MEAN TO A NORMAL DISTRIBUTION IS REASONABLY GOOD.
THE WEAK LAW OF LARGE NUMBERS CAN PROVIDE GUIDANCE ON HOW LARGE A SAMPLE IS REQUIRED TO ACHIEVE A PRESCRIBED LEVEL OF ACCURACY IN ESTIMATING THE MEAN. SINCE THE LAW IS SO GENERAL (APPLYING TO ANY DISTRIBUTION WITH FINITE VARIANCE), THAT GUIDANCE IS NOT VERY USEFUL. MORE REASONABLE ESTIMATES OF SAMPLE SIZES CAN BE OBTAINED IF IT CAN BE ASSUMED THAT THE SAMPLING DISTRIBUTION IS A SPECIFIC DISTRIBUTION, SUCH AS POISSON OR NORMAL.
THE CENTRAL LIMIT THEOREM APPLIES TO (SIMPLE) RANDOM SAMPLING. IN MANY PRACTICAL APPLICATIONS, THE SAMPLE DESIGN IS QUITE DIFFERENT FROM SIMPLE RANDOM SAMPLING, AND THE SAMPLE DESIGN MUST BE TAKEN INTO ACCOUNT IN ESTIMATING SAMPLE SIZE.
IN ANY EVENT, THIS PRESENTATION ASSUMES THAT THE SAMPLE SIZES ARE SUFFICIENTLY LARGE THAT THE LAW OF LARGE NUMBERS AND THE CENTRAL LIMIT THEOREM CAN REASONABLY BE INVOKED.
THE DELTA METHOD
DETERMINING THE PROBABILITY DISTRIBUTION OF A RANDOM VARIABLE THAT IS A FUNCTION OF ANOTHER RANDOM VARIABLE MAY BE COMPLICATED, INVOLVING COMPLEX VARIABLE AND PARAMETER TRANSFORMATION AND INTEGRATION. A SIMPLE APPROXIMATION TO THE DISTRIBUTION OF A FUNCTION OF A RANDOM VARIABLE IS PROVIDED BY THE DELTA METHOD. (IT IS CALLED THE DELTA METHOD BECAUSE IT IS BASED ON A TAYLOR SERIES EXPANSION (WHICH INVOLVES SMALL DIFFERENCES, OR "DELTAS".)
IF A SEQUENCE Yn
OF RANDOM VARIABLES (SUCH AS ![]() CONVERGES TO A NORMAL DISTRIBUTION N(μ,σ2/n),
THEN A FUNCTION, g(Yn) CONVERGES TO THE NORMAL DISTRIBUTION
N(g(μ),(g'(μ)))2σ2/n.
CONVERGES TO A NORMAL DISTRIBUTION N(μ,σ2/n),
THEN A FUNCTION, g(Yn) CONVERGES TO THE NORMAL DISTRIBUTION
N(g(μ),(g'(μ)))2σ2/n.
6. STATISTICAL INFERENCE
STATISTICAL INFERENCE IS THE METHODOLOGY FOR INFERRING CHARACTERISTICS OF A DISTRIBUTION (CDF F OR PDF f) FROM A RANDOM SAMPLE, (X1,...,Xn), FROM THAT DISTRIBUTION.
THIS PRESENTATION IS LIMITED TO INFERENCE USING RANDOM SAMPLES. THIS DOES NOT INCLUDE SAMPLING FROM A FINITE POPULATION WITHOUT REPLACEMENT (IN WHICH CASE THE RANDOM VARIABLES ARE NOT INDEPENDENT). IN THIS PRESENTATION, ALL OF THE RANDOM VARIABLES DEFINING THE SAMPLE (X1,...,Xn) ARE INDEPENDENT (AND FROM THE SAME DISTRIBUTION).
WE SHALL USE THE TERMS POPULATION, PARENT POPULATION, OR SAMPLED POPULATION TO REFER TO THE PROBABILITY SPACE ON WHICH A RANDOM VARIABLE IS DEFINED. (THE TERM UNIVERSE IS SOMETIMES USED.) THE TERM TARGET POPULATION REFERS TO A POPULATION OF INTEREST. IT MAY OR MAY NOT BE POSSIBLE OR PRACTICAL TO SELECT A RANDOM SAMPLE FROM THE TARGET POPULATION, BUT FEASIBLE TO SELECT A RANDOM SAMPLE FROM A RELATED POPULATION (I.E., THE SAMPLED POPULATION).
WE MAY REFER TO SELECTING A SAMPLE FROM A DISTRIBUTION (THE JOINT DISTRIBUTION f(x1,...,xn)) OR TO SELECTING A SAMPLE FROM A POPULATION.
A STATISTIC IS A FUNCTION OF A RANDOM VARIABLE. WITH RESPECT TO SAMPLES (WHICH ARE RANDOM VARIABLES), A STATISTIC IS ANY FUNCTION OF THE SAMPLE THAT DOES NOT CONTAIN ANY UNKNOWN PARAMETERS. EXAMPLES OF STATISTICS ARE THE ENTIRE SAMPLE, THE MINIMUM OBSERVATION IN THE SAMPLE, A SAMPLE MEAN, A SAMPLE QUANTILE, A SAMPLE MEDIAN, A SAMPLE RANGE, AN INTERQUARTILE RANGE, AND A SAMPLE VARIANCE.
THE TERM STATISTIC IS USED IN TWO SENSES. IT MAY REFER TO THE RANDOM VARIABLES DEFINING THE SAMPLE, IN WHICH CASE IT IS ALSO A RANDOM VARIABLE, OR IT MAY REFER TO THE REALIZED VALUE OF THE SAMPLE, IN WHICH CASE IT IS A VECTOR OF KNOWN NUMERICAL VALUES. AS MENTIONED, WE SHALL USE UPPER-CASE LETTERS TO REFER TO RANDOM VARIABLES AND LOWER-CASE LETTERS TO REFER TO THE REALIZED VALUES. WHICH SENSE OF THE TERM "RANDOM VARIABLE" IS INTENDED IS INFERRED FROM CONTEXT.
STATISTICS ARE FUNCTIONS OF RANDOM VARIABLES AND ARE THEREFORE ALSO RANDOM VARIABLES. THEIR PROBABILITY DISTRIBUTIONS ARE CALLED SAMPLING DISTRIBUTIONS.
STATISTICAL INFERENCE IS BASED ON STATISTICS AND THE THEORY OF PROBABILITY.
AS MENTIONED, THE TWO MAIN BRANCHES OF STATISTICAL INFERENCE ARE ESTIMATION AND HYPOTHESIS TESTING. ESTIMATION IS CONCERNED WITH INFERRING THE VALUES OF CHARACTERISTICS OF A DISTRIBUTION, SUCH AS ITS MEAN. HYPOTHESIS TESTING IS CONCERNED WITH MAKING DECISIONS ABOUT THE VALUES OF CHARACTERISTICS OF ONE OR MORE DISTRIBUTIONS, SUCH AS WHETHER THE MEANS OF THE TWO DISTRIBUTIONS ARE EQUAL.
STATISTICAL INFERENCE MAY BE CATEGORIZED ACCORDING AS THE DISTRIBUTION FUNCTION OF INTEREST DEPENDS ON A SMALL NUMBER OF PARAMETERS (FIXED CONSTANTS THAT DETERMINE THE DISTRIBUTION EXACTLY). HERE, THE "DISTRIBUTION FUNCTION OF INTEREST" IS THE SAMPLING DISTRIBUTION OF STATISTICS OF INTEREST. IF THE DISTRIBUTION FUNCTION DOES NOT DEPEND ON ANY PARAMETERS, OR ON A NUMBER OF PARAMETERS THAT INCREASES AS THE SAMPLE SIZE INCREASES, THEN THE INFERENCE IS NONPARAMETRIC; OTHERWISE IT IS PARAMETRIC. THIS PRESENTATION WILL DEAL PRIMARILY WITH PARAMETRIC INFERENCE, NOT NONPARAMETRIC INFERENCE. (NOTE: IN SAMPLING FROM FINITE POPULATIONS, THE TERM "POPULATION PARAMETER" MAY REFER TO A QUANTITY THAT IS A FUNCTION OF ALL OF THE MEMBERS OF THE POPULATION, SUCH AS THE POPULATION MEAN OR VARIANCE – THAT DEFINITION HAS NOTHING TO DO WITH A PARAMETER THAT SPECIFIES AN ANALYTIC FUNCTION.)
STATISTICAL INFERENCE MAY ALSO BE CHARACTERIZED ACCORDING AS THE QUANTITIES TO BE ESTIMATED ARE CONSIDERED FIXED (DETERMINISTIC) OR AS RANDOM VARIABLES. THE FORMER TYPE OF INFERENCE IS CALLED "CLASSICAL" OR "FREQUENTIST" – ALL OF THE INFORMATION ON WHICH THE INFERENCE IS BASED IS CONTAINED IN THE SAMPLE AND ASSUMPTIONS ABOUT THE FORM OF THE DISTRIBUTION FUNCTION (E.G., WHETHER IT IS NORMAL). THE LATTER TYPE OF INFERENCE IS CALLED "BAYESIAN" – USE IS MADE OF INFORMATION THAT IS AVAILABLE OUTSIDE THE SAMPLE, SUCH AS PRIOR BELIEF ABOUT LIKELY VALUES OF DISTRIBUTION CHARACTERISTICS OR PARAMETERS. IN THIS PRESENTATION WE SHALL CONSIDER BOTH CLASSICAL METHODS AND BAYESIAN METHODS.
WE SHALL DISCUSS TOPICS OF STATISTICAL INFERENCE IN THE FOLLOWING ORDER.
CLASSICAL PARAMETRIC METHODS
PARAMETRIC ESTIMATION
CLASSICAL POINT ESTIMATION
PROPERTIES OF POINT ESTIMATORS
METHOD OF MOMENTS
METHOD OF MAXIMUM LIKELIHOOD
METHOD OF LEAST SQUARES
DELTA METHOD
INTERVAL ESTIMATION
LARGE-SAMPLE THEORY (LAWS OF LARGE NUMBERS, CENTRAL LIMIT THEOREM)
NONPARAMETRIC METHODS
ESTIMATION
HYPOTHESIS TESTING
NUMERICAL METHODS PART 1 (SIMPLE MODELS)
NEWTON-RAPHSON
ITERATIVE REWEIGHTED LEAST SQUARES
VARIANCE ESTIMATION (BOOTSTRAP)
CLASSICAL HYPOTHESIS TESTING
STATISTICAL POWER
THE ROC CURVE
CONFIDENCE SETS
TESTS FOR INDEPENDENCE
GOODNESS-OF-FIT TESTS
BAYESIAN INFERENCE; STATISTICAL DECISION THEORY
STANDARD STATISTICAL MODELS
UNIVARIATE MODELS
LINEAR STATISTICAL MODELS
LINEAR REGRESSION MODELS
ANALYSIS OF VARIANCE MODELS
LOGISTIC REGRESSION MODELS
GENERAL LINEAR MODEL
GENERALIZED LINEAR MODEL
GENERALIZED ESTIMATING EQUATIONS
TRUNCATED, CENSORED AND LATENT-VARIABLE MODELS
TREATMENT OF MISSING DATA; SMALL-AREA ESTIMATION; CAUSAL MODELS
NUMERICAL METHODS, PART II (MORE COMPLEX MODELS)
EM ALGORITHM
MCMC ALGORITHM
TESTS OF GOODNESS OF FIT AND MODEL ADEQUACY
MULTIVARIATE MODELS
GENERAL LINEAR MODEL
LOG-LINEAR MODELS (FOR CATEGORICAL DATA)
FACTOR ANALYSIS
CLASSIFICATION
TIME-SERIES MODELS
EXPERIMENTAL DESIGN; QUASIEXPERIMENTAL DESIGN
SAMPLE SURVEY
7. CLASSICAL PARAMETRIC ESTIMATION
PARAMETRIC ESTIMATION IS CONCERNED WITH ESTIMATION OF THE PARAMETERS THAT DEFINE PROBABILITY DISTRIBUTIONS. SEVERAL EXAMPLES OF PARAMETRIC PROBABILITY DISTRIBUTIONS WERE PRESENTED ABOVE, INCLUDING THE BINOMIAL DISTRIBUTION (PARAMETER p); THE NORMAL DISTRIBUTION (PARAMETERS μ, σ2); THE POISSON DISTRIBUTION (PARAMETER λ).
WE MAY DENOTE THE CLASS OF DISTRIBUTIONS OF INTEREST AS:
{f(x;θ): θєΘ)}
WHERE Θ DENOTES THE k-DIMENSIONAL CARTESIAN PRODUCT OF THE REAL LINE, Rk, AND θ = (θ1,...,θk) IS A PARAMETER. THE PROBLEM OF INTEREST IS TO ESTIMATE θ OR A FUNCTION OF θ.
EXAMPLES:
FOR A NORMAL DISTRIBUTION, X~N(μ,σ2), IT IS DESIRED TO ESTIMATE THE MEAN, μ, AND THE VARIANCE, σ2. IN THE NOTATION PRESENTED ABOVE, θ = (μ,σ) OR θ = (μ, σ2). MATHEMATICALLY, σ2 IS EASIER TO DEAL WITH THAN σ, SO THE PARAMETER IS USUALLY SPECIFIED AS (μ, σ2). IF θ IS DEFINED AS (μ, σ), THEN THE ESTIMATION PROBLEM IS TO ESTIMATE THE FUNCTION (μ, σ2).
ANOTHER EXAMPLE OF A QUANTITY TO BE ESTIMATED WOULD BE A QUANTILE, SUCH AS THE VALUE OF x FOR WHICH P(X>x) = .05. IN THIS CASE THE FUNCTION TO BE ESTIMATED IS DETERMINED AS FOLLOWS:
P(X > x) = .05
P((X-μ)/σ > (x-μ)/σ) = .05
P(Z > (x-μ)/σ) = .05
1 – Ф((x-μ)/σ) = .05
Ф((x-μ)/σ) = .95
(x-μ)/σ = Ф-1(.95)
x = μ + σ Ф-1(.95),
SO IN THIS CASE, THE PROBLEM IS TO ESTIMATE THE FUNCTION
g(μ,θ) = μ + σ Ф-1(.95).
CLASSICAL POINT ESTIMATION
AN ESTIMATOR IS ANY
STATISTIC (KNOWN FUNCTION OF OBSERVED RANDOM VARIABLES) USED TO ESTIMATE
(GUESS, APPROXIMATE, INFER) THE VALUE OF A FUNCTION g(θ) OF THE PARAMETER, θ,
DEFINING THE SAMPLING DISTRIBUTION. IF θ DENOTES THE PARAMETER, THEN AN
ESTIMATOR OF θ WILL BE DENOTED BY ![]() , AND AN ESTIMATOR OF g(θ) WILL BE DENOTED BY
, AND AN ESTIMATOR OF g(θ) WILL BE DENOTED BY ![]() . THE FUNCTION g(θ) IS CALLED THE ESTIMAND.
. THE FUNCTION g(θ) IS CALLED THE ESTIMAND.
AN ESTIMATE IS THE NUMERICAL VALUE OF AN ESTIMATOR OBTAINED FROM A PARTICULAR REALIZATION OF THE SAMPLE. AS WITH RANDOM VARIABLES, WE SHALL USE UPPER-CASE LETTERS TO DENOTE ESTIMATORS (WHICH ARE RANDOM VARIABLES) AND LOWER-CASE LETTERS TO DENOTE ESTIMATES (WHICH ARE NUMBERS OR VECTORS OF NUMBERS).
PROPERTIES OF POINT ESTIMATORS
IT IS DESIRED THAT, ON AVERAGE, THE VALUES OF AN ESTIMATOR BE CLOSE (IN SOME DEFINED SENSE) TO THE VALUE OF THE ESTIMAND. STANDARD MEASURES OF CLOSENESS OF AN ESTIMATOR TO THE ESTIMAND ARE THE VARIANCE, THE BIAS, AND THE MEAN-SQUARED ERROR.
![]()
![]()
![]()
NOTE THAT BIAS OF AN ESTIMATOR (AND HENCE THE MSE) IS ALWAYS RELATIVE TO A PARTICULAR ESTIMAND.
THE VARIANCE OF AN ESTIMATOR IS A MEASURE OF ITS REPEATABILITY (OR RELIABILITY, OR PRECISION). (IT IS NOT RELATIVE TO A PARTICULAR ESTIMAND.) THE BIAS IS A MEASURE OF SYSTEMATIC ERROR, OR VALIDITY. THE MSE IS A MEASURE THAT COMBINES BOTH PRECISION AND VALIDITY; IT IS A MEASURE OF ACCURACY.
AN ESTIMATOR IS UNBIASED IF ITS EXPECTED VALUE IS EQUAL TO THE ESTIMAND, I.E., THE BIAS IS ZERO.
AN ESTIMATOR IS CONSISTENT IF ITS BIAS DECREASES TO ZERO AS THE SAMPLE SIZE INCREASES.
THERE IS A SUBSTANTIAL THEORY OF ESTIMATION, AND THIS PRESENTATION WILL ADDRESS THE TOPIC ONLY SUPERFICIALLY. THE STANDARD REFERENCE IN THE FIELD IS THEORY OF POINT ESTIMATION BY E. L. LEHMANN (WILEY, 1983).
THERE ARE A NUMBER OF WAYS OF FINDING ESTIMATORS. THIS PRESENTATION WILL NOW DESCRIBE THREE OF THEM: THE METHOD OF MOMENTS, THE METHOD OF MAXIMUM LIKELIHOOD, AND THE METHOD OF LEAST-SQUARES.
METHOD OF MOMENTS
THE METHOD OF MOMENTS FINDS ESTIMATES BY SETTING THE SAMPLE MOMENTS EQUAL TO THEIR EXPECTED VALUES, AND SOLVING FOR THE VALUES OF THE PARAMETERS.
SUPPOSE THAT THE PARAMETER VECTOR HAS k COMPONENTS: θ = (θ1,...,θk).
THE j-TH MOMENT, Mj, OF A DISTRIBUTION OF A RANDOM VARIABLE X IS THE EXPECTED VALUE OF Xj:
Mj = Mj(θ) = Eθ(Xj) = ∫xjdFθ(x)
THE j-TH SAMPLE MOMENT IS THE SAMPLE AVERAGE OF Xj:
![]()
THE METHOD-OF-MOMENTS
ESTIMATOR ![]() IS DEFINED TO BE THE VALUE OF θ THAT SATISFIES THE
SIMULTANEOUS EQUATIONS
IS DEFINED TO BE THE VALUE OF θ THAT SATISFIES THE
SIMULTANEOUS EQUATIONS
![]()
EXAMPLE: BERNOULLI DISTRIBUTION
EXAMPLE: NORMAL DISTRIBUTION
PROPERTIES OF METHOD-OF-MOMENT ESTIMATORS
THE METHOD-OF-MOMENTS
ESTIMATOR ![]() HAS THE
FOLLOWING PROPERTIES (UNDER SUITABLE CONDITIONS):
HAS THE
FOLLOWING PROPERTIES (UNDER SUITABLE CONDITIONS):
1. THE ESTIMATE EXISTS WITH PROBABILITY TENDING TO ONE.
2. THE ESTIMATE IS
ASYMPTOTICALLY NORMAL: ![]()
where
![]()
AS WASSERMAN OBSERVES, IT IS NOT NECESSARY TO CALCULATE THE VARIANCE USING THE PRECEDING FORMIDABLE EXPRESSION. INSTEAD THE VARIANCE CAN BE CALCULATED USING THE BOOTSTRAP METHOD (TO BE DISCUSSED). MOREOVER, THE VARIANCE MAY BE OF LITTLE INTEREST, IF THE METHOD-OF-MOMENT ESTIMATORS ARE SIMPLY TO BE USED AS STARTING VALUES FOR ANOTHER ESTIMATION METHOD (E.G., A NUMERICAL SOLUTION FOR A MAXIMUM LIKELIHOOD ESTIMATOR).
METHOD OF MAXIMUM LIKELIHOOD
THE LIKELIHOOD FUNCTION OF n IID RANDOM VARIABLES, X1,...,Xn HAVING PARAMETRIC PDF f(X;θ) IS THE JOINT DENSITY OF THE RANDOM VARIABLES, CONSIDERED AS A FUNCTION OF THE PARAMETER (θ):
![]()
THE LOG-LIKELIHOOD FUNCTION IS
![]()
THE MAXIMUM LIKELIHOOD
ESTIMATOR (MLE), ![]() , IS THE VALUE THAT MAXIMIZES THE LIKELIHOOD,
, IS THE VALUE THAT MAXIMIZES THE LIKELIHOOD, ![]() .
.
THE SAME MAXIMIZING VALUE
IS OBTAINED BY MAXIMIZING ![]() OR
OR ![]() . IT IS OFTEN SIMPLER TO WORK WITH
. IT IS OFTEN SIMPLER TO WORK WITH ![]() THAN WITH
THAN WITH ![]() .
.
EXAMPLE: BERNOULLI DISTRIBUTION
EXAMPLE: NORMAL DISTRIBUTION
PROPERTIES OF MAXIMUM LIKELIHOOD ESTIMATORS
MAXIMUM LIKELIHOOD ESTIMATORS (MLEs) POSSESS SEVERAL DESIRABLE PROPERTIES:
1. A MLE IS CONSISTENT, I.E., CONVERGE IN PROBABILITY TO THE TRUE VALUE OF THE PARAMETER BEING ESTIMATED
2. A MLE IS EQUIVARIANT,
I.E.. IF ![]() IS THE MLE OF
IS THE MLE OF ![]() THEN
THEN ![]() IS THE MLE OF
IS THE MLE OF ![]() .
.
3. A MLE IS ASYMPTOTICALLY
NORMAL: ![]() CONVERGES IN DISTRIBUTION TO N(0,1), WHERE
CONVERGES IN DISTRIBUTION TO N(0,1), WHERE ![]() DENOTES THE ESTIMATED STANDARD ERROR OF
DENOTES THE ESTIMATED STANDARD ERROR OF ![]() . (FURTHERMORE, FOR MANY APPLICATIONS,
. (FURTHERMORE, FOR MANY APPLICATIONS, ![]() CAN BE DETERMINED ANALYTICALLY.)
CAN BE DETERMINED ANALYTICALLY.)
4. A MLE IS ASYMPTOTICALLY OPTIMAL (EFFICIENT), I.E., IT HAS THE SMALLEST ASYMPTOTIC VARIANCE OF ANY ESTIMATOR.
AN APPROXIMATE EXPRESSION FOR THE STANDARD ERROR OF THE MLE IS THE FOLLOWING.
SINGLE-PARAMETER MODELS
THE SCORE FUNCTION IS DEFINED AS
![]()
THE FISHER INFORMATION IS DEFINED AS
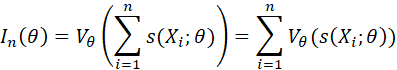
WHERE ![]() DENOTES THE VARIANCE OPERATOR.
DENOTES THE VARIANCE OPERATOR.
SINCE ![]() IT FOLLOWS THAT
IT FOLLOWS THAT ![]() AND
AND
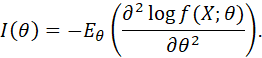
DENOTING ![]() , THE FOLLOWING PROPERTIES HOLD FOR THE MLE (UNDER
SUITABLE CONDITIONS):
, THE FOLLOWING PROPERTIES HOLD FOR THE MLE (UNDER
SUITABLE CONDITIONS):
1. ![]()
2. ![]()
THE METHOD OF LEAST SQUARES
FOR THE TWO PRECEDING ESTIMATION TECHNIQUES, THE METHOD OF MOMENTS AND THE METHOD OF MAXIMUM LIKELIHOOD, IT IS NECESSARY TO SPECIFY THE PROBABILITY DISTRIBUTION FOR THE MODEL ERROR TERMS. WITH THE METHOD OF LEAST SQUARES, IT IS NOT NECESSARY TO MAKE ANY ASSUMPTIONS ABOUT THE DISTRIBUTION OF THE MODEL ERROR TERMS.
IF ![]() DENOTES THE PARAMETER ESTIMATE, AND
DENOTES THE PARAMETER ESTIMATE, AND ![]() DENOTES THE ESTIMATED (PREDICTED, FITTED) VALUE OF Y
FOR THE i-th OBSERVATION, THEN THE ESTIMATED MODEL ERROR TERMS, OR MODEL
RESIDUALS, ARE DEFINED TO BE
DENOTES THE ESTIMATED (PREDICTED, FITTED) VALUE OF Y
FOR THE i-th OBSERVATION, THEN THE ESTIMATED MODEL ERROR TERMS, OR MODEL
RESIDUALS, ARE DEFINED TO BE
![]()
THE LEAST-SQUARES ESTIMATES OF THE PARAMETERS ARE THE VALUE OF THE RESIDUAL SUM OF SQUARES
![]()
THE LEAST-SQUARES METHOD OF ESTIMATION IS OLD, ATTRIBUTED TO GAUSS AND LEGENDRE. IN ITS BASIC FORM PRESENTED ABOVE, IT IS REFERRED TO AS THE METHOD OF “ORDINARY LEAST SQUARES” OR OLS.
ALTHOUGH THE METHOD DOES NOT DEPEND ON ANY ASSUMPTIONS ABOUT THE DISTRIBUTION OF THE MODEL ERROR TERMS, THE PROPERTIES OF ESTIMATORS PRODUCED BY THE METHOD CERTAINLY DEPEND ON THESE ASSUMPTIONS. IN ORDER FOR THE LEAST-SQUARES ESTIMATES TO POSSESS DESIRABLE PROPERTIES SUCH AS UNBIASEDNESS OR CONSISTENCY, IT IS NECESSARY THAT CERTAIN ASSUMPTIONS BE MADE ABOUT THE PROBABILITY DISTRIBUTION OF AN UNDERLYING PROBABILITY DISTRIBUTION THAT GENERATES THE DATA.
M ESTIMATION
WE HAVE DISCUSSED SEVERAL TYPES OF ESTIMATION PROCEDURES: METHOD OF MOMENTS, MAXIMUM LIKELIHOOD AND LEAST SQUARES. IN SOME APPLICATIONS, THESE PROCEDURES DO NOT WORK PARTICULARLY WELL. FOR EXAMPLE, MAXIMUM LIKELIHOOD ESTIMATORS MAY BE BIASED AND INEFFICIENT. A MORE GENERAL TYPE OF ESTIMATION PROCEDURE IS M-ESTIMATION. WITH THIS APPROACH, ESTIMATES ARE FOUND BY MINIMIZING A CRITERION FUNCTION. THE CRITERION FUNCTION IS SELECTED SO THAT THE ESTIMATOR HAS DESIRABLE PROPERTIES IN TERMS OF BIAS AND EFFICIENCY, AND YET CONVERGES TO THE DESIRED PARAMETER VALUES, PARTICULARLY WHEN THE DATA MAY NOT BE FROM AN ASSUMED DISTRIBUTION.
THE LEAST-SQUARES METHOD IS AN EXAMPLE OF AN M-ESTIMATOR (IT MINIMIZES A SUM OF SQUARES, NOT THE LIKELIHOOD FUNCTION DIRECTLY, YET IN THE CASE OF A NORMAL DISTRIBUTION IT CONVERGES TO THE CORRECT PARAMETER VALUES).
THIS PRESENTATION DOES NOT PROVIDE DETAILS ON THE METHOD OF M-ESTIMATION. FOR A REFERENCE, SEE WOOLDRIDGE OP. CIT.
INTERVAL ESTIMATES AND CONFIDENCE SETS
THIS PRESENTATION FOCUSES ON ESTIMATION IN THE CASE OF LARGE SAMPLES, I.E., SAMPLES SUFFICIENTLY LARGE THAT THE LAWS OF LARGE NUMBERS AND THE CENTRAL LIMIT THEOREM MAY BE APPLIED. IN THIS CASE, ONCE A SUITABLE ESTIMATOR AND ITS STANDARD ERROR ARE OBTAINED, CONFIDENCE INTERVALS MAY BE CONSTRUCTED.
IN THE PRECEDING CASE, LET
![]()
(WHERE zα/2 DENOTES THE VALUE OF A STANDARD NORMAL RANDOM VARIABLE, Z, HAVING PROBABILITY α/2 TO THE RIGHT) THEN
![]()
THIS PRESENTATION DOES NOT PRESENT PROOFS, BUT IN THIS CASE, THE PROOF IS SIMPLE AND IMPORTANT TO UNDERSTAND. IT IS AS FOLLOWS:
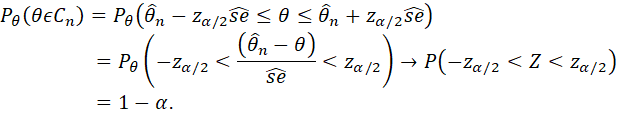
FOR EXAMPLE, FOR α = .05, zα/2 = 1.96, so
![]()
IS AN APPROXIMATE 95 PERCENT CONFIDENCE INTERVAL FOR θ.
A KEY POINT TO REALIZE IN THE PRECEDING PROOF IS THAT θ IS NOT A RANDOM VARIABLE. THE PROBABILITY STATEMENTS REFER TO THE RANDOM VARIABLE Z. IN REPEATED SAMPLING, THE PROBABILITY IS 95 PERCENT THAT THE CONFIDENCE INTERVAL (Cn) – WHICH IS THE RANDOM VARIABLE – WILL INCLUDE θ (WHICH IS A FIXED NUMBER, NOT A RANDOM VARIABLE).
INTERVALS OF THE TYPE
![]()
(AN ESTIMATOR PLUS AND MINUS A MULTIPLE OF ITS STANDARD ERROR) ARE SOMETIMES REFERRED TO AS WALD INTERVALS. THE QUANTITY
![]()
(WHERE θ IS KNOWN) IS REFERRED TO AS A WALD STATISTIC.
THE DELTA METHOD (LINEARIZATION)
ONCE WE HAVE AN ESTIMATOR OF A PARAMETER, IT IS STRAIGHTFORWARD TO FIND AN ESTIMATOR OF A DIFFERENTIABLE FUNCTION OF THAT ESTIMATOR. THE PROCEDURE FOR DOING THIS IS CALLED THE DELTA METHOD, OR LINEARIZATION.
IF τ = g(θ) WHERE g(θ) IS DIFFERENTIABLE FUNCTION AND g'(θ)≠0 THEN
![]()
WHERE
![]()
AND
![]()
CONFIDENCE INTERVALS MAY BE CONSTRUCTED FOR τ JUST AS THEY WERE BEFORE FOR θ (I.E., AS THE ESTIMATE PLUS AND MINUS A MULTIPLE OF ITS STANDARD ERROR).
MULTIPARAMETER MODELS
THE PRECEDING PROPERTIES OF MAXIMUM LIKELIHOOD ESTIMATORS IN THE CASE OF A SINGLE PARAMETER CAN BE EXTENDED TO THE CASE OF MULTIPLE PARAMETERS. DETAILS FOR DOING THIS ARE PROVIDED IN WASSERMAN, PP. 133-34. THE FORMULAS ARE SIMILAR, WITH MATRICES REPLACING CERTAIN SCALAR QUANTITIES. A SUMMARY OF THE METHOD FOLLOWS (FOLLOWING WASSERMAN):
LET THE VECTOR
![]()
DENOTE THE DISTRIBUTION PARAMETER AND LET
![]()
DENOTE THE MAXIMUM LIKELIHOOD ESTIMATOR OF θ.
LET
![]()
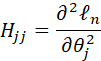
AND
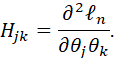
THE FISHER INFORMATION MATRIX IS DEFINED AS
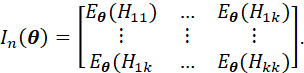
DENOTE THE INVERSE OF In AS Jn(θ) = In-1(θ).
THEN, UNDER SUITABLE CONDITIONS, WE HAVE
![]()
AND, IF θj
DENOTES THE j-th DIAGONAL ELEMENT OF ![]() THEN
THEN
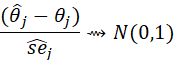
WHERE
![]()
IS THE j-th DIAGONAL
ELEMENT OF Jn. THE APPROXIMATE COVARIANCE OF ![]() AND
AND ![]() IS
IS
![]()
THE MULTIPARAMETER VERSION OF THE DELTA METHOD IS AS FOLLOWS:
LET τ = g(θ1,,,θk) BE A DIFFERENTIABLE FUNCTION WITH GRADIENT
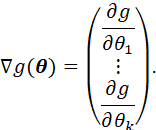
ASSUME THAT ![]() IS NOT ZERO, AND LET
IS NOT ZERO, AND LET ![]() THEN
THEN
![]()
WHERE
![]()
8. NONPARAMETRIC METHODS
THE FOCUS OF THIS PRESENTATION IS ON PARAMETRIC MODELS, I.E., MODELS FOR WHICH THE DISTRIBUTION OF THE RANDOM VARIABLE(S) OF INTEREST ARE SPECIFIED BY A PARAMETER (SCALAR OR VECTOR-VALUED). THERE IS A SUBSTANTIAL BODY OF STATISTICAL THEORY DEALING WITH MODELS THAT ARE NOT PARAMETRIC. A NONPARAMETRIC MODEL CORRESPONDS TO A DISTRIBUTION FUNCTION THAT DOES NOT DEPEND ON A PARAMETER, OR ON A NUMBER OF PARAMETERS THAT INCREASES WITH THE SAMPLE SIZE (SUCH AS A POWER SPECTRUM).
THIS PRESENTATION IS RESTRICTED TO PARAMETRIC MODELS NOT BECAUSE NONPARAMETRIC MODELS ARE UNIMPORTANT, BUT BECAUSE PARAMETRIC MODELS ARE IN SUBSTANTIALLY WIDER USE AND IT IS DESIRABLE TO RESTRICT THE SCOPE OF THE PRESENTATION TO A MANAGEABLE EXTENT.
NONPARAMETRIC METHODS ARE SOMETIMES REFERRED TO AS "DISTRIBUTION-FREE" METHODS. THIS IS SOMEWHAT A MISNOMER, SINCE IT MIGHT BE TAKEN TO MEAN THAT NO DISTRIBUTION IS INVOLVED. WHAT IT MEANS IS THAT THE METHODS WORK NO MATTER WHAT THE FORM OF THE DISTRIBUTION IS.
(IN FACT, THE UNDERLYING DISTRIBUTION MAY VERY WELL BE A PARAMETRIC ONE, SUCH AS A NORMAL DISTRIBUTION – IT IS JUST NOT REQUIRED TO ASSUME THIS. IF THE UNDERLYING DISTRIBUTION IS PARAMETRIC AND THIS INFORMATION IS NOT TAKEN ADVANTAGE OF, NONPARAMETRIC METHODS WILL GENERALLY BE LESS EFFICIENT (FOR A GIVEN SAMPLE SIZE) THAN APPROPRIATE PARAMETRIC METHODS.)
IN GENERAL, NONPARAMETRIC METHODS REQUIRE FEWER ASSUMPTIONS OR WEAKER ASSUMPTIONS ABOUT THE DISTRIBUTION THAN DO PARAMETRIC METHODS. ALSO, NONPARAMETRIC TESTS MAY BE APPLIED TO SITUATIONS IN WHICH SAMPLE SIZES ARE SMALL; THIS PRESENTATION FOCUSES ON INFERENCE FROM LARGE SAMPLES.
NONPARAMETRIC METHODS MAY BE CLASSIFIED AS "TRADITIONAL" OR "MODERN." TRADITIONAL NONPARAMETRIC METHODS DEAL WITH NONPARAMETRIC TESTS OF A NUMBER OF BASIC TESTS OF HYPOTHESIS, SUCH AS TESTING WHETHER TWO SAMPLES COME FROM THE SAME DISTRIBUTION. MODERN NONPARAMETRIC METHODS DEAL WITH ESTIMATION OF THE CDF AND DENSITY, SMOOTHING, NONPARAMETRIC REGRESSION, AND VARIANCE ESTIMATION.
IN THIS PRESENTATION, WE SHALL DESCRIBE NONPARAMETRIC METHODS OF VARIANCE ESTIMATION.
A BOOK THAT PRESENTS TRADITIONAL NONPARAMETRIC METHODS IS NONPARAMETRIC STATISTICS BY SIDNEY SIEGEL (McGRAW-HILL, 1956). A BOOK THAT PRESENTS MODERN NONPARAMETRIC METHODS IS ALL OF NONPARAMETRIC STATISTICS BY LARRY WASSERMAN (SPRINGER, 2006).
TRADITIONAL NONPARAMETRIC METHODS FOCUS ON TESTS OF HYPOTHESIS AND ESTIMATION OF MEASURES OF ASSOCIATION. MODERN NONPARAMETRIC METHODS FOCUS MORE ON ESTIMATION.
TOPICS COVERED IN SIEGEL'S BOOK INCLUDE:
ONE-SAMPLE GOODNESS-OF-FIT TESTS
CHI-SQUARE TEST
KOLMOGOROV-SMIRNOV TEST
RUNS TEST
TESTS COMPARING TWO RELATED SAMPLES
CHI-SQUARE (McNEMAR TEST)
SIGN TEST
WILCOXON MATCHED-PAIRS SIGNED-RANKS TEST
WALSCH TEST
RANDOMIZATION TEST
TESTS COMPARING TWO INDEPENDENT SAMPLES
FISHER EXACT PROBABILITY TEST
CHI-SQUARE TEST
MEDIAN TEST
MANN-WHITNEY U TEST
KOLMOGOROV-SMIRNOV TEST
WALD-WOLFOWITZ RUNS TEST
TESTS FOR COMPARING k RELATED SAMPLES (k>2)
COCHRAN Q TEST
FRIEDMAN TWO-WAY ANALYSIS OF VARIANCE BY RANKS
TESTS FOR COMPARING k INDEPENDENT SAMPLES (k>2)
CHI-SQUARE TEST
MEDIAN TEST
KRUSKAL-WALLIS ONE-WAY ANALYSIS OF VARIANCE BY RANKS
MEASURES OF CORRELATION
THE CONTINGENCY COEFFICIENT
THE SPEARMAN RANK CORRELATION COEFFICIENT
THE KENDALL RANK CORRELATION COEFFICIENT
THE KENDALL PARTIAL RANK CORRELATION COEFFICIENT
THE KENDALL COEFFICIENT OF CONCORDANCE
TO THE ABOVE SHOULD BE ADDED CRAMER'S COEFFICIENT OF ASSOCIATION (DENOTED AS V OR Ф) FOR NOMINAL LEVEL-OF-MEASUREMENT VARIATES.
9. NUMERICAL METHODS (OPTIMIZATION, SIMULATION), PART 1 (SIMPLE MODELS; ESTIMATION OF VARIANCES)
NUMERICAL METHODS FOR DETERMINING MLEs (OPTIMIZATION)
FOR MOST OF THE EXAMPLES SHOWN ABOVE, IT WAS GENERALLY POSSIBLE TO DETERMINE THE MAXIMIZING PARAMETER VALUE FOR THE LIKELIHOOD FUNCTION BY SETTING THE DERIVATIVES WITH RESPECT TO THE PARAMETERS EQUAL TO ZERO AND SOLVING THE RESULTING EQUATIONS. THIS IS NOT ALWAYS POSSIBLE TO DO, EVEN FOR SOME SIMPLE MODELS, SUCH AS THE LOGISTIC REGRESSION MODEL. IN SUCH CASES, WHERE ANALYTICAL SOLUTIONS ARE NOT POSSIBLE, NUMERICAL METHODS ARE USED TO FIND THE MAXIMUM LIKELIHOOD ESTIMATOR.
TWO NUMERICAL METHODS THAT ARE WIDELY USED ARE THE NEWTON-RAPHSON METHOD AND THE ITERATIVE REWEIGHTED LEAST-SQUARES METHOD. THESE WILL NOW BE DESCRIBED IN SUMMARY DETAIL. A THIRD SPECIALIZED METHOD, THE DEMING-STEPHAN ITERATIVE PROPORTIONAL FITTING METHOD, WILL ALSO BE SUMMARIZED.
THE NEWTON-RAPHSON METHOD
THE NEWTON-RAPHSON METHOD (OR NEWTON'S METHOD) OF OPTIMIZATION (FINDING A MAXIMIZING VALUE OF A FUNCTION) WORKS FOR PROBLEMS IN WHICH THE FIRST AND SECOND DERIVATIVES OF THE LIKELIHOOD FUNCTION (OR LOG-LIKELIHOOD FUNCTION) WITH RESPECT TO THE PARAMETERS ARE AVAILABLE. FOR SPECIFICITY, WE SHALL ASSUME THAT WE ARE MAXIMIZING THE LOG-LIKELIHOOD FUNCTION.
THE METHOD IS BASED ON USING THE FIRST TWO TERMS OF A TAYLOR-SERIES EXPANSION OF THE FIRST DERIVATIVE OF THE LIKELIHOOD FUNCTION AROUND THE PARAMETER VALUE. THE MAXIMIZING VALUES CORRESPOND TO SETTING THIS EQUAL TO ZERO. (THE BASIC NEWTON'S METHOD IS USED TO FIND THE ZERO (ROOT) OF A FUNCTION, NOT OF ITS FIRST DERIVATIVE. THE METHOD WORKS SIMPLY BY EXTRAPOLATING THE TANGENT (GRADIENT) OF THE FUNCTION AT THE LAST ITERATION VALUE TO ITS ZERO, AND USING THAT AS THE NEXT ITERATION VALUE.)
FOR THE CASE IN WHICH THERE IS A SINGLE PARAMETER, THE METHOD PROCEEDS AS FOLLOWS.
![]()
SOLVING FOR ![]() YIELDS THE FOLLOWING APPROXIMATION:
YIELDS THE FOLLOWING APPROXIMATION:
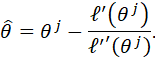
THIS EXPRESSION SUGGESTS THE FOLLOWING ITERATIVE ALGORITHM FOR ESTIMATING θ:
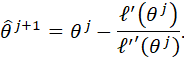
FOR THE CASE IN WHICH THE PARAMETER IS A VECTOR, θ = (θ1,...,θk),THE ALGORITHM IS SIMILAR, WITH THE INVERSE OF THE SECOND DERIVATIVE REPLACED BY A MATRIX:
![]()
WHERE ![]() IS THE MLE,
IS THE MLE, ![]() IS THE VECTOR OF PARTIAL DERIVATIVES AND H (THE
"HESSIAN" MATRIX) IS THE MATRIX OF SECOND PARTIAL DERIVATIVES OF THE LOG-LIKELIHOOD.
IS THE VECTOR OF PARTIAL DERIVATIVES AND H (THE
"HESSIAN" MATRIX) IS THE MATRIX OF SECOND PARTIAL DERIVATIVES OF THE LOG-LIKELIHOOD.
CLEARLY, THE NEWTON-RAPHSON METHOD WORKS ONLY FOR MLEs FOR WHICH THE SECOND DERIVATIVE (OR MATRIX H) ARE NONZERO. THIS IMPLIES THAT THERE IS A CERTAIN AMOUNT OF CURVATURE TO THE LIKELIHOOD FUNCTION, WHICH IS USUALLY THE CASE.
ITERATIVE REWEIGHTED LEAST SQUARES (IRLS)
THE NEWTON-RAPHSON METHOD IS A GENERALLY APPLICABLE METHOD FOR DETERMINING THE MAXIMIZING VALUES OF A FUNCTION, BUT FOR SOLVING MAXIMUM LIKELIHOOD PROBLEMS (ESPECIALLY FOR MEMBERS OF THE EXPONENTIAL FAMILY), THERE IS AN IMPROVED ALGORITHM, THE ITERATIVE (OR ITERATIVELY) REWEIGHTED LEAST SQUARES (IRLS) ALGORITHM, FOR DETERMINING THE MAXIMUM LIKELIHOOD ESTIMATORS. THIS METHOD WORKS BY REPLACING THE OBSERVED HESSIAN MATRIX BY THE EXPECTED HESSIAN MATRIX.
(OPTIONAL: DETAILS ON THE RELATIONSHIP OF IRLS TO NEWTON-RAPHSON). JUSTIFICATION FOR THE IRLS ALGORITHM IS SUMMARIZED IN THE ARTICLE, "ITERATIVELY REWEIGHTED LEAST SQUARES FOR MAXIMUM LIKELIHOOD ESTIMATION, AND SOME ROBUST AND RESISTANT ALTERNATIVES" BY P. J. GREEN (JOURNAL OF THE ROYAL STATISTICAL SOCIETY, SERIES B (METHODOLOGICAL), VOL. 46, NO. 2 (1984), PP. 149-192), POSTED AT INTERNET WEB SITE http://www.stat.wisc.edu/courses/st771-newton/papers/green.pdf.
THE REGRESSION FUNCTION IS SPECIFIED BY THE INVERSE LINK FUNCTION η = η(β) WHERE β = (β1,...,βp). (FOR EXAMPLE, IN THE CASE OF LOGISITIC REGRESSION, yi ~ B(ni, {1+exp(-Σxijβi)}-1 ) THE INVERSE LINK FUNCTION IS ηi = {1+exp(-Σxijβi)}-1 (IN THIS PRESENTATION, THE PARAMETER ηi WAS PREVIOUSLY DENOTED pi). THE LIKELIHOOD FUNCTION IS
![]()
NOTE THAT GREEN'S η CORRESPONDS TO μ IN THE LINK TABLE GIVEN EARLIER.)
THE LIKELIHOOD EQUATIONS ARE
![]()
WHERE u IS THE n-VECTOR {∂L/∂η} AND D IS THE n x p MATRIX {∂η/∂β}. THE NEWTON-RAPHSON EQUATIONS CORRESPOND TO
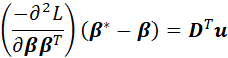
WHERE ![]() IS THE UPDATED ESTIMATE. AS DESCRIBED EARLIER, THE
PRECEDING EQUATION IS OBTAINED FROM THE FIRST TWO TERMS OF A TAYLOR SERIES
EXPLANSION FOR ∂L/∂β. THE ITERATION IS REPEATED UNTIL CONVERGENCE (FOR
A LOG-LIKELIHOOD THAT IS QUADRATIC IN β, CONVERGENCE OCCURS IN ONE
STEP).
IS THE UPDATED ESTIMATE. AS DESCRIBED EARLIER, THE
PRECEDING EQUATION IS OBTAINED FROM THE FIRST TWO TERMS OF A TAYLOR SERIES
EXPLANSION FOR ∂L/∂β. THE ITERATION IS REPEATED UNTIL CONVERGENCE (FOR
A LOG-LIKELIHOOD THAT IS QUADRATIC IN β, CONVERGENCE OCCURS IN ONE
STEP).
A RESULT FROM DIFFERENTIAL CALCULUS IS
![]()
THE VECTOR ANALOG OF THIS RESULT IS
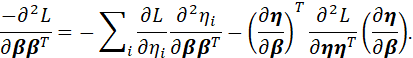
AS MENTIONED EARLIER,
![]()
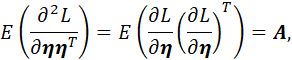
SAY. SUBSTITUTING THE PRECEDING RESULTS INTO THE NEWTON-RAPHSON EQUATION THAT PRECEDED THEM WE OBTAIN
![]()
IT IS ASSUMED THAT D IS OF FULL RANK AND A IS POSITIVE DEFINITE, IN WHICH CASE THE PRECEDING EQUATION CAN BE SOLVED FOR β*.
INSTEAD OF REGARDING THIS SYSTEM A GENERAL SYSTEM OF EQUATIONS, NOTE THAT IT IS THE SET OF NORMAL EQUATIONS FOR A WEIGHTED LEAST-SQUARES REGRESSION, I.E., β* IS THE SOLUTION TO THE QUADRATIC-FORM MINIMIZATION PROBLEM
minimize (A-1u + D(β – β*))T A (A-1u + D(β – β*))
I.E.,
β* = min arg (A-1u + D(β – β*))T A (A-1u + D(β – β*)).
THIS PROBLEM IS THE EQUIVALENT OF REGRESSING (A-1u + Dβ) ONTO THE COLUMNS OF D USING THE WEIGHT MATRIX A.
THIS IS THE ITERATIVE REWEIGHTED LEAST-SQUARES ALGORITHM.
(END OF OPTIONAL SECTION.)
ITERATIVE PROPORTIONAL FITTING (DEMING-STEPHAN)
A GENERAL METHOD OF FINDING MAXIMUM LIKELIHOOD ESTIMATES FOR CONTINGENCY TABLES IS THE DEMING-STEPHAN METHOD OF ITERATIVE PROPORTIONAL FITTING. THIS METHOD IS NOT DESCRIBED HERE, BUT IS DESCRIBED IN AGRESTI OP. CIT.
NUMERICAL METHODS FOR VARIANCE ESTIMATION (SIMULATION; BOOTSTRAP, JACKKNIFE, BRR)
IT WAS MENTIONED IN THE PRECEDING SECTION THAT ONE OF THE "MODERN" METHODS OF NONPARAMETRIC STATISTICS WAS THE ESTIMATION OF VARIANCES. THERE ARE SEVERAL SUCH METHODS, INCLUDING THE BOOTSTRAP METHOD, THE JACKKNIFE METHOD, AND THE METHOD OF BALANCED REPEATED REPLICATION (BRR).
THE JACKKNIFE METHOD IS ORIENTED NOT ONLY TO THE ESTIMATION OF THE VARIANCE OF AN ESTIMATOR, BUT TO ESTIMATING BIAS AS WELL. IT WILL NOT BE DESCRIBED HERE, OTHER THAN TO MENTION THAT IT CONSISTS OF CALCULATING A SEQUENCE OF STATISTICS BY OMITTING EACH OF THE OBSERVATIONS IN TURN, AND COMBINING THE MEMBERS OF THE SEQUENCE IN A CERTAIN WAY.
THE BOOTSTRAP METHOD IS BASED ON THE USE OF SIMULATION (I.E., A SO-CALLED "MONTE CARLO METHOD."
THE BOOTSTRAP METHOD IS VERY STRAIGHTFORWARD. A SEQUENCE OF INDEPENDENT RANDOM SAMPLES IS SELECTED FROM THE AVAILABLE SAMPLE (THE OBSERVED SAMPLE, THE DATA), AND THE STATISTIC OF INTEREST IS CALCULATED FOR EACH SUCH SAMPLE. THE SAMPLE VARIANCE OF THESE QUANTITIES IS CALCULATED. THIS SAMPLE VARIANCE IS AN ESTIMATE OF THE VARIANCE OF THE STATISTIC OF INTEREST. THE NUMBER OF SELECTED SAMPLES IS USUALLY TAKEN TO BE SEVERAL HUNDRED.
WASSERMAN PROVIDES A COMPACT DESCRIPTION OF THE BOOTSTRAP METHOD FOR ESTIMATING A VARIANCE:
1. LET THE SAMPLE (DATA) BE X1,...,Xn. SELECT A SAMPLE X1*,...,Xn* WITH REPLACEMENT FROM X1,...,Xn.
2. CALCULATE THE STATISTIC (ESTIMATE) OF INTEREST, Tn* = g(X1,...,Xn).
3. REPEAT STEPS 1 AND 2 B TIMES, TO OBTAIN Tn,1*,...,Tn,b*.
4. CALCULATE
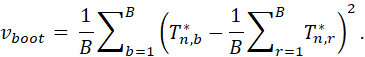
THE BOOTSTRAP ESTIMATE OF THE VARIANCE IS vboot.
THE BOOTSTRAP METHOD CAN BE USED TO ESTIMATE THE VARIANCE OF ANY ESTIMATOR, SUCH AS A MEDIAN, AN PERCENTILE, OR AN INTERQUARTILE RANGE. IN PARTICULAR, IT MAY BE USED TO ESTIMATE CONFIDENCE INTERVALS. SEE WASSERMAN FOR DETAILS.
10. CLASSICAL HYPOTHESIS TESTING
STATISTICAL HYPOTHESIS TESTING ADDRESSES THE PROBLEM OF MAKING A DECISION, BASED ON SAMPLE DATA. THE GENERAL THEORY OF HYPOTHESIS TESTING FALLS WITHIN THE DOMAIN OF THE TOPIC OF STATISTICAL DECISION THEORY. THERE ARE TWO GENERAL APPROACHES TO STATISTICAL DECISION THEORY – THE CLASSICAL ("FREQUENTIST") APPROACH, IN WHICH THE DISTRIBUTIONAL PARAMETER IS ASSUMED TO BE A FIXED VALUE AND THE DECISION IS BASED SOLELY ON THE SAMPLE DATA, AND THE BAYESIAN APPROACH, IN WHICH THE PARAMETER IS ASSUMED TO HAVE A PROBABILITY DISTRIBUTION, AND INFORMATION ABOUT THE PARAMETER OUTSIDE THE SAMPLE IS SUMMARIZED IN THIS DISTRIBUTION. THIS PRESENTATION SECTION ADDRESSES CLASSICAL DECISION THEORY. THE STANDARD REFERENCE ON THIS SUBJECT IS TESTING STATISTICAL HYPOTHESES BY E. L. LEHMANN (2nd ED. WILEY, 1986).
THERE ARE SEVERAL APPROACHES TO CLASSICAL TESTING OF HYPOTHESES, INVOLVING ALTERNATIVE CRITERIA SUCH AS POWER, EXPECTED LOSS, INVARIANCE, UNBIASEDNESS, COMPLETENESS, AND SUFFICIENCY. WE SHALL RESTRICT CONSIDERATION TO POWER.
THE PROBLEM OF HYPOTHESIS
TESTING MAY BE FORMULATED AS FOLLOWS. LET ![]() DENOTE THE CLASS OF ALL PROBABILITY DISTRIBUTIONS
BASED ON A PARAMETER θ. LET Θ DENOTE THE PARAMETER SPACE, I.E., θ є Θ. LET US
DIVIDE THE PARAMETER SPACE INTO TWO MUTUALLY EXCLUSIVE AND EXHAUSTIVE SUBSETS, ΘH
AND ΘK. THE PROBLEM IS TO DECIDE, BASED ON A SAMPLE, WHETHER THE
VALUE OF THE PARAMETER IS IN ΘH OR ΘK.
DENOTE THE CLASS OF ALL PROBABILITY DISTRIBUTIONS
BASED ON A PARAMETER θ. LET Θ DENOTE THE PARAMETER SPACE, I.E., θ є Θ. LET US
DIVIDE THE PARAMETER SPACE INTO TWO MUTUALLY EXCLUSIVE AND EXHAUSTIVE SUBSETS, ΘH
AND ΘK. THE PROBLEM IS TO DECIDE, BASED ON A SAMPLE, WHETHER THE
VALUE OF THE PARAMETER IS IN ΘH OR ΘK.
IN CLASSICAL TESTING OF HYPOTHESES, IT IS ASSUMED THAT THERE IS A SINGLE, UNKNOWN VALUE OF θ. SINCE ΘH AND ΘK ARE MUTUALLY EXCLUSIVE AND EXHAUSTIVE, θ IS IN ONE AND ONLY ONE OF THEM.
THE STATEMENT THAT θ є ΘH IS CALLED THE NULL HYPOTHESIS, OFTEN DENOTED BY H OR H0. THE STATEMENT THAT θ є ΘK IS CALLED THE ALTERNATIVE HYPOTHESIS, OFTEN DENOTED BY K OR H1. IF AN HYPOTHESIS CONTAINS A SINGLE POINT (I.E., COMPLETELY SPECIFIES A DISTRIBUTION), IT IS CALLED A SIMPLE HYPOTHESIS; OTHERWISE IT IS CALLED A COMPOSITE HYPOTHESIS. IF THE TERM "HYPOTHESIS" IS USED WITHOUT A MODIFIER, IT USUALLY REFERS TO THE NULL HYPOTHESIS (BUT MAY REFER TO EITHER HYPOTHESIS, DEPENDING ON CONTEXT). THE RATIONALE FOR THIS POSITION IS THAT THE SAMPLE MAY PROVIDE INSUFFICIENT EVIDENCE TO ACCEPT OR REJECT EITHER HYPOTHESIS WITH REASONABLE PROBABILITY, AND "NOT ACCEPTED" IS A LESS ASSERTIVE STATEMENT THAN "ACCEPTED."
THE DECISION TO BE MADE IS WHETHER θ LIES IN ΘH OR ΘK. MAKING THIS DECISION IS CALLED TESTING THE HYPOTHESIS. IF IT IS DECIDED THAT θ є ΘH, IT IS SAID THAT THE NULL HYPOTHESIS HAS BEEN ACCEPTED, AND THE ALTERNATIVE HYPOTHESIS HAS BEEN REJECTED. IF IT IS DECIDED THAT θ є ΘK, IT IS SAID THAT THE ALTERNATIVE HYPOTHESIS HAS BEEN ACCEPTED, AND THE NULL HYPOTHESIS HAS BEEN REJECTED. (SOME AUTHORS OBJECT TO USE OF THE EXPRESSION THAT AN HYPOTHESIS IS "ACCEPTED," AND PREFER TO STATE THAT A HYPOTHESIS IS "NOT REJECTED.")
A DECISION IS MADE ACCORDING TO A RULE, BASED ON A SAMPLE. FOR A NONRANDOMIZED DECISION RULE, THE SAMPLE SPACE IS DIVIDED INTO TWO COMPLEMENTARY REGIONS, SH AND SK. IF THE SAMPLE FALLS IN SH, THE NULL HYPOTHESIS IS ACCEPTED. IF IT FALLS IN SK, THE NULL HYPOTHESIS IS REJECTED. SH IS CALLED THE REGION OF ACCEPTANCE AND SK IS CALLED THE REGION OF REJECTION, OR THE CRITICAL REGION. FOR A RANDOMIZED DECISION RULE, THE DECISION TO ACCEPT OR REJECT IS MADE WITH PROBABILITY LESS THAN ONE. WE SHALL CONSIDER ONLY NONRANDOMIZED DECISION RULES.
IN MAKING A TEST OF HYPOTHESIS, ONE MAY MAKE A CORRECT DECISION OR TWO TYPES OF ERROR. A TYPE 1 ERROR IS MADE IF IT IS DECIDED THAT THE ALTERNATIVE HYPOTHESIS IS TRUE WHEN THE NULL HYPOTHESIS IS IN FACT TRUE (I.E., ERRONEOUS REJECTION OF THE NULL HYPOTHESIS). A TYPE 2 ERROR IS MADE IF IT IS DECIDED THAT THE NULL HYPOTHESIS IS TRUE WHEN IN FACT THE ALTERNATIVE HYPOTHESIS IS TRUE (I.E., ERRONEOUS ACCEPTANCE OF THE NULL HYPOTHESIS).
GIVEN A CRITICAL REGION AND A VALUE FOR θ, THE PROBABILITIES OF MAKING A TYPE 1 ERROR AND A TYPE 2 ERROR MAY BE DETERMINED. BY VARYING THE CRITICAL REGION, IT IS POSSIBLE TO CONTROL THE PROBABILITIES OF MAKING THE TWO TYPES OF ERROR (FOR SPECIFIED θ). FOR A SPECIFIED SAMPLE SIZE, BOTH PROBABILITIES CANNOT BE SIMULTANEOUSLY CONTROLLED. IT IS CONVENTIONAL TO SPECIFY A MAXIMUM VALUE FOR THE PROBABILITY OF A TYPE 1 ERROR (E.G., .05, .01 OR .001), AND TO MINIMIZE (BY SPECIFYING THE TEST OR THE SAMPLE SIZE) THE PROBABILITY OF A TYPE 2 ERROR SUBJECT TO THIS CONSTRAINT.
IF ![]() , THE TEST IS CALLED A SIZE α TEST.
, THE TEST IS CALLED A SIZE α TEST.
IF IF ![]() , THE, THE TEST IS CALLED A LEVEL α TEST.
, THE, THE TEST IS CALLED A LEVEL α TEST.
FOR SIMPLE SITUATIONS, THE SIZE AND LEVEL ARE OFTEN THE SAME.
(THE TERM
"SIGNIFICANCE LEVEL" IS SOMETIMES USED FOR SIZE OR LEVEL, BUT ITS USE
IS GENERALLY AVOIDED IN TESTS OF HYPOTHESIS SINCE IT IS ALSO USED IN TESTS OF
SIGNIFICANCE. FOR TESTS OF SIGNIFICANCE, THE DECISION IS BASED ON THE
PROBABILITY ![]() , WHERE Xn IS THE OBSERVED SAMPLE),
E.G., IF IT IS DECIDED TO REJECT THE NULL HYPOTHESIS IF P<.01 AND P IS
OBSERVED TO BE .005, THEN THE NULL HYPOTHESIS IS REJECTED. THERE IS NO
CONSIDERATION OF ANY OTHER TEST ATTRIBUTE, SUCH AS POWER, INVARIANCE,
SUFFICIENCY, OR UNBIASEDNESS.)
, WHERE Xn IS THE OBSERVED SAMPLE),
E.G., IF IT IS DECIDED TO REJECT THE NULL HYPOTHESIS IF P<.01 AND P IS
OBSERVED TO BE .005, THEN THE NULL HYPOTHESIS IS REJECTED. THERE IS NO
CONSIDERATION OF ANY OTHER TEST ATTRIBUTE, SUCH AS POWER, INVARIANCE,
SUFFICIENCY, OR UNBIASEDNESS.)
THE PROBABILITY OF REJECTING THE NULL HYPOTHESIS FOR A SPECIFIED VALUE OF θ IN Θ (ALL Θ, INCLUDING ΘH AND ΘK) IS CALLED THE POWER OF THE TEST AGAINST ALTERNATIVE θ. CONSIDERED AS A FUNCTION OF θ, THE PROBABILITY OF REJECTION Pθ(XєSK) IS CALLED THE POWER FUNCTION. IN QUALITY CONTROL THE POWER FUNCTION IS CALLED THE OPERATING CHARACTERISTIC (OC) CURVE.
THE SIZE OF A TEST IS OFTEN SET AT A PARTICULAR LEVEL, SUCH AS .01 OR .05, AND THE SAMPLE SIZE IS DETERMINED TO ACHIEVE A SPECIFIED POWER AGAINST A SPECIFIED ALTERNATIVE.
AS MENTIONED, THERE ARE A NUMBER OF CRITERIA FOR DETERMINING A TEST OF HYPOTHESIS, I.E., FOR DETERMINING THE CRITICAL REGION FOR THE TEST. IN THIS SECTION (CLASSICAL TESTS OF HYPOTHESIS), WE SHALL RESTRICT CONSIDERATION TO POWER. FOR A TEST BETWEEN TWO SIMPLE HYPOTHESES, THE NEYMAN-PEARSON LEMMA STATES THAT A TEST BASED ON THE RATIO OF THE LIKELIHOODS UNDER THE TWO HYPOTHESES HAS HIGHER POWER THAN ANY OTHER TEST OF THE SAME SIZE.
EXAMPLE (VERY SIMPLE, TO DEMONSTRATE CONCEPTS):
CHOOSE BETWEEN H0: f(X) = f0(X) and H1: f(X) = f1(X), BASED ON A SINGLE OBSERVATION, x = x.
FIGURE 26. TWO PROBABILITIES OF ERROR.
THE NEYMAN-PEARSON LEMMA (MOOD, GRAYBILL, BOES) (THE LIKELIHOOD RATIO TEST). LET X1,...Xn BE A RANDOM SAMPLE FROM f(x;θ), WHERE θ IS ONE OF THE TWO KNOWN VALUES θ0 OR θ1, AND LET 0 < α < 1 BE FIXED. LET k* BE A POSITIVE CONSTANT AND C* BE A SUBSET OF THE SAMPLE SPACE THAT SATISFY:
1. ![]()
2. ![]()
AND λ≥k* if (x1,...,xn) ϵ C*c.
THEN, THE TEST CORRESPONDING TO THE CRITICAL REGION C* IS A MOST POWERFUL TEST OF THE HYPOTHESIS H0: θ=θ0 VERSUS THE ALTERNATIVE H1: θ=θ1.
EXAMPLE: TEST OF MEAN FOR A NORMAL DISTRIBUTION
THE NEYMAN-PEARSON LEMMA
(LIKELIHOOD RATIO TEST) CAN BE USED TO SHOW THAT THE MOST POWERFUL TEST OF THE
HYPOTHESIS H0: μ = μ0 VERSUS THE ALTERNATIVE H1:
μ = μ1>μ0 IS THE FAMILIAR ONE, TO ACCEPT H0
IF ![]() AND REJECT H0 IF
AND REJECT H0 IF ![]() WHERE k IS SET SO THAT PH0(
WHERE k IS SET SO THAT PH0(![]() ) = α.
) = α.
THE NEYMAN-PEARSON LEMMA REFERS TO THE PROBLEM OF TESTING A SIMPLE HYPOTHESIS AGAINST A SIMPLE ALTERNATIVE. THE BASIC CONCEPT OF THE NEYMAN-PEARSON LEMMA, OF BASING A TEST ON THE RATIO OF LIKELIHOODS, IS EXTENDED THROUGH THE GENERALIZED LIKELIHOOD-RATIO TEST, WHICH IS OFTEN A GOOD TEST.
THE GENERALIZED LIKELIHOOD-RATIO TEST (MOOD, GRAYBILL, BOES). LET Θ0 AND Θ1 DENOTE DISJOINT SUBSETS OF THE PARAMETER SPACE, Θ. LET L(θ;x1,...xn) BE THE LIKELIHOOD FUNCTION FOR A SAMPLE X1,...,Xn HAVING JOINT DENSITY fX1,...,Xn(x1,...,xn;θ) WHERE θϵΘ. THE GENERALIZED LIKELIHOOD RATIO, DENOTED BY λ OR λn, IS DEFINED TO BE
![]()
THE GENERALIZED LIKELIHOOD RATIO TEST PRINCIPLE STATES THAT THE HYPOTHESIS H0: θϵΘ0 IS TO BE REJECTED AGAINST THE ALTERNATIVE H1: θϵΘ-Θ0 IF AND ONLY IF λ≤λ0 WHERE λ0 IS A FIXED CONSTANT SATISFYING 0≤λ0≤1.
OTHER METHODS OF FINDING TESTS (THAN BASED ON POWER): LOSS FUNCTIONS; THE CONFIDENCE-SET (CONFIDENCE-INTERVAL) METHOD
EXAMPLE: DETERMINING SAMPLE SIZE TO ACHIEVE A SPECIFIED POWER LEVEL
SUPPOSE THAT THE FOLLOWING LIKELIHOOD-RATIO TEST IS BEING USED TO TEST H0: μ=μ0 VERSUS THE ALTERNATIVE H1: μ>μ0 FOR A NORMAL DISTRIBUTION HAVING KNOWN VARIANCE σ2. LET US SUPPOSE THAT THE SIZE OF THE TEST IS α = .05. THE TEST IS
REJECT H0 IF ![]() , WHERE z1-α IS THE 1-α PERCENTAGE POINT OF
A STANDARD NORMAL VARIATE. THE PROBABILITY OF A TYPE II ERROR IF μ = μ1
IS
, WHERE z1-α IS THE 1-α PERCENTAGE POINT OF
A STANDARD NORMAL VARIATE. THE PROBABILITY OF A TYPE II ERROR IF μ = μ1
IS
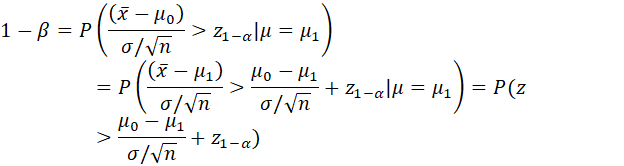
WHICH IMPLIES
![]()
SOLVING FOR n YIELDS
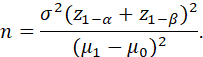
COMPARING TESTS: THE RECEIVER OPERATING CHARACTERISTIC (ROC) CURVE
Receiver Operating Characteristic analysis is a methodology for comparing alternative decision systems. The following paragraphs summarize this methodology. Standard references in this methodology are Green, David M. and John A. Swets, Signal Detection Theory and Psychophysics (Wiley, 1966) and Swets, John A., and Ronald M. Pickett, Evaluation of Diagnostic Systems: Methods from Signal Detection Theory (Academic Press, 1982).
For discussion purposes, we consider the problem of assessing the accuracy for a two-alternative decision problem, e.g., deciding whether a particular threat is present or not present – a "yes/no" decision problem. This decision must be made from a series of tests (corresponding to multiple sources). The essential characteristics of a two-alternative decision problem are embodied in a stimulus-response matrix, as shown below:
![]()
A false positive (or false alarm) is the decision that the threat is present when it is not; in decision theory this is called a Type 1 error. A false negative (or miss) is the decision that the threat is not present, when it is; in decision theory this is called a Type 2 error.
By varying the decision criteria, the probabilities of the two types of error may be adjusted (traded off). By changing the diagnostic procedures (e.g., adding sources or sensors, improving sensors), the probabilities of both types of error may be reduced. A problem that arises is that there are often a large number of stimulus-response matrices (one for each decision criterion), so that this way of describing system performance becomes cumbersome. The challenge is how to summarize the performance of a decision system succinctly. A solution to this problem is found in the Receiving Operating Characteristic (ROC) graph, which displays the probability of a correct decision ("hit") versus the probability of a false positive. An example of a ROC curve is shown in Figure 3 (below).
In comparing two decision systems for the same value of P(S|n), the system having the higher value of P(S|s) is selected. In comparing decision systems over a range of values of P(S|n), a more general decision criterion is used, such as selecting the system for which the Bayes risk (expected loss) is less.
A considerable number of decision problems may be formulated as two-alternative decision problems. A standard methodology for estimating the probability that a threat is present is a logistic regression model:
Logistic Regression Model: ![]()
Estimate:![]()
Decision criterion: decide “yes” if pest > c and “no” if pest <= c
Vary c and calculate the proportion of hits and false positives, and plot on a ROC graph (each value of c yields a different point on the curve).
Examples of ROC curves are presented in Logistic Regression Examples Using the SAS System (SAS Institute, 1995). An automated capability for producing ROC curves will be integrated into the ABDFAS (in Phase II), without the need for accessing statistical software packages (such as SAS or Stata).
![]()
ITEMS RELATED TO TESTS OF HYPOTHESIS, ADDRESSED IN OTHER SECTIONS:
THE UNION-INTERSECTION PRINCIPLE
THE PRINCIPLE OF CONDITIONAL ERROR
TESTS FOR INDEPENDENCE, RANDOMNESS, OUTLIERS
GOODNESS-OF-FIT TESTS AND TESTS OF MODEL ADEQUACY.
11. BAYESIAN INFERENCE
IN THE CLASSICAL APPROACH TO STATISTICAL INFERENCE, NOTHING IS KNOWN ABOUT THE UNKNOWN PARAMETER (EXCEPT ITS DOMAIN AND RANGE), AND ESTIMATES AND TESTS OF HYPOTHESES ARE BASED SOLELY ON THE SAMPLE DATA. IN THE BAYESIAN APPROACH, THE UNKNOWN PARAMETER IS ASSUMED TO BE A RANDOM VARIABLE, AND KNOWLEDGE ABOUT IT PRIOR TO SAMPLING IS SUMMARIZED IN A PROBABILITY DISTRIBUTION. ESTIMATES AND TESTS OF HYPOTHESIS ARE OBTAINED BY COMBINING THE PRIOR KNOWLEDGE AND THE SAMPLE DATA, USING BAYES' RULE.
PRIOR TO SAMPLING, THE DISTRIBUTION OF THE PARAMETER, Θ, IS ASSUMED TO BE fΘ (θ). THE DISTRIBUTION fΘ (θ) IS CALLED THE PRIOR DISTRIBUTION OF Θ.
THE SAMPLING DISTRIBUTION (OF X CONDITIONAL ON Θ) IS fX|Θ(x|θ).
THE CONDITIONAL DISTRIBUTION OF Θ GIVEN THE SAMPLE X = (X1,...,Xn) = (x1,...,xn) = x IS CALLED THE POSTERIOR DISTRIBUTION, AND IS (BY BAYES' FORMULA):
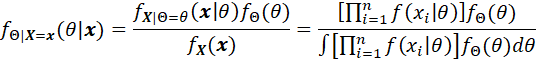
IN CLASSICAL STATISTICAL INFERENCE, ALL OF THE INFORMATION AVAILABLE IS INCLUDED IN THE LIKELIHOOD FUNCTION. IN BAYESIAN INFERENCE, ALL OF THE INFORMATION AVAILABLE IS INCLUDED IN THE POSTERIOR DISTRIBUTION.
OBSERVE THAT THE POSTERIOR
DISTRIBUTION IS PROPORTIONAL TO THE LIKELIHOOD FUNCTION, ![]() TIMES THE PRIOR DISTRIBUTION:
TIMES THE PRIOR DISTRIBUTION:
![]()
WHERE
![]()
IS A NORMALIZING CONSTANT (NOT DEPENDENT ON θ).
BAYESIAN ESTIMATION IS A PARAMETRIC APPROACH (SINCE IT FOCUSES ON THE DISTRIBUTION OF A PARAMETER).
IN CLASSICAL ESTIMATION,
AN ESTIMATOR IS CHOSEN THAT IS IN SOME SENSE CLOSE TO THE UNKNOWN VALUE OF THE QUANTITY
BEING ESTIMATED (A FUNCTION, g(θ), OF THE UNKNOWN PARAMETER, θ, WHICH IS ASSUMED
TO BE FIXED). IN BAYESIAN ESTIMATION, THE QUANTITY BEING ESTIMATED IS ANY
CHARACTERISTIC OF THE POSTERIOR DISTRIBUTION OF θ, SUCH AS THE MEAN, MEDIAN,
MODE, VARIANCE OR SKEWNESS. A STANDARD WAY OF DECIDING WHICH ESTIMATOR TO USE
IS TO INTRODUCE A LOSS FUNCTION, WHICH SPECIFIES THE LOSS ASSOCIATED WITH DECIDING
ON ![]() AS THE ESTIMATE WHEN Θ = θ IS THE TRUE VALUE, AND TO
USE THE ESTIMATOR THAT MINIMIZES THE EXPECTED LOSS.
AS THE ESTIMATE WHEN Θ = θ IS THE TRUE VALUE, AND TO
USE THE ESTIMATOR THAT MINIMIZES THE EXPECTED LOSS.
THAT IS, IF IT IS DESIRED
TO ESTIMATE θ AND THE LOSS FUNCTION IS ![]() ,
,![]() , THE ESTIMATOR IS THE FUNCTION
, THE ESTIMATOR IS THE FUNCTION ![]() THAT MINIMIZES
THAT MINIMIZES
![]()
FOR QUADRATIC LOSS, ![]() , THE ESTIMATOR OF θ IS THE MEAN OF THE POSTERIOR
DISTRIBUTION. FOR ABSOLUTE LOSS,
, THE ESTIMATOR OF θ IS THE MEAN OF THE POSTERIOR
DISTRIBUTION. FOR ABSOLUTE LOSS, ![]() , THE ESTIMATOR OF θ IS THE MEDIAN OF THE POSTERIOR
DISTRIBUTION.
, THE ESTIMATOR OF θ IS THE MEDIAN OF THE POSTERIOR
DISTRIBUTION.
CALCULATION OF THE EXPECTED VALUES THAT ARISE IN BAYESIAN ESTIMATION CAN BE COMPLICATED. FOR ANALYTICAL EXAMPLES, IT IS CUSTOMARY TO USE PRIOR DISTRIBUTIONS THAT ARE "MATCHED" TO THE SAMPLING DISTRIBUTION SO THAT THE POSTERIOR DISTRIBUTION IS OF THE SAME "CLASS" AS THE PRIOR DISTRIBUTION (E.G., IF THE PRIOR IS NORMAL, THEN THE POSTERIOR IS, ALSO, SO THAT IT IS POSSIBLE TO OBTAIN A CLOSED-FORM EXPRESSION FOR THE POSTERIOR DISTRIBUTION). SUCH A PRIOR DISTRIBUTION IS CALLED A "CONJUGATE" DISTRIBUTION. A "NATURAL" CONJUGATE PRIOR IS ONE THAT IS OF THE SAME FUNCTIONAL FORM AS THE LIKELIHOOD FUNCTION (I.E., OF THE SAMPLING DISTRIBUTION).
EXAMPLE: BERNOULLI DISTRIBUTION
EXAMPLE: NORMAL DISTRIBUTION
NATURAL AND CONJUGATE DISTRIBUTIONS WERE MORE IMPORTANT PRIOR TO THE AGE OF COMPUTERS, WHERE IT WAS VERY DESIRABLE TO OBTAIN ANALYTICAL SOLUTIONS. ONCE COMPUTERS WERE GENERALLY AVAILABLE, NUMERICAL METHODS COULD BE USED TO DETERMINE POSTERIOR DISTRIBUTION WITH EASE, IF ANALYTICAL SOLUTIONS WERE NOT AVAILABLE.
COMMENT: THIS PRESENTATION IS FOCUSED ON APPLICATIONS HAVING LARGE SAMPLE SIZES. IN SUCH CASES, THE AMOUNT OF INFORMATION IN THE SAMPLE DOMINATES THE PRIOR INFORMATION, THE RESULTS FOR THE CLASSICAL APPROACH AND THE BAYESIAN APPROACH ARE SIMILAR, AND THERE IS LITTLE BENEFIT TO BE REALIZED FROM THE ADDITIONAL COMPLICATION OF THE BAYESIAN APPROACH. FOR LARGE SAMPLES, THE POSTERIOR MEAN IS CLOSE TO THE MAXIMUM LIKELIHOOD ESTIMATE.
STATISTICAL DECISION THEORY
THE PRECEDING DISCUSSION HAS PRESENTED A SMALL NUMBER OF FACTS ABOUT STATISTICAL INFERENCE. A GENERAL FRAMEWORK FOR STATISTICAL INFERENCE IS CONTAINED WITHIN THE SUBJECT OF STATISTICAL DECISION THEORY. REFERENCES ON THIS SUBJECT INCLUDE THE FOLLOWING:
REFERENCES ON STATISTICAL DECISION THEORY.
12. STANDARD STATISTICAL MODELS
THE PRECEDING DISCUSSION HAS DISCUSSED BASIC CONCEPTS IN STATISTICAL INFERENCE, AND HAS PRESENTED A NUMBER OF EXAMPLES INVOLVING SIMPLE PROBABILITY DISTRIBUTIONS. STATISTICAL INFERENCE DEALS WITH A LARGE VARIETY OF PROBABILISTIC PHENOMENA, AND IN MANY APPLICATIONS THE PHENOMENA OF INTEREST CANNOT BE REPRESENTED DIRECTLY IN TERMS OF THE SIMPLE PROBABILITY DISTRIBUTIONS DESCRIBED ABOVE. IN SOME INSTANCES, THE PARTICULAR DISTRIBUTIONS DESCRIBED ABOVE MAY DESCRIBE THE PHENOMENA WELL (E.G., SAMPLING INSPECTION OR PERFORMANCE MONITORING), BUT IN MOST CASES THE THEORY PRESENTED ABOVE SERVES AS "BUILDING BLOCKS" THAT MUST BE EXTENDED TO BE OF PRACTICAL VALUE.
EXAMPLES OF MORE COMPLEX APPLICATIONS INCLUDE EVALUATION OF SOCIAL AND ECONOMIC PROGRAMS, INVOLVING ANALYSIS OF SURVEY DATA, CAUSAL ANALYSIS, AND ANALYSIS OF TIME SERIES (LONGITUDINAL) DATA. STATISTICAL METHODS FOR ADDRESSING THESE APPLICATIONS WILL NOW BE DISCUSSED.
USEFUL STATISTICAL MODELS
IN MANY APPLICATIONS, THE RANDOM VARIABLES OF PRIMARY INTEREST DO NOT HAVE SIMPLE OR STANDARD DISTRIBUTIONS, SUCH AS A BINOMIAL OR NORMAL DISTRIBUTION, BUT IT IS POSSIBLE TO TRANSFORM THE VARIABLES IN SUCH A WAY THAT THE TRANSFORMED VARIABLES HAVE SIMPLE DISTRIBUTIONS (THAT IS, COMMON DISTRIBUTIONS, OR DISTRIBUTIONS THAT DEPEND ON A SMALL NUMBER OF PARAMETERS). SUCH TRANSFORMATIONS CONSTITUTE A MODEL (OR STATISTICAL MODEL OR STOCHASTIC MODEL OR PROBABILISTIC MODEL).
IF THE MODEL INVOLVES A PARAMETRIC DISTRIBUTION, THEN THE MODEL IS A PARAMETRIC MODEL. OTHERWISE IT IS A NONPARAMETRIC MODEL. IF A MODEL INCLUDES BOTH PARAMETRIC AND NONPARAMETRIC COMPONENTS, IT IS CALLED A SEMIPARAMETRIC MODEL.
FOR EXAMPLE, IT MAY BE KNOWN THAT THE LOGARITHM OF EARNINGS OBEYS A NORMAL DISTRIBUTION. IN THIS CASE, IF X DENOTES EARNINGS AND Y = log(X), THEN Y IS NORMALLY DISTRIBUTED. OR, IT MAY BE KNOWN THAT THE DISTRIBUTION OF AN OBSERVED CHARACTERISTIC IS A MIXTURE OF TWO SIMPLER DISTRIBUTIONS, SUCH AS EARNINGS OF MEAN AND WOMEN, WHERE EACH SEX HAS A DIFFERENT DISTRIBUTION.
THE PRECEDING ARE VERY SIMPLE EXAMPLES OF MODELS. MODELS MAY BE FAR MORE COMPLICATED, BUT, IF A PARAMETRIC MODEL IS SOUGHT, IT IS ALWAYS ATTEMPTED TO FIND A PARSIMONIOUS REPRESENTATION (MODEL) OF THE REAL-WORLD PROCESS UNDER STUDY, I.E., A REPRESENTATION INVOLVING A SMALL NUMBER OF PARAMETERS (SINCE SIMPLICITY GENERALLY FACILITATES UNDERSTANDING).
A STATISTICAL MODEL MAY BE DESCRIBED (SPECIFIED, CHARACTERIZED, DETERMINED) EITHER AS A PROBABILITY DISTRIBUTION OR BY A SET OF RELATIONSHIPS (EQUATIONS) AMONG VARIABLES (RANDOM VARIABLES AND NON-RANDOM VARIABLES) THAT SPECIFY A PROBABILITY DISTRIBUTION.
A COMMON WAY TO SPECIFY A MODEL IS TO SPECIFY IT IN TERMS OF A CONDITIONAL EXPECTATION. (SEE WOOLDRIDGE P. 18.) IF y IS A RANDOM VARIABLE AND x IS A SET OF OBSERVED VARIABLES (RANDOM VARIABLES OR NON-RANDOM), THEN y CAN BE DECOMPOSED AS
y = E(y|x) + u
E(u|x) = 0.
THE PRECEDING IS DEFINITIONAL; ANY RANDOM VARIABLE MAY BE WRITTEN AS A CONDITIONAL EXPECTATION E(y|x) PLUS AN ERROR TERM THAT HAS CONDITIONAL MEAN ZERO.
THERE IS AVAILABLE A VAST ARRAY OF MODELS OF PROBABILISTIC PHENOMENA. THIS PRESENTATION WILL NOW DESCRIBE A NUMBER OF CLASSES OF MODELS, AND PRESENT EXAMPLES. THERE IS ABSOLUTELY NO ATTEMPT HERE TO DESCRIBE A THOROUGH VARIETY OF MODELS. A SELECTED FEW MODELS WILL BE DISCUSSED AS A MEANS TO DESCRIBING A FEW GENERAL METHODS OF STATISTICAL INFERENCE (SUCH AS THE EM ALGORITHM).
THE POINT TO CONSTRUCTING A MODEL OF A PHENOMENON OR PROCESS IS TO FACILITATE UNDERSTANDING AND OBTAIN ESTIMATES OF HIGHER ACCURACY (LOWER MEAN-SQUARED ERROR; HIGHER PRECISION AND/OR LOWER BIAS) AND TESTS OF HYPOTHESIS OF HIGHER POWER. STATISTICAL INFERENCES ABOUT A PROBABILISTIC PHENOMENON WILL BE BASED ON A STATISTICAL MODEL OF THE PHENOMENON. IN ORDER FOR THE INFERENCES TO BE VALID, THE MODEL MUST BE A VALID (UNBIASED) REPRESENTATION OF THE PHENOMENON UNDER STUDY. THE DISCUSSION WILL INCLUDED CONSIDERATION OF TESTS OF MODEL ADEQUACY.
UNIVARIATE MODELS
THE TERMS UNIVARIATE, BIVARIATE, AND MULTIVARIATE REFER TO THE NUMBER OF RANDOM VARIABLES INVOLVED IN A MODEL (I.E., ONE, TWO, OR TWO OR MORE). SOME MODELS MAY INVOLVE BOTH RANDOM VARIABLES AND DETERMINISTIC (NON-STOCHASTIC) VARIABLES. IF A MODEL CONTAINS A SINGLE RANDOM VARIABLE AND ADDITIONAL NON-STOCHASTIC VARIABLES, IT IS REFERRED TO AS A MULTI-VARIABLE UNIVARIATE MODEL, NOT AS A MULTIVARIATE MODEL (I.E., A MULTIVARIATE MODEL MUST CONTAIN AT LEAST TWO RANDOM VARIABLES).
LINEAR STATISTICAL MODELS
A CLASS OF STATISTICAL MODELS THAT HAS PROVEN TO BE OF SUBSTANTIAL VALUE IN MODELING A WIDE VARIETY OF PHENOMENA IS THE CLASS OF LINEAR MODELS. MANY NONLINEAR MODELS MAY BE TRANSFORMED TO LINEAR MODELS, EITHER BY TRANSFORMATION OF THE RANDOM VARIABLE OF INTEREST OR BY TRANSFORMING THE MODEL PARAMETERS. THE CLASS OF LINEAR MODELS WILL NOW BE DESCRIBED.
SIMPLE LINEAR MODELS
LINEAR REGRESSION WITH A SINGLE REGRESSOR
AS MENTIONED, THE BASIC THEORY PRESENTED ABOVE CENTERS ON RANDOM SAMPLING FROM BASIC PROBABILITY DISTRIBUTIONS. IN GENERAL, PRACTICAL APPLICATIONS INVOLVE MORE COMPLICATED DISTRIBUTIONS. ONE OF THE SIMPLEST AND MOST WIDELY USED APPLICATIONS IS SAMPLING FROM A NORMAL DISTRIBUTION IN WHICH THE MEAN OF THE RANDOM VARIABLE (Y, CALLED THE EXPLAINED VARIABLE, REGRESSAND, PREDICTED VARIABLE OR DEPENDENT VARIABLE) IS A LINEAR FUNCTION OF ANOTHER VARIABLE. THAT OTHER VARIABLE (X, CALLED THE EXPLANATORY VARIABLE, REGRESSOR, PREDICTOR OR INDEPENDENT VARIABLE) MAY BE A RANDOM VARIABLE OR NOT A RANDOM VARIABLE (I.E., AN ORDINARY, DETERMINISTIC VARIABLE, A NUMBER THAT MAY BE DIFFERENT FOR EACH MEMBER OF THE SAMPLE). THE SIMPLER CASE IS THE LATTER, AND WE WILL NOW CONSIDER IT.
IN THIS APPLICATION, THE SAMPLE DATA CONSIST OF n VALUES OF A RANDOM VARIABLE, Y, AND ANOTHER VARIABLE, X (A REAL VARIABLE, NOT A RANDOM VARIABLE).
IN GENERAL, THE FUNCTION
E(Y|X=x) IS CALLED THE REGRESSION CURVE (OR REGRESSION FUNCTION) OF
Y ON x, OFTEN DENOTED AS ![]() .
.
IN THIS APPLICATION, IT IS ASSUMED THAT THE REGRESSION CURVE IS LINEAR (I.E., IS A REGRESSION LINE):
E(Y|X=x) = β0 + β1 x
THE INFERENCE PROBLEM IS TO ESTIMATE THE VALUES OF β0 AND β1 (THE MODEL PARAMETERS).
APPLYING THE METHOD OF MAXIMUM LIKELIHOOD, WE WRITE DOWN THE LIKELIHOOD FUNCTION OF THE SAMPLE AND MAXIMIZE IT WITH RESPECT TO β0 AND β1. FOR THIS PROBLEM, WE SHALL ASSUME THAT THE PROBABILITY DISTRIBUTION OF THE RANDOM VARIABLE IS A NORMAL DISTRIBUTION WITH MEAN β0 + β1 x AND VARIANCE σ2, WHERE σ2 IS UNKNOWN (AS ARE β0 AND β1). IN OUR PREVIOUS NOTATION, THE DISTRIBUTION PARAMETER IS θ = (β0, β1, σ2).
IN THE PRECEDING SPECIFICATION OF THE MODEL, AN EXPRESSION WAS GIVEN FOR THE EXPECTED VALUE OF THE RANDOM VARIABLE AS A FUNCTION OF EXPLANATORY VARIABLES. A SECOND WAY OF SPECIFYING THE MODEL IS BY MEANS OF AN EQUATION THAT DESCRIBES EACH OBSERVATION:
yi = β0 + β1 xi + єi
where the єi are independent normally distributed random variables having mean zero and variance σ2, and the xi's are known numbers (not random variables).
A THIRD WAY OF SPECIFYING A MODEL IS TO SPECIFY THE JOINT PROBABILITY DISTRIBUTION FUNCTION OF THE RANDOM VARIABLES OF THE MODEL (I.E., OF THE SAMPLE, GIVEN THE MODEL SPECIFICATION).
ALL THREE OF THE PRECEDING METHODS FOR SPECIFYING A MODEL ARE EQUIVALENT, IN THE SENSE THAT THEY CORRESPOND TO THE SAME JOINT PROBABILITY DISTRIBUTION. (THERE ARE OTHER WAYS OF SPECIFYING MODELS. FOR EXAMPLE, A NORMAL DISTRIBUTION IS CHARACTERIZED BY (DEFINED BY) ITS FIRST AND SECOND MOMENTS (MEANS, VARIANCES, COVARIANCES). HENCE A NORMAL MODEL MAY BE SPECIFIED BY THESE MOMENTS.)
THE LIKELIHOOD FUNCTION IS THE JOINT PDF OF THE RVs, VIEWED AS A FUNCTION OF THE PARAMETERS. THIS IS:
![]()
THE MAXIMUM LIKELIHOOD ESTIMATE OF θ = (β0, β1, σ2) IS FOUND BY DETERMINING THE VALUES OF β0, β1, AND σ2 THAT MAXIMIZE THIS QUANTITY. THESE ARE THE SAME VALUES THAT MAXIMIZE THE LOGARITHM OF THIS QUANTITY, OR THE LOG-LIKELIHOOD:
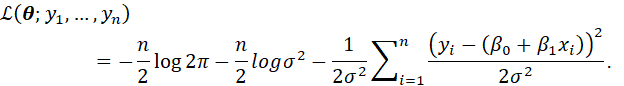
SINCE THIS IS A DIFFERENTIABLE FUNCTION OF THE PARAMETERS, THE MAXIMUM LIKELIHOOD ESTIMATES OF θ = (β0, β1, σ2) ARE FOUND BY SETTING THE PARTIAL DERIVATIVES OF THIS EXPRESSION WITH RESPECT TO β0, β1, AND σ2 EQUAL TO ZERO. THIS RESULTS IN THE FOLLOWING THREE EQUATIONS (CALLED THE NORMAL EQUATIONS), WHERE THE SOLUTIONS ARE DENOTED WITH CARETS:
![]()
![]()
![]()
SOLVING THESE EQUATIONS
FOR ![]() 0,
0, ![]() 1, AND
1, AND ![]() 2 RESULTS
IN THE FOLLOWING ESTIMATES:
2 RESULTS
IN THE FOLLOWING ESTIMATES:
![]()
![]()
![]()
WHERE
![]()
AND
![]()
THE PRECEDING EXAMPLE ILLUSTRATES THE METHOD OF MAXIMUM LIKELIHOOD FOR ESTIMATING THE PARAMETERS OF A MODEL, WHERE THE LIKELIHOOD FUNCTION IS OF A SIMPLE ANALYTICAL FORM AND DIFFERENTIABLE WITH RESPECT TO THE PARAMETERS. IN THIS EXAMPLE, IT IS POSSIBLE TO FIND CLOSED-FORM EXPRESSIONS (EXPLICIT FUNCTIONS: FORMULAS (NOT ALGORITHMS) THAT MAY BE SOLVED FOR THE PARAMETERS) FOR THE ESTIMATES.
IT IS EASY TO SHOW THAT ![]() 0 AND
0 AND ![]() 1 ARE
UNBIASED ESTIMATES OF β0 AND β1. THE ESTIMATOR
1 ARE
UNBIASED ESTIMATES OF β0 AND β1. THE ESTIMATOR ![]() 2 IS NOT
UNBIASED. ITS EXPECTED VALUE IS (n-2)/n TIMES σ2, SO THAT (n/(n-2))
2 IS NOT
UNBIASED. ITS EXPECTED VALUE IS (n-2)/n TIMES σ2, SO THAT (n/(n-2))![]() 2 IS AN
UNBIASED ESTIMATE OF σ2. (ALTHOUGH MLEs ARE CONSISTENT, THEY MAY BE
BIASED.)
2 IS AN
UNBIASED ESTIMATE OF σ2. (ALTHOUGH MLEs ARE CONSISTENT, THEY MAY BE
BIASED.)
THE PRECEDING MODEL CAN BE EXTENDED TO THE CASE WHERE THE xi ARE RANDOM VARIABLES UNCORRELATED WITH THE єi. THE ESTIMATES REMAIN THE SAME, BUT THEIR DISTRIBUTIONAL PROPERTIES ARE DIFFERENT (SO THAT TESTS OF SIGNIFICANCE ABOUT THE MODEL PARAMETERS (REGRESSION COEFFICIENTS) ARE DIFFERENT). (THIS EXTENSION WILL BE DISCUSSED LATER.)
ESTIMATION BY THE METHOD OF LEAST SQUARES
THE PRECEDING DISCUSSION ILLUSTRATES THE APPROACH OF ESTIMATING THE PARAMETERS OF THE LINEAR STATISTICAL MODEL USING THE METHOD OF MAXIMUM LIKELIHOOD, ASSUMING THAT THE MODEL ERROR TERMS HAVE A NORMAL DISTRIBUTION. IT TURNS OUT THAT FOR THE LINEAR STATISTICAL MODEL THE MAXIMUM LIKELIHOOD ESTIMATES ARE THE SAME AS THE “LEAST-SQUARES” ESTIMATES, I.E., THOSE FOR WHICH THE SUM OF SQUARES OF THE ERROR TERMS (THE DEVIATIONS BETWEEN THE OBSERVED VALUE OF THE DEPENDENT VALUE AND THE VALUE ESTIMATED BY THE MODEL) IS MINIMIZED.
THE METHOD OF LEAST SQUARES DESCRIBED ABOVE IS THE MOST BASIC VERSION, AND IT IS REFERRED TO AS “ORDINARY LEAST SQUARES,” OR OLS. AS MENTIONED, THE LEAST-SQUARES PROCEDURE MAY BE APPLIED WITHOUT ANY CONSIDERATION OF THE PROBABILITY DISTRIBUTION OF THE UNDERLYING RANDOM VARIABLES. IF CERTAIN ASSUMPTIONS ARE MADE ABOUT THE PROBABILITY RELATIONSHIPS, THEN ASSERTIONS MAY BE MADE ABOUT PROPERTIES OF THE ESTIMATES, SUCH AS UNBIASEDNESS OR CONSISTENCY.
A STANDARD ASSUMPTION IS THAT THE MODEL ERROR TERMS (THE u’s) HAVE MEAN ZERO, CONSTANT VARIANCE, ARE INDEPENDENT, AND ARE UNCORRELATED WITH THE EXPLANATORY VARIABLES OF THE MODEL (THE x’s). A STRONGER STATEMENT IS THAT E(u|x)=0. THIS STATEMENT IMPLIES THAT u IS UNCORRELATED WITH ANY FUNCTION OF x.
IN THE FOLLOWING, WE SHALL REFER TO OLS ESTIMATES AND CONDITIONS UNDER WHICH THEY ARE UNBIASED OR CONSISTENT. IN MOST CASES, THE RESULTS REQUIRE ONLY THAT u IS UNCORRELATED WITH x, BUT IN SOME INSTANCES THE STRONGER CONDITION E(u|x)=0 IS REQUIRED. (THESE LECTURE NOTES MAY SIMPLY REFER TO “OLS CONDITIONS,” WITHOUT SPECIFYING THE EXACT CONDITIONS REQUIRED IN A PARTICULAR SITUATION. FOR DETAILS, SEE WOOLDRIDGE.)
AN EXPLANATORY VARIABLE x IS SAID TO BE ENDOGENOUS IF IT IS CORRELATED WITH u. IF x IS UNCORRELATED WITH u IT IS SAID TO BE EXOGENOUS. IF E(u|x)=0, THEN x IS EXOGENOUS. ENDOGENEITY MAY RESULT FOR SEVERAL REASONS, INCLUDING OMITTED VARIABLES, MEASUREMENT ERROR AND SIMULTANEITY (TO BE DISCUSSED).
MULTIPLE LINEAR REGRESSION
AN OBVIOUS GENERALIZATION OF THE PRECEDING LINEAR MODEL INVOLVING A SINGLE REGRESSOR IS TO ALLOW FOR MULTIPLE REGRESSORS, I.E., THE MODEL IS
yi = β0 + β1 x1i + β2 x2i + ... + βk xki + єi
where the єi are independent normally distributed random variables having mean zero and variance σ2, and the xji's are known numbers (not random variables).
IN THE PRECEDING MODEL, THE x's ARE FIXED NUMBERS, NOT RANDOM VARIABLES. AS IN THE CASE OF A SINGLE REGRESSOR, THE MODEL MAY BE EXTENDED TO THE CASE IN WHICH THE x's ARE RANDOM VARIABLES. IN THAT CASE, THE ESTIMATES REMAIN THE SAME, BUT THE DISTRIBUTIONAL PROPERTIES ARE DIFFERENT.
WORKING WITH THIS MODEL, INVOLVING SEVERAL REGRESSOR VARIABLES, BECOMES CUMBERSOME UNLESS VECTOR AND MATRIX NOTATION IS USED. IN VECTOR / MATRIX NOTATION, THE MODEL IS AS FOLLOWS:
yi = xi' β + єi
where
β = (β0, β1, ..., βk)'
xi = (1, x1i, x2i,...,xki)'.
THE PRECEDING MODEL SPECIFIES A SINGLE OBSERVATION. FOR THE COMPLETE SAMPLE, THE MODEL IS REPRESENTED AS:
Y = Xβ + є
where
Y = (y1, y2, ..., yn)'
X = (x1, x2,..., xn)'
and
є = (є1, є2, ..., єn)'.
IN MATRIX NOTATION, THE NORMAL EQUATIONS ARE
X'Xβ = X'Y.
SOLVING THESE FOR β (ASSUMING THAT THE MATRIX X'X IS INVERTIBLE) YIELDS THE SOLUTION
![]()
IT CAN BE SHOWN THAT THE EXPECTED
VALUE OF ![]() IS β (
IS β (![]() ) AND THAT THE VARIANCE
OF
) AND THAT THE VARIANCE
OF ![]() IS
IS
![]()
THE SAMPLING DISTRIBUTION
OF ![]() IS NORMAL (WITH THE JUST-STATED MEAN AND VARIANCE).
IS NORMAL (WITH THE JUST-STATED MEAN AND VARIANCE).
THE ESTIMATED REGRESSION FUNCTION IS
![]()
THE QUANTITY
![]()
WHERE ![]() IS THE VECTOR OF RESIDUALS IS AN UNBIASED ESTIMATE OF
σ2. AN APPROXIMATE 1-α CONFIDENCE INTERVAL FOR βj IS
IS THE VECTOR OF RESIDUALS IS AN UNBIASED ESTIMATE OF
σ2. AN APPROXIMATE 1-α CONFIDENCE INTERVAL FOR βj IS
![]()
WHERE ![]() IS THE j-TH DIAGONAL ELEMENT OF THE MATRIX
IS THE j-TH DIAGONAL ELEMENT OF THE MATRIX ![]() . (THESE RESULTS ARE NOT OBVIOUS, AND REQUIRE
DERIVATION.)
. (THESE RESULTS ARE NOT OBVIOUS, AND REQUIRE
DERIVATION.)
THE REGRESSION MODEL IS A SPECIFIC EXAMPLE OF THE GENERAL LINEAR STATISTICAL MODEL, OR THE GENERAL LINEAR MODEL (GLM), WHICH WILL BE DISCUSSED IN GREATER DETAIL LATER. IN THIS EXAMPLE THE Xs ARE FIXED NUMBERS (NOT RANDOM VARIABLES) AND THE ERRORS ARE UNCORRELATED AND OF CONSTANT VARIANCE. THE MODEL CAN BE EXTENDED IN A NUMBER OF WAYS, E.G., WHERE THE Y VARIABLE IS MULTIVARIATE, THE Xs ARE RANDOM VARIABLES, AND THE ERRORS ARE CORRELATED OR NOT OF CONSTANT VARIANCE.
THE BASIC "REGRESSION-MODEL" VERSION OF THE GENERAL LINEAR MODEL WAS DEFINED ABOVE:
Y = Xβ + є
WHERE THE X's ARE DETERMINISTIC AND THE є' ARE INDEPENDENTLY DISTRIBUTED NORMAL RANDOM VARIABLES WITH MEAN 0 AND VARIANCE σ2.
EXTENSIONS OF THIS MODEL INCLUDE ALLOWING THE VARIANCE OF THE є's TO VARY (HETEROSCEDASTICITY), THE X's TO BE RANDOM VARIABLES, AND THE DISTRIBUTION OF THE є's TO BE NON-NORMAL.
IF THE VARIANCE OF THE RESIDUALS (є's) IS σi2 FOR THE i-th OBSERVATION, THEN THE MODEL MAY BE EASILY TRANSFORMED TO CONSTANT VARIANCES (BY MULTIPLICATION OF EACH OBSERVATION BY THE INVERSE OF ITS STANDARD DEVIATION), OR THE "WEIGHTED LEAST-SQUARES" FORMULA MAY BE APPLIED.
WE ASSUME
E(є) = 0
V(є) = Vσ2
AND
є ~ N(0, Vσ2)
THEN THE WEIGHTED LEAST-SQUARES ESTIMATE (WHICH IS THE BEST LINEAR UNBIASED ESTIMATE) IS
![]()
THE PRECEDING EXAMPLE CONSIDERS THE CASE OF A UNIVARIATE DEPENDENT VARIABLE (Y). THE GLM MAY BE EXTENDED TO THE MULTIVARIATE CASE; THIS WILL BE DISCUSSED LATER.
THE CASE IN WHICH THE Xs ARE RVs.
IN THE PRECEDING VERSION OF THE GENERAL LINEAR MODEL, THE EXPLANATORY VARIABLES (Xs) WERE ASSUMED TO BE DETERMINISTIC, OR "FIXED". IN MANY APPLICATIONS, SUCH AS ECONOMICS, THIS ASSUMPTION IS UNTENABLE, AND IT MUST BE ASSUMED THAT THE X's ARE RANDOM VARIABLES. IN THIS CASE, IT MUST BE ASSUMED THAT THE X's ARE UNCORRELATED WITH THE MODEL ERROR TERMS. OTHERWISE, THE ESTIMATES MAY BE BIASED.
IF ALL OF THE X's ARE RANDOM VARIABLES, THEN THE MODEL IS CALLED A RANDOM-EFFECTS MODEL. IF ALL OF THE X's ARE FIXED, THEN THE MODEL IS CALLED A FIXED-EFFECTS MODEL. IF SOME EFFECTS ARE RANDOM AND SOME ARE FIXED, THE MODEL IS CALLED A MIXED MODEL.
THE PROCEDURES FOR CONSTRUCTING ESTIMATES AND MAKING TESTS OF HYPOTHESIS DIFFER FOR THE THREE CASES (RANDOM EFFECTS, FIXED EFFECTS, MIXED MODEL).
MULTIVARIATE MODELS
THE PRECEDING DISCUSSION HAS FOCUSED ON UNIVARIATE MODELS, I.E., MODELS IN WHICH THE MODEL ERROR TERM IS REPRESENTED BY A SINGLE RANDOM VARIABLE, REPRESENTED BY A SINGLE PROBABILITY DISTRIBUTION. THESE MODELS MAY BE EXTENDED TO THE CASE IN WHICH THE MODEL DEPENDENT VARIABLE IS A VECTOR, AND THE MODEL ERROR TERMS ARE HENCE REPRESENTED BY A JOINT PROBABILITY DISTRIBUTION, I.E., TO THE MULTIVARIATE CASE.
MULTIVARIATE MODELS FALL INTO SEVERAL CATEGORIES. MAJOR DISTINCTIONS INCLUDE WHETHER THE DEPENDENT VARIABLES OF THE MODEL ARE CONTINUOUS OR DISCRETE; WHETHER SAMPLING IS DONE FOR MANY TIMES OR A FEW; AND WHETHER THE MODEL INCLUDES EXOGENOUS VARIABLES. THIS PRESENTATION DOES NOT GO INTO DETAIL ON THE TOPIC OF MULTIVARIATE MODELS AND MULTIVARIATE ANALYSIS. SOME DISCUSSION OF THE TOPIC IS PRESENTED LATER, IN THE CASE OF DISCRETE DEPENDENT VARIABLES. THE SUBJECT OF MULTIVARIATE ANALYSIS FOR CONTINUOUS RANDOM VARIABLE IS VAST, AND WILL BE COVERED IN A SEPARATE PRESENTATION.
THE GENERAL REFERENCES BY GREENE (ECONOMETRIC ANALYSIS) AND WOOLDRIDGE (ECONOMETRIC ANALYSIS OF CROSS SECTION AND PANEL DATA) CITED EARLIER CONTAIN RELATIVELY LITTLE INFORMATION ON MULTIVARIATE ANALYSIS. SOME MORE COMPREHENSIVE REFERENCES ON THIS SUBJECT ARE THE FOLLOWING:
Roy, S. N. Some Aspects of Multivariate Analysis, Wiley, 1957
Anderson, T. W., An Introduction to Multivariate Statistical Analysis, Wiley, 1958
Hamilton, James D., Time Series Analysis, Princeton University Press, 1994
Lütkepohl, Helmut, New Introduction to Multiple Time Series Analysis, Springer, 2007
Berridge, Damon M., and Robert Crouchley, Multivariate Generalized Linear Mixed Models using R, CRC Press, 2011
Cooley, William W. and Paul R. Lohnes, Multivariate Data Analysis, Wiley, 1971
Harman, Harry H., Modern Factor Analysis, 2nd ed. revised, University of Chicago Press, 1967
MODELS INVOLVING TIME: TIME SERIES MODELS AND PANEL-DATA MODELS
IN SOME APPLICATIONS OBSERVATIONS ARE TAKEN FOR A NUMBER OF POINTS IN TIME, AND IT IS KNOWN OR POSSIBLE THAT TIME MAY HAVE AN EFFECT ON OTHER VARIABLES. THE METHODOLOGIES USED TO ANALYZE MODELS INVOLVING TIME DIFFER ACCORDING AS THE NUMBER OF TIME POINTS IS SMALL OR LARGE, AND WHETHER THE MODEL CONTAINS EXOGENOUS VARIABLES. IF THE NUMBER OF TIME POINTS IS SMALL, THE MODEL IS REFERRED TO AS A PANEL-DATA MODEL; IF THE NUMBER OF TIME POINTS IS LARGE AND EVENLY-SPACED, THE MODEL IS REFERRED TO AS A TIME-SERIES MODEL.
THIS PRESENTATION CONTAINS LITTLE INFORMATION ABOUT MODELS INVOLVING TIME. THE LITERATURE ON THIS SUBJECT IS VAST. REFERENCES INCLUDE THE FOLLOWING:
Greene, William H., Econometric Analysis, 7th ed, Prentice Hall, 2012
Wooldridge, Jeffrey M., Econometric Analysis of Cross Section and Panel Data, 2nd ed., The MIT Press, 2010
Hamilton, James D., Time Series Analysis, Princeton University Press, 1994
Lütkepohl, Helmut, New Introduction to Multiple Time Series Analysis, Springer, 2007
Box, George E. P., Gwilym M. Jenkins and Gregory C Reinsel, Time Series Analysis, Forecasting and Control, 3rd ed, Prentice-Hall International, 1994
Jenkins, Gwilym M. and Donald G. Watts, Spectral Analysis and its applications, Holden-Day, 1968
Glass, Gene V., Victor L. Wilson and John M. Gottman, Design and Analysis of Time-Series Experiments, Information Age Publishing, 2008
Harvey, Andrew, The Econometric Analysis of Time Series, 2nd ed,. The MIT Press, 1990
Harvey, Andrew, Time Series Models, 2nd ed., The MIT Press, 1993
Harvey, Andrew C., Forecasting, structural time series models and the Kalman Filter, Cambridge University Press, 1989
DETAILED INFORMATION ON THE SUBJECT OF TIME-SERIES ANALYSIS AND ANALYSIS OF PANEL DATA WILL BE PRESENTED IN A SEPARATE PRESENTATION. THE FOLLOWING SUBSECTION DISCUSSES A PARTICULAR TOPIC IN ANALYSIS OF PANEL DATA, VIZ., THE ISSUE OF UNOBSERVED VARIABLES.
ASSUMPTIONS IN THE GENERAL LINEAR MODEL, AND THE EFFECTS OF INVALID ASSUMPTIONS
IN THE PRECEDING DISCUSSION OF THE GENERAL LINEAR MODEL, A NUMBER OF ASSUMPTIONS WERE MADE. THESE INCLUDE:
THE MODEL ERROR TERMS HAVE MEAN ZERO
THE MODEL ERROR TERMS ARE INDEPENDENT
THE MODEL EXPLANATORY VARIABLES ARE EITHER FIXED (DETERMINISTIC) VARIABLES OR RANDOM VARIABLES (OR A MIXTURE OF BOTH)
THE MODEL ERROR TERMS ARE UNCORRELATED WITH THE EXPLANATORY VARIABLES (IF THEY ARE RANDOM VARIABLES)
THE MODEL ERROR TERMS HAVE CONSTANT VARIANCE
THE MATRIX X’X IS NONSINGULAR (INVERTIBLE, OF FULL RANK)
THE MODEL IS CORRECTLY SPECIFIED (E.G., THERE ARE NO UNOBSERVED (OMITTED, HIDDEN) VARIABLES; THERE ARE NO ERRORS IN MEASURING THE VARIABLES (DEPENDENT OR EXPLANATORY); THE FUNCTIONAL FORM OF THE MODEL IS CORRECT)
THERE ARE NO MISSING VALUES (OF EITHER THE DEPENDENT OR INDEPENDENT VARIABLES)
ASSUMPTIONS MAY BE MADE ABOUT THE DISTRIBUTION OF THE MODEL ERROR TERMS, SUCH AS NORMALITY
IF THE PRECEDING ASSUMPTIONS ARE SATISFIED, THEN THE PARAMETER ESTIMATES HAVE DESIRABLE PROPERTIES, SUCH AS UNBIASEDNESS, CONSISTENCY, EFFICIENCY AND ASYMPTOTIC NORMALITY. IF SOME OF THE ASSUMPTIONS ARE RELAXED, SOME OF THESE PROPERTIES MAY FAIL TO HOLD, E.G., THE ESTIMATES COULD BE BIASED AND INCONSISTENT, OR THEY MAY BE BIASED BUT CONSISTENT.
THE FOLLOWING SUBSECTIONS WILL DISCUSS EACH OF THESE ITEMS, BRIEFLY. IN MOST CASES, RESULTS ARE STATED WITHOUT PROOF. (FOR PROOFS, SEE GREENE, WOOLDRIDGE, OR JOHNSTON, OP. CIT.)
THE MODEL ERROR TERMS HAVE MEAN ZERO
IF THE PHENOMENON, OR PROCESS, UNDER INVESTIGATION HAS A NONZERO MEAN, THEN THE MODEL SHOULD ALLOW FOR A MEAN. THIS IS ACCOMPLISHED BY SETTING THE VALUE OF AN EXPLANATORY VARIABLE EQUAL TO ONE FOR ALL OBSERVATIONS. IF THE PROCESS HAS A MEAN BUT A MEAN IS NOT ALLOWED FOR IN THE MODEL, THE MODEL IS MISSPECIFIED AND THE OTHER MODEL PARAMETERS (REGRESSION COEFFICIENTS) WILL BE BIASED.
THE MODEL ERROR TERMS ARE INDEPENDENT
IF THE MODEL ERROR TERMS ARE NOT INDEPENDENT, ESTIMATES MAY OR MAY NOT BE SERIOUSLY AFFECTED. A WEAKER ASSUMPTION THAT MAY BE MADE IS MEAN INDEPENDENCE, E(u|x)=0. IF AT LEAST THIS LATTER CONDITION DOES NOT HOLD, THEN PARAMETER ESTIMATES MAY BE BIASED. IF THE MODEL ERROR TERMS ARE CORRELATED (AMONG THEMSELVES – NOT WITH THE EXPLANATORY VARIABLES), THEN THE PARAMETER ESTIMATES MAY BE UNBIASED, BUT THEY ARE STILL CONSISTENT. BETTER ESTIMATES ARE OBTAINED BY USING GENERAL LEAST SQUARES INSTEAD OF ORDINARY LEAST SQUARES, TO TAKE INTO ACCOUNT THE NATURE OF THE CORRELATIONAL STRUCTURE OF THE VARIANCE MATRIX OF THE MODEL ERROR TERMS. (SEE WOOLDRIDGE CHAPTER 7 FOR DISCUSSION.)
THE MODEL EXPLANATORY VARIABLES ARE EITHER FIXED (DETERMINISTIC) VARIABLES OR RANDOM VARIABLES (OR A MIXTURE OF BOTH)
WHETHER THE EXPLANATORY VARIABLES ARE FIXED OR RANDOM (OR A MIXTURE OF BOTH) DOES NOT AFFECT BIAS OR CONSISTENCY. WHAT IS AFFECTED IS TESTS OF SIGNIFICANCE OF MODEL PARAMETERS. THESE TESTS MUST TAKE INTO ACCOUNT RANDOM VARIABILITY OF THE REGRESSORS (EXPLANATORY VARIABLES).
THE MODEL ERROR TERMS ARE UNCORRELATED WITH THE EXPLANATORY VARIABLES (IF THEY ARE RANDOM VARIABLES)
IF THE EXPLANATORY VARIABLES ARE FIXED, THEN THERE IS NO CONSIDERATION OF CORRELATION OF THE MODEL ERROR TERMS WITH THEM (SINCE THEY ARE NOT RANDOM VARIABLES). IF THE EXPLANATORY VARIABLES ARE RANDOM, THEN IT IS ESSENTIAL THAT THE MODEL ERROR TERMS BE UNCORRELATED WITH THEM. OTHERWISE, THE PARAMETER ESTIMATES MAY BE BIASED. CORRELATION BETWEEN THE ERROR TERMS AND THE EXPLANATORY VARIABLES IS POTENTIALLY VERY SERIOUS: IF CORRELATION EXISTS BETWEEN A SINGLE EXPLANATORY VARIABLE (IN A MODEL CONTAINING SEVERAL EXPLANATORY VARIABLES) AND THE MODEL ERROR TERM, THEN ALL OF THE PARAMETER ESTIMATES MAY BE BIASED (NOT JUST THE ESTIMATE ASSOCIATED WITH THE SINGLE EXPLANATORY VARIABLE THAT IS CORRELATED WITH THE MODEL ERROR TERM).
THE MODEL ERROR TERMS HAVE CONSTANT VARIANCE
IF THE MODEL ERROR TERMS DO NOT HAVE CONSTANT VARIANCE (I.E., ARE HOMOSCEDASTIC), THEN THE PARAMETER ESTIMATES MAY BE BIASED. THERE ARE TWO WAYS TO ADDRESS THIS PROBLEM: EITHER TRANSFORM THE ORIGINAL RANDOM VARIABLE (THE DEPENDENT VARIABLE) TO ONE HAVING CONSTANT VARIANCE; OR USE THE WEIGHTED-LEAST-SQUARES APPROACH DESCRIBED EARLIER. (TO DO THE LATTER REQUIRES KNOWLEDGE OF WHAT THE VARIANCE OF EACH OBSERVATION IS.) FOR EXAMPLE, STOCK PRICES MAY BE APPROXIMATELY LOG-NORMALLY DISTRIBUTED, IN WHICH CASE TAKING LOGARITHMS WILL PRODUCE A VARIABLE WITH CONSTANT VARIANCE. IF THE DEPENDENT VARIABLE IS DISCRETE, SUCH AS A BINARY-VALUED RANDOM VARIABLE, THE VARIANCE WILL NOT BE CONSTANT. A GENERAL METHOD FOR ADDRESSING THIS SITUATION IS DESCRIBED LATER (IN THE SUBSECTIONS TITLED LOGISTIC REGRESSION AND GENERALIZED LINEAR MODEL).
THE MATRIX X’X IS NONSINGULAR (INVERTIBLE, OF FULL RANK)
IF THE MATRIX X’X IS SINGULAR, THE ESTIMATES DESCRIBED EARLIER (WHICH INVOLVE THE INVERSE OF THIS MATRIX) CANNOT BE CALCULATED. THE SOURCE OF SINGULARITY IS LINEAR DEPENDENCIES AMONG THE EXPLANATORY VARIABLES, SUCH AS INCLUDING TWO CONSTANT TERMS, OR SEVERAL VARIABLES THAT SUM TO A CONSTANT (E.G., PERCENTAGES THAT SUM TO 100).
THE SOLUTION TO THIS PROBLEM IS TO REDUCE THE NUMBER OF EXPLANATORY VARIABLES SO THAT NO LINEAR DEPENDENCIES ARE PRESENT AMONG THEM.
THE MODEL IS CORRECTLY SPECIFIED (I.E., THERE ARE NO UNOBSERVED (OMITTED, HIDDEN) VARIABLES; THERE ARE NO ERRORS IN MEASURING THE VARIABLES (DEPENDENT OR EXPLANATORY); SIMULTANEITY; THE FUNCTIONAL FORM OF THE MODEL IS CORRECT)
MODEL SPECIFICATION ERRORS
IF THE MODEL IS NOT CORRECTLY SPECIFIED, THE PARAMETER ESTIMATES MAY BE BIASED. (THE TERM “NOT CORRECTLY SPECIFIED” COULD REFER TO ANY SPECIFICATION ERROR, SUCH AS AN INCORRECT FUNCTIONAL FORM (E.G., LINEAR INSTEAD OF NONLINEAR), MISSING VARIABLES, MISSING INTERACTION TERMS, HETEROSCEDASTICITY), BUT IS INTENDED HERE TO COVER WHATEVER INVALID ASSUMPTIONS ARE NOT ADDRESSED BY THE OTHER TOPIC HEADINGS OF THIS SUBSECTION.)
SIMULTANEITY
SIMULTANEITY REFERS TO THE SITUATION IN WHICH ONE OR MORE OF THE EXPLANATORY VARIABLES IS DETERMINED SIMULTANEOUSLY WITH THE DEPENDENT VARIABLE. IN THIS CASE THOSE EXPLANATORY VARIABLES WILL BE CORRELATED WITH THE MODEL ERROR TERMS. THIS PROBLEM IS ADDRESSED EITHER BY CONSIDERING A TIME-SERIES MODEL (DISCUSSED LATER) OR A SIMULTANEOUS-EQUATION MODEL (SEE WOOLDRIDGE, CHAPTER 9).
MEASUREMENT ERRORS
IN THE PRECEDING DISCUSSION OF THE GENERAL LINEAR MODEL, IT WAS ASSUMED THAT THE VALUES OF THE DEPENDENT VARIABLE (Y) AND THE EXPLANATORY VARIABLES (Xs) ARE KNOWN EXACTLY.
MEASUREMENT ERRORS IN THE DEPENDENT (RESPONSE) VARIABLE DO NOT CAUSE A PROBLEM IF THE MEASUREMENT ERROR IS UNCORRELATED WITH THE EXPLANATORY VARIABLES. OTHERWISE, THE ESTIMATES MAY BE INCONSISTENT AND BIASED. THE PRECISION OF THE ESTIMATES WILL BE REDUCED.
MEASUREMENT ERRORS IN INDEPENDENT VARIABLES MAY BE PROBLEMATIC. IF THE MEASUREMENT ERROR IN AN EXPLANATORY VARIABLE IS UNCORRELATED WITH ALL OF THE EXPLANATORY VARIABLES (INCLUDING THE ONE WITH MEASUREMENT ERROR), THEN THE USUAL OLS ASSUMPTIONS ARE SATISFIED, AND THE PARAMETER ESTIMATES ARE CORRECT. ALL THAT HAPPENS IS THAT THE ERROR VARIANCE IS INCREASED.
IF THE MEASUREMENT ERROR IS UNCORRELATED WITH THE TRUE (UNOBSERVED) VALUE OF THE EXPLANATORY VARIABLE CONTAINING MEASUREMENT ERROR, THEN IT (THE MEASUREMENT ERROR) MUST BE CORRELATED WITH THE OBSERVED (MEASURED) VALUE OF THAT VARIABLE. IN THIS CASE, THE ASSUMPTION THAT THE MODEL ERROR IS UNCORRELATED WITH THE EXPLANATORY VARIABLES IS VIOLATED, AND THE PARAMETER ESTIMATES ARE ALL INCONSISTENT. THIS SITUATION IS CALLED THE “CLASSICAL ERRORS-IN-VARIABLES PROBLEM.” IF THE TRUE VALUE OF THE EXPLANATORY VARIABLE CONTAINING MEASUREMENT ERROR IS UNCORRELATED WITH THE OTHER EXPLANATORY VARIABLES, THEN IT CAN BE SHOWN THAT THE COEFFICIENTS FOR THE OTHER EXPLANATORY VARIABLES CONVERGE IN PROBABILITY TO THE CORRECT VALUES, BUT THE COEFFICIENT FOR THE MEASUREMENT-ERROR VARIABLE IS ATTENUATED. (SEE WOOLDRIDGE CHAPTER 4 FOR DETAILS.)
RESULTS IN TWO SPECIAL CASES ARE AS FOLLOWS. IF THERE IS A SINGLE EXPLANATORY VARIABLE, x1, THEN THE ESTIMATE OF ITS COEFFICIENT CONVERGES IN PROBABILITY TO THE FOLLOWING VALUE:
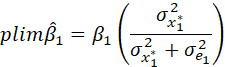
WHERE x1* DENOTES THE TRUE (UNOBSERVED) VALUE OF THE EXPLANATORY VARIABLE AND x1 DENOTES THE OBSERVED VALUE (CONTAINING MEASUREMENT ERROR).
IF THERE ARE K EXPLANATORY VARIABLES, WITH ONLY THE K-TH ONE, xK, CONTAINING MEASUREMENT ERROR, THEN, IF xK* IS UNCORRELATED WITH ALL xj, j≠K (SO THAT xK ALSO IS), THEN
![]()
AND
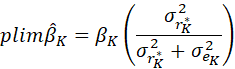
WHERE rK* IS THE LINEAR PROJECTION ERROR IN
![]()
UNOBSERVED VARIABLES
AN IMPORTANT CONSIDERATION IN RANDOM EFFECTS MODELS AND MIXED-EFFECTS MODELS IS THE PROBABILISTIC NATURE OF UNOBSERVED VARIABLES. THE PRESENCE OF UNOBSERVED VARIABLES MAY OR MAY NOT BIAS THE ESTIMATES OF THE COEFFICIENTS OF THE OTHER MODEL VARIABLES. THE ISSUE IS THAT IN USING THE ORDINARY-LEAST SQUARES METHOD OF ESTIMATION IN A GENERAL LINEAR MODEL, THE MODEL ERROR TERMS MAY NOT BE CORRELATED WITH ANY OF THE EXPLANATORY VARIABLES. (UNOBSERVED VARIABLES ARE ALSO CALLED UNOBSERVED EFFECTS, UNOBSERVED COMPONENTS, LATENT VARIABLES, AND UNOBSERVED HETEROGENEITY.)
IF THE UNOBSERVED VARIABLE IS UNCORRELATED WITH THE OTHER EXPLANATORY VARIABLES, NO PROBLEM EXISTS. THE UNOBSERVED VARIABLE IS SIMPLY INCLUDED IN THE MODEL ERROR TERM, THE ESTIMATION PROCEEDS AS USUAL, AND THE PARAMETER ESTIMATES ARE UNBIASED.
IF THE UNOBSERVED VARIABLE IS CORRELATED WITH THE OBSERVED EXPLANATORY VARIABLES, THEN THE PARAMETER ESTIMATES WILL BE BIASED AND INCONSISTENT. ONE APPROACH TO THIS PROBLEM IS TO INCLUDE AN EXPLANATORY VARIABLE IN THE MODEL THAT IS CORRELATED WITH THE UNOBSERVED VARIABLE AND SUCH THAT, CONDITIONAL ON THE OTHER EXPLANATORY VARIABLES, THE UNOBSERVED VARIABLE IS UNCORRELATED WITH THE OTHER EXPLANATORY VARIABLES.
UNOBSERVED VARIABLES IN PANEL-DATA MODELS
IN THE CASE OF PANEL DATA (DATA OBSERVED AT MORE THAN ONE TIME), A VERY USEFUL APPROACH EXISTS FOR DEALING WITH UNOBSERVED VARIABLES IN CERTAIN SITUATIONS. WOOLDRIDGE PROVIDES A DETAILED DESCRIPTION OF UNOBSERVED (OMITTED) VARIABLES. HERE FOLLOWS A BRIEF SUMMARY OF MAJOR POINTS. (SEE WOOLDRIDGE CHAPTER 10 FOR DETAILS.)
THE APPROACH TO BE DESCRIBED APPLIES TO THE SITUATION WHERE PANEL SAMPLING IS DONE AT MORE THAN ONE LEVEL, SUCH AS VILLAGES AND HOUSEHOLDS AT THE FIRST AND SECOND LEVELS AND INDIVIDUALS AT THE THIRD LEVEL, AND TIME-INVARIANT UNOBSERVED VARIABLES OCCUR AT THE THIRD LEVEL. IN THIS EXAMPLE, THE UNOBSERVED VARIABLES ARE INDIVIDUAL CHARACTERISTICS, SUCH AS INTELLIGENCE AND AMBITION, WHICH ARE UNOBSERVED BUT MAY BE REASONABLY ASSUMED TO REMAIN CONSTANT BETWEEN THE TWO TIMES OF THE PANELS.
CASE 1: THE OMITTED VARIABLE IS NOT CORRELATED WITH THE OTHER EXPLANATORY VARIABLES. THE SITUATION IS AS FOLLOWS (SEE WOOLDRIDGE 2ND ED. CHAPTER 10 FOR DETAILS. THIS PRESENTATION USES WOOLDRIDGE’S NOTATION).
The model is:
yit = xitβ + ci + uit
where β is a K x 1 vector, xit is a 1 x K vector, the ui are independent with mean zero and variance σ2 and uncorrelated with the xit’s; and ci for all t, with variance σc2, is uncorrelated with the xit’s and has mean zero conditional on the xit’s. (To retain consistency with the notational conventions used by Wooldridge, we depart from standard notation is not using a prime to denote the xit row vector.) We define
vit = ci + uit
and rewrite the model as
yi = xitβ + vit.
In order to use OLS to estimate the parameters (β), the vit must be uncorrelated with the xit. If this condition holds, then OLS estimation may be used. This approach is referred to as “pooled ordinary least squares,” the descriptor “pooled” referring to the fact that all of the data, both cross-sectional and over time, are combined (or “pooled”). The condition that ci is uncorrelated with the vit and xit are uncorrelated imposes substantial restrictions on the xit. For example, if lagged dependent variables are included as explanatory variables, the assumption is violated (since yi,t-1 and ci must be correlated).
RANDOM EFFECTS METHOD AND RANDOM EFFECTS ESTIMATORS
THE USE OF POOLED OLS IS NOT EFFICIENT, SINCE IT DOES NOT EXPLICITLY TAKE INTO ACCOUNT THE SERIAL CORRELATION INTRODUCED BY THE FACT THAT ci ARE THE SAME OVER TIME. IMPROVED ESTIMATES MAY BE OBTAINED BY USING GENERALIZED LEAST SQUARES. THAT APPROACH IS CALLED THE “RANDOM EFFECTS METHOD,” AND THE ESTIMATORS ARE CALLED “RANDOM EFFECTS ESTIMATORS.” THIS USE OF THE TERM HAS NOTHING TO DO WITH THE USE OF THE TERM “RANDOM EFFECTS” TO INDICATE WHETHER THE MODEL EXPLANATORY VARIABLES ARE RANDOM. IN THIS CONTEXT, IT SIMPLY MEANS THAT THE TIME-INVARIANT UNOBSERVED VARIABLE IS BEING INCLUDED IN THE MODEL ERROR TERM.
THE RANDOM EFFECTS APPROACH PLACES THE UNOBSERVED TIME-INVARIANT EFFECT ci IN THE MODEL ERROR TERM, AND ASSUMES THAT IT IS UNCORRELATED WITH THE xit. IN MANY APPLICATIONS, THIS ASSUMPTION CANNOT BE MADE. IN THAT CASE AN ALTERNATIVE IS TO USE A “FIXED EFFECTS” APPROACH, WHICH ALLOWS FOR THE ci TO BE ARBITRARILY CORRELATED WITH THE xij.
FIXED EFFECTS METHODS
THERE ARE TWO APPROACHES TO FIXED-EFFECTS ESTIMATION. THE FIRST IS TO AVERAGE THE DATA OVER THE TIME VARIABLE, AND THE SECOND IS TO TAKE DIFFERENCES BETWEEN SUCCESSIVE TIMES. THE FIRST APPROACH IS CALLED USING A FIXED EFFECTS TRANSFORMATION OR WITHIN TRANSFORMATION, AND THE ESTIMATOR IS CALLED A FIXED-EFFECTS ESTIMATOR. THE SECOND APPROACH IS CALLED FIRST DIFFERENCING OR USING A FIRST-DIFFERENCING TRANSFORMATION, AND THE ESTIMATOR IS CALLED A FIRST-DIFFERENCE ESTIMATOR.
FIXED-EFFECTS (FE) ESTIMATOR
TO RECAPITULATE, THE MODEL IS
yit = xitβ + ci + uit.
THIS EQUATION IS CALLED A “STRUCTURAL” EQUATION.
USING THE FIXED-EFFECTS TRANSFORMATION, WE AVERAGE THE DATA OVER TIME (t = 1,…,T) TO OBTAIN:
![]()
WHERE
![]()
![]()
AND
![]()
WE SUBTRACT THE PRECEDING
EQUATION FOR ![]() FROM THE MODEL (STRUCTURAL) EQUATION FOR EACH t TO
OBTAIN:
FROM THE MODEL (STRUCTURAL) EQUATION FOR EACH t TO
OBTAIN:
![]()
OR
![]()
WHERE
![]()
![]()
AND
![]()
SINCE THE INDIVIDUAL
SPECIFIC EFFECT ci IS TIME-INVARIANT, IT IS ELIMINATED FROM THE
EQUATION. THE MODEL EQUATION SHOWN JUST ABOVE (IN TERMS OF ![]() IS AN ESTIMATING EQUATION, NOT A STRUCTURAL EQUATION.
IS AN ESTIMATING EQUATION, NOT A STRUCTURAL EQUATION.
NOTE THAT BY SUBTRACTING THE MEAN FROM ALL VARIABLES, WE HAVE INTRODUCED A LINEAR DEPENDENCY IN THE DATA (I.E., THE SUM OF EACH VARIABLE OVER ALL T TIME PERIODS IS ZERO). WITH THIS DEPENDENCY, THE CROSS-PRODUCTS MATRIX X’X WOULD BE SINGULAR, AND THE OLS ESTIMATION PROCEDURE WOULD FAIL (SINCE X’X WOULD NOT BE INVERTIBLE). THIS DEPENDENCY MAY BE REMOVED BY DISCARDING THE (TRANSFORMED) DATA FROM ANY ONE OF THE T TIME PERIODS. (WHICH TIME PERIOD IS DROPPED MAKES NO DIFFERENCE; THE SIMPLEST APPROACH IS TO DROP THE DATA FOR THE FINAL (T-th) TIME PERIOD – THE MATHEMATICAL NOTATION IS SIMPLER IN THIS CASE (SEE WOOLDRIDGE P. 312-313.)
UNDER THE ASSUMPTION THAT THE MODEL ERROR TERMS ARE UNCORRELATED WITH THE EXPLANATORY VARIABLES, THE OLS ESTIMATES ARE CONSISTENT.
FOR THE RANDOM-EFFECTS ESTIMATOR, WE ASSUMED THAT ci WAS UNCORRELATED WITH xi. FOR THE FIXED-EFFECTS ESTIMATOR, WE ASSUME THAT ci AND xi ARE UNCORRELATED WITH uit FOR ALL t, BUT ci MAY HAVE ANY RELATIONSHIP TO THE xi.
SINCE ci MAY BE ANY FUNCTION OF xi, ITS EFFECT CANNOT BE DISTINGUISHED FROM ANY OTHER TIME-CONSTANT VARIABLE, USING THIS APPROACH.
THE PRECEDING HAS DESCRIBED THE FIRST APPROACH TO FIXED-EFFECTS ESTIMATION, I.E., THE TIME-DEMEANING OF THE DATA BY AVERAGING EACH VARIABLE OVER ALL T TIME PERIODS, AND SUBTRACTING THE MEAN FROM EACH VARIABLE. THIS PROCEDURE REMOVES THE UNOBSERVED VARIABLE c FROM THE ESTIMATING EQUATION. THE SECOND APPROACH FOR REMOVING c IS TO TRANSFORM THE DATA BY DIFFERENCING. THAT APPROACH WILL NOW BE DESCRIBED.
FIRST-DIFFERENCE (FD) ESTIMATOR
WITH THE FIRST-DIFFERENCING APPROACH, WE CALCULATE THE DIFFERENCES BETWEEN CORRESPONDING OBSERVATIONS IN SUCCESSIVE TIME PERIODS:
![]()
WHERE
![]()
![]()
AND
![]()
THE PRECEDING TRANSFORMATION IS CALLED A FIRST-DIFFERENCING TRANSFORMATION. IT REMOVES ALL VARIABLES THAT ARE TIME-INVARIANT FROM ONE TIME PERIOD TO THE NEXT, SUCH AS THE UNOBSERVED VARIABLE, c, WHICH IS TIME-INVARIANT OVER ALL T PERIODS.
THE PRECEDING TRANSFORMED EQUATION IS USED AS AN ESTIMATING EQUATION. NOTE THAT AFTER TRANSFORMING, DATA ARE AVAILABLE FOR ONE LESS TIME PERIOD THAN FOR THE ORIGINAL (RAW) DATA.
IT CAN BE SHOWN THAT THE
TRANSFORMED ERROR TERMS ![]() ARE UNCORRELATED WITH THE TRANSFORMED EXPLANATORY
VARIABLES
ARE UNCORRELATED WITH THE TRANSFORMED EXPLANATORY
VARIABLES ![]() ,
,
![]()
SO THE OLS ESTIMATES OBTAINED FROM THE TRANSFORMED DATA ARE CONSISTENT. MOREOVER, IT CAN BE SHOWN THAT STRICT EXOGENEITY HOLDS:
![]()
SO THAT THE FIRST-DIFFERENCE ESTIMATOR IS UNBIASED CONDITIONAL ON X.
THE RANK CONDITION FOR OLS ESTIMATION IS THAT THE CROSS-PRODUCTS MATRIX OF THE FIRST-DIFFERENCED DATA IS NONSINGULAR. THIS IMPLIES THAT ALL VARIABLES THAT ARE FIXED ACROSS ALL TIME PERIODS CANNOT BE INCLUDED IN THE MODEL. IT IS ALSO POSSIBLE THAT FIRST DIFFERENCING CAN INTRODUCE ADDITIONAL COLLINEARITIES IN THE DATA, SUCH AS FOR ANY VARIABLE THAT INCREASES BY A FIXED AMOUNT FROM YEAR TO YEAR.
FOR THE CASE OF TWO TIME PERIODS (T=2), THE FIXED-EFFECTS APPROACH AND THE FIRST-DIFFERENCING APPROACH PRODUCE IDENTICAL ESTIMATES. THE FIRST-DIFFERENCE APPROACH IS SIMPLER TO PROGRAM (BUT THIS IS NO LONGER A CONSIDERATION IN THE AGE OF READILY AVAILABLE STATISTICAL COMPUTER PROGRAMS). FOR MORE THAN TWO TIME PERIODS (T>2), WHICH APPROACH IS MORE EFFICIENT DEPENDS ON WHAT ASSUMPTIONS ARE MADE ABOUT HOMOSCEDASTICITY AND SERIAL CORRELATION. IF IT IS ASSUMED THAT THE u’s ARE HOMOSCEDASTIC AND HAVE NO SERIAL CORRELATION, THEN THE FE ESTIMATES ARE MORE EFFICIENT. WITH HIGH SERIAL CORRELATION, THE FD ESTIMATES ARE MORE EFFICIENT. (SEE WOOLDRIDGE PP. 317-318 FOR DISCUSSION.) THE ASSUMPTION OF SERIAL CORRELATION MAY BE TESTED.
MANY PROGRAM EVALUATIONS INVOLVE SIMPLY TWO PANELS (A BASELINE AND ENDLINE), IN WHICH CASE THIS ISSUE IS IRRELEVANT (SINCE THE FE AND FD ESTIMATES ARE IDENTICAL IN THIS CASE). IN THE CASE OF TWO TIME PERIODS, THE TRANSFORMED DATA ARE AVAILABLE FOR A SINGLE TIME PERIOD, AND ALL STATISTICAL PROCEDURES DEVELOPED FOR CROSS-SECTIONAL DATA MAY BE APPLIED DIRECTLY.
COMPARISON OF FE AND FD ESTIMATORS TO RE ESTIMATORS
IF THE EXPLANATORY VARIABLES IN xi DO NOT VARY MUCH OVER TIME, THE FE AND FD ESTIMATES CAN BE OF LOW PRECISION (SINCE THE DIFFERENCE WILL HAVE LITTLE VARIATION). IN THIS CASE THE RE ESTIMATES MAY BE MUCH MORE PRECISE. THE KEY ISSUE IS WHETHER ci CAN BE ASSUMED TO BE UNCORRELATED WITH THE xit. WHETHER THIS CONDITION HOLDS MAY BE TESTED USING A HAUSMAN TEST. THIS TEST IS BASED ON THE DIFFERENCE BETWEEN THE RE AND FE ESTIMATES. THE FE IS CONSISTENT WHEN ci AND xit ARE CORRELATED, BUT THE RE IS INCONSISTENT. A STATISTICALLY SIGNIFICANT DIFFERENCE BETWEEN THE FE AND RE ESTIMATORS IS HENCE TAKEN AS EVIDENCE AGAINST THE RE ASSUMPTION.
THERE ARE LIMITATIONS ON THE HAUSMAN TEST. SINCE THE FE APPROACH PRODUCES ESTIMATES ONLY FOR TIME-VARYING EXPLANATORY VARIABLES, THE FE AND RE COEFFICIENTS CANNOT BE COMPARED ON TIME-CONSTANT VARIABLES OR ON VARIABLES THAT VARY ONLY ACROSS TIME.
THERE ARE NO MISSING VALUES (OF EITHER THE DEPENDENT OR INDEPENDENT VARIABLES)
IN COLLECTION SAMPLE DATA, MISSING VALUES MAY OCCUR IN EITHER THE DEPENDENT VARIABLE OR THE EXPLANATORY VARIABLES. THE EFFECTS OF THE OCCURRENCE OF MISSING VALUES MAY BE MILD OR SEVERE. ESSENTIAL FEATURES OF MISSING DATA ANALYSIS IS WHETHER THE MISSING-VALUE MECHANISM DEPENDS ON THE DEPENDENT VARIABLE, ON OBSERVED EXPLANATORY VARIABLES, OR ON UNOBSERVED VARIABLES. MUCH RESEARCH HAS BEEN DONE ON THIS TOPIC, AND IT IS WELL UNDERSTOOD.
SINCE THIS TOPIC IS BROAD, IT IS COVERED IN A SEPARATE PRESENTATION. (THE MATERIAL ON TIME-INVARIANT UNOBSERVED VARIABLES IN PANEL-DATA MODELS PRESENTED ABOVE COULD HAVE BEEN INCLUDE IN THAT PRESENTATION, RATHER THAN IN SUMMARY FORM HERE.)
TWO STANDARD REFERENCES ON MISSING DATA ARE THE FOLLOWING:
Little, Roderick J. A., and Donald R. Rubin, Statistical Analysis with Missing Data, 2nd ed., Wiley, 2002
Ho, Daniel, Kosuke Imai, Gary King, and Elizabeth Stuart. 2007. “Matching as Nonparametric Preprocessing for Reducing Model Dependence in Parametric Causal Inference.” Political Analysis, 15, Pp. 199–236. (Available from Internet website https://gking.harvard.edu/files/matchp.pdf .)
ASSUMPTIONS MAY BE MADE ABOUT THE DISTRIBUTION OF THE MODEL ERROR TERMS, SUCH AS NORMALITY
IF DISTRIBUTION-FREE METHODS SUCH AS THE METHOD OF MOMENTS OR LEAST-SQUARES ARE USED, IT IS NOT NECESSARY TO MAKE ASSUMPTIONS ABOUT THE PROBABILITY DISTRIBUTION OF THE MODEL ERROR TERMS, SUCH AS NORMALITY. IN THESE CASES, THE LAW OF LARGE NUMBERS AND CENTRAL LIMIT THEOREM WILL BE USED TO MAKE PROBABILITY STATEMENTS ABOUT ESTIMATES. IN SOME MODELS, DISTRIBUTIONAL ASSUMPTIONS ARE MADE. THE EFFECTS OF DEPARTURES FROM THE DISTRIBUTIONAL ASSUMPTION MAY BE MILD OR SEVERE. FOR EXAMPLE, IN THE CASE OF A HECKMAN TWO-STAGE ESTIMATOR OF SELECTION EFFECTS (UNOBSERVED VARIABLES), A NORMAL DISTRIBUTION IS ASSUMED. IT IS KNOWN THAT IF THE UNDERLYING DISTRIBUTION DEPARTS FROM NORMAL THEN SEVERE ERRORS IN ESTIMATION MAY OCCUR.
ANALYSIS OF VARIANCE.
IT IS CUSTOMARY TO SUMMARIZE THE RESULTS OF A REGRESSION ANALYSIS IN A TABLE, CALLED AN ANALYSIS OF VARIANCE TABLE. THIS TABLE SHOWS THE PROPORTION OF THE VARIANCE THAT IS ASSOCIATED WITH DIFFERENT VARIABLES OR SETS OF VARIABLES IN A MODEL. THIS IS INVARIABLY DONE FOR MODELS INVOLVING RANDOM EXPLANATORY VARIABLES, BUT IT IS OFTEN DONE FOR ALL MODELS. THE RESULTS ARE EASIER TO INTERPRET WHEN EXPLANATORY VARIABLES ARE UNCORRELATED (ORTHOGONAL), AS IN THE CASE OF AN EXPERIMENTAL DESIGN.
THE METHOD OF LEAST SQUARES; RELATIONSHIP TO MLE
THE PRECEDING EXAMPLE IS AN ILLUSTRATION OF THE ESTIMATION METHOD OF MAXIMUM LIKELIHOOD. THE ESSENTIAL ASPECT OF THE METHOD IS THAT IT REQUIRES SPECIFICATION OF THE LIKELIHOOD FUNCTION, THAT IS, THE PROBABILITY DISTRIBUTION FUNCTION OF THE SAMPLE. NOTE THAT IN THIS EXAMPLE, THE MAXIMIZATION OF THE LIKELIHOOD FUNCTION REDUCES TO THE PROBLEM OF MINIMIZING THE SUM OF SQUARES OF THE MODEL RESIDUALS (THE DIFFERENCES BETWEEN THE OBSERVED VALUES AND THE MODEL-SPECIFIED VALUES). THE PROCEDURE OF ESTIMATING MODEL PARAMETERS TO MINIMIZE THE SQUARED MODEL RESIDUALS (OR "DEVIATIONS") WAS DEVELOPED BY GAUSS (AND OTHERS) IN THE 1800s, LONG BEFORE THE METHOD OF MAXIMUM LIKELIHOOD WAS INTRODUCED. IT IS CALLED "GAUSS'S METHOD" OR THE "METHOD OF LEAST SQUARES." IT IS A PROCEDURE FOR DETERMINING ESTIMATES THAT MAKES NO REFERENCE TO ANY PROBABILITY DISTRIBUTION. IT SIMPLY FINDS THE LINE FOR WHICH THE SUM OF THE SQUARED DEVIATIONS OF THE OBSERVED VALUES FROM THE LINE IS A MINIMUM.
IN THE CASE IN WHICH THE MODEL RESIDUALS ARE NORMALLY DISTRIBUTED, THE MAXIMUM LIKELIHOOD METHOD AND THE METHOD OF LEAST SQUARES PRODUCE THE SAME ESTIMATES. THIS DOES NOT NECESSARILY HOLD FOR OTHER DISTRIBUTIONS. USING THE METHOD OF MAXIMUM LIKELIHOOD, IT IS POSSIBLE TO MAKE PROBABILITY STATEMENTS ABOUT THE ESTIMATES (SUCH AS CONFIDENCE INTERVALS). WITH THE METHOD OF LEAST SQUARES, NO DISTRIBUTION IS SPECIFIED, AND THIS IS NOT POSSIBLE.
IN THE PRECEDING EXAMPLE, IT WAS POSSIBLE TO DETERMINE THE MAXIMUM OF THE LIKELIHOOD FUNCTION ANALYTICALLY. WHILE THIS IS POSSIBLE IN MANY SIMPLE APPLICATIONS, IT IS NOT, IN GENERAL, POSSIBLE, AND NUMERICAL METHODS ARE USED TO DETERMINE THE MAXIMUM LIKELIHOOD ESTIMATOR.
LOGISTIC REGRESSION
THE LINEAR REGRESSION MODEL DESCRIBED ABOVE IS SUITABLE FOR SITUATIONS IN WHICH THE DEPENDENT VARIABLE (Y) IS CONTINUOUS AND THE DISTRIBUTION OF THE MODEL ERROR TERMS REASONABLY DESCRIBED BY A NORMAL DISTRIBUTION. THE EXPLANATORY VARIABLES (Xs) MAY BE CONTINUOUS OR DISCRETE. FOR SITUATIONS IN WHICH Y IS DISCRETE, THE NORMAL LIKELIHOOD FUNCTION IS NOT APPROPRIATE. THIS SECTION WILL DISCUSS A MODEL THAT IS APPROPRIATE FOR A BINARY (0-1) RANDOM VARIABLE.
WE CONSIDER THE SITUATION IN WHICH THE DEPENDENT VARIABLE IS BINARY, E.G., TAKES ON THE VALUES 0 AND 1. IN THIS CASE, WE SHALL ASSUME THAT THE DISTRIBUTION OF THE Ys IS BERNOULLI:
Yi|Xi=xi ~ Bernoulli(pi).
FOR THIS MODEL, EACH OF THE OBSERVATIONS IS BERNOULLI WITH PARAMETER pi. THE pi DEPEND ON EXPLANATORY VARIABLES (Xs), JUST AS Y DEPENDED ON THEM IN THE LINEAR REGRESSION MODEL.
THE ISSUE TO ADDRESS HERE IS WHAT MODEL TO USE TO DESCRIBE THE pi AS A FUNCTION OF PARAMETERS. WHAT IS NEEDED IS A MODEL IN WHICH THE VALUE OF pi IS CONSTRAINED TO THE INTERVAL (0,1). THERE ARE A NUMBER OF CANDIDATE MODELS THAT COULD BE CONSIDERED, BUT THE MOST WIDELY USED ONE IS BASED ON THE LOGISTIC FUNCTION, ex/(1+ex) (HENCE THE NAME "LOGISTIC REGRESSION"). WITH THIS APPROACH, THE MODEL USED TO REPRESENT pi AS A FUNCTION OF k PARAMETERS IS:
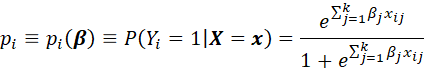
OR
![]()
WHERE
![]()
FOR EACH OBSERVATION THE PROBABILITY FUNCTION IS
![]()
SO THAT THE LIKELIHOOD FUNCTION FOR THE SAMPLE IS
![]()
THE PROBLEM IS TO DETERMINE THE VALUE OF β = (β1,...,βk) THAT MAXIMIZES THIS EXPRESSION. UNLIKE THE CASE OF THE LINEAR REGRESSION MODEL CONSIDERED ABOVE, THIS EXPRESSION IS TOO COMPLEX TO USE THE TECHNIQUE OF SETTING THE DERIVATIVES WITH RESPECT TO THE βi EQUAL TO ZERO. INSTEAD, NUMERICAL METHODS MUST BE USED. WASSERMAN DESCRIBES AN ALGORITHM FOR DETERMINING THE VALUES OF THE βi.
THE PRECEDING EXAMPLE OF A LOGISTIC REGRESSION IS SIMPLY ONE WAY IN WHICH THE GENERAL LINEAR MODEL MAY BE EXTENDED. IN ITS BASIC FORM, THE ERROR TERMS OF THE GENERAL LINEAR MODEL ARE USUALLY ASSUMED TO BE NORMALLY DISTRIBUTED. BY MEANS OF A SUITABLE TRANSFORMATION, SUCH AS THE LOGISTIC TRANSFORMATION SHOWN ABOVE, THE GLM MODEL CAN BE USED TO DESCRIBE A WIDE RANGE OF PHENOMENA, SUCH AS A BINARY DEPENDENT VARIABLE IN THE LOGISTIC REGRESSION MODEL. THE TRANSFORMATION USED TO CONVERT THE MEAN OF THE OBSERVED RANDOM VARIABLE TO ONE FOR WHICH THE GLM IS SUITABLE IS CALLED THE LINK FUNCTION. A TABLE OF OTHER LINK FUNCTIONS IS PRESENTED BELOW.
THIS EXTENSION OF THE GENERAL LINEAR MODEL, INVOLVING A TRANSFORMATION OF THE PARAMETER, IS CALLED A GENERALIZED LINEAR MODEL. SUCH TRANSFORMATIONS ARE AVAILABLE FOR ALL MEMBERS OF THE EXPONENTIAL FAMILY OF DISTRIBUTIONS.
THE LINK FUNCTION IS THE FUNCTION THAT SHOWS THE RELATIONSHIP η = g(μ) OF THE LINEAR FUNCTION η = Xβ OF THE GLM TO THE MEAN μ OF THE DISTRIBUTION. FOR EXAMPLE, IN THE LOGISTIC REGRESSION EXAMPLE GIVEN EARLIER, THE LINK FUNCTION IS
η = g(μ) = ln (μ/(1 – μ)).
(IN THE NOTATION USED EARLIER, THIS WOULD BE
logit (p) = ln (p/(1-p)).)
THE FOLLOWING TABLE IS FROM HILBE AND ROBINSON (PP. 102-103) AND HARDIN AND HILBE (PP. 7-10).
|
GLM Link and Inverse Link Functions |
||
|
Link Name |
Link Function η = g(μ) |
Inverse Link μ = g-1(μ) |
|
Complementary log-log |
ln{-ln(1-μ)} |
1 – exp{-exp(η)} |
|
Identity |
μ |
η |
|
Inverse square |
1/μ2 |
1/√η |
|
Log |
ln(μ) |
exp(η) |
|
Log-log |
-ln{-ln(μ)) |
exp{-exp(-η} |
|
Logit |
ln(μ/(1-μ)) |
eη/(1+eη) |
|
Negative binomial (α) |
ln(αμ/(1+αμ)) |
1/[α(exp(-η)-1)] |
|
Probit |
Φ-1(μ) |
Φ(η) |
|
Reciprocal |
1/ |
1/η |
NOTE THAT THERE IS SOME CONFUSION ABOUT NAMING OF LINK FUNCTIONS. SOME AUTHORS USE THE NAME OF THE LINK FUNCTION GIVEN IN THE PRECEDING TABLE, WHEREAS OTHERS USE THE NAME OF THE INVERSE FUNCTION. SINCE THE LINK FUNCTION IS THE FUNCTION THAT TRANSFORMS THE EXPECTED VALUE μ TO THE LINEAR PREDICTOR Xβ, THE NAMES USED ABOVE ARE MORE APPROPRIATE.
|
Power Links |
||
|
Power |
Link Name |
Model Canonical Link |
|
3 |
Cube |
None |
|
2 |
Square |
None |
|
1 |
Identity |
Gaussian |
|
0 |
Log |
Poisson |
|
0.5 |
Square Root |
None |
|
-1 |
Inverse |
Gamma |
|
-2 |
Inverse Quadratic |
Inverse Gaussian |
|
-3 |
Inverse Cubic |
None |
IT IS EMPHASIZED THAT THE TRANSFORMATION INVOLVED IN DEFINING GENERALIZED LINEAR MODELS IS A TRANSFORMATION OF THE PARAMETER, NOT OF THE RANDOM VARIABLE.
FOR EXAMPLE, A SIMPLE REGRESSION MODEL MAY PRODUCE NEGATIVE ESTIMATES FOR A VARIABLE THAT CAN ONLY TAKE ON POSITIVE VALUES. IN THIS CASE, USE OF AN EXPONENTIAL LINK FUNCTION MAY BE APPROPRIATE.
WHEN MORE THAN ONE LINK FUNCTION MAY BE GENERALLY APPLICABLE (E.G., HAVE THE CORRECT DOMAIN), THEN CAREFUL CONSIDERATION SHOULD BE GIVEN TO THE EXACT NATURE OF THE TRANSFORMATION. FOR EXAMPLE, A PROBIT LINK FUNCTION MAY BE DESIRED IN ORDER TO USE A BIVARIATE NORMAL DISTRIBUTION TO REPRESENT CORRELATION BETWEEN THE ERROR TERMS OF THE SELECTION MODEL AND THE OUTCOME MODEL. THE LOGIT LINK FUNCTION IS SYMMETRIC IN P AND 1-P. IF THIS IS NOT APPROPRIATE, THEN A COMPLEMENTARY LOG-LOG LINK FUNCTION MAY BE MORE APPROPRIATE.
THE WIKIPEDIA ARTICLE ON GENERALIZED LINEAR MODELS PROVIDES A GOOD SUMMARY.
13. TRUNCATED, CENSORED, AND LATENT-VARIABLE MODELS
THE PROBLEM OF DETERMINING THE DISTRIBUTION OF A FUNCTION OF A PARAMETER WAS DISCUSSED EARLIER, AND ILLUSTRATED WITH A SIMPLE EXAMPLE. A PROBLEM THAT ARISES ON OCCASION IS THAT OF DETERMINING THE DISTRIBUTION OF A RANDOM VARIABLE THAT IS CENSORED OR TRUNCATED.
A TRUNCATED RANDOM VARIABLE IS ONE FOR WHICH OBSERVATIONS IN A CERTAIN RANGE VALUES ARE OMITTED.
A CENSORED RANDOM VARIABLE IS ONE FOR WHICH VALUES IN A CERTAIN RANGE ARE REPLACED BY A COMMON VALUE. FOR EXAMPLE, IN CODING SURVEY DATA, ALL SALARIES ABOVE $250,000 MAY BE REPLACED BY $250,000.
FOR THIS SECTION, WE SHALL ASSUME THAT THE RANDOM VARIABLE OF INTEREST IS CONTINUOUS, MORE SPECIFICALLY, NORMALLY DISTRIBUTED.
THE RESULTS PRESENTED HERE ARE FROM ECONOMETRIC ANALYSIS, 7th ED. BY WILLIAM H. GREENE (PRENTICE HALL / PEARSON, 2013).
TRUNCATED RANDOM VARIABLES
TRUNCATED RANDOM VARIABLE: IF f(x) IS THE PDF OF A CONTINUOUS RANDOM VARIABLE AND a IS A CONSTANT, THEN
![]()
THIS RESULT FOLLOWS DIRECTLY FROM THE DEFINITION OF CONDITIONAL PROBABILITY. THE TRUNCATED DENSITY IS PROPORTIONAL TO THE ORIGINAL DENSITY, REWEIGHTED TO SUM OR INTEGRATE TO ONE.
AN EXAMPLE OF A TRUNCATED DISTRIBUTION WOULD BE A RANDOM SAMPLE OF ALL INCOMES EXCEEDING $100,000 (WHERE THE ORIGINAL UNTRUNCATED DISTRIBUTION IS ALL INCOMES).
A RANDOM VARIABLE WHOSE DISTRIBUTION IS TRUNCATED IS CALLED A TRUNCATED RANDOM VARIABLE.
MOMENTS OF A TRUNCATED NORMAL DISTRIBUTION: IF x ~ N(μ,σ2) AND a IS A CONSTANT, THEN
E(x|truncation) = μ +σλ(α)
V(x|truncation) = σ2(1 – δ(σ))
WHERE
α = (a – μ)/σ, φ(α) IS THE STANDARD NORMAL DENSITY AND
λ(α) = φ(α)/(1 – Φ(α)) if truncation is x > a
λ(α) = -φ(α)/Φ(α) if truncation is x < a
AND
δ(α) = λ(α)( λ(α) – α).
ALSO, 0 < δ(α) < 1 FOR ALL VALUES OF α.
THE FUNCTION λ(α) IS CALLED THE INVERSE MILLS RATIO.
THE FUNCTION φ(α)/(1 – Φ(α)) IS CALLED THE HAZARD FUNCTION FOR THE STANDARD NORMAL DISTRIBUTION.
CENSORED RANDOM VARIABLES
A CENSORED DISTRIBUTION IS A MIXTURE OF A DISCRETE AND CONTINUOUS DISTRIBUTIONS. THE DISCRETE PART IS THE VALUE (OR VALUES) TO WHICH VALUES IN CERTAIN RANGES ARE SET.
IF y* ~ N(μ,σ2) AND y = a if y* ≤ a OR ELSE y = y*, THEN THE PROBABILITY FUNCTION OF y IS
P(y = a) = P(y* ≤ a) = Φ(a)
f(y) = Ф(y) for y ≥ a.
NOTE THAT, IN CONTRAST TO TRUNCATION, THE DENSITY ABOVE THE CENSORING POINT IS NOT RESCALED, BUT IS THE ORIGINAL DENSITY. THE PROBABILITY MASS FROM THE ORIGINAL DENSITY THAT FALLS BELOW THE TRUNCATION POINT IS AGGREGATED INTO A DISCRETE POINT.
THE TRUNCATED AND CENSORED MODELS DIFFER ONLY IN THAT IN THE TRUNCATED MODEL THE DISTRIBUTION OF INTEREST INCLUDES ONLY THE TRUNCATED OBSERVATIONS, WHEREAS IN THE CENSORED MODEL THE DISTRIBUTION OF INTEREST INCLUDES BOTH THE CENSORED AND UNCENSORED OBSERVATIONS. (SHOW GRAPH.)
MOMENTS OF A CENSORED NORMAL VARIATE: IF y* ~ N(μ,σ2) AND y = a if y* ≤ a OR ELSE y = y*, THEN
E(y) = Φa + (1 – Φ)(μ + σλ)
V(y) = σ2(1- Φ)[(1 - δ) + (α – λ)2Φ]
WHERE
Φ[(a – μ)/σ)] = Φ(α) = P(y* ≤ a) = Φ,
λ = Ф/(1 – Φ)
AND
δ = λ2 – λα.
INCIDENTAL TRUNCATION AND SAMPLE SELECTION
A MODEL THAT OCCURS FREQUENTLY IN IMPACT ANALYSIS OF SOCIAL AND ECONOMIC PROGRAMS IS A BIVARIATE ONE IN WHICH SAMPLE SELECTION IS DETERMINED BY ONE OF THE RANDOM VARIABLES AND OUTCOME IS DETERMINED BY THE SECOND RANDOM VARIABLE, RELATED TO THE FIRST. (IN THE PRECEDING SECTION, THE TRUNCATION WAS DELIBERATE, BASED ON THE VALUE OF THE RANDOM VARIABLE OF INTEREST. IN THIS SECTION, THE TRUNCATION IS NOT DELIBERATE (OR BASED ON THE RANDOM VARIABLE OF INTEREST) HENCE THE DESCRIPTOR "INCIDENTAL".)
THIS MODEL WILL BE DESCRIBED IN DETAIL IN ANOTHER PRESENTATION (ON CAUSAL ANALYSIS), AND IS SUMMARIZED HERE FOR A PARTICULAR CASE. THIS SPECIAL CASE WILL ASSUME THAT THE BIVARIATE DISTRIBUTION IS NORMAL. IN THIS CASE, THE DEPENDENCE BETWEEN THE TWO VARIATES IS CHARACTERIZED BY THE CORRELATION COEFFICIENT.
SUPPOSE THAT y AND z HAVE A NORMAL BIVARIATE DISTRIBUTION WITH CORRELATION ρ. WHAT IS OF INTEREST IS THE DISTRIBUTION OF y GIVEN THAT z EXCEEDS A PARTICULAR VALUE.
WE SHALL GENERALIZE THE PROBLEM SOMEWHAT BY ALLOWING THE MEAN OF THE DISTRIBUTION OF z and y TO BE DEFINED BY LINEAR FUNCTIONS OF PARAMETERS (I.E., LINEAR REGRESSION MODELS). IN THIS CASE, WE PROCEED AS FOLLOWS (PER GREENE).
THE SAMPLE SELECTION MODEL IS
zi* = wi' + ui
AND THE MODEL FOR THE OBSERVED OUTCOME IS
yi = xi' + ei.
THE SAMPLE SELECTION RULE IS THAT yi IS OBSERVED ONLY WHEN zi* IS GREATER THAN ZERO.
WE SHALL SHOW EXPRESSIONS FOR THE MEAN AND VARIANCE OF THE OBSERVED RANDOM VARIABLE (THE INCIDENTALLY TRUNCATED ONE). THE RESULTS ARE A GENERALIZATION FOR THE BIVARIATE CASE OF WHAT WAS PRESENTED ABOVE FOR A SINGLE RANDOM VARIABLE. THE DIFFERENCE IS THAT WE ARE DEALING NOW WITH A JOINT (BIVARIATE) DISTRIBUTION, NOT A UNIVARIATE ONE.
THE TRUNCATED JOINT DENITY OF y AND z IS
![]()
TO OBTAIN THE MARGINAL DENSITY OF y, WE AVERAGE OVER z, I.E., INTEGRATE THIS EXPRESSION WITH RESPECT TO z.
WE SHALL SIMPLY STATE EXPRESSIONS FOR THE MEAN AND VARIANCE OF y, AND THEN PRESENT DETAILS FOR THE MARGINAL DENSITY. SUBSTANTIAL DETAIL IS PRESENTED FOR THIS MODEL BECAUSE IT IS A STANDARD MODEL USED IN PROGRAM IMPACT ANALYSIS. (IT IS GENERALLY REFERRED TO AS A HECKMAN MODEL, AFTER THE MAN WHO POPULARIZED ITS USE (AND WON A NOBEL PRIZE IN ECONOMICS FOR THIS). IT IS ALSO CALLED A TYPE II TOBIT MODEL.)
MOMENTS OF AN INCIDENTALLY TRUNCATED BIVARIATE NORMAL DISTRIBUTION: IF y AND z HAVE A BIVARIATE NORMAL DISTRIBUTION WITH MEANS μy AND μz, STANDARD DEVIATIONS σy AND σz, AND CORRELATION ρ, THEN
E(y|z>a) = μy + ρ σyλ(αz)
AND
V(y|z>a) = σ2y(1 – ρ2δ(αz)
WHERE
α = (a – μz)/σz, λ(αz) = φ(αz)/(1 – Φ(αz)) AND δ(αz) = λ(αz)(λ(αz) – αz).
IF THE TRUNCATION IS z < a THEN λ(αz) = -φ(αz)/Φ(αz).
THE PRECEDING ARE THEORETICAL RESULTS. IN A PRACTICAL APPLICATION, WE WANT TO ESTIMATE THE PARAMETERS (THE MEANS, STANDARD DEVIATIONS AND CORRELATION COEFFICIENT). IN GENERAL, THE MEANS WILL DEPEND ON OTHER VARIABLES. THE STANDARD PROCEDURE IS TO REPRESENT THE MEANS OR FUNCTIONS OF THE MEANS AS FUNCTIONS OF A LINEAR COMBINATION OF PARAMETERS IN A MULTIPLE REGRESSION MODEL OR IN A GENERALIZED LINEAR MODEL.
THE FOLLOWING DETAILS ARE PRESENTED IN GREENE OP. CIT. (PP. 872-880) AND WOOLDRIDGE, ECONOMETRIC ANALYSIS OF CROSS SECTION AND PANEL DATA (THE MIT PRESS, 2ND ED. 2010 (PP. 802-808).
FOR WHAT FOLLOWS WE SHALL ASSUME THE FOLLOWING MODELS FOR z AND y.
THE MODEL ON WHICH SAMPLE SELECTION IS BASED IS
zi* = wi'γ + ui.
THE MODEL FOR THE OBSERVED OUTCOME IS
yi = xi'β + ei.
THE OUTCOME yi IS OBSERVED ONLY WHEN zi* IS GREATER THAN ZERO. (NOTE THAT THE CUTOFF POINT MAY BE ANY VALUE, AND THAT THE VARIANCE OF THE DISTRIBUTION OF z IS IRRELEVANT, SO IT IS ARBITRARILY SET EQUAL TO ONE.)
IN THIS EXAMPLE, THE MEAN OF z IS wi'γ AND THE MEAN OF y IS E(y) = xi'β. AS AN EXAMPLE OF A GENERALIZED LINEAR MODEL, wi'γ MIGHT BE THE MEAN OF logit(p) FOR THE PARAMETER p OF A BERNOULLI RANDOM VARIABLE (I.E., A LOGISTIC REGRESSION MODEL, WITH LINK FUNCTION logit(p) = log(p/(1 – p))) AND xi'β MIGHT BE THE MEAN OF log(y) (I.E., A LOG MODEL, WITH LINK FUNCTION log(μ)).
THE EXPECTED VALUE OF y GIVEN THAT IT IS OBSERVED IS
E(yi | yi is observed) = E(yi | zi*>0) = E(yi | ui > -wi'γ) = xi'β + E(ei | ui > -wi'γ) = xi'β + ρσeλi(αu) = xi'β = βλi(αu)
WHERE αu = -wi'γ/σu, λ(αu) = φ(wi'γ/σu)/Φ(wi'γ/σu), AND βλ = ρσe. HENCE WE MAY WRITE
yi | zi* > 0 = E(yi | zi* > 0) + vi = xi'β + βλλi(αu) + vi.
ESTIMATION OF PARAMETERS
THE KEY POINT TO OBSERVE HERE IS THAT ORDINARY-LEAST-SQUARES (OLS) ESTIMATES OF β WOULD BE BIASED BECAUSE OF THE OMITTED VARIABLE βλλi(αu). THE OLS ESTIMATE BASED ON x AND λ WOULD BE CONSISTENT INEFFICIENT BECAUSE THE VARIANCE OF vi IS NOT CONSTANT.
TO DERIVE THE MAXIMUM LIKELIHOOD ESTIMATES OF THE PARAMETERS, IT IS NECESSARY TO SPECIFY THE JOINT PROBABILITY DENSITY.
THE SELECTION MODEL IS
zi* = wi'γ + ui, zi = 1 if zi*>0, zi = 0 otherwise.
THE OUTCOME MODEL IS
yi = xi'β + ei, observed only if zi = 1.
THE JOINT DENSITY OF ui AND ei IS BIVARIATE NORMAL (0,0,1,σe,ρ).
WHAT IS OBSERVED IS THE VALUES OF z (0 OR 1) AND THE VALUE OF y IF z = 1. THE JOINT DENSITY OF z AND y IS OBTAINED AS FOLLOWS.
IF y IS NOT OBSERVED, THEN THE JOINT DENSITY IS:
P(y, z =0) = 1 – Φ(wi'γ).
IF y IS OBSERVED, THEN THE JOINT DENSITY IS (DROPPING THE i SUBSCRIPTS):
f(y, z = 1) = P(z = 1| y) f(y) = P(z* > 0 | y) f(y) = P(w'γ + u > 0| y = x'β + e) f(y) = P(u > -w'γ | y = x'β + e) f(y).
NOW, IF u AND e ARE DISTRIBUTED N(0,0,1,σe,ρ), THEN u | e IS DISTRIBUTED N* = N(eρ/σ,1-ρ2), AND z = u – eρ/σ IS DISTRIBUTED N(0, 1-ρ2), SO THE PRECEDING PROBABILITY IS EQUAL TO
PN*(z + eρ/σ > -w'γ | y = x'β + e) f(y) = PN*(z > -w'γ - (y - x'β) ρ/σ > 0) f(y) = Φ([w'γ + (y - x'β) ρ/σ]/(1-ρ2)-1/2) f(y).
NOW f(y) = φ[(y - x'β)/σe]/σe. COMBINING THE PRECEDING RESULTS GIVES THE FOLLOWING FOR THE JOINT DENSITY (ADDING BACK THE SUBSCRIPTS):
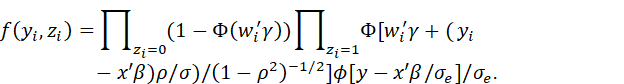
THE LOG-LIKELIHOOD FUNCTION IS HENCE
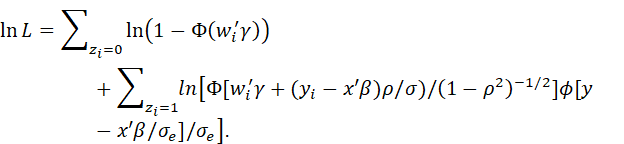
THE MAXIMUM LIKELIHOOD ESTIMATES OF THE MODEL PARAMETERS ARE OBTAINED BY MAXIMIZING THE PRECEDING EXPRESSION. THE EXPRESSION IS COMPLICATED, AND NUMERICAL METHODS ARE REQUIRED TO DETERMINE THE SOLUTION. WHEN THIS MODEL WAS FIRST INTRODUCED, NUMERICAL METHODS WERE NOT IN WIDE USE IN SOLVING MLE PROBLEMS, AND ANALYTICAL SOLUTIONS WERE FREQUENTLY SOUGHT, EVEN IF APPROXIMATE. HECKMAN PROPOSED A TWO-STEP PROCEDURE FOR OBTAINING A CONSISTENT ESTIMATES. THE TWO-STEP METHOD EXHIBITS SOME WEAKNESSES, AND IS NOT GENERALLY RECOMMENDED. DISCUSSION OF THESE PROBLEMS IS PRESENTED IN PP. 698-699 AND 805-806 OF WOOLDRIDGE OP. CIT.)
WOOLDRIDGE GIVES A SIMILAR EXPRESSION IN THE CASE IN WHICH A GENERALIZED LINEAR MODEL IS USED WITH LINK FUNCTION log(μ) (AN EXPONENTIAL TYPE II TOBIT MODEL). (PP. 697-699 OP. CIT.)
14. TREATMENT OF MISSING DATA; SMALL-AREA ESTIMATION; CAUSAL MODELS
MISSING DATA
MISSING DATA OCCUR IN MOST PRACTICAL APPLICATIONS OF STATISTICS. MISSING DATA OCCUR FOR A VARIETY OF REASONS, AND MANIFEST IN A VARIETY OF WAYS. MISSING DATA ARE PROBLEMATIC IN STATISTICS BECAUSE ITS PRESENCE INTRODUCES BIASES AND REDUCES THE PRECISION OF ESTIMATES. THERE ARE TWO BASIC CATEGORIES OF MISSING DATA: (1) MISSING OBSERVATIONS; AND (2) MISSING ITEMS FROM OBSERVATIONS (I.E., MISSING COMPONENTS FROM VECTOR-VALUED RANDOM VARIABLES).
THE SEMINAL BOOKS ON THE STATISTICAL TREATMENT OF MISSING DATA ARE STATISTICAL ANALYSIS WITH MISSING DATA, 2ND ED., BY RODERICK J. A. LITTLE AND DONALD B. RUBIN (WILEY, 2002) AND MULTIPLE IMPUTATION FOR NONRESPONSE IN SURVEYS BY DONALD B. RUBIN (WILEY, 1987). THESE BOOKS DESCRIBE METHODOLOGICALLY SOUND APPROACHES FOR HANDLING MISSING DATA, IN SITUATIONS IN WHICH A PROBABILISTIC MODEL CAN BE SPECIFIED AND ESTIMATED TO DESCRIBE THE MISSING DATA EVENT.
PRIOR TO THE PUBLICATION OF RUBIN'S BOOKS, A VARIETY OF AD-HOC PROCEDURES WERE USED TO HANDLE MISSING DATA. THESE METHODS WERE NOT BASED ON FORMAL PROBABILITY MODELS OF NONRESPONSE, BUT ON THE APPLICATION OF PROCEDURES THAT APPEARED TO REDUCE THE BIAS AND LOSS OF PRECISION FROM MISSING DATA, BASED ON JUDGMENT. THE PROBLEM WITH THESE APPROACHES IS THAT ALTHOUGH THEY MAY REDUCE BIAS AND INCREASE THE PRECISION OF ESTIMATES, LACKING A PROBABILITY MODEL FOR MISSINGNESS, THERE IS NO OBJECTIVE WAY TO ASSESS THEIR WORTH FROM A STATISTICAL POINT OF VIEW.
THE MODERN METHOD OF HANDLING MISSING DATA IS TO SPECIFY A PROBABILISTIC MODEL FOR MISSINGNESS AND COMBINE IT WITH THE PROBABILISTIC MODEL FOR THE OUTCOME VARIABLES OF INTEREST, AND TO PERFORM MAXIMUM LIKELIHOOD ESTIMATION OF THE COMPLETE LIKELIHOOD FUNCTION, INCLUDING BOTH MODELS. BECAUSE THE LIKELIHOOD FUNCTION IS COMPLICATED, NUMERICAL METHODS ARE USED TO CONSTRUC THE ESTIMATES.
SINCE AN ENTIRE PRESENTATION IS ALLOCATED TO THE ISSUE OF STATISTICAL ANALYSIS WITH MISSING DATA, NOTHING MORE WILL BE SAID ABOUT THAT TOPIC HERE. THE SAID PRESENTATION DESCRIBES THE VARIOUS AD-HOC METHODS AND THE LIKELIHOOD-BASED APPROACH.
SMALL-AREA ESTIMATION
SMALL-AREA ESTIMATION IS CONCERNED WITH THE PROBLEM OF CONSTRUCTING ESTIMATES FOR SUBPOPULATIONS (DOMAINS OF STUDY) FOR WHICH TOO FEW OBSERVATIONS ARE AVAILABLE TO ENABLE CONSTRUCTION OF DIRECT DESIGN-BASED ESTIMATES BASED ON THE NORMALLY AVAILABLE DATA, SUCH AS THOSE FROM A ROUTINE SAMPLE SURVEY. THE PROBLEM IS ADDRESSED THROUGH THE USE OF INCORPORATION OF AUXILIARY DATA FROM ADDITIONAL SOURCES AND THE USE OF MODELS THAT DESCRIBE THE RELATIONSHIP OF THE CHARACTERISTICS OF THE SUBPOPULATION OF INTEREST TO OTHER DATA OR INFORMATION. THE RESULTING ESTIMATES ARE CALLED "MODEL-BASED" OR "MODEL-ASSISTED" OR "INDIRECT" ESTIMATES.
A VARIETY OF STATISTICAL TECHNIQUES ARE EMPLOYED IN THE FIELD OF SMALL-AREA ESTIMATION, INCLUDING WEIGHTING AND CALIBRATION PROCEDURES, GENERALIZED REGRESSION ESTIMATES, DEMOGRAPHIC TECHNIQUES AND BAYESIAN METHODS.
BECAUSE THE MODELS USED IN SMALL-AREA ESTIMATION ARE COMPLICATED, IT IS GENERALLY NECESSARY TO USE NUMERICAL METHODS TO CONSTRUCT DESIRED ESTIMATES.
A STANDARD REFERENCE ON THE SUBJECT OF SMALL-AREA ESTIMATION IS SMALL-AREA ESTIMATION BY J. N. K. RAO (WILEY, 2003).
SINCE AN ENTIRE PRESENTATION IS DEVOTED TO THIS TOPIC, NO FURTHER DISCUSSION IS PRESENTED HERE.
CAUSAL MODELS AND CAUSAL ANALYSIS
MOST OF THE FIELD OF STATISTICS DEALS WITH ASSOCIATIONAL ANALYSIS, NOT WITH CAUSAL ANALYSIS. THE WORD "CAUSAL" APPEARS IN VERY FEW STATISTICS TEXTS. IN ORDER TO MAKE CAUSAL INFERENCES, A CAUSAL MODEL MUST BE SPECIFIED. STATISTICAL METHODS CAN THEN BE USED TO MAKE ESTIMATES OF CAUSAL EFFECTS, IN ACCORDANCE WITH THE CAUSAL MODEL.
THERE ARE TWO BASIC ASPECTS OF CAUSAL INFERENCE: (1) SPECIFICATION OF A CAUSAL MODEL; AND (2) SPECIFICATION OF STATISTICAL METHODS FOR ESTIMATING CAUSAL EFFECTS FROM DATA.
IN CAUSAL INFERENCE, IT IS ESSENTIAL FOR MODEL SPECIFICATIONS TO BE CORRECT, TAKING INTO ACCOUNT BOTH THE CAUSAL RELATIONSHIPS INVOLVED IN AN APPLICATION AND WHATEVER SAMPLE SELECTION PHENOMENA MAY BE PRESENT. THE SAMPLE SELECTION MODELS ARE IN EFFECT MISSING DATA MODELS, AND THEY THEREFORE GENERALLY REQUIRE THE USE OF NUMERICAL METHODS FOR ESTIMATION (BASED ON THE METHOD OF MAXIMUM LIKELIHOOD OR BAYESIAN ANALYSIS).
TEXTS DEALING WITH THE SUBJECT OF CAUSAL MODELING AND ANALYSIS ARE THE FOLLOWING:
PEARL, JUDEA, CAUSALITY: MODELS, REASONING AND INFERENCE, 2ND ED., CAMBRIDGE UNIVERSITY PRESS, 2009.
MORGAN, STEPHEN L. AND CHRISTOPHER WINSHIP, COUNTERFACTUALS AND CAUSAL INFERENCE: METHODS AND PRINCIPLES FOR SOCIAL RESEARCH, CAMBRIDGE UNIVERSITY PRESS, 2007.
ANGRIST, JOSHUA D. AND JÖRN-STEFFEN PISCHKE, MOSTLY HARMLESS ECONOMETRICS: AN EMPIRICIST'S COMPANION, PRINCETON UNIVERSITY PRESS, 2009
LEE, MYOUNG-JAE, MICRO-ECONOMETRICS FOR POLICY, PROGRAM AND TREATMENT EFFECTS, OXFORD UNIVERSITY PRESS, 2005
SINCE AN ENTIRE PRESENTATION ADDRESSES THE SUBJECT OF CAUSAL ANALYSIS AND MODELING, NO FURTHER DETAILS ARE PRESENTED HERE.
15. NUMERICAL METHODS PART 2 (COMPLEX MODELS)
AN EARLIER SECTION DESCRIBED THREE NUMERICAL METHODS: (1) THE NEWTON-RAPHSON METHOD; (2) THE ITERATIVE REWEIGHTED LEAST SQUARES METHOD; (3) THE ITERATIVE PROPORTIONAL FITTING PROCEDURE OF DEMING AND STEPHAN; AND (4) THE BOOTSTRAP METHOD FOR ESTIMATING VARIANCES AND OTHER DISTRIBUTIONAL CHARACTERISTICS. THE FIRST THREE OF THESE ARE OPTIMIZATION METHODS AND THE LAST IS A SIMULATION METHOD.
THE BOOTSTRAP METHOD IS GENERALLY APPLICABLE TO ANY SITUATION. THE DEMING-STEPHAN ITERATIVE PROPORTIONAL FITTING PROCEDURE IS A SPECIALIZED METHOD FOR FINDING MAXIMUM LIKELIHOOD ESTIMATES FOR CONTINGENCY TABLES. THE ITERATIVE REWEIGHTED LEAST SQUARES IS APPROPRIATE FOR USE IN THE SPECIAL APPLICATION OF A GENERALIZED LINEAR MODEL FOR THE EXPONENTIAL FAMILY OF DISTRIBUTIONS. THE NEWTON-RAPHSON METHOD WORKS BEST IN SITUATIONS INVOLVING A SMALL NUMBER OF PARAMETERS AND A RELATIVELY WELL-BEHAVED LIKELIHOOD FUNCTION (E.G., ONE WITHOUT SEVERAL LOCAL MAXIMA).
THE NUMERICAL METHODS PRESENTED EARLIER ARE FOR RELATIVELY SIMPLE SITUATIONS, SUCH AS A SMALL NUMBER OF PARAMETERS. ALSO, THE NEWTON-RAPHSON METHOD REQUIRES THAT THE FIRST AND SECOND DERIVATIVES OF THE PROBABILITY DENSITY FUNCTION BE AVAILABLE. FOR MORE COMPLEX SITUATIONS (E.G., NO PARTIAL DERIVATIVES, LARGE NUMBER OF PARAMETERS), OTHER NUMERICAL METHODS ARE AVAILABLE. FOUR OF THEM WILL NOW BE DESCRIBED. THEY ARE DESCRIBED IN SUMMARY DETAIL, AND NOT COVERED IN ADDITIONAL DETAIL IN THIS SERIES OF PRESENTATIONS.
THE ALGORITHMS DESCRIBED HERE ADDRESS BOTH THE PROBLEMS OF ITEM MISSINGNESS AND OBSERVATION MISSINGNESS.
THE EXPECTATION-MAXIMIZATION (EM) ALGORITHM
THE EXPECTATION-MAXIMIZATION (EM) ALGORITHM IS A GENERAL NUMERICAL METHOD FOR DETERMINING MAXIMUM LIKELIHOOD VALUES FOR COMPLEX LIKELIHOOD FUNCTIONS WHERE THE MAXIMIZING VALUES CANNOT BE FOUND DIRECTLY. IT IS USED PARTICULARLY IN APPLICATIONS INVOLVING MISSING DATA. THE METHOD IS DETERMINISTIC (I.E., NOT A SIMULATION (MONTE CARLO) METHOD). IT IS DESCRIBED IN MANY PLACES, SUCH AS LITTLE AND RUBIN OP. CIT. OR HILBE AND ROBINSON OP. CIT.
THE METHOD CAN BE APPLIED TO SITUATIONS IN WHICH DATA ARE MISSING FOR SOME VARIABLES, OR WHERE LATENT (HIDDEN, MISSING) VARIABLES OR PARAMETERS ARE PRESENT.
THE METHOD CONSISTS OF REPEATING THE FOLLOWING STEPS:
1. FIRST EXPECTATION STEP: USING OBSERVED DATA, CALCULATE THE MAXIMUM LIKELIHOOD ESTIMATES OF THE MISSING DATA AND ANY MISSING MODEL PARAMETERS. THIS STEP PRODUCES THE CONDITIONAL EXPECTATION OF THE MISSING DATA OR MISSING PARAMETERS, GIVEN THE OBSERVED DATA AND PARAMETERS.
2. FIRST MAXIMIZATION STEP: USE THE CONDITIONAL EXPECTATIONS OF STEP 1 AS VALUES FOR THE MISSING DATA AND MISSING PARAMETERS IN THE LIKELIHOOD FUNCTION TO CALCULATE VALUES OF THE MISSING DATA AND MISSING PARAMETERS.
3. SECOND (AND LATER) EXPECTATION STEP: USING THE OBSERVED DATA AND ESTIMATED VALUES, CALCULATE THE MAXIMUM LIKELIHOOD ESTIMATES OF THE ORIGINAL MISSING DATA AND ORIGINAL MISSING PARAMETERS.
4. USE THE CONDITIONAL EXPECTATIONS FROM STEP 3, CALCULATE NEW VALUES OF THE ORIGINAL MISSING DATA AND ORIGINAL MISSING PARAMETERS.
STEPS 3 AND 4 ARE REPEATED UNTIL CONVERGENCE.
ALTHOUGH THE METHOD EXPLICITLY CALCULATES INDIVIDUAL MISSING VALUES, THE POINT IS TO CALCULATE THE VALUES OF SUFFICIENT STATISTICS ON WHICH THE LIKELIHOOD FUNCTION DEPENDS (USING THOSE INDIVIDUAL VALUES).
SIMULATION METHODS
THE FOLLOWING GENERAL METHODS ARE USED FOR NUMERICAL APPROXIMATION OF MULTIDIMENSIONAL INTEGRALS. THEY ARE USEFUL FOR SITUATIONS INVOLVING A LARGE NUMBER OF PARAMETERS, FOR EXAMPLE, IN CALCULATIONS ASSOCIATED WITH LARGE HIERARCHICAL BAYES MODELS, THAT MAY REQUIRE INTEGRATION OVER HUNDREDS OR THOUSANDS OF UNKNOWN PARAMETERS.
MARKOV CHAIN MONTE CARLO
THE MARKOV CHAIN MONTE CARLO (MCMC) METHOD IS A GENERAL METHOD THAT INCLUDES THE NEXT TWO METHODS TO BE DESCRIBED, THE METROPOLIS-HASTINGS ALGORITHM AND GIBBS SAMPLER.
THE MCMC METHOD IS SIMILAR TO THE TRADITIONAL MONTE CARLO APPROACH TO NUMERICAL INTEGRATION EXCEPT FOR THE FACT THAT IN TRADITIONAL MONTE CARLO SIMULATION SUCCESSIVE SAMPLES ARE INDEPENDENT. IN MCMC, THE LOCATION OF THE NEXT SAMPLE DEPENDS ON THE OUTCOME OF THE PRECEDING ONE. THE MCMC WORKS BY INITIATING AN ENSEMBLE OF "WALKERS" THAT MOVE AROUND RANDOMLY. THE VALUE OF THE INTEGRAND IS CALCULATED AND A DECISION IS MADE WHETHER TO CONTINUE SAMPLING CLOSE TO THAT POINT OR FARTHER AWAY.
THE METHOD MAY BE USED TO APPROXIMATE A HISTOGRAM OR TO CALCULATE AN INTEGRAL, SUCH AS AN EXPECTED VALUE.
THE EQUILIBRIUM DISTRIBUTION OF THE MARKOV CHAIN IS THE DESIRED DISTRIBUTION. THE STATE OF THE CHAIN AFTER A NUMBER OF STEPS IS A SAMPLE FROM THE DESIRED DISTRIBUTION.
METROPOLIS-HASTINGS ALGORITHM
THE METROPOLIS-HASTINGS ALGORITHM IS A MARKOV-CHAIN MONTE CARLO METHOD. IT WORKS AS FOLLOWS (FOLLOWING WASSERMAN).
THE PROBLEM IS TO EVALUATE THE INTEGRAL
I = ∫h(x) f(x)dx.
THE APPROACH IS TO CONSTRUCT A MARKOV CHAIN X1, X2,... WHOSE STATIONARY DISTRIBUTION IS f. BY THE LAW OF LARGE NUMBERS FOR MARKOV CHAINS, THE SUM
![]()
LET q(y|x) BE AN ARBITRARY DISTRIBUTION THAT IS EASY TO SAMPLE FROM. IT IS CALLED THE PROPOSAL DISTRIBUTION. SELECT X0 ARBITRARILY. THE SEQUENCE X0, X1,...Xi IS GENERATED AS FOLLOWS. SUPPOSE THAT Xi HAS BEEN GENERATED.
1. GENERATE A PROPOSAL OR CANDIDATE VALUE Y ~ q(y | Xi).
2. EVALUATE r ≡ r(Xi, Y) WHERE
![]()
3. SET
![]()
GIBBS SAMPLER
THE GIBBS SAMPLER IS AN MCMC DESIGNED SO SAMPLE FROM A COMPLEX MULTIVARIATE DISTRIBUTION. THE ESSENCE OF THE ALGORITHM IS DESCRIBED HERE, FOLLOWING LITTLE AND RUBIN OP. CIT.
LET p(x1, x2,...,xp) BE A JOINT MULTIVARIATE DISTRIBUTION OF RANDOM VARIABLES X1,X2,...,Xp. SUPPOSE THAT IT IS DIFFICULT TO SAMPLE THE JOINT (VECTOR) RV DIRECTLY, BUT THAT IT IS EASY TO SAMPLE FROM THE CONDITIONAL DISTRIBUTION FROM ANY ONE OF THE RVs. SUPPOSE THAT WE HAVE INITIAL VALUES x1(0),...,xp(0). THEN, GIVEN THE VALUES OF x1(t),...,xp(t), THE VALUES FOR THE NEXT ITERATION ARE PROVIDED BY SAMPLING FROM EACH OF THE FOLLOWING CONDITIONAL DISTRIBUTIONS:
x1(t+1) ~ p(x1 | x2(t), x3(t),...,xp(t)
x2(t+1) ~ p(x2 | x1(t+1), x3(t),...,xp(t)
x3(t+1) ~ p(x3 | x1(t+1), x2(t+1),x4(t),...,xp(t)
...
xp(t+1) ~ p(xp | x1(t+1), x2(t+1),...,xp-1(t+1).
IT CAN BE PROVED THAT UNDER GENERAL CONDITIONS THE DISTRIBUTION OF THE SEQUENCE x1(t),...,xp(t) CONVERGES TO THE JOINT DISTRIBUTION OF X1,...,Xp.
16. TESTS OF GOODNESS OF FIT, MODEL ADEQUACY, VALIDITY AND QUALITY
WHENEVER A MODEL IS FITTED TO DATA, THE ISSUE ARISES OF WHETHER IT IS A VALID REPRESENTATION OF THE PHYSICAL PROCESS UNDER STUDY. THE ADEQUACY OF A MODEL IS TESTED IN A VARIETY OF WAYS, BY TESTING HYPOTHESES ABOUT SPECIFIC MODEL ASSUMPTIONS, OVERALL GOODNESS OF FIT TO THE DATA, AND MODEL PARSIMONY. THIS SECTION IDENTIFIES AND SUMMARIZES A NUMBER OF MEASURES OF GOODNESS OF FIT AND MODEL ADEQUACY.
TESTS OF GOODNESS OF FIT
TESTS OF GOODNESS OF FIT ASSESS HOW CLOSE THE OBSERVATIONS ARE TO THE VALUES PREDICTED BY THE MODEL. GOODNESS OF FIT TESTS INCLUDE THE FOLLOWING:
1. TESTING WHETHER MODEL RESIDUALS (ERROR TERMS) FOLLOW A NORMAL DISTRIBUTION: THE KOLMOGOROV-SMIRNOV TEST.
2. TESTING WHETHER MODEL RESIDUALS ARE UNCORRELATED ("WHITE NOISE"): THE DURBIN-WATSON TEST.
3. TESTING WHETHER MODEL EFFECTS ARE FIXED OR RANDOM: THE HAUSMAN TEST.
4. TESTING WHETHER A SAMPLE IS FROM A SPECIFIED DISTRIBUTION: THE KOLMOGOROV-SMIRNOV TEST.
5. TESTING WHETHER A SEQUENCE OF NUMBERS IS CONSISTENT WITH HAVING BEEN SELECTED AT RANDOM: THE RUNS TEST FOR RANDOMNESS; THE CHI-SQUARE TEST.
6. TESTING WHETHER TWO SAMPLES ARE DRAWN FROM THE SAME DISTRIBUTION: THE KOLMOGOROV-SMIRNOV TWO-SAMPLE TEST.
7. TESTING WHETHER TWO RANDOM VARIABLES ARE INDEPENDENT: THE CHI-SQUARE TEST.
8. TESTING FOR OUTLIERS AND EXTREME VALUES: GRUBB'S TEST (FOR NORMAL DISTRIBUTION); DIXON'S Q TEST (FOR NORMAL DISTRIBUTION); COCHRAN'S C TEST (FOR NORMAL DISTRIBUTION).
9. TESTING FOR THE SIGNIFICANCE OF A VARIABLE OR VARIABLES IN A MODEL (E.G., A REGRESSION MODEL; FIXED EFFECTS AND RANDOM EFFECTS): t TEST; F TEST; LIKELIHOOD RATIO TEST.
GENERAL TESTS OF MODEL QUALITY
THE TESTS DESCRIBED ABOVE ARE TESTS OF SPECIFIC MODEL FEATURES OR ASSUMPTIONS. THERE MAY BE SEVERAL CANDIDATE MODELS THAT APPEAR TO FIT THE DATA ADEQUATELY, AND ARE VALID REPRESENTATIONS OF A PROCESS. AN ISSUE TO ADDRESS IS HOW TO SELECT A PREFERRED MODEL FROM SEVERAL THAT APPEAR TO BE GENERALLY ADEQUATE.
HAVING A CLOSE FIT OF A MODEL TO DATA IS GENERALLY DESRIABLE, BUT, BY ITSELF, IS NOT A SUFFICIENT CRITERION FOR MODEL QUALITY. THE FIT OF A MODEL MAY BE IMPROVED BY ADDING PARAMETERS TO THE MODEL. MODEL PARSIMONY IS IMPORTANT, I.E., IF TWO MODELS BOTH APPEAR TO BE VALID REPRESENTATIONS OF REALITY, THEN THE MODEL HAVING THE SMALLER NUMBER OF PARAMETERS IS GENERALLY PREFERRED. (THIS IS ALSO REFERRED TO AS THE PRINCIPLE OF "OCCAM'S RAZOR").
THE MOST GENERALLY ACCEPTED MEASURE OF MODEL QUALITY IS THE AKAIKE INFORMATION CRITERION. IT IS USED TO COMPARE THE RELATIVE OVERALL QUALITY OF ALTERNATIVE MODELS.
THE AKAIKE INFORMATION CRITERION IS BASED ON THE LOSS IN INFORMATION ASSOCIATED WITH A PARTICULAR MODEL, COMPARED TO A PERFECT MODEL (IN WHICH THE MODEL PREDICTS EACH OBSERVATION EXACTLY).
THE AIC MEASURE (OR VALUE) FOR A MODEL IS THE QUANTITY:
AIC = 2k -2ln (L)
WHERE k IS THE NUMBER OF ESTIMATED PARAMETERS IN THE MODEL AND L IS THE MAXIMUM VALUE OF THE LIKELIHOOD FUNCTION FOR THE MODEL.
THE QUALITY OF SEVERAL MODELS IS COMPARED BY CALCULATING THE AIC VALUE FOR EACH ONE. THE ONE HAVING THE MINIMUM VALUE OF THE AIC IS THE PREFERRED MODEL.
NOTE THAT THE DIFFERENCE IN THE AIC VALUES FOR TWO DIFFERENT MODELS IS EQUAL TO THE LOGARITHM OF THE LIKELIHOOD RATIO:
AIC1 – AIC2 = -2(ln(L1) – ln(L2)) = -2 ln(L1/L2).
FOR A SINGLE MODEL, THE DEVIANCE IS DEFINED AS THE DIFFERENCE BETWEEN THE LOG-LIKELIHOOD FOR THE ESTIMATED MODEL AND FOR A HYPOTHETICAL MODEL THAT FITS THE DATA PERFECTLY:
D = 2∑i{ln L(yi; yi) – ln L(μi; yi).
A NOTE OF CAUTION IS IN ORDER CONCERNING CALCULATION OF THE AIC IN COMMERCIAL STATISTICAL SOFTWARE PACKAGES. BOTH MAXIMUM LIKELIHOOD ESTIMATION AND THE AIC INVOLVE CALCULATION OF THE LOG-LIKELIHOOD. IN CALCULATION OF THE LOG-LIKELIHOOD FUNCTION, SOME PACKAGED DISCARD CONSTANTS THAT HAVE NO EFFECT ON THE MAXIMIZATION. IN COMPARING MODELS USING THE AIC, IT IS IMPORTANT TO ASSURE THAT ALL CONSTANTS ARE RETAINED, SO THAT COMPARISONS BETWEEN MODELS ARE VALID.
BAYESIAN INFORMATION CRITERION
THE BAYESIAN INFORMATION CRITERION (OR SCHWARZ CRITERION) IS SIMILAR TO THE AIC, USING A SLIGHTLY DIFFERENT CRITERION:
BIC = k ln(n) – 2 ln (L)
WHERE N IS THE SAMPLE SIZE (NUMBER OF OBSERVATIONS IN THE DATA SET).
THE BIC IS APPROPRIATE FOR SITUATIONS IN WHICH n IS MUCH LARGER THAN k.
DESPITE ITS NAME, THE BIC IS NOT BASED ON INFORMATION THEORY.
17. MULTIVARIATE MODELS
EXTENSION OF THE GENERAL LINEAR MODEL TO THE MULTIVARIATE CASE
[TO BE DONE, IN ANOTHER PRESENTATION.]
MULTIVARIATE MODELS FOR CATEGORICAL VARIABLES
LOG-LINEAR MODELS
WE SHALL NOW CONSIDER A CLASS OF MODELS THAT IS VERY USEFUL FOR REPRESENTING CATEGORICAL DATA. THIS IS THE CLASS OF LOG-LINEAR MODELS. WE SHALL ILLUSTRATE THE METHOD MAINLY IN THE CASE OF A SIMPLE TWO-BY-TWO CROSS-TABULATION (OR CONTINGENCY TABLE). WE SHALL DISCUSS THIS EXAMPLE IN SOMEWHAT MORE DETAIL THAN IS NECESSARY, TO ILLUSTRATE HOW THE CHOICE OF A MODEL MAY BE DEPENDENT ON MANY FACTORS.
THE APPROACH OF USING LOG-LINEAR MODELS TO DESCRIBE DEPENDENCIES IN CONTINGENCY TABLES BY MEANS OF A PARAMETRIC MODEL IS SUBSTANTIALLY MORE USEFUL THAN THE SIMPLER APPROACH OF SIMPLY TESTING THE HYPOTHESIS OF INDEPENDENCE. THE LOG-LINEAR APPROACH CAN BE USED TO DESCRIBE THE NATURE OF RELATIONSHIPS, AND TO COMPARE THE RESULTS OF DIFFERENT INVESTIGATIONS (IN A MUCH MORE DETAILED MANNER THAN "IS OR IS NOT DEPENDENT").
THE FOLLOWING EXAMPLE IS ADAPTED FROM ONE PRESENTED IN STATISTICAL METHODS FOR RATES AND PROPORTIONS, BY JOSEPH FLIESS (WILEY, 1ST ED. 1973, 2ND ED. 1981 (CURRENT EDITION IS THE 3RD, 2003). OTHER USEFUL REFERENCES ON LOG-LINEAR MODELS INCLUDE AN INTRODUCTION TO CATEGORICAL DATA ANALYSIS BY ALAN AGRESTI (WILEY, 1996) AND CATEGORICAL DATA ANALYSIS BY ALAN AGRESTI (WILEY, 1990). USE OF THE LINEAR LOGISTIC MODEL FOR ANALYSIS OF BINARY DATA WAS POPULARIZED BY D. R. COX IN THE MONOGRAPH, ANALYSIS OF BINARY DATA (METHUEN, 1970).
THIS EXAMPLE CONSIDERS THE RELATIONSHIP BETWEEN SMOKING AND LUNG CANCER. THE DATA ARE COMPLETELY HYPOTHETICAL.
THERE ARE THREE METHODS OF SAMPLE SELECTION THAT MAY BE CONSIDERED:
1. A NATURALISTIC, OR CROSS-SECTIONAL STUDY
2. A PROSPECTIVE STUDY (ALSO CALLED A FOLLOW-UP, COHORT, OR FORWARD-GOING STUDY)
3. A RETROSPECTIVE STUDY (OR CASE-CONTROL STUDY)
NO FURTHER SPECIFICATION IS MADE HERE OF THE NATURE OF THE SELECTION PROCESS FOR THE SAMPLE (E.G., THIS IS NOT AN EXPERIMENTAL DESIGN WITH RANDOMIZED ASSIGNMENT OF A TREATMENT TO UNITS), AND NO CAUSAL MODEL IS SPECIFIED, SO NO CAUSAL INFERENCES ARE IMPLIED. THE ANALYSIS SIMPLY DESCRIBES ASSOCIATIVE RELATIONSHIPS.
FOR ALL THREE SAMPLE DESIGNS, THE TOTAL SAMPLE SIZE WILL BE THE SAME. WHAT DIFFERS IS THE ALLOCATION OF THE SAMPLE TO THE SMOKERS AND LUNG CANCER VICTIMS.
BEFORE EXAMINING THE SAMPLE DESIGNS IN GREATER DETAIL, LET US DISCUSS THE POPULATION DISTRIBUTION AND ANALYSIS GOALS FURTHER.
IN A STUDY OF THE RELATIONSHIP OF SMOKING AND CANCER, A MAIN QUANTITY OF INTEREST WOULD BE THE DIFFERENCE IN THE CONDITIONAL PROBABILITIES OF CANCER FOR SMOKERS AND NON-SMOKERS:
P(C=1|S=1) – P(C=1|S=0)
WHERE C DENOTES THE CANCER ATTRIBUTE (C=0 DENOTING NO CANCER, C=1 DENOTING CANCER) AND S DENOTES THE SMOKING ATTRIBUTE (S=0 DENOTING NON-SMOKER, S=1 DENOTING SMOKER.
LET US DENOTE THE JOINT PROBABILITIES OF CANCER AND SMOKING AS FOLLOWS:
P(C=0, S=0) = π00
P(C=1, S=0) = π10
P(C=0, S=1) = π01
P(C=1, S=1) = π11
FROM THE FORMULA FOR CONDITIONAL PROBABILITY WE HAVE:
![]() .
.
NOW LET US EXAMINE THE THREE SAMPLE DESIGNS FURTHER.
CROSS-SECTIONAL SAMPLE DESIGN
FOR THE FIRST SAMPLE SELECTION METHOD, THE TOTAL SAMPLE SIZE IS HELD FIXED (AT n = 1,000, SAY), AND A SIMPLE RANDOM SAMPLE IS SELECTED FROM A POPULATION OF INTEREST. A CROSSTABULATION TABLE IS CONSTRUCTED TO SHOW THE DISTRIBUTION OF THE SAMPLE OVER THE CATEGORIES. THE SAMPLING DISTRIBUTION IS A MULTINOMIAL DISTRIBUTION OVER THE FOUR CATEGORIES OF THE TABLE.
|
Sample Distribution for a Cross-sectional Study |
|||
|
Cancer status |
|||
|
Smoking status |
No cancer |
Cancer |
Total |
|
Non-smoker |
800 |
100 |
900 |
|
Smoker |
50 |
50 |
100 |
|
Total |
850 |
150 |
1000 (fixed) |
THE FOLLOWING TABLE SHOWS THE PROPORTIONS OF THE SAMPLE OVER THE CATEGORIES.
|
Joint Proportions for the Cross-sectional Study |
|||
|
Cancer status |
|||
|
Smoking status |
No cancer |
Cancer |
Total |
|
Non-smoker |
p11=.8 |
p12=.1 |
p1.=.9 |
|
Smoker |
p21=.05 |
p22=.05 |
p2.=.1 |
|
Total |
p.1=.85 |
p.2=.15 |
1. |
THE KEY POINT TO REALIZE IS THAT FOR THE CROSS-SECTIONAL SAMPLE, ALL OF THE TABLE PROBABILITIES MAY BE ESTIMATED. IN FACT, EACH CELL PROPORTION pij IS AN ESTIMATE OF THE CORRESPONDING PROBABILITY πij, AND THE MARGINAL PROBABILITIES ARE ESTIMATES OF THE CORRESPONDING MARGINAL PROBABILITIES (E.G., p.1 IS AN ESTIMATE OF π01 + π11). THIS MEANS THAT, IN PARTICULAR THE QUANTITY
![]()
CAN BE ESTIMATED.
PROSPECTIVE SAMPLE DESIGN
FOR THE PROSPECTIVE SAMPLE DESIGN, LET US ASSUME THAT A SAMPLE OF 500 SMOKERS AND 500 NON-SMOKERS IS SELECTED. ASSUME THAT THE SAMPLE DISTRIBUTION IS AS IN THE FOLLOWING TABLE.
|
Sample Distribution for a Prospective Study |
|||
|
Cancer status |
|||
|
Smoking status |
No cancer |
Cancer |
Total |
|
Non-smoker |
445 |
55 |
500 (fixed) |
|
Smoker |
250 |
250 |
500 (fixed) |
|
Total |
695 |
305 |
1000 |
THE FOLLOWING TABLE SHOWS THE PROPORTIONS OF THE SAMPLE OVER THE CATEGORIES FOR THIS SAMPLE.
|
Joint Proportions for the Prospective Study |
|||
|
Cancer status |
|||
|
Smoking status |
No cancer |
Cancer |
Total |
|
Non-smoker |
p11=.445 |
p12=.055 |
p1.=.5 (fixed) |
|
Smoker |
p21=.25 |
p22=.25 |
p2.=.5 (fixed) |
|
Total |
p.1=.695 |
p.2=.305 |
1. |
A KEY POINT TO REALIZE HERE IS THAT THE INDIVIDUAL JOINT PROBABILITIES CANNOT BE ESTIMATED FROM THIS DESIGN, SINCE THE PROPORTIONS OF SMOKERS AND NONSMOKERS HAVE EACH BEEN FIXED (AT .5). HOWEVER, THE CONDITIONAL PROBABILITIES OF CANCER, GIVEN SMOKING STATUS, CAN BE ESTIMATED: π00/(π00+π10), π01/(π01+π11), π10/(π00+π10), π11/(π01+π11). THIS MEANS THAT FOR THE PROSPECTIVE DESIGN, THE DIFFERENCE
![]()
CAN BE ESTIMATED. (NONE OF THE TABLE PROPORTIONS REFER TO THE GENERAL POPULATION, BUT TO THE POPULATION OF HALF SMOKERS AND HALF NON-SMOKERS.)
RETROSPECTIVE SAMPLE DESIGN
FOR THE RETROSPECTIVE SAMPLE DESIGN, LET US ASSUME THAT A SAMPLE OF 500 CANCER VICTIMS AND 500 NON-CANCER VICTIMS IS SELECTED. ASSUME THAT THE SAMPLE DISTRIBUTION IS AS IN THE FOLLOWING TABLE.
|
Sample Distribution for a Retrospective Study |
|||
|
Cancer status |
|||
|
Smoking status |
No cancer |
Cancer |
Total |
|
Non-smoker |
471 |
333 |
804 |
|
Smoker |
29 |
167 |
196 |
|
Total |
500 (fixed) |
500 (fixed) |
1000 |
THE FOLLOWING TABLE SHOWS THE PROPORTIONS OF THE SAMPLE OVER THE CATEGORIES FOR THIS SAMPLE.
|
Joint Proportions for the Prospective Study |
|||
|
Cancer status |
|||
|
Smoking status |
No cancer |
Cancer |
Total |
|
Non-smoker |
p11=.471 |
p12=.333 |
p1.=.804 |
|
Smoker |
p21=.029 |
p22=.167 |
p2.=.196 |
|
Total |
p.1=.5 |
p.2=.5 |
1. |
FOR THIS DESIGN, AS FOR THE PROSPECTIVE DESIGN, THE INDIVIDUAL JOINT PROBABILITIES CANNOT BE ESTIMATED. THE CONDITIONAL PROBABILITIES THAT CAN BE ESTIMATED ARE: π00/(π00+π01), π01/(π00+π01), π10/(π10+π11), π11/(π10+π11). UNFORTUNATELY, THESE ARE NOT THE CONDITIONAL PROBABILITIES REQUIRED TO ESTIMATE THE DIFFERENCE
![]() .
.
SO, IN SUMMARY WE SEE THAT THE DIFFERENCE IN THE PROBABILITY OF CONRACTING CANCER FOR SMOKERS AND NON-SMOKERS IS ESTIMABLE FOR THE CROSS-SECTIONAL DESIGN AND THE PROSPECTIVE DESIGN, BUT NOT FOR THE RETROSPECTIVE DESIGN.
THIS DOES NOT MEAN, HOWEVER, THAT THE RETROSPECTIVE DESIGN IS NOT USEFUL. THERE ARE A NUMBER OF MEASURES OF ASSOCIATION THAT MAY BE DEFINED FOR A TWO-WAY CLASSIFICATION TABLE. ONE OF THEM THAT IS WIDELY USED IS THE ODDS (RATIO OF TWO PROBABILITIES).
THE ODDS OF CONTRACTING CANCER CONDITIONAL ON SMOKING STATUS ARE π01/π00 AND π11/π10. THE ODDS IS THE RATIO OF THESE:
(π01/π00)/(π11/π10) = (π01π10)/(π00π11).
THE LOGARITHM OF THIS QUANTITY, OR THE "LOG ODDS" IS:
LOG((π01π10)/(π00π11)) = LOG(π01/π00) - LOG(π11/π10).
THIS IS STILL NOT VERY HELPFUL. WHAT IS INTERESTING TO OBSERVE, HOWEVER, IS THAT THE DIFFERENCES OF THE LOG ODDS OF THE QUANTITIES
![]()
WHICH ARE ESTIMABLE FROM THE PROSPECTIVE DESIGN, AND
![]()
WHICH ARE ESTIMABLE FROM THE RETROSPECTIVE DESIGN, ARE IDENTICAL.
THE LOGISTIC FUNCTION IS
![]()
THE LOGISTIC TRANSFORM OF A PROBABILITY, p, (OR THE LOG ODDS, OR LOGIT) IS THE INVERSE OF THIS:
![]()
THE DIFFERENCE IN THE LOG ODDS FOR THE PROSPECTIVE DESIGN IS:
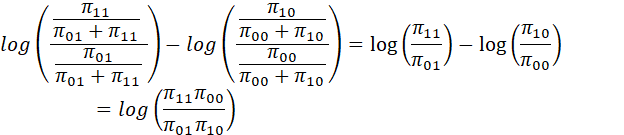
THE DIFFERENCE IN THE LOG ODDS FOR THE PROSPECTIVE DESIGN IS:
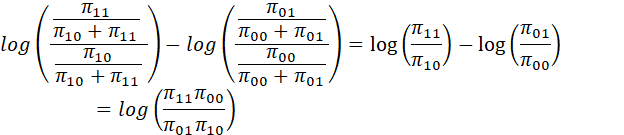
THESE QUANTITIES ARE
EXACTLY THE SAME. (THE QUANTITY ![]() IS CALLED THE CROSS-PRODUCT RATIO (AS IS
IS CALLED THE CROSS-PRODUCT RATIO (AS IS ![]() .)
.)
IN SUMMARY, IF WE ARE INTERESTED IN ESTIMATING THE RELATIONSHIP OF CANCER TO SMOKING, BUT SAMPLING IS BASED ON THE INVERSE APPROACH OF FIXING CANCER AND OBSERVING SMOKING, THEN WE CAN ESTIMATE THE DIFFERENCE IN PROBABILITIES ON A LOGISTIC SCALE. THIS CAN B DONE ONLY ON THE LOGISTIC SCALE, AND NOT ON ANY OTHER SCALE.
WE SHALL NOW DESCRIBE A MODEL THAT INCORPORATES THE PRECEDING RESULTS, AND ESTIMATE THE MODEL PARAMETERS USING THE METHOD OF MAXIMUM LIKELIHOOD.
FOR CROSS-SECTIONAL STUDIES, THE TOTAL SAMPLE SIZE IS FIXED, BUT NO ROW OR COLUMN TOTALS ARE. THE DISTRIBUTION OF THE IJ INDIVIDUAL CELL FREQUENCIES (WHERE I DENOTES THE NUMBER OF ROWS AND J DENOTES THE NUMBER OF COLUMNS OF THE TABLE, IN THIS EXAMPLE I = 2 AND J = 2) IS A MUNTINOMIAL DISTRIBUTION WITH PARAMETER n = TOTAL SAMPLE SIZE.
FOR PROSPECTIVE STUDIES, THE TOTALS OF THE EXPLANATORY VARIABLE (SAY, ROW, AS IN THE EXAMPLE, SMOKER STATUS) ARE FIXED, AND THE DISTRIBUTION OF EACH ROW OF J COUNTS IN AN INDEPENDENT MULTINOMIAL SAMPLE ON THE DEPENDENT VARIABLE.
FOR RETROSPECTIVE STUDIES, THE TOTALS OF THE DEPENDENT VARIABLE (COLUMN) IS FIXED, AND THE DISTRIBUTION OF EACH COLUMN OF I COUNTS IS AN INDEPENDENT MULTINOMIAL SAMPLE ON THE EXPLANATORY VARIABLE.
WE SHALL ILLUSTRATE THE DERIVATION OF THE MAXIMUM LIKELIHOOD ESTIMATES FOR THE CASE OF CROSS-SECTIONAL SAMPLING.
THE SAMPLING DISTRIBUTION IS MULTINOMIAL WITH PARAMETERS n (THE TOTAL NUMBER OF COUNTS IN THE TABLE), k=IJ (THE NUMBER OF CELLS IN THE TABLE) AND PROBABILITIES pi, i=1,...,k, WHERE EACH OF THE pi IS ONE OF THE JOINT PROBABILITIES πij, i = 1, ..., I, j = 1, ..., J:
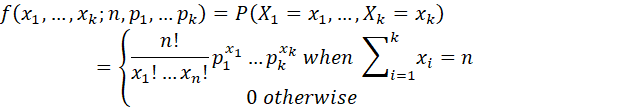
FOR NONNEGATIVE INTEGERS x1, ..., xk. NOW, IF THE OBJECTIVE WERE SIMPLY TO ESTIMATE THE PROBABILITIES pi, THEN WE WOULD DIFFERENTIATE THIS EXPRESSION WITH RESPECT TO THE pi, SET THE DERIVATIVES EQUAL TO ZERO, AND OBTAIN THE ESTIMATES:
![]()
(OR, IN THE πij NOTATION, πij = nij/n). (A DETAILED DESCRIPTION OF THE PROCEDURE FOR DETERMINING THE MAXIMUM LIKELIHOOD ESTIMATES IS SHOWN ON PP. 40-41 OF CATEGORICAL DATA ANALYSIS BY ALAN AGRESTI (WILEY, 1990).)
THE PARAMETER ESTIMATES ARE THE SAME FOR THE PROSPECTIVE AND RETROSPECTIVE SAMPLING PROCEDURES (INDEPENDENT MULTINOMIAL SAMPLING) AS FOR THE CROSS-SECTIONAL SAMPLING PROCEDURE (MULTINOMIAL SAMPLING), BECAUSE OF THE SIMILARITY THE LIKELIHOOD FUNCTION IN ALL THREE CASES.
NOTE THAT IN THE PRECEDING EXAMPLES, ONE OF THE VARIABLES HAS BEEN CALLED AN EXPLANATORY VARIABLE AND THE OTHER A DEPENDENT VARIABLE. THIS DISTINCTION IS A LITTLE MISLEADING, BECAUSE THIS ANALYSIS IS BASED SOLELY ON THE ASSOCIATIVE RELATION BETWEEN THE VARIABLES, WITH NO REPRESENTATION OF CAUSALITY IN THE MODEL.
IN THIS EXAMPLE, WE ARE INTERESTED IN ESTIMATING THE DEGREE OF ASSOCIATION OF C AND S, AND IN TESTING THE HYPOTHESIS OF NO ASSOCIATION (INDEPENDENCE). IF ALL WE WERE INTERESTED IN DOING WAS TESTING FOR INDEPENDENCE, WE COULD APPLY A CHI-SQUARE TEST. TO ESTIMATE THE DEGREE OF ASSOCIATION, WE PROCEED AS FOLLOWS, DEVELOPING A LOG-LINEAR MODEL. (ESTIMATING A DEGREE OF ASSOCIATION WOULD BE USEFUL, FOR EXAMPLE, IN COMPARING THE RESULTS OF DIFFERENT STUDIES.)
WE SHALL DEVELOP A MODEL IN WHICH THE LOG ODDS IS THE MEASURE OF ASSOCIATION. (THE PRESENTATION HERE FOLLOWS THAT OF AGRESTI OP. CIT., PP. 131-3 AND 152-3.)
LOGLINEAR MODEL FOR TWO DIMENSIONS
INDEPENDENCE MODEL
SUPPOSE THAT WE HAVE A MULTINOMIAL SAMPLE OF n OBSERVATIONS OVER THE N = IJ CELLS OF AN I x J TWO-WAY TABLE (CONTINGENCY TABLE). LET πij DENOTE THE PROBABILITY OF OCCURRENCE FOR THE CELL IN ROW i AND COLUMN j. LET πi+ DENOTE THE SUM OF THE PROBABILITIES OVER THE i-th ROW AND π+j THE SUM OF THE PROBABILITIES OVER THE j-th COLUMN.
IF THE ROW AND COLUMN VARIABLES ARE INDEPENDENT, THEN πij = πi+π+j, i = 1,...,I, j = 1,...,J, AND THE EXPECTED FREQUENCIES IN CELL (i,j) ARE mij = n πi+π+j.
LINEAR MODELS ARE EASIER TO WORK WITH THAN MULTIPLICATIVE MODELS. TAKING LOGARITHMS, THE MODEL FOR THE EXPECTED FREQUENCIES IS
log mij = log n + log πi+ + log π+j
A PROBLEM WITH THE PRECEDING MODEL AS IT STANDS IS THAT THERE IS A LINEAR DEPENDENCY AMONG THE π's (THEY SUM TO ONE), SO THAT, AS IT STANDS, THE MODEL PARAMETERS ARE NOT ESTIMABLE. THIS PROBLEM IS ADDRESSED BY IMPOSING CONSTRAINTS ON THE MODEL. THIS IS TYPICALLY DONE BY TRANSFORMING THE ABOVE MODEL SPECIFICATION TO THE FOLLOWING ONE:
![]()
WHERE
![]()
![]()
![]()
AND THE PARAMETERS ![]() AND
AND ![]() SATISFY
SATISFY
![]()
NOTE THAT THE EXPONENTS X AND Y IN THE PRECEDING FORMULAS ARE NOT POWERS, BUT SIMPLY PART OF THE SYMBOLOGY USED TO REPRESENT THE VARIABLES.
THE PRECEDING MODEL IS CALLED A LOGLINEAR MODEL OF INDEPENDENCE FOR A TWO-WAY CONTINGENCY TABLE.
DEPENDENCE MODEL
TO ALLOW FOR DEPENDENCE BETWEEN THE ROW AND COLUMN VARIABLES, WE INCORPORATE ADDITIONAL PARAMETERS INTO THE MODEL:
INSTEAD OF mij = n πi+π+j THE MODEL IS mij = n πi+π+jθij. WHILE IT MAY APPEAR THAT WE HAVE ADDED IJ ADDITIONAL PARAMETERS (THE θij), THIS IS NOT THE CASE. THE NUMBER OF PARAMETERS CANNOT EXCEED THE NUMBER OF CELLS (IJ) IN THE TABLE.
FOR EXAMPLE, FOR A 2x2 CONTINGENCY TABLE, IN ORDER FOR THE MARGINAL PROBABILITIES TO BE MAINTAINED, THE FOLLOWING CONSTRAINTS ARE REQUIRED:
θ11 = 1/θ21 = 1/θ12 = θ22,
SO THAT (IN THE CASE OF A 2x2 CONTINGENCY TABLE) THERE IS ACTUALLY ONLY ONE ADDITIONAL PARAMETER, θ11. LET US DENOTE THIS PARAMETER SIMPLY AS θ (OF COURSE, IN LARGER TABLES, THERE WOULD BE MORE SUCH PARAMETERS).
WITH THE ADDITIONAL PARAMETERS, THE LOG-LINEAR MODEL BECOMES:
![]()
JUST AS THE ![]() AND
AND ![]() WERE NORMALIZED TO SUM TO ZERO, IT IS CUSTOMARY TO
NORMALIZE THE
WERE NORMALIZED TO SUM TO ZERO, IT IS CUSTOMARY TO
NORMALIZE THE ![]() TO SUM TO ZERO:
TO SUM TO ZERO:
![]()
WITH THESE CONSTRAINTS, THE NUMBER OF LINEARLY INDEPENDENT "DEPENDENCE" PARAMETERS IS (I-1)(J-1). FOR THE INDEPENDENCE MODEL, THE NUMBER OF LINEARLY INDEPENDENT PARAMETERS IS I + J – 1, AND FOR THE DEPENDENCE MODEL, IT IS AT MOST IJ (FOR A "SATURATED" MODEL, WHICH FITS THE DATA EXACTLY).
THERE IS A CORRESPONDENCE BETWEEN THE PARAMETERS OF A LOG-LINEAR MODEL AND THE LOG ODDS. FOR THE INDEPENDENCE MODEL OF A 2x2 CONTINGENCY TABLE, THE LOG ODDS (LOGIT) IS (FOR THE ZERO-SUM CONSTRAINTS)
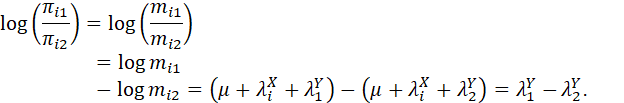
NOTE THAT THIS IS THE SAME
FOR BOTH TABLE ROWS (AND, SINCE ![]() = -
= -![]() , EQUALS 2
, EQUALS 2![]() . THE ANTILOG OF THIS, exp(2
. THE ANTILOG OF THIS, exp(2![]() ), IS THE ODDS THAT THE COLUMN CLASSIFICATION IS
CATEGORY 1 RATHER THAN 2.
), IS THE ODDS THAT THE COLUMN CLASSIFICATION IS
CATEGORY 1 RATHER THAN 2.
FOR THE DEPENDENCE MODEL IN THE CASE OF A 2x2 CONTINGENCY TABLE, THE LOG ODDS RATIO IS
![]()
WHERE θ IS THE LOG ODDS RATIO. EXPANDING THIS EXPRESSION IN TERMS OF THE m's YIELDS
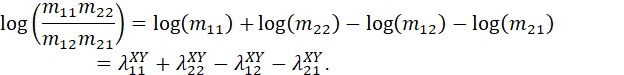
FOR THE ZERO CONSTRAINTS
IT IS TRUE THAT ![]() , SO THAT
, SO THAT
![]()
IT FOLLOWS THAT (FOR A 2x2 TABLE)
![]()
(THAT IS, THE ODDS RATIO
IS THE ANTILOG OF FOUR TIMES THE ASSOCIATION PARAMETER ![]() ).
).
FOR THE LOG-LINEAR MODEL, THERE IS NO DISTINCTION BETWEEN THE VARIABLES, WITH RESPECT TO DEPENDENT-VARIABLE (RESPONSE-VARIABLE) AND INDEPENDENT-VARIABLE (EXPLANATORY-VARIABLE) STATUS. IF ONE OF THE VARIABLES IS A DEPENDENT VARIABLE AND THE OTHER IS AN INDEPENDENT VARIABLE, THE MODEL THAT EXPRESSES THE RELATIONSHIP BETWEEN THE TWO IN TERMS OF THE ODDS RATIO IS THE LOGISTIC REGRESSION (LOGIT) MODEL. FOR AN I x J x 2 TABLE, THIS MODEL IS:
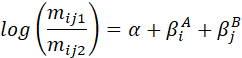
AGRESTI (PP. 152-153) SHOWS THAT THIS IS EQUIVALENT TO THE LOG-LINEAR MODEL
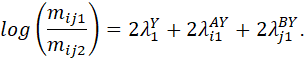
ESTIMATION OF MODEL PARAMETERS
FOR LOG-LINEAR MODELS OF CONTINGENCY TABLES, THE METHOD OF DIFFERENTIATING THE LOG-LIKELIHOOD FUNCTION AND SETTING THE DERIVATIVES EQUAL TO ZERO WORKS IN CERTAIN CASES. THE PROCEDURE FOR CONSTRUCTING THESE ESTIMATES IS SHOWN IN AGRESTI OP. CIT. FOR SATURATED MODELS FOR THREE-WAY TABLES. THE PROCEDURE RECOGNIZES THAT THE COUNTS IN EACH OF THE TABLE CELLS IS A POISSON RANDOM VARIABLE WITH EXPECTED VALUES mijk.
FOR UNSATURATED MODELS, DIRECT SOLUTIONS MAY NOT BE POSSIBLE, AND IT IS NECESSARY TO USE ITERATIVE (NUMERICAL) METHODS TO OBTAIN THE MAXIMUM LIKELIHOOD ESTIMATES OF THE MODEL PARAMETERS. TWO METHODS DESCRIBED IN AGRESTI ARE ITERATIVE PROPORTIONAL FITTING AND THE NEWTON-RAPHSON METHOD.
ADDITIONAL TOPICS IN MULTIVARIATE ANALYSIS
THE UNION-INTERSECTION PRINCIPLE
FACTOR ANALYSIS
CLASSIFICATION ANALYSIS
DISCRIMINANT ANALYSIS
18. TIME-SERIES MODELS
[TO BE DONE, IN ANOTHER PRESENTATION.]
SHORT SERIES: PANEL DATA, LONGITUDINAL MODELS
LONG SERIES, UNIVARIATE: ARMA MODELS; ARIMA MODELS; INTERVENTION ANALYSIS; ARCH MODELS; GARCH MODELS; THE KALMAN FILTER; STATE-SPACE MODELS; MULTIVARIATE TIME SERIES MODELS; COINTEGRATED SERIES
LONG SERIES, MULTIVARIATE
19. EXPERIMENTAL DESIGN; QUASI-EXPERIMENTAL DESIGNS
[TO BE DONE, IN ANOTHER PRESENTATION.]
20. SAMPLE SURVEY
[TO BE DONE, IN ANOTHER PRESENTATION.]
(MOSTLY COVERED ELSEWHERE; MODEL-BASED AND MODEL-ASSISTED)
MODEL CALIBRATION; WEIGHTING; GENERALIZED REGRESSION MODELS (GREG)
FndID(210)
FndTitle(STATISTICAL INFERENCE: REVIEW OF THEORY NEEDED AS BACKGROUND FOR OTHER TOPICS (CAUSAL ANALYSIS, ANALYSIS OF MISSING DATA, AND ANALYSIS OF PANEL DATA), LECTURE NOTES)
FndDescription(STATISTICAL INFERENCE: REVIEW OF THEORY NEEDED AS BACKGROUND FOR OTHER TOPICS (CAUSAL ANALYSIS, ANALYSIS OF MISSING DATA, AND ANALYSIS OF PANEL DATA), LECTURE NOTES)
FndKeywords(statistical methods; statistical inference; monitoring and evaluation; statistics course; short course; sample survey; causal inference; statistical design and analysis; sample size determination)