SMALL AREA ESTIMATION: LECTURE NOTES

THIS COURSE WAS FIRST PRESENTED TO THE BAHAMAS DEPARTMENT OF STATISTICS, AND INCLUDED MANY EXAMPLES RELATING TO THEIR SMALL-AREA ESTIMATION REQUIREMENTS. RATHER THAN MODIFY THE COURSE TO A "GENERIC" VERSION IN WHICH ALL REFERENCES TO ACTUAL PLACES WERE "DE-IDENTIFIED," THE EXAMPLES PRESENTED IN THE ORIGINAL PRESENTATION HAVE BEEN RETAINED.

2.OUTLINE

1. ESTIMATION FOR DOMAINS (ISLANDS) HAVING LARGE SAMPLE SIZES: DESIGN-BASED ESTIMATION (“DIRECT” ESTIMATION; PRESENT APPROACH)

SUMMARY OF CURRENT PROCEDURES

REFERENCES

2. SMALL-AREA ESTIMATION: CONCEPTS AND EXAMPLES

CONCEPTS AND EXAMPLES

DEVELOPMENT PLAN FOR FIRST YEAR AND FOR FUTURE YEARS

ALTERNATIVE APPROACHES TO SMALL-AREA ESTIMATION

TECHNICAL BACKGROUND: REVIEW OF MATRIX ALGEBRA, GENERAL LINEAR STATISTICAL MODEL

3. ESTIMATION FOR DOMAINS HAVING NO SAMPLE: MODEL-BASED ESTIMATION (“INDIRECT” ESTIMATES)

4. ESTIMATION FOR DOMAINS HAVING SMALL SAMPLES: DESIGN-BASED ESTIMATION (“DIRECT” ESTIMATES)

5. ESTIMATION FOR DOMAINS HAVING SMALL SAMPLES: MODEL-ASSISTED ESTIMATION

6. CONSTRUCTION OF ANNUAL ESTIMATE FROM THE MAY AND NOVEMBER ESTIMATES

7. COMPUTATION (DATA PROCESSING)

8. RECOMMENDATIONS FOR ANALYSIS OF MAY AND NOV. DATA

9. CONSIDERATIONS FOR FUTURE DEVELOPMENT

3. ESTIMATION FOR DOMAINS (ISLANDS) HAVING LARGE SAMPLE SIZES: DESIGN-BASED ESTIMATION (“DIRECT” ESTIMATION)

THIS IS THE PRESENT APPROACH

SAMPLE DESIGN FOR LABOUR FORCE SURVEY (LFS): STRATIFIED MULTISTAGE SAMPLE DESIGN

STRATA: ISLANDS

FIRST-STAGE SAMPLE UNITS (PRIMARY SAMPLE UNITS, PSUs): ENUMERATION AREAS (EAs, GEOGRAPHIC DISTRICTS OF SIMILAR SIZE (NUMBER OF HOUSEHOLDS))

SECOND-STAGE SAMPLE UNITS (SECONDARY SAMPLE UNITS, SSUs): HOUSEHOLDS

ELEMENTS (ULTIMATE SAMPLE UNITS): IN-SCOPE (“ELIGIBLE”) INDIVIDUALS

THE FIRST- AND SECOND-STAGE UNITS ARE SELECTED WITHOUT REPLACEMENT

SCOPE OF INFERENCE: IN THE FOLLOWING, IT IS ASSUMED, UNLESS OTHERWISE STATED, THAT THE INFERENCES ARE BEING MADE FOR THE POPULATION BEING SURVEYED (E.G., NEW PROVIDENCE, GRAND BAHAMAS, OTHER FAMILY ISLANDS INCLUDED IN THE SURVEY).

ESTIMATE OF TOTAL UNEMPLOYED: THE “π ESTIMATOR” OR “HORVITZ-THOMPSON” ESTIMATOR:

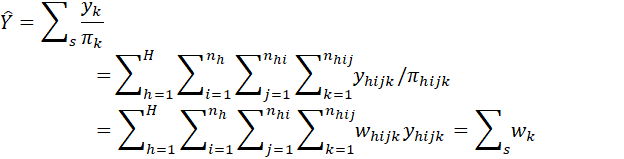
where

s = sample

H = number of strata

n_h = number of EAs selected in stratum h

n_hi = number of households selected in EA hi

n_hij = number of in-scope indivicuals in household hij

y_hijk = observed value (0 = employed, 1 = unemployed) for individual hijk

w_hijk = sample weight for individual hijk = 1/π_hijk where π_hijk = probability of inclusion of individual hijk in sample

THE VARIANCE OF THIS ESTIMATOR IS:

WHERE U DENOTES THE TOTAL POPULATION AND

AN UNBIASED ESTIMATE OF THE VARIANCE IS:

THE PRECEDING “DOUBLE-SUM” FORM OF THE ESTIMATED VARIANCE IS COMPUTATIONALLY BURDENSOME, AND MUCH SIMPLER EXPRESSIONS CAN BE DERIVED FOR HIGHLY STRUCTURED DESIGNS. FOR COMPLEX DESIGNS, ALTERNATIVE METHODS, SUCH AS TAYLOR-SERIES LINEARIZATION OR RESAMPLING METHODS (E.G., THE “BOOTSTRAP”) ARE USED TO ESTIMATE THE VARIANCE.

FOR THE PRESENT LFS DESIGN, THE ABOVE FORMULA LEADS TO THE FOLLOWING COMUPUTATIONALLY SIMPLER FORM:

where

and

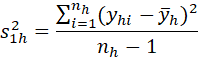
where

= total for cluster hi in stratum h

= mean of totals for clusters in stratum h

AND IT IS ASSUMED THAT THE FIRST-STAGE SAMPLING FRACTION, f_1h, IS SMALL.

THE ESTIMATED VARIANCE IS USED TO CALCULATE CONFIDENCE INTERVALS. FOR EXAMPLE, FOR LARGE SAMPLES, A 95% CONFIDENCE INTERVAL IS:

WHERE IS THE ESTIMATED STANDARD ERROR OF .

THE PRECEDING ESTIMATES ARE “DESIGN-BASED” ESTIMATES. THEY ARE THE TYPE CURRENTLY USED FOR ANALYSIS OF THE LABOUR FORCE SURVEY (LFS) DATA.

IT IS POSSIBLE THAT MORE PRECISE ESTIMATES MAY BE OBTAINED BY POST-STRATIFYING ON AGE, SEX, INDUSTRY AND OCCUPATION (“POSTSTRATIFIED” ESTIMATES).

IN THE CURRENT SAMPLE DESIGN, NOT ALL ISLANDS ARE SAMPLED EACH YEAR. NATIONAL ESTIMATES (TOTAL, MEANS, PROPORTIONS) ARE BASED ON THE ISLANDS THAT ARE SAMPLED. AS AN ESTIMATE FOR THE ENTIRE COUNTRY, THIS ESTIMATE IS BIASED (SINCE THE CHARACTERISTICS (E.G., UNEMPLOYMENT RATES) FOR THE NON-SAMPLED ISLANDS MAY DIFFER FROM THOSE OF THE SAMPLED ISLANDS).

THIS PRESENTATION WILL DESCRIBE METHODS THAT MAY BE USED TO CONSTRUCT ESTIMATES THAT HAVE LOWER BIAS AND HIGHER PRECISION THAN THE DESIGN-BASED ESTIMATES THAT ARE CURRENTLY USED. THE ALTERNATIVE ESTIMATES ARE CALLED “SMALL-AREA ESTIMATES.” THEY MAY BE USED TO CONSTRUCT ESTIMATES FOR ANY SMALL SUBPOPULATIONS (“DOMAINS,” “DOMAINS OF STUDY”), NOT JUST GEOGRAPHIC AREAS (SUCH AS ISLANDS).

A DOMAIN (OR AREA) IS CONSIDERED “SMALL” IF THE SAMPLE SIZE FOR THAT DOMAIN IS SO SMALL THAT THE PRECISION OF THE STANDARD DESIGN-BASED ESTIMATE (DESCRIBED ABOVE) FOR THAT DOMAIN IS TOO LOW TO BE USEFUL. FOR SOME OF THE SMALL-AREA ESTIMATES TO BE DESCRIBED, THE SAMPLE SIZE FOR THE DOMAIN MAY, IN FACT, BE ZERO.

THE SMALL-AREA ESTIMATORS ARE CALLED “MODEL-BASED” OR “MODEL ASSISTED.” THE TERM “MODEL ASSISTED” IS USED IF SOME SAMPLE DATA ARE AVAILABLE FOR THE DOMAIN, AND THE ESTIMATOR MAKES USE OF BOTH THE MODEL AND THE SAMPLE DESIGN. IF THERE ARE NO SAMPLE DATA FOR THE DOMAIN, THE TERM “MODEL BASED” (OR “MODEL DEPENDENT”) IS USED.

FOR THE DESIGN-BASED ESTIMATES, ALL OF THE RANDOM VARIATION IS SAMPLING VARIATION. THE ONLY RANDOM VARIABLE INVOLVED IS THE SAMPLE MEMBERSHIP INDICATOR VARIABLE:

WHERE s DENOTES THE SAMPLE. THE MEAN, VARIANCE AND COVARIANCE OF I_k ARE:

E(I_k) = π_k

V(I_k) = π_k(1 – π_k) = Δ_kk

C(I_k, I_l)= π_kl – π_kπ_l = Δ_kl

FOR THE DESIGN-BASED ESTIMATORS, THE POPULATION BEING SURVEYED IS CONSIDERED FIXED – THE RANDOM VARIATION DERIVES FROM THE RANDOM SAMPLE-SELECTION PROCESS.

FOR THE MODEL-BASED AND MODEL-ASSISTED ESTIMATORS TO BE CONSIDERED, ANOTHER SOURCE OF RANDOM VARIATION WILL BE INVOLVED – THE RANDOM VARIATION ASSOCIATED WITH SELECTING THE FIXED SAMPLE POPULATION FROM A CONCEPTUALLY LARGER INFINITE POPULATION. THE “MODEL” ON WHICH AN ESTIMATOR IS BASED DESCRIBES HOW THE FIXED SAMPLE IS RELATED TO THE INFINITE POPULATION.

COMPUTATIONAL PROCEDURES:

ALL COMPUTATIONS (ESTIMATES AND ESTIMATED VARIANCES OF ESTIMATES) FOR THE DESIGN-BASED APPROACH MAY BE DONE USING THE STATA svyset AND svy COMMANDS. (svyset SPECIFIES THE SAMPLE DESIGN AND svy: IS A “PREFIX” COMMAND THAT PRECEDES ESTIMATION COMMANDS, SUCH AS “proportion” OR “regress”.)

A FEW EXAMPLES OF STATA OUTPUT ARE IMBEDDED IN THESE NOTES. MANY MORE EXAMPLES ARE INCLUDED IN COMPUTER-OUTPUT HANDOUTS. THESE HANDOUTS INCLUDE A STATA COMMAND FILE (“DO” FILE, Do1BahamasLFS2013May.do) AND A CORRESPONDING OUTPUT (“LOG” FILE, Do1BahamasLFS2013May.log).

NOTE ON ESTIMATION OF PRECISION.

IN ORDER TO OBTAIN CORRECT ESTIMATES OF THE PRECISION (STANDARD ERRORS) OF ESTIMATES, IT IS NECESSARY TO SPECIFY ALL ASPECTS OF THE SURVEY SAMPLE DESIGN, INCLUDING ALL LEVELS OF SAMPLING. IT IS NOT SUFFICIENT SIMPLY TO SPECIFY THE SURVEY WEIGHTS (RECIPROCALS OF PROBABILITIES OF SELECTION). UNBIASED ESTIMATES OF UNEMPLOYMENT RATES (AND MANY OTHER QUANTITIES OF INTEREST) MAY BE OBTAINED USING JUST THE WEIGHTS, BUT THIS IS NOT TRUE FOR ESTIMATING VARIANCES (AND HENCE, FOR CONSTRUCTING CONFIDENCE INTERVALS AND MAKING TESTS OF HYPOTHESES).

TO EMPHASIZE, IN MAKING DESIGN-BASED ESTIMATES, IT IS INSUFFICIENT TO FOCUS ATTENTION ON THE WEIGHTS, WITHOUT INCLUDING A COMPLETE SPECIFICATION OF THE SURVEY DESIGN.

IN ALL DATA FILES, THE COMPLETE DESIGN SHOULD BE SPECIFIED, INCLUDING ISLAND, PSU (ENUMERATION DISTRICT) AND HOUSEHOLD. THE fpc’s SHOULD ALSO BE SPECIFIED.

ALTHOUGH ESTIMATION OF VARIANCES IS VERY IMPORTANT, LITTLE ATTENTION WILL BE GIVEN TO THIS TOPIC IN THIS PRESENTATION. THE STATA PROGRAM PACKAGE PERFORMS ALL OF THE REQUIRED VARIANCE CALCLATIONS, AS LONG AS THE DESIGN OR MODEL IS CORRECTLY SPECIFIED.

USING JUST THE SAMPLE WEIGHTS, THE svyset AND svy COMMANDS ARE:

svyset _n [pweight=weight] (the _n specifies that individuals (not clusters) were randomly selected; the weight is an individual weight – this is a hypothetical example, not the correct LFS design)

svy: proportion employed

svy: proportion employed, over(island)

TAKING INTO ACCOUNT THE SURVEY DESIGN, THE STATA svy COMMAND IS:

svyset [psu] [weight] [,design_options] [|| ssu, design_options]…[options]

E.G.,

svyset enumdist [pweight=weighted], strata(island) fpc(fpced) || hhold, fpc(fpchh)

svy: proportion employed

svy: proportion employed, over(island)

NOTE: FOR THE EXAMPLES TO BE PRESENTED LATER, THE AVAILABLE DATASET DID NOT CONTAIN THE SURVEY DESIGN PARAMETERS. HENCE, THE EXAMPLES ARE PRESENTED FOR A “FICTITIOUS” SURVEY IN WHICH INDIVIDUALS WERE ASSUMED TO BE SELECTED USING SIMPLE RANDOM SAMPLING WITH REPLACEMENT, WITH THE SPECIFIED SURVEY WEIGHT.

REFERENCES

THE LITERATURE ON SMALL-AREA ESTIMATES IS VERY LARGE. A DESCRIPTION OF THE MATERIAL PRESENTED HERE MAY BE FOUND IN:

RAO, J. N. K., SMALL AREA ESTIMATION, WILEY, 2003

ADDITIONAL REFERENCES INCLUDE:

SÄRNDAL, CARL-ERIK, BENGT SWENSSON, AND JAN WRETMAN, MODEL ASSISTED SURVEY SAMPLING, SPRINGER-VERLAG, 1992

VALLIANT, RICHARD, ALAN H. DORFMAN AND RICHARD M. ROYALL, FINITE POPULATION SAMPLING AND INFERENCE: A PREDICTION APPROACH, WILEY, 2000

VALLIANT, RICHARD, JILL A. DEVER AND FRAUKE KREUTER, PRACTICAL TOOLS FOR DESIGNING AND WEIGHTING SURVEY SAMPLES, SPRINGER-VERLAG, 2013

LONGFORD, NICHOLAS T., MISSING DATA AND SMALL-AREA ESTIMATION: MODERN ANALYTICAL EQUIPMENT FOR THE SURVEY STATISTICIAN, SPRINGER-VERLAG, 2005

COCHRAN, WILLIAM G., SAMPLING TECHNIQUES, 3^RD ED., WILEY, 1977

LOHR, SHARON L., SAMPLING: DESIGN AND ANALYSIS, 2ND ED., CENGAGE LEARNING, 2009

AS STATED, THIS PRESENTATION IS BASED ON THE J. N. K. RAO BOOK, SMALL AREA ESTIMATION.

4. SMALL-AREA ESTIMATION: CONCEPTS, EXAMPLES, DEVELOPMENT PLAN, ALTERNATIVE APPROACHES AND TECHNICAL BACKGROUND

4.1 CONCEPTS AND EXAMPLES

TRADITIONAL, DESIGN-BASED, APPROACH. EXAMPLE:

SAMPLE OF SIZE n, POPULATION OF SIZE N:

ESTIMATE OF MEAN =

VARIANCE OF ESTIMATED MEAN = (1 – n/N) σ²/n = fpc σ²/n

WHERE fpc = 1 – n/N.

IF THE SAMPLE SIZE, n, IS SUFFICIENTLY LARGE, AND/OR THE fpc IS SUFFICIENTLY SMALL, THIS ESTIMATE MAY BE OF ADEQUATE PRECISION (E.G., A 95% CONFIDENCE INTERVAL IS SUFFICIENTLY NARROW).

FOR SOME DOMAINS (SUBPOPULATIONS OF SPECIAL INTEREST, SUCH AS ISLANDS), THE SAMPLE SIZE MAY BE TOO SMALL (OR EVEN EQUAL TO ZERO). WHAT TO DO? THE ANSWER IS “SMALL-AREA ESTIMATION”: MODEL-BASED OR MODEL-ASSISTED ESTIMATORS, INSTEAD OF DESIGN-BASED ESTIMATORS.

EXAMPLES

EXAMPLE 1: MODEL-BASED ESTIMATOR (USING NO BAHAMAS SURVEY DATA)

SUPPOSE THAT WE HAD NO SAMPLE DATA ON THE BAHAMAS. HOW COULD WE ESTIMATE THE UNEMPLOYMENT RATE? WE WOULD BASE AN ESTIMATE ON PUBLISHED DATA FOR SIMILAR ECONOMIES.

OPTION a. SUPPOSE THAT THE UNEMPLOYMENT RATE FOR THE WORLD’S HIGH-INCOME COUNTRIES FOR 2014 IS _{High, 2014} = 7%, WITH AN ESTIMATED STANDARD ERROR (SE() OR SIMPLY SE) OF 1%. SUPPOSE FURTHER THAT THE BAHAMAS UNEMPLOYMENT RATE HAS HISTORICALLY BEEN OBSERVED TO BE ABOUT TWICE THIS RATE.

THEN WE COULD ESTIMATE

_{Bahamas, 2014} = 2 x _{High, 2014} = 14%,

WITH AN ESTIMATED STANDARD ERROR (SE) OF 2 x 1% = 2%.

PROBLEM: AS AN ESTIMATE OF THE BAHAMAS UNEMPLOYMENT RATE IS LIKELY TO BE BIASED (EXPECTED VALUE NOT CORRECT). CONFIDENCE INTERVALS BASED ON THE WORLD VALUES FOR AND SE WOULD NOT BE CORRECT (THE LIKELIHOOD OF INCLUDING THE BAHAMAS VALUE WOULD BE VERY LOW, NOT THE DESIRED VALUE (SUCH AS A NOMINAL 95%)).

OPTION b. SUPPOSE THAT THE BAHAMAS UNEMPLOYMENT RATE HAS BEEN OBSERVED TO BE SIMILAR TO THE UNEMPLOYMENT RATE IN OTHER TOURIST-ORIENTED CARIBBEAN NATIONS. SUPPOSE _{Car, 2013} = 17%, SE = 2%. THEN WE COULD ESTIMATE

_{BahamasFromCar, 2014} = _{Car, 2013} = 17%, SE = 2%.

THE BIAS OF THIS ESTIMATE IS LIKELY TO BE LESS THAN THE PREVIOUS ONE, BUT IT IS STILL LIKELY (AND COULD BE SHOWN FROM HISTORICAL DATA) TO BE SUBSTANTIALLY BIASED.

OPTION c. SUPPOSE THAT THE BAHAMAS UNEMPLOYMENT RATE HAS BEEN OBSERVED TO BE SIMILAR TO THE UNEMPLOYMENT RATE IN TOURIST-ORIENTED PARTS OF FLORIDA, TIMES 1.5. SUPPOSE _{Fla, 2013} = 10%, SE = 3%. THEN WE COULD ESTIMATE

_{BahamasFromFla, 2014} = _{Fla, 2013} = 1.5 x 10% = 15%, SE = 1.5 x 3% = 4.5%.

OPTION d (COMPOSITE ESTIMATOR). SUPPOSE THE US UNEMPLOYMENT FIGURES ARE AVAILABLE FOR 2014, AND FLORIDA TOURIST-AREA FIGURES ARE AVAILABLE FOR 2013. SUPPOSE THAT THE BAHAMAS RATE IS ABOUT TWICE THE USA RATE. WE COULD CONSIDER A COMPOSITE ESTIMATOR:

_{Bahamas, 2014} = α (_{BahamasFromUSA, 2014}) + (1- α) (_{BahamasFromFla, 2013})

where

_{BahamasFromUSA, 2014} = 2 x μ_{USA, 2014}

_{BahamasFromFla, 2013} = 1.5 x μ_Fla,
2013

and

THE PRECEDING MODELS, AND SIMILAR ONES, COULD BE DEVELOPED FROM AVAILABLE DATA, AND THE ONE WITH THE MINIMUM MEAN SQUARED ERROR USED. THE ESTIMATES INVOLVE NO BAHAMAS SAMPLE DATA. THEY ARE MODEL-BASED. (THEY ARE SUBJECTIVE, A PRIORI, ESTIMATES, SINCE THEY USE NO SAMPLE DATA.)

DIGRESSION: THE ROLE OF THE MEAN SQUARED ERROR (MSE)

IN CONSIDERING SMALL-AREA ESTIMATORS, IT IS IMPORTANT TO CONSIDER BOTH THE VARIANCE AND THE BIAS OF AN ESTIMATOR. IF THE QUANTITY BEING ESTIMATED IS DENOTED BY θ AND ITS ESTIMATOR IS DENOTED BY , THEN THE VARIANCE AND BIAS OF THE ESTIMATOR ARE DEFINED BY

NOTE THAT THE BIAS OF AN ESTIMATOR IS RELATIVE TO WHAT IS BEING ESTIMATED (IN THIS CASE, θ).

THE MEAN SQUARED ERROR (MSE) OF AN ESTIMATOR IS:

IT IS DESIRED TO USE ESTIMATORS HAVING SMALL VARIANCE AND SMALL BIAS, THAT IS, SMALL MSE.

THE PRESENCE OF SMALL BIAS IS ACCEPTABLE FOR TWO REASONS:

FOR MANY PARAMETERS, IT IS DIFFICULT TO FIND AN UNBIASED ESTIMATOR

AN ESTIMATOR WITH SOME BIAS MAY HAVE A SMALLER VARIANCE AND MSE THAN AN UNBIASED ESTIMATOR.

THE PRESENCE OF BIAS CORRUPTS CONFIDENCE INTERVAL ESTIMATES, SUCH THAT THE TRUE CONFIDENCE COEFFICIENT IS SMALLER THAN THE NOMINAL (INTENDED, DESIRED) VALUE. IT IS IMPORTANT THAT THE BIAS RATIO,

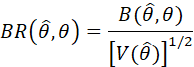
BE SMALL. THE PROBABILITY THAT θ IS CONTAINED IN THE INTERVAL

IS CALLED THE COVERAGE PROBABILITY, AND IS GIVEN BY

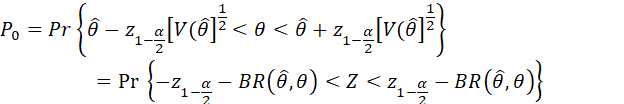
WHERE Z IS THE STANDARDIZED NORMAL N(0,1) RANDOM VARIABLE. IT IS CLEAR THAT THE COVERAGE PROBABILITY EQUALS THE NOMINAL CONFIDENCE LEVEL (1 – α) ONLY IF IS ZERO. IF THE BIAS RATIO IS LESS THAN 50%, THE DISTORTION IS SMALL (LESS THAN ABOUT 3%).

EXAMPLE 2. MODEL-ASSISTED ESTIMATORS (BASED ON BOTH SURVEY DATA AND A MODEL APART FROM THE SURVEY DESIGN)

SUPPOSE THAT WE HAVE A LARGE SAMPLE OF DATA FOR THE THREE LARGEST ISLANDS, SO THAT WE HAVE A HIGH-PRECISION ESTIMATE FOR THEM. SUPPOSE ALSO THAT WE HAVE SAMPLE SURVEY DATA FOR A SMALLER ISLAND, SAY ELEUTHERA, BUT THAT THE SAMPLE SIZE IS SMALL AND THE PRECISION OF THE DESIGN-BASED ESTIMATE IS TOO LOW FOR THE ESTIMATE TO BE OF PRACTICAL VALUE. THE ESTIMATE CAN BE IMPROVED BY COMBINING THE SURVEY DATA WITH AUXILIARY DATA.

THE TERM “AUXILIARY DATA” REFERS TO ANY DATA RELATING TO ESTIMATING THE PARAMETER OF INTEREST, ADDITIONAL TO WHAT IS ALREADY USED. FOR EXAMPLE, EMPLOYMENT STATUS MAY BE THE VARIABLE OF PRIMARY INTEREST FOR ESTIMATING THE UNEMPLOYMENT RATE, AND AN ESTIMATE OF THE UNEMPLOYMENT RATE MIGHT BE BASED ON THIS VARIABLE ALONE. VARIABLES RELATED TO EMPLOYMENT STATUS MIGHT BE AGE, SEX, OCCUPATION AND INDUSTRY, AND A MORE PRECISE ESTIMATE MIGHT BE OBTAINED BY TAKING THESE VARIABLES INTO ACCOUNT. WITH RESPECT TO EMPLOYMENT STATUS, THEY ARE AUXILIARY DATA.

AUXILIARY DATA MAY REFER TO DATA FROM THE SAME SMALL AREA, OR TO DATA FROM OTHER AREAS. IT MAY REFER TO VARIABLES OBSERVED ONLY FOR EACH SAMPLE UNIT IN THE SURVEY QUESTIONNAIRE (SUCH AS AGE, SEX, OCCUPATION, INDUSTRY, ISLAND) OR TO VARIABLES OBSERVED FROM NON-SURVEY SOURCES, SUCH AS ADMINISTRATIVE RECORDS, CENSUS RECORDS, OR DATA FROM OUTSIDE THE COUNTRY.

IF THE VARIANCE OF THE ESTIMATOR REMAINS APPROXIMATELY PROPORTIONAL TO THE INVERSE OF THE SAMPLE SIZE OF THE SMALL AREA, THE ESTIMATOR IS CALLED A “DIRECT ESTIMATOR” (WHETHER IT IS BASED ON AUXILIARY DATA OR NOT). IF THE VARIANCE OF THE ESTIMATOR IS PROPORTIONAL TO THE INVERSE OF THE TOTAL SURVEY SAMPLE SIZE (OF ALL AREAS, NOT JUST THE SMALL AREA), THE ESTIMATOR IS CALLED AN “INDIRECT ESTIMATOR.”

FOR MODEL-ASSISTED ESTIMATORS, THE MODEL MAY BE IMPLIED OR EXPLICIT. THE STATISTICAL PROPERTIES OF THE ESTIMATORS (UNBIASEDNESS, CONSISTENCY, VARIANCE FORMULAS) DEPEND ON THE DESIGN, AND NOT ON WHETHER THE MODEL IS CORRECTLY SPECIFIED.

ESTIMATORS MAY BE BASED SOLELY ON A MODEL THAT DOES NOT INVOLVE THE SAMPLE DESIGN. SUCH ESTIMATORS ARE CALLED “MODEL-BASED” OR “MODEL-DEPENDENT” OR “PURE MODEL-BASED” ESTIMATORS. THE MODEL PARAMETERS MAY BE ESTIMATED FROM SAMPLE DATA. (THE MODEL PARAMETERS COULD BE A PRIORI ESTIMATES, E.G., ESTIMATED FROM PAST SURVEYS.)

IT IS A SOURCE OF CONFUSION THAT THE TERM “MODEL BASED” MAY REFER EITHER TO “MODEL-ASSISTED” ESTIMATORS OR TO “PURE MODEL-BASED” ESTIMATORS. THE IMPORTANT DISTINCTION IS WHETHER THE PROPERTIES OF THE ESTIMATORS RELATE TO THE SURVEY DESIGN (E.G., ARE “DESIGN-UNBIASED” OR “DESIGN-CONSISTENT”) OR NOT (E.G., ARE “MODEL-UNBIASED” OR “MODEL-CONSISTENT”). SOME ESTIMATORS ARE BOTH DESIGN-CONSISTENT AND MODEL-CONSISTENT. (WE SHALL DEFINE THESE TERMS SHORTLY.)

IN THE FOLLOWING, WE SHALL CONSIDER BOTH DIRECT AND INDIRECT ESTIMATORS, ESTIMATORS BASED ON IMPLICIT AND EXPLICIT MODELS, AND ESTIMATORS THAT ARE DESIGN-CONSISTENT AND MODEL-CONSISTENT.

SOME DEFINITIONS AND CLARIFICATIONS OF TERMS

AN ESTIMATOR IS “DESIGN-UNBIASED” IF THE EXPECTATION OF THE ESTIMATOR EQUALS THE QUANTITY BEING ESTIMATED, WHERE THE EXPECTATION IS CALCULATED USING THE DESIGN PROBABILITIES.

AN ESTIMATOR IS “DESIGN-CONSISTENT” IF IT IS UNBIASED OR IF ITS BIAS TENDS TO ZERO AS THE SAMPLE SIZE INCREASES AND ITS VARIANCE TENDS TO ZERO AS THE SAMPLE SIZE INCREASES. (THESE DEFINITIONS ARE NOT RIGOROUS, SINCE THEY DO NOT ADDRESS THE FACT THAT THE SAMPLE SIZE MAY NOT INCREASE INDEFINITELY, FOR A FINITE POPULATION.)

THE TERMS MODEL-UNBIASED AND MODEL-CONSISTENT ARE SIMILARLY DEFINED, BUT WITH RESPECT TO A SPECIFIED SUPERPOPULATION MODEL FROM WHICH THE SURVEYED POPULATION IS CONSIDERED TO HAVE BEEN SELECTED.

THE TERM “MODEL-BASED” IS SOMEWHAT MISLEADING, SINCE A SURVEY DESIGN IS IN FACT SPECIFIED BY A MATHEMATICAL / STATISTICAL MODEL. THE TERM “MODEL-BASED” IMPLIES THAT THAT THE SURVEYED POPULATION IS CONSIDERED TO HAVE BEEN SELECTED FROM A SUPERPOPULATION (AND THE “MODEL” DESCRIBES HOW).

CONTINUATION OF EXAMPLE…

SUPPOSE THAT WE HAVE AN ESTIMATE FROM THE THREE LARGEST ISLANDS:

_{Direct,3largest, 2014} =18%, SE = 2%

AND AN ESTIMATE FROM SURVEY DATA FOR ELEUTHERA:

_{Direct1,Elu, 2014} = 25%, SE = 20%.

THE GOAL IS TO ESTIMATE THE UNEMPLOYMENT RATE FOR ELEUTHERA. THE PROBLEM IS THAT THE DIRECT (DESIGN-BASED) ESTIMATE FOR ELEUTHERA IS OF LOW PRECISION. WE MAY CONSIDER A NUMBER OF ALTERNATIVE SOLUTIONS.

OPTION a: SIMPLE DESIGN-BASED ESTIMATE (DIRECT ESTIMATE BASED ON OBSERVATION OF EMPLOYMENT STATUS, WITH NO AUXILIARY DATA): USE THE 3-LARGEST-ISLAND ESTIMATE AS THE ESTIMATE FOR ELEUTHERA

_{Direct2,Elu, 2014} = _{Direct,3largest, 2014} =18%, SE = 2%

THIS ESTIMATOR IS HIGH-PRECISION, BUT PROBABLY SUBSTANTIALLY BIASED (SINCE THE LABOUR-FORCE CHARACTERISTICS OF ELEUTHERA SURELY DIFFER SUBSTANTIALLY FROM THOSE OF THE THREE LARGEST ISLANDS).

OPTION b. SIMPLE DESIGN-BASED ESTIMATE (DIRECT ESTIMATE BASED ON OBSERVATION OF EMPLOYMENT STATUS, WITH NO AUXILIARY DATA): BASE THE ELEUTHERA ESTIMATE ON THE ELEUTHERA SAMPLE:

_{Direct1,Elu, 2014} = 25%, SE = 20%

THIS ESTIMATOR IS UNBIASED, BUT THE PRECISION IS SO LOW THAT IT IS NOT USEFUL.

OPTION c. COMPLEX DESIGN-BASED ESTIMATE (DIRECT ESTIMATE, USING AUXILIARY DATA): IT IS BASED ON ELEUTHERA SAMPLE, BUT USES AUXILIARY DATA. GENERALIZED REGRESSION ESTIMATE (INCLUDES THE USUAL DESIGN-BASED RATIO AND REGRESSION ESTIMATES AS SPECIAL CASES). WILL SHOW EXAMPLES LATER.

OPTION d. MODEL-ASSISTED ESTIMATE (INDIRECT ESTIMATE): CONSTRUCT A SYNTHETIC ESTIMATE BASED ON THE RATES FOR THE INDUSTRIAL CATEGORIES ESTIMATED FOR THE THREE LARGEST ISLANDS. FOR EXAMPLE, SUPPOSE THAT THE UNEMPLOYMENT RATE IS RELATED TO INDUSTRIAL CATEGORY. THEN A SYNTHETIC ESTIMATE WOULD BE:

where

= estimated unemployment rate for industrial category i on 3 largest islands

N_Elu,i = population count in industrial category i for Eleuthera, from the last (most recent) Census

N_Elu = population count for Eleuthera from last Census.

THIS ESTIMATE IS BIASED (SINCE THE INDUSTRY-SPECIFIC RATES FOR ELEUTHERA MAY DIFFER FROM THE 3 LARGEST ISLANDS), BUT, IF THE RELATIONSHIP IS REASONABLY STRONG, THE BIAS WILL BE LOW. ITS PRECISION SHOULD BE HIGH, SINCE IT IS BASED ON THE (LARGE) 3-ISLAND SAMPLE.

OPTION e. COMPOSITE ESTIMATE (INDIRECT ESTIMATE): WEIGHTED AVERAGE OF DIRECT ESTIMATE (UNBIASED, LOW PRECISION) AND INDIRECT ESTIMATE (BIASED, HIGH PRECISION).

WHERE α IS SPECIFIED AS SHOWN EARLIER (FUNCTION OF MSEs, WHICH ARE ESTIMATED FROM HISTORICAL DATA).

THIS ESTIMATE WOULD BE PREFERRED TO THE PRECEDING ONES. ITS PRECISION CAN BE ESTIMATED FROM THE 3-ISLAND SURVEY DATA. ITS BIAS CAN BE ESTIMATED FROM HISTORICAL DATA. THE WEIGHTING PARAMETER (α) IS SELECTED TO MINIMIZE THE MSE (VARIANCE + BIAS²) OF THE ESTIMATE.

THE PRECEDING EXAMPLE IS A VERY SIMPLE EXAMPLE OF A MODEL-ASSISTED ESTIMATE – A SYNTHETIC ESTIMATE BASED ON A WEIGHTED MEAN INVOVLVING A SINGLE AUXILIARY VARIABLE (UNEMPLOYMENT RATES IN INDUSTRIAL CATEGORIES). A MODEL IS IMPLIED, NOT SPECIFIED OR CONSTRUCTED (TESTED, VALIDATED).

FOR THE MODEL-ASSISTED APPROACHES, THE MODEL IS USED SIMPLY TO SUGGEST A FORM FOR THE ESTIMATOR. EVEN IF THE MODEL IS NOT CORRECT THE ESTIMATOR IS STILL DESIGN-CONSISTENT.

A BETTER APPROACH IS TO DEVELOP A TESTED (VALIDATED) MODEL OF THE RELATIONSHIP OF UNEMPLOYMENT RATE TO EXPLANATORY VARIABLES (NOT JUST INDUSTRIAL CATEGORY), AND DERIVE A “BEST LINEAR UNBIASED” (BLU) ESTIMATE OR OTHER ESTIMATE (E.G., A LOGISTIC REGRESSION MODEL) HAVING GOOD STATISTICAL PROPERTIES.

IF THE MODEL IS CORRECTLY SPECIFIED, THE ESTIMATES ARE MODEL-CONSISTENT.

4.2 DEVELOPMENT PLANS

PLAN FOR FIRST YEAR

PRELIMINARY ANALYSIS. IT IS RECOMMENDED TO USE THE COMPOSITE INDIRECT ESTIMATES BASED ON SIMPLE DIRECT ESTIMATES AND SIMPLE INDIRECT MODELS INVOLVING AUXILIARY DATA. THE ESTIMATES WILL BE DERIVED FROM “CROSS-SECTIONAL” MODELS BASED ON DATA FROM A SINGLE SURVEY ROUND (E.G., MAY AND NOVEMBER, SEPARATELY). AFTER THE NOVEMBER SURVEY, COMPOSITE ESTIMATES WILL BE CONSTRUCTED FOR THE YEAR.

FINAL ANALYSIS. DEVELOP "PANEL SURVEY" MODELS FROM TWO SUCCESSIVE SURVEY ROUNDS (MAY AND NOVEMBER).

PLAN FOR FUTURE YEARS, THE FOLLOWING IMPROVEMENTS MAY BE CONSIDERED:

1. DEVELOP IMPROVED VALIDATED CROSS-SECTIONAL MODELS FOR A SINGLE SURVEY ROUND.

2. DEVELOP IMPROVED AND VALIDATED MODELS FROM TWO SUCCESSIVE SURVEY ROUNDS (MAY AND NOVEMBER; CROSS-SECTIONAL AND PANEL MODELS).

3. DEVELOP VALIDATED MODELS FROM THREE SUCCESSIVE SURVEY ROUNDS (MAY, NOVEMBER, MAY).

4. DEVELOP VALIDATED MODELS FROM FOUR SUCCESSIVE SURVEYS (MAY AND NOVEMBER IN TWO SUCCESSIVE YEARS).

5. DEVELOP VALIDATED MODELS FROM SEVERAL SUCCESSIVE YEARS (TIME SERIES ANALYSIS).

6. EXAMINE BAYESIAN ESTIMATION, AS WELL AS THE FREQUENTIST-APPROACH METHOD DESCRIBED ABOVE.

THIS COMPLETES A “SURVEY” OF THE PROPOSED APPROACH (CONCEPTS AND EXAMPLES). WE WILL NOW DESCRIBE THE METHODOLOGY IN GREATER DETAIL. FIRST, WE WILL PRESENT AN OVERVIEW OF THE VARIOUS APPROACHES TO SMALL-AREA ESTIMATION, AND A BRIEF SUMMARY OF MATRIX ALGEBRA AND THE GENERAL LINEAR STATISTICAL MODEL.

4.3 ALTERNATIVE APPROACHES TO SMALL-AREA ESTIMATION

IN WHAT FOLLOWS, NO FORMULAS WILL BE GIVEN FOR VARIANCES OF ESTIMATORS OR ESTIMATES OF VARIANCE OF ESTIMATORS. FOR THE ESTIMATORS TO BE CONSIDERED, THEY ARE COMPLICATED AND APPROXIMATE, AND THEY WILL BE CALCULATED USING A STATISTICAL SOFTWARE PACKAGE (STATA).

NOTE: THE LITERATURE ON SMALL-AREA ESTIMATION IS LARGE, AND MANY ALTERNATIVE PROCEDURES ARE AVAILABLE. FOR THE FIRST YEAR, IT IS RECOMMENDED TO KEEP THE APPROACH SIMPLE (YET BASED ON SOUND THEORETICAL CONCEPTS).

HERE FOLLOWS A SUMMARY OF THE VARIOUS APPROACHES TO ESTIMATION FOR SMALL DOMAINS.

1. DIRECT ESTIMATOR: USE SAMPLE DATA FROM THE DOMAIN.

a. WITHOUT AUXILIARY DATA (FROM THE DOMAIN OR OUTSIDE OF IT). THIS IS THE TRADITIONAL APPROACH. SUCH ESTIMATES ARE NOT AVAILABLE IF THE SAMPLE SIZE IS TOO SMALL (OR ZERO).

b. WITH AUXILIARY DATA

MODEL-ASSISTED ESTIMATOR: GENERALIZED REGRESSION (“GREG”) ESTIMATOR (OR GENERAL REGRESSION ESTIMATOR)

SPECIAL CASES:

RATIO ESTIMATOR (THE USUAL DESIGN-BASED ESTIMATOR)

REGRESSION ESTIMATOR (THE USUAL)

POST-STRATIFIED ESTIMATOR (THE USUAL)

2. INDIRECT ESTIMATOR: USE SAMPLE DATA FROM OUTSIDE THE DOMAIN

SYNTHETIC ESTIMATOR: USE A RELIABLE DIRECT ESTIMATOR FOR A LARGE AREA COVERING SEVERAL SMALL AREAS, AND DERIVE AN INDIRECT ESTIMATE FOR A SMALL AREA UNDER THE ASSUMPTION THAT THE SMALL AREAS HAVE THE SAME CHARACTERISTICS AS THE LARGE AREA.

SPECIAL CASES:

RATIO SYNTHETIC ESTIMATOR

REGRESSION SYNTHETIC ESTIMATOR

STRUCTURE-PRESERVING ESTIMATION (SPREE), ITERATIVE PROPORTIONAL FITTING (IPF), RAKING. EXTENSION OF SYNTHETIC ESTIMATION, MAKING FULLER USE OF RELIABLE DIRECT ESTIMATES (SUCH AS CENSUS COUNTS).

3. COMPOSITE ESTIMATOR (WEIGHTED AVERAGE OF DIRECT AND INDIRECT ESTIMATORS; SPECIAL CASE: JAMES-STEIN ESTIMATORS (“SHRINKAGE” ESTIMATORS))

4. MODEL-BASED ESTIMATORS

NO SAMPLE DATA FOR THE DOMAIN, BUT BASE ESTIMATOR ON A MODEL DEVELOPED FROM THE FULL SURVEY DATA. UNLIKE GREG ESTIMATOR, THE MODEL IS VALIDATED, AND THE ESTIMATOR IS “MINIMUM VARIANCE” FOR LINEAR ESTIMATORS BASED ON THE COMPLETE (FULL SURVEY) SAMPLE.

GENERAL LINEAR MODEL (REGRESSION MODEL)

GENERALIZED LINEAR MODEL (E.G., LOGISTIC REGRESSION MODEL)

LOTS OF VARIATIONS:

FREQUENTIST, BAYESIAN

CROSS-SECTIONAL OR LONGITUDINAL (OR BOTH)

4.4 TECHNICAL BACKGROUND

4.4.1 REVIEW OF MATRIX ALGEBRA

A COLUMN VECTOR IS A VERTICAL ARRAY OF A SEQUENCE OF n ELEMENTS

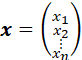IN THIS APPLICATION, THE ELEMENTS ARE SYMBOLS OR VARIABLES OR NUMBERS.

VECTORS ARE INDICATED BY BOLDFACE OR UNDERLINED FONT. A VECTOR CONSISTING OF ONE ELEMENT IS CALLED A SCALAR. FOR EXAMPLE, x MAY DENOTE A SCALAR AND x AND x MAY DENOTE VECTORS.

THE ELEMENT x_i IS CALLED THE i-th COMPONENT OF x. THE NUMBER OF COMPONENTS IN x IS VARIOUSLY CALLED THE DIMENSION OR SIZE OR LENGTH OF x. (THE TERMS “LENGTH” AND “SIZE” HAVE DIFFERENT MEANINGS, TO BE DEFINED LATER.)

THE TRANSPOSE OF x, DENOTED BY x’ or x^T IS THE ROW VECTOR OF LENGTH n, OR .

A MATRIX X OF m ROWS AND n COLUMNS (AN “m by n” MATRIX) IS A RECTANGULAR ARRAY OF ELEMENTS:

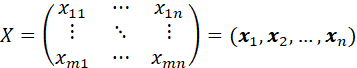
IF x_ij DENOTES THE ELEMENT IN ROW i AND COLUMN j OF MATRIX X, THEN THE TRANSPOSE X’ (OR X^T) IS DEFINED AS THE MATRIX HAVING ELEMENT x_ji IN ROW i AND COLUMN j. NOTE THAT A MATRIX HAVING JUST ONE ROW OR ONE COLUMN IS A VECTOR (OR, IF JUST ONE ROW AND ONE COLUMN, A SCALAR).

IF A MATRIX HAS THE SAME NUMBER OF ROWS AS COLUMNS, IT IS CALLED “SQUARE,” AND THE NUMBER OF ROWS (OR COLUMNS) IS CALLED THE SIZE OR ORDER OF THE MATRIX.

THE PRODUCT OF A SCALAR a AND A VECTOR x WHOSE i-th COMPONENT IS x_i IS THE VECTOR WHOSE i-th COMPONENT is ax_i: a x’ = (ax₁, ax₂,…,ax_n).

IF VECTORS a AND b ARE OF THE SAME LENGTH n, THE VECTOR PRODUCT (OR INNER PRODUCT) IS

THE PRODUCT OF AN n BY m MATRIX A AND AN m BY k MATRIX B IS THE n BY k MATRIX WHOSE i,j-th ELEMENT (I.E., ENTRY IN ROW i AND COLUMN j) IS THE VECTOR PRODUCT OF THE i-th ROW OF A AND THE j-th COLUMN OF B. NOTE THAT THE PRODUCT IS DEFINED ONLY IF THE MATRICES ARE CONFORMABLE, I.E., THE NUMBER OF COLUMNS OF A IS EQUAL TO THE NUMBER OF ROWS OF B.

IN MATRIX NOTATION, A SYSTEM OF SIMULTANEOUS EQUATIONS

y₁ = a₁₁ x₁ + a₁₂ x₂

y₂ = a₂₁ x₁ + a₂₂ x₂

MAY BE REPRESENTED AS

y = A x

WHERE y’ = (y₁, y₂), x’ = (x₁, x₂) AND A = (a₁, a₂) WHERE a₁’ = (a₁₁, a₂₁) AND a₂’ = (a₁₂, a₂₂).

THE INVERSE OF A SQUARE n BY n MATRIX A IS A MATRIX B = A^-1 SUCH THAT AB = I_n, WHERE I_n (THE IDENTITY MATRIX OF ORDER n) IS A SQUARE n BY n MATRIX HAVING 1’s ALONG THE DIAGONAL AND 0’s ELSEWHERE. IF IT EXISTS, IT IS UNIQUE, AND A^-1 A = I_n. IF THE INVERSE EXISTS, THE MATRIX IS CALLED NONSINGULAR OR INVERTIBLE.

THE RANK, r, OF A MATRIX IS THE NUMBER OF LINEARLY INDEPENDENT ROWS OR COLUMNS (WHICH ARE EQUAL). FOR A SQUARE MATRIX, IF r=n, THE MATRIX IS SAID TO BE OF FULL RANK, AND IT IS INVERTIBLE.

EXAMPLES:

THE MATRIX

IS OF RANK 2. ITS INVERSE IS THE SAME MATRIX.

THE MATRIX

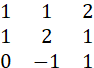
IS SINGULAR (NON-INVERTIBLE), SINCE THE THIRD ROW IS THE FIRST MINUS THE SECOND. IT IS OF RANK 2.

THE MATRIX

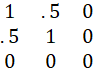
IS SINGULAR, AND OF RANK 2.

A SYMMETRIC MATRIX IS A SQUARE MATRIX FOR WHICH x_ij = x_ji. NOTE THAT A CORRELATION MATRIX IS SYMMETRIC.

A SYMMETRIC n x n REAL MATRIX A IS SAID TO BE POSITIVE DEFINITE IF x^TAx IS POSITIVE FOR EVERY NON-ZERO COLUMN VECTOR x OF n REAL NUMBERS. CORRELATION MATRICES OF FULL RANK ARE POSITIVE DEFINITE.

IF THE SYSTEM OF EQUATIONS SHOWN ABOVE IS SOLVABLE, THE SOLUTION IS x = A^-1 y.

IF x DENOTES AN n-COMPONENT VECTOR, THEN THE VARIANCE OF A VECTOR RANDOM VARIABLE x (DENOTED BY VAR(x) OR V(x) OR var(x)) IS DEFINED TO BE THE n BY n MATRIX Σ WHOSE ij-th ELEMENT IS COV(x_i, x_j). THE i-th DIAGONAL ELEMENT IS THE VARIANCE OF x_i. (THE VARIANCE OF A VECTOR x IS ALSO CALLED THE VARIANCE MATRIX OR THE VARIANCE-COVARIANCE MATRIX OR THE DISPERSION MATRIX.)

IF x AND y DENOTE ANY TWO SCALAR RANDOM VARIABLES AND a DENOTES A SCALAR CONSTANT, THEN VAR(ax) = a²x AND VAR(x + y) = VAR(x) + VAR(y) + 2 COV(x,y).

IF a IS A SCALAR, WE HAVE V(ax) = a²V(x). IF a IS A VECTOR OF LENGTH n, WE HAVE V(ax) = a V(x) a’. IF A IS A MATRIX HAVING n COLUMNS, THEN V(Ax) = AV(x)A’. IF A COVARIANCE MATRIX, Σ, IS OF FULL RANK, IT IS POSITIVE DEFINITE AND HAS A UNIQUE MATRIX SQUARE ROOT, DENOTED BY Σ^1/2. WE HAVE Σ^1/2Σ^1/2 = Σ AND Σ^-1/2Σ^-1/2 = Σ^-1.

EXAMPLE (GAUSS-JORDAN ELIMINATION, SWEEP OPERATOR, SOLUTION OF EQUATIONS, CONSTRUCTION OF MATRIX INVERSE)

REFERENCE: JAMES H. GOODNIGHT, “A TUTORIAL ON THE SWEEP OPERATOR,” THE AMERICAN STATISTICIAN, AUGUST 1979, VOL. 33, NO. 3.

THE FOLLOWING SYSTEM OF LINEAR EQUATIONS WILL BE SOLVED BY PERFORMING, ON BOTH SIDES OF THE EQUATION, A SEQUENCE OF ROW OPERATIONS EQUIVALENT TO PREMULTIPLYING BY A MATRIX. NOTE THAT BY PERFORMING THE SAME OPERATIONS ON AN IDENTITY MATRIX, THE INVERSE IS OBTAINED.

2 x + y = 2

.5 x -.75 y = 1.5

IN MATRIX NOTATION, THIS SYSTEM IS

A x = c

WHERE

AND

SWEEP-OUT PROCEDURE (CAN BE APPLIED TO SYSTEM OF ANY NUMBER OF VARIABLES):

1. MULTIPLY EACH EQUATION BY INVERSE OF FIRST COEFFICIENT (IF NOT EQUAL TO 0, BY 1 OTHERWISE):

x + .5 y = 1

x – 1.5 y = 3

2. SUBTRACT FIRST EQUATION FROM THE OTHERS (IN THIS EXAMPLE JUST FROM THE SECOND EQUATION):

x + .5 y = 1

0 x – 2 y = 2

3. MULTIPLY EACH EQUATION BY INVERSE OF SECOND COEFFICIENT (IF NOT EQUAL TO 0, BY 1 OTHERWISE):

2 x + y = 2

0 x + y = -1

4. SUBTRACT THE SECOND EQUATION FROM EACH OF THE OTHERS (IN THIS EXAMPLE, JUST FROM THE FIRST EQUATION):

2 x + 0 y = 3

0 x + y = -1

5. MULTIPLY EACH EQUATION BY INVERSE OF DIAGONAL ELEMENT:

x = 1.5

y = -1

NOTE THAT THE SYSTEM HAS BEEN SOLVED WITHOUT EXPLICITLY CALCULATING THE INVERSE. THE INVERSE MAY BE OBTAINED BY MULTIPLYING ALL OF THE TRANSFORMING MATRICES TOGETHER (AS NOTED, THE INVERSE IS OBTAINED IN PRACTICE BY PERFORMING ALL OF THE EXECUTED ROW OPERATIONS ON AN IDENTITY MATRIX):

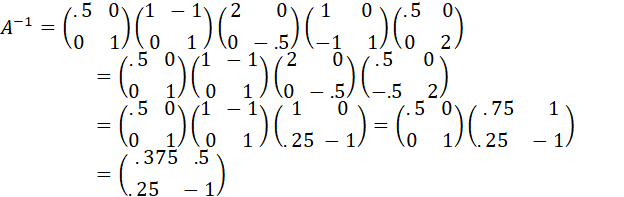
7. CHECK ON CORRECTNESS OF INVERSE:

8. CHECK ON CORRECTNESS OF SOLUTION:

4.4.2 REVIEW OF GENERAL LINEAR STATISTICAL MODEL (GENERAL LINEAR MODEL, GLM)

THE LINEAR STATISTICAL MODEL

y_i = b₁x_1i + b₂x_2i + … + b_px_pi + e_i =

MAY BE REPRESENTED IN VECTOR NOTATION AS:

y_i = x_i’b + e_i, i = 1,…,n

y = Xb + e

where

y’ = (y₁,…,y_n) = vector of n observations on the explained (dependent) variable

x_i.’ = (x_i1,…,x_ip) = vector of p observed explanatory variables for the i-th observation, i = 1,…,n

x._j’ = (x_1j,…,x_nj) = vector of n observations on the j-th explanatory variable, j = 1,…,p

X = (x.₁,…,x._p) = n by p “data” matrix of p explanatory (independent) variables; element x_ij is the i-th observation for the j-th variable

b’ = (b₁,…,b_p) = vector of p parameters (regression coefficients)

e’ = (e₁,…,e_n) = vector of n error terms (model residuals)

n = number of observations

p = number of parameters (b’s).

IT IS ASSUMED (HERE) THAT THE e’s ARE A SEQUENCE OF INDEPENDENT AND IDENTICALLY DISTRIBUTED RANDOM VARIABLES WITH MEAN ZERO AND VARIANCE σ². THE x’s ARE ASSUMED (HERE) TO BE FIXED NUMBERS, NOT RANDOM VARIABLES.

THE “LEAST-SQUARES” ESTIMATES OF THE b’s ARE THE VALUES FOR WHICH THE SUM OF SQUARES OF THE ESTIMATED MODEL RESIDUALS, Σ_i(y_i – x_i’b)², IS A MINIMUM.

THE LEAST-SQUARES ESTIMATES OF THE b’s CAN BE SHOWN TO BE GIVEN BY

THE VARIANCE OF IS

VAR() = VAR((X’X)^-1X’y) = VAR((X’X)^-1X’(Xb+e)) =VAR((X’X)^-1(X’X)b + (X’X)^-1X’e = VAR(b + (X’X)^-1X’e) = VAR(b) + VAR(X’X)^-1X’e) = 0 + (X’X)^-1X’VAR(e)X(X’X)^-1 = (X’X)^-1X’ σ² I X(X’X)^-1 = σ² ((X’X)^-1(X’X)(X’X)^-1 = σ²(X’X)^-1,

I.E.,

VAR() = σ²(X’X)^-1.

THE ESTIMATE OF y GIVEN (ANY VECTOR) x IS

THE VARIANCE OF GIVEN (ANY VECTOR) x IS

VAR() = VAR(x’) = x’ var() x = x’ σ²(X’X)^-1 x.

THE VARIANCE OF GIVEN ALL OF THE SAMPLE VALUES OF x, I.E., GIVEN X, IS

VAR() = σ² X(X’X)^-1X’.

THE VECTOR OF ESTIMATED RESIDUALS IS

THE RESIDUAL SUM OF SQUARES IS HENCE

AN UNBIASED ESTIMATE OF σ² IS

THE ESTIMATED VARIANCE OF b IS OBTAINED BY SUBSTITUTING THE ESTIMATE FOR σ² IN THE EXPRESSION FOR THE VARIANCE OF b:

THE MATRIX X’X IS THE MATRIX OF CROSS-PRODUCTS OF THE EXPLANATORY VARIABLES, AND THE VECTOR X’y IS THE VECTOR OF CROSS PRODUCTS OF THE DEPENDENT VARIABLE y WITH EACH OF THE p EXPLANATORY VARIABLES.

THE LEAST-SQUARES ESTIMATES () ARE THE ONES FOR WHICH THE MODEL ERROR TERMS (RESIDUALS) ARE UNCORRELATED WITH THE EXPLANATORY VARIABLES. IN GEOMETRIC TERMS, THIS MEANS THAT THE ERROR VECTOR e IS ORTHOGONAL TO THE HYPERPLANE GENERATED BY THE COLUMNS OF X:

X’e = X’(y – Xb) = X’(y – Xb) = X’y – X’Xb = X’y – X’Xb = 0.

THIS IMPLIES THAT IS THE SOLUTION TO

X’y – X’X = 0

X’X = X’y

= (X’X)^-1X’y

(ASSUMING THAT X’X IS INVERTIBLE).

A SIMPLER WAY OF REMEMBERING THE FORMULA IS TO OBSERVE THAT IF

y = Xb + e

THEN, MULTIPLYING BOTH SIDES BY X’,

X’y = X’Xb + X’e.

IF WE REQUIRE X’e=0, THEN IT FOLLOWS THAT b MUST SATISFY

X’y = X’X

WHICH ARE THE “NORMAL EQUATIONS” OBTAINED BY MINIMIZING THE RESIDUAL SUM OR SQUARES. ASSUMING THAT X’X IS INVERTIBLE,

= (X’X)^-1X’y.

IT IS IMPORTANT TO REMEMBER THE GENERAL FORM OF THIS ESTIMATOR, BECAUSE IT OCCURS REPEATEDLY IN FORMULAS ASSOCIATED WITH THE GENERALIZED REGRESSION (GREG) ESTIMATOR USED IN SMALL-AREA ESTIMATION.

WEIGHTED LEAST-SQUARES ESTIMATES (OPTIONAL)

THE LEAST-SQUARES ESTIMATES ARE NOT THE ONLY ONES IN COMMON USE. “GENERALIZED” OR “WEIGHTED” LEAST-SQUARES ESTIMATES ARE OBTAINED BY INTRODUCING WEIGHTING FACTORS. THESE FACTORS MAY ACCOUNT FOR DIFFERING VARIANCES OR SELECTION PROBABILITIES. FOR EXAMPLE, IF THE e’s ARE UNCORRELATED WITH VARIANCES var(e_i) , THEN IT MAY BE DESIRED TO MINIMIZE THE WEIGHTED SUM

WHERE w_i = var(e_i)^-1. MORE GENERALLY, IF V DENOTES THE VARIANCE MATRIX OF THE e’s, IT MAY BE DESIRED TO MINIMIZE

THE SOLUTION (ASSUMING THAT X’V^-1X IS INVERTIBLE) IS

(THIS ESTIMATOR IS THE MAXIMUM LIKELIHOOD ESTIMATOR, IF e IS NORMALLY DISTRIBUTED.)

THIS FORMULA MAY BE REMEMBERED BY MULTIPLYING BOTH SIDES OF

y = Xb + e

BY X’V^-1, OBTAINING

X’V^-1y = X’V^-1Xb + X’V^-1e

IF WE REQUIRE X’V^-1e = 0 WE OBTAIN

X’V^-1y = X’V^-1X

WITH THE RESULT

ALTERNATIVELY, WE MAY TRANSFORM

z = Σ^-1/2 y.

THE MODEL BECOMES

z = Σ^-1/2X b + Σ^-1/2e

WHERE THE VARIANCE OF u = Σ^-1/2 e IS NOW A DIAGONAL MATRIX WITH EVERY DIAGONAL ELEMENT HAS THE SAME VALUE (SAY, σ²). THIS MODEL SATISFIES THE REQUIREMENTS OF THE GENERAL LINEAR MODEL.

AS BEFORE, THE NORMAL EQUATIONS MAY BE OBTAINED BY PREMULTIPLYING BOTH SIDES OF THE EQUATION BY THE TRANSPOSE OF THE COEFFICIENT OF b (I.E., BY X’Σ^-1/2), YIELDING

X’Σ^-1/2 z = X’Σ^-1/2Σ^-1/2X b+X’Σ^-1/2Σ^-1/2 e = X’V^-1X b + X’V^-1 e

AND SETTING THE LAST TERM EQUAL TO ZERO, TO OBTAIN

X’Σ^-1/2Σ^-1/2y = X’V^-1X

X’V^-1y = X’V^-1X

AS BEFORE.

THIS EXPRESSION WILL BE SEEN AGAIN, IN THE GREG FORMULAS.

RANDOM-EFFECTS MODELS AND MIXED-EFFECTS MODELS

IN THE PRECEDING, IT IS ASSUMED THAT THE EXPLANATORY VARIABLES x ARE FIXED NUMBERS (NOT RANDOM VARIABLES). SUCH A MODEL IS CALLED A “FIXED EFFECTS” MODEL. A MORE GENERAL MODEL IS THE “MIXED” MODEL, WHICH CONTAINS EXPLANATORY VARIABLES THAT ARE BOTH FIXED AND RANDOM:

y = x’b + z’c + e

y = Xb + Zc + e

WHERE z = (z₁, …,z_q)’ IS A VECTOR OF RANDOM VARIABLES UNCORRELATED WITH THE e’s. FOR EXAMPLE, THE x’s MIGHT INCLUDE AGE, SEX, OCCUPATION AND INDUSTRY INDICATOR VARIABLES, AND THE z’s MIGHT INCLUDE ISLAND INDICATOR VARIABLES.

A NOTE ON NOTATION

THE NOTATION IN THE LITERATURE OF SMALL-AREA ESTIMATION IS CONFUSING. FOR INFINITE-POPULATION MODELS, IT IS CUSTOMARY TO USE UPPER-CASE LETTERS NEAR THE END OF THE ALPHABET (X, Y, Z) FOR RANDOM VARIABLES AND LOWER-CASE LETTERS (x, y, z) FOR REALIZATIONS OF RANDOM VARIABLES. COLUMN-VECTOR RANDOM VARIABLES ARE DENOTED IN BOLDFACE. FOR A LINEAR MODEL, THE DATA MATRIX (COLUMN LIST OF ROW VECTORS FOR EACH OBSERVATION) IS USUALLY DENOTED BY X. PARAMETERS ARE GENERALLY INDICATED BY GREEK LETTERS (α, β, σ) OR BY LATIN LETTERS NEAR THE BEGINNING OF THE ALPHABET (E.G., b FOR A REGRESSION COEFFICIENT. ESTIMATES ARE INDICATED BY CARETS, E.G., .

FOR SAMPLE SURVEY, IT IS CUSTOMARY TO USE LOWER-CASE LETTERS FOR SAMPLE VALUES (x, y, n) AND UPPER-CASE LETTERS FOR POPULATION VALUES (X, Y, N), WITH AN OVER-BAR TO INDICATE A MEAN, AND A CARET TO INDICATE AN ESTIMATE.

THIS PRESENTATION WILL GENERALLY FOLLOW THE NOTATION USED BY J. N. K. RAO IN SMALL AREA ESTIMATION. NOTE THAT RAO USES SLIGHTLY DIFFERENT NOTATION FOR FINITE-POPULATION MODELS AND INFINITE-POPULATION MODELS. (FOR EXAMPLE, RAO USES B FOR THE VECTOR OF REGRESSION COEFFICIENTS IN THE FINITE-POPULATION CASE, AND β FOR THE INFINITE-POPULATION CASE. IN THE FINITE-POPULATION CASE HE DOES NOT USE A SYMBOL FOR THE DATA MATRIX (HE USES X SPECIFICALLY TO DENOTE A COLUMN VECTOR OF POPULATION TOTALS, NOT A GENERAL DATA MATRIX (SEE p. 13 OF THE RAO TEXT)).

4.4.3 MORE ON THE REGRESSION MODEL (OPTIONAL)

DERIVATION OF THE LEAST-SQUARES ESTIMATES FOR A TWO-PARAMETER REGRESSION MODEL, WITHOUT USING MATRIX ALGEBRA.

The model for an individual observation is

y = a + b x + e

or, using index i for the i-th observation,

y_i = a + b x_i + e_i.

We wish to determine values of a and b such that the sum of squares of the residuals (model error terms) is a minimum, i.e., determine a and b so that

Σ(e_i²) = Σ(y_i – a – b x_i)²

is a minimum (the symbol Σ denotes summation over the index i).

This optimization problem is solved by differentiating the preceding expression with respect to a and b, setting the derivatives equal to zero, and solving for a and b. Denote the optimal values by and .

Setting the derivatives with respect to a and b equal to zero we obtain

-2Σ(y_i – – x_i) = 0

-2Σx_i(y_i – – x_i) = 0

Σy_i = n+ Σx_i

Σx_iy_i = Σx_i + Σx_i².

Solving the first equation for a we obtain

= Σy_i/n – Σx_i/n =

Substituting this expression into the second equation and solving for we obtain

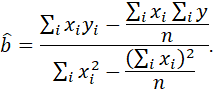
DERIVATION OF THE LEAST-SQUARES ESTIMATES FOR A REGRESSION MODEL, USING MATRIX ALGEBRA.

The model for an individual observation is

y = a + b x + e

or, using index i for the i-th observation,

y_i = a + b x_i + e_i.

In matrix notation, this is (as described earlier)

y = Xb + e.

The sum of squares of the model residuals is

e’e = (y – Xb)’(y – Xb) = y’y – y’Xb – b’X’y + b’X’Xb = y’y – 2y’Xb + b’X’Xb.

We shall differentiate this expression with respect to b, set it equal to zero, and solve for b (denoting the solution as ). The rules for differentiating linear functions and quadratic forms are as follows.

Let y = f(x) denote a scalar-valued function of a vector x’ = (x₁, x₂, …,x_n). The vector of partial derivatives

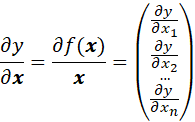
is called the gradient vector, or simply the gradient.

For a linear function

the derivative (gradient) is

(note that the gradient vector is a column vector, a, not a row vector a’).

For a quadratic form,

we have

for any matrix A, and

if A is symmetric. Differentiating the expression for e’e with respect to b (i.e., forming the vector of partial derivatives, or the gradient vector) we obtain:

Setting this equal to zero and solving for b (denoting the solution by ) we obtain

GEOMETRIC INTERPRETATION OF REGRESSION SOLUTION

THE LENGTH, OR EUCLIDEAN LENGTH, OR NORM, OF A VECTOR e IS GIVEN BY THE PYTHAGOREAN THEOREM:

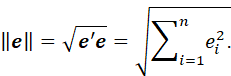
THE ANGLE BETWEEN TWO VECTORS a AND b SATISFIES:

TWO VECTORS a AND b ARE ORTHOGONAL (“PERPENDICULAR”) IF THEIR INNER PRODUCT a’b IS ZERO (IN WHICH CASE THE ANGLE, θ, IS 90 DEGREES).

THE COVARIANCE BETWEEN TWO RANDOM VARIABLES X AND Y IS DEFINED AS

σ_XY = COV(X, Y) = E(X – E(X))(Y – E(Y)).

THE CORRELATION IS

ρ_XY = σ_XY / σ_X σ_Y

WHERE σ_X and σ_Y DENOTE THE STANDARD DEVIATIONS OF X AND Y. THE SAMPLE COVARIANCE AND CORRELATION ARE DEFINED SIMILARLY, WITH SUMS OVER THE SAMPLE UNITS IN PLACE OF EXPECTATIONS.

THE TERMS VARIANCE, COVARIANCE AND CORRELATION APPLY TO RANDOM VARIABLES AND RANDOM SAMPLES. THE TERM ORTHOGONAL APPLIES TO ANY VECTORS (RANDOM OR NOT).

THE MATRIX EXPRESSION

y = Xb

MEANS THAT THE COLUMN VECTOR y CAN BE EXPRESSED AS A LINEAR COMBINATION OF THE COLUMNS OF X.

THE EXPRESSION

y = Xb + e

MEANS THAT y CAN BE EXPRESSED AS A LINEAR COMBINATION OF THE COLUMNS OF X PLUS AN “ADJUSTMENT”, e.

IF IS THE LEAST-SQUARES ESTIMATOR OF b, THEN X’e = 0, I.E., THE COLUMN VECTOR OF MODEL RESIDUALS IS ORTHOGONAL TO THE COLUMN VECTORS OF THE DATA MATRIX X (BY CONSTRUCTION). IF EACH COLUMN VECTOR OF X REPRESENTS A RANDOM VARIABLE, THEN AN UNDERLYING ASSUMPTION OF THE REGRESSION MODEL IS THAT EACH OF THESE EXPLANATORY VARIABLES IS UNCORRELATED WITH THE MODEL ERROR TERM.

THE LEAST-SQUARES ESTIMATE OF THE REGRESSION PARAMETER b IS THE VECTOR THAT MINIMIZES

WE SAW ABOVE THAT THIS SOLUTION MAKES e ORTHOGONAL TO THE COLUMNS OF X.

[END OF OPTIONAL SECTION, “MORE ON THE REGRESSION MODEL”]

4.4.4 DETAILED NUMERICAL EXAMPLE (INCLUDING COMPARISON TO STATA OUTPUT)

WE SHALL EXAMINE IN DETAIL AN EXAMPLE OF A VERY SIMPLE REGRESSION ANALYSIS, USING A SIMULATED DATA SET CONSISTING OF 12 OBSERVATIONS CONSISTING OF ONE DEPENDENT VARIABLE (y) AND ONE EXPLANATORY VARIABLE (x).

AFTER COMPLETING THE ANALYSIS “BY HAND,” THE SAME MODEL WILL BE ANALYZED USING STATA, AND THE RESULTS COMPARED. SOME RESULTS WILL BE SHOWN USING MATRIX ALGEBRA. THE VARIANCE OF A LINEAR COMBINATION (LINEAR FUNCTION, LINEAR FORM) OF THE PARAMETERS WILL BE ESTIMATED.

THE PURPOSE OF THIS EXAMPLE IS TO INCREASE FAMILIARITY WITH THE LINEAR REGRESSION MODEL, WHICH IS A FOUNDATION FOR MODEL-BASED ESTIMATION (AND SMALL-AREA ESTIMATION), TO SHOW COMPARISONS BETWEEN COMPUTATIONS WITH AND WITHOUT MATRIX ALGEBRA, AND TO ILLUSTRATE CONSTRUCTION OF ESTIMATES AND VARIANCES OF ESTIMATES IN ADDITION TO THE USUAL ONES (OF THE INDIVIDUAL REGRESSION PARAMETERS).

A SIMPLE LINEAR MODEL

y = b₁ + b₂ x + e

WILL BE FITTED.

FOR AN INDIVIDUAL OBSERVATION, THE MODEL IS

y_i = b₁ + b₂ x_i + e_i, i = 1,…,n

IN MATRIX NOTATION, THE MODEL IS

y = Xb + e

WHERE y = (y₁,…,y_n)’, X = (1,x), 1 = (1,…,1)’, x = (x₁,…,x_n), b = b₁, b₂)’, e = (e₁,…e_n)’.

THE LEAST-SQUARES ESTIMATES ARE

WITH

WHERE

AND

THE FOLLOWING EXAMPLE IS A TWO-PARAMETER MODEL. AS WILL BE SEEN, CALCULATIONS DONE WITHOUT USING MATRIX ALGEBRA ARE QUITE CUMBERSOME, EVEN FOR THIS SIMPLE TWO-PARAMETER MODEL. THE MATRIX-ALGEBRA FORMULAS ARE QUITE SIMPLE IN FORM, AND EASY TO PROGRAM.

AFTER THIS EXAMPLE, WE SHALL PRESENT ESTIMATION FORMULAS IN MATRIX ALGEBRA (BUT CONTINUE TO SHOW SOME SIMPLE MODELS IN BOTH IN MATRIX AND NON-,MATRIX NOTATION). THE MATRIX NOTATION IS CONSIDERED ESSENTIAL TO UNDERSTANDING THE NATURE OF THE GENERALIZED REGRESSION (GREG) SMALL-AREA ESTIMATORS IN GENERAL CASES – WITHOUT MATRIX NOTATION, THE GENERAL FORMULAS WOULD BE INCOMPREHENSIBLE.

DATA:

y x

6.95 1

8.57 2

10.61 3

12.64 4

16.57 5

18.07 6

19.00 7

19.67 8

22.36 9

23.88 10

25.73 11

29.60 12

Sums and sums of squares (subscripts dropped):

Σx_i= Σx = 78

Σx² = 650

Σy = 213.65

Σy² = 4351.505

Σxy = 1666.38

xmean = Σx/n = 78/12 = 6.5

ymean = Σy/n = 213.63/12 = 17.80417

Estimates (carets dropped, since they are not representable in Stata program code; many decimal places are retained to preserve accuracy and to facilitate comparison to the Stata program output, which retains many decimal places):

b₂ = (Σxy – Σx Σy /n)/(Σx² – (Σx)²/n) = (1666.38 – (78)(213.65)/12)) / (650 – 78²/12) = 1.941643357

b₁ = ymean – b₂ xmean = 17.80417 – 1.941643357 (6.5) = 5.183488182

Predictions (estimates of the expected value of y for a given x, ypred = b₁ + b₂ x) and residuals (resid = y – ypred):

x y ypred resid

1 6.95 7.125 -.175

2 8.57 9.067 -.497

3 10.61 11.008 -.398

4 12.64 12.950 -.310

5 16.57 14.892 1.678

6 18.07 16.833 1.237

7 19.00 18.775 .225

8 19.67 20.717 -1.046

9 12.36 22.658 -.298

10 23.88 24.600 -.720

11 25.73 26.541 -.812

12 29.60 28.483 1.117

(The term “prediction” may also refer to a forecast of an individual value, given x. The numerical value of that prediction is the same as the prediction of the expected value, given x, but the variance (and hence the confidence intervals) are larger for forecasting individual values. In the present application, we are interested only in predicting expected values, given x.)

Estimated variance:

This may be calculated directly by squaring each residual and summing:

s² = Σresid² / (n-2) = 8.5375071 / 10 = .85375071.

It may also be calculated (without the need to calculate each residual) from:

which yields (4351.505 – 5.183488182 ( 213.65) – (1.941643357) (1666.38)) / 10 = .853709269. For this calculation method, it is necessary to retain many decimal places (since the result is the difference between two relatively large numbers).

Estimated root-mean-squared error:

s = sqrt(.85375) = .92399.

Variances and covariance of estimates:

var(b₁) = s² Σx² / (n (Σx² – (Σx)²/n) = .85375 (650) / (12 (650 – 78²/12)) = .3234

var(b₂) = s² / (Σx² – (Σx)²/n) = .85375 / (650 – 78²/12) = .005970

cov(b₁, b₂) = -s² xmean / (Σx² – (Σx)²/n) = -.85375 (6.5) / (650 – 78²/12) = -.03881.

Standard deviations and correlations:

sd(b₁) = sqrt(.3234) = .56868

sd(b₂) = sqrt(.005970) = .077266

corr(b₁, b₂) = -.03881/((.56868)(.077266)) = -.88326.

We shall now estimate the variance of the estimated value (predicted value, expected value) of y given a value of the explanatory variable, x.

We have

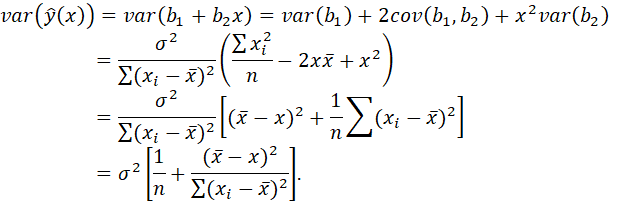
Hence we see that for the value x = , the prediction is

5.183 + 1.942 (6.5) = 17.806.

The variance of the prediction is

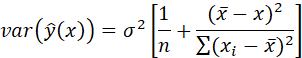
so that the estimated variance for x = is

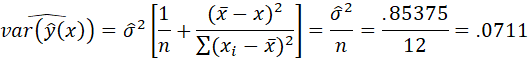
and the standard error is sqrt(.0711) = .267.

For the value x = 3, the prediction is

5.183 + 1.942 (3) = 11.009.

The variance of this prediction is

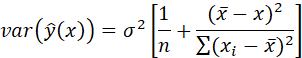
which is estimated as

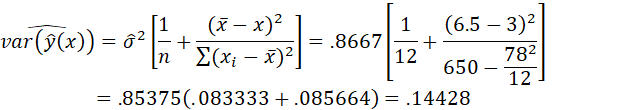
and the standard error is sqrt(.14428) = .3798.

Stata Output

FOLLOWING IS THE COMPUTER PROGRAM OUTPUT FROM THE STATA regress PROCEDURE. IN ADDITION TO THE ESTIMATES PRESENTED ABOVE, IT CONTAINS THE RESULTS ASSOCIATED WITH VARIOUS TESTS OF HYPOTHESIS (F, t, p, 95% confidence limits), WHICH ARE NOT DESCRIBED IN THESE PRESENTATION NOTES (BUT WHICH ARE ADDRESSED IN THE DISCUSSION).

. regress y x

Source | SS df MS Number of obs = 12

-------------+------------------------------ F( 1, 10) = 631.46

Model | 539.106994 1 539.106994 Prob > F = 0.0000

Residual | 8.53750641 10 .853750641 R-squared = 0.9844

-------------+------------------------------ Adj R-squared = 0.9829

Total | 547.644501 11 49.7858637 Root MSE = .92399

------------------------------------------------------------------------------

y | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

x | 1.941643 .0772676 25.13 0.000 1.76948 2.113806

_cons | 5.183485 .5686742 9.12 0.000 3.916399 6.45057

------------------------------------------------------------------------------

. predict resid, residuals

. predict ypred, xb

. list y x etrunc resid ypred

+--------------------------------------------+

| y x etrunc resid ypred |

|--------------------------------------------|

1. | 6.95 1 -.05 -.1751282 7.125128 |

2. | 8.57 2 -.43 -.4967717 9.066772 |

3. | 10.61 3 -.39 -.3984151 11.00842 |

4. | 12.64 4 -.36 -.3100578 12.95006 |

5. | 16.57 5 1.57 1.678298 14.8917 |

|--------------------------------------------|

6. | 18.07 6 1.07 1.236655 16.83335 |

7. | 19 7 0 .2250118 18.77499 |

8. | 19.67 8 -1.33 -1.046632 20.71663 |

9. | 22.36 9 -.64 -.2982744 22.65828 |

10. | 23.88 10 -1.12 -.7199192 24.59992 |

|--------------------------------------------|

11. | 25.73 11 -1.27 -.8115622 26.54156 |

12. | 29.6 12 .6 1.116795 28.48321 |

+--------------------------------------------+

. *Examine variances and covariances. standard deviations, correlations.

. *REMEMBER: regress places the constant term last, i.e., b1 is the slope

. *and b2 is the intercept.

. tempname b V S

. matrix `b'=e(b)

. matrix list `b'

__00000J[1,2]

x _cons

y1 1.9416434 5.1834846

. matrix `V'=e(V)

. matrix list `V'

symmetric __00000K[2,2]

x _cons

x .00597028

_cons -.03880685 .32339039

. matrix `S'=corr(`V')

. matrix list `S'

symmetric __00000L[2,2]

x _cons

x 1

_cons -.88317609 1

. *Check on calculation of correlation between two estimates.

. *Note reversal if indices, to match manual calculations above.

. scalar sdb2new=sqrt(`V'[1,1])

. scalar sdb1new=sqrt(`V'[2,2])

. scalar corb1b2=covb1b2/(sqrt(`V'[1,1])*sqrt(`V'[2,2]))

. display sdb1new, sdb2new, corb1b2

.56867424 .07726761 -.88317609

. *Place the total residual sum of squares here, after observing the results from regress

. *(since total will change them, and predict will operate on the wrong output).

. gen float ressq = resid*resid

. total ressq

Total estimation Number of obs = 12

--------------------------------------------------------------

| Total Std. Err. [95% Conf. Interval]

-------------+------------------------------------------------

ressq | 8.537507 2.910141 2.132328 14.94268

--------------------------------------------------------------

. tempname resvar resss

. matrix `resss' = e(b)

. matrix list `resss'

symmetric __00000N[1,1]

ressq

y1 8.5375067

. scalar `resvar' = `resss'[1,1]/(`nobs'-2.)

. scalar `ressd' = sqrt(`resvar')

. display `resvar', `ressd'

.85375067 .92398632

. save Example1.dta, replace

file Example1.dta saved

. *Construct estimates of linear combinations, and standard errors.

. *Rerun regress (after total).

. regress y x

Source | SS df MS Number of obs = 12

-------------+------------------------------ F( 1, 10) = 631.46

Model | 539.106994 1 539.106994 Prob > F = 0.0000

Residual | 8.53750641 10 .853750641 R-squared = 0.9844

-------------+------------------------------ Adj R-squared = 0.9829

Total | 547.644501 11 49.7858637 Root MSE = .92399

------------------------------------------------------------------------------

y | Coef. Std. Err. t P>|t| [95% Conf. Interval]

-------------+----------------------------------------------------------------

x | 1.941643 .0772676 25.13 0.000 1.76948 2.113806

_cons | 5.183485 .5686742 9.12 0.000 3.916399 6.45057

------------------------------------------------------------------------------

. *Remove data set from memory.

. clear

. *Check that estimates are still in memory.

. tempname ests

. matrix `ests' = e(b)

. matrix list `ests'

__00000O[1,2]

x _cons

y1 1.9416434 5.1834846

. set obs 2

obs was 0, now 2

. egen ID=seq()

. gen float x=0.

. replace x=6.5 if ID==1

(1 real change made)

. replace x=3.0 if ID==2

(1 real change made)

. predict yhatx, xb

. predict stdp, stdp

. predict stdf, stdf

. predict stdr, stdr

. list

+------------------------------------------------------+

| ID x yhatx stdp stdf stdr |

|------------------------------------------------------|

1. | 1 6.5 17.80417 .2667319 .9617154 .8846495 |

2. | 2 3 11.00842 .3798445 .9990157 .8422997 |

+------------------------------------------------------+

THE RESULTS OF THE MANUAL CALCULATIONS AND THE STATA OUTPUT AGREE.

THE PRECEDING EXAMPLE INVOLVED JUST TWO MODEL PARAMETERS (AN INTERCEPT AND A SLOPE). IT IS SEEN THAT WITHOUT USING MATRIX NOTATION, THE FORMULAS ARE COMPLICATED AND EXTENSIVE. FOR ADDITIONAL PARAMETERS, IT IS SIMPLY IMPRACTICAL NOT TO USE MATRIX ALGEBRA.

THE MATRIX FORMULAS ARE USEFUL FOR UNDERSTANDING THE MODELS AND ESTIMATES. THEY WILL BE USED IN THE GREG SMALL-AREA ESTIMATES. IT IS NOT NECESSARY TO PERFORM ANY MATRIX CALCULATIONS MANUALLY – THEY ARE ALL CALCULATED BY STATA. THIS IS TRUE BOTH FOR THE FORMULAS INVOVLED IN ESTIMATION AND IN THE WEIGHT CALIBRATION ASSOCIATED WITH GREG.

5. ESTIMATION FOR DOMAINS HAVING NO SAMPLE: MODEL-BASED ESTIMATION (“INDIRECT” ESTIMATES)

GENERAL LINEAR MODEL (GLM, REGRESSION MODEL, ANOVA)

where

y = explained variable (dependent variable, regressand), e.g., unemployment status

x_j = j-th explanatory variable (independent variable, regressor variable), e.g., age, sex, occupation, industry

b_j = model parameter (regression coefficient)

p = number of model parameters

e = error term.

THE FIRST EXPLANATORY VARIABLE IS OFTEN A CONSTANT TERM (ALL 1’s). THE x_j’s AND e ARE ASSUMED TO BE UNCORRELATED. IT IS OFTEN ASSUMED THAT THE e’s ARE INDEPENDENT AND IDENTICALLY DISTRIBUTED RANDOM VARIABLES FOR DIFFERENT OBSERVATIONS, WITH MEAN ZERO AND VARIANCE σ². THE x’s MAY BE FIXED NUMBERS OR RANDOM VARIABLES. THE PARAMETERS b_j MAY BE ESTIMATED BY THE METHOD OF LEAST SQUARES OR THE METHOD OF MAXIMUM LIKELIHOOD (IF THE LATTER METHOD IS USED, THE PROBABILITY DISTRIBUTION OF THE e’s (AND x’s, IF THEY ARE RANDOM VARIABLES) IS SPECIFIED).

IF THE x’s ARE RANDOM VARIABLES, THEY MUST BE UNCORRELATED WITH THE e’s.

FOR THE i-th OBSERVATION, THE MODEL IS

WHERE n DENOTES THE NUMBER OF OBSERVATIONS.

IN MATRIX NOTATION, THE GLM IS WRITTEN AS

where

x’ = (x₁,…,x_p)

where

y’ = (y₁,…,y_n) (observation vector)

b’ = (b₁,…,b_p) (parameter vector)

e’ = (e₁,…,e_n) (error vector, model residuals)

X = data matrix (element x_ij is i-th observation for j-th variable).

IF THE MEAN OF THE e’s IS ZERO, THE MODEL MAY BE WRITTEN AS:

THE LEAST-SQUARES ESTIMATE OF b IS GIVEN BY

THE EXPLANATORY VARIABLES (x’s) MAY BE CONTINUOUS OR DISCRETE. FOR EXAMPLE:

Age = numerical age in years (actually discrete, but considered continuous)

Age1 = categorical variable, e.g., = 1 if age is between 15 and 19, 0 otherwise

Sex = 0 if male, 1 if female (a binary (0-1) variable)

Island indicator variables, e.g., Island3 = 1 if Abaco, 0 otherwise

Occupational category, e.g., SOC8 = 1 if SOC code is between 7000 and 7999, 0 otherwise

Industrial category, e.g., SIC2 = 1 if the SIC code is between 1000 and 3500, 0 otherwise

THE GLM IS LINEAR IN THE PARAMETERS, BUT DOES NOT HAVE TO BE LINEAR IN THE EXPLANATORY VARIABLES. FOR EXAMPLE, IT MAY CONTAIN TERMS SUCH AS x₁ x₂ OR x₁² OR log x₃.

CATEGORICAL VARIABLES HAVING MORE THAN TWO VALUES (CATEGORIES) ARE NOT REPRESENTED IN THE MODEL BY A SINGLE VARIABLE, BUT BY A SET OF INDICATOR VARIABLES. A SEPARATE INDICATOR VARIABLE IS DEFINED FOR EACH CATEGORY. FOR EXAMPLE:

SUPPOSE

island = 1 for New Providence, 2 for Grand Bahama and 3 for Other Family Islands.

THEN WE MIGHT DEFINE THE THREE ISLAND INDICATOR VARIABLES

_Iisland_1 = 1 for New Providence, 0 otherwise

_Iisland_2 = 2 for Grand Bahama, 0 otherwise

_Iisland_3 = 3 for Other Family Islands, 0 otherwise

IT IS IMPORTANT THAT THE EXPLANATORY VARIABLES ARE NOT LINEARLY DEPENDENT, OR ELSE THE X’X CROSS-PRODUCTS MATRIX CANNOT BE INVERTED. FOR EXAMPLE, NOT ALL OF THE ISLAND INDICATOR VARIABLES MAY BE INCLUDED IN A MODEL, SINCE THEY SUM TO 1 (I.E., ARE LINEARLY DEPENDENT).

A PROBLEM ARISES IF THE EXPLAINED VARIABLE (y) IS BINARY, SINCE THE LINEAR MODEL WOULD ALLOW FOR VALUES OUTSIDE OF THE INTERVAL (0,1). IN THIS CASE, IT IS USEFUL TO CONSIDER AN EXTENSION OF THE GENERAL LINEAR MODEL, CALLED THE GENERALIZED LINEAR MODEL.

IN THE GENERAL LINEAR MODEL, THE MEAN IS REPRESENTED AS A LINEAR FUNCTION (x’b). IN THE GENERALIZED LINEAR MODEL, AN APPROPRIATE FUNCTION OF THE MEAN OF THE EXPLAINED VARIABLE IS REPRESENTED BY A LINEAR FUNCTION. FOR EXAMPLE, THE LOGISTIC MODEL IS:

IN THIS CASE, THE PARAMETERS ARE ESTIMATED BY THE METHOD OF MAXIMUM LIKELIHOOD (NOT BY LEAST-SQUARES).

THE PRECEDING (LOGISTIC) MODEL IS A NONLINEAR RELATIONSHIP BETWEEN p AND THE EXPLANATORY VARIABLES, BUT A LINEAR RELATIONSHIP BETWEEN logit(p) AND THE EXPLANATORY VARIABLES.

EXAMPLE: REGRESSION MODEL OF UNEMPLOYMENT RATE AS A FUNCTION OF AGE, SEX, OCCUPATION AND INDUSTRY

The following variables are present in the 2013 LFS data file:

employ = 1 if employed, 2 if unemployed, 3 if not in labour force

*Recode:

drop if employ==3

generate int employed=0

replace employed=1 if employ==1

sex = Male or Female

age = numerical age in years

i62_business_act = standard industrial code

i63_duties = standard occupational code

island = 1 for New Providence, 2 for Grand Bahama, and 3 for Other Family Islands

Define the following variables, for use in examining basic distributional characteristics overall and by island. (Stata code is shown below.)

gen int agecat=0

replace agecat=1 if age>=15

replace agecat=2 if age>=20

replace agecat=3 if age>=30

replace agecat=4 if age>=40

replace agecat=5 if age>=50

replace agecat=6 if age>=60

replace agecat=7 if age>=70 & age<=99

*This will include missing and literals.

replace agecat=8 if age>99

gen int siccat=0

replace siccat=1 if i62_business_act>=1000

replace siccat=2 if i62_business_act>=3500

replace siccat=3 if i62_business_act>=3600

replace siccat=4 if i62_business_act>=4000

replace siccat=5 if i62_business_act>=4500

replace siccat=6 if i62_business_act>=4900

replace siccat=7 if i62_business_act>=5500

replace siccat=8 if i62_business_act>=5800

replace siccat=9 if i62_business_act>=6400

replace siccat=10 if i62_business_act>=6800

replace siccat=11 if i62_business_act>=6900

replace siccat=12 if i62_business_act>=7700

replace siccat=13 if i62_business_act>=8400

replace siccat=14 if i62_business_act>=8500

replace siccat=15 if i62_business_act>=8600

replace siccat=16 if i62_business_act>=9000

replace siccat=17 if i62_business_act>=9400

replace siccat=18 if i62_business_act>=9700

*Not stated.

replace siccat=19 if i62_business_act>=9900 & i62_business_act<=9999

*Missing.

replace siccat=20 if i62_business_act>9999

gen int occcat=0

replace occcat=1 if i63_duties>=1000

replace occcat=2 if i63_duties>=2000

replace occcat=3 if i63_duties>=3000

replace occcat=4 if i63_duties>=4000

replace occcat=5 if i63_duties>=5000

replace occcat=6 if i63_duties>=6000

replace occcat=7 if i63_duties>=7000

replace occcat=8 if i63_duties>=8000

replace occcat=9 if i63_duties>=9000 & i63_duties<=9999

*Missing.

replace occcat=11 if i63_duties>9999

USED STATA COMMAND tabulate TO EXAMINE DISTRIBUTIONS OF PRECEDING VARIABLES, AND RELATIONSHIP TO UNEMPLOYMENT RATE AND ISLAND.

WE SHALL EXAMINE TWO SIMPLE MODELS. IN THE FIRST, THE UNEMPLOYMENT RATE DIFFERS BY ISLAND. IN THE SECOND, THE UNEMPLOYMENT RATE IS ALSO RELATED TO INDUSTRY CODE.

AN ANALYSIS OF VARIANCE WAS CONDUCTED TO ASSESS WHETHER THE UNEMPLOYMENT RATE DIFFERED BY ISLAND. THE RESULTS OF THIS ANALYSIS INDICATED THAT THE UNEMPLOYMENT RATE IS STATISTICALLY SIGNIFICANTLY DIFFERENT BY ISLAND, AND THAT THE STANDARD DEVIATION OF THE UNEMPLOYMENT RATE OVER ISLANDS IS .0188 (ESTIMATED FROM STATA PROCEDURE xtmixed.

. xtmixed employed cons1 || island: , ml emiterate(10)

note: cons1 dropped because of collinearity

Performing EM optimization:

Performing gradient-based optimization:

Iteration 0: log likelihood = -1438.9801

Iteration 1: log likelihood = -1438.9801

Computing standard errors:

Mixed-effects ML regression Number of obs = 3984

Group variable: island Number of groups = 3

Obs per group: min = 562

avg = 1328.0

max = 2813

Wald chi2(0) = .

Log likelihood = -1438.9801 Prob > chi2 = .

------------------------------------------------------------------------------

employed | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

_cons | .8575724 .0128158 66.92 0.000 .8324539 .8826909

------------------------------------------------------------------------------

Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]

-----------------------------+------------------------------------------------

island: Identity |

sd(_cons) | .0188222 .0124777 .0051332 .0690167

-----------------------------+------------------------------------------------

sd(Residual) | .3470524 .0038899 .3395114 .3547609

------------------------------------------------------------------------------

LR test vs. linear regression: chibar2(01) = 1.68 Prob >= chibar2 = 0.0978

EXAMPLE 1: VERY SIMPLE MODEL: USE NATIONAL ESTIMATE

MODEL:

Unemployment rate y is a binomial random variable with mean

μ_i = μ + d_i

where

μ = overall (national) unemployment rate

μ_i = unemployment rate for island i

d_i = deviation of island rate from national rate (random effect).

IT IS ASSUMED THAT d_i IS A RANDOM VARIABLE WITH MEAN 0 AND STANDARD DEVIATION .0188 OR VARIANCE .00035 (ESTIMATED USING xtmixed). WE HAVE A NATIONAL ESTIMATE OF μ = .16 WITH STANDARD ERROR .0058 (ESTIMATED USING svy).

. svy: proportion employed

(running proportion on estimation sample)

Survey: Proportion estimation

Number of strata = 1 Number of obs = 4108

Number of PSUs = 4108 Population size = 197289

Design df = 4107

--------------------------------------------------------------

| Linearized

| Proportion Std. Err. [95% Conf. Interval]

-------------+------------------------------------------------

employed |

0 | .1611405 .0057512 .1498649 .172416

1 | .8388595 .0057512 .827584 .8501351

--------------------------------------------------------------

WE COULD THEN ESTIMATE THE UNEMPLOYMENT RATE FOR ISLAND i AS .16 WITH MEAN SQUARED ERROR (MSE) = .0188² + .0058² = .00035 + .00003364 = .00038 OR ROOT MSE = .02. THIS YIELDS AN APPROXIMATE 95% CONFIDENCE INTERVAL OF .16 +/- .04 = (.12, .20).

NOTE THAT THE PRECEDING CONFIDENCE INTERVAL IS MUCH WIDER THAN THE CONFIDENCE INTERAL FOR THE UNEMPLOYMENT RATE FOR THE THREE SAMPLED ISLANDS (SE = .0058, HENCE .16 +/- 1.96 (.0058) = (.1486, .1713)).

EXAMPLE 2. A SLIGHTLY MORE COMPLICATED MODEL.

LINEAR STATISTICAL MODEL, WITH ISLAND MEAN RANDOM:

μ_i = μ + b₁ _Isiccat_18 + b₂ _Isiccat_19 + d_i

USING xtmixed, OBTAIN sd(d_i) = .020, sd() = .014.

. *Estimate island standard deviation, with two siccat variables.

. xtmixed employed _Isiccat_18 _Isiccat_19 || island: , ml emiterate(10)

Performing EM optimization:

Performing gradient-based optimization:

Iteration 0: log likelihood = -1411.2256

Iteration 1: log likelihood = -1411.2256

Computing standard errors:

Mixed-effects ML regression Number of obs = 3984

Group variable: island Number of groups = 3

Obs per group: min = 562

avg = 1328.0

max = 2813

Wald chi2(2) = 55.92

Log likelihood = -1411.2256 Prob > chi2 = 0.0000

------------------------------------------------------------------------------

employed | Coef. Std. Err. z P>|z| [95% Conf. Interval]

-------------+----------------------------------------------------------------

_Isiccat_18 | .0150794 .0273164 0.55 0.581 -.0384597 .0686185

_Isiccat_19 | -.3765748 .0506059 -7.44 0.000 -.4757605 -.277389

_cons | .8606127 .0136536 63.03 0.000 .8338522 .8873732

------------------------------------------------------------------------------

Random-effects Parameters | Estimate Std. Err. [95% Conf. Interval]

-----------------------------+------------------------------------------------

island: Identity |

sd(_cons) | .0204437 .0126111 .0061021 .0684918

-----------------------------+------------------------------------------------

sd(Residual) | .3446259 .0038626 .3371379 .3522803

------------------------------------------------------------------------------

LR test vs. linear regression: chibar2(01) = 2.36 Prob >= chibar2 = 0.0623

HENCE MSE IS APPROXIMATELY = .020² + .014² = .0004 + .000196 = .000596 OR ROOT MSE = .024. THIS YIELDS AN APPROXIMATE 95% CONFIDENCE INTERVAL OF .16 +/- .048 = (.112, .208).

IT WOULD HAVE BEEN EXPECTED THAT A MORE COMPLEX MODEL (WITH MORE EXPLANATORY VARIABLES) WOULD LEAD TO A NARROWER CONFIDENCE INTERVAL. THE MODEL IS VERY WEAK. THE STANDARD ERRORS OF THE ESTIMATED VARIANCES ARE SUBSTANTIAL, AND THIS TURNED OUT NOT TO BE THE CASE. IN ANY EVENT, THE CONFIDENCE INTERVAL IN THE TWO EXAMPLES ARE OF SIMILAR SIZE. BY TAKING INTO ACCOUNT THE EXPECTED BIAS ASSOCIATED WITH THE VARIANCE OF THE ISLAND MEANS, THE CONFIDENCE INTERVALS ARE MUCH LARGER THAN THOSE THAT WOULD HAVE BEEN OBTAINED HAD THE VARIANCE OF THE ISLAND MEANS BEEN IGNORED.

THIS HYPOTHETICAL EXAMPLE ILLUSTRATES THE FACT THAT THERE IS LITTLE OR NO ADVANTAGE IN USING A WEAK PARAMETRIC MODEL OVER THE MOST SIMPLE MODEL OF EXAMPLE 1, UNLESS THE MODEL HAS SOME DESCRIPTIVE POWER.

DESPITE THE SHORTCOMINGS OF THIS CONTRIVED EXAMPLE, IT IS USED IN THE COMPUTER PROGRAM TO ILLUSTRATE CALCULATIONS.

AS MENTIONED, THE LINEAR REGRESSION MODEL HAS THE DRAWBACK THAT IT MAY LEAD TO PREDICTIONS OF THE PROBABILITY OF EMPLOYMENT LESS THAN ZERO OR GREATER THAN ONE. THIS IS MORE A PROBLEM WITH PREDICTION OF INDIVIDUAL SCORES THAN AVERAGES OVER GROUPS, AND IT MAY BE VIEWED AS A GROUND FOR DISQUALIFYING THIS MODEL FOR USE WITH BINARY DEPENDENT VARIABLES. THIS DRAWBACK IS OFTEN IGNORED IN SAMPLE SURVEY APPLICATIONS, WHICH ARE PRIMARILY CONCERNED WITH ESTIMATION OF GROUP MEANS OR TOTALS, AND NOT WITH PREDICTION OF INDIVIDUAL VALUES.

THIS SAME DIFFICULTY ARISES IN CONNECTION WITH THE GREG, USED TO CONSTRUCT DESIGN-BASED ESTIMATES FOR SMALL AREAS FOR WHICH SURVEY DATA ARE AVAILABLE (NEXT SECTION). IF IT IS DESIRED TO USE THE GREG ESTIMATOR, WHICH IS A LINEAR ESTIMATOR, THEN THIS DRAWBACK MUST BE ACCEPTED. SINCE THE MODEL-BASED ESTIMATES TYPICALLY DO NOT USE WEIGHTS, THERE IS NO COMPELLING REASON IN MODEL-BASED ANALYSIS TO RESTRICT THE ANALYSIS TO THE USE OF LINEAR ESTIMATORS.

SOME EXAMPLES OF MODEL-BASED ANALYSIS WILL NOW BE EXAMINED, USING STATA COMPUTER PROGRAM OUTPUT.

[DISCUSSION OF COMPUTER OUTPUT HANDOUT]

ESTIMATION OF UNEMPLOYMENT RATES, USING MODEL

FOR A LINEAR MODEL

WHERE v DENOTES THE ISLAND MEAN. ONCE THE MODEL PARAMETERS HAVE BEEN ESTIMATED, THE ESTIMATED UNEMPLOYMENT RATE IS OBTAINED USING THE EQUATION

WHERE x DENOTES THE VALUES OF THE AUXILIARY VARIABLE FOR THE ISLAND OF INTEREST (E.G., THE VALUES OF THE PROPORTIONS OF THE LABOUR-FORCE POPULATION IN THE VARIOUS SIC-CODE CATEGORIES, IF THAT MODEL IS USED). THE MEAN SQUARED ERROR IS OBTAINED FROM THE EQUATION

THE QUANTITY IS OBTAINED AS STATA OUTPUT FROM THE STATA PROGRAM USED TO ESTIMATE THE PARAMETERS , AND THE QUANTITY VAR(v) IS OBTAINED FROM THE STATA PROGRAM xtmixed.

6. ESTIMATION FOR DOMAINS HAVING SMALL SAMPLES: DESIGN-BASED ESTIMATION (“DIRECT” ESTIMATES)

FIRST, CONSIDER THE FOLLOWING ESTIMATOR FOR THE COMPLETE (ALL-COUNTRY) SAMPLE (NOT FOR A SMALL AREA).

BASIC ESTIMATOR, WITH NO AUXILIARY DATA:

WE SHALL CONSIDER THE CASE OF ESTIMATION OF TOTALS.

IT IS ASSUMED THAT THE SAMPLE SIZE IS SMALL, SO THAT THE PRECISION OF THE PRECEDING ESTIMATES IS TOO LOW FOR THEM TO BE OF VALUE. THE OBJECTIVE IS TO USE AUXILIARY DATA TO IMPROVE THE PRECISION OF THE DESIGN-BASED ESTIMATE. A STANDARD APPROACH IS TO USE A GENERALIZED REGRESSION ESTIMATOR, OR GREG.

GENERALIZED REGRESSION ESTIMATOR:

REFER TO pp. 13-25 OF RAO TEXT (SMALL AREA ESTIMATION).

where

i-th observation = (y_i, x_i1i,…,x_pi) = (y_i, x_i^T)

X = (X₁,…X_p)^T = vector of known population totals

and

IS THE SOLUTION OF THE SAMPLE-WEIGHTED LEAST-SQUARES EQUATIONS:

WITH SPECIFIED CONSTANTS c_i >0.

FOR THE MOMENT WE WILL NOT SPECIFY THE c’s. (THEY WILL BE SET TO CONSTRUCT SPECIAL CASES.)

THE PRECEDING MODEL IS A LINEAR MODEL, IN WHICH THE CONSTANT TERM IS THE DESIGN-BASED ESTIMATE AND THE EXPLANATORY VARIABLES ARE DEMEANED AUXILIARY VARIABLES. THE GREG ESTIMATOR IS AN ADJUSTMENT TO THE USUAL DESIGN-BASED ESTIMATE, TAKING INTO ACCOUNT THE AUXILIARY VARIABLES.

WHILE THE GREG IS A LINEAR MODEL, IT IS NOT THE GENERAL LINEAR MODEL (GLM) DESCRIBED EARLIER. THE GLM ESTIMATES PARAMETERS BY MINIMIZING THE SUM OF SQUARES OF THE ESTIMATED MODEL RESIDUALS. THE GREG IS A “CALIBRATION ESTIMATOR” THAT SATISFIES CALIBRATION CONSTRAINTS IN A WAY THAT MODIFIES THE SURVEY DESIGN WEIGHTS IN A MINIMAL FASHION.

AMONG ALL ESTIMATORS OF THE FORM WITH WEIGHTS a_i SATISFYING , THE GREG WEIGHTS w_i* MINIMIZE A CHI-SQUARED DISTANCE,

BETWEEN THE DESIGN WEIGHTS w_i AND THE CALIBRATION WEIGHTS a_i. SEE RAO pp. 13-25 FOR A PROOF OF THIS. THE MINIMIZATION IS ACCOMPLISHED IN A FASHION SIMILAR TO THE PROCEDURE FOR DETERMINING THE GLM LEAST-SQUARES ESTIMATES (I.E., BY DIFFERENTIATING WITH RESPECT TO THE a’s, SETTING THE DERIVATIVES EQUAL TO ZERO, AND SOLVING FOR THE OPTIMAL VALUES OF a_i (DENOTED AS w_i*)).

THE GREG ESTIMATOR IS A LINEAR FUNCTION OF y, AND IT MAY BE REPRESENTED AS

where

THE REVISED WEIGHT w_j* IS THE PRODUCT OF THE DESIGN WEIGHT w_j(s) AND THE ESTIMATION WEIGHT g_j(s). IT IS CALLED THE “CALIBRATION WEIGHT.” NOTE THAT THE WEIGHTS DEPEND ON THE x’s, NOT ON THE y’s. (HENCE, THE WEIGHTS ARE THE SAME NO MATTER WHAT DEPENDENT VARIABLE IS UNDER CONSIDERATION.)

KEY POINT: THE GREG ESTIMATOR IS A LINEAR ESTIMATOR, AND IT LEADS TO REVISED SAMPLE WEIGHTS. IT HAS THE DESIRABLE PROPERTIES THAT THE ESTIMATE OF A LINEAR COMBINATION OF ESTIMATES IS THE SAME LINEAR COMBINATION OF THE ESTIMATES, AND THE WEIGHTED SUM OF THE VALUES FOR AN AUXILIARY VARIABLE IS EQUAL TO THE CONTROL TOTAL. FOR A NONLINEAR ESTIMATOR, SUCH AS ONE BASED ON A LOGISTIC-REGRESSION MODEL, THIS PROPERTY WOULD NOT HOLD.

THIS LATTER POINT,

IS EASY TO SHOW (SEE p. 25 OF RAO TEXT):

Considering as an operator on x, we have

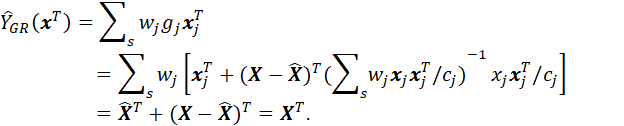
BY SPECIFYING CERTAIN VALUES FOR THE c’s, THE USUAL DESIGN-BASED AUXILIARY-INFORMATION ESTIMATORS MAY BE OBTAINED.

FOR EXAMPLE, IN THE CASE OF A SINGLE AUXILIARY VARIABLE x, IF c_j = x_j, WE OBTAIN THE USUAL RATIO ESTIMATOR

AND

IF ONLY THE POPULATION SIZE IS KNOWN, WE SET x_i =1, RESULTING IN X=N AND .

IF THERE IS A SINGLE AUXILIARY VARIABLE x AND WE SET x_i = (1, x_i)^T AND c_j= 1, WE OBTAIN THE USUAL REGRESSION ESTIMATOR

where

with

and

ALSO, IT MAY BE SHOWN (RAO, p. 14) THAT THE POSTSTRATIFIED ESTIMATOR

MAY BE OBTAINED BY SETTING x_i EQUAL TO THE STRATUM INDICATOR VARIABLE

x_i = (x_1i,…,x_hi)^T

with x_hi = 1 if the i-th observation is in the h-th stratum and c_i =1.

and

with s_.h denoting the sample of elements belonging to poststratum h.

VARIANCES OF THE ESTIMATORS (USED TO CONSTRUCT CONFIDENCE INTERVALS) MAY BE OBTAINED EITHER BY THE USUAL TAYLOR-SERIES LINEARIZATION METHOD BY SUBSTITUTING THE ESTIMATED MODEL RESIDUALS e_i IN PLACE OF y_i IN THE USUAL VARIANCE FORMULA, OR BY SUBSTITUTING g_ie_i IN THE FORMULA, OR BY THE RESAMPLING (SIMULATION) METHOD (“BOOTSTRAP”). (NOTE: THE BOOTSTRAP MAY BE USED TO CONSTRUCT CONFIDENCE INTERVALS DIRECTLY, WITHOUT THE NEED FOR ESTIMATING THE VARIANCE.)

THE TAYLOR SERIES METHOD (LINEARIZATION, DELTA METHOD) FOR ESTIMATING THE VARIANCE OF FUNCTIONS IS BASED ON A TAYLOR SERIES EXPANSION. (OPTIONAL)

If z = f(x), a differentiable function of x, then by Taylor’s Theorem, z may be approximated by

z = f(x₀) + f’(x₀)(x – x₀).

For example, setting x₀ = ,

z = f() + f’())(x – ),

so that

var(z) = (f’())² var(x).

For example, if z = 1/x, then we have the approximation

var(1/x) = (1/)² var(x).

For a function of two variables, we have z = f(x,y) and the approximation

z = f(x₀,y₀) + f_x(x₀,y₀)(x – x₀) + f_y(x₀,y₀)(y – y₀) + 2f_x(x₀,y₀) f_y(x₀,y₀) (x – x₀)(y – y₀)

z = f(,) + f_x(,)(x – ) + f_y(,)(y – ) + 2f_x(,) f_y(,) (x – )(y – )

leading to

var(z) = f_x²(,) var(x) + f_y²(,) var(y) + 2f_x(,) f_x(,) cov(x,y).

For example, if z = x/y, then we have the approximation

var(x/y) = (1/)² var(x) + (/²)² var(y) – 2 (/³) cov(x,y)

= (/)² (var(x) / ² + var(y) / ² – 2 cov(x,y) / () ).

[END OF OPTIONAL SECTION ON TAYLOR SERIES METHOD.]

THE PRECEDING FORMULAS PERTAIN TO USING THE GENERALIZED REGRESSION (GREG) ESTIMATOR FOR THE ENTIRE POPULATION.

THE GREG APPROACH MAY BE USED TO CONSTRUCT DESIGN-BASSED ESTIMATES FOR SMALL AREAS (DOMAINS). THE REGRESSION-MODEL ESTIMATION MAY BE ESTIMATED FROM THE FULL SAMPLE (“SURVEY REGRESSION”) OR JUST FOR THE SMALL AREA. IN EITHER CASE, THE VARIANCE OF THE ESTIMATOR IS DOMINATED BY THE VARIANCE OF THE FIRST TERM, . THIS MEANS THAT THE VARIANCE IS INVERSELY PROPORTIONAL TO THE SAMPLE SIZE FOR THE SMALL AREA. IN ESSENCE, THE GREG ESTIMATOR MAKES EFFECTIVE USE OF AUXILIARY INFORMATION FROM WITHIN THE SMALL AREA, BUT LIMITED USE OF INFORMATION FROM OUTSIDE THE AREA (BECAUSE IT IS SIMPLY AN ADJUSTMENT TO THE USUAL DESIGN-BASED ESTIMATOR BASED ON WITHIN-SMALL-AREA DATA).

ANOTHER LIMITATION OF THE GREG ESTIMATOR IS THAT, AS A LINEAR ESTIMATOR, IF USED TO ESTIMATE PROPORTIONS IT MAY PRODUCE ESTIMATES FALLING OUTSIDE OF THE RANGE (0,1). AS DISCUSSED EARLIER, THIS IS NOT CONSIDERED A FATAL DRAWBACK. IF IT IS DESIRED TO USE THE GREG (CALIBRATION-WEIGHT) APPROACH, THEN IT IS NECESSARY TO USE A LINEAR MODEL.

THE TWO PRECEDING LIMITATIONS SHOULD BE KEPT IN MIND IN DECIDING WHETHER TO USE GREG ESTIMATES. WHILE GREG ESTIMATORS HAVE DESIRABLE PROPERTIES, THEY ARE NOT THE ONLY ESTIMATORS AVAILABLE FOR SMALL-AREA ESTIMATION.

THE NEXT SECTION EXAMINES AN ALTERNATIVE APPROACH TO SMALL-AREA ESTIMATION, VIZ., THE USE OF COMPOSITE ESTIMATORS.

7. ESTIMATION FOR DOMAINS HAVING SMALL SAMPLES: MODEL-ASSISTED ESTIMATION (“INDIRECT” ESTIMATION)

RECALL, IN THE EXAMPLES GIVEN EARLIER ABOUT ESTIMATING THE BAHAMAS UNEMPLOYMENT RATE USING TWO DIFFERENT ESTIMATORS, THAT A COMPOSITE ESTIMATOR WAS FORMED AS A WEIGHTED AVERAGE OF TWO ESTIMATORS, WHERE THE WEIGHTS WERE INVERSELY RELATED TO THE MEAN SQUARED ERRORS. THIS APPROACH WILL BE USED HERE.

SUPPOSE THAT WE HAVE TWO ESTIMATORS FOR A SMALL AREA, ONE A DESIGN-BASED (“DIRECT”) ESTIMATOR BASED ON A SMALL SAMPLE SIZE, AND ONE A MODEL-BASED (“INDIRECT”) ESTIMATE. THE DESIGN-BASED ESTIMATE IS UNBIASED BUT HAS A LARGE VARIANCE, AND THE MODEL-BASED ESTIMATE IS BIASED BUT HAS A SMALL VARIANCE.

THE COMPOSITE ESTIMATOR IS:

where

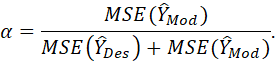
THE GOAL HERE IS TO MINIMIZE THE MEAN SQUARED ERROR OF THE ESTIMATOR. THE MEAN SQUARED ERROR IS EQUAL TO

MSE = VARIANCE + BIAS².

THE DESIGN-BASED ESTIMATES ARE UNBIASED, SO

THE BIAS MAY BE ESTIMATED FROM HISTORICAL DATA (TO ESTIMATE THE MEAN DIFFERENCE BETWEEN AN ISLAND’S UNEMPLOYMENT RATE AND THAT OF THE THREE ISLANDS THAT ARE ALWAYS INCLUDED IN THE SURVEY). ALTERNATIVELY, IT MAY BE ESTIMATED FROM AN ANALYSIS OF VARIANCE (ANOVA) IN WHICH ISLAND IS A RANDOM EFFECT. THE VARIANCE OF THE ISLAND VARIABLE IS THE VARIANCE OF THE BIAS (OVER THE SAMPLE OF ISLANDS). IF OTHER EXPLANATORY VARIABLES ARE INCLUDED IN THE MODEL (SUCH AS INDUSTRIAL CATEGORY INDICATOR VARIABLES), A MIXED-EFFECTS ANOVA IS USED (E.G., USING STATA COMMAND xtmixed.

SUCH AN ANALYSIS WAS DONE (USING THE SAMPLE DATA SET AND A HYPOTHETICAL SURVEY DESIGN), AND SHOWED THAT THE STANDARD DEVIATION OF THE ISLAND MEANS WAS ABOUT .02, OR VARIANCE = .0004.

HENCE WE OBTAIN

IN SUMMARY, THE PROCEDURE FOR ESTIMATING THE UNEMPLOYMENT RATE FOR SMALL ISLANDS IS:

IF NO SAMPLE IS AVAILABLE FOR THE SMALL ISLAND, USE THE MODEL-BASED ESTIMATE (FROM THE STATA POSTESTIMATION COMMAND predict).

NOTE THAT THE SIMPLEST MODEL IS TO USE THE NATIONAL ESTIMATE AND ESTIMATE THE ISLAND VARIANCE AS , WHERE v IS THE ISLAND-TO-ISLAND VARIANCE (SEE EXAMPLE 2 CONSIDERED EARLIER).

IF SOME SAMPLE DATA ARE AVAILABLE FOR THE SMALL ISLAND, CALCULATE BOTH THE USUAL DESIGN-BASED ESTIMATE (FROM THE SAMPLE DATA) AND THE MODEL-BASED ESTIMATE (FROM THE MODEL), AND FORM A WEIGHTED MEAN OF THE TWO ESTIMATES, AS DESCRIBED ABOVE.

THIS ESTIMATE IS REFERRED TO AS A COMPOSITE ESTIMATE FOR THE SMALL AREA, COMBINING A DIRECT DESIGN-BASED ESTIMATE AND AN INDIRECT MODEL-BASED ESTIMATE. THIS PROCEDURE BALANCES THE POTENTIAL BIAS OF THE MODEL-BASED ESTIMATE WITH THE INSTABILITY (LARGE STANDARD ERROR) OF THE DESIGN-BASED ESTIMATE. (THE POTENTIAL BIAS ARISES SINCE THE MODEL MAY NOT BE CORRECT FOR THE SMALL AREA.)

NOTE THAT THIS ESTIMATE IS BASED ON DATA FROM A SINGLE LFS ROUND (MAY OR NOVEMBER).

8. CONSTRUCTION OF AN ANNUAL ESTIMATE FROM THE MAY AND NOVEMBER ESTIMATES

THE PRECEDING MATERIAL HAS BEEN LIMITED TO THE CONSTRUCTION OF ESTIMATES USING DATA FROM A SINGLE SURVEY (MAY OR NOVEMBER). AFTER THE NOVEMBER SURVEY IS COMPLETED, IT IS ALSO OF INTEREST TO CONSTRUCT AN ANNUAL ESTIMATE OF THE UNEMPLOYMENT RATE (OR OTHER PARAMETERS OF INTEREST, FOR THE FULL POPULATION AND FOR SUBPOPULATIONS).

THERE ARE TWO MAIN APPROACHES TO THIS PROBLEM:

1. DESIGN-BASED APPROACH (RECOMMENDED FOR THIS YEAR): CONSTRUCT THE MAY AND NOVEMBER ESTIMATES SEPARATELY, AND CONSTRUCT A COMBINED ANNUAL ESTIMATE FROM THOSE ESTIMATES AND A KNOWLEDGE OF THE PROPORTION OF MATCHING SAMPLE UNITS AND THE CORRELATION BETWEEN MATCHING SAMPLE UNITS. NOTE THAT THIS CORRELATION IS DIFFERENT FOR EVERY DEPENDENT VARIABLE OR SUBPOPULATION CONSIDERED.

2. PANEL-DATA MODEL-BASED APPROACH: COMBINE THE MAY AND NOVEMBER DATA SETS INTO A SINGLE “PANEL” DATA SET, AND CONSTRUCT AN ESTIMATE FROM THIS DATA SET. THIS APPROACH REQUIRES UNIQUE IDENTIFICATION OF SAMPLE UNITS OCCURRING IN BOTH SURVEYS (TO KEEP TRACK OF WHICH SAMPLE UNITS ARE MATCHED). ESTIMATION IS DONE USING STATA PROGRAMS xtreg OR xtmixed, AS APPROPRIATE. THIS APPROACH IS A CONVENIENT GENERAL APPROACH FOR CONSTRUCTING ESTIMATES FOR MANY PARAMETERS OF INTEREST (I.E., NOT JUST THE UNEMPLOYMENT RATE). THIS APPROACH TAKES INTO ACCOUNT STRATIFICATION AND CLUSTERING, BUT DOES NOT TAKE INTO ACCOUNT THE fpc (SINCE THE fpc IS NOT AN INPUT PARAMETER FOR xtreg or xtmixed). (IT MAY BE USED FOR fpc’s NEAR 0 (FIXED-EFFECTS OR RANDOM-EFFECTS MODELS) OR 1 (FIXED-EFFECTS MODEL). THE STATA SURVEY PROCEDURES ARE NOT DESIGNED FOR TIME-SERIES APPLICATIONS, AND THE TIME SERIES PROCEDURES ARE NOT DESIGNED FOR DESCRIPTIVE SURVEYS.)

WE SHALL NOW DESCRIBE THE FIRST APPROACH, WHICH IS REFERRED TO AS ESTIMATION OF MEANS OR TOTALS IN THE CASE OF REPEATED SURVEYS, OR OF SAMPLING ON TWO OCCASIONS.

REFERENCES:

DES RAJ, SAMPLING THEORY, MCGRAW-HILL BOOK COMPANY, 1968 (REVISED AS SAMPLE SURVEY THEORY BY DES RAJ AND PROMOD CHANDHOK, 2012).

DES RAJ, “ON SAMPLING OVER TWO OCCASIONS WITH PROBABILITY PROPORTIONATE TO SIZE,” ANNALS OF MATHEMATICAL STATISTICS, VOL. 36, 1965.

BEFORE CONSTRUCTING A COMBINED ANNUAL ESTIMATE, AN IMPROVED ESTIMATE OF THE CURRENT VALUE (MAY OR NOVEMBER) WILL BE CONSTRUCTED, USING DATA FROM BOTH SURVEYS.

CURRENT ESTIMATES

BASED ON THE SURVEY DATA FROM A SINGLE ROUND (MAY OR NOVEMBER), A CURRENT ESTIMATE MAY BE CONSTRUCTED, USING DATA FROM THAT SINGLE ROUND. AN IMPROVED ESTIMATE MAY BE OBTAINED BY COMBINING DATA FROM TWO SUCCESSIVE SURVEY ROUNDS.

THE POPULATION IS SAMPLED ON TWO OCCASIONS, MAY AND NOVEMBER. A PORTION OF THE MAY SAMPLE IS RETAINED (MATCHED) IN THE NOVEMBER SURVEY. LET y DENOTE THE MEASUREMENT FOR THE FIRST SURVEY AND x DENOTE THE MEASUREMENT FOR THE SECOND SURVEY.

CLOSED-FORM SOLUTIONS TO THIS PROBLEM ARE AVAILABLE ONLY FOR SPECIAL CASES. IN THE FOLLOWING WE SHALL DESCRIBE THE CASE IN WHICH SIMPLE RANDOM SAMPLING IS USED, THE SAME-SIZE SAMPLE IS USED IN BOTH SURVEYS, AND IT IS DESIRED TO ESTIMATE THE MEAN. THE fpc IS IGNORED, AND THE VARIANCE IS ASSUMED TO BE THE SAME FOR BOTH SURVEYS. IN THE SECOND REFERENCED CITED ABOVE, RAJ DESCRIBES THE CASE IN WHICH CLUSTERS ARE SELECTED WITH PROBABILITIES PROPORTIONAL TO SIZE.

THE FOLLOWING NOTATION (MAINLY FOLLOWING THE RAJ TEXT) IS USED:

n = sample size for each survey

λ = proportion of first-survey sample units that are retained in the second survey (i.e., the proportion of “matching” units)

m = sample size of matching units in second survey = nλ

μ = proportion of sample units that are not matched

u = n – m = nμ = number of non-matching sample units

x = measurement in first survey (e.g., unemployment)

y = measurement in second survey

M_h = mean on occasion h (h = 1 for first survey, h = 2 for second survey)

σ² = variance

ρ = correlation between matching sample units (i.e., of unemployment for individuals in the same household).

WE SHALL CONSIDER TWO ESTIMATORS. ONE IS BASED ON A SIMPLE “DIFFERENCE ESTIMATOR,” AND THE OTHER IS THE MINIMUM-VARIANCE ESTIMATOR.

CURRENT ESTIMATE BASED ON A DIFFERENCE ESTIMATOR

WE BEGIN BY CONSTRUCTING AN ESTIMATE OF M₂ FOR THE SECOND OCCASION (OR “ROUND”), USING DATA FROM BOTH ROUNDS. SUPPOSE THAT WE INITIALLY CONSIDER THE FOLLOWING ESTIMATE FOR ROUND 1, BASED ON DATA JUST FROM THAT ROUND:

FOR ESTIMATING M₂, WE HAVE TWO INDEPENDENT ESTIMATES:

ESTIMATE BASED ON THE UNMATCHED PART:

ESTIMATE FOR THE MATCHED PART, BASED ON A DIFFERENCE ESTIMATOR:

IT MAY BE SHOWN (SEE RAJ) THAT THE VARIANCES OF THESE TWO ESTIMATORS ARE:

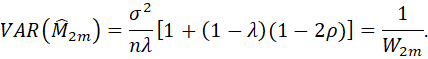
THE COMBINED ESTIMATE IS OBTAINED BY FORMING A WEIGHTED AVERAGE OF THE TWO PRECEDING ESTIMATES, WHERE THE WEIGHTS ARE INVERSES OF THE RESPECTIVE VARIANCES:

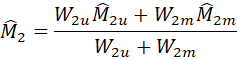
WITH VARIANCE:

) =

NOTE THAT THE VARIANCE DEPENDS ON THE CORRELATION, ρ, BETWEEN MATCHING SAMPLE UNITS IN THE TWO SURVEY ROUNDS. (CORRELATION IS INTRODUCED BY MATCHING OF SAMPLE UNITS, E.G., BY RETAINING SAMPLE UNITS FROM A PREVIOUS SURVEY.)

THE PRECEDING IS A CURRENT ESTIMATE FOR THE SECOND ROUND, USING DATA FROM BOTH ROUNDS. A SIMILAR IMPROVED ESTIMATE COULD BE CONSTRUCTED FOR THE FIRST SURVEY ROUND (BUT IT IS OF LESS INTEREST, SINCE SIX MONTHS HAVE PASSED).

THE PRECEDING ESTIMATOR, BASED ON A DIFFERENCE ESTIMATOR, IS CONCEPTUALLY SIMPLE. A MORE COMPLEX ESTIMATOR IS THE MINIMUM-VARIANCE ESTIMATOR.

MINIMUM-VARIANCE CURRENT ESTIMATE

THE FOLLOWING NOTATION IS INTRODUCED:

= mean for unmatched sample, first round

= mean for matched sample, first round

= mean for unmatched sample, first round

= mean for matched sample, first round

(A single prime indicates that the mean is based on units sampled on a single occasion, and a double prime indicates that the mean is based on units sampled on two occasions.)

IT CAN BE SHOWN THAT THE BEST LINEAR ESTIMATOR OF M₂ IS GIVEN BY:

WITH VARIANCE

ONCE AGAIN, THE VARIANCE DEPENDS ON THE CORRELATION, ρ, BETWEEN MATCHING SAMPLE UNITS IN SUCCESSIVE SURVEY ROUNDS.

ESTIMATION OF MEAN ON TWO OCCASIONS (ANNUAL MEAN)

THE MINIMUM-VARIANCE ESTIMATE OF THE ANNUAL MEAN IS OBTAINED BY SUMMING THE PRECEDING MINIMUM-VARIANCE ESTIMATE FOR M₂ AND A SIMILAR ONE FOR M₁:

WITH VARIANCE:

IF, INSTEAD OF USING THE PRECEDING MINIMUM-VARIANCE ESTIMATOR, THE ANNUAL MEAN IS ESTIMATED BY TAKING THE SIMPLE AVERAGE ON EACH OCCASION, THE ESTIMATOR IS:

WITH VARIANCE

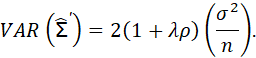
THE RELATIVE GAIN IN PRECISION IN USING OVER IS

THE FOLLOWING TABLE SHOWS THE RELATIVE PERCENTAGE GAIN IN PRECISION IN USING OVER FOR COMBINATIONS OF ρ AND λ. (RESULTS FOR λ AND 1-λ ARE IDENTICAL.)

ρ	Λ
ρ	1	1/2	1/3	1/4	0
.5	0	4.2	3.7	3.1	0
.6	0	5.6	5.0	4.2	0
.7	0	7.2	6.4	5.3	0
.8	0	8.8	7.8	6.6	0
.9	0	10.6	9.5	7.8	0

THIS TABLE SHOWS THAT THE RELATIVE PERCENTAGE GAIN IN PRECISION IS NOT HIGH, EVEN FOR HIGH VALUES OF ρ. THE PRESENT LFS SURVEY DESIGN INVOLVES MATCHING ENUMERATION DISTRICTS, NOT MATCHING HOUSEHOLDS. IT IS EXPECTED THAT THE VALUE OF ρ IS NOT LARGE. AN ANALYSIS OF VARIANCE (STATA PROCEDURE loneway) CAN BE DONE TO ESTIMATE ρ (NEEDED FOR THE ESTIMATION FORMULA) IF A COMBINED MAY-NOVEMBER DATA BASE IS ASSEMBLED. OTHERWISE, IF THIS IS NOT DONE AND THE ANNUAL ESTIMATE IS TAKEN SIMPLY AS THE MEAN OF THE MAY AND NOVEMBER MEANS, RELATIVELY LITTLE LOSS IN PRECISION WOULD BE EXPECTED.

SAMPLING ON MORE THAN TWO OCCASIONS

THE PRECEDING SHOW HOW TO CONSTRUCT COMBINED ESTIMATES FROM TWO SUCCESSIVE SURVEYS. SIMILAR METHODS CAN BE EMPLOYED TO COMBINE RESULTS FROM THREE OR MORE SURVEYS. IN THE FIRST REFERENCE CITED EARLIER, RAJ DISCUSSES A SPECIAL CASE IN WHICH SUCCESSIVE SURVEYS ARE ASSUMED TO FOLLOW AN AUTOREGRESSIVE PROCESS. (TO APPLY THIS APPROACH TO DATA THAT INCLUDE TWO SURVEYS IN THE SAME YEAR, THE AUTOREGRESSIVE MODEL WOULD HAVE TO INCLUDE A SEASONAL COMPONENT.)

IF IT IS DESIRED TO BASE ESTIMATES ON MORE THAN TWO SURVEYS, IT IS RECOMMENDED THAT DATA FROM SUCCESSIVE SURVEYS BE ASSEMBED INTO A SINGLE DATA BASE, AND THAT PANEL-DATA OR TIME-SERIES MODELING BE USED TO CONSTRUCT THE ESTIMATES.

THE AVAILABILITY OF A COMBINED MULTI-YEAR DATA BASE WOULD BROADEN THE OPPORTUNITIES FOR MAKING SMALL-AREA ESTIMATES UTILIZING BOTH CROSS-SECTIONAL AND TIME-SERIES DATA.

9. COMPUTATION (DATA PROCESSING)

THE CALCULATIONS FOR CONSTRUCTING THE PRECEDING ESTIMATES MAY BE DONE USING THE STATA STATISTICAL PROGRAM PACKAGE (THE LATEST VERSION POSSESSED BY THE DEPARTMENT).

THE MAY DATA SET WILL BE STORED IN A MICROSOFT WINDOWS FOLDER NAMED DataAnalysis/BahamasLFS2014May, THE NOVEMBER DATA SET IN DataAnalysis/BahamasLFS2014Nov, AND THE COMBINED DATA SET (IF ASSEMBLED) IN DataAnalysis/BahamasLFS2014Comb. THE DO FILE FOR MAY WILL BE NAMED Do1BahamasLFS2014May.do, AND THE CORRESPONDING LOG FILE WILL BE NAMED Do1BahamasLFS2014May.log.

FOR EACH SURVEY, ALL OF THE ANALYSIS WILL BE DOCUMENTED IN A STATA “DO” (COMMAND, .DO) FILE, LIBERALLY EMBEDDED WITH COMMENTS TO DESCRIBE WHAT ANALYSIS IS BEING DONE. IT IS INTENDED THAT THE DO FILE WILL CONSTRUCT ALL ESTIMATES SHOWN IN THE DEPARTMENT’S ANNUAL REPORT. THAT IS, IF THE DO FILE IS EXECUTED WITH THE CLEANED SURVEY DATA FILE, THE OUTPUT (LOG) FILE WILL CONTAIN ALL OF THE ESTIMATES INCLUDED IN THE ANNUAL REPORT, WITH FULL EXPLANATION AND LABELING. IT IS HIGHLY RECOMMENDED THAT THIS SAME APPROACH BE USED FOR CLEANING THE RAW SURVEY DATA FILE, I.E., A DO FILE COULD BE EXECUTED TO CONVERT THE RAW DATA FILE TO THE CLEAN DATA FILE USED IN THIS ANALYSIS.

THE DO FILE WILL CONTAIN A HEADER (SERIES OF COMMENTS AT THE BEGINNING) THAT SPECIFIES THE FOLLOWING, FOR EXAMPLE (FOR THE MAY 2014 APPLICATION, IN DO FILE Do1BahamasLFS2014May.do):

version 10.0

set more off

clear

capture log close

*In the following line, specify the name of the folder in which the data files are located.

global direct1 "C:\DataAnalysis\BahamasLFS2014\"

log using "$direct1\Do1BahamasLFS2014May.log", replace

*Place file header following the preceding statement, so it shows up in the log file.

*File name: Do1BahamasLFS2014May.do

*Project: Bahamas LFS 2014 May

*Creator: Joseph Caldwell

*Date created: 23 June 2014

*Modifier:

*Date modified: 23 June 2014

*Purpose: Construct estimates of unemployment, using direct and indirect estimators.

*Input files: Bahamas_LFS_May2014_individual.dta

*Note that the input file is NEVER modified.

*Output files: ResultsFile.dta.

*Called programs: None.

*Log file: Do1BahamasLFS2014May.log

*Repeat, as comments, commands prior to turning log on:

*version 10.0

*set more off

*clear

*capture log close

*In the following line, specify the name of the folder in which the data files are located.

*global direct1 "C:\DataAnalysis\BahamasLFS2014May\"

*log using "$direct1\Do1BahamasLFS2014May.log", replace

USING SAMPLE COMPUTER OUTPUT, EXAMPLES WILL BE PRESENTED AND DISCUSSED FOR THE MAIN STATA PROCEDURES TO BE USED IN THE DATA ANALYSIS. THESE INCLUDE (BUT ARE NOT LIMITED TO) THE FOLLOWING:

describe

summarize

tabulate

svy

mean

proportion

total

regress

logit

anova

loneway

xtreg

xtmixed

THE PRINTOUT WILL INCLUDE EXAMPLES OF MATRIX OPERATIONS.

[EXAMINE SAMPLE COMPUTER PRINTOUT.]

10. RECOMMENDATIONS FOR ANALYSIS OF MAY AND NOVEMBER SURVEY DATA

FOR MAY:

1. CONSTRUCT DESIGN-BASED ESTIMATES OF MAY DATA SET (USING A COMPLETE SPECIFICATION OF THE SURVEY DESIGN). (FOR THIS ANALYSIS, MAKE USE OF THE STATA svy COMMAND.)

2. ASSEMBLE AVAILABLE AUXILIARY DATA THAT RELATES TO EMPLOYMENT / UNEMPLOYMENT (E.G., AGE, INDUSTRIAL CATEGORY, OCCUPATION, PREVALENCE OF TOURIST OPERATIONS)

3. ASSEMBLE HISTORICAL DATA ON EMPLOYMENT RATES FOR INDIVIDUAL ISLANDS (TO ESTIMATE BIASES).

4. DEVELOP MODELS RELATING UNEMPLOYMENT TO AUXILIARY VARIABLES, AND ESTIMATE THE VARIANCE BETWEEN ISLANDS (OR THE BIAS OF THE ISLAND ESTIMATE FROM THE NATIONAL ESTIMATE).

5. CONSTRUCT WHATEVER SMALL-AREA ESTIMATES ARE FEASIBLE.

6. USE THE “BEST” ESTIMATE, WHERE “BEST” REFERS BOTH TO ACCURACY OF THE ESTIMATE AND THE AMOUNT OF EXPERTISE AND EFFORT REQUIRED TO CONSTRUCT IT.

FOR NOVEMBER:

PRELIMINARY ANALYSIS

1. CONSTRUCT NOVEMBER CURRENT ESTIMATE, BASED ON NOVEMBER SURVEY DATA (SAME AS STEPS 1-6 LISTED ABOVE).

2. ASSEMBLE A COMBINED MAY-NOVEMBER DATA SET, TO ESTIMATE THE CORRELATIONS REQUIRED TO ESTIMATE THE VARIANCE OF AN ANNUAL ESTIMATE BASED ON THE MAY AND NOVEMBER DATA, AND CONSTRUCT THE COMBINED NATIONAL ESTIMATE. IF RESOURCES DO NOT PERMIT CONSTRUCTION OF THE COMBINED DATA SET, USE THE AVERAGE OF THE TWO SURVEYS AND A CONSERVATIVE ESTIMATE OF THE VARIANCE.

FINAL ANALYSIS

ANALYZE THE COMBINED MAY-NOVEMBER DATA SET AS A TWO-ROUND PANEL SAMPLE, USING THE STATA COMMANDS xtset AND xtreg.

11. CONSIDERATIONS FOR FUTURE DEVELOPMENT

THE PRECEDING APPROACH IS RELATIVELY SIMPLE, AND MAY BE IMPLEMENTED THIS YEAR. ALL PROCESSING CAN BE DONE USING STATA. THIS APPROACH CAN BE IMPLEMENTED SEPARATELY FOR THE MAY AND NOVEMBER SURVEYS. WHEN THE TWO ESTIMATES ARE AVAILABLE, THEY MAY BE COMBINED INTO A SINGLE ANNUAL ESTIMATE BY FORMING A COMPOSITE ESTIMATOR LIKE THE ONE ABOVE, BUT WITH THE WEIGHTS INVERSELY PROPORTIONAL TO THE ESTIMATE VARIANCES. (BOTH ESTIMATES ARE UNBIASED ESTIMATES OF THE UNEMPLOYMENT RATES FOR THE SURVEY TIME, SO NO BIAS IS INVOLVE (HENCE VARIANCES ARE USED IN THE WEIGHTS, NOT MEAN SQUARED ERRORS).)

AFTER COMPLETING THIS PRELIMINARY ANALYSIS, THE DATA SHOULD BE ANALYZED AS A TWO-ROUND PANEL DATA SET (USING THE STATA xtset AND xtreg COMMANDS).

AS STATED EARLIER, THE FOLLOWING IMPROVEMENTS MAY BE IMPLEMENTED IN FUTURE YEARS:

1. DEVELOP IMPROVED AND VALIDATED CROSS-SECTIONAL MODELS FOR A SINGLE SURVEY ROUND.

2. DEVELOP IMPROVED AND VALIDATED MODELS FROM TWO SUCCESSIVE SURVEY ROUNDS (MAY AND NOVEMBER; CROSS-SECTIONAL AND PANEL MODELS).

3. DEVELOP VALIDATED MODELS FROM THREE SUCCESSIVE SURVEY ROUNDS (MAY, NOVEMBER, MAY).

4. DEVELOP VALIDATED MODELS FROM FOUR SUCCESSIVE SURVEYS (MAY AND NOVEMBER IN TWO SUCCESSIVE YEARS).

5. DEVELOP VALIDATED MODELS FROM SEVERAL SUCCESSIVE YEARS (TIME SERIES ANALYSIS).

6. EXAMINE BAYESIAN ESTIMATION, AS WELL AS THE FREQUENTIST-APPROACH METHOD DESCRIBED ABOVE.

FndID(205)

FndTitle(SMALL AREA ESTIMATION: LECTURE NOTES)

FndDescription(SMALL AREA ESTIMATION: LECTURE NOTES)

FndKeywords(small area estimation; small area statistics; short course)